Landauer’s Princple for Fermionic Fields in One-Dimensional Bags
Abstract
:1. Introduction
2. Model Setup
3. Vacuum State
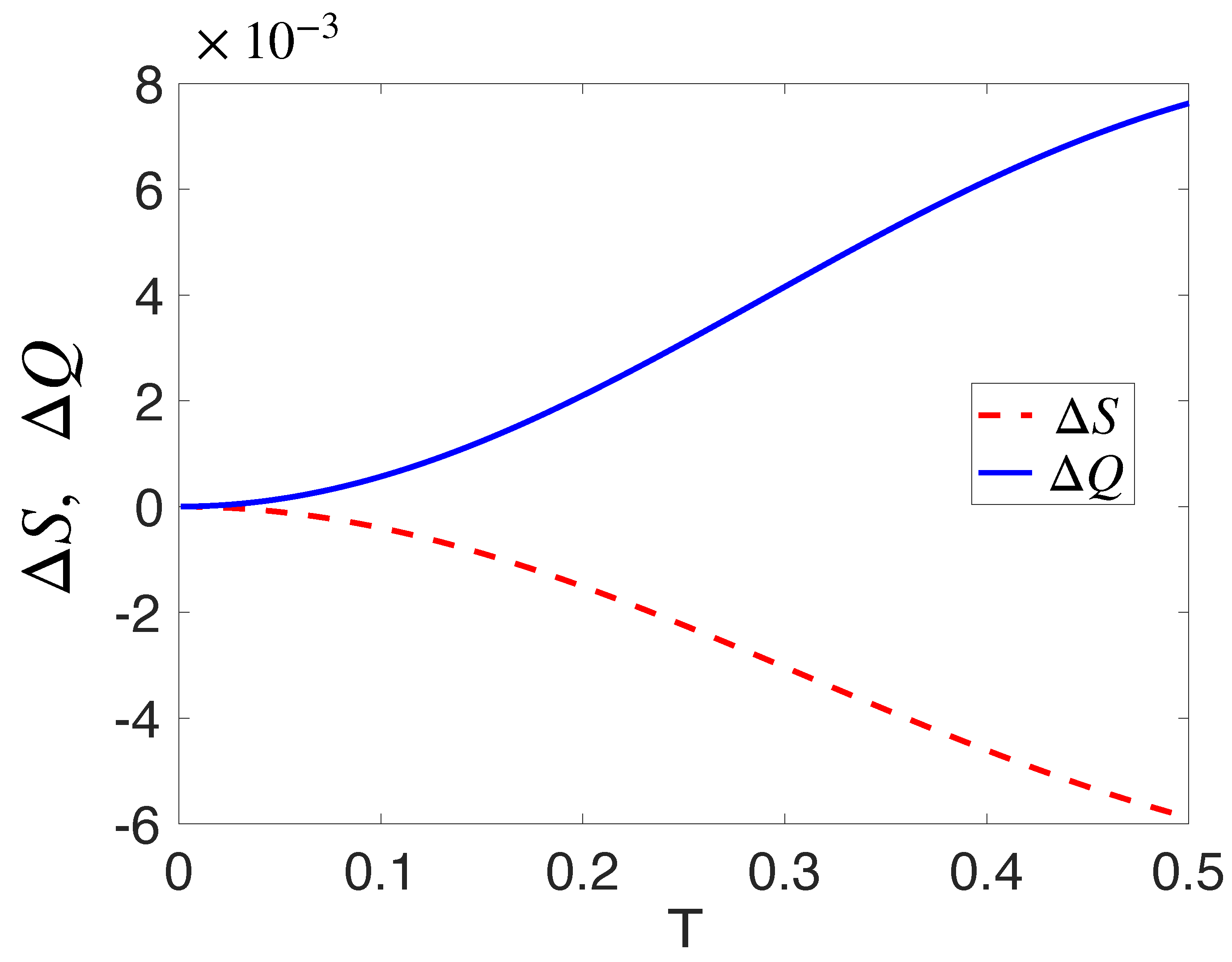
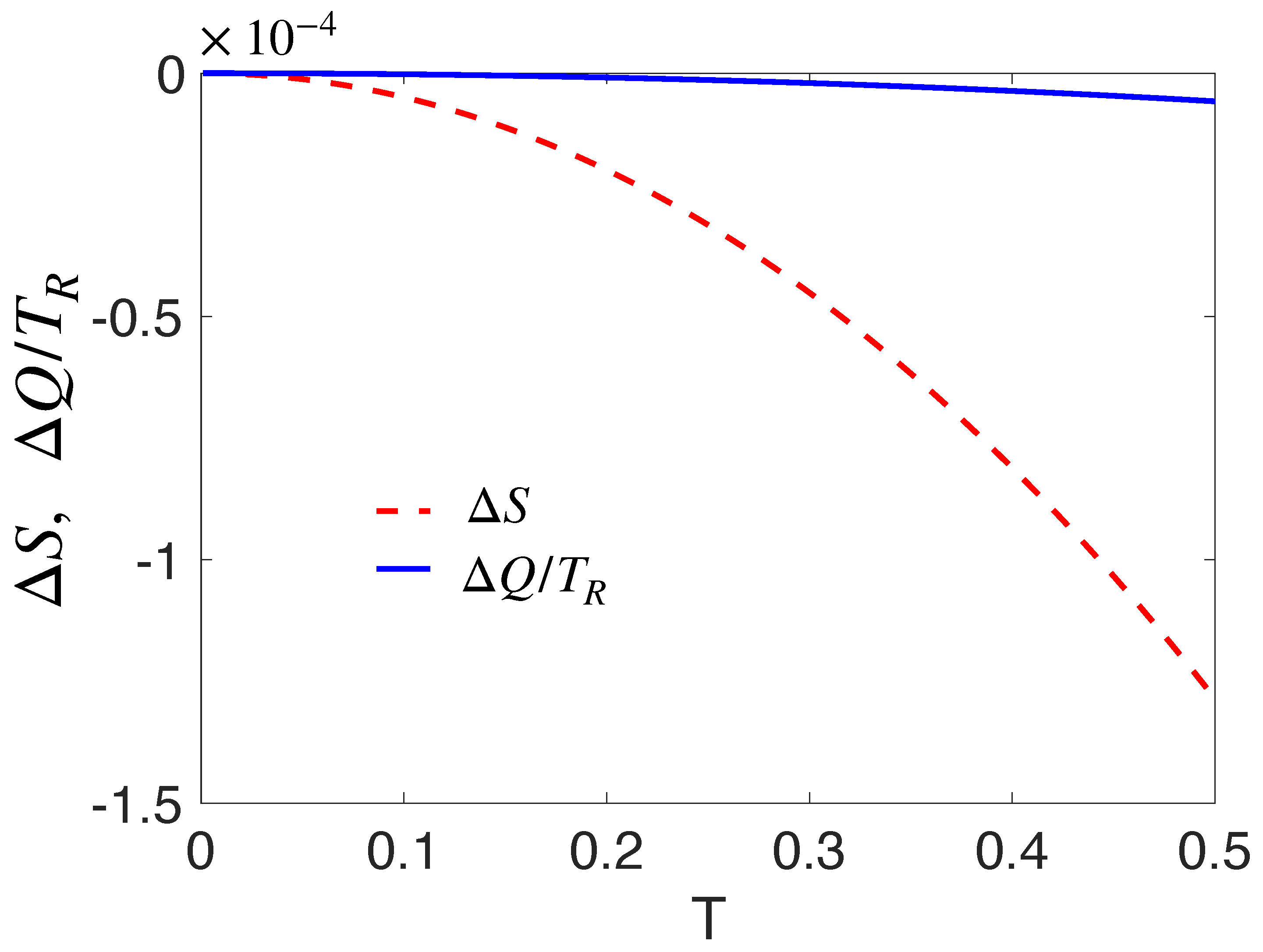
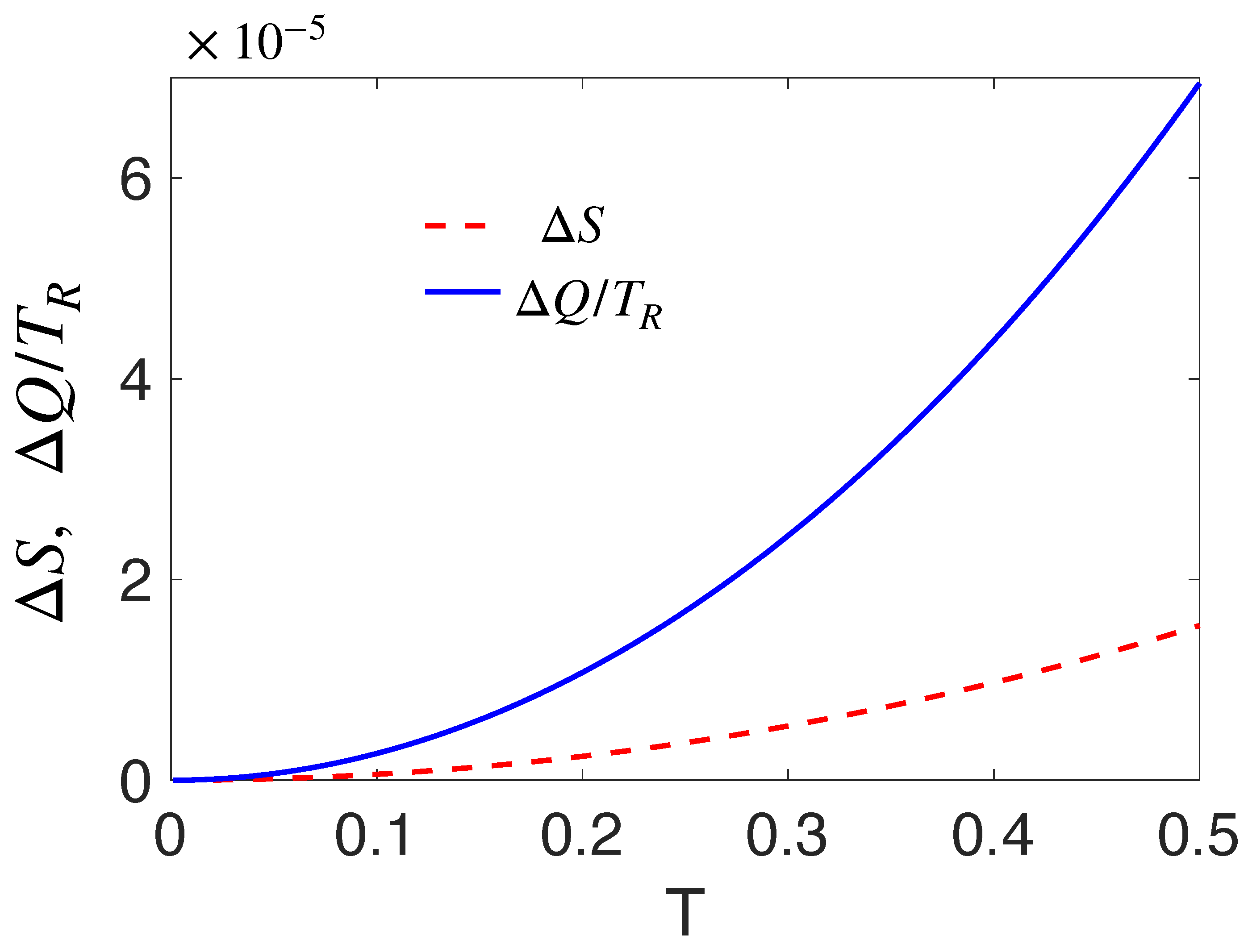
4. Thermal State
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, B.L.; Jacobson, T.A. Directions in General Relativity; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Polo-Gomez, J.; Garay, L.J.; Martin-Martinez, E. A detector-based measurement theory for quantum field theory. Phys. Rev. D 2022, 105, 065003. [Google Scholar] [CrossRef]
- Higuchi, A.; Iso, S.; Ueda, K.; Yamamoto, K. Entanglement of the vacuum between left, right, future, and past. Phys. Rev. D 2017, 96, 083531. [Google Scholar] [CrossRef]
- Reznik, B. Entanglement from the vacuum. Found. Phys. 2003, 33, 167–176. [Google Scholar] [CrossRef]
- Swingle, B. Mutual information and the structure of entanglement in quantum field theory. arXiv 2010, arXiv:1010.4038. [Google Scholar]
- Hollands, S.; Sanders, K. Entanglement measures and their properties in quantum field theory. arXiv 2018, arXiv:1702.04924. [Google Scholar]
- Summers, S.J.; Werner, R. Bell’s Inequalities and Quantum Field Theory. 1. General Setting. J. Math. Phys. 1987, 28, 2440. [Google Scholar] [CrossRef]
- Summers, S.J.; Werner, R. Bell’s inequalities and quantum field theory. II. Bell’s inequalities are maximally violated in the vacuum. J. Math. Phys. 1987, 28, 2448. [Google Scholar] [CrossRef]
- Reznik, B.; Retzker, A.; Silman, J. Violating Bell’s inequalities in vacuum. Phys. Rev. A 2005, 71, 042104. [Google Scholar] [CrossRef]
- Summers, S.J.; Werner, R. The vacuum violates Bell’s inequalities. Phys. Lett. 1985, 110A, 5. [Google Scholar] [CrossRef]
- Perche, T.R.; Lima, C.; Martin-Martinez, E. Harvesting entanglement from complex scalar and fermionic fields with linearly coupled particle detectors. arXiv 2022, arXiv:2111.12779. [Google Scholar] [CrossRef]
- Cong, W.; Tjoa, E.; Mann, R.B. Entanglement harvesting with moving mirrors. J. High Energ. Phys. 2019, 2019, 21. [Google Scholar] [CrossRef]
- Valentini, A. Non-local correlations in quantum electrodynamics. Phys. Lett. A 1991, 153, 321–325. [Google Scholar] [CrossRef]
- Maeso-Garcia, H.; Polo-Gomez, J.; Martin-Martinez, E. Entanglement harvesting: State dependence and covariance. arXiv 2022, arXiv:2208.13801. [Google Scholar] [CrossRef]
- Perche, T.R.; Ragula, B.; Martin-Martinez, E. Harvesting entanglement from the gravitational vacuum. arXiv 2022, arXiv:2210.14921. [Google Scholar]
- Landauer, R. Irreversibility and Heat Generation in the Computing Process. IBM J. Res. Dev. 1961, 5, 183. [Google Scholar] [CrossRef]
- Landauer, R. The physical nature of information. Phys. Lett. A 1996, 217, 188. [Google Scholar] [CrossRef]
- Herrera, L. Landauer Principle and General Relativity. Entropy 2020, 22, 340. [Google Scholar] [CrossRef]
- Daffertshofer, A.; Plastino, A.R. From Landauer’s principle to Tolman’s temperature. Phys. Lett. A 2007, 362, 243–245. [Google Scholar] [CrossRef]
- Reeb, D.; Wolf, M.M. An improved Landauer principle with finite-size corrections. New J. Phys. 2014, 16, 103011. [Google Scholar] [CrossRef]
- Xu, H.; Ong, Y.C.; Yung, M.-H. Landauer’s principle in Qubit-Cavity quantum-field-theory interaction in vacuum and thermal states. Phys. Rev. A 2022, 105, 012430. [Google Scholar] [CrossRef]
- Xu, H.; Ong, Y.C.; Yung, M.-H. Decoherence and Landauer’s Principle in Qubit-Cavity Quantum-Field-Theory Interaction. arXiv 2022, arXiv:2207.06702. [Google Scholar] [CrossRef]
- Torres, B.S.L.; Perche, T.R.; Landulfo, A.G.S.; Matsas, G.E.A. Neutrino flavor oscillations without flavor states. Phys. Rev. D 2020, 102, 093003. [Google Scholar] [CrossRef]
- Perche, T.R.; Martin-Martinez, E. Antiparticle detector models in QFT. Phys. Rev. D 2021, 104, 105021. [Google Scholar] [CrossRef]
- Mamaev, S.G.; Trunov, N.N. Vacuum expectation values of the energy-momentum tensor of quantized fields on manifolds with different topologies and geometries. III. Sov. Phys. 1980, 23, 551–554. [Google Scholar] [CrossRef]
- Saghian, R.; Valuyan, M.A.; Seyedzahedi, A.; Gousheh, S.S. Casimir energy for a massive Dirac field in one spatial dimension: A direct approach. Int. J. Mod. Phys. A 2012, 27, 1250038. [Google Scholar] [CrossRef]
- Unruh, W.G.; Weiss, N. Acceleration radiation in interacting field theories. Phys. Rev. D 1984, 29, 1656. [Google Scholar] [CrossRef]
- Fosco, C.D.; Hansen, G. Dynamical Casimir effect from fermions in an oscillating bag in 1 + 1 dimensions. Phys. Rev. D 2022, 105, 016004. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B. Baryon structure in the bag theory. Phys. Rev. D 1974, 10, 2599. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.-S.; Liu, Y.; Zhang, R. Landauer’s Princple for Fermionic Fields in One-Dimensional Bags. Symmetry 2023, 15, 1663. https://doi.org/10.3390/sym15091663
Cao Y-S, Liu Y, Zhang R. Landauer’s Princple for Fermionic Fields in One-Dimensional Bags. Symmetry. 2023; 15(9):1663. https://doi.org/10.3390/sym15091663
Chicago/Turabian StyleCao, Yu-Song, Yanxia Liu, and Rong Zhang. 2023. "Landauer’s Princple for Fermionic Fields in One-Dimensional Bags" Symmetry 15, no. 9: 1663. https://doi.org/10.3390/sym15091663
APA StyleCao, Y.-S., Liu, Y., & Zhang, R. (2023). Landauer’s Princple for Fermionic Fields in One-Dimensional Bags. Symmetry, 15(9), 1663. https://doi.org/10.3390/sym15091663





