Abstract
The nucleon-pair shell model (NPSM) within the framework of a broken symmetry basis is studied. The results demonstrate the validity of such a scheme, which in turn leads to a significant reduction in the dimensionality of the multi-pair configuration space. Specifically, in the case of an axially-deformed basis, the results yield a satisfactory description of the low-lying spectrum, even without the need for applying the projection procedure. In the case of a triaxially-deformed basis, the result of variation after angular momentum projection suggest a potential for using the NPSM to find exact solutions in a semi-magic system.
PACS:
21.60.Cs
1. Introduction
Atomic nuclei are self-bounded quantum many-body systems. The modeling of such systems is one of the crucial challenging problems in theoretical nuclear physics. Much progress has been made on this topic over the years, including the Green’s function Monte Carlo method [,], various full configuration interaction (FCI) approaches, the so-called no-core shell model (NCSM) [], the symmetry-adapted no-core shell model [], etc. Most of these methods mentioned above are limited to cases for light nuclei. The coupled-cluster method (CC) [] has been applied to both light nuclei and medium mass nuclei around closed shells. The equation of motion method also been applied to various nuclear problems [,,]. While a mean-field theory can in principle be applied across the whole chart of the nuclides [], within such a framework there is no guarantee that all important correlations can be addressed equitably. Additionally, while valence space shell models (SM) play an important role in describing and understanding nuclear structures [,,,,,,], complete SM studies remain out of reach for the heavy mass nuclei because of the huge number of configurations encountered []. In addition, several alternative models that use broken rotational symmetry bases have been advanced, with good angular momenta restored by various projection techniques, such as the projected Hartree-Fock [,], including variation after projection [,], the Hartree Fock-Bogoliubov theories [,,,], and projected relativistic mean-field calculations [], the Monte Carlo shell model [,], the projected shell model [,,], a projected configuration interaction [] as well as the so-called projected generator coordinate methods [,].
In 1993, a novel technique known as generalized Wick theory was proposed to calculate the commutators for coupled operators and fermion clusters by Chen et al. [,]. Based on this approach, a nucleon pair shell model (NPSM) was developed [], in which the building blocks of the configuration space were nucleon-pairs. Due to successes of the interacting boson model (IBM) [], the model space of the NPSM was truncated to the pair subspace, and hence this method is called the SD-pair shell model (SDPSM). Within the latter framework it has been shown that the collectivity of the low-lying states can be described well within the pair subspace [,,]. Additionally, it has been found that within the framework of the M-scheme for NPSM, the computational time required for calculating the matrix elements can be reduced significantly [,].
However, at a more fundamental level, the truncation of the NPSM should be carefully re-examined because the convergence of the theory has not yet been demonstrated. To address this issue, the basis should be constructed for more kinds of collective pairs, with the pair structure coefficients examined using variation procedures [,,,]. However, the dimensionality of the many-pair model space increases rapidly with the number of collective pairs, hindering its further study. In the NPSM, the nucleon-pairs always have good angular momentum J and third component M, so the many-body basis maintains its the rotational invariance. Therefore, both the total and intermediate angular momentum J or third component M, depending upon the J- and M-scheme adopted, should be good quantum numbers. To work with a complete subspace, a group of multi-pair basis should be considered, and hence in this paper we introduce the concept of symmetry broken pairs within a NPSM framework, and include some early results for semi-magic nuclei.
The remainder of this paper is organized as follows: in Section 2, a review of the NPSM and the angular momentum projection schemes is presented. In Section 3, some initial applications of the concept of symmetry broken pairs within the NPSM framework are explored. Finally, in Section 4, a summary of current results is given along with a suggestion regarding potential next steps.
2. The Model
In this section we introduce the model and establish labeling conventions, etc. In the following sub-sections to this introduction we establish the overarching framework of the theory by introducing two novel sub-schemes to the NPSM; namely, the axially-deformed NPSM and a triaxially-deformed NPSM. Regarding applications, in this paper, which is a preliminary report, we only discuss semi-magic nuclei.
The general form of the shell model Hamiltonian between identical nucleon pairs is that which is adopted in [],
where stands for an oscillator single-particle orbital (nlj), is the single-particle creation operator, is the single-particle annihilation operator, is the single-particle energy and the symbol × represent angular momentum coupling, which is given by
where is Clebsch–Gordan (CG) coefficient [].
2.1. NPSM Framework
The building blocks of the NPSM are collective pairs with good angular momentum J and a third component M, designated as , which is built from many distinct non-collective pairs [],
where the parameters are the pair-structure coefficients, which can be determined by variational methods. With this, the multi-pair basis can be constructed in both the M-scheme [,] and the J-scheme [,], respectively,
and
In the M-scheme, the multi-pair basis is constructed by taking the inner product of the pair operator, as given by Equation (3). In the J-scheme, on the other hand, the multi-pair basis is formed by successively coupling the pair operator to angular momentum ranging from to J. When considering specific collective pairs, a set of multi-pair bases is constructed, and these bases depend on the pair structure coefficients associated with each pair. Such many-pair bases are non-normal and non-orthogonal, the Hamiltonian kernel and norm kernel must be transformed into a ortho-normal basis []. The matrix elements of the Hamiltonian can be carried out by using the commutator relations between collective pairs [,,,]. Finally, the Hamiltonian can be diagonalized in such a subspace, with the sum running over relatively few of the lowest-lying energies; specifically, minimizing the following average energy [].
2.2. Symmetry Broken Basis
Taking into consideration the broken rotational symmetry of nucleon pairs, the collective pairs with good angular momentum J are mixed. To circumvent this issue, a new model can be constructed using two different approaches. In the following two sub-sections, we introduce these two models. Specifically, in first part of this section, the concept of an axially-deformed NPSM is introduced, while the second part focuses on a triaxially-deformed NPSM.
2.2.1. Axially-Deformed Basis
First, we introduce what is meant by axially-deformed pairs. In particular, it is determined by summing over collective pairs with the same quantum number M but different angular momenta J, as defined in Equation (3).
where the axial-deformed pairs maintain the third component of angular momentum as a good quantum number. A set of multi-pair basis states with fixed total third component M is constructed, after the collective pairs are introduced,
The Hamiltonian can then be diagonalized in a subspace with the fixed total third component M.
The transitions are given by
where,
with the effective charge with the reduced transition matrix elements are given by
The transition probability is given by []
where is the energy of the transition. The half-life of the transition is then simply
In this model, no angular momentum projection is needed as the angular momentum J is determined by its third component, namely M.
2.2.2. Triaxially-Deformed Basis
The triaxially-deformed pairs can be constructed by mixing the collective pairs. Unlike the axially-deformed pairs, the triaxially-deformed pairs involve summation over both the angular momentum J as well as the third component M of a set of collective pairs.
where both the angular momentum J and third component M are mixed, and hence break the rotational invariance. The multi-pair basis is given by
Since all rotational symmetry is broken, only one basis exists for a given set of collective pairs. In this case, the triaxially-deformed pairs are chosen to be different from each other, with the pair structure coefficients independent for different triaxially-deformed pairs.
The rotational symmetry can be restored by a standard projection process; namely, by introducing a quadrature over orthogonal functions. For an arbitrary rotation operation applied to a state with a well-defined angular momentum state , it only mixes the third component of angular momentum M, and not the J value itself [].
where is a Wigner D matrix, is the rotation operator over the Euler angles
wherein and are the generators of rotations about the z and y axes, respectively. The Wigner D functions are the matrix elements of the rotation operator in a basis with good angular momentum quantum numbers, and the Wigner D functions compose of a complete orthogonal set,
To carry out the angular momentum projection procedure, an expression for the rotation of basis states is required. For a given rotation applied to a triaxially-deformed basis state, this can be expressed as the inner product of the rotated collective pairs.
where the rotated triaxially-deformed collective pairs are given by
In particular, the rotation of symmetry broken basis states can be interpreted in another way. For any basis that breaks rotational symmetry, such as a triaxially-deformed basis , it can be expanded in terms of states with good angular momenta, denoted as .
where is a coefficient. An application of the rotation operator to this basis is then given by,
where K indicates the quantum number in the initial state, and M denotes the third component in the rotated state. Therefore, the norm kernel and Hamiltonian kernel with a good angular momentum quantum number can be obtained by using the orthogonal relation of the Wigner D function, as given by Equation (18).
The norm matrix elements are projected out by the standard equation,
The Hamiltonian matrix elements are given
Finally, the generalized eigenvalue problems for every J are solved, where the solutions are labeled by r,
The transitions are given by
wherein the reduced transition matrix elements are given by
where is the angular momentum projection operator. In this work, we only perform variation after projection on a triaxially-deformed basis.
3. Numerical Results
In this section, we use two real cases to demonstrate the advantages of the symmetry broken basis. In the first sub-section, the low-lying structure of Sn is studied within an axially-deformed basis. In the second half sub-section, the structure of O is studied with the triaxially-deformed basis.
3.1. Axially-Deformed Basis
As a preliminary report, the low-lying spectra of Sn are studied for the axially-deformed basis. We assume that the nucleus Sn is a closed core and the 82–126 shell (0h, 1f, 1f, 2p, 2p, and 0i) is chosen as the valence neutron shell. As regards the single-particle energies, they are taken from the experiment and given in Table 1. In particular, the low-lying spectra of and Sn are used to fix the neutron SP energies. The only exception is neutron , whose corresponding levels are still missing. Their values are taken from [], within which one can find how these can be determined.

Table 1.
Neutron SP energies (in MeV).
The two-body matrix elements of the effective interaction are derived from the CD-Bonn NN potential []. The strong short-range repulsion term is renormalized by integrating out the high-momentum components above a certain cutoff momentum , see []. A smooth potential , keeping the physics of bare nucleon-nucleon interaction up to , is constructed, and can be used in calculations of shell model effective interactions. In this work, is fixed as 2.2 fm. Then the shell model effective interaction, with the Coulomb force for protons, is carried out within the framework of -box folded-diagram expansion [,,]. In this paper, the -box is calculated up to the second order in .
Usually, the collective pairs with the lowest angular momenta J, such as S (J = 0), D (J =2) and G (J = 4), are considered in the NPSM. For the low-lying states, these collective pairs should be dominant. The dimension of the multi-pair basis increases dramatically when more types of collective pairs are included. Originally those many-pair basis are non-normal and non-orthogonal, the Hamiltonian matrix elements should be transformed to a normal orthogonal basis. To this end, one must to diagonalize the norm matrix, which is very difficult for large configuration spaces. Alternatively, the dimension of the configuration space will be reduced when the rotation symmetry is broken. For the semi-magic nucleus Sn, the shell model space with M = 0 is 31,124. However, when considering open-shell cases in this region, the dimension of the model space increases dramatically, surpassing the computational capabilities of our current supercomputer facility.
Figure 1 illustrates the slow increase in dimension for the case with axially-deformed basis. In the figure, we only present the dimension with M = 0, and we include the collective pair with angular momentum J up to 10.
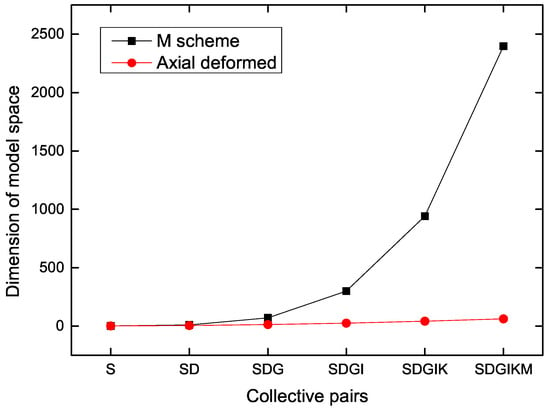
Figure 1.
The dimension of configuration space for three identical pairs against the types of collective pairs are presented. The spherical basis in the M-scheme and the axially-deformed basis are shown. The collective pair S, D, G, I, K and M are the pairs of angular momentum J = 0, 2, 4, 6, 8 and 10, respectively.
In the following results, we specifically limit our configurations to SDG collective pairs. Although the angular momentum J of each collective pair is mixed, the third component M is a good quantum number and the total M of each multi-pair basis is also a good quantum number. The effective Hamiltonian is diagonalized in this subspace and the pair-structure coefficients are determined by searching for the minimum energy.
The lowest energy levels in each axially-deformed subspace with a different third component M in the NPSM are shown in Figure 2, where the shell model calculations are carried out using KSHELL code []. It is seen that the results from the NPSM are close to the SM. The shift of level from the NPSM to SM is 0.059 MeV, and the shift of is 0.095 MeV. The transition probability can be evaluated using the Equation (9), where an effective neutron charge of = 0.65e was used. The is 0.22 W.u., whereas the exact solution given by the shell model is 0.34 W.u. The experimental value is 0.36 (8) W.u. []. The corresponding predicted half-life of the state is 979.66 ns according to NPSM by using Equation (13), and 633.90 ns according to SM. The experimental half-life is 210(45) ns []. As we can see, the scheme can provide a satisfied spectrum, but the transition is smaller than the exact solution. These results also suggest the low-lying levels of Sn can be described in the SDG pair subspace. Overall, the results suggest that the NPSM can reproduce the spectrum very well with the axially-deformed basis.
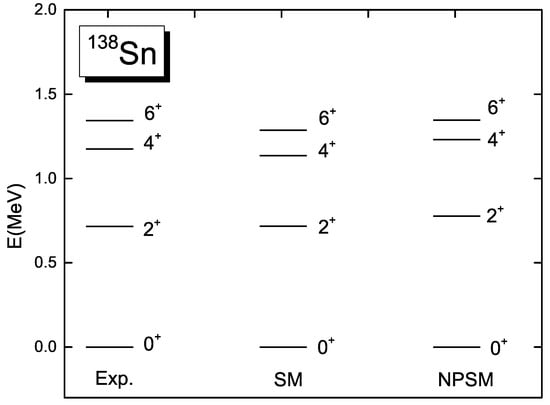
Figure 2.
The low-lying spectra of Sn are studied in the shell model and NPSM with the axially-deformed basis.
3.2. Triaxially-Deformed Basis
The NPSM was also studied with the triaxially-deformed basis, which entails rotation symmetry breaking. In general, the symmetry is restored numerically. There are two ways to recover the rotational symmetry: variation before projection (VBP) and variation after projection (VAP). Here, the VAP method is used. The low-lying levels of the O nucleus were studied with the USDA interaction []. Only one basis is used for each level in our variation procedure. The results given in Figure 3 show that the NPSM is consistent with the SM. For example, the first level from SM is MeV, the one from NPSM is also MeV, level from the SM is the same as for the NPSM, with any difference falling outside the accuracy limitation of the computational facility that was used in the analysis.
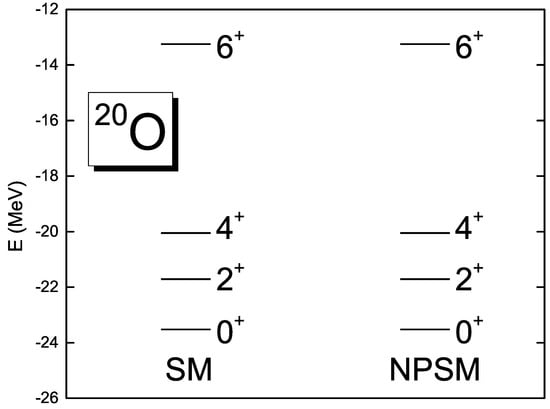
Figure 3.
The low-lying spectra of O are studied in the shell model and NPSM with the triaxially-deformed basis.
To generate more levels with the same angular momenta J, more bases should be used in the configuration space. For example, if we want to obtain the second states, the first level should be calculated first, which can be described by one basis, after determining the parameters for the first basis, the second basis is considered in the model space, then the parameters of the second basis are fixed by a variation procedure.
As shown in Figure 4, the lowest five levels with J = 2 and J = 4 are calculated in the SM and NPSM with the triaxially-deformed basis. We found that the difference between the NPSM and SM is negligible within the machine precision limit. For the decay , experimental data is available [], indicating a value of W.u. We can also compare the transition probability from our model with the SM one. The shell model predicts a transition probability of 1.52 W.u., while the VAP approach yields 1.50 W.u. The corresponding half-lives are 7.3(3) ps for the experimental data, 8.9 ps for the shell model, and 9.0 ps for the VAP approach. Those results suggest that if the VAP is adopted, there may be no significant difference between the NPSM and SM.
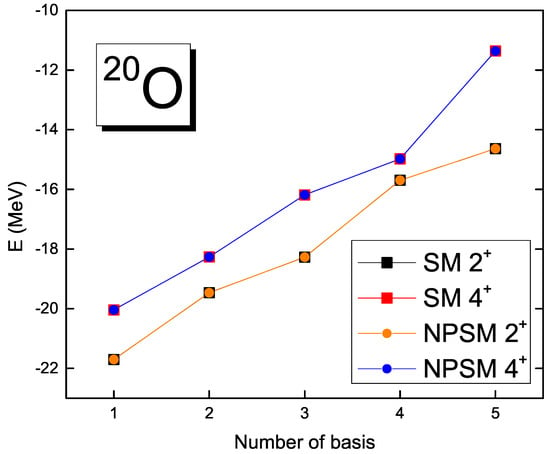
Figure 4.
The levels with J = 2 and J = 4 of O are calculated in the SM and NPSM with the triaxially-deformed basis.
4. Summary and Discussion
In this paper, the validity of the symmetry broken basis concept in the NPSM was examined. The results show that the NPSM with an axially-deformed basis can reproduce the low-lying spectra of a semi-magic nucleus well.
Further, if the triaxially-deformed basis and variation after projection method are used for a semi-magic nucleus, the difference between the NPSM and SM seems to be negligible. These results suggest that the axially-deformed basis and triaxially-deformed basis may provide a satisfactory description for studying low-lying spectra. The case for a proton-neutron coupled system will be studied in a following publication.
Author Contributions
Conceptualization, L.L., Y.L. and J.P.D.; Methodology, B.H., S.Z., F.P. and J.P.D.; Software, B.H., S.Z. and Y.Z.; Validation, B.H., S.Z. and F.P.; Formal Analysis, B.H., Y.Z. and L.L.; Investigation, B.H., Y.Z., Y.L. and F.P.; Resources, L.L. and F.P.; Data Curation, B.H.; Writing—Original Draft Preparation, B.H., S.Z., Y.L. and F.P.; Writing—Review and Editing, S.Z., Y.Z., Y.L. and J.P.D.; Visualization, B.H. and Y.Z.; Supervision, Y.L.; Project Administration, Y.L.; Funding Acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of China (11475091, 11875171, 11875158, 12175097, 12275141), China’s Postdoctoral Science Foundation (2020M680849), Special Foundation for theoretical physics Research Program of China (12047534), Natural Science Foundation of Tianjin (20JCYBJC01510), the U.S. National Science Foundation (OIA-1738287 and PHY-1913728), the U.S. Department of Energy (DE-SC0005248), and the LSU-LNNU joint research program (9961). The work was carried out at National Supercomputer Center in Tianjin, and the calculations were performed on TianHe-1(A).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carlson, J.; Schiavilla, R. Structure and dynamics of few-nucleon systems. Rev. Mod. Phys. 1998, 70, 743. [Google Scholar]
- Pieper, S.C.; Wiringa, R.B. Quantum Monte Carlo Calculations of Light Nuclei. Annu. Rev. Nucl. Part. Sci. 2001, 51, 53. [Google Scholar] [CrossRef]
- Barrett, B.R.; Navratil, P.; Vary, J.P. Ab initio no core shell model. Prog. Part. Nucl. Phys. 2012, 69, 1022919. [Google Scholar]
- Dytrych, T.; Launey, K.D.; Draayer, J.P.; Maris, P.; Vary, J.P.; Saule, E.; Catalyurek, U.; Sosonkina, M.; Langr, D.; Caprio, M.A. Collective Modes in Light Nuclei from First Principles. Phys. Rev. Lett. 2013, 111, 252501. [Google Scholar] [CrossRef] [PubMed]
- Hagen, G.; Papenbrock, T.; Hjorth-Jensen, M.; Dean, D.J. Coupled-cluster computations of atomic nuclei. Rep. Prog. Phys. 2014, 77, 096302. [Google Scholar] [CrossRef]
- Gregorio, G.D.; Knapp, F.; Iudice, N.L.; Vesely, P. Odd nuclei spectroscopy within a self-consistent multiphonon approach. J. Phys. Conf. Ser. 2018, 866, 012007. [Google Scholar] [CrossRef]
- Vesely, P.; Gregorio, G.D.; Knapp, F.; Iudice, N.L. A center of mass free equation of motion method and its application to 4He. J. Phys. Conf. Ser. 2023, 2453, 012008. [Google Scholar] [CrossRef]
- Rowe, D.J. Equations-of-Motion Method and the Extended Shell Model. Rev. Mod. Phys. 1968, 40, 153. [Google Scholar] [CrossRef]
- Bender, M.; Heenen, P.-H.; Reinhard, P.-G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121. [Google Scholar]
- Roth, R. Importance truncation for large-scale configuration interaction approaches. Phys. Rev. C 2009, 79, 064324. [Google Scholar] [CrossRef]
- Bertulani, C. Nuclear Physics in a Nutshell; Princeton University Press: Princeton, NJ, USA, 2007; p. 119. [Google Scholar]
- Talmi, I.; Barrett, B. Simple Models of Complex Nuclei: The Shell Model and Interacting Boson Model. Phys. Today 1994, 47, 102. [Google Scholar] [CrossRef]
- Lawson, R.D. Theory of the Nuclear Shell Model; Oxford University Press: New York, NY, USA, 1980. [Google Scholar]
- Otsuka, T.; Honma, M.; Mizusaki, T.; Shimizu, N.; Utsuno, Y. New-generation Monte Carlo shell model for the K computer era. Prog. Part. Nucl. Phys. 2001, 47, 319. [Google Scholar] [CrossRef]
- Caurier, E.; Martinez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427. [Google Scholar] [CrossRef]
- Koonin, S.E.; Dean, D.J.; Langanke, K. Shell model Monte Carlo methods. Phys. Rep. 1996, 278, 1–77. [Google Scholar] [CrossRef]
- Iachello, F.; Talmi, I. Shell-model foundations of the interacting boson model. Rev. Mod. Phys. 1987, 59, 339. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P.; Strayer, M.R. The Nuclear Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Gunye, M.R.; Warke, C.S. Strayer, The Nuclear Many-Body Problem. Phys. Rev. 1967, 456, 1087. [Google Scholar] [CrossRef]
- Rodríguez, T.R.; Egido, J.L.; Robledo, L.M.; Rodríguez-Guzmán, R. Quality of the restricted variation after projection method with angular momentum projection. Phys. Rev. C 2005, 71, 044313. [Google Scholar] [CrossRef]
- Hara, K.; Hayashi, A.; Ring, P. Exact angular momentum projection of cranked Hartree-Fock-Bogoliubov wave functions. Nucl. Phys. A 1982, 385, 14. [Google Scholar] [CrossRef]
- Enami, K.; Tanabe, K.; Yoshinaga, N. Microscopic description of high-spin states: Quantum-number projections of the cranked Hartree-Fock-Bogoliubov self-consistent solution. Phys. Rev. C 1999, 59, 135. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Ring, P. Symmetry-projected Hartree–Fock–Bogoliubov equations. Nucl. Phys. A 2000, 665, 71. [Google Scholar] [CrossRef]
- Yao, J.M.; Meng, J.; Ring, P.; Arteaga, D.P. Three-dimensional angular momentum projection in relativistic mean-field theory. Phys. Rev. C 2009, 79, 044312. [Google Scholar] [CrossRef]
- Honma, M.; Mizusaki, T.; Otsuka, T. Nuclear Shell Model by the Quantum Monte Carlo Diagonalization Method. Phys. Rev. Lett. 1996, 77, 3315. [Google Scholar] [CrossRef]
- Abe, T.; Maris, P.; Otsuka, T.; Shimizu, N.; Tsunoda, Y.; Utsuno, Y.; Vary, J.P.; Yoshida, T. Recent development of Monte Carlo shell model and its application to no-core calculations. J. Phys. Conf. Ser. 2013, 454, 012066. [Google Scholar] [CrossRef]
- Hara, K.; Sun, Y. Projected Shell Model and High-Spin Spectroscopy. Int. J. Mod. Phys. E 1995, 4, 637. [Google Scholar] [CrossRef]
- Sun, Y.; Hara, K. Fortran code of the Projected Shell Model: Feasible shell model calculations for heavy nuclei. Comput. Phys. Commun. 1997, 104, 245. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Hara, K. Triaxial Projected Shell Model Approach. Phys. Rev. Lett. 1999, 82, 3968. [Google Scholar] [CrossRef]
- Gao, Z.-C.; Horoi, M. Angular momentum projected configuration interaction with realistic Hamiltonians. Phys. Rev. C 2009, 79, 014311. [Google Scholar] [CrossRef]
- Rodríguez-Guzmán, R.; Egido, J.L.; Robledo, L.M. Quadrupole collectivity in N = 28 nuclei with the angular momentum projected generator coordinate method. Phys. Rev. C 2002, 65, 024304. [Google Scholar] [CrossRef]
- Yao, J.M.; Meng, J.; Ring, P.; Vretenar, D. Configuration mixing of angular-momentum-projected triaxial relativistic mean-field wave functions. Phys. Rev. C 2010, 81, 044311. [Google Scholar] [CrossRef]
- Chen, J.-Q. The Wick theorem for coupled fermion clusters. Nucl. Phys. A 1993, 562, 218. [Google Scholar] [CrossRef]
- Chen, J.Y.; Chen, B.Q.; Klein, A. Factorization of commutators: The Wick theorem for coupled operators. Nucl. Phys. A 1993, 554, 61. [Google Scholar]
- Chen, J.-Q. Nucleon-pair shell model: Formalism and special cases. Nucl. Phys. A 1997, 626, 686. [Google Scholar] [CrossRef]
- Iachello, F. The Interacting Boson Model; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Luo, Y.-A.; Chen, J.-Q.; Draayer, J. Nucleon-pair shell model calculations of the even–even Xe and Ba nuclei. Nucl. Phys. A 2000, 669, 101. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Yoshinaga, N.; Yamaji, S.; Arima, A. Validity of the SD-pair truncation of the shell model. Phys. Rev. C 2000, 62, 014316. [Google Scholar] [CrossRef]
- Zhao, Y.; Arima, A. A collective pair-condensed configuration variational method for pairwise approximation calculations. Phys. Rep. 2014, 545, 4. [Google Scholar]
- He, B.C.; Li, L.; Luo, Y.A.; Zhang, Y.; Pan, F.; Draayer, J.P. Nucleon pair shell model in M scheme. Phys. Rev. C 2020, 102, 024304. [Google Scholar] [CrossRef]
- Lei, Y.; Lu, Y.; Zhao, Y.M. Nucleon-pair approximation with uncoupled representation. Chin. Phys. C 2021, 45, 054103. [Google Scholar] [CrossRef]
- Fu, G.J.; Lei, Y.; Zhao, Y.M.; Pittel, S.; Arima, A. Nucleon-pair approximation of the shell model with isospin symmetry. Phys. Rev. C 2013, 87, 044310. [Google Scholar] [CrossRef]
- Fu, G.J.; Shen, J.J.; Zhao, Y.M.; Arima, A. Spin-aligned isoscalar pair correlation in 96Cd, 94Ag, and 92Pd. Phys. Rev. C 2013, 87, 044310. [Google Scholar] [CrossRef]
- Cheng, Y.Y.; Zhao, Y.M.; Arima, A. Nucleon-pair approximation with particle-hole excitations. Phys. Rev. C 2018, 97, 024303. [Google Scholar] [CrossRef]
- Meng, X.-f.; Wang, F.-r.; Luo, Y.-a.; Pan, F.; Draayer, J.P. SD-pair shell model study for 126Xe and 128Ba. Phys. Rev. C 2008, 77, 047304. [Google Scholar] [CrossRef]
- Wang, J.-Q.; Gao, Z.-C.; Ma, Y.-J.; Chen, Y.S. New algorithm in the variation after projection calculations for non-yrast nuclear states. Phys. Rev. C 2018, 98, 021301. [Google Scholar] [CrossRef]
- Suhonen, J. From Nucleons to Nucleus; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Andreozzi, F.; Coraggio, L.; Covello, A.; Gargano, A.; Kuo, T.T.S.; Porrino, A. Structure of neutron-rich nuclei around 132Sn. Phys. Rev. C 1997, 56, R16. [Google Scholar] [CrossRef]
- Machleidt, R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys. Rev. C 2001, 63, 024001. [Google Scholar] [CrossRef]
- Bogner, S.; Kuo, T.T.S.; Coraggio, L.; Covello, A.; Itaco, N. Low momentum nucleon-nucleon potential and shell model effective interactions. Phys. Rev. C 2002, 65, 051301. [Google Scholar] [CrossRef]
- Hjorth-Jensen, M.; Kuo, T.T.; Osnes, E. Realistic effective interactions for nuclear systems. Phy. Rep. 1995, 261, 125. [Google Scholar] [CrossRef]
- Coraggio, L.; Covello, A.; Gargano, A.; Itaco, N.; Kuo, T. Shell-model calculations and realistic effective interactions. Prog. Part. Nucl. Phys. 2009, 62, 135. [Google Scholar] [CrossRef]
- Coraggio, L.; Covello, A.; Gargano, A.; Itaco, N.; Kuo, T. Effective shell-model hamiltonians from realistic nucleon–nucleon potentials within a perturbative approach. Ann. Phys. 2012, 327, 2125. [Google Scholar] [CrossRef][Green Version]
- Shimizu, N.; Mizusaki, T.; Utsuno, Y.; Tsunoda, Y. Thick-restart block Lanczos method for large-scale shell-model calculations. Comput. Phys. Commun. 2019, 344, 372. [Google Scholar] [CrossRef]
- Simpson, G.S.; Gey, G.; Jungclaus, A.; Taprogge, J.; Nishimura, S.; Sieja, K.; Doornenbal, P.; Lorusso, G.; Söderström, P.-A.; Sumikama, T.; et al. Yrast 6+ Seniority Isomers of 136,138Sn. Phys. Rev. Lett. 2014, 113, 132502. [Google Scholar] [CrossRef]
- Brown, B.A.; Richter, W.A. New “USD” Hamiltonians for the sd shell. Phys. Rev. C 2006, 74, 034315. [Google Scholar] [CrossRef]
- Tilley, D.; Cheves, C.; Kelley, J.; Raman, S.; Weller, H. Energy levels of light nuclei, A = 20. Nucl. Phys. A 1998, 636, 249. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).