Asymmetric Right-Skewed Size-Biased Bilal Distribution with Mathematical Properties, Reliability Analysis, Inference and Applications

Abstract

Asymmetric distributions, as opposed to symmetric distributions, may be more resilient to extreme values or outliers. Furthermore, when data show substantial skewness, asymmetric distributions can shed light on the underlying processes or phenomena being investigated. In this direction, the size-biased Bilal distribution (SBBD) is suggested in this study as a generalization to the Bilal distribution. The length-biased and area-biased Bilal distributions are discussed in detail as two special cases. The main statistical properties of the distribution including the rth moment, coefficients of variation, skewness, kurtosis, moment generating function, incomplete moments, moments of residual life, harmonic mean, Fisher’s information, and the Rényi entropy as a measure of uncertainty are presented. Graphical representations of the cumulative distribution, probability density, odds, survival, hazard, reversed hazard rate, and cumulative hazard functions are presented for further explanation of the distribution behavior. In addition, the methods of moments and maximum likelihood estimates are taken into account for estimating the model parameters. A simulation study is carried out to see the efficiency of the maximum likelihood in terms of standard errors and bias. Real data sets of precipitation and myeloid leukemia patients are considered to show the practical significance of the suggested distributions as an alternative to some well-known distributions such as the Rama, Rani, Bilal, and exponential distributions. It is found that the size-biased Bilal distribution is right-skewed and has a superior fitting performance compared to the other distributions in this study.

1. Introduction

One of the most crucial objectives of a statistician is to describe real-world situations using probability distributions. In many real-world applications, including the fields of medicine, actuarial science, engineering, industry, and finance, modeling and interpreting lifetime data are crucial. This has led researchers to concentrate on creating families of probability distributions in recent decades. The size-biased distributions appear when the gathered data in actual life scenarios are assigned based on a weight function rather than randomly. Size-biased distribution refers to the distribution that results in sampling process selecting sample units with a probability that is proportional to some size measure of the unit. The concept of weighted distributions was first proposed by [1] to accurately model real data. Over the last 25 years, some fitting models for scanned data have been collected using the weighted distributions technique. Assume that the random variable X has a probability density function (pdf) $f(x)$; then, the pdf of the weighted random variable $X_w$ is obtained using the following:

$$f_w(x)=\frac{w(x)f(x)}{E[w(X)]}$$

(1)

such that $E[w(X)]$ exists and the normalization factor, $w(x)$, makes the overall probability equal to 1. The concept of length-biased sampling was first introduced by [2], and then [3] formulated and explored this idea broadly in the context of modeling statistical data when the conventional method of employing standard distributions was proven to be ineffective. Ref. [3] introduced a special case of the weighted distribution known as size-biased distribution of order $t$ and if the weighted function has the form $w(x)=x^t,$ the pdf is obtained using the following:

$$f_t(x)=\frac{x^t\hspace{0.17em}f(x)}{E_t(X)}.$$

(2)

For $t=1$ and $t=2$, the obtained distributions are called length-biased and area-biased distributions, respectively.

Furthermore, due to the importance of the weighted distributions, many researchers studied it in various cases. Ref. [4] talked about using weighted binomial distribution to model human families and determine the size of wildlife families. The relationship between initial reliability measures and size-biased distribution was outlined by [5]. Ref. [6] provided the theory of bivariate weighted distribution. Ref. [7] proposed the length-biased weighted Maxwell distribution. Ref. [8] suggested size-biased weighted transmuted Weibull distribution. Length and area-biased Maxwell distributions were introduced by [9]. Ref. [10] proposed size-biased Ishita distribution. Weighted power Lomax distribution and its length-biased form were proposed by [11]. For modeling skewed and heavy-tailed data, Ref. [12] presented the normal weighted inverse Gaussian distribution. Ref. [13] offered weighted generalized Quasi Lindley distribution. Ref. [14] suggested generalized weighted exponential distribution. Ref. [15] introduced weighted Gamma–Pareto distribution, and [16] investigated a modified weighted Pareto distribution of Type I.

Ref. [17] offered a new continuous lifetime distribution, called Bilal distribution (BD), which is demonstrated to belong with the class of novel renewal failure rates that are better than average. The Bilal distribution’s density function is always unimodal, with around 25% and 28% less skewness and kurtosis than the exponential distribution’s density function, respectively. The distribution function, qth quantiles, and failure rate function, on the other hand, are in compact form, and the distinct moments are expressed explicitly in terms of the exponential function. He defined the probability density function of BD as follows:

$$f_{BD}(x;\theta )=\frac{6}{\theta }\left(1-{\mathrm{e}}^{-\frac{x}{\theta }}\right){\mathrm{e}}^{-\frac{2x}{\theta }},x\ge 0,\theta >0$$

(3)

where $E_{BD}(X)=\frac{5}{6}\theta$, $V_{BD}(X)=\frac{13}{36}{\theta }^2$, coefficient of variation $CV=0.72$, kurtosis $Ku=6.443786982$, and the corresponding cumulative distribution function (CDF) is defined as follows:

$$F_{BD}(x;\theta )=1-\left(3-2{\mathrm{e}}^{-\frac{x}{\theta }}\right){\mathrm{e}}^{-\frac{2x}{\theta }},x\ge 0,\theta >0$$

(4)

It is of interest to note here that base Bilal distribution has a one parameter and the suggested modifications each has one parameter with suitable weight functions which yields more flexibility in modeling a variety of real data sets for simple usage. The novelty of this research lies in combination the Bilal distribution with the weighted distribution to modify the Bilal distribution for modeling real data sets. To our knowledge, this is the first work on length-biased and area-biased Bilal distributions. The rest of this paper is organized as follows: The size-biased Bilal distribution and some of its properties are presented in Section 2. Section 3 addresses some certain distributional features of the suggested length-biased and area-biased Bilal distributions. In Section 4, the applicability of the proposed models is demonstrated based on two real data sets. Finally, the paper is concluded in Section 5.

2. Structure of the SBBD

This section introduces the size-biased Bilal distribution of the order t, expressed using Equation (2). Then, the length and area-biased Bilal distributions are derived as two special cases. The pdf of the size-biased Bilal random variable, $X_{SBBD}^{}$, of order t is expressed using

$$f_{SBBD}(x;\theta )=\frac{x^t\hspace{0.17em}{f}_{BD}(x;\theta )}{E_{BD}(X^t)}=\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}{x}^t{e}^{-\frac{2x}{\theta }}\left(1-e^{-\frac{x}{\theta }}\right), x>0,\hspace{0.17em}\theta >0,$$

(5)

and the corresponding CDF is as follows:

$$F_{SBBD}(x;\theta )=\frac{2^{t+1}\left[\Gamma (t+1)-\Gamma \left(t+1,\frac{3x}{\theta }\right)\right]+3^{t+1}\left[\Gamma \left(t+1,\frac{2x}{\theta }\right)-t\Gamma (t)\right]}{\left(2^{t+1}-3^{t+1}\right)\Gamma (t+1)},t=1,2,\dots ;\hspace{0.17em}x,\theta >0,$$

(6)

where $\Gamma (t)={\displaystyle \underset{0}{\overset{\infty }{\int }}{z}^{t-1}{e}^{-z}dz}$ is the gamma function and $\Gamma (a,t)={\displaystyle \underset{t}{\overset{\infty }{\int }}{z}^{a-1}{e}^{-z}dz}$ is the incomplete gamma function. Figure 1 shows the pdf plots of SBBD for various schemes, where $\theta =0.9$ and 0.3 with t = 1, 2, 3, 4, 5, 6, 7. It is clear that SBBD can take various shapes depending on the value of the parameters $\theta$ and t. For example, when $t=1$, SBBD is skewed to the right for both values $\theta =0.9,0.3,$ increasing and then decreasing as in both the plots, and is semi-symmetric for $t=7$ with $\theta =0.3$. These different shapes give the distribution more flexibility in modeling some type of data.

Figure 1. The plots of SBBD for $\theta =0.9$ (left) and $\theta =0.3$ (right) with $t=1, 2, 3$, 4, 5, 6, 7.

Theorem 1.

The rth moment of the size-biased Bilal distributed random variable, X_SBBD, is obtained using the following equation:

$$E\left(X^r\right)=\frac{{\theta }^r\left(2^{r+t+1}-3^{r+t+1}\right)\Gamma (r+t+1)}{6^r\left(2^{t+1}-3^{t+1}\right)\Gamma (t+1)},\theta >0,r+t>-2$$

(7)

Proof. 

To prove the theorem, the rth moment is defined as follows:

$$\begin{array}{ll}E\left(X^r\right)& ={\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^r{f}_{SBBD}(x;\theta )}\hspace{0.17em}dx\\ & ={\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^r\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}{x}^t{e}^{-\frac{2x}{\theta }}\left(1-e^{-\frac{x}{\theta }}\right)}\hspace{0.17em}dx\\ & =\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}\left({\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^{r+1}{e}^{-\frac{2x}{\theta }}}\hspace{0.17em}dx-{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^{r+t}{e}^{-\frac{3x}{\theta }}}\hspace{0.17em}dx\right)\\ & =\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}\left(\frac{\Gamma (r+t+1)}{{\left(\frac{2}{\theta }\right)}^{r+t+1}}-\frac{\Gamma (r+t+1)}{{\left(\frac{3}{\theta }\right)}^{r+t+1}}\right)\\ & =\frac{6^{t+1}{\theta }^{-t-1}\Gamma (r+t+1){\theta }^{r+t+1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}\left(\frac{3^{r+t+1}-2^{r+t+1}}{6^{r+t+1}}\right)\\ & =\frac{{\theta }^r\left(2^{r+t+1}-3^{r+t+1}\right)(r+t)!}{6^r\left(2^{t+1}-3^{t+1}\right)\hspace{0.17em}t!}.\end{array}$$

□

For $r=1,2,3,4$ in Equation (7), we obtain the first four moments, respectively, for the origin of X:

$$E\left(X\right)=\frac{\theta \left(2^{t+2}-3^{t+2}\right)(t+1)!}{6\left(2^{t+1}-3^{t+1}\right)t!}, E\left(X^2\right)=\frac{{\theta }^2\left(2^{t+3}-3^{t+3}\right)(t+2)!}{36\left(2^{t+1}-3^{t+1}\right)t!},$$

$$E\left(X^3\right)=\frac{{\theta }^3\left(2^{t+4}-3^{t+4}\right)(t+3)!}{216\left(2^{t+1}-3^{t+1}\right)t!}, E\left(X^4\right)=\frac{{\theta }^4\left(2^{t+5}-3^{t+5}\right)(t+4)!}{1296\left(2^{t+1}-3^{t+1}\right)t!}.$$

Theorem 2.

If X has a SBBD, then the moment generating functions of X_SBBD is obtained using the following equation:

$$M_X(w)=\frac{6^{t+1}}{3^{t+1}-2^{t+1}}\left[{\left(2-\theta w\right)}^{-(t+1)}-{\left(3-\theta w\right)}^{-(t+1)}\right],w<\frac{3}{\theta },t>-2.$$

(8)

Proof. 

The proof is similar to the proof of Theorem (1), considering the following:

$$M_X(w)={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{wx}{f}_{SBBD}(x;\theta )}\hspace{0.17em}dx.$$

□

Theorem 3.

The rth incomplete moment of the SBBD is defined as follows:

$$E\left(X_{IM-SBBD}^r\right)=\frac{3^{r+t+1}\left[\Gamma \left(r+t+1,\frac{2h}{\theta }\right)-\Gamma (r+t+1)\right]+2^{r+t+1}\left[\Gamma (r+t+1)-\Gamma \left(r+t+1,\frac{3h}{\theta }\right)\right]}{\left(2^{t+1}-3^{t+1}\right)\Gamma (t+1)}.$$

(9)

Proof. 

Recall the pdf in (5), the incomplete rth moment of the SBBD can be proved as follows:

$$\begin{array}{l}E\left(X_{IM-LBBD}^r\right)={\displaystyle \underset{0}{\overset{h}{\int }}{x}_{}^r{f}_{LBBD}(x;\theta )}dx\\ =\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}{\displaystyle \underset{0}{\overset{h}{\int }}{x}_{}^{r+t}\left(e^{-\frac{2x}{\theta }}-e^{-\frac{3x}{\theta }}\right)}dx\\ =\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}\left[\begin{array}{l}\theta 2^{-r-t-1}{h}^{r+t}{\left(\frac{h}{\theta }\right)}^{-r-t}\left(\Gamma (r+t+1)-\Gamma \left(r+t+1,\frac{2h}{\theta }\right)\right)\\ -\theta 3^{-r-t-1}{h}^{r+t}{\left(\frac{h}{\theta }\right)}^{-r-t}\left(\Gamma (r+t+1)-\Gamma \left(r+t+1,\frac{3h}{\theta }\right)\right)\end{array}\right]\\ =\frac{6^{t+1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}\left[2^{-r-t-1}\left(\Gamma (r+t+1)-\Gamma \left(r+t+1,\frac{2h}{\theta }\right)\right)-3^{-r-t-1}\left(\Gamma (r+t+1)-\Gamma \left(r+t+1,\frac{3h}{\theta }\right)\right)\right]\\ =\frac{3^{r+t+1}\left[\Gamma \left(r+t+1,\frac{2h}{\theta }\right)-\Gamma (r+t+1)\right]+2^{r+t+1}\left[\Gamma (r+t+1)-\Gamma \left(r+t+1,\frac{3h}{\theta }\right)\right]}{\left(2^{t+1}-3^{t+1}\right)\Gamma (t+1)}.\end{array}$$

□

Rényi entropy is a statistical mechanics and information theory concept that gauges how random or uncertain a system is. The Rényi entropy of the random variable X as defined by [18] is expressed using $H_{\alpha }(X)=\frac{1}{1-\alpha }\log \left({\displaystyle \underset{0}{\overset{\infty }{\int }}f{(x)}^{\alpha }dx}\right),$ $\alpha >0$,$\alpha \ne 1$.

Theorem 4.

The Rényi entropy of the SBBD is obtained using the following:

$$H_{\alpha }\left(X_{SBBD}\right)=\frac{1}{1-\alpha }\log \left\{{\left(\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}\right)}^{\alpha }{\displaystyle \sum _{j=0}^{\alpha }{(-1)}^{\alpha -j}\left(\begin{array}{c}\alpha \\ j\end{array}\right)}(\alpha t)!{\left(\frac{3\alpha -j}{\theta }\right)}^{-(\alpha t+1)}\right\}.$$

(10)

Proof. 

The Rényi entropy of the size-biased distributed random variable X can be derived as follows:

$$\begin{array}{ll}{H}_{\alpha }\left(X_{LBBD}\right)& =\frac{1}{1-\alpha }\log {\displaystyle \underset{0}{\overset{\infty }{\int }}{\left(\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}{x}^t{e}^{-\frac{2x}{\theta }}\left(1-e^{-\frac{x}{\theta }}\right)\right)}^{\alpha }dx}\\ & =\frac{1}{1-\alpha }\log \left\{{\left(\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}\right)}^{\alpha }{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^{\alpha t}{e}^{-\frac{2\alpha x}{\theta }}{\left(1-e^{-\frac{x}{\theta }}\right)}^{\alpha }dx}\right\}\\ & =\frac{1}{1-\alpha }\log \left\{{\left(\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}\right)}^{\alpha }{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^{\alpha t}{e}^{-\frac{2\alpha x}{\theta }}{\displaystyle \sum _{j=0}^{\alpha }{(-1)}^{\alpha -j}\left(\begin{array}{c}\alpha \\ j\end{array}\right)\hspace{0.17em}\hspace{0.17em}{\left(e^{-\frac{x}{\theta }}\right)}^{\alpha -j}}dx}\right\}\\ & =\frac{1}{1-\alpha }\log \left\{{\left(\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}\right)}^{\alpha }{\displaystyle \sum _{j=0}^{\alpha }{(-1)}^{\alpha -j}\left(\begin{array}{c}\alpha \\ j\end{array}\right)}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^{\alpha t}{e}^{-\frac{2\alpha x}{\theta }}{\left(e^{-\frac{x}{\theta }}\right)}^{\alpha -j}dx}\right\}\\ & =\frac{1}{1-\alpha }\log \left\{{\left(\frac{6^{t+1}{\theta }^{-t-1}}{\Gamma (t+1)\left(3^{t+1}-2^{t+1}\right)}\right)}^{\alpha }{\displaystyle \sum _{j=0}^{\alpha }{(-1)}^{\alpha -j}\left(\begin{array}{c}\alpha \\ j\end{array}\right)}(\alpha t)!{\left(\frac{3\alpha -j}{\theta }\right)}^{-(\alpha t+1)}\right\}.\end{array}$$

□

3. Special Cases of the SBBD

In this section, by setting $t=1,2$ in Equation (5), we obtain the pdfs of the suggested length-biased Bilal distribution (LBBD) and area-biased Bilal distribution (ABBD), respectively:

$$f_{LBBD}(x;\theta )=\frac{36}{5\hspace{0.17em}{\theta }^2}\left(x-x{\mathrm{e}}^{-\frac{x}{\theta }}\right){\mathrm{e}}^{-\frac{2x}{\theta }},\hspace{0.17em}\hspace{0.17em}x>0,\theta >0,$$

(11)

$$f_{ABBD}(x;\theta )=\frac{108}{19\hspace{0.17em}{\theta }^3}\left(x^2-x^2{e}^{-\frac{x}{\theta }}\right)e^{-\frac{2x}{\theta }},\hspace{0.17em}\hspace{0.17em}x>0,\theta >0.$$

(12)

For various distribution parameter values, the pdf plots of the LBBD and ABBD are shown in Figure 2. The pdfs of the recommended distributions are skewed to the right and become more flat as the values of $\theta$ increase. Furthermore, depending on the parameter values, the pdfs of the ABBD and LBBD can display a variety of behaviors.

Figure 2. The pdf plots of the LBBD and ABBD when $\theta =1,2,3,4,5,6,7$.

The CDFs of the LBBD and ABBD, respectively, are expressed using the following:

$$F_{LBBD}(x;\theta )=1-\frac{9e^{-\frac{2x}{\theta }}(\theta +2x)-4e^{-\frac{3x}{\theta }}(\theta +3x)}{5\theta },$$

(13)

$$F_{ABBD}(x;\theta )=1-\frac{27}{19\hspace{0.17em}{\theta }^2}{e}^{-\frac{2x}{\theta }}\left({\theta }^2+2x^2+2\theta x\right)+\frac{4}{19}{e}^{-\frac{3x}{\theta }}\left(\frac{9x^2}{{\theta }^2}+\frac{6x}{\theta }+2\right).$$

(14)

Some of the CDFs plots of the LBBD and ABBD when $\theta =1,2,3,4,5,6,7$ are presented in Figure 3.

Figure 3. The CDFs plots of the LBBD and ABBD when θ = 1, 2, 3, 4, 5, 6, 7.

3.1. Moments and Related Measure

The moments and related measures, coefficients of variation (Cv), skewness (Sk), and kurtosis (Ku), the incomplete moments and moment of the residual lifetime, moment generating function, reliability functions of the proposed distributions are all described in this section in closed expressions. Also, the parameters estimation, Fisher’s information and entropies, as well as the order statistics are presented.

The rth moments of the LBBD and ABBD by setting $t=1,2$ in Equation (7), respectively, are obtained using the following:

$$E\left(X_{LBBD}^r\right)=\frac{1}{5}{\left(\frac{\theta }{6}\right)}^r\left(3^{r+2}-2^{r+2}\right)\Gamma (r+2) \mathrm{and} E\left(X_{ABBD}^r\right)=\frac{1}{38}\left(\frac{27}{2^r}\hspace{0.33em}-\frac{8}{3^r}\hspace{0.33em}\right){\theta }^r\Gamma (r+3),$$

for $\theta >0$ and $r=1,2,\dots$.

An alternative formulation of a real-valued random variable’s probability distribution is the moment-generating function (mgf). The mgf of the LBBD and ABBD, respectively, are expressed using the following:

$$M_{XLBBD}(w)=-\frac{36(2\theta w-5)}{5{\left({\theta }^2{w}^2-5\theta w+6\right)}^2} \mathrm{and} M_{XABBD}(w)=\frac{216}{19}\left(\frac{1}{{(\theta w-3)}^3}-\frac{1}{{(\theta w-2)}^3}\right).$$

The Lorenz ([19]) and Benforroni [20] curves are used to measure inequality using the incomplete moments of a probability distribution. The rth incomplete moments of the LBBD and ABBD from Theorem (2) by setting $t=1,2$, respectively, are defined as follows:

$$\begin{array}{ll}E\left(X_{IM-LBBD}^r\right)& ={\displaystyle \underset{0}{\overset{h}{\int }}{x}_{}^r{f}_{LBBD}(x;\theta )}dx\\ & =\frac{1}{5}{\left(\frac{\theta }{6}\right)}^r\left\{2^{r+2}\left[\Gamma \left(r+2,\frac{3h}{\theta }\right)-(r+1)!\right]+3^{r+2}\left[(r+1)!-\Gamma \left(r+2,\frac{2h}{\theta }\right)\right]\right\},\end{array}$$

and

$$\begin{array}{ll}E\left(X_{IM-ABBD}^r\right)& ={\displaystyle \underset{0}{\overset{h}{\int }}{x}_{}^r{f}_{ABBD}(x;\theta )}dx\\ & =\frac{4}{19}{\left(\frac{\theta }{3}\right)}^r\left\{{\left(\frac{3}{2}\right)}^{r+3}\left[(r+2)!-\Gamma \left(r+3,\frac{2h}{\theta }\right)\right]+\left[\Gamma \left(r+3,\frac{3h}{\theta }\right)-(r+2)!\right]\right\}.\end{array}$$

The residual life is the time after a component lives up to time $(t\ge 0)$ until the time of failure, which is determined by the conditional random variable $X-t|X>t$. Hence, the rth moment of the residual lifetime (MRL) of the LBBD and ABBD, respectively, are distinct:

$$\begin{array}{ll}E\left(X_{MRL-LBBD}^r\right)& =\frac{1}{S_{LBBD}(s;\theta )}{\displaystyle \underset{s}{\overset{\infty }{\int }}{\left(x-s\right)}_{}^r{f}_{LBBD}(x;\theta )}dx\\ & =\frac{1}{S_{LBBD}(s;\theta )}\left\{\frac{{\theta }^{r-1}\Gamma (r+1)}{5\left(6^r\right)}{e}^{-\frac{3s}{\theta }}\left[3^{r+2}{e}^{s/\theta }(\theta +\theta r+2s)-2^{r+2}(\theta +\theta r+3s)\right]\right\},\end{array}$$

$$\begin{array}{ll}E\left(X_{MRL-ABBD}^r\right)& =\frac{1}{S_{ABBD}(s;\theta )}{\displaystyle \underset{s}{\overset{\infty }{\int }}{\left(x-s\right)}_{}^r{f}_{ABBD}(x;\theta )}dx\\ & =\frac{1}{S_{ABBD}(s;\theta )}\left\{\frac{{\theta }^{r-2}\Gamma (r+1)}{19\left(3^r\right)\left(2^{r+1}\right)}{e}^{-\frac{3s}{\theta }}\left\{\begin{array}{l}{3}^{r+3}{e}^{s/\theta }\left[{\theta }^2(r+1)(r+2)+4\theta (r+1)s+4s^2\right]\\ -2^{r+3}\left[{\theta }^2(r+1)(r+2)+6\theta (r+1)s+9s^2\right]\end{array}\right\}\right\}.\end{array}$$

The harmonic means of the LBBD and ABBD are defined as follows:

$$H_{LBBD}=\frac{5\theta }{6} \mathrm{and} H_{ABBD}=\frac{19\hspace{0.17em}\theta }{15}.$$

The rth quartiles of the LBBD and ABBD, respectively, are the solutions for $Q_r$ in the following equations:

$$\frac{e^{-\frac{3Q_r}{\theta }}}{5\theta }\left[9e^{Q_r/\theta }\left(\theta +2Q_r\right)-4\left(\theta +3Q_r\right)\right]=\frac{r}{4},$$

and

$$\frac{e^{-\frac{3Q_r}{\theta }}}{19{\theta }^2}\left[27e^{Q/\theta }\left({\theta }^2+2Q_r^2+2\theta Q_r\right)-4\left(2{\theta }^2+9Q_r^2+6\theta Q_r\right)\right]=\frac{r}{4}, r=1,2,3,$$

where $Q_1,Q_2$ and $Q_3$ are respectively called the first, second and third quartiles.

The coefficient of skewness is used to determine the skewness of the distribution and is expressed as $Sk=\frac{E\left(X^3\right)-3\mu {\sigma }^2-{\mu }^3}{{\sigma }^3}$. For the LBBD and ABBD, correspondingly, the coefficients of skewness are expressed as $S{k}_{LBBD}=1.23386$ and $S{k}_{ABBD}=0.514944.$

The top of the distribution’s flatness is measured by the coefficient of kurtosis, which can be defined as $Ku=\frac{E\left(X^4\right)-4\mu E\left(X^3\right)+6E\left(X^2\right){\sigma }^2+3E\left(X^4\right)}{{\sigma }^4}.$ The LBBD and ABBD has the coefficient of kurtosis $K{u}_{LBBD}=5.35547$ and $K{u}_{ABBD}=1.07703$, respectively. The Cv is defined as $Cv=\frac{\sigma }{\mu }$و and for the LBBD and ABBD, they are expressed as $C{v}_{LBBD}=0.591959$ and $C{v}_{ABBD}=4.79273$, respectively.

Table 1 presents the values of the mean and standard deviation (SD) of the LBBD and ABBD for different selections of $\theta$. According to Table 1, as the value of $\theta$ rises, the mean and standard deviation values of the LBBD and ABBD rise as well.

Table 1. The mean and standard deviation of the LBBD and ABBD for various values of θ.

$\mathit{\theta }$	${\mathit{\mu }}_{\mathit{A}\mathit{B}\mathit{B}\mathit{D}}$	${\mathit{\sigma }}_{\mathit{A}\mathit{B}\mathit{B}\mathit{D}}^{}$	${\mathit{\mu }}_{\mathit{L}\mathit{B}\mathit{B}\mathit{D}}$	${\mathit{\sigma }}_{\mathit{L}\mathit{B}\mathit{B}\mathit{D}}^{}$
0.1	0.1711	0.0881	0.1267	0.0750
0.2	0.3421	0.1762	0.2533	0.1500
0.3	0.5132	0.2643	0.3800	0.2249
0.4	0.6842	0.3523	0.5067	0.2999
0.5	0.8553	0.4404	0.6333	0.3749
0.6	1.0263	0.5285	0.7600	0.4499
0.7	1.1974	0.6166	0.8867	0.5249
0.8	1.3684	0.7047	1.0133	0.5999
0.9	1.5395	0.7927	1.1400	0.6748
1	1.7105	0.8808	1.2667	0.7498
1.1	1.8816	0.9689	1.3933	0.8248
1.2	2.0526	1.0570	1.5200	0.8998
1.3	2.2237	1.1451	1.6467	0.9748
1.4	2.3947	1.2332	1.7733	1.0497
1.5	2.5658	1.3212	1.9000	1.1247
1.6	2.7368	1.4093	2.0267	1.1997
1.7	2.9079	1.4974	2.1533	1.2747
1.8	3.0790	1.5855	2.2800	1.3497
1.9	3.2500	1.6736	2.4067	1.4247
2	3.4211	1.7617	2.5333	1.4996
2.1	3.5921	1.8497	2.6600	1.5746
2.2	3.7632	1.9378	2.7867	1.6496
2.3	3.9342	2.0259	2.9133	1.7246
2.4	4.1053	2.1140	3.0400	1.7996
2.5	4.2763	2.2021	3.1667	1.8745

3.2. Reliability Functions

The survival function is frequently used to predict the probability that an event will not occur after a specific amount of time or threshold in domains like survival analysis and reliability engineering, among others. The survival function is defined as $S(x)=1-F(x)$, and for the LBBD and ABBD, respectively, it is characterized as

$$S_{LBBD}(x;\theta )=\frac{9e^{x/\theta }(\theta +2x)-4(\theta +3x)}{5\theta }{e}^{-\frac{3x}{\theta }},$$

and

$$S_{ABBD}(x;\theta )=\frac{27{\mathrm{e}}^{x/\theta }\left(2x^2+2x\theta +{\theta }^2\right)-4\left(9x^2+6x\theta +2{\theta }^2\right)}{19{\theta }^2}{\mathrm{e}}^{-\frac{3x}{\theta }}.$$

Figure 4 shows the survival functions plots of the LBBD and ABBD for $\theta =0.1,0.2,\dots ,0.7.$ The plots reveal that the survival functions curves decreases and are skewed to the right. The distances between each two curves depend on the parameters’ values.

Figure 4. The survival function plots of the LBBD and ABBD for parameter choices.

In survival analysis and reliability engineering, the hazard function is a basic idea. It is utilized to simulate the instantaneous probability of an event (such as death, failure, or the occurrence of a specific event) occurring at a given time, given that it has not yet happened at that time. It is the ratio between the pdf and survival function of a random variable X, $H(x)=\frac{f(x)}{1-F(x)}$. For the LBBD and ABBD, the hazard functions, respectively, are expressed using

$$H_{LBBD}(x;\theta )=\frac{36x\left(e^{x/\theta }-1\right)}{9\theta e^{x/\theta }(\theta +2x)-4\theta (\theta +3x)},$$

and

$$H_{ABBD}(x;\theta )=\frac{108x^2\left(e^{x/\theta }-1\right)}{27\theta e^{x/\theta }\left({\theta }^2+2x^2+2\theta x\right)-4\theta \left(2{\theta }^2+9x^2+6\theta x\right)}.$$

Figure 5 presents the hazard functions of the LBBD and ABBD for some parameter choices, and it is clear that the hazard functions curves are increasing with different ranges depending on the parameter value.

Figure 5. The hazard functions plot of the LBBD and ABBD for some parameter choices.

The reversed hazard rate (RH) function is distinct as the ratio between the life probability density to its distribution function as $RH(x)=\frac{f(x)}{F(x)}$. The RH functions for the LBBD and ABBD, respectively, are defined as

$$R{H}_{LBBD}(x;\theta )=\frac{36x\left(e^{x/\theta }-1\right)}{\theta \left(5\theta e^{\frac{3x}{\theta }}-9e^{x/\theta }(\theta +2x)+4(\theta +3x)\right)},$$

and

$$R{H}_{ABBD}(x;\theta )=\frac{108x^2\left(e^{x/\theta }-1\right)}{19{\theta }^3{e}^{\frac{3x}{\theta }}-27\theta e^{x/\theta }\left({\theta }^2+2x^2+2\theta x\right)+4\theta \left(2{\theta }^2+9x^2+6\theta x\right)}.$$

Figure 6 displays some plots of the reversed hazard functions of the LBBD and ABBD for selected values of the parameters as $\theta =0.1,0.2,\dots ,0.7$, where the reversed hazard functions are decreasing for these parameter values.

Figure 6. The LBBD and ABBD reversed hazard functions plots for various values of θ.

The odds function is obtained as the ratio between $F(x)$ and $S(x)$ as $O(x)=\frac{F(x)}{S(x)}.$ The LBBD and ABBD have the odds functions, respectively, defined by the following:

$$O_{LBBD}(x;\theta )=\frac{5\theta e^{\frac{3x}{\theta }}-9e^{x/\theta }(\theta +2x)+4(\theta +3x)}{9e^{x/\theta }(\theta +2x)-4(\theta +3x)},$$

$$O_{ABBD}(x;\theta )=\frac{4\left(2{\theta }^2+9x^2+6\theta x\right)-27e^{x/\theta }\left({\theta }^2+2x^2+2\theta x\right)+19{\theta }^2{e}^{\frac{3x}{\theta }}}{27e^{x/\theta }\left({\theta }^2+2x^2+2\theta x\right)-4\left(2{\theta }^2+9x^2+6\theta x\right)}.$$

Some plots of the odds functions of the LBBD and ABBD for $\theta =0.1,0.2,\dots ,0.7$ are presented in Figure 7, which indicate that the curves are increasing for all parameter values.

Figure 7. Plots of the LBBD and ABBD odds functions at some values of θ.

The cumulative hazard (CH) function of a random variable X from a univariate continuous distribution is defined as $CH(x)=-ln\left(1-F(x)\right)$. The CH for the LBBD and ABBD, respectively, are expressed as

$$C{H}_{LBBD}(x;\theta )=-ln\left(\frac{9e^{x/\theta }(\theta +2x)-4(\theta +3x)}{5\theta }{e}^{-\frac{3x}{\theta }}\right),$$

and

$$C{H}_{ABBD}(x;\theta )=-ln\left(\frac{27{\mathrm{e}}^{x/\theta }\left(2x^2+2x\theta +{\theta }^2\right)-4\left(9x^2+6x\theta +2{\theta }^2\right)}{19{\theta }^2}{\mathrm{e}}^{-\frac{3x}{\theta }}\right).$$

Figure 8 shows some plots of the LBBD and ABBD cumulative hazard functions at various values of $\theta =0.1,0.2,\dots ,0.7.$ It is obvious that the odds function of both distributions is increasing and its values are larger for small values of $\theta$.

Figure 8. The plots of the LBBD and ABBD cumulative hazard functions for $\theta =0.1,0.2,\dots ,0.7$.

3.3. Parameters Estimation

The method of moments (MOMs) and maximum likelihood technique are used in this section to estimate the LBBD and ABBD parameters. Let $X_1,X_2,\dots ,X_n$ be a random sample of size n selected from a pdf $f(x)$ and CDF $F(x)$. The method of moments estimators of the distributions parameter are ${\tilde{\theta }}_{LBBD}=\frac{15}{19}\overline{X}$ and ${\tilde{\theta }}_{ABBD}=\frac{38}{65}\overline{X}$, where $\overline{X}={\displaystyle \sum _{i=1}^n\frac{x_i}{n}}$ is the sample mean.

To find the maximum likelihood estimators of the distribution parameter, let $x_1,x_2,\dots ,x_n$ be the sample observations of $X_1,X_2,\dots ,X_n$ from the LBBD and ABBD. The log-likelihood functions are, respectively, obtained using the following:

$$\ln {(L)}_{LBBD}=n\log \left(\frac{36}{5}\right)+n\log \frac{1}{{\theta }^2}-2{\displaystyle \sum }_{i=1}^n\frac{x_i}{\theta }+{\displaystyle \sum }_{i=1}^n\log x_i+{\displaystyle \sum }_{i=1}^n\log \left(1-e^{-\frac{x_i}{\theta }}\right),$$

$$\ln {(L)}_{ABBD}=n\log \left(\frac{108}{19}\right)+n\log \frac{1}{{\theta }^3}-2{\displaystyle \sum }_{i=1}^n\frac{x_i}{\theta }+{\displaystyle \sum }_{i=1}^n\log x_i^2+{\displaystyle \sum }_{i=1}^n\log \left(1-{\mathrm{e}}^{-\frac{x_i}{\theta }}\right).$$

The partial derivatives of these equations with respect to the parameter $\theta$ are obtained using the following:

$$\frac{\partial \ln {(L)}_{LBBD}}{\partial \theta }={\displaystyle \sum _{i=1}^n\frac{2x_i}{{\theta }^2}}-{\displaystyle \sum _{i=1}^n\frac{x_i{e}^{-\frac{x_i}{\theta }}}{{\theta }^2\left(1-e^{-\frac{x_i}{\theta }}\right)}}-\frac{2n}{\theta }, \frac{\partial ln{(L)}_{ABBD}}{\partial \theta }={\displaystyle \sum _{i=1}^n\frac{2x_i}{{\theta }^2}}-{\displaystyle \sum _{i=1}^n\frac{x_i{e}^{-\frac{x_i}{\theta }}}{{\theta }^2\left(1-e^{-\frac{x_i}{\theta }}\right)}}-\frac{3n}{\theta }.$$

The exact solution of these nonlinear equations is not easy, so one may maximize them by using some optimization approaches as the Newton–Raphson method. Table 2 provides some values of the MLE ${\widehat{\theta }}_{ABBD}$ and ${\widehat{\theta }}_{LBBD}$, and the corresponding standard errors (SE) for various distributions parameter with sample sizes n = 40, 80, 120, 160, 200, 240, and 500.

Table 2. The MLE ${\widehat{\theta }}_{ABBD}$ and ${\widehat{\theta }}_{LBBD}$ with SE for selected values of $\theta$ and n.

n	$\mathit{\theta }$	${\widehat{\mathit{\theta }}}_{\mathit{A}\mathit{B}\mathit{B}\mathit{D}}$	$\mathit{S}\mathit{E}\left({\widehat{\mathit{\theta }}}_{\mathit{A}\mathit{B}\mathit{B}\mathit{D}}\right)$	${\widehat{\mathit{\theta }}}_{\mathit{L}\mathit{B}\mathit{B}\mathit{D}}$	$\mathit{S}\mathit{E}\left({\widehat{\mathit{\theta }}}_{\mathit{L}\mathit{B}\mathit{B}\mathit{D}}\right)$
	2	2.0002	0.1628	2.0003	0.1871
	3	3.0003	0.2442	3.0005	0.2807
40	5	5.0005	0.4069	5.0008	0.4678
	7	7.0007	0.5697	7.0011	0.6549
	10	10.0010	0.8141	10.0016	0.9356
	2	2.0023	0.1152	2.0027	0.1325
	3	3.0034	0.1728	3.0040	0.1987
80	5	5.0057	0.2881	5.0066	0.3312
	7	7.0080	0.4033	7.0093	0.4637
	10	10.0114	0.5762	10.0133	0.6624
	2	2.0010	0.0940	2.0011	0.1081
	3	3.0014	0.1410	3.0017	0.1621
120	5	5.0024	0.2350	5.0029	0.2702
	7	7.0033	0.3291	7.0040	0.3783
	10	10.0048	0.4700	10.0057	0.5405
	2	2.0004	0.0814	2.0005	0.0936
	3	3.0006	0.1221	3.0008	0.1404
160	5	5.0010	0.2035	5.0013	0.2339
	7	7.0014	0.2849	7.0018	0.3275
	10	10.0020	0.4070	10.0026	0.4680
	2	1.9996	0.0728	1.9997	0.0837
	3	2.9995	0.1092	2.9995	0.1255
200	5	4.9991	0.1819	4.9991	0.2092
	7	6.9988	0.2547	6.9988	0.2928
	10	9.9982	0.3640	9.9983	0.4183
	2	1.9997	0.0664	1.9997	0.0764
	3	2.9995	0.0997	2.9995	0.1146
240	5	4.9992	0.1661	4.9992	0.1909
	7	6.9989	0.2325	6.9989	0.2673
	10	9.9984	0.3322	9.9985	0.3819
	2	1.9995	0.0460	1.9994	0.0529
	3	2.9992	0.0690	2.9992	0.0794
500	5	4.9987	0.1151	4.9986	0.1323
	7	6.9982	0.1611	6.9980	0.1852
	10	9.9974	0.2301	9.9972	0.2645

Table 2 demonstrates that the standard errors values for both MLE estimators ${\widehat{\theta }}_{ABBD}$ and ${\widehat{\theta }}_{LBBD}$, which shows that distributions parameters are decreasing for larger sample sizes for fixed parameter values.

3.4. Fisher’s Information and Entropies

This subsection introduces the Fisher’s information (FI) as well as the Rényi entropy of the LBBD and ABBD.

Theorem 5.

The Fisher’s information of ABBD and LBBD, respectively, are as follows:

$$F{I}_{ABBD}(\theta )=\frac{3.77457}{{\theta }^2} \mathrm{and} F{I}_{LBBD}(\theta )=\frac{2.85636}{{\theta }^2}.$$

Proof. 

Take the log of the ABBD pdf as

$$\log \left(f_{LBBD}(x;\theta )\right)=\log \left(\frac{36}{5{\theta }^2}\right)+\log (x)+\log \left(1-{\mathrm{e}}^{-\frac{x}{\theta }}\right)-\frac{2x}{\theta }.$$

The first and second derivatives of $\log \left(f_{LBBD}(x;\theta )\right)$ with respect to $\theta$ respectively are as follows:

$$\frac{\partial }{\partial \theta }\log \left(f_{LBBD}(x;\theta )\right)=\frac{x}{{\theta }^2}\left(\frac{1}{1-e^{x/\theta }}+2\right)-\frac{2}{\theta },$$

$$\frac{{\partial }^2}{\partial {\theta }^2}\log \left(f_{LBBD}(x;\theta )\right)=\frac{2}{{\theta }^3}\left(\theta +x\left(\frac{1}{e^{x/\theta }-1}-2\right)\right)-\frac{x^2{e}^{x/\theta }}{{\theta }^4{\left(e^{x/\theta }-1\right)}^2}.$$

Hence,

$$\begin{array}{ll}F{I}_{LBBD}(\theta )& =-E\left(\frac{{\partial }^2}{\partial {\theta }^2}log\left[f_{LBBD}(x;\theta )\right]\right)\\ & =-\frac{36}{5{\theta }^5}{\displaystyle \underset{0}{\overset{\infty }{\int }}\left[2x\left(\theta +x\left(\frac{1}{e^{x/\theta }-1}-2\right)\right)-\frac{x^3{e}^{x/\theta }}{\theta {\left(e^{x/\theta }-1\right)}^2}\right]}\left(1-{\mathrm{e}}^{-\frac{x}{\theta }}\right){\mathrm{e}}^{-\frac{2x}{\theta }}dx\\ & =-\frac{2195-24{\pi }^4}{50{\theta }^2}=\frac{2.85636}{{\theta }^2}.\end{array}$$

Similarly,

$$\begin{array}{ll}F{I}_{ABBD}(\theta )& =-E\left(\frac{{\partial }^2}{\partial {\theta }^2}log\left[f_{ABBD}(x;\theta )\right]\right)\\ & =-\frac{24\left(109-108Zeta\left[5\right]\right)}{19{\theta }^2}=\frac{3.77457}{{\theta }^2}.\end{array}$$

□

Some values of the Fisher’s information for both of LBBD and ABBD are presented in Table 3 for selected values of the parameter $\theta$.

Table 3. Fisher’s information values of the LBBD and ABBD for some values of θ.

$\mathit{\theta }$	$\mathit{F}{\mathit{I}}_{\mathit{L}\mathit{B}\mathit{B}\mathit{D}}(\mathit{\theta })$	$\mathit{F}{\mathit{I}}_{\mathit{A}\mathit{B}\mathit{B}\mathit{D}}(\mathit{\theta })$	$\mathit{\theta }$	$\mathit{F}{\mathit{I}}_{\mathit{L}\mathit{B}\mathit{B}\mathit{D}}(\mathit{\theta })$	$\mathit{F}{\mathit{I}}_{\mathit{A}\mathit{B}\mathit{B}\mathit{D}}(\mathit{\theta })$
1	3.77457	2.85636	12	0.02621	0.01984
2	0.94364	0.71409	13	0.02234	0.01690
3	0.41940	0.31737	14	0.01926	0.01457
4	0.23591	0.17852	15	0.01678	0.01270
5	0.15098	0.11425	16	0.01474	0.01116
6	0.10485	0.07934	17	0.01306	0.00988
7	0.07703	0.05829	18	0.01165	0.00882
8	0.05898	0.04463	19	0.01046	0.00791
9	0.04660	0.03526	20	0.00944	0.00714
10	0.03775	0.02856	21	0.00856	0.00648
11	0.03120	0.02361	22	0.00780	0.00590

Table 3 reveals that the values decrease as the distribution’s parameter values rise, and they eventually approach zero for high parameter values.

According to information theory, a random variable’s entropy measures the average amount of uncertainty, information, or surprise that could result from its potential outcomes. From Equation (10), the Rényi entropies of the LBBD and ABBD, respectively, are obtained using the following:

$$H_{\alpha }\left(X_{LBBD}\right)=\frac{1}{1-\alpha }\log \left[{\left(\frac{36}{5{\theta }^2}\right)}^{\alpha }{\displaystyle \sum _{j=0}^{\alpha }\alpha !{(-1)}^{\alpha +j}\left(\begin{array}{c}\alpha \\ j\end{array}\right)\hspace{0.17em}\hspace{0.17em}{\left(\frac{3\alpha -j}{\theta }\right)}^{-\left(\alpha +1\right)}}\right],$$

$$H_{\alpha }\left(X_{ABBD}\right)=\frac{1}{1-\alpha }\log \left[{\left(\frac{108}{19{\theta }^3}\right)}^{\alpha }{\displaystyle \sum _{j=0}^{\alpha }(2\alpha )!{(-1)}^{\alpha +j}\left(\begin{array}{c}\alpha \\ j\end{array}\right){\left(\frac{3\alpha -j}{\theta }\right)}^{-\left(2\alpha +1\right)}}\right].$$

Table 4 presents the values of the suggested Rényi entropies of the distributions. It is evident that when the values of $\alpha$ for $\theta =3.8$ increase, the Rényi entropies values decrease. Also, for fixed $\alpha$, the Rényi entropies values of $\theta =3$ are less than their counterparts when $\theta =8$.

Table 4. $H_{\alpha }\left(X_{ABBD}\right)$ values with $\theta =3.8$ for some values of $\alpha$.

	$\mathit{\theta }=3$		$\mathit{\theta }=8$
$\mathit{\alpha }$	LBBD	ABBD	LBBD	ABBD
2	1.91705	2.1183	2.89788	3.09913
3	1.83624	2.03994	2.81706	3.02077
4	1.78815	1.99309	2.76898	2.97392
5	1.75559	1.96127	2.73642	2.94210
6	1.73178	1.93796	2.71261	2.91879
7	1.71348	1.92001	2.69431	2.90083
8	1.69888	1.90568	2.67971	2.88651
9	1.68693	1.89392	2.66776	2.87475
10	1.67692	1.88408	2.65775	2.86491
11	1.66840	1.87570	2.64923	2.85653
12	1.66104	1.86845	2.64187	2.84928
13	1.65462	1.86212	2.63545	2.84295
14	1.64895	1.85654	2.62978	2.83737
15	1.64390	1.85156	2.62473	2.83239
16	1.63938	1.84710	2.62021	2.82793
17	1.63530	1.84308	2.61613	2.82390
18	1.63160	1.83942	2.61243	2.82025
19	1.62822	1.83608	2.60905	2.81691
20	1.62512	1.83302	2.60595	2.81385
21	1.62227	1.83021	2.60310	2.81104

3.5. Order Statistics

In statistical theory, order statistics are essential, especially in the idea of extreme value. Consider a random sample $X_1,$ $X_2, \dots ,$ $X_m$ of size m selected from $f(x)$ with $F(x).$ Let $X_{(1:m)},$ $X_{(2:m)},\dots ,X_{(m:m)}$ be the corresponding order statistics of the sample. The jth order statistics pdf is defined as follows:

$$f_{(j:m)}(x)=\frac{m!}{(j-1)!(m-j)!}\times {\left[F(x)\right]}^{j-1}{\left[1-F(x)\right]}^{m-j}f(x), \mathrm{for}j=1,2,\dots ,m.$$

(15)

For simplicity, we use ${\left[1-F(x)\right]}^{m-j}={\displaystyle \sum _{a=0}^{\infty }\left(\begin{array}{c}m-j\\ a\end{array}\right)}{(-1)}^a{[F(x)]}^a$. Now, Equation (15) will be

$$f_{(j:m)}(x)=\frac{m!}{(j-1)!(m-j)!}f(x){\displaystyle \sum _{a=0}^{\infty }\left(\begin{array}{c}m-j\\ a\end{array}\right)}{(-1)}^a{[F(x)]}^{a+j-1}.$$

Therefore, the pdf for the LBBD and ABBD jth order statistics, respectively, are obtained using

$$\begin{array}{ll}{f}_{LBBD(j:m)}(x;\theta )& =\frac{m!}{(j-1)!(m-j)!}\frac{36}{5\hspace{0.17em}{\theta }^2}x\left(1-{\mathrm{e}}^{-\frac{x}{\theta }}\right){\mathrm{e}}^{-\frac{2x}{\theta }}{\displaystyle \sum _{a=0}^{\infty }\left(\begin{array}{c}m-j\\ a\end{array}\right)}{(-1)}^a\\ & \times {\left[1-\frac{9}{5\theta }{\mathrm{e}}^{-\frac{2x}{\theta }}\left(2x+\theta \right)-4{\mathrm{e}}^{-\frac{3x}{\theta }}\left(3x+\theta \right)\right]}^{a+j-1},\end{array}$$

(16)

and

$$\begin{array}{ll}{f}_{ABBD(j:m)}(x;\theta )& =\frac{108\hspace{0.17em}m!}{19\hspace{0.17em}{\theta }^3(j-1)!(m-j)!}{x}^2{e}^{-\frac{2x}{\theta }}\left(1-e^{-\frac{x}{\theta }}\right){\displaystyle \sum _{a=0}^{\infty }\left(\begin{array}{c}m-j\\ a\end{array}\right)}{(-1)}^a\\ & \times {\left[1-\frac{27}{19\hspace{0.17em}{\theta }^2}{e}^{-\frac{2x}{\theta }}\left({\theta }^2+2x^2+2\theta x\right)+\frac{4}{19}{e}^{-\frac{3x}{\theta }}\left(\frac{9x^2}{{\theta }^2}+\frac{6x}{\theta }+2\right)\right]}^{a+j-1}.\end{array}$$

(17)

For $j=1,m$ in Equations (16) and (17), for both LBBD and ABBD, respectively, we can obtain the pdfs of the minimum (min) and maximum (max) order statistics. Figure 9 shows three-dimensional plots of the pdf of the min and max order statistics of the ABBD and LBBD when $m=7$.

Figure 9. Three-dimensional plots of the minimum and maximum order statistics pdfs of the ABBD and LBBD for m = 7.

4. Applications to Real Data

In this section, we demonstrate the applicability of the proposed ABBD and LBBD distributions using two real data sets.

The first data consists of thirty consecutive measurements of March precipitation (in inches) throughout a 30-year period in Minneapolis. The data set values are 0.32, 0.47, 0.52, 0.59, 0.77, 0.81, 0.81, 0.9, 0.96, 1.18, 1.20, 1.20, 1.31, 1.35, 1.43, 1.51, 1.62, 1.74, 1.87, 1.89, 1.95, 2.05, 2.10, 2.20, 2.48, 2.81, 3.0, 3.09, 3.37, and 4.75. The same data are considered by [21,22].

The second one consists the survival times (in months) of 20 acute myeloid leukemia patients discussed by [23], and the observations are 2.226, 2.113, 3.631, 2.473, 2.720, 2.050, 2.061, 3.915, 0.871, 1.548, 2.746, 1.972, 2.265, 1.200, 2.967, 2.808, 1.079, 2.353, 0.726, and 1.958.

The descriptive statistics for both data sets are presented in Table 5, and it is clear that both data sets are skewed to the right. The density, histogram, box and total time on test (TTT) plots for both data sets are shown in Figure 10. The P-P plots of the fitted distributions for the both data sets are displayed in Figure 11. The estimated pdfs of the suggested and competitive distributions are shown in Figure 12.

Table 5. Descriptive statistics of the data sets.

Data	n	Mean	SD	Median	Min	Max	Range	Skew	Kurtosis	SE
Set 1	30	1.68	1	1.47	0.32	4.75	4.43	1.03	0.93	0.18
Set 2	20	2.18	0.84	2.17	0.73	3.92	3.19	0.11	−0.57	0.19

Figure 10. The density, TTT, box and histogram plots for first (green) and second (blue) data sets.

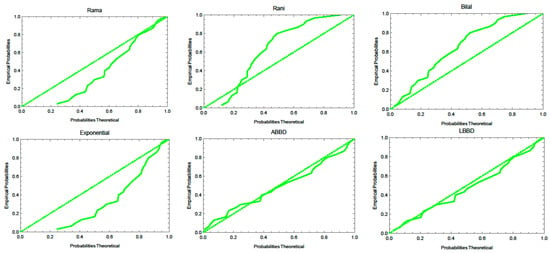
Figure 11. The P-P plots of the fitted distributions for the first (green) and second (blue) data sets.

Figure 12. The estimated pdfs of the competitive distributions for the first (green) and second (blue) data sets.

Since the proposed distributions in this study have just one parameter, we compared them to certain existing distributions that likewise have just one parameter for a fair comparison.

In order to explain how adaptable LBBD and ABBD are, we are going to evaluate them in contrast to a variety of well-recognized models, including Rani ([24]), Exponential, Rama ([25]) and Bilal distributions with pdfs, which are respectively expressed as follows:

o

$f(x;\theta )=\frac{{\theta }^5}{{\theta }^5+24}\left(\theta +x^4\right){\mathrm{e}}^{-\theta x},x>0,\theta >0,$

o

$f\left(x;\theta \right)=\theta e^{-\theta x},x\ge 0,\theta >0,$

o

$f\left(x;\theta \right)=\frac{{\theta }^4}{{\theta }^3+6}\left(1+x^3\right)e^{-\theta x},x>0,\theta >0,$

o

$f(x;\theta )=\frac{6}{\theta }\left(1-{\mathrm{e}}^{-\frac{x}{\theta }}\right){\mathrm{e}}^{-\frac{2x}{\theta }},x\ge 0,\theta >0.$

We used the maximum likelihood method to estimate these distributions parameters and fit them to the data sets. To compare the results, we used the negative maximized log-likelihood values ($\mathcal{l}$), the Hannan–Quinn information criterion (HQIC), the Bayesian information criterion (BIC), the Akaike information criterion (AIC), and the Consistent Akaike information criterion (CAIC) defined as $\mathrm{AIC}=-2\mathcal{l}+2\kappa$, $\mathrm{CAIC}=-2\mathcal{l}+\frac{2\kappa \hspace{0.17em}n}{n-\kappa -1}$, $\mathrm{BIC}=-2\mathcal{l}+\kappa \hspace{0.17em}\ln (n)$, $\mathrm{HQIC}=2\kappa \ln \left(\ln (n)\right)-2\mathcal{l}$, where n is the sample size and $\kappa$ is the number of parameters. The results are displayed in Table 6 and the best model is indicated by lower AIC, BIC, CAIC, HQIC values for goodness of statistics. For the first data set, the LBBD fits the data better than other distributions and similarly, the ABBD fits the second data set due to the lowest values of these measures. Therefore, both suggested models are considered as best fitted models as compared to the competitors considered in this study. These results are supported by Figure 10, Figure 11 and Figure 12 where it is seen that the proposed models fit both data sets well.

Table 6. The AIC, CAIC, BIC, HQIC, and K-S values for the data sets.

Data	Measures	Model
		ABBD	LBBD	Rama	Exp	Rani	Bilal
Data Set 1	AIC	79.361	78.183	90.880	92.949	96.997	80.734
	CAIC	79.504	78.326	91.023	93.092	97.140	80.877
	BIC	80.762	79.584	92.281	94.350	98.398	82.136
	HQIC	79.810	78.632	91.328	93.397	97.445	81.183
	Erro	0.092	0.143	0.134	0.109	0.111	0.265
	MML	38.681	38.091	44.440	45.474	47.499	39.367
	MLE	0.976	1.322	1.634	0.597	1.833	2.019
Data Set 2	AIC	53.648	56.329	64.411	73.248	66.567	61.55
	CAIC	53.870	56.552	64.633	73.470	66.789	61.774
	BIC	54.644	57.325	65.407	74.244	67.562	62.548
	HQIC	53.842	56.524	64.605	73.443	66.761	61.746
	Erro	0.148	0.229	0.140	0.102	0.122	0.4247
	MML	25.824	27.165	31.206	35.624	32.283	29.776
	MLE	1.283	1.737	1.403	0.458	1.630	2.645

5. Conclusions

In this study, size-biased Bilal distribution is suggested as a modification of the base Bilal distribution. Two special cases of the SBBD are derived, LBBD and ABBD. The survival function, hazard function, reversed hazard rate function, odds function, and cumulative hazard function of the LBBD and ABBD are obtained. Further statistical features include moments, incomplete moments, moment generating function, and the rth moment. Fisher’s information and entropies, order statistics and harmonic mean are presented. Also, the method of moments and the maximum likelihood estimation methods are used for estimating the unknown distributions parameters. Finally, using two real data sets, the suggested model’s applicability is demonstrated. According to the findings in this study, the ABBD and LBBD models may be deemed as competitive models with superior capacity than the other models studied in this paper. As expected, the new distributions are probable to garner interest from academics in other fields. In the future, the ranked set sampling techniques can be used to estimate the distribution parameters (see [26]).