Applications of Convolutional Neural Networks to Extracting Oracle Bone Inscriptions from Three-Dimensional Models

Abstract

In recent years, high-fidelity three-dimensional (3D) oracle bone models (3D-OBMs) have received extensive attention from oracle bone experts due to their unparalleled reducibility to real oracle bone. In the research process of 3D-OBMs, the first procedure is to extract oracle bone inscriptions (OBIs) from the model to form individual oracle bone characters (OBCs). However, the manual extraction of OBIs is a time-consuming and labor-intensive task that relies heavily on oracle bone knowledge. To address these problems, we propose a texture-mapping-based OBI extractor (tm-OBIE), which leverages the symmetrical characteristics of the texture mapping process and is able to extract 3D-OBIs from 3D-OBMs saved as a wavefront file. The OBIs in the texture file were first located using a trained 2D object detector. After that, the 3D mesh area, where the OBIs are located, was obtained using an inverse texture mapping method. Thirdly, a specific 2D plane was fitted using the centroid of triangular faces in the flat regions of the mesh via a singular value decomposition (SVD) method. Finally, by measuring the distances between the triangle meshes and the fitted plane, the meshes of the 3D-OBIs were obtained. This paper verifies the feasibility of this method via experiments and analyzes the possibility of using the algorithm framework for extracting other ancient characters from their corresponding 3D models.

1. Introduction

OBIs are defined as ancient Chinese characters engraved on the shells and bones in the Shang Dynasty more than 3000 years ago. As the earliest systematic Chinese language materials discovered so far, OBIs are hugely valuable to research. In recent years, OBI interpretation and oracle bone rejoining have served as two important research directions in oracle bone science [1].

The purpose of OBI interpretation is to interpret the meaning of OBCs that have not yet been recognized. One of the current mainstream ideas for OBI interpretation is finding the corresponding OBCs from modern Chinese characters through “the line of evolution of Chinese character”, as shown in Figure 1.

Figure 1. The evolution of a Chinese character, this figure presents an evolutionary path of a specific Chinese character(which means “its” in English).

Figure 1 shows how a Chinese character has evolved from the oracle bone age to modern times; the leftmost character is part of an OBI, while the rightmost character is a modern Chinese character. During the process, point features were retrieved, which can be seen in Figure 2. Although these characters exist in different historical periods, they follow similar evolutionary laws in strokes and structures. If the OBC in a certain evolution line is vacant and characters in other periods are relatively complete, the writing form of this character might be deduced through the law of evolution, which would lead to the interpretation of the specific OBC. Recently, progress has been made in the evolution of ancient Chinese characters based on generative adversarial network (GAN) [2].

Figure 2. The process of extracting oracle bone characters using a computer.

The process of oracle bone rejoining is finding oracle fragments that belong to one entity. Figure 3a shows two successfully rejoined oracle bones. Since the rejoining process requires frequent comparisons of edge features and OBC features, it is laborious and time-consuming work. Computer-aided oracle bone rejoining involves using a program to automatically extract and analyze the features of oracle bones. It can be used to present a small number of potentially matchable pairs to users via the comparison of OBC and edge eigenvalues to reduce the burden on users [3]. Figure 3b presents a computer-aided successfully rejoined pattern of two oracle bones. Since the same ancient inscriber tends to have unique eigenvalues for OBCs, experts usually judge whether the OBCs in two oracle bones are carved by the same inscriber, so as to indirectly judge whether or not the two oracle bones can be rejoined.

Figure 3. Example of successfully rejoined oracle bones. (a) A set of rejoined bones. (b) A set of computer-aided rejoined bones.

Thus far, computer-aided OBI interpretation or oracle bone rejoining has relied on digital replicas of real oracle bones; an example of the two-dimensional images can be seen in Figure 4a. In the process of collecting two-dimensional images of oracle bones, it is difficult for amateur collectors to strictly follow collection standards in order to obtain images with consistent specifications. However, inconsistent image specifications can lead to inconsistent object scales, making it difficult to directly utilize these images even if a unified scale reference is added during the collection process. Moreover, in two-dimensional images, the front and sides of the oracle bones tend to overlap with each other, and the OBCs are distorted due to the shooting angle. In the upper left corner of Figure 4a, the front and sides of the oracle bone overlap, which results in a blurred fracture surface. In contrast, in Figure 4b, the 3D model of the identical oracle bone, the corresponding fracture surface can be clearly depicted. Additionally, the 2D images are unable to reflect the depth features of the OBCs that are closely related to their inscribing style. Experts are able to infer the inscriber and the historical period of the characters from the inscribing style, which is essential for OBI interpretation and oracle bone rejoining.

Figure 4. The 2D images of oracle bone vs. 3D models. (a) An image of oracle bone. (b) 3D-OBM. (c) 3D-OBC Scratch with background. (d) 3D-OBC Scratch.

In recent years, the technology of high-precision 3D scanners has greatly developed. These scanners are able to acquire the real size of the object with an accuracy range of 0.08 mm. The 3D-OBMs reconstructed by the scanner provide brilliant materials for the study of oracle bone science. Aside from providing the real size of the OBIs, 3D-OBMs are also able to display the depths of the OBCs. Figure 4c shows an OBC in the 3D mesh model that is obtained from the 3D model shown in Figure 4b. The OBC in 3D mesh model provides much more detail than its corresponding 2D image, which encourages OBI interpretation and oracle bone rejoining. By analyzing the features of the stroke intersection areas acquired from the 3D model, experts are endowed with the ability to deduce the inscribing sequence of the oracle bone strokes, which helps identifying the inscriber and historical period that the OBC belongs to, thus accelerating the process of OBI interpretation. The writing styles of the OBCs in the oracle bone fragments that can be rejoined together are essentially the same, especially the width and the depth of their strokes. If the individual character mesh model can be obtained from the 3D-OBMs (as shown in Figure 4d), then the width and depth features of its strokes can be further extracted to support the oracle bone rejoining research area.

Obtaining 3D-OBCs from the 3D-OBMs is regarded as the first step towards the efficient utilization of 3D-OBMs. However, the manual extraction of 3D-OBCs requires proficiency in 3D editing software (e.g., 3Dmax) and is time-consuming and labor-intensive work. It seems that the automatic extraction of 3D-OBCs may relieve the burden on the user to some extent. Nevertheless, to the best of the authors’ knowledge, no research has focused on the process of automatically extracting 3D-OBCs, which, although simple at first glance, is actually notoriously difficult to undertake. To make it even more difficult, since the concept of 3D-OBM has just been proposed, there is not an adequate number of 3D-OBMs available for machine learning. Focusing on the automatic extraction process of 3D-OBCs, we propose the tm-OBIE, which includes 3D-OBC plane extraction based on the inverse mapping method of texture and the scratch extraction method based on the feature of the distance between the scratch and its fitting plane. The contributions of the paper are as follows.

① This is the first attempt to design an automatic 3D-OBC extractor. We analyzed the characteristics of the 3D-OBMs in detail and proposed an effective framework.

② To overcome the lack of 3D texture datasets, a transfer learning method, which utilizes the 2D images of the oracle bones to train object detector, was proposed. The detector was further used to mark the OBCs in the 3D texture images. Given the specific rectangle mark within the texture image, the inverse mapping method was used to segment the individual 3D-OBC with its corresponding adjacent surface. We conducted a thorough performance analysis of three mainstream object detectors.

③ Considering the characteristics of the curved surface where the 3D-OBC is situated, we proposed a method to extract the scratch of the 3D-OBCs. First of all, the focuses of the featured triangles near the 3D-OBC were selected using the three-neighbor method. After that, an SVD algorithm was used to fit the focusing points to form a fitting plane. Finally, the distances between the fitting plane and each triangle were calculated to obtain the scratch of the 3D-OBCs.

The rest of the paper is arranged as follows: in the second chapter, studies related to oracle bone information processing and 3D-OBC extraction are discussed. In the third chapter, the construction of dataset used in this paper is discussed, and the framework and algorithms of tm-OBIE are elaborately depicted. In the fourth chapter, comprehensive experiments to verify the availability and performance of the tm-OBIE are described. In the fifth chapter, the advantages and disadvantages, applicability, and potential application value of the algorithm are described. Finally, in the sixth chapter, a conclusion is presented, summarizing the paper and presenting future research directions.

2. Related Studies

2.1. Oracle Bone Information Processing

OBCs play a significant role in 2D-oriented computer-aided OBI interpretation and oracle bone rejoining. In OBI interpretation, object detection technology is first utilized to obtain the individual OBC. After that, OBC features are retrieved via classical methods or deep learning methods to feed into different models for further analysis. In the process of oracle bone rejoining, the first step is to obtain a single OBC from the images of different oracle bones. Then, after the feature extraction process, the inscribing style of each oracle bone is formed, and oracle bones with similar inscribing styles are regarded as potentially rejoinable oracle bones. Both of these two research directions are related to OBC detection and OBC feature extraction and analysis.

In the OBC detection period, the experts adopt object detection technology to label the characters with rectangle boxes within the 2D oracle bone images for further segmentation [4]. Thus far, two kinds of deep-learning-based object detectors have been widely used: the one-stage detector and the two-stage detector. The one-stage detector directly extracts features via a convolutional neural network (CNN) to predict target classification and location. The two-stage detector inherits and extends the one-stage detector. Before the classification and detection stage, the detector generates some preselected bounding boxes via a region proposal algorithm, and then another CNN determines the final bounding box as the predictor of certain targets. The two-stage detector is superior to the one-stage detector in theoretical and practical accuracy, which is represented by the Fast R-CNN [5], Faster R-CNN [6] and Mask R-CNN [7]. Although the one-stage detector lags behind the two-stage kind in terms of accuracy, it has a faster training convergence and detection speed. Besides, the latest one-stage detectors are becoming more and more close to the two-stage detector in terms of accuracy. The mainstream one-stage object detectors are SSD [8] and YOLO [9]. Regarding 3D-OBC extraction, one of the most important step is to obtain the location of each OBC within the 2D texture image. According to the research content, we trained three detectors which belong to Faster R-CNN, YOLO and SSD, respectively, and analyzed their performance.

In current research on OBIs, experts and scholars usually regard OBIs as a special kind of graphics, and thus the feature extraction of OBIs is borrowed from computer vision. Generally speaking, there are two kinds of feature extraction methods: the classical extraction methods and the deep-learning-based method. Classical feature extraction methods usually find feature values through a specific paradigm, during which the image is preprocessed (such as binarization and grayscale processing) to remove redundant information. Deep learning methods tend to send the original picture into the neural network, convert these features into weights, and embed them in the neural network under specific training conditions. When using classical methods to extract OBC features, different levels of features, which include region images [10] of oracle bones, graph models [11], point sets [12], and edge features of the OBCs [13], can be extracted for further analysis. The features obtained via classical methods are analyzed directly or fed into classical models for further research. In OBI interpretation, the point set is fed into complex networks to explore the evolution of OBC. Simultaneously, the OBC similarity matching problems in oracle bone rejoining are related to both classical and deep learning feature extraction methods. Although the stroke length, inflection point, stroke distance and other feature values can be obtained and directly compared using classical methods, its deeper features can only be obtained and compared using deep learning methods. The UCN [14] and NCN [15] provide methods for OBC comparison. The UCN uses deep metric learning to directly learn mapping relationships to preserve geometric and semantic similarity. The NCN method learns geometric and semantic consistency constraints between neighborhoods directly from training data. Feature extraction based on traditional methods has its own advantages and disadvantages compared with that based on deep learning. The extraction process of the former method is compatible with human logic, and the extracted feature values are highly interpretable, so they also have strong reusability. However, the shortcomings are significant; these features are usually incomprehensive and inaccurate, with a poor robustness. Although the features extracted using the latter methods are more comprehensive and robust, their features defy interpretability and reusability. At the same time, the feature extraction methods of deep learning require a large amount of training data as evidence, which further limits its usage scenarios. In a word, both approaches have their place in oracle bone research. The first problem of 3D-OBC extraction is how to represent the extracted OBIs. We have two options: the 3D-OBC with a background (Figure 4c) and without a background (Figure 4d). Referencing to the research in this section, if we want to retrieve features using a classical method, we have to eliminate the background with the 3D-OBC. Therefore, the 3D-OBC extraction without a background is more suitable in oracle research.

2.2. OBC Related 3D Segmentation and Object Detection

The purpose of mesh segmentation research is to segment a complete 3D mesh model into some disconnected parts according to certain criteria. If we are able to segment the triangular faces where the OBI is located from the rest according to semantics, then the 3D-OBC extraction problem will be solved. At present, there is a lot of research on semantic segmentation, which can be divided into classical methods and deep learning methods. Classical contour-based methods can solve the mesh segmentation problem by evolving the dividing lines between different parts of the model, which are suitable for segmenting 3D mesh models with clear boundaries between the parts to be segmented and the main part [16,17,18,19]. Since the 3D-OBMs are full of inscriptions, classical segmentation methods are unable to retrieve the OBIs from the main part. Furthermore, these segmentation methods have shortcomings that heavily rely on local seed or initial cluster center selection, when the initial conditions are not accurately determined, the segmentation effect is greatly reduced. Although deep-learning-based mesh segmentation methods [20,21,22] have made great progress in accuracy and segmentation speed, they heavily rely on training datasets. To the best of the authors’ knowledge, there is no open-source 3D data set related to oracle bones, which makes the training process impossible.

The development of 3D object detection research comes from the unremitting progress of autonomous driving technology, where the vehicles need to perceive the location and category information of the objects on the street with the help of 3D object detection technology. The autonomous driving-oriented 3D object detections tend to project the 3D models to the 2D plane, using the CNN-based 2D object detection network to acquire the approximate location and category information of the underlying objects. Finally, the precise locations of the objects are estimated using parameter regression algorithms. At first, a cylindrical projection method was used to obtain the 2D projection map. The height and distance information for the point were encoded into two channels, respectively, and a fully convolutional neural network was used to estimate the 3D bounding box of the vehicle [23]. Since then, scholars have optimized detection accuracy and speed by modifying the projection algorithm and the structure of the network. The improvements in detection speed include the introduction of a dilated convolution network to replace the fully convolutional network [24,25,26], a reference to the concept of a high-speed 2D object detector YOLO as the pre-detection part, and the introduction of a pre-pooling convolution method [27]. The improvements in detection accuracy include the introduction of multi-channel projection, the use of the Faster R-CNN detector as a pre-detector [28], and the elimination of cognitive uncertainty and occasional uncertainty in observational noise [29].

Since the texture files in the 3D-OBMs are essentially a projection of 3D to 2D, 3D object detection methods in autonomous driving have a certain reference value. However, unlike autonomous driving related methods, multiple views of a certain 3D-OBM are mapped to a single 2D image. To address this problem, the paper refers to the method in a 3D classification paper [30], in which multiple views have been projected into a cylinder and the cylinder has been unfolded to a 2D image.

3. Material and Methods

3.1. The Construction of Datasets

The paper involves two datasets, a two-dimensional oracle bone image dataset (2D Dataset) and a 3D-OBM dataset (3D Dataset). The images in the 2D dataset come from oracle collection books written by oracle experts (e.g., “Collection of oracle bone inscriptions”) and from private oracle bone collectors. We scanned the books in full page view, manually segmented the individual images, and processed them. The 2D dataset consists of 1723 images with the resolution between 1024 × 1024 and 2405 × 4277. All the OBCs within the images were manually labeled by the oracle bone experts. Figure 5 presents two labeled images within the dataset. The green rectangles indicate the existence of the OBC within this region.

Figure 5. An example of the image manually labeled by an expert. (a) Annotation of an oracle bone image from collection book. (b) Annotation of an oracle bone image from private collector.

At present, many supporting software of high-precision 3D scanners provide a 3D model output in alias wavefront format. The alias wavefront format consists of three separate files, the 3D mesh file (ends with .obj), the material and environment control file (ends with. mtl), and the 2D texture file (ends with .jpg). The first file records the backbone of the 3D model in the form of polygon mesh (typically a triangular mesh). Specifically, the file includes the set of vertices for each polygon mesh, the 3D space coordinates of each vertex, the normal vector for each polygon and the mapping information from material file to mesh. An example of the visualization of the single 3D-OBM mesh file is shown in Figure 6a. Intuitively, although the model displays the spatial features of 3D-OBM, it lacks the texture and lighting features of the object surface, which are recorded in the other two files.

Figure 6. An example of wavefront 3D-OBM. (a) 3D-OBM mesh file, (b) 3D-OBM texture file, (c) complete 3D-OBM.

The second file shows the lighting, surface material, etc. The third texture file can be viewed as a 2D image formed by mapping the surface texture of the 3D model to the 2D plane using a UV unwrapping method; an example of the texture image from 3D-OBM is shown in Figure 6b. It is worth mentioning that for the 3D-OBM, we can always find a way to map the texture of the front and back surfaces to the 2D image completely and continuously. The combination of the three files results in a complete 3D-OBM, as shown in Figure 6c.

Regarding the 3D dataset, we collected data from 50 oracle bones that are part of a private collection using an Artec3D^TM Micro scanner, and then processed the data using Artec Studio to obtain the 3D-OBMs. Some of the models can be seen in Figure 7.

Figure 7. Example of 3D-OBM within 3D dataset.

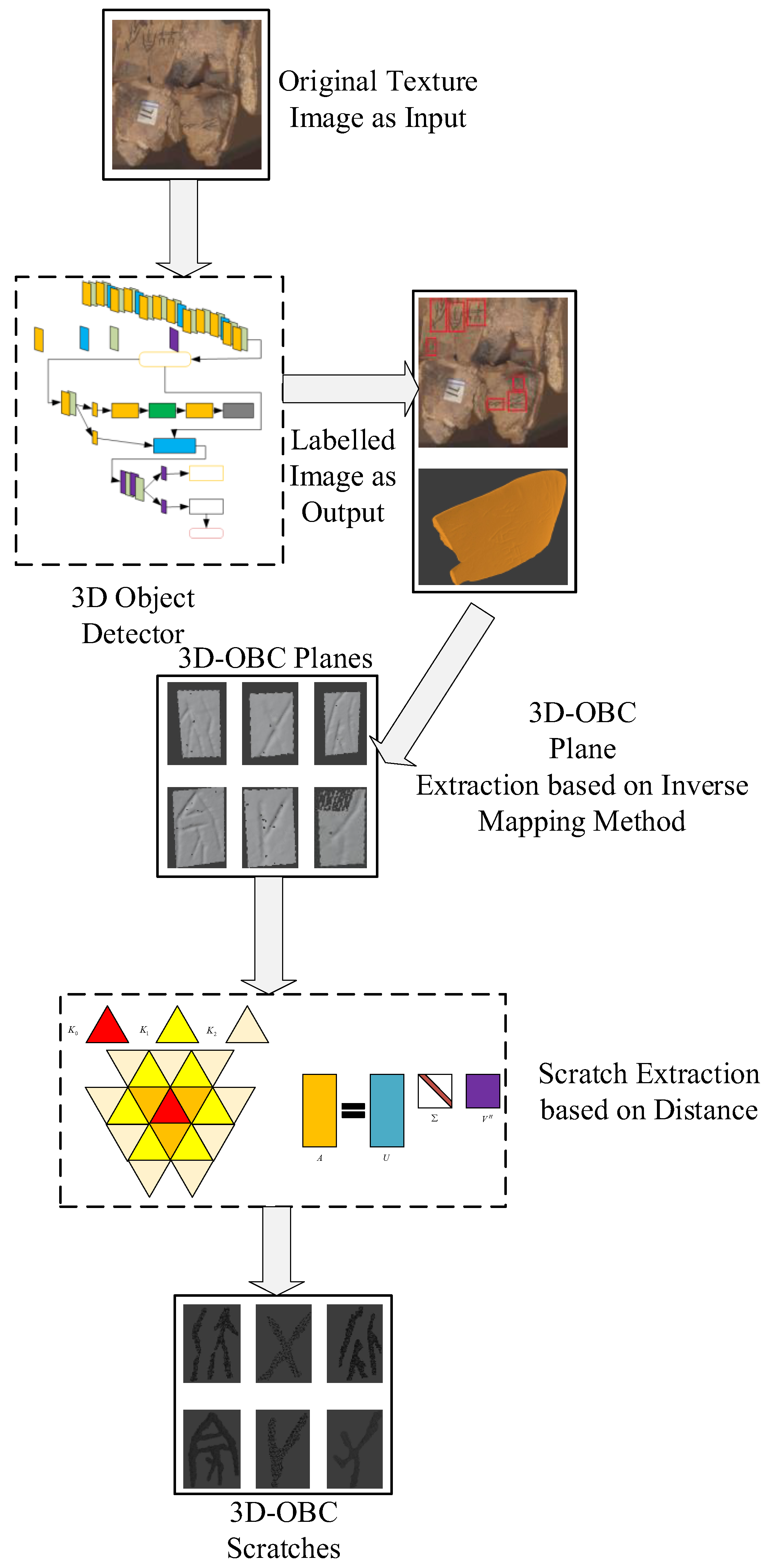
3.2. The Framework of tm-OBIE

The overall process framework of the method is shown in Figure 8. Firstly, the texture images in the wavefront 3D model file group were input into the trained 2D image detector, and the label coordinates of each OBC in the image were obtained. After that, the inverse mapping method was utilized to segment the 3D-OBM into 3D-OBC planes (the rectangle plane which contain the scratches of the OBC itself). Finally, in order to retrieve the 3D-OBIs from the planes, the weighted N-nearest neighbor normal vector variance method was used to obtain the triangular faces of the seeds. Then, a method called singular value decomposition (SVD) was used to generate a plane to fit these triangular faces. Then, the triangular faces of the 3D-OBC scratches were selected based on the distance between the plane.

Figure 8. The framework of tm-OBIE.

3.3. 3D-OBC Plane Extraction Based on Inverse Mapping Method

The texture image is an image formed by mapping the color information of the triangular surface in the 3D model to the 2D space (this process is called UV unwrapping). The supporting software of existing 3D scanners tend to coherently map the adjacent triangular faces in the 3D model to the 2D texture image. Therefore, from the 2D texture image, the location of the bounding box surrounding each OBC can be obtained via the trained two-dimensional object detector, and then the triangular surfaces of the separate OBC with backgrounds can be segmented using the texture inverse mapping method. An example of texture inverse is shown in Figure 9. In this example, the location of a 3D-OBC within its corresponding 3D-OBM can be obtained via its texture image.

Figure 9. An example of texture inverse. (a) The texture image of an 3D-OBM, (b) The corresponding 3D-OBM.

The corresponding algorithm can be seen in Algorithm 1.

Algorithm 1: The Inverse Mapping Algorithm

Input: The triangular mesh set $S$ and the two coordinates of the diagonal vertexes of the bounding box which annotates the OBC in the Texture Image denoted as $V_0\left(x_0,y_0\right)$ and $V_1\left(x_1,y_1\right)$; Output: The set $F$ containing the triangular meshes of the 3D-OBC scratches with backgrounds; 1: $F\leftarrow \varnothing$ 2: for each triangular mesh $s_i$ in set $S$ do 3:  $v_i\left(x_i,y_i\right)\leftarrow$ the focus of $s_i;$ 4:  $\mathbf{i}\mathbf{f} x_i\le \left|x_1-x_0\right|$$\mathrm{and} y_i\le \left|y_1-y_0\right|$ 5:   $\mathrm{add} s_i$ to $F$; 6:  end 7: end

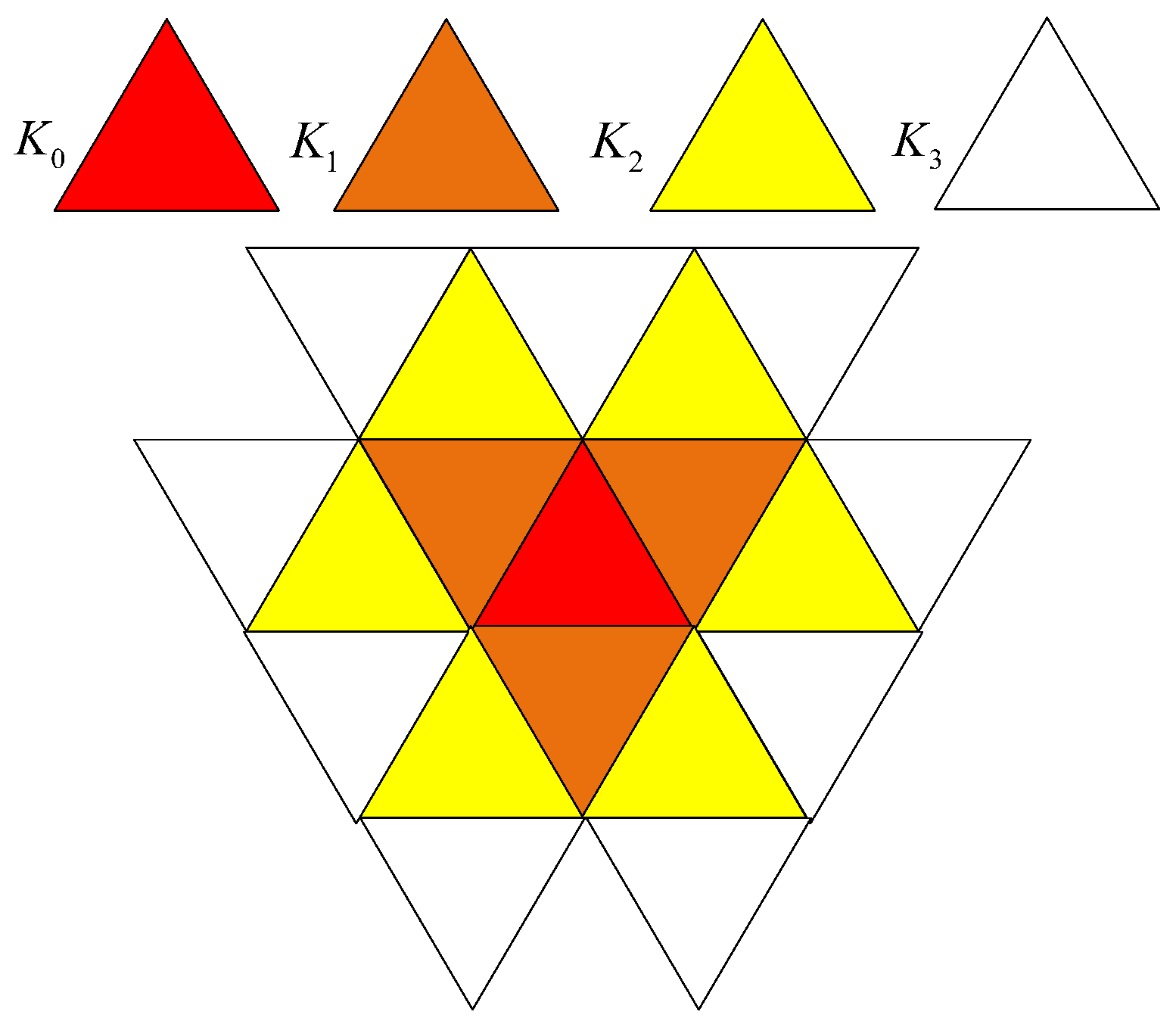
3.4. Scratch Extraction Based on Distance

The 3D-OBMs in this paper are all presented in the form of triangular meshes, and there is an adjacency relationship between the triangular meshes, as shown in Figure 10. In Figure 10, $K_0$ represents any single triangular mesh of the 3D-OBM. Any triangular mesh that shares an edge with $K_0$ is defined as its 1-neighboring meshes, which are represented by $K_1$. In this figure, the $K_1$ neighboring meshes are colored orange. The 2-neighboring meshes are defined as all the 1-neighboring meshes of $K_1$ except $K_1$ and itself, which is represented by $K_2$ and colored yellow. Likewise, the 3-neighboring meshes are defined as all the 1-neighboring meshes of their $K_2$ neighboring meshes except $K_2$, $K_1$ and itself, which is defined as $K_3$ and colored as white triangle. Define $k_n^i\left(n=1,2,3;i=1\dots N_n\right)$ as a certain triangular mesh within the $n$-neighboring mesh set of $K_0$, where $N_n$ represents the number of elements that $K_n$ contains. Define $K_n^i\left(n=1,2,3;i=1\dots N_n\right)$ as the 1-neighboring meshes of $k_n^i$ and $K_2$ and $K_3$ can be calculated using Equations (1) and (2).

$$K_2={{\displaystyle \bigcup }}_{i=1}^{N_1}{K}_1^i-K_1-K_0$$

(1)

$$K_3={{\displaystyle \bigcup }}_{i=1}^{N_2}{K}_2^i-K_2-K_1-K_0$$

(2)

Figure 10. The adjacency relationship between the triangular meshes.

Define ${\mathit{n}}_{\mathit{n}}^{\mathit{i}}$ as the normal vector of triangular mesh $k_n^i$ and ${\mathit{n}}_{\mathbf{0}}$ as the normal vector of triangular mesh $K_0$. The pose difference between the triangular face $K_0$ and its adjacent faces can be represented by $Va{r}^{{\mathit{n}}_{\mathbf{0}}}$, which can be calculated via Equation (3). It is worth noting that $\alpha$,$\beta$ and $\chi$ are hyperparameters that indicate the degree of dependence of the results on adjacent triangles regarding distance.

$$\begin{gathered} Va{r}^{{\mathit{n}}_{\mathbf{0}}}=\alpha \cdot \frac{1}{N_1}{{\displaystyle \sum }}_{i=1}^{N_1}\Vert {\mathit{n}}_{\mathbf{1}}^{\mathit{i}}-{\mathit{n}}_{\mathbf{0}}\Vert {}^2+\beta \cdot \frac{1}{N_2}{{\displaystyle \sum }}_{p=1}^{N_2}\Vert {\mathit{n}}_{\mathbf{2}}^{\mathit{p}}-{\mathit{n}}_{\mathbf{0}}\Vert {}^2+\chi \cdot \frac{1}{N_3}{{\displaystyle \sum }}_{q=1}^{N_3}\Vert {\mathit{n}}_{\mathbf{3}}^{\mathit{q}}-{\mathit{n}}_{\mathbf{0}}\Vert {}^2 \\ (0<\chi <\beta <\alpha <1 and \alpha +\beta +\chi =1) \end{gathered}$$

(3)

Triangular Mesh Fitting Method based on SVD

In the next step, we need to find a plane parallel to the plane where the OBC is located. Suppose a function describing the plane can be represented as $ax+by+cz+d=0$. Given a triangular mesh set $S^k$, define $s_i^k \left(k=1,2,\dots N_k\right)$ as any single triangular mesh of $S^k$, $N_k$ as the number of elements in $S^k$. Define ${\mathit{G}}_{\mathit{i}}^{\mathit{k}}\left(x_i^k,y_i^k,z_i^k\right)$ as the geometrical center of $s_i^k$, and the coordinate mean of ${\mathit{G}}_{\mathit{i}}^{\mathit{k}}$ can be calculated by Equation (4).

$${\mathit{G}}_{\mathbf{0}}^{\mathit{k}}\left({\overline{x}}_0^k,{\overline{y}}_0^k,{\overline{z}}_0^k\right)=\frac{1}{N_k}\left({{\displaystyle \sum }}_{i=1}^{N_k}{x}_i^k,{{\displaystyle \sum }}_{i=1}^{N_k}{y}_i^k,{{\displaystyle \sum }}_{i=1}^{N_k}{z}_i^k\right)$$

(4)

Construct matrix $\mathit{A}$ using Equation (5).

$$\mathit{A}=\left[\begin{array}{ccc}{x}_1^k-{\overline{x}}_0^k& y_1^k-{\overline{y}}_0^k& z_1^k-{\overline{z}}_0^k\\ x_2^k-{\overline{x}}_0^k& y_2^k-{\overline{y}}_0^k& z_2^k-{\overline{z}}_0^k\\ x_3^k-{\overline{x}}_0^k& y_3^k-{\overline{y}}_0^k& z_3^k-{\overline{z}}_0^k\\ \dots & \dots & \dots \\ x_{N_k}^k-{\overline{x}}_0^k& y_{N_k}^k-{\overline{y}}_0^k& z_{N_k}^k-{\overline{z}}_0^k\end{array}\right]$$

(5)

Then, perform SVD on matrix $\mathit{A}$ via Equation (6), and the parameters of the fitting plane can be calculated by Equations (7) and (8).

$$\mathit{A}=\mathit{S}\mathit{V}\mathit{D}$$

(6)

$$\left(a,b,c\right)=\left(v_{n,1},v_{n,2},v_{n,3}\right)$$

(7)

$$d=-\left(a\cdot {\overline{x}}_0^k+b\cdot {\overline{y}}_0^k+c\cdot {\overline{z}}_0^k\right)$$

(8)

The algorithm can be seen in Algorithm 2.

Algorithm 2: The Scratch Extraction Algorithm based on Distance

Input: The hyperparameters $\alpha$, $\beta$, $\chi$, $var L im$ and $d$; The discriminate set of triangular meshes corresponding to each 3D-OBC $S^k\left(k=1,2,\dots ,N_s\right)$, where $N_s$ denote the total number of 3D-OBCs; Output: The set $R^k$ containing the triangular meshes of the 3D-OBC scratches; 1: for $k\leftarrow 1$ to $N_s$ do 2:  $R^k\leftarrow \varnothing$; 3:  for each triangular mesh $s_i$ in set $S^k$ do 4:   $R\leftarrow \varnothing$; 5:   calculate $K_1$, $K_2$ and $K_3$; 6:   calculate $Va{r}^{n_n}$; 7:   if $Va{r}^{n_n}\le var L im$ then 8:    add $s_i$ to $R$; 9:    end 10:   given $R$, calculate plane $P$ using $SVD$ method; 11:   for each triangular mesh $s_i$ in set $S^k$ do 12:    calculate the distance $d_k$ between $s_i$ and $P$; 13:    if $d_k\le d$ then 14:     add $s_i$ to $R^k$ 15:    end 16:   end 17:  end 18: end

4. Experiments and Analysis

As can be seen above, the overall procedure consists of three major steps. Firstly, a trained object detector marks the region where the OBCs are located. Secondly, the rectangle regions enclosing the single OBC are extracted from a whole 3D-OBM. Thirdly, the 3D-OBCs are extracted from the rectangle regions. Using these steps, as described in this section, three experiments were conducted in order to prove the feasibility of the method.

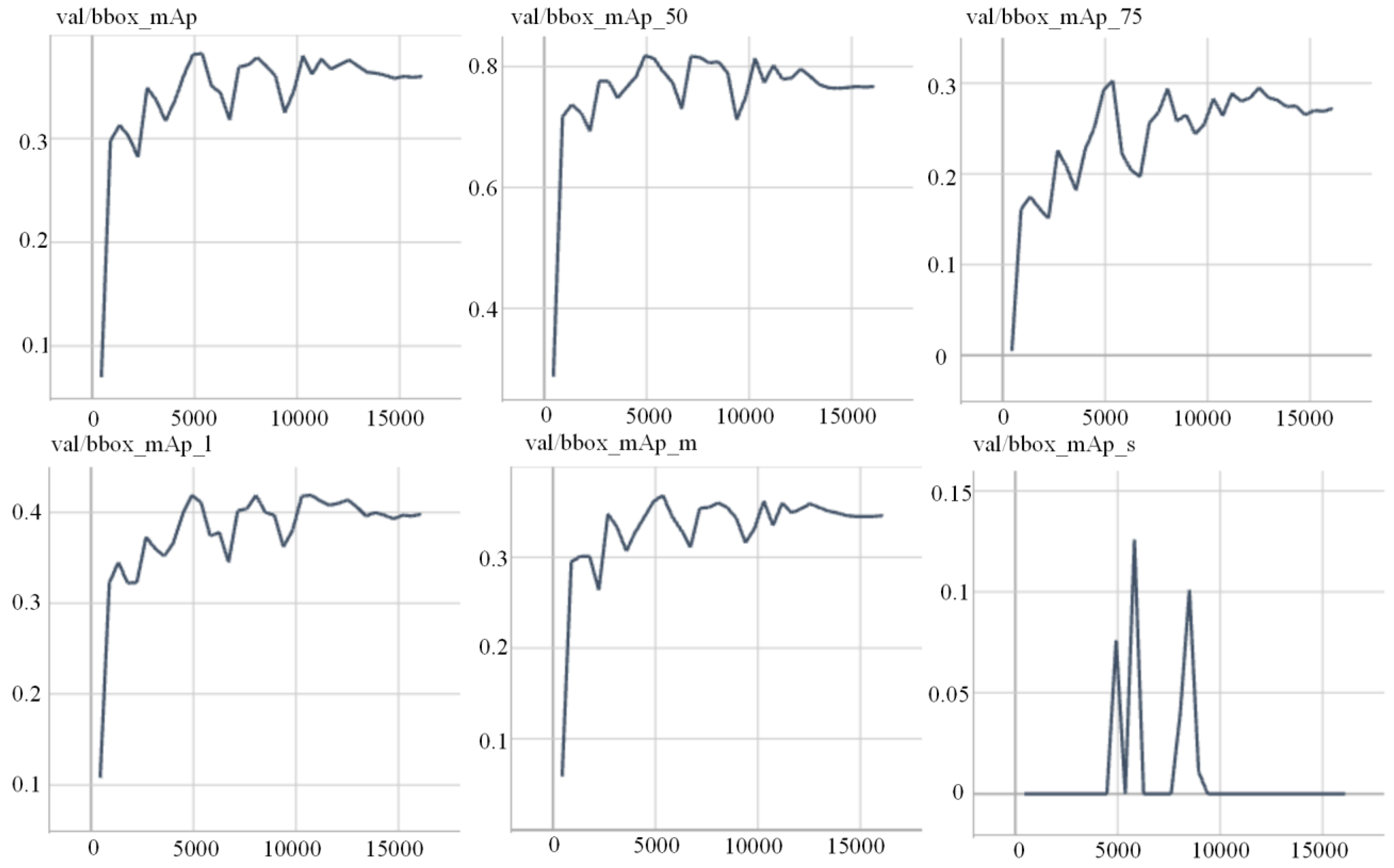
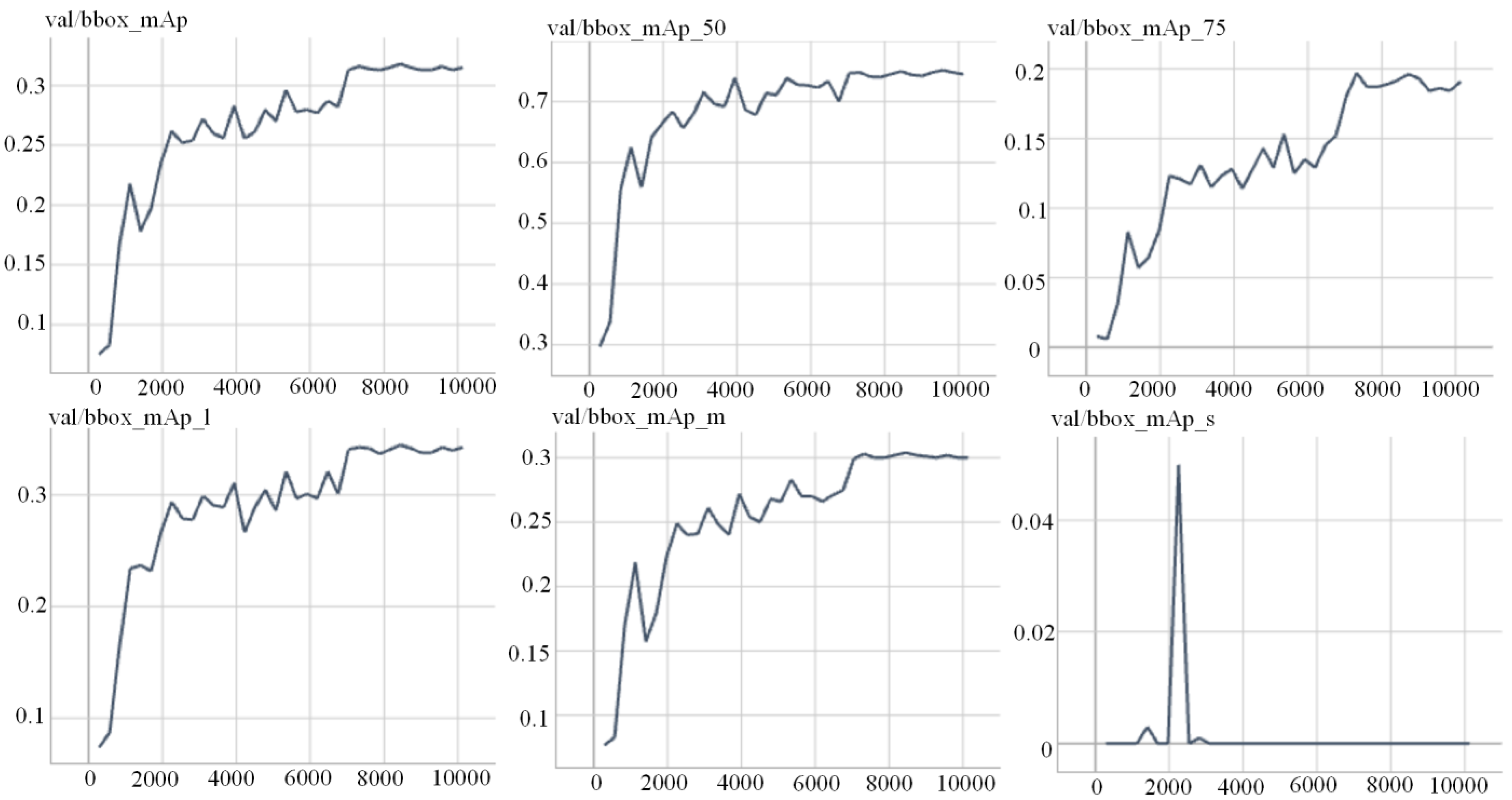
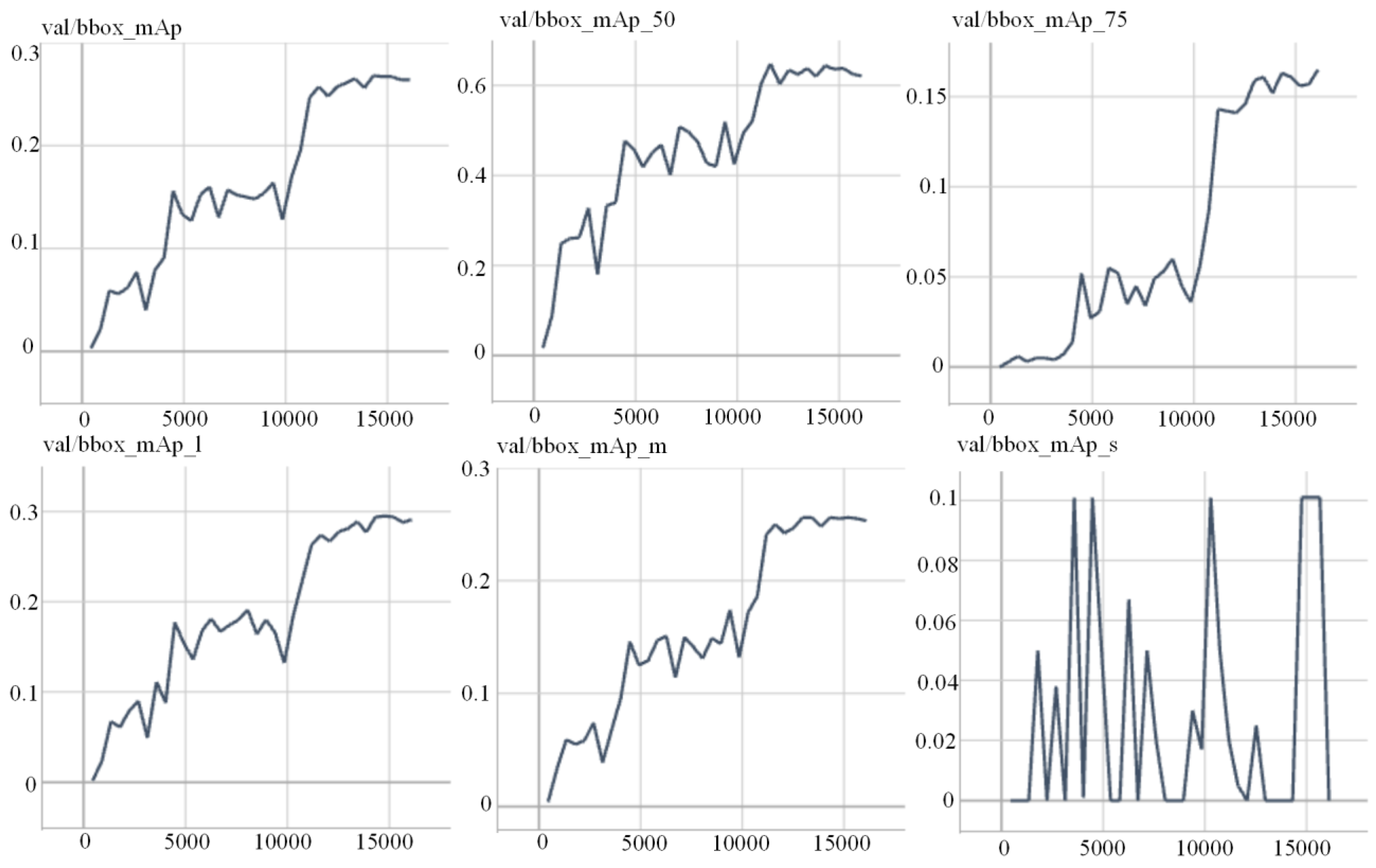
4.1. OBC Detection Experiment

In this experiment, we compared three different object detectors (YOLO v7, Faster R-CNN, SSD) to select the most suitable detector for the OBCs. In this experiment, 1723 images of the oracle bones that contain OBCs were used. All the images are from the 2D dataset mentioned above. We randomly selected 1300 images as the training set, and the remaining images (423 images) as the validation set. In this section, we describe the performance of each object detector, which is measured in average precision (AP) and mean average precision (mAP).

The software and hardware configurations of the experiment are shown in Table 1 and Table 2. Before these three models were trained, we loaded the pre-trained weights. During the training process, we went through the update process of the complete weights and no layer in the network was frozen. The Adamw optimizer, which employs a dynamic learning rate strategy, was used during the training process. Moreover, we did not use data augmentation strategy in this experiment. The main parameters can be seen in Table 3.

Table 1. Software configuration.

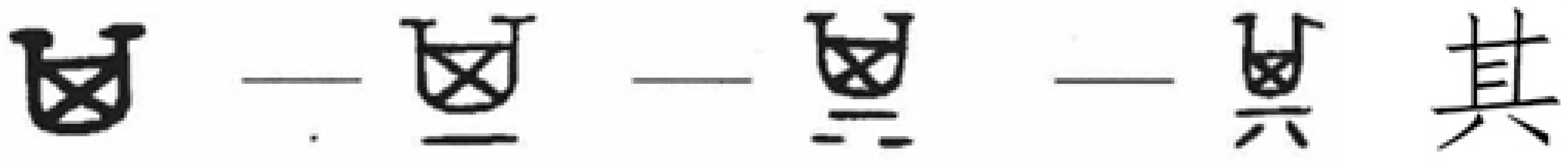
Title	Content
OS	Ubuntu v20.04
Python IDE	Pycharm v.2021.3
Framework for Deep Learning	Pytorchv1.7 & Apex & CUDA10.1 & Cudnn v8.0.5
CV Library	Open CV v.3.7

Table 2. Hardware configuration.

Title	Content
CPU	Intel(R) Xeon(R) E5-2683 v3@2.00GHz
RAM	DDR4 2133 Mhz× 4(32 GB in total)
Graphic Cards	Nvidia(R) RTX 3090× 4(each with 24 GB vram)
Hard Disk	Intel(R) SSDSC2KW512G8(512 GB)

Table 3. Main training parameters.

Name	Batch Size	Learn Rate (Initial)	Weight Decay
Faster R-CNN	8	10−4	5 × 10−2
SSD	16	10−4	5 × 10−2
YOLO v7	8	10−4	5 × 10−2

In Figure 11, Figure 12 and Figure 13, the horizontal axis represents the number of steps. Each batch processing during the training process is equivalent to executing one step. When the performance indicator (mAp) stabilized, the training process ceased. Note that the number of steps in the three experiments was not completely consistent, and SSD training has the least number of steps. According to the indexes, all of the three object detectors are eligible for coordinating the OBCs in the texture image. Additionally, Faster R-CNN performs better than the other detectors.

Figure 11. The main performance of Faster R-CNN.

Figure 12. The main performance of SSD.

Figure 13. The main performance of YOLO v7.

4.2. Inverse Mapping Experiment

This experiment aimed to verify Algorithm 1, inverse mapping algorithm. In this experiment, we used the best performing Faster R-CNN detector to obtain each coordination of OBC within the texture image and slice the 3D-OBMs into triangular meshes. Simultaneously, we manually extracted the rectangular area where the OBCs were located in the 3D-OBM, forming a ground-truth sample. The number of ground-truth samples is 298. All of the 50 3D-OBMs involved in this experiment are from the previously mentioned 3D dataset. Then, we compared these samples using the IoU (Intersection over Union) index, namely the number of the triangular tablets from the intersection of the samples (the ground truth and that obtained using Algorithm 1) divided by the number of the triangular tablets from the union of the samples.

The angle of the 3D-OBM can be seen in Figure 14a, and the whole texture can be seen in Figure 14b. In this experiment, the object detector is directly used in the texture file to find the coordinate information of a single OBC in the form of a bounding box; an example can be seen in Figure 15. In Figure 15, each of the red rectangle boxes corresponds to an OBC.

Figure 14. An example of the 3D-OBM and its texture file. (a) Complete model; (b) texture file.

Figure 15. An example of the OBC detecting effect.

Figure 16 shows an example of processed 3D-OBCs. Figure 16a–c show an example of the OBC from the texture file, Figure 16d–f are their corresponding ground truths and OBCs obtained using Algorithm 1. The left side of Figure 16d–f are ground truths, and the right side are OBCs obtained using Algorithm 1.

Figure 16. An example of processed 3D-OBCs, (a–c) present three OBCs which are extracted from texture images, (d–f) present corresponding ground truths and OBCs obtained using our methods.

Regarding the performance index IoU, the values range from 0.75 to 0.99, with the mean value being 0.89. From the actual effect, this algorithm can also meet usage needs.

4.3. Scratch Extraction Experiment

In the previous experiment, we were able to obtain a single 3D-OBC with a rectangle plane. However, this model may not be sufficient for our research. We need to extract the OBC scratch from the plane using Algorithm 2. In this experiment, by using the ground-truth samples in the inverse mapping experiment, we manually extracted the scratches from the 3D-OBC planes to form a ground-truth sample and compared this sample with those obtained using Algorithm 2. The number of ground-truth samples is 298. In this experiment, distance played a vital role. Figure 16 shows the impact of different values on the extraction results.

In Figure 17a, the value of d is too large, resulting in the preservation of the triangular surfaces beyond the OBC scratch. On the contrary, in Figure 17b, the value of d is too small, resulting in the absence of triangular surfaces within the OBC scratch. Moreover, the value of d is suitable in Figure 17c. Generally speaking, the value of d is a hyperparameter that should be adjusted during the experiment; the values may vary from 3.0 to 3.1. The process of solving the optimal value of d requires repeated iteration and refinement. For the same batch of unearthed oracle bones, once we find the optimal value for a certain OBC, this value is also applicable to the extraction process of all other OBCs. As shown in Figure 18a–c, ground-truth scratches were situated on the left side and the corresponding obtained scratches were situated on the right side, according to Algorithm 2. In this experiment, we still used the IoU index to measure the performance just as in experiment 4.2. The value of IoU in this experiment ranges from 0.51 to 0.95, with the mean value being 0.78.

Figure 17. The obtained scratches with different values: (a) d = 3.01, (b) d = 3.03, (c) d = 3.02.

Figure 18. Examples of obtained scratches, in (a–c), ground-truth scratches are in the left and obtained scratches are in the right.

5. Discussion

On the basis of experimental analysis, assuming that we already have high-precision 3D-OBMs, the key factors determining the final scratch extraction effect include the performance of the 2D object detector, the geometric shape of the oracle bone tablets and the density of the 3D-OBCs. Figure 19 provides some examples in which the object detectors failed to function properly, thus resulting in scratch extraction failure in the following process.

Figure 19. Example of the poor performance OBC detection, (a) detection omission and multiple bounding boxes within a single OBC, (b) bounding box overlap, (c) partial detection.

In the upper half of Figure 19a, the 2D object detectors are annotated in two bounding boxes within one OBC. This phenomenon is related to the IoU training parameters of a specific object detector. Regarding certain object detectors, a suitable parameter will eventually be found after numerous experiments, eliminating this phenomenon. In the lower part of Figure 19a, the object detector just misses the OBC. This situation is usually caused by insufficient training samples for the object detector, and increasing the numbers of training samples and training epochs is helpful for solving this problem. In Figure 19b, the boxes of the adjacent OBCs overlap, and this means that the scratch extraction failed in the process that followed. Since this phenomenon is caused by the overly dense inscribing style of some OBCs, we are unable to eliminate this phenomenon by improving the algorithms. In Figure 19c, only part of the OBC is detected and bound with a box. This phenomenon is related to image and OBC size, occurring when the OBC size significantly differs from that in the training dataset, and can be improved during training process with data augmentation method.

However, in the experiment, we found some samples that were not suitable for scratch extraction. Since our method assumes that the OBCs exist in a flat or approximately flat plane (this assumption is reasonable since the OBCs are small in size), when the plane containing OBCs clearly appears uneven, our method cannot be effective. Figure 20 provides an example of a narrow and curved 3D-OBM, and we were unable to extract any OBC scratch within this model. Fortunately, most of the oracle bone tablets appear flat.

Figure 20. The example of an 3D-OBM that defies scratch extraction.

The tm-OBIE method has the advantage that the rotation of the 3D model does not affect the results. Since the core idea of the algorithm is to segment the rectangular area containing OBC via an inverse mapping method. The texture file is created upon the construction of 3D-OBM and will not change with the rotation of the model itself. In addition to retrieving the OBCs, our method also inspires the extraction of other engraved characters. Engraved characteristics such as inscriptions on gold in ancient China and steel often have a large number of photos as research materials. When experts try to perform a character extraction on 3D models of such materials containing these characters, they may refer to our method.

6. Conclusions

The paper proposes an algorithm framework for extracting scratches from 3D-OBMs. The experiment focuses on analyzing the applicability of the algorithm and verifying its feasibility. At the same time, the algorithm framework also provides inspiration for the extraction of other ancient characters, such as the ancient Chinese inscriptions on gold. Regarding the shortcomings of the algorithm framework, our team focused on solving the extraction of densely inscribed OBCs and OBCs inscribed on non-planar plane, in order to contribute to the research directions in oracle sciences, such as interpretation and oracle bone conjugation.