Complex-Variable Dynamic System of Layla and Majnun Model with Analytic Solutions

Abstract

A complex Layla and Majnun model system (CLMMS) is suggested in this study for a complex variable in the open-unit disk. Analytic solutions are discovered by using a technique of bounded turning functions. The set of necessary conditions is illustrated involving some special cases.

1. Introduction

Complex variables are crucial when studying dynamic systems. Complex variables offer a potent mathematical foundation for evaluating and comprehending the actions and outcomes of dynamic systems, which are systems which shift over time. Complex variables are frequently employed for displaying signals or functions that change over time in the context of dynamic systems. Complex numbers can be represented in the form $\zeta =\chi +i\eta ,$ where $\chi$ and $\eta$ are real numbers and i is the imaginary unit, and they have both real and imaginary components. We may explain dynamic characteristics using both amplitude (the real component) and phase (the imaginary part) information using this approach. One of the most important complex variable dynamic systems is the Layla and Majnun model describing the intensity or strength over time of the love between Layla and Majnun (see [1,2,3,4]).

Layla and Majnun’s romantic ties have been addressed in a mathematical model of a complex variable. The most basic description of the nonlinear system with two complex variables is given as follows [1,2,3,4]:

$$\begin{array}{c}\hfill {\displaystyle \frac{d\Omega }{d\chi }}={\varrho }_1\Omega \left(\chi \right)+{\Lambda }^2\left(\chi \right)+{\varsigma }_1\\ \hfill {\displaystyle \frac{d\Lambda }{d\chi }}={\varrho }_2\Lambda \left(\chi \right)+{\Omega }^2\left(\chi \right)+{\varsigma }_2,\end{array}$$

(1)

where $\Omega$ and $\Lambda$ indicate a falling out between them, while ${\varrho }_1,{\varrho }_2$ and ${\varsigma }_1,{\varsigma }_2$ are the connection constants of the system satisfying ${\varrho }_1<0,{\varrho }_2<0,{\varsigma }_1>0$ (everyone admits sympathy for Majnun) and ${\varsigma }_2<0$. By using the Caputo fractional-order derivative, System (1) is presented as a complex system (four-dimensional real system of fractional differential equations) by many researchers. Figure 1 shows the behavior of the solutions of System (1), while Figure 2 shows the distribution of the critical points of the system where ${\varrho }_1=1,{\varrho }_2=1$ and different values of $({\varsigma }_1,{\varsigma }_2).$ For example, the system does not have critical points in cases (c) and (f). And it admits double critical points for (a): (1, 0) and (1.2, 0.453); (b): (−0.474, 0.725) and (1.395, 0.946); (d): (0.741, −0.7) and (1.545, 1.138); (e): (1.188, 0.662) and (0.773, −0.152).

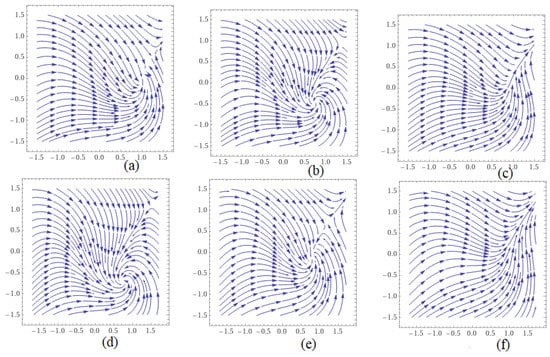
Figure 1. Integral curves for System (1) for fixed value ${\varrho }_1=1,{\varrho }_2=1$ (equally feeling in love) and different values of ${\varsigma }_1,{\varsigma }_2,$ where (a) $:({\varsigma }_1,{\varsigma }_2)=(1,-1)$, (b) $:({\varsigma }_1,{\varsigma }_2)=(0.5,-1)$, (c) $:({\varsigma }_1,{\varsigma }_2)=(1,-0.5)$, (d) $:({\varsigma }_1,{\varsigma }_2)=(0.25,-1.25)$, (e) $:({\varsigma }_1,{\varsigma }_2)=(0.75,-0.75)$ and (f) $:({\varsigma }_1,{\varsigma }_2)=(1.25,-0.25)$.

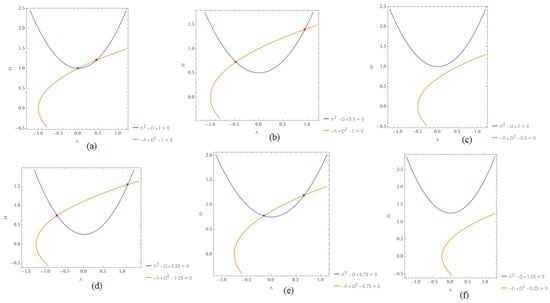
Figure 2. The distribution of the critical points of System (1) for fixed value ${\varrho }_1=1,{\varrho }_2=1$ and different values of ${\varsigma }_1,{\varsigma }_2,$ where (a)$:({\varsigma }_1,{\varsigma }_2)=(1,-1),$ (b) $:({\varsigma }_1,{\varsigma }_2)=(0.5,-1),$ (c) $:({\varsigma }_1,{\varsigma }_2)=(1,-0.5)$, (d) $:({\varsigma }_1,{\varsigma }_2)=(0.25,-1.25),$ (e) $:({\varsigma }_1,{\varsigma }_2)=(0.75,-0.75)$ and (f) $:({\varsigma }_1,{\varsigma }_2)=(1.25,-0.25)$.

For complex value functions $\Omega ={\Omega }_r+i{\Omega }_j$ and $\Lambda ={\Lambda }_r+i{\Lambda }_j,$ the complex system corresponding to (1) becomes:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d{\Omega }_r}{d\chi }}={\varrho }_1{\Omega }_r\left(\chi \right)-{\Lambda }_j^2\left(\chi \right)+{\Lambda }_r^2\left(\chi \right)+{\varsigma }_1\hfill \\ \hfill & {\displaystyle \frac{d{\Omega }_j}{d\chi }}={\varrho }_1{\Omega }_j\left(\chi \right)-2{\Lambda }_j\left(\chi \right){\Lambda }_r\left(\chi \right)\hfill \\ \hfill & {\displaystyle \frac{d{\Lambda }_r}{d\chi }}={\varrho }_2{\Lambda }_r\left(\chi \right)-{\Omega }_j^2\left(\chi \right)+{\Omega }_r^2\left(\chi \right)+{\varsigma }_2\hfill \\ \hfill & {\displaystyle \frac{d{\Lambda }_j}{d\chi }}={\varrho }_2{\Lambda }_j\left(\chi \right)+2{\Omega }_r\left(\chi \right){\Omega }_j\left(\chi \right)\hfill \end{array}$$

(2)

$$({\Omega }_r\left(0\right)={\omega }_0,{\Omega }_j\left(0\right)={\omega }_1,{\Lambda }_r\left(0\right)={\lambda }_0,{\Lambda }_j\left(0\right)={\lambda }_1).$$

System (2) is studied in [3] when ${\varsigma }_1=1$ and ${\varsigma }_2=-1$ using a fractional-derivative-type Atangana–Baleanu operator.

A bounded solution in the context of dynamic systems is a trajectory or actions taken by a system that over time stays within predetermined bounds or constraints. In numerous situations, bounded solutions are preferred to provide stability as well as prevent the system from deviating or reaching infinity. For instance, a linear dynamic system is stable and has bounded solutions if the system matrix’s eigenvalues contain negative real portions. Similar methods can be used to demonstrate the boundedness of solutions in nonlinear systems, such as certain circumstances or Lyapunov functions [5,6]. Turning Points: In a dynamic system, a turning point occurs when the derivative, which represents the rate of change, of the system variables equals zero. This state is also referred to as a critical point or equilibrium point. The system is at equilibrium or in a state of steady motion when it reaches a turning point. For instance, a turning point occurs in a one-dimensional system described by a differential equation when the system variable’s temporal derivative is equal to zero. This shows that the system’s driving forces and resistible forces are in equilibrium. It is possible to learn more about a system’s stability and dynamics by observing how it behaves close to a turning point. The stability of a turning point can be examined for linear systems employing eigenvalues and eigenvectors. To analyze actions close to a turning point in nonlinear systems, various approaches may be needed, such as linearization or phase plane analysis (see [7,8]).

In the present study, we consider System (1) (CLMMS) for a complex variable $\chi$ in the open-unit disk $\Theta :=\{\chi \in \mathbb{C}:|\chi |<1\},$ as follows:

$$\begin{array}{c}\hfill {\displaystyle \frac{d\Omega }{d\chi }}={\varrho }_1\Omega \left(\chi \right)+{\Lambda }^2\left(\chi \right)+1\\ \hfill {\displaystyle \frac{d\Lambda }{d\chi }}={\varrho }_2\Lambda \left(\chi \right)+{\Omega }^2\left(\chi \right)+1,\end{array}$$

(3)

Suppose that the functions $\Omega$ and $\Lambda$ in System (3) are analytic in $\Theta .$ We shall investigate a set of sufficient conditions to obtain univalent solution in $\Theta$. The technique is based on the bounded turning functions of a dynamic system of a complex variable.

2. Methods and Results

It is feasible to locate explicit analytic univalent solutions in specific circumstances. For instance, the unit disk for any other simply linked domain in the complex plane is guaranteed to have a conformal (analytic univalent) mapping according to the Riemann mapping theorem. With a few exceptions, the explicit form of such a mapping is often unknown. Finding analytic univalent solutions, however, can be a difficult challenge in general. In complex analysis, many equations and issues lack explicit solutions. To analyze the behavior of solutions, one frequently uses existence and uniqueness theorems or numerical techniques. It is important to note that complex analysis offers a variety of methods and instruments for creating or describing analytical univalent functions. This involves numerous geometric or algebraic processes, such as conformal mappings, Schwarz–Christoffel mappings, and others. The particular strategy to be utilized will depend on the issue at present.

Definition 1.

Let $f\left(\chi \right)$ be an analytic function, where χ is a complex variable. Geometrically, it is said that $f\left(\chi \right)$ is a bounded turning analytic function if, for each zero of $f\left(\chi \right)$, there is a positive constant M that means that, for any closed curve C encircling the zero in the counterclockwise direction, the spiraling number of $f\left(\chi \right)$ around C is less than or equal to M. Mathematically, for a normalized analytic function in Θ of the form [7]

$$f\left(\chi \right)=\chi +\sum _{n=2}^{\infty }{a}_n{\chi }^n\chi \in \Theta ,$$

(4)

is called a bounded turning function (BTF) if and only if its first derivative has a positive real part, i.e.,

$$\Re \left(f^{\prime }\left(\chi \right)\right)>0,{}^{\prime }=df\left(\chi \right)/\chi ,\chi \in \Theta .$$

As a consequence of the above inequality, f is univalent in $\Theta .$

In this part, we illustrate different methods to obtain the bounded turning solutions for System (3). To proceed with different types of methods, let $\Omega$ and $\Lambda$ of the form (4) be as follows:

$$\Omega \left(\chi \right)=\chi +\sum _{n=2}^{\infty }{\omega }_n{\chi }^n,\chi \in \Theta ,$$

(5)

and

$$\Lambda \left(\chi \right)=\chi +\sum _{n=2}^{\infty }{\lambda }_n{\chi }^n,\chi \in \Theta .$$

(6)

A mathematical function that demonstrates both symmetry and boundedness in its behavior is known as a symmetric and bounded turning function. A symmetric and bounded turning function would display equilibrium action around a point of symmetry (often the origin of the open-unit disk) while being constrained within particular bounds by the combination of symmetry and boundedness. For example, the Julia set fractals $J\left(\chi \right)={\chi }^2+t,$ where t is a constant, admit a bounded turning function with symmetry behavior whenever $\Re \left(\chi \right)>0$ (see Figure 3).

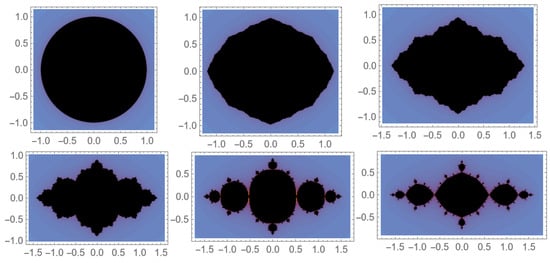
Figure 3. Example of symmetrical bounded turning function. It represents to Julia set functions $J\left(\chi \right)$ in a complex domain where from the upper left $t=0,-0.2,-0.4,-0.6,-0.8,-1$, respectively.

2.1. Miller–Mocanu–Maxwell Method (MMMM)

This method is based on special types of analytic functions called Bazilevic functions. This class has a variety of intriguing characteristics as well as relationships to other branches of complex analysis and number theory. It can be applied, for instance, to research the distribution of values for specific analytic functions and the Riemann zeta function’s behavior in a crucial area [9].

Lemma 1.

Let σ be analytic in Θ and ϵ be real number. Then

$$\Re \left(\sigma \left(\chi \right)+{\displaystyle \frac{ϵ\chi {\sigma }^{\prime }\left(\chi \right)}{\sigma \left(\chi \right)}}\right)>0\Rightarrow \Re \left(\sigma \left(\chi \right)\right)>0,\chi \in \Theta .$$

We have the following result:

Proposition 1.

Assume function (5). If it satisfies the inequality

$$\begin{array}{cc}\hfill & \Re \left({\displaystyle \frac{{\varrho }_1(ϵ\chi {\Omega }^{\prime }(\chi )+\Omega (\chi )(2\Lambda {(\chi )}^2+1))+{\varrho }_1^2\Omega {(\chi )}^2+\Lambda {(\chi )}^4+\Lambda {(\chi )}^2}{{\varrho }_1\Omega (\chi )+\Lambda {(\chi )}^2+1}}\right)\hfill \\ \hfill & +2\Re \left({\displaystyle \frac{ϵ\chi \Lambda (\chi ){[\Lambda (\chi )]}^{\prime }}{({\varrho }_1\Omega (\chi )+\Lambda {(\chi )}^2+1)}}\right)>-1,\hfill \end{array}$$

(7)

then $\Re \left({\Omega }^{\prime }(\chi )\right)>0.$

Proof. 

Putting

$${\sigma }_1(\chi ):={\varrho }_1\Omega (\chi )+{\Lambda }^2(\chi )+1,\chi \in \Theta .$$

Then

$$\begin{array}{cc}\hfill \Re \left({\sigma }_1(\chi )+{\displaystyle \frac{ϵ\chi {\sigma }_1^{\prime }(\chi )}{{\sigma }_1(\chi )}}\right)& =\Re \left([{\varrho }_1\Omega (\chi )+{\Lambda }^2(\chi )+1]+{\displaystyle \frac{ϵ\chi {[{\varrho }_1\Omega (\chi )+{\Lambda }^2(\chi )+1]}^{\prime }}{[{\varrho }_1\Omega (\chi )+{\Lambda }^2(\chi )+1]}}\right)\hfill \\ \hfill & =\Re \left([{\varrho }_1\Omega (\chi )+{\Lambda }^2(\chi )+1]+{\displaystyle \frac{ϵ\chi [{\varrho }_1{\Omega }^{\prime }(\chi )+2\Lambda (\chi ){\Lambda }^{\prime }(\chi )}{[{\varrho }_1\Omega (\chi )+{\Lambda }^2(\chi )+1]}}\right)\hfill \\ \hfill & =\Re \left({\displaystyle \frac{{\varrho }_1ϵ\chi {[\Omega (\chi )]}^{\prime })}{({\varrho }_1\Omega (\chi )+{[\Lambda (\chi )]}^2+1)}}\right)+2\Re \left({\displaystyle \frac{ϵ\chi \Lambda (\chi ){[\Lambda (\chi )]}^{\prime })}{({\varrho }_1\Omega (\chi )+{[\Lambda (\chi )]}^2+1)}}\right)\hfill \\ \hfill & +\Re \left({\varrho }_1\Omega (\chi )\right)+\Re \left({[\Lambda (\chi )]}^2\right)+1\hfill \\ \hfill & =\Re \left({\displaystyle \frac{{\varrho }_1(ϵ\chi {\Omega }^{\prime }(\chi )+\Omega (\chi )(2\Lambda {(\chi )}^2+1))+{\varrho }_1^2\Omega {(\chi )}^2+\Lambda {(\chi )}^4+\Lambda {(\chi )}^2}{{\varrho }_1\Omega (\chi )+\Lambda {(\chi )}^2+1}}\right)\hfill \\ \hfill & +2\Re \left({\displaystyle \frac{ϵ\chi \Lambda (\chi ){[\Lambda (\chi )]}^{\prime }}{({\varrho }_1\Omega (\chi )+\Lambda {(\chi )}^2+1)}}\right)+1\hfill \\ \hfill & >0.\hfill \end{array}$$

Thus, in view of Lemma 1, we obtain $\Re ({\varrho }_1\Omega (\chi )+{\Lambda }^2(\chi )+1)=\Re ({\Omega }^{\prime }(\chi ))>0.$ □

Similarly, we obtain the following result

Proposition 2.

Assume function (6). If it satisfies the inequality

$$\begin{array}{cc}\hfill & \Re \left({\displaystyle \frac{{\varrho }_2(ϵ\chi {\Lambda }^{\prime }(\chi )+\Lambda (\chi )(2\Omega {(\chi )}^2+1))+{\varrho }_2^2\Lambda {(\chi )}^2+\Omega {(\chi )}^4+\Omega {(\chi )}^2}{{\varrho }_2\Lambda (\chi )+\Omega {(\chi )}^2+1}}\right)\hfill \\ \hfill & +2\Re \left({\displaystyle \frac{ϵ\chi \Omega (\chi ){[\Omega (\chi )]}^{\prime }}{({\varrho }_2\Lambda (\chi )+\Omega {(\chi )}^2+1)}}\right)>-1,\hfill \end{array}$$

(8)

then $\Re \left({\Lambda }^{\prime }(\chi )\right)>0.$

Proof. 

Putting

$${\sigma }_2(\chi ):={\varrho }_2\Lambda (\chi )+{\Omega }^2(\chi )+1,\chi \in \Theta .$$

Then

$$\begin{array}{cc}\hfill \Re \left({\sigma }_2(\chi )+{\displaystyle \frac{ϵ\chi {\sigma }_2^{\prime }(\chi )}{{\sigma }_2(\chi )}}\right)& =\Re \left([{\varrho }_2\Lambda (\chi )+{\Omega }^2(\chi )+1]+{\displaystyle \frac{ϵ\chi {[{\varrho }_2\Lambda (\chi )+{\Omega }^2(\chi )-1]}^{\prime }}{[{\varrho }_2\Omega (\chi )+{\Omega }^2(\chi )+1]}}\right)\hfill \\ \hfill & =\Re \left([{\varrho }_2\Lambda (\chi )+{\Omega }^2(\chi )+1]+{\displaystyle \frac{ϵ\chi [{\varrho }_2{\Lambda }^{\prime }(\chi )+2\Omega (\chi ){\Omega }^{\prime }(\chi )}{[{\varrho }_2\Lambda (\chi )+{\Omega }^2(\chi )-1]}}\right)\hfill \\ \hfill & =\Re \left({\displaystyle \frac{{\varrho }_2ϵ\chi {[\Lambda (\chi )]}^{\prime }}{({\varrho }_2\Lambda (\chi )+{[\Omega (\chi )]}^2+1)}}\right)+2\Re \left({\displaystyle \frac{ϵ\chi \Omega (\chi ){[\Omega (\chi )]}^{\prime }}{({\varrho }_2\Lambda (\chi )+{[\Omega (\chi )]}^2+1)}}\right)\hfill \\ \hfill & +\Re \left({\varrho }_2\Lambda (\chi )\right)+\Re \left({[\Omega (\chi )]}^2\right)+1\hfill \\ \hfill & =\Re \left({\displaystyle \frac{{\varrho }_2(ϵ\chi {\Lambda }^{\prime }(\chi )+\Lambda (\chi )(2\Omega {(\chi )}^2+1))+{\varrho }_2^2\Lambda {(\chi )}^2+\Omega {(\chi )}^4+\Omega {(\chi )}^2}{{\varrho }_2\Lambda (\chi )+\Omega {(\chi )}^2+1}}\right)\hfill \\ \hfill & +2\Re \left({\displaystyle \frac{ϵ\chi \Omega (\chi ){[\Omega (\chi )]}^{\prime }}{{\varrho }_2\Lambda (\chi )+\Omega {(\chi )}^2+1}}\right)+1\hfill \\ \hfill & >0.\hfill \end{array}$$

Thus, in view of Lemma 1, we obtain $\Re ({\varrho }_2\Lambda (\chi )+{\Omega }^2(\chi )+1)=\Re ({\Lambda }^{\prime }(\chi ))>0.$ □

The existence of a univalent solution of System (3) is concluded in the next result.

Corollary 1.

Consider the solution $(\Omega ,\Lambda )$ of System (3), which satisfies inequalities (7) and (8). Then System (3) has a univalent solution.

Proof. 

By Propositions 1 and 2, we have the solution $(\Omega ,\Lambda )$ of bounded turning. But according to the Nashiro–Warschawski theorem [7] (page 74), we confirm that $(\Omega ,\Lambda )$ is univalent solution. □

2.2. Subordination Method

The idea of subordination is utilized in complex analysis to contrast and establish connections between analytic functions specified on the complex plane [7]. The idea of one function being “less complex” than another is provided by subordination. Understanding many characteristics of analytic functions, such as inequalities, growth rates, and geometric aspects, makes use of the premise of subordination especially well. It gives us a way to compare and comprehend the intricate dynamics of different functions by relating the behavior of one function to that of another.

Definition 2.

Two analytic functions φ and ψ in Θ are subordinated if there occurs an analytic function κ with $\kappa \left(0\right)=0$ and $\left|\kappa \right|<1$ such that

$$\phi \left(\chi \right)=\psi \left(\kappa \right(\chi \left)\right),\chi \in \Theta .$$

The subordination is symbolized by $\phi \prec \psi .$ It is common to refer to κ in this context as a subordination function.

In complicated analysis, utilizing subordination has the following unique benefits:

• Simplification: Subordination enables us to swap out a complicated function for a more straightforward one. We may frequently streamline the examination of the original function and make it simpler to analyze by identifying an appropriate subordinate function.
• Properties that help construct mappings between various domains in the complex plane include subordination. Complex differential equations can be broken down into shorter versions using these mappings, which will make them easier to analyze and solve.
• Value estimation for complex functions: In some areas of the complex plane, subordination offers a method for estimating the values of complex functions. We can derive upper or lower bounds on the values of a function by juxtaposing it to a known subordinate function, which can be helpful in a variety of applications.
• Subordination can be used to prove the uniqueness of solutions to some specific classes of complex differential equations. We can ascertain whether a special solution exists by contrasting several solutions and examining their interrelationships via subordination.
• Subordination methods are useful for researching the analytic continuation of complex functions. Analytic continuation is the procedure of expanding a function’s domain past its originally specified area. Understanding subordination facilitates comprehension of the function’s behavior in these broadened domains.

It is crucial to keep in mind that the use of subordination in complicated analysis can change based on the particular issue at hand. Although there may be benefits to subordination in some circumstances, it may not always be appropriate or required. The nature of the problem and the intended goals of the study ultimately determine the choice of methodologies and procedures. We have the following outcome [9]:

Lemma 2.

Let ϑ be analytic-defined in a starlike domain in Θ (a subset of the complex plane that includes the origin (0) and is symmetric in comparison to the real axis is referred to as a starlike domain in Θ). If $\vartheta \left(0\right)=0$ and analytic function $v\left(\chi \right)=\nu +{\nu }_m{\chi }^m+{\nu }_{m+1}{\chi }^{m+1}+\dots$ satisfies

$$\chi v^{\prime }\left(\chi \right)\prec \vartheta \left(\chi \right),\chi \in \Theta ,$$

then

$$v\left(\chi \right)\prec \nu +m^{-1}{\int }_0^{\chi }{\displaystyle \frac{\vartheta \left(y\right)}{y}}dy,$$

which is the best dominant and the last integral formula defined in a convex domain in Θ.

The next result gives the exact solution of System (3) in $\Theta .$

Proposition 3.

Let the solution of System (3) $(\Omega ,\Lambda )$ be as defined in (5) and (6), respectively. Moreover, consider two analytic functions, a starlike function ${\vartheta }_1$ with ${\vartheta }_1\left(0\right)=0$ and ${\kappa }_1$ with ${\kappa }_1\left(0\right)=0$ and $|{\kappa }_1|<1.$ If

$$\chi {\Omega }^{\prime }\left(\chi \right)={\vartheta }_1\left({\kappa }_1\left(\chi \right)\right),$$

(9)

then there is an analytic function ${\tau }_1$ with ${\tau }_1\left(0\right)=0$ and $|{\tau }_1|<1$ such that

$$\Omega \left(\chi \right)={\int }_0^{{\tau }_1\left(\chi \right)}{\displaystyle \frac{{\vartheta }_1\left(y\right)}{y}}dy.$$

Similarly, consider two analytic functions, a starlike function ${\vartheta }_2$ with ${\vartheta }_2\left(0\right)=0$ and ${\kappa }_2$ with ${\kappa }_2\left(0\right)=0$ and $|{\kappa }_2|<1.$ If

$$\chi {\Lambda }^{\prime }\left(\chi \right)={\vartheta }_2\left({\kappa }_2\left(\chi \right)\right),$$

(10)

then there is an analytic function ${\tau }_2$ with ${\tau }_2\left(0\right)=0$ and $|{\tau }_2|<1,$

$$\Lambda \left(\chi \right)={\int }_0^{{\tau }_2\left(\chi \right)}{\displaystyle \frac{{\vartheta }_2\left(y\right)}{y}}dy.$$

Proof. 

From (9) and Definition 2, we have

$$\chi {\Omega }^{\prime }\left(\chi \right)\prec {\vartheta }_1\left(\chi \right).$$

Thus, in view of Lemma 2 with $m=1$ and $\nu =0$, we have

$$\Omega \left(\chi \right)\prec {\int }_0^{\chi }{\displaystyle \frac{{\vartheta }_1\left(y\right)}{y}}dy.$$

Again by Definition 2, there is an analytic function ${\tau }_1$ with ${\tau }_1\left(0\right)=0$ and $|{\tau }_1|<1$; we obtain

$$\Omega \left(\chi \right)={\int }_0^{{\tau }_1\left(\chi \right)}{\displaystyle \frac{{\vartheta }_1\left(y\right)}{y}}dy.$$

In a manner similar to the above conclusion, we obtain

$$\Lambda \left(\chi \right)={\int }_0^{{\tau }_2\left(\chi \right)}{\displaystyle \frac{{\vartheta }_2\left(y\right)}{y}}dy.$$

Note that the solution is convex in $\Theta .$ □

Example 1.

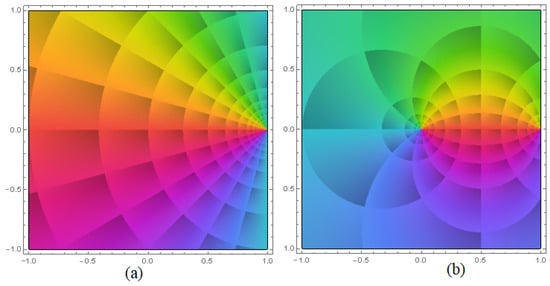
Assume that ${\vartheta }_1\left(\chi \right)={\vartheta }_2\left(\chi \right)=\chi /{(1-\chi )}^2$, which is the extreme starlike function in $\Theta .$ And let ${\tau }_1\left(\chi \right)=\chi$ (the Schwarz lemma). Then the solution is

$$\Omega \left(\chi \right)=\Lambda \left(\chi \right)={\displaystyle \frac{\chi }{1-\chi }},$$

where $\chi /(1-\chi )$ is the extreme convex function in Θ (Koebe function) (see Figure 4).

Figure 4. Solution of example (1), where (a) is ${\vartheta }_1$ and (b) is $\Omega \left(\chi \right)=\Lambda \left(\chi \right)$.

2.3. Clunie–Jack Lemma Method

According to the Jack lemma [10], the zeros of a function $\psi \left(\chi \right)$ are isolated if $\psi \left(\chi \right)$ is analytic $\Theta$ on the complex plane and $\psi \left(\chi \right)$ is not identically zero on $\Theta$. In simpler terms, there exists a tiny disk focused at ${\chi }_0$ so that $\psi \left(\chi \right)$ is also zero only at ${\chi }_0$ if there is a point ${\chi }_0\in \Theta$ that makes $\psi \left({\chi }_0\right)$ = 0. This finding is significant because it demonstrates that, unlike conventional continuous functions, analytic functions always have isolated zeros. The Jack lemma’s proof depends on the notion that power series expansions could locally depict analytical functions and that a power series’ zeros are likewise isolated. The Jack lemma has numerous uses in complex analysis, including investigating the existence of complete function zeros and a factorization of meromorphic functions [9].

The statement of the generalized Jack lemma (Clunie–Jack lemma) is as follows:

Lemma 3

([9], p. 19). For ${\chi }_0\in \Theta$ and $f_0=\left|{\chi }_0\right|$, let $\psi \left(\chi \right)={\psi }_n{\chi }^n+{\psi }_{n+1}{\chi }^{n+1}+\cdots$ be analytic on ${\Theta }_{f_0}\cup \left\{f_0\right\}$ such that $\psi \not\equiv 0$ and $n\ge 1$. If $|\psi \left({\chi }_0\right)|=max\{|\psi \left(\chi \right)|:\chi \in {\Theta }_{f_0}\},$ then there is an $m\ge n$ with

• $\Re \left({\displaystyle \frac{{\chi }_0{\psi }^{\prime }\left({\chi }_0\right)}{\psi \left({\chi }_0\right)}}\right)=m$ and
• ${\displaystyle \Re \left(\frac{{\chi }_0{\psi }^{″}\left({\chi }_0\right)}{{\psi }^{\prime }\left({\chi }_0\right)}+1\right)\ge m}$.

Theorem 1.

Assume the following inequality

$$\begin{array}{c}\hfill \Re \left(1+\frac{\chi {[\Omega \left(\chi \right)]}^{″}}{{[\Omega \left(\chi \right)]}^{\prime }}\right)<1+\frac{\wp }{2},\chi \in \Theta ,\wp >0.\end{array}$$

(11)

Let $2\ge 1+\wp$ and ${\displaystyle \frac{[\Omega (\chi \left)\right]}{\chi }}\ne 0.$ Then $\Re {[\Omega \left(\chi \right)]}^{\prime }>0,\chi \in \Theta$ and $[\Omega (\chi \left)\right]$ is univalent.

Proof. 

Firstly, we prove that ${[\Omega \left(\chi \right)]}^{\prime }\ne 0$ for all $\chi \in \Theta$ and $\chi \ne 0$. In view of the definition of the function $\Omega ,$ it is clear that ${[\Omega \left(0\right)]}^{\prime }=1$). If there is ${\chi }_1$, $0<|{\chi }_1|<1$ and ${[\Omega \left(\chi \right)]}^{\prime }={(\chi -{\chi }_1)}^{m_1}\psi \left(\chi \right),$ such that $m_1\ge 1$ and $\psi$ is analytic in $\Theta$ and $\psi \left({\chi }_1\right)\ne 0,$ then

$$1+\frac{\chi {[\Omega \left(\chi \right)]}^{″}}{{[\Omega \left(\chi \right)]}^{\prime }}=1+\frac{m_1\chi }{\chi -{\chi }_1}+\frac{\chi {[\Omega \left(\chi \right)]}^{\prime }}{\psi \left(\chi \right)}.$$

Thus, we obtain $1+{\displaystyle \frac{\chi {[\Omega \left(\chi \right)]}^{″}}{{[\Omega \left(\chi \right)]}^{\prime }}}\to \infty$ when $\chi \to {\chi }_1$, which contradicts (11).

Assume that

$$\begin{array}{c}\hfill {[\Omega \left(\chi \right)]}^{\prime }={\left(1-h\left(\chi \right)\right)}^{\frac{\wp }{n-1}},\end{array}$$

(12)

where $0<\wp /(n-1)\le 1$. Since ${[\Omega \left(\chi \right)]}^{\prime }\ne 0$ for all $\chi \in \Theta$, then $h\left(\chi \right)=h_{n-1}{\chi }^{n-1}+\cdots$ is analytic in $\Theta$ with $h\left(0\right)=0$. Moreover, a computation implies that

$$\begin{array}{cc}\hfill \left(1+\frac{\chi {[\Omega \left(\chi \right)]}^{″}}{{[\Omega \left(\chi \right)]}^{\prime }}\right)=& 1-\frac{\wp \chi h^{\prime }\left(\chi \right)}{(n-1)(1-h(\chi \left)\right)}.\hfill \end{array}$$

Consider the equality ${max}_{|\chi |\le |{\chi }_0|}|h\left(\chi \right)|=|h\left({\chi }_0\right)|=1.$ In view of Lemma 3, we obtain

$$\begin{array}{c}\hfill {\chi }_0{h}^{\prime }\left({\chi }_0\right)=kh\left({\chi }_0\right);(k\ge n-1;h\left({\chi }_0\right)=e^{i\theta };\theta \in \mathbb{R}).\end{array}$$

This yields

$$\begin{array}{cc}\hfill \Re \left(1+\frac{{\chi }_0{[\Omega \left({\chi }_0\right)]}^{″}}{{[\Omega \left({\chi }_0\right)]}^{\prime }}\right)& =1-\frac{\wp }{n-1}\Re \left(\frac{k{e}^{i\theta }}{1-e^{i\theta }}\right).\hfill \end{array}$$

As a consequence, we have

$$\begin{array}{cc}\hfill \Re \left(1+\frac{{\chi }_0{[\Omega \left({\chi }_0\right)]}^{″}}{{[\Omega \left({\chi }_0\right)]}^{\prime }}\right)& =1+\frac{k\wp }{2}\ge 1+\frac{\wp }{2},\hfill \end{array}$$

which is in contradiction with (11). That is $\left|h\right(\chi \left)\right|<1,\chi \in \Theta$, and by (12), we obtain

$$\begin{array}{c}\hfill |arg\left({[\Omega \left(\chi \right)]}^{\prime }\right)|=\wp |arg\left((1-h\left(\chi \right))\right|<\frac{\wp }{(n-1)}\frac{\pi }{2}\le \frac{\pi }{2},\end{array}$$

where $2\ge 1+\wp ,$ which implies $\Re {[\Omega \left(\chi \right)]}^{\prime }>0,\chi \in \Theta$. Let

$$\begin{array}{c}\hfill {\left(\frac{\chi }{[\Omega (\chi \left)\right]}\right)}^2{[\Omega \left(\chi \right)]}^{\prime }-1=Q\left(\chi \right).\end{array}$$

(13)

Then $Q\left(\chi \right)=q_1\chi +\cdots$ is analytic in $\Theta$. A logarithmic differentiation yields

$$\begin{array}{c}\hfill 1+\frac{\chi {[\Omega \left(\chi \right)]}^{″}}{{[\Omega \left(\chi \right)]}^{\prime }}=\frac{\chi Q^{\prime }\left(\eta \right)}{1+Q\left(\chi \right)}+2\frac{\chi {[\Omega \left(\chi \right)]}^{\prime }}{[\Omega (\chi \left)\right]}-1.\end{array}$$

(14)

According to (14), we obtain

$$\begin{array}{c}\hfill \Re \left(\frac{\chi Q^{\prime }\left(\chi \right)}{1+Q\left(\chi \right)}+2\frac{\chi {[\Omega \left(\chi \right)]}^{\prime }}{[\Omega (\chi \left)\right]}-1\right)<\frac{2+\wp }{2}.\end{array}$$

(15)

That is

$$\begin{array}{c}\hfill \frac{\chi {[\Omega \left(\chi \right)]}^{\prime }}{[\Omega (\chi \left)\right]}\prec \frac{1-\chi }{1-k\chi },\end{array}$$

where $0<k=1/(1+\wp )<1,\wp >0$ which brings $\Re \left(\frac{\chi {[\Omega \left(\chi \right)]}^{\prime }}{[\Omega (\chi \left)\right]}\right)>0.$

But (15) indicates

$$\begin{array}{c}\hfill \Re \left(\frac{\chi Q^{\prime }\left(\chi \right)}{1+Q\left(\chi \right)}-1\right)<1+\frac{\wp }{2}-2\Re \left(\frac{\chi {[\Omega \left(\chi \right)]}^{\prime }}{[\Omega (\chi \left)\right]}\right)<\frac{2+\wp }{2}.\end{array}$$

(16)

For ${\chi }_0\in \Theta$ with $\left|Q\right({\chi }_0\left)\right|=1$. Now by Lemma 3, we have

$$\begin{array}{c}\hfill {\chi }_0{Q}^{\prime }\left({\chi }_0\right)=kQ\left({\chi }_0\right);(k\ge 1;Q\left({\eta }_0\right)=e^{i\theta };\theta \in \mathbb{R}).\end{array}$$

Thus,

$$\begin{array}{c}\hfill \Re \left(\frac{{\chi }_0{Q}^{\prime }\left({\chi }_0\right)}{1+Q\left({\chi }_0\right)}-1\right)=\Re \left(\frac{k{e}^{i\theta }}{1+e^{i\theta }}\right)-1=\frac{k-2}{2}.\end{array}$$

Hence,

$$\Re \left(\frac{{\chi }_0{Q}^{\prime }\left({\chi }_0\right)}{Q\left({\chi }_0\right)}-1\right)\ge 1+\frac{\wp }{2},$$

where $k\ge 1$. This yields a contradiction with the assumption. That is

$$\left|Q\right(\chi \left)\right|<1,\chi \in \Theta ,\chi \in \Theta .$$

Moreover, we have that (13) admits

$$\begin{array}{c}\hfill \left|{\left(\frac{\chi }{[\Omega (\chi \left)\right]}\right)}^2{[\Omega \left(\chi \right)]}^{\prime }-1\right|<1,\chi \in \Theta ,\end{array}$$

which gives the second part of the theorem. □

In a manner similar to Theorem 1, we have the following result

Theorem 2.

Assume the following inequality

$$\begin{array}{c}\hfill \Re \left(1+\frac{\chi {[\Lambda \left(\chi \right)]}^{″}}{{[\Lambda \left(\chi \right)]}^{\prime }}\right)<1+\frac{\delta }{2},\chi \in \Theta ,\delta >0.\end{array}$$

(17)

Assume that $2\ge 1+\delta ,$ and ${\displaystyle \frac{[\Lambda (\chi \left)\right]}{\chi }}\ne 0.$ Then

$$\Re {[\Lambda \left(\chi \right)]}^{\prime }>0,\chi \in \Theta ,$$

and $[\Lambda (\chi \left)\right]$ is univalent.

2.4. Schur Functions Method

After the mathematician Issai Schur, Schur functions are a significant class of symmetric functions in mathematics. They are crucial to algebraic geometry, representational theory and combinatorial combinatorics (see [11]). Any combination of the variables in a symmetric function results in the same result. The theory of Young tableaux and the representational theory of the symmetric group are used for establishing Schur functions, which are symmetric functions. A class of complex-valued functions known as Schur analytic functions have been established on the open-unit disk of the complex plane, which is the collection of all complex numbers with absolute values less than 1. Because they are holomorphic, these functions have the unique characteristic of appearing complex differentiable wherever in the open-unit disk.

Definition 3.

If a function $\varsigma \left(\chi \right),\chi \in \Theta$ matches the criteria below, it is referred to as a Schur analytic function.

• Analysis: In the open-unit disk, the function $\varsigma \left(\chi \right)$ is holomorphic. It has a derivative at each location on the disk, according to this.
• Unit disk boundary behavior: As χ gets closer to a point on the unit disk boundary, the function $\varsigma \left(\chi \right)$ limits practically everywhere. With the exception of a set of measure zero, this restriction holds for practically all of the points on the unit circle.
• The norm-preserving property, which is represented as $\left|\varsigma \right(\chi \left)\right|\le 1$ for any $\chi \in \Theta$ is satisfied by the function $\varsigma \left(\chi \right)$.

Relationship through Schur Polynomials

Use of Schur polynomials results in one particular relationship between Schur functions and analytic functions. A class of symmetric polynomials known as Schur polynomials can be defined in terms of either power sum symmetric functions or elementary symmetric functions. The theory of Schur functions is closely related to these polynomials. By using their power-series expansions, which contain coefficients that can be stated as an expression of the function’s derivatives at a certain point, analytical functions may be expressed. Such expansions frequently have coefficients that can be calculated combinatorially and involve symmetric functions like Schur polynomials. In this sense, understanding Schur functions can help us understand the characteristics and coefficients of some analytic functions. In conclusion, although Schur functions and analytic functions are separate mathematical ideas, there are linkages between them, especially when Schur polynomials are used. The analysis of symmetric functions and their applications to representation theory, combinatorics and other branches of mathematics lead to these relationships. In this part, we used the connection between a class of Schur functions and the class of analytic functions to obtain the analytic solution of System (3). In [12], the authors presented two different types of Schur function, iterating integrally and integro-differentials. For the integral iteration, it was acting on the normalized function (such as (5) and (6)), as follows:

$$\begin{array}{cc}\hfill & s_0(\Omega \left(\chi \right))=\Omega \left(\chi \right)=\chi +\sum _{n=2}^{\infty }{\omega }_n{\chi }^n\hfill \\ \hfill & s_1\left(\chi \right)={\chi }^{-1}\left(2{\int }_0^{\chi }{s}_0\left(w\right)dw\right)=2{\chi }^{-1}\left({\displaystyle \frac{{\chi }^2}{2}}+\sum _{n=2}^{\infty }{\omega }_n{\displaystyle \frac{{\chi }^{n+1}}{n+1}}\right)\hfill \\ \hfill & =\chi +\sum _{n=2}^{\infty }\left({\displaystyle \frac{2}{n+1}}\right){\omega }_n{\chi }^n;\hfill \\ \hfill & s_2(\Omega \left(\chi \right))={\chi }^{-1}\left(2{\int }_0^{\chi }{s}_1\left(w\right)dw\right)=2{\chi }^{-1}\left({\displaystyle \frac{{\chi }^2}{2}}+\sum _{n=2}^{\infty }{\omega }_n\left({\displaystyle \frac{2}{n+1}}\right){\displaystyle \frac{{\chi }^{n+1}}{n+1}}\right)\hfill \\ \hfill & =\chi +\sum _{n=2}^{\infty }{\left({\displaystyle \frac{2}{n+1}}\right)}^2{\omega }_n{\chi }^n;\hfill \\ \hfill & ⋮\hfill \\ \hfill & s_k(\Omega \left(\chi \right))={\chi }^{-1}\left(2{\int }_0^{\chi }{s}_{k-1}\left(w\right)dw\right)=2{\chi }^{-1}\left({\displaystyle \frac{{\chi }^2}{2}}+\sum _{n=2}^{\infty }{\varphi }_n{\left({\displaystyle \frac{2}{n+1}}\right)}^{k-1}{\displaystyle \frac{{\chi }^{n+1}}{n+1}}\right)\hfill \end{array}$$

(18)

$$=\chi +\sum _{n=2}^{\infty }{\left({\displaystyle \frac{2}{n+1}}\right)}^k{\omega }_n{\chi }^n.$$

It is clear that $s_k$ is a normalized function and the coefficients are dominated by the Riemann–Zeta function. A new process is given here, by assuming the non-normalized function

$$f\left(\chi \right)={\displaystyle \frac{\chi -i}{\chi +i}}$$

$$=-1-2i\chi +2{\chi }^2+2i{\chi }^3-2{\chi }^4+O\left({\chi }^5\right)$$

then (see Figure 5)

$$\begin{array}{cc}\hfill s\left(f\right(\chi \left)\right)& ={\displaystyle \frac{{\int }_0^{\chi }f\left(\zeta \right)d\zeta }{\chi }}\hfill \\ \hfill & ={\displaystyle \frac{\chi -2ilog[i+\chi ]}{\chi }}\hfill \\ \hfill & =\pi /\chi -1-i\chi +\left(2{\chi }^2\right)/3+\left(i{\chi }^3\right)/2+O\left({\chi }^4\right).\hfill \end{array}$$

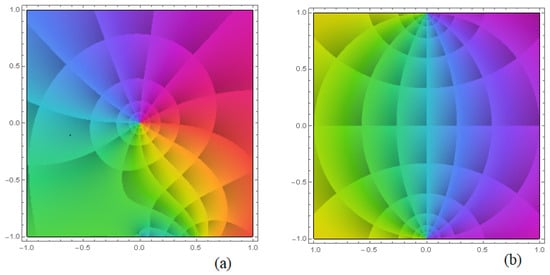
Figure 5. (a) The complex plot of $s\left(\chi \right)$ under the function $(\chi -i)/(\chi +i)$ in (b).

Now define a normalized Schur function as follows (see Figure 6):

$$\begin{array}{cc}\hfill & S\left(f\left(\chi \right)\right)=-\chi \left({\displaystyle \frac{1+s\left(f\right(\chi \left)\right)}{1-s\left(f\right(\chi \left)\right)}}\right)\hfill \\ \hfill & =\chi +{\displaystyle \frac{2{\chi }^2}{\pi }}+{\displaystyle \frac{4{\chi }^3}{{\pi }^2}}+{\displaystyle \frac{(8+2i\pi ){\chi }^4}{{\pi }^3}}\hfill \\ \hfill & -{\displaystyle \frac{4(-12-6i\pi +{\pi }^2){\chi }^5}{3{\pi }^4}}+{\displaystyle \frac{(96+72i\pi -22{\pi }^2-3i{\pi }^3){\chi }^6}{3{\pi }^5}}\hfill \\ \hfill & +{\displaystyle \frac{4(240+240i\pi -105{\pi }^2-25i{\pi }^3+3{\pi }^4){\chi }^7}{15{\pi }^6}}\hfill \\ \hfill & +{\displaystyle \frac{2(2880+3600i\pi -2040{\pi }^2-675i{\pi }^3+137{\pi }^4+15i{\pi }^5){\chi }^8}{45{\pi }^7}}\hfill \\ \hfill & -{\displaystyle \frac{4(-6720-10080i\pi +7000{\pi }^2+2940i{\pi }^3-812{\pi }^4-147i{\pi }^5+15{\pi }^6){\chi }^9}{105{\pi }^8}}\hfill \\ \hfill & +{\displaystyle \frac{(107520+188160i\pi -154560{\pi }^2-78400i{\pi }^3+27076{\pi }^4+6566i{\pi }^5-1089{\pi }^6-105i{\pi }^7){\chi }^{10}}{210{\pi }^9}}\hfill \\ \hfill & +{\displaystyle \frac{967680+1935360i\pi -1834560{\pi }^2-1088640i{\pi }^3+448980{\pi }^4+134568i{\pi }^5-29531{\pi }^6-4566i{\pi }^7}{945{\pi }^{10}}}\hfill \\ \hfill & {\displaystyle \frac{+420{\pi }^8}{945{\pi }^{10}}}\times {\chi }^{11}\hfill \\ \hfill & +O\left({\chi }^{12}\right).\hfill \end{array}$$

(19)

Figure 6. The complex plot of $S\left(f\right(\chi )$).

Making the power series in (18) and (19) equal and comparing the connections yields the following result:

Proposition 4.

Consider the solution of System (4) $(\Omega ,\Lambda )$ as in Equations (5) and (6), respectively. Then

$$\begin{array}{cc}\hfill & |{\omega }_2|\le {\displaystyle \frac{2/\pi }{{(2/3)}^k}}={\displaystyle \frac{0.63661}{{(2/3)}^k}}\le {\displaystyle \frac{\zeta \left(2\right)/2}{{(2/3)}^k}};\hfill \\ \hfill & |{\omega }_3|\le {\displaystyle \frac{4/{\pi }^2}{{(1/2)}^k}}={\displaystyle \frac{0.40528}{{(1/2)}^k}}\le {\displaystyle \frac{\zeta \left(3\right)/2}{{(1/2)}^k}};\hfill \\ \hfill & |{\omega }_4|\le {\displaystyle \frac{\sqrt{64+4{\pi }^2}/{\pi }^3}{{(2/5)}^k}}={\displaystyle \frac{0.32807}{{(2/5)}^k}}\le {\displaystyle \frac{\zeta \left(4\right)/2}{{(2/5)}^k}};\hfill \\ \hfill & |{\omega }_5|\le {\displaystyle \frac{{\displaystyle \frac{(4\sqrt{{(240\pi -25{\pi }^3)}^2+{(240-105{\pi }^2+3{\pi }^4)}^2})}{\left(15{\pi }^6\right)}}}{{(1/3)}^k}}={\displaystyle \frac{0.14}{{(1/3)}^k}}\le {\displaystyle \frac{\zeta \left(5\right)/2}{{(1/3)}^k}};\hfill \\ \hfill & \dots \hfill \\ \hfill & |{\omega }_n|\le {\displaystyle \frac{\zeta \left(n\right)/2}{{\left({\displaystyle \frac{2}{n+1}}\right)}^k}},k\ge 0,\hfill \end{array}$$

where $\zeta \left(n\right)$ indicates the Riemann–Zeta Function. The same goes for the coefficients of $\Lambda .$

3. Conclusions and Discussions

The analytic solution of the Layla and Majnun model of a complex variable is considered in the open-unit disk. We suggested a new complex dynamic system of the model by replacing the negative sympathy coefficient by a positive one. The solution is presented using different methods from the field of geometric function theory. Firstly, we obtained a solution which is of bounded turning function (univalent solution) using MMMM. The technique is based on a positive real part. Secondly, we obtained an analytic solution by employing the concept of subordination. In this case, we obtain an exact formula of the solution (Alexander integral formula). Thirdly, the Clunie–Jack lemma method, which is the generalized statement of the Jack lemma, is applied to obtain an analytic solution of bounded turning function, as well. In this case, the solution is univalent in the open-unit disk. Finally, the Schur functions method is utilized to describe an analytic solution, which is symmetric in a complex domain. We suggested new normalized Schur functions to obtain a normalized analytic solution.

Mathematical symmetric formulas that offer a straightforward method for computing the answer to a problem are known as analytical or closed-form solutions. These remedies offer a number of advantages:

• Efficiency and Simplicity: Analytic solutions frequently offer a clear and succinct formula for arriving at the solution. When the formula is developed, it can be applied effectively and with less computation overhead than iterative or numerical approaches.
• Exactness and Precision: Within the boundaries of the mathematical model, analytical solutions produce highly accurate answers. They are not susceptible to numerical instability or approximation errors, as can happen with iterative or numerical methods. They are therefore very helpful when high accuracy is required.
• Knowledge and Insight: The underlying linkages and relationships in a problem are frequently revealed by analytical solutions. They can shed light on the characteristics and actions of the system under investigation. Analytical solutions help in the interpretation and analysis of the data by enabling a greater understanding of the issue.
• Generalization and Predictability: The conventional method for deriving analytical solutions is to build them on a set of general rules or presumptions. Once developed, they can be used in a variety of particular scenarios that fall within the same problem area. Without the need for intensive numerical simulations, this generalizability facilitates predictability and the investigation of various scenarios.
• Interpretability and Communication: Analytical answers are frequently given in a mathematical format, which makes them simple to comprehend and convey to others. They offer concise explanations and promote knowledge and research exchange among disciplines.
• Improvements related to a particular problem: In certain cases, distinct problem areas can benefit from tried-and-true analytical techniques that offer special benefits. For instance, there are known analytical solutions for some physical systems that provide precise predictions or illuminate underlying physical principles.