Abstract
Graph burning was introduced to simulate the spreading of news/information/rumors in social networks. The symmetric undirected graph is considered here. That is, vertex u can spread the information to vertex v, and symmetrically vertex v can also spread information to vertex u. When it is modeled as a graph burning process, a vertex can be set on fire directly or burned by its neighbor. Thus, the task is to find the minimum sequence of vertices chosen as sources of fire to burn the entire graph. This problem has been proved to be NP-hard. In this paper, from a new perspective, we introduce a generalized model called the Independent Cascade Graph Burning model, where a vertex v can be burned by one of its burning neighbors u only if the influence that u gives to v is larger than a given threshold . We determine the graph burning number with this new Independent Cascade Graph Burning model for several graphs and operation graphs and also discuss its upper and lower bounds.
1. Introduction
Bonato et al. [1,2,3] introduced the concept of the graph burning problem as a model for social contagion. Given a finite connected graph G, the burning process on G is a discrete-time process defined as follows.
Initially, all vertices are unburned. One vertex can be set on fire directly or burned by its neighbor. At each step, only one vertex is selected to be set on fire, and simultaneously all those vertices which have caught fire at the last step will burn all their neighbors. The process does not stop until the entire graph is burned. Furthermore, if a vertex is burned, the vertex remains in this state until the end of the process. The vertices selected as the sources of fire are called the burning sequences; the shortest burning sequence is called the optimum burning sequence. The length of the optimum burning sequence is called the burning number . Note that the smaller the burning number is, the faster a contagion (such as news or gossip) spreads in the network. For a given network, finding the optimum burning sequence has important applications in reality.
The graph burning problem has been proved to be NP-hard [4], and several approximation algorithms [4,5,6] and heuristics [7,8,9] were proposed. Among them, the Burning Farthest-First (BFF) algorithm [6] has a better approximation ratio, which is . For heuristics, the Forward-Looking Search Strategy (GFSS) [8] and Component-Based Recursive Heuristic (CBRH) algorithm [7] perform better. In addition to the above studies on algorithms, researchers have paid attention to the bounds of the burning number [1,10,11] and calculated the burning number for some special graphs, such as generalized Petersen graphs [12], theta graphs [13], graph products [14,15], spiders and path forests [16].
The above mentioned graph burning model was used to simulate the spreading of news/information/rumors in social networks. It is supposed that if a person obtains news (or other social information) at time , all their neighbors will obtain the news at time t and spread the news at time . However, in reality, we find that a person may not accept the news and further spread it to their neighbors if they receive this news from only one of their neighbors. Based on this fact, Li et al. [17] proposed the generalized r-burning process of G where a person will accept the news only if they received the news from more than just their r neighbors, where r is a preset integer that serves as a threshold. This threshold, ‘r’, defines the minimum number of sources needed before the individual considers the news credible enough for further propagation. They studied the generalized r-burning number for several graphs and operation graphs.
However, in reality, the following situation may happen. For instance, as shown in Figure 1a, if a person, namely A, has two friends, namely B and C. B is popular, while C is not. As a result, the influence of A on these two friends is different. For B, since they have many friends, A will have less influence on B. On the contrary, for C, since C has fewer friends, A is very likely to be an important friend to C. So, A is likely to have more influence on C than on B. Assume that at some step t, A is active/burned. It may happen that at time , A can burn C but cannot burn B. However, in the above graph burning models, vertex A’s activation ability on its neighbors is not distinguished. Thus, we should introduce another model which can take this difference into account.
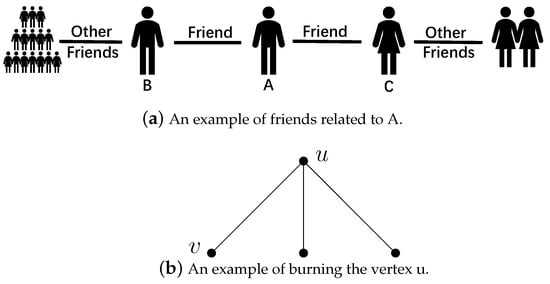
Figure 1.
Two examples of different friends of a person and a burning vertex.
In the information diffusion research field, there is another information diffusion model called the Independent Cascade Model (abbreviated as the IC Model) [18] where whether a vertex can activate its neighbors successfully or not depends on a threshold. Inspired by the IC model, in this paper we propose a new generalized Independent Cascade graph burning model for G, where a burned vertex v can successfully burn its unburned neighbor w only if the influence that v exerts on w is larger than a given threshold . Note that when , it turns to be the traditional graph burning problem. Our task is still to find the minimum sequence of vertices that can be chosen as sources of fire to burn the entire graph. The minimum number of vertices or steps is called the IC burning number of a graph G with a given threshold .
2. Terminology
All graphs considered in this paper are finite and simple. For notation and terminology not defined here, refer to Bondy and Murty [19].
During the burn process in the IC model, we call a vertex burned outsideif is selected to be set on fire and burned inside if is burned by its neighbor. For a given threshold , if all vertices of the graph are burned after k time steps, we call the fire source sequence a -burning sequence of graph G. Clearly, the generalized burning number is the length of a minimum burning sequence among all -burning sequences for graph G. If , we call sequence an optimum -burning sequence of G.
In reality, the influence a vertex u receives from its neighbor w can be an arbitrary value in , only with the restriction that the sum of influences that it receives should not be larger than 1. For simplicity, in this paper, we assume a vertex u receives equal influence from each of its neighbors, which is . Note that u’s neighbors have equal chance to activate u, but u has a different chance to activate its neighbors. For example, as shown in Figure 1b, the influence from to u is because u has three friends, while the influence from u to is 1 because has only one friend u. Then, whether a vertex can be burned by its neighbor depends heavily on its degree. The more friends a vertex has, the more difficult it is for one of its friends to activate it. For a vertex u, if the number of its neighbors is less than (i.e., the influence from each of its neighbors is greater than ), vertex u can be burned by any one of its burned neighbors. See Figure 1b; assume or is burned at time , then u will be burned by or at time t if and will not if . On the contrary, if u is burned at time , then will be burned by u at time t for any but will be burned by u at time t only if .
For convenience, we assign a parameter to each vertex u, representing the influence that it receives from each of its neighbors. For a directed graph, , where is the in-degree of vertex u. Clearly, while , where is the maximum degree of the graph G.
3. The Bounds for the IC Burning Number of Graphs
If G is a graph and u, v are two vertices of G, and the distance between them is denoted by . A shortest path between u and v is denoted by , and the is defined as where as described above. The open neighborhood is the set of vertices at distance one from a vertex v. Notice that . Meanwhile, the closed neighborhood is the set of vertices at most one from a vertex v. In other words, . Given a positive integer k, the k-th closed neighborhood of u is defined to be the set , which is denoted by . Similarly, given a positive integer k and fraction , the k-th closed -neighborhood of u is defined to be the set and is denoted by . Suppose that () is a burning sequence for a given graph G.
The following set equation holds:
We denote simply by .
Observation 1.
Suppose G is a connected graph with n vertices and are two fractions with . Then, .
From the definition of the IC burning number, the following result can be directly obtained.
Theorem 1.
Suppose G is a connected graph with n vertices and for , where . Then, .
Next, we discuss the extremal cases of the IC burning number.
Theorem 2.
Suppose G is a connected graph with n vertices and is the minimum degree of G. Then, if and only if .
Proof.
Let be a -burning sequence of graph G and be a vertex with .
First, if , then . Otherwise, assume . Let the first fire source , then will be burned in the second step. Meanwhile, we can choose another vertex other than as . Then, we find that there are at least three vertices that will be burned in two steps. Furthermore, thus, there exist at most vertices unburned in the first two steps. So, we obtain , which contradicts to . Therefore, .
On the other hand, if , according to Theorem 1, we can easily obtain . □
Theorem 3.
Suppose G is a graph with n vertices and is the maximum degree. Then, is an optimum β-burning sequence for G if and only if one of the following conditions is met:
(1) , and for all .
(2) , and for all .
Proof.
Assume that is an optimum -burning sequence for G. According to Equation (1), , which shows that every vertex in set is adjacent to , and the influence of its neighbors on it is more than . Since these vertices can only be burned by in the second step, there are two possible cases for : (1) If , then it implies that and for any , . (2) If , then we must have and for any , .
Conversely, since G has at least two vertices, then .
If , and there is a vertex such that while for any , then let . If and for any , then let be any vertices in . If and for any , then let . In each case, can burn graph G; thus, it is an optimum -burning sequence for G. □
Given a graph G, suppose is a -burning sequence. Obviously, if vertex and , then , i.e., is a fire source. From the above observation, a bound on the IC burning number of G can be easily concluded.
Theorem 4.
Suppose G is a connected graph with n vertices, and is a degree sequence such that with . If , then , and .
Proof.
Clearly, we have , so the influence that each vertex receives from its neighbors is less than in graph G. As a result, these vertices are firstly chosen as source fires in the -burning process of graph G and let . Then, we directly obtain . □
At the end of this section, we discuss a bound of IC burning number with certain domination numbers. If D is a subset of , D’s k-th closed neighborhood is denoted by as defined above. If D satisfies the condition that for every vertex , there exists a vertex and , then D is called a k-step dominating set. Meanwhile, we can define -way k-step dominating set of G. A k-step dominating set D is called a -way k-step dominating set of G if for any either or there exists such that . The -way k-step domination number of G denoted by is the number of the vertices in a minimum -way k-step dominating set of G.
From the above definition of -way k-step dominating set of G, we obtain
Theorem 5.
Suppose G is a connected graph with n vertices. Then, .
4. The IC Burning Number of Some Special Graphs
Given a graph G and a vertex v, the eccentricity of v is defined as . The radius is the minimum eccentricity over the vertex set G, which is denoted by rad(G), and the diameter is the maximum eccentricity over the vertex set G, which is denoted by diam(G).
Given two graphs G and H, their Cartesian product is denoted by . In , two vertices and are adjacent if and only if either and , or and .
We first list several known results for the traditional graph burning number that will be used later.
Proposition 1
([1]). Suppose G is a path with n vertices, then .
Proposition 2
([17]). Suppose G is a complete bipartite graph with , then .
Proposition 3
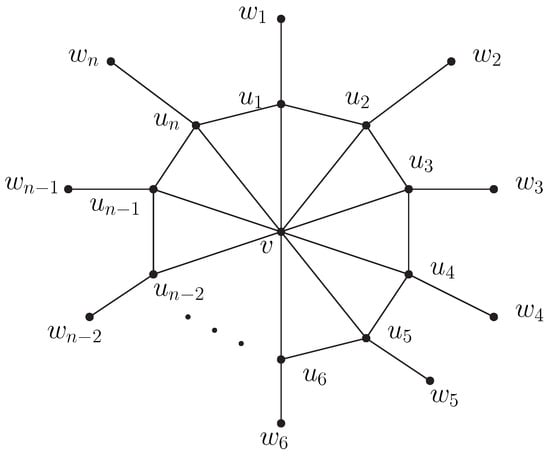
([17]). Suppose G is a Helm graph (See Figure 2 for Helm graph.) with , then .

Figure 2.
An example of a Helm () graph.
Proposition 4
([2]). Suppose G is a graph with radius rad(G) and diameter diam(G). Then
Proposition 5
([14]). Suppose two graphs G and H are connected graphs, then
For the new generalized graph burning IC model, we present the following results for .
Theorem 6.
Suppose is a path with n vertices and . Then
Proof.
Suppose with and for .
Case 1. .
Note that for . From Proposition 1, we obtain .
Case 2. .
It is easy to obtain and . Here, we consider cases for . We let , , and for . Clearly, (, , …, ) is a -burning sequence of and thus . On the other hand, consider for , so we obtain . Thus, while . □
Theorem 7.
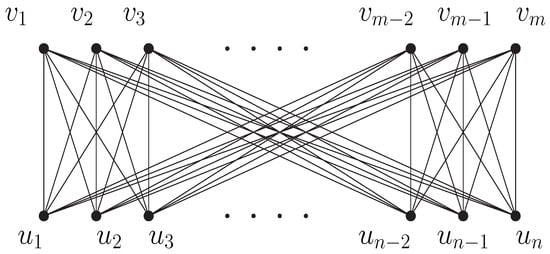
Suppose is a complete bipartite graph with and (See Figure 3). Then

Figure 3.
An example of ().
Proof.
Suppose the vertices of are divided into two parts, A = {,, …, } and B = {,, …, }. Then, for and for . We complete the proof by analyzing the following three cases.
Case 1. .
In this case, . From Proposition 2, we directly obtain while .
Case 2. .
First, let for . Obviously, is a -burning sequence of , which implies . On the other hand, because for all , according to Theorem 1, we obtain . Thus, while .
Case 3. .
According to Theorem 1, it is easy to obtain . Then, we directly obtain while . □
The Helm graph, which has vertices, is obtained by adding a pendant edge at each vertex to the cycle of the n-wheel graph; see Figure 2.
Theorem 8.
Suppose G is a Helm graph with and . Then
Proof.
Let v be the center vertex in the Helm graph and be pendant edges. Meanwhile, for .
Case 1. .
Case 1.1. .
For a Helm graph G with , it should be noted that the diameter and radius of G are 3 and 2, respectively. From Proposition 4, we obtain . However, note that , and according to Theorem 3, it follows that .
Case 1.2. .
In these cases, the diameter and radius of the Helm graph G are 4 and 2, respectively. If , from Proposition 4, we directly obtain . If , we choose , , and . Obviously, is a -burning sequence; thus, . On the other hand, it is clear that from Proposition 3. Thus, we obtain when .
In summary, we have for .
Case 2. .
Case 2.1. .
For the case and , we let , , , and . Obviously, is a -burning sequence of G, which means . On the other hand, for , so we have . Note that in any optimum -burning sequences, must be burned later than , which means . So, we obtain while .
Similarly, for , we let , , , and . Clearly, is a -burning sequence of G, which means . On the other hand, for , which means . We obtain while .
So, when , for all .
Case 2.2. .
Let for and . Obviously, is a -burning sequence of G, which means . Now, we prove . In fact, for , which implies that there are vertices that cannot be burned by any of their neighbors. These vertices must be chosen as the sources fires in any optimum -burning sequences. So, clearly . We directly obtain for . □
The fan graph is obtained by connecting to every vertex in the path , where , which is denoted by . The vertex of is called the center of the fan graph. See Figure 4.
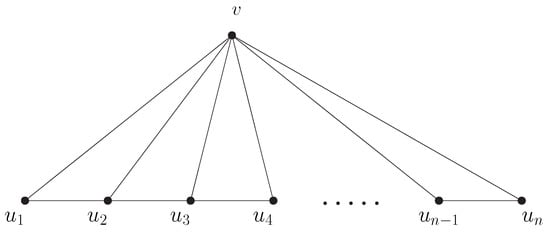
Figure 4.
An example of a fan () graph.
Theorem 9.
Suppose G is a fan graph with and . Then
Proof.
Let v be the center vertex in the fan graph G and .
Case 1. .
Whether is less than or not, we choose first and . Obviously, is the -burning sequence of G when . From the definition, we obtain . On the other hand, for any graph G with more than two vertices, we have . Thus, we have .
Case 2. .
Let , and for . Obviously, is a -burning sequence of G and thus . On the other hand, considering for , all vertices () and v must be chosen as source fires in any optimum -burning sequences of G. At least steps are thus required to burn all the vertices in G. So, we obtain .
Case 3. .
It is easy to see that all these vertices should be set on fire directly, so we obtain while . □
Given and an integer k such that , we define the generalized Petersen graph as a graph on vertices with vertex set
and edge set
Theorem 10.
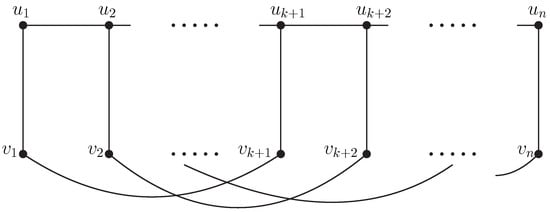

Suppose G is a generalized Petersen graph (See Figure 5) with , k is an integer with , and . The values of for generalized Petersen graphs are listed in the following Table 1.

Figure 5.
An example of a generalized Petersen () graph.

Table 1.
of generalized Petersen graphs.
Proof.
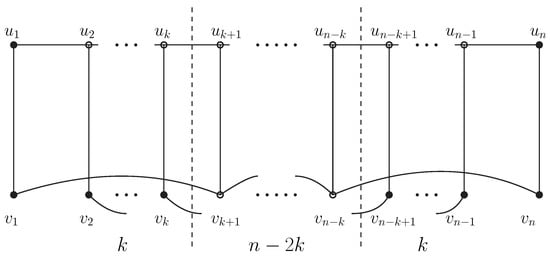
Suppose and are two partite sets of G. Now, we divide the following four cases to complete the proof.
Case 1. .
If , , we borrow the results directly from [12]; see Table 1.
Case 2. .
Case 2.1. .
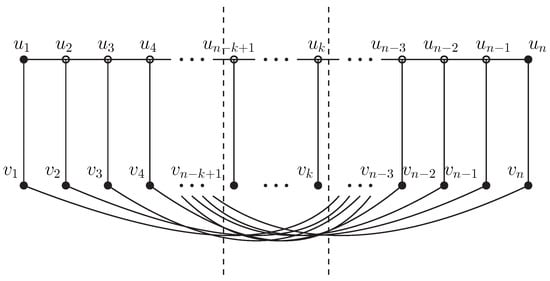
There exists at least one vertex in whose degree is 1; see Figure 6, where the solid dots represent that they can be burned by their neighbors, and the hollow dots indicate that they can only be source of fires. For clarity, we converted the graph to another form as shown in Figure 7.

Figure 6.
The state of vertices of G in Case 2.1.

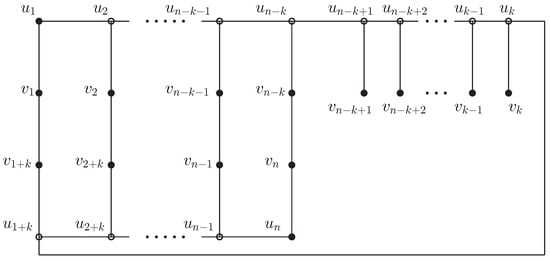
Figure 7.
The state of vertices of G in Case 2.1 with another form.
First, we consider the case for . As for the case and , from simple verification, we obtain for both and . Then, we consider the cases for . We let , , for and . Obviously, is a -burning sequence of G. From the definition, we obtain . On the other hand, the vertices for must be chosen as the source fires in any optimum -burning sequences of G. Suppose that is burned in step t, then will be burned in step . Therefore, no matter how the source fires are chosen, all vertices of G cannot be burned in steps, which implies that . Thus, while .
Next, we consider the case for . In this case, and implies . See Figure 7.
From simple verification, we obtain for . Here, we consider the cases for . Let for . Obviously, is the -burning sequence of G. From the definition, we obtain . On the other hand, the vertices for must be chosen as the source fires in any optimum -burning sequences of G, and we have . Thus, we obtain .
Case 2.2. .
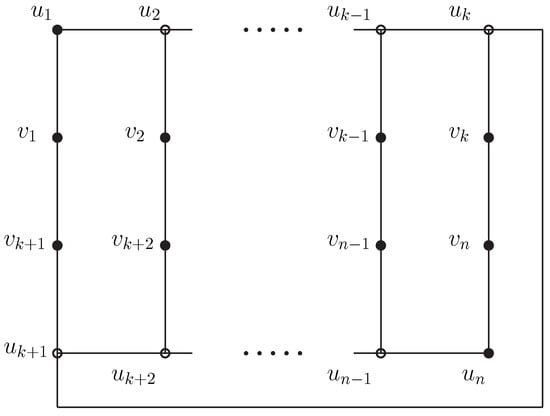
The degree of all the vertices in set is 2 in this case. We can also convert the graph to another form as shown in Figure 8.

Figure 8.
The state of vertices of G in Case 2.2.
First, we consider the case for , which means , and it is not hard to see . As for the cases when , we let , , and for . Clearly, is a -burning sequence of G. Hence, we obtain . On the other hand, all vertices in set except and must be chosen as source fires in any optimum -burning sequences of G. Thus, at least steps are required to burn all the vertices of G. So, we obtain .
Case 2.3. .
From simple checking, we obtain for and . As for other cases, see Figure 9. Let , and . Obviously, the degree of each vertex in A is 3, and the degree of each vertex in both and is 2. All vertices with degree 3 in this graph must be sources of fires, which means . On the other hand, let , , for and for as source fires. It is easy to check that is a -burning sequence of G. Thus, .

Figure 9.
The state of vertices of G in Case 2.3.
Case 3. .
Case 3.1. .
As shown in Figure 6, all vertices except with degree 1 cannot be burned by their neighbors; thus, . Furthermore, also notice that is a -burning sequence of G. Thus, while .
Case 3.2. .
In this case, all vertices should be the sources of fire, so while . □
Theorem 11.
Suppose and are two paths with and . Then
Proof.
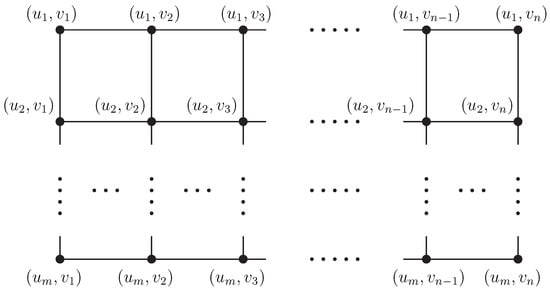
Suppose and . There are four cases related to the degree of vertices in graph , when . Note that , for and , and the degree of the vertex is equal to 4 otherwise.
Case 1. .
When , . Because and are both paths, from Proposition 1, their burning numbers are and , respectively. Furthermore, it is easy to calculate their radii, and , respectively. Then, we borrow the results in Proposition 5 directly here, which are while .
Case 2. .
From simple verification, we obtain for and for both and . Then, we consider other cases.
We claim that , is an optimum -burning sequence in . Clearly, the above sequence is a -burning sequence of , so . On the other hand, the number of vertices with influence less than is which implies that . So, we have .
Case 3. .
As shown in Figure 10, all vertices except with degree 2 cannot be burned by their neighbor; thus, . Furthermore, also notice that is a -burning sequence of . Thus, while .

Figure 10.
An example of a () graph.
Case 4. .
All vertices should be set on fires directly; thus, . □
5. Conclusions and Future Work
In this paper, we introduced a new generalized graph burning model called the Independent Cascade Graph Burning model (abbreviated as the IC Model), which is more realistic than the traditional graph burning model. Regarding the IC burning number, we carried out the following work:
- The upper and lower bounds of the IC burning numbers of general graphs were discussed.
- The IC burning numbers of several special graphs were determined.
As for future research, we are interested in related algorithms to calculate IC burning numbers on large networks, and we also intend to calculate the IC burning number of some other special graphs.
Author Contributions
Methodology, X.Q. and Z.C.; derivation, J.S.; supervision, X.Q. and Z.C.; writing—original draft preparation, J.S.; writing—review and editing, X.Q. and Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (CN) with No. 11971271; and the Natural Science Foundation of Shandong Province with No. ZR2019MA008.
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Acknowledgments
The authors would like to express their gratitude to the editor and the anonymous reviewers. Their insightful and constructive comments greatly improved the quality and presentation of this paper.
Conflicts of Interest
The authors have no relevant financial or non-financial interest to disclose.
References
- Bonato, A.; Janssen, J.; Roshanbin, E. How to burn a graph. Internet Math. 2016, 12, 85–100. [Google Scholar] [CrossRef]
- Bonato, A.; Janssen, J.; Roshanbin, E. Burning a Graph as a Model of Social Contagion. Algorithms and Models for the Web Graph; Springer International Publishing: Cham, Switzerland, 2014; pp. 13–22. [Google Scholar]
- Roshanbin, E. Burning a Graph as a Model for the Spread of Social Contagion; Dalhousie University: Halifax, NS, Cananda, 2016. [Google Scholar]
- Bessy, S.; Bonato, A.; Janssen, J.; Rautenbach, D.; Roshanbin, E. Burning a graph is hard. Discret. Appl. Math. 2017, 232, 73–87. [Google Scholar] [CrossRef]
- Bonato, A.; Kamali, S. Approximation algorithms for graph burning. In Proceedings of the International Conference on Theory and Applications of Models of Computation, Kitakyushu, Japan, 13–16 April 2019. [Google Scholar]
- Garcia-Diaz, J.; Perez-Sansalvador, J.C.; Rodriguez-Henriquez, L.; Cornejo-Acosta, J.A. Burning graphs through farthest-first traversal. IEEE Access 2022, 10, 30395–30404. [Google Scholar] [CrossRef]
- Gautam, R.K.; Kare, A.S.; Bhavani, S.D. Faster heuristics for graph burning. Appl. Intell. 2022, 52, 1351–1361. [Google Scholar] [CrossRef] [PubMed]
- Simon, M.; Huraj, L.; Luptakova, I.D.; Pospichal, J. Heuristics for spreading alarm throughout a network. Appl. Sci. 2019, 9, 3269. [Google Scholar] [CrossRef]
- Farokh, Z.R.; Tahmasbi, M.; Tehran, Z.; Bual, Y. New heuristics for burning graphs. arXiv 2020, arXiv:2003.09314. [Google Scholar]
- Bessy, S.; Bonato, A.; Janssen, J.; Rautenbach, D. Bounds on the burning number. Discret. Appl. Math. 2018, 235, 16–22. [Google Scholar] [CrossRef]
- Land, M.R.; Lu, L.Y. An Upper Bound on the Burning Number of Graphs. In Algorithms and Models for the Web Graph; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–8. [Google Scholar]
- Sim, K.A.; Tan, T.S.; Wong, K.B. On the Burning Number of Generalized Petersen Graphs. Bull. Malays. Math. Sci. Soc. 2017, 41, 1657–1670. [Google Scholar] [CrossRef]
- Liu, H.Q.; Zhang, R.T.; Hu, X.L. Burning number of theta graphs. Appl. Math. Comput. 2019, 361, 246–257. [Google Scholar] [CrossRef]
- Mitsche, D.; Pralat, P.; Roshanbin, E. Burning number of graph products. Theor. Comput. Sci. 2018, 746, 124–135. [Google Scholar] [CrossRef]
- Jyothsna, B.; Radhakrishnan, N.B. Burning Number of some Families and some Products of Graphs. Int. J. Pure Appl. Math. 2018, 118, 1489–1500. [Google Scholar]
- Bonato, A.; Lidbetter, T. Bounds on the burning numbers of spiders and path-forests. Theor. Comput. Sci. 2019, 794, 12–19. [Google Scholar] [CrossRef]
- Li, Y.K.; Qin, X.X.; Li, W. The generalized burning number of graphs. Appl. Math. Comput. 2021, 411, 126306. [Google Scholar] [CrossRef]
- Kempe, D.; Kleinberg, J.; Tardos, E. Maximizing the Spread of Influence through a Social Network. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 24–27 August 2003; pp. 137–146. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Elsevier Science Publishing Co., Inc.: New York, NY, USA, 1976; Volume 290, p. 10017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).