Inertial Viscosity Approximation Methods for General Split Variational Inclusion and Fixed Point Problems in Hilbert Spaces

Abstract

The purpose of this paper is to find a common element of the fixed point set of a nonexpansive mapping and the set of solutions of the general split variational inclusion problem in symmetric Hilbert spaces by using the inertial viscosity iterative method. Some strong convergence theorems of the proposed algorithm are demonstrated. As applications, we use our results to study the split feasibility problem and the split minimization problem. Finally, the numerical experiments are presented to illustrate the feasibility and effectiveness of our theoretical findings, and our results extend and improve many recent ones.

1. Introduction

The Hilbert space theory and the nonlinear fixed point problem are an important field in mathematics and optimization. Symmetry is closely related to the fixed point problem. And Hilbert space is one kind of reflexive space, and a reflexive Hilbert space is called a symmetric space. Let $\mathcal{H}$ be a real symmetric Hilbert space and $S:\mathcal{H}\to \mathcal{H}$ be a mapping. The set of fixed points of S is denoted by $Fix\left(S\right)$. It is known that S is a contraction if there exists a constant $\rho \in (0,1)$ such that $\parallel Sx-Sy\parallel \le \rho \parallel x-y\parallel , \forall x,y\in \mathcal{H}$.

Let $T:\mathcal{H}\to 2^{\mathcal{H}}$ be a set valued mapping. Then, T is said to be monotone if $⟨x-y,u-v⟩\ge 0$ for all $x,y\in \mathcal{H}$ with $u\in Tx$ and $v\in Ty$. A monotone mapping T is maximal monotone if its graph $G\left(T\right)=\left\{\right(x,y),y\in Tx\}$ is not properly contained in the graph of any other monotone mapping. The resolvent operator $J_{\beta }^T$ of mapping T defined by $J_{\beta }^T={(I+\beta T)}^{-1}$ for each $\beta >0$.

It is worth noting that the split variational inclusion problem serves as a model in image reconstruction, radiation therapy and sensor networks [1,2,3]. There are many other special cases of split variational inclusion problem, such as split feasibility problem, variational inclusion problem, fixed point problem, split equilibrium problem and split minimization problem; see [4,5,6,7,8,9,10] and the references therein. Let ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ be two real Hilbert spaces, and let $B_1:{\mathcal{H}}_1\to 2^{{\mathcal{H}}_1}$ and $B_2:{\mathcal{H}}_2\to 2^{{\mathcal{H}}_2}$ be maximal monotone mappings. In fact, the following is a split variational inclusion problem: to find a point $x\in {\mathcal{H}}_1$ such that

$$0\in B_{1}x,\mathrm{and}0\in B_{2}Ax,$$

where $A:{\mathcal{H}}_1\to {\mathcal{H}}_2$ is a bounded linear operator. Several iterative algorithms for finding the set of solutions of the split variational inclusion problem have been studied by many authors [11,12,13]. Particularly, in 2012, Byrne et al. [14] introduced the following iteration process for given $x_0\in {\mathcal{H}}_1, \lambda >0$:

$$x_{n+1}=J_{\lambda }^{B_1}[x_n+ϵA^{*}(J_{\lambda }^{B_2}-I)A{x}_n],$$

where $ϵ\in (0,\frac{2}{\parallel A^{*}A\parallel })$. They established the weak and strong convergence of the algorithm to solve the split variational inclusion problem. In 2014, Kazmi and Rivi [13] proved a strong convergence result of the following algorithm to a solution of the split variational inclusion problem and the fixed point problem of a nonexpansive mapping in Hilbert space:

$$\left\{\begin{array}{cc}\hfill & u_n=J_{\lambda }^{B_1}[x_n+ϵA^{*}(J_{\lambda }^{B_2}-I)A{x}_n],\hfill \\ \hfill & x_{n+1}={\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)S{u}_n.\hfill \end{array}\right.$$

On the other hand, many authors are increasingly interested in using inertial techniques to build efficient iterative algorithms due to the effect that inertial techniques have to speed up convergence, see [15,16,17,18,19,20,21] and references therein. In 2001, Alvarez and Attouch [22] introduced the following inertial proximal point method to solve the variational inclusion problem:

$$x_{n+1}=J_{{\lambda }_n}^{B_1}[x_n+{\theta }_n(x_n-x_{n-1})],$$

where $\left\{{\theta }_n\right\}\in [0,1)$, $\left\{{\lambda }_n\right\}>0$. They proved that the sequence converges weakly to a zero of the maximal monotone operator B. Thenceforward, in 2017, Chuang et al. [23] extended this method to the hybrid inertial proximal algorithm in Hilbert spaces. They proved that their iterative sequence converges weakly to the solution of the split variational inclusion problem. In 2018, Cholamjiak et al. [20] obtained strong convergence results by combining the inertial technique of the Halpern iteration method. Moreover, in 2020, Pham et al. [24] proposed an algorithm which is a combination of Mann method and inertial method for solving the split variational inclusion problem in real Hilbert spaces:

$$\left\{\begin{array}{cc}\hfill & x_0,x_1\in {\mathcal{H}}_1,\hfill \\ \hfill & w_n=x_n+{\alpha }_n(x_n-x_{n-1}),\hfill \\ \hfill & y_n=J_{\beta }^{B_1}(I-{\lambda }_n{A}^{*}(I-J_{\beta }^{B_2}A))w_n,\hfill \\ \hfill & x_{n+1}=(1-{\theta }_n-{\beta }_n)x_n+{\theta }_n{y}_n.\hfill \end{array}\right.$$

They proved that the sequence $\left\{x_n\right\}$ converges strongly to a solution of the split variational inclusion problem with two set-valued maximal monotone mappings.

Motivated and inspired by the above work, we consider the following general split variational inclusion problem of finding a point $x\in {\mathcal{H}}_1$ such that

$$x\in \bigcap _{i=1}^N{B}_i^{-1}\left(0\right),\mathrm{and}Ax\in \bigcap _{i=1}^N{K}_i^{-1}\left(0\right),$$

where $B_i:{\mathcal{H}}_1\to {\mathcal{H}}_1,K_i:{\mathcal{H}}_2\to {\mathcal{H}}_2,i=1,2,\dots ,N$ are two families of maximal monotone mappings. The solution set of the general split variational inclusion problem is denoted by $\Gamma$. We present an inertial viscosity iterative algorithm for the general split variational inclusion problem and the fixed point problem of a nonexpansive mapping:

$$\left\{\begin{array}{cc}\hfill & z_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ \hfill & w_n={\Sigma }_{i=1}^N{\gamma }_{i,n}{J}_{{\beta }_{i,n}}^{B_i}[z_n-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n],\hfill \\ \hfill & x_{n+1}={\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)[{\delta }_n{w}_n+(1-{\delta }_n)S{w}_n].\hfill \end{array}\right.$$

(1)

Then, the strong convergence theorem of this algorithm is proved. We apply this iterative scheme to studying the split feasibility problem and the split minimization problem. Finally, we give the numerical experiments to illustrate the feasibility and effectiveness of our main theorem. Our results extend and improve many recent ones [12,13,14,20,23,24].

2. Preliminaries

Let $\mathcal{C}$ be a nonempty closed convex subset of a real symmetric Hilbert space $\mathcal{H}$ with inner product $⟨·,·⟩$ of regularity and symmetry and norm $\parallel ·\parallel$. $x_n\rightharpoonup x$ and $x_n\to x$ denote the weak convergence and strong convergence of the sequence $\left\{x_n\right\}$ to a point x, respectively. A mapping $P_{\mathcal{C}}:\mathcal{H}\to \mathcal{C}$ is called the metric projection if $\parallel x-P_{\mathcal{C}}x\parallel \le \parallel x-y\parallel , \forall y\in \mathcal{C}$. It is known that $P_{\mathcal{C}}$ is nonexpansive and

$$⟨x-P_{\mathcal{C}}x,y-P_{\mathcal{C}}x⟩\le 0, \forall y\in \mathcal{C}.$$

The following lemmas and concepts will be needed to prove our main results.

Definition 1. 

Suppose $S:\mathcal{H}\to \mathcal{H}$ is a mapping. Then, S is called nonexpansive if

$$\parallel Sx-Sy\parallel \le \parallel x-y\parallel , \forall x,y\in \mathcal{H},$$

S is said to be firmly nonexpansive if

$${\parallel Sx-Sy\parallel }^2\le ⟨Sx-Sy,x-y⟩, \forall x,y\in \mathcal{H}.$$

Lemma 1 

([11]). Suppose $\mathcal{H}$ is a real Hilbert space. Then, for all $x,y\in \mathcal{H}, \kappa \in R$, the following statements are hold:

(i) 

$\parallel x+y\parallel \le {\parallel x\parallel }^2+2⟨x+y,y⟩$;

(ii) 

${\parallel \kappa x+(1-\kappa )y\parallel }^2={\kappa \parallel x\parallel }^2{-\kappa (1-\kappa )\parallel x-y\parallel }^2+(1-\kappa ){\parallel y\parallel }^2$.

Lemma 2 

([17]). Assume $\left\{a_n\right\}$ is a sequence of nonnegative real numbers satisfying:

$$a_{n+1}\le (1-{\alpha }_n)a_n+{\alpha }_n{b}_n,n\ge 0,$$

where $\left\{{\alpha }_n\right\}\subset (0,1)$ and $\left\{b_n\right\}\subset R$ such that:

(i) 

${lim}_{n\to \infty }{\alpha }_n=0$ and ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty ;$

(ii) 

either ${lim\; sup}_{n\to \infty }{b}_n\le 0$ or ${\sum }_{n=0}^{\infty }\left|{\alpha }_n{b}_n\right|<\infty .$

Then ${lim}_{n\to \infty }{a}_n=0$.

Lemma 3 

([25]). Suppose $S:\mathcal{C}\to \mathcal{H}$ is a nonexpansive mapping, and $\left\{x_n\right\}$ is a sequence in $\mathcal{C}$. If $x_n\rightharpoonup u$ and ${lim}_{n\to \infty }\parallel x_n-S{x}_n\parallel =0$, then $Su=u$.

Lemma 4 

([26]). Suppose that $\left\{a_n\right\}$ is a sequence of nonnegative real numbers satisfying $a_{n_i}<a_{n_i+1}$ for all $i\in \mathbb{N}$, where $\left\{n_j\right\}$ is a subsequence of $\left\{n\right\}$. Then, there exists a nondecreasing sequence $\left\{l_j\right\}\subset \mathbb{N}$ such that $l_j\to \infty$ and $j\in \mathbb{N}$, we have

$$a_{l_j}<a_{l_j+1}\mathrm{and}{a}_j<a_{l_j+1}.$$

In fact, $l_j=max\{k\le j:a_k<a_{k+1}\}$.

Lemma 5 

([27]). Let $B:\mathcal{H}\to 2^{\mathcal{H}}$ be a set-valued maximal monotone mapping and $\beta >0$, the following relations hold:

(i) 

For each $\beta >0$, the resolvent mapping $J_{\beta }^B$ is is a single-valued and firmly nonexpansive mapping;

(ii) 

$D\left(J_{\beta }^B\right)=\mathcal{H},F\left(J_{\beta }^B\right)=B^{-1}\left(0\right)=\{x\in D\left(B\right),0\in Bx\}$;

(iii) 

$(I-J_{\beta }^B)$ is a firmly nonexpansive mapping;

(iv) 

Suppose that $B^{-1}\left(0\right)\ne \varnothing$, then for all $x\in \mathcal{H}$, $z\in B^{-1}\left(0\right)$ and $\parallel J_{\beta }^B{x-z\parallel }^2\le {\parallel x-z\parallel }^2-{\parallel J_{\beta }^{B}x-x\parallel }^2$;

(v) 

Suppose that $B^{-1}\left(0\right)\ne \varnothing$, then for all $x\in \mathcal{H}$, $p\in B^{-1}\left(0\right)$ and $⟨x-J_{\beta }^{B}x,J_{\beta }^{B}x-p⟩\ge 0$.

Lemma 6. 

Assume that ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ are two real Hilbert spaces. Let $A:{\mathcal{H}}_1\to {\mathcal{H}}_2$ be a linear and bounded operator with its adjoint $A^{*}$. Let $B_i:{\mathcal{H}}_1\to {\mathcal{H}}_1,K_i:{\mathcal{H}}_2\to {\mathcal{H}}_2,i=1,2,\dots ,N$ are two families of maximal monotone mappings. Let $J_{{\beta }_i}^{B_i}$ and $J_{{\beta }_i}^{K_i}$ be the resolvent mapping of $B_i$ and $K_i$, respectively. Suppose that the solution set of the the solution set Γ is nonempty and ${\beta }_i>0, {\lambda }_i>0$. Then, for any $z\in H_1$, z is a solution of general split variational inclusion problem if and only if $J_{{\beta }_i}^{B_i}[z-{\lambda }_i{A}^{*}(I-J_{{\beta }_i}^{K_i})Az]=z$.

Proof. 

⇒ Let $z\in \Gamma$, then $z\in {\bigcap }_{i=1}^N{B}_i^{-1}\left(0\right)$ and $Az\in {\bigcap }_{i=1}^N{K}_i^{-1}\left(0\right)$. From Lemma 5(ii), we have that

$$\begin{array}{c}\hfill J_{{\beta }_i}^{B_i}[z-{\lambda }_i{A}^{*}(I-J_{{\beta }_i}^{K_i})Az]=J_{{\beta }_i}^{B_i}[z-{\lambda }_i{A}^{*}(Az-J_{{\beta }_i}^{K_i}Az)]=J_{{\beta }_i}^{B_i}z=z.\end{array}$$

⇐ Let $J_{{\beta }_i}^{B_i}[z-{\lambda }_i{A}^{*}(I-J_{{\beta }_i}^{K_i})Az]=z$ and $p\in \Gamma$. From Lemma 5(v), for any $p\in B_i^{-1}\left(0\right)$, we get

$$⟨(z-{\lambda }_i{A}^{*}(I-J_{{\beta }_i}^{K_i})Az)-z,z-p⟩\ge 0,$$

which implies that $⟨A^{*}(I-J_{{\beta }_i}^{K_i})Az,z-p⟩\le 0$, then $⟨Az-J_{{\beta }_i}^{K_i}Az,Az-Ap⟩\le 0$. For any $w\in K_i^{-1}\left(0\right)$, we also use Lemma 5(v) to obtain

$$\begin{array}{c}\hfill ⟨Az-J_{{\beta }_i}^{K_i}Az,w-J_{{\beta }_i}^{K_i}Az⟩\le 0,\end{array}$$

Thus, we observe that

$$\begin{array}{c}\hfill ⟨Az-J_{{\beta }_i}^{K_i}Az,w-J_{{\beta }_i}^{K_i}Az+Az-Ap⟩\le 0,\end{array}$$

which means for any $p\in B_i^{-1}\left(0\right)$ and $w\in K_i^{-1}\left(0\right)$, we have

$$\begin{array}{c}\hfill \parallel Az-J_{{\beta }_i}^{K_i}{Az\parallel }^2\le ⟨Az-J_{{\beta }_i}^{K_i}Az,Ap-w⟩.\end{array}$$

Since $p\in \Gamma$, then $p\in {\bigcap }_{i=1}^N{B}_i^{-1}\left(0\right)$ and $Ap\in {\bigcap }_{i=1}^N{K}_i^{-1}\left(0\right)$, we get $Az=J_{{\beta }_i}^{K_i}Az$, then $Az\in F\left(J_{{\beta }_i}^{K_i}\right)=K_i^{-1}\left(0\right)$, so $Az\in {\bigcap }_{i=1}^N{K}_i^{-1}\left(0\right)$. It follows that

$$\begin{array}{c}\hfill z=J_{{\beta }_i}^{B_i}[z-{\lambda }_i{A}^{*}(I-J_{{\beta }_i}^{K_i})Az]=J_{{\beta }_i}^{B_i}z,\end{array}$$

which implies $z\in F\left(J_{{\beta }_i}^{B_i}\right)=B_i^{-1}\left(0\right)$, so $z\in {\bigcap }_{i=1}^N{K}_i^{-1}\left(0\right)$. Therefore $z\in \Gamma$. □

3. Main Results

Theorem 1. 

Let ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ be two real Hilbert spaces. Let $A:{\mathcal{H}}_1\to {\mathcal{H}}_2$ be a bounded linear operator and $A^{*}$ be the adjoint operator of A. Suppose that $B_i:{\mathcal{H}}_1\to {\mathcal{H}}_1\mathit{and}{K}_i:{\mathcal{H}}_2\to {\mathcal{H}}_2,i=1,2,\dots ,N$ are two families of maximal monotone mappings. Let $f:{\mathcal{H}}_1\to {\mathcal{H}}_1$ be a contraction with coefficient $\rho \in (0,1)$ and $S:{\mathcal{H}}_1\to {\mathcal{H}}_1$ be a nonexpansive mapping such that $Fix\left(S\right)\bigcap \Gamma \ne \varnothing$. Suppose $\left\{{\alpha }_n\right\},\left\{{\delta }_n\right\},\left\{{\gamma }_{i,n}\right\}\subset (0,1)$. Assume that $\left\{{\beta }_{i,n}\right\},\left\{{\lambda }_{i,n}\right\}$ are sequences of positive real numbers and $x_0,x_1\in {\mathcal{H}}_1$. If the sequence $\left\{x_n\right\}$ defined by (1) satisfies the following conditions:

(i) 

Let the parameter ${\theta }_n$ chosen as

$${\theta }_n=\left\{\begin{array}{cc}\hfill & min\{\theta ,\frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }\}\mathit{if}{x}_n\ne x_{n-1},\hfill \\ \hfill & \theta \mathit{otherwise},\hfill \end{array}\right.$$

where $\theta >0$, ${ϵ}_n$ is a positive real sequence such that ${ϵ}_n=o\left({\alpha }_n\right)$;

(ii) 

${lim}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$, ${\delta }_n\subset [a,b]\subset (0,1)$;

(iii) 

${\sum }_{i=1}^N{\gamma }_{i,n}=1$, ${\gamma }_{i,n}\subset [c,d]\subset (0,1)$, ${\lambda }_{i,n}\in (0,\frac{2}{{\parallel A\parallel }^2})$,

then $\left\{x_n\right\}$ converges strongly to an element ${\omega }^{†}\in Fix\left(S\right)\bigcap \Gamma$, where ${\omega }^{†}=P_{Fix\left(S\right)\bigcap \Gamma }f\left({\omega }^{†}\right)$.

Proof. 

Let ${\omega }^{†}\in Fix\left(S\right)\bigcap \Gamma$, then we have ${\omega }^{†}=J_{{\beta }_{i,n}}^{B_i}{\omega }^{†}$, $A{\omega }^{†}=J_{{\beta }_{i,n}}^{K_i}A{\omega }^{†}$ and $S{\omega }^{†}={\omega }^{†}$. By the convexity of ${\parallel ·\parallel }^2$, we obtain

$$\begin{array}{cc}\hfill \parallel w_n-{\omega }^{†}{\parallel }^2& =\parallel {\Sigma }_{i=1}^N{\gamma }_{i,n}{J}_{{\beta }_{i,n}}^{B_i}[z_n-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n]-{\omega }^{†}{\parallel }^2\hfill \\ \hfill & \le {\Sigma }_{i=1}^N{\gamma }_{i,n}{\parallel J_{{\beta }_{i,n}}^{B_i}[z_n-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n]-{\omega }^{†}\parallel }^2.\hfill \end{array}$$

(2)

It follows from Lemma 5 that $J_{{\beta }_{i,n}}^{B_i}[I-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A]$ are nonexpansive. Then, we get

$$\begin{array}{cc}& \parallel J_{{\beta }_{i,n}}^{B_i}[z_n-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n]-{\omega }^{†}{\parallel }^2\hfill \\ & \le \parallel z_n-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n-{\omega }^{†}{\parallel }^2\hfill \\ & = \parallel z_n-{\omega }^{†}{\parallel }^2+{\lambda }_{i,n}^2{\parallel A^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n\parallel }^2+2{\lambda }_{i,n}⟨z_n-{\omega }^{†},A^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n⟩\hfill \\ & = \parallel z_n-{\omega }^{†}{\parallel }^2+{\lambda }_{i,n}^2⟨(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n,A{A}^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n⟩+2{\lambda }_{i,n}⟨A(z_n-{\omega }^{†}),(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n⟩\hfill \\ & \le \parallel z_n-{\omega }^{†}{\parallel }^2+{\lambda }_{i,n}^2{\parallel A\parallel }^2{\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel }^2\hfill \\ & + 2{\lambda }_{i,n}⟨A(z_n-{\omega }^{†})+(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n-(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n,(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n⟩\hfill \\ & = \parallel z_n-{\omega }^{†}{\parallel }^2+{\lambda }_{i,n}^2{\parallel A\parallel }^2\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n{\parallel }^2-2{\lambda }_{i,n}{\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel }^2\hfill \\ & + 2{\lambda }_{i,n}⟨J_{{\beta }_{i,n}}^{K_i}A{z}_n-A{\omega }^{†},(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n⟩\hfill \\ & \le \parallel z_n-{\omega }^{†}{\parallel }^2-(2{\lambda }_{i,n}-{\lambda }_{i,n}^2{\parallel A\parallel }^2\parallel )\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n{\parallel }^2\hfill \\ & = \parallel z_n-{\omega }^{†}{\parallel }^2+{\lambda }_{i,n}({\lambda }_{i,n}{\parallel A\parallel }^2-2)\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n{\parallel }^2.\hfill \end{array}$$

which means

$$\begin{array}{cc}\hfill \parallel w_n-{\omega }^{†}{\parallel }^2& \le {\Sigma }_{i=1}^N{\gamma }_{i,n}{\parallel J_{{\beta }_{i,n}}^{B_i}[z_n-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n]-{\omega }^{†}\parallel }^2\hfill \\ \hfill & \le \parallel z_n-{\omega }^{†}{\parallel }^2+{\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}({\lambda }_{i,n}{\parallel A\parallel }^2-2)\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n{\parallel }^2.\hfill \end{array}$$

(3)

From condition (i), we have

$$\begin{array}{cc}\hfill \parallel z_n-{\omega }^{†}\parallel & = \parallel x_n+{\theta }_n(x_n-x_{n-1})-{\omega }^{†}\parallel \hfill \\ \hfill & \le \parallel x_n-{\omega }^{†}\parallel +{\theta }_n\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & = \parallel x_n-{\omega }^{†}\parallel +{\alpha }_n\frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & \le \parallel x_n-{\omega }^{†}\parallel +{\alpha }_n{M}_1,\hfill \end{array}$$

$M_1>0$ is a constant. Define $y_n={\delta }_n{w}_n+(1-{\delta }_n)S{w}_n$, then we have

$$\begin{array}{cc}\hfill \parallel y_n-{\omega }^{†}\parallel & \le {\delta }_n\parallel w_n-{\omega }^{†}\parallel +(1-{\delta }_n)\parallel S{w}_n-{\omega }^{†}\parallel \hfill \\ \hfill & \le {\delta }_n\parallel w_n-{\omega }^{†}\parallel +(1-{\delta }_n)\parallel w_n-{\omega }^{†}\parallel \hfill \\ \hfill & = \parallel w_n-{\omega }^{†}\parallel .\hfill \end{array}$$

(4)

We compute that:

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-{\omega }^{†}\parallel \hfill \\ \hfill & = \parallel {\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)y_n-{\omega }^{†}\parallel \hfill \\ \hfill & \le {\alpha }_n\parallel f\left(x_n\right)-{\omega }^{†}\parallel +(1-{\alpha }_n)\parallel y_n-{\omega }^{†}\parallel \hfill \\ \hfill & \le {\alpha }_n\rho \parallel x_n-{\omega }^{†}\parallel +(1-{\alpha }_n)(\parallel x_n-{\omega }^{†}\parallel +{\alpha }_n{M}_1)\hfill \\ \hfill & \le [1-{\alpha }_n(1-\rho )]\parallel x_n-{\omega }^{†}\parallel +{\alpha }_n{M}_1\hfill \\ \hfill & \le max\{\parallel x_n-{\omega }^{†}\parallel ,\frac{M_1}{1-\rho }\}\le \cdots \le max\{\parallel x_0-{\omega }^{†}\parallel ,\frac{M_1}{1-\rho }\}.\hfill \end{array}$$

which implies that $x_n$ is bounded; hence, $z_n$, $w_n$, $y_n$ and $S{w}_n$ is also bounded.

Since $\left\{x_n\right\}$ is bounded and $\parallel z_n-{\omega }^{†}\parallel \le \parallel x_n-{\omega }^{†}\parallel + {\alpha }_n{M}_1$, there exists a constant $M_2>0$, we have

$$\begin{array}{cc}\hfill & \parallel z_n-{\omega }^{†}{\parallel }^2\le {\parallel x_n-{\omega }^{†}\parallel }^2+{\alpha }_n{M}_2.\hfill \end{array}$$

(5)

Therefore, using (3), we observe that

$$\begin{array}{cc}\hfill \parallel w_n-{\omega }^{†}{\parallel }^2& \le \parallel z_n-{\omega }^{†}{\parallel }^2+{\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}({\lambda }_{i,n}{\parallel A\parallel }^2-2)\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n{\parallel }^2\hfill \\ \hfill & \le |x_n-{\omega }^{†}{\parallel }^2+{\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}({\lambda }_{i,n}{\parallel A\parallel }^2-2)\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n{\parallel }^2+{\alpha }_n{M}_2.\hfill \end{array}$$

(6)

It follows from (2) that

$$\begin{array}{cc}& \parallel J_{{\beta }_{i,n}}^{B_i}[z_n-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n]-{\omega }^{†}{\parallel }^2\hfill \\ & \le \parallel z_n-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n-{\omega }^{†}{\parallel }^2\hfill \\ & \le ⟨w_n-{\omega }^{†},z_n+{\lambda }_{i,n}{A}^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n-{\omega }^{†}⟩\hfill \\ & = \frac{1}{2}\parallel z_n+{\lambda }_{i,n}{A}^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n-{\omega }^{†}{\parallel }^2+\frac{1}{2}{\parallel w_n-{\omega }^{†}\parallel }^2\hfill \\ & - \frac{1}{2}{\parallel w_n-{\omega }^{†}-z_n-{\lambda }_{i,n}{A}^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n+{\omega }^{†}\parallel }^2\hfill \\ & = \frac{1}{2}\parallel z_n-{\omega }^{†}+{\lambda }_{i,n}{A}^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n{\parallel }^2+\frac{1}{2}{\parallel w_n-{\omega }^{†}\parallel }^2\hfill \\ & - \frac{1}{2}{\parallel w_n-z_n-{\lambda }_{i,n}{A}^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel }^2\hfill \\ & = \frac{1}{2}\parallel w_n-{\omega }^{†}{\parallel }^2+\frac{1}{2}\parallel z_n-{\omega }^{†}{\parallel }^2+\frac{1}{2}{\lambda }_{i,n}^2{\parallel A^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel }^2+⟨z_n-{\omega }^{†},{\lambda }_{i,n}{A}^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n⟩\hfill \\ & - \frac{1}{2}\parallel w_n-z_n{\parallel }^2-\frac{1}{2}{\lambda }_{i,n}^2{\parallel A^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel }^2+⟨w_n-z_n,{\lambda }_{i,n}{A}^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n⟩\hfill \\ & = \frac{1}{2}\parallel w_n-{\omega }^{†}{\parallel }^2+\frac{1}{2}\parallel z_n-{\omega }^{†}{\parallel }^2-\frac{1}{2}{\parallel w_n-z_n\parallel }^2+⟨w_n-{\omega }^{†},{\lambda }_{i,n}{A}^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n⟩\hfill \\ & \le \frac{1}{2}\parallel w_n-{\omega }^{†}{\parallel }^2+\frac{1}{2}\parallel z_n-{\omega }^{†}{\parallel }^2-\frac{1}{2}\parallel w_n-z_n{\parallel }^2+{\lambda }_{i,n}\parallel w_n-{\omega }^{†}\parallel \parallel A^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel ,\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill \parallel w_n-{\omega }^{†}{\parallel }^2& \le {\Sigma }_{i=1}^N{\gamma }_{i,n}{\parallel J_{{\beta }_{i,n}}^{B_i}[z_n-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n]-{\omega }^{†}\parallel }^2\hfill \\ \hfill & \le \frac{1}{2}\parallel w_n-{\omega }^{†}{\parallel }^2+\frac{1}{2}\parallel z_n-{\omega }^{†}{\parallel }^2-\frac{1}{2}\parallel w_n-z_n{\parallel }^2+{\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}\parallel w_n-{\omega }^{†}\parallel \parallel A^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel ,\hfill \end{array}$$

hence, by (5),

$$\begin{array}{cc}\hfill \parallel w_n-{\omega }^{†}{\parallel }^2& \le \parallel z_n-{\omega }^{†}{\parallel }^2-\parallel w_n-z_n{\parallel }^2+2{\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}\parallel w_n-{\omega }^{†}\parallel \parallel A^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel \hfill \\ \hfill & \le \parallel x_n-{\omega }^{†}{\parallel }^2-\parallel w_n-z_n{\parallel }^2+2{\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}\parallel w_n-{\omega }^{†}\parallel \parallel A^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel +{\alpha }_n{M}_2.\hfill \end{array}$$

(7)

Furthermore,

$$\begin{array}{cc}\hfill \parallel y_n-{\omega }^{†}{\parallel }^2& = \parallel {\delta }_n{w}_n+(1-{\delta }_n)S{w}_n-{\omega }^{†}{\parallel }^2\hfill \\ \hfill & = ⟨y_n-{\omega }^{†},{\delta }_n{w}_n+(1-{\delta }_n)S{w}_n-{\omega }^{†}⟩\hfill \\ \hfill & = \frac{1}{2}\parallel {\delta }_n{w}_n+(1-{\delta }_n)S{w}_n-{\omega }^{†}{\parallel }^2+\frac{1}{2}\parallel y_n-{\omega }^{†}{\parallel }^2-\frac{1}{2}{\parallel y_n-{\omega }^{†}-{\delta }_n{w}_n+(1-{\delta }_n)S{w}_n+{\omega }^{†}\parallel }^2\hfill \\ \hfill & = \frac{1}{2}\parallel {\delta }_n(w_n-{\omega }^{†})+(1-{\delta }_n)(S{w}_n-{\omega }^{†}){\parallel }^2+\frac{1}{2}\parallel y_n-{\omega }^{†}{\parallel }^2-\frac{1}{2}{\parallel {\delta }_n(y_n-w_n)+(1-{\delta }_n)(y_n-S{w}_n)\parallel }^2\hfill \\ \hfill & = \frac{1}{2}{\delta }_n^2\parallel w_n-{\omega }^{†}{\parallel }^2+\frac{1}{2}{(1-{\delta }_n)}^2{\parallel S{w}_n-{\omega }^{†}\parallel }^2+{\delta }_n(1-{\delta }_n)⟨w_n-{\omega }^{†},S{w}_n-{\omega }^{†}⟩\hfill \\ \hfill & + \frac{1}{2}\parallel y_n-{\omega }^{†}{\parallel }^2-\frac{1}{2}{\delta }_n^2\parallel y_n-w_n{\parallel }^2-\frac{1}{2}{(1-{\delta }_n)}^2{\parallel y_n-S{w}_n\parallel }^2-{\delta }_n(1-{\delta }_n)⟨y_n-w_n,y_n-S{w}_n⟩\hfill \\ \hfill & \le \frac{1}{2}{\delta }_n^2\parallel w_n-{\omega }^{†}{\parallel }^2+\frac{1}{2}{(1-{\delta }_n)}^2\parallel w_n-{\omega }^{†}{\parallel }^2+{\delta }_n(1-{\delta }_n){\parallel w_n-{\omega }^{†}\parallel }^2\hfill \\ \hfill & + \frac{1}{2}\parallel y_n-{\omega }^{†}{\parallel }^2-\frac{1}{2}{\delta }_n^2\parallel y_n-w_n{\parallel }^2-\frac{1}{2}{(1-{\delta }_n)}^2{\parallel y_n-S{w}_n\parallel }^2\hfill \\ \hfill & = \frac{1}{2}\parallel y_n-{\omega }^{†}{\parallel }^2+\frac{1}{2}\parallel w_n-{\omega }^{†}{\parallel }^2-\frac{1}{2}{\delta }_n^2\parallel y_n-w_n{\parallel }^2-\frac{1}{2}{(1-{\delta }_n)}^2{\parallel y_n-S{w}_n\parallel }^2,\hfill \end{array}$$

which indicates that

$$\begin{array}{c}\hfill \parallel y_n-{\omega }^{†}{\parallel }^2 \le \parallel w_n-{\omega }^{†}{\parallel }^2-{\delta }_n^2\parallel y_n-w_n{\parallel }^2-{(1-{\delta }_n)}^2{\parallel y_n-S{w}_n\parallel }^2,\end{array}$$

(8)

Moreover, for some $M_3>0$,

$$\begin{array}{cc}\hfill \parallel z_n-{\omega }^{†}{\parallel }^2& = \parallel x_n+{\theta }_n(x_n-x_{n-1})-{\omega }^{†}{\parallel }^2\hfill \\ \hfill & = \parallel x_n-{\omega }^{†}+{\theta }_n(x_n-x_{n-1}){\parallel }^2\hfill \\ \hfill & = \parallel x_n-{\omega }^{†}{\parallel }^2+{\theta }_n^2{\parallel x_n-x_{n-1}\parallel }^2+2{\theta }_n⟨x_n-{\omega }^{†},x_n-x_{n-1}⟩\hfill \\ \hfill & \le \parallel x_n-{\omega }^{†}{\parallel }^2+{\theta }_n^2\parallel x_n-x_{n-1}{\parallel }^2+2{\theta }_n\parallel x_n-{\omega }^{†}\parallel \parallel x_n-x_{n-1}\parallel \hfill \\ \hfill & = \parallel x_n-{\omega }^{†}{\parallel }^2+{\theta }_n\parallel x_n-x_{n-1}\parallel ({\theta }_n\parallel x_n-x_{n-1}\parallel +2\parallel x_n-{\omega }^{†}\parallel )\hfill \\ \hfill & \le \parallel x_n-{\omega }^{†}{\parallel }^2+{\theta }_n\parallel x_n-x_{n-1}\parallel M_3.\hfill \end{array}$$

(9)

Observe that

$$\begin{array}{cc}\hfill \parallel x_{n+1}-{\omega }^{†}{\parallel }^2& =\parallel {\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)y_n-{\omega }^{†}{\parallel }^2\hfill \\ \hfill & \le ⟨{\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)y_n-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & =(1-{\alpha }_n)⟨y_n-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩+{\alpha }_n⟨f\left(x_n\right)-f\left({\omega }^{†}\right),x_{n+1}-{\omega }^{†}⟩+{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & \le \frac{1-{\alpha }_n}{2}[\parallel y_n-{\omega }^{†}{\parallel }^2+\parallel x_{n+1}-{\omega }^{†}{\parallel }^2]+\frac{{\alpha }_n}{2}[{\rho }^2\parallel x_n-{\omega }^{†}{\parallel }^2+\parallel x_{n+1}-{\omega }^{†}{\parallel }^2]\hfill \\ \hfill & +{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & \le \frac{1}{2}\parallel x_{n+1}-{\omega }^{†}{\parallel }^2+\frac{1-{\alpha }_n}{2}\parallel y_n-{\omega }^{†}{\parallel }^2+\frac{{\alpha }_n}{2}{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩,\hfill \end{array}$$

then from (3), (4) and (9) and conditions (ii), we get

$$\begin{array}{cc}\hfill \parallel x_{n+1}-{\omega }^{†}{\parallel }^2& \le (1-{\alpha }_n)\parallel y_n-{\omega }^{†}{\parallel }^2+{\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & \le (1-{\alpha }_n)(\parallel x_n-{\omega }^{†}{\parallel }^2+{\theta }_n\parallel x_n-x_{n-1}\parallel M_3)+{\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & = [1-{\alpha }_n(1-{\rho }^2)]\parallel x_n-{\omega }^{†}{\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩+{\alpha }_n(1-{\alpha }_n)\frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel M_3.\hfill \end{array}$$

(10)

It follows from (4) and (6) that

$$\begin{array}{cc}\hfill \parallel x_{n+1}-{\omega }^{†}{\parallel }^2& \le (1-{\alpha }_n)\parallel y_n-{\omega }^{†}{\parallel }^2+{\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & \le (1-{\alpha }_n)(\parallel x_n-{\omega }^{†}{\parallel }^2+{\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}({\lambda }_{i,n}{\parallel A\parallel }^2-2)\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n{\parallel }^2+{\alpha }_n{M}_2)\hfill \\ \hfill & + {\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & = [1-{\alpha }_n(1-{\rho }^2)]{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩+(1-{\alpha }_n){\alpha }_n{M}_2\hfill \\ \hfill & + (1-{\alpha }_n){\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}({\lambda }_{i,n}{\parallel A\parallel }^2-2)\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n{\parallel }^2,\hfill \end{array}$$

(11)

and by (4) and (7), we have that

$$\begin{array}{cc}\hfill \parallel x_{n+1}-{\omega }^{†}{\parallel }^2& \le (1-{\alpha }_n)\parallel y_n-{\omega }^{†}{\parallel }^2+{\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & \le (1-{\alpha }_n)(\parallel x_n-{\omega }^{†}{\parallel }^2-\parallel w_n-z_n{\parallel }^2+2{\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}\parallel w_n-{\omega }^{†}\parallel \parallel A^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel +{\alpha }_n{M}_2)\hfill \\ \hfill & + {\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & = [1-{\alpha }_n(1-{\rho }^2)]{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩+(1-{\alpha }_n){\alpha }_n{M}_2\hfill \\ \hfill & - (1-{\alpha }_n)\parallel w_n-z_n{\parallel }^2+2(1-{\alpha }_n){\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}\parallel w_n-{\omega }^{†}\parallel \parallel A^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel .\hfill \end{array}$$

(12)

It follows from (3) and (8) and conditions (ii), we deduce

$$\begin{array}{cc}\hfill \parallel x_{n+1}-{\omega }^{†}{\parallel }^2& \le (1-{\alpha }_n)\parallel y_n-{\omega }^{†}{\parallel }^2+{\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & \le (1-{\alpha }_n)(\parallel w_n-{\omega }^{†}{\parallel }^2-{\delta }_n^2\parallel y_n-w_n{\parallel }^2)+{\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & \le (1-{\alpha }_n)(\parallel x_n-{\omega }^{†}{\parallel }^2+{\alpha }_n{M}_2-{\delta }_n^2\parallel y_n-w_n{\parallel }^2)+{\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & =[1-{\alpha }_n(1-{\rho }^2)]{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩+(1-{\alpha }_n){\alpha }_n{M}_2\hfill \\ \hfill & -(1-{\alpha }_n){\delta }_n^2{\parallel y_n-w_n\parallel }^2,\hfill \end{array}$$

(13)

and

$$\begin{array}{cc}\hfill \parallel x_{n+1}-{\omega }^{†}{\parallel }^2& \le (1-{\alpha }_n)\parallel y_n-{\omega }^{†}{\parallel }^2+{\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & \le (1-{\alpha }_n)(\parallel w_n-{\omega }^{†}{\parallel }^2-{(1-{\delta }_n)}^2\parallel y_n-S{w}_n{\parallel }^2)+{\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & \le (1-{\alpha }_n)(\parallel x_n-{\omega }^{†}{\parallel }^2+{\alpha }_n{M}_2-{(1-{\delta }_n)}^2\parallel y_n-S{w}_n{\parallel }^2)+{\alpha }_n{\rho }^2{\parallel x_n-{\omega }^{†}\parallel }^2\hfill \\ \hfill & + 2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩\hfill \\ \hfill & =[1-{\alpha }_n(1-{\rho }^2)]{\parallel x_n-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩+(1-{\alpha }_n){\alpha }_n{M}_2\hfill \\ \hfill & -(1-{\alpha }_n){(1-{\delta }_n)}^2{\parallel y_n-S{w}_n\parallel }^2.\hfill \end{array}$$

(14)

Next, we consider the convergence of the sequence $\{\parallel x_n-{\omega }^{†}\parallel \}$ in two cases.

Case 1: There exists a $n_0$ such that $\parallel x_{n+1}-{\omega }^{†}\parallel \le \parallel x_n-{\omega }^{†}\parallel$ for each $n\ge n_0$. This indicates that $\{\parallel x_n-{\omega }^{†}\parallel \}$ is convergent. Thus, from (11), (13) and (14), we have

$$\begin{array}{cc}\hfill & (1-{\alpha }_n){\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}(2-{\lambda }_{i,n}{\parallel A\parallel }^2)\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n{\parallel }^2\hfill \\ \hfill & \le [1-{\alpha }_n(1-{\rho }^2)]\parallel x_n-{\omega }^{†}{\parallel }^2-{\parallel x_{n+1}-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩+(1-{\alpha }_n){\alpha }_n{M}_2\to 0,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & (1-{\alpha }_n){\delta }_n^2{\parallel y_n-w_n\parallel }^2\hfill \\ \hfill & =[1-{\alpha }_n(1-{\rho }^2)]\parallel x_n-{\omega }^{†}{\parallel }^2-{\parallel x_{n+1}-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩+(1-{\alpha }_n){\alpha }_n{M}_2\to 0,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & (1-{\alpha }_n){(1-{\delta }_n)}^2{\parallel y_n-S{w}_n\parallel }^2\hfill \\ \hfill & =[1-{\alpha }_n(1-{\rho }^2)]\parallel x_n-{\omega }^{†}{\parallel }^2-{\parallel x_{n+1}-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩+(1-{\alpha }_n){\alpha }_n{M}_2\to 0.\hfill \end{array}$$

Then, by the restriction conditions, we can get

$$\begin{array}{c}\hfill \parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel \to 0;\parallel y_n-w_n\parallel \to 0;\parallel y_n-S{w}_n\parallel \to 0.\end{array}$$

(15)

From (12), we have

$$\begin{array}{cc}& (1-{\alpha }_n){\parallel w_n-z_n\parallel }^2\hfill \\ & \le [1-{\alpha }_n(1-{\rho }^2)]\parallel x_n-{\omega }^{†}{\parallel }^2-{\parallel x_{n+1}-{\omega }^{†}\parallel }^2+2{\alpha }_n⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩+(1-{\alpha }_n){\alpha }_n{M}_2\hfill \\ & +2(1-{\alpha }_n){\Sigma }_{i=1}^N{\gamma }_{i,n}{\lambda }_{i,n}\parallel w_n-{\omega }^{†}\parallel \parallel A^{*}(J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel \to 0,\hfill \end{array}$$

Then, we obtain

$$\begin{array}{c}\hfill \parallel w_n-z_n\parallel \to 0.\end{array}$$

(16)

From the definition of $z_n$, we obtain

$$\begin{array}{c}\hfill \parallel x_n-z_n\parallel = {\theta }_n\parallel x_n-x_{n-1}\parallel \le {\alpha }_n{M}_1\to 0.\end{array}$$

(17)

From (15) and (16), we get

$$\begin{array}{cc}\hfill & \parallel x_n-w_n\parallel \le \parallel x_n-z_n\parallel + \parallel z_n-w_n\parallel \to 0,\hfill \\ \hfill & \parallel x_n-y_n\parallel \le \parallel x_n-w_n\parallel + \parallel w_n-y_n\parallel \to 0,\hfill \\ \hfill & \parallel S{w}_n-w_n\parallel \le \parallel S{w}_n-y_n\parallel + \parallel y_n-w_n\parallel \to 0.\hfill \end{array}$$

(18)

From (ii) and (18), we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}-x_n\parallel & \le \parallel x_{n+1}-y_n\parallel + \parallel y_n-x_n\parallel \hfill \\ \hfill & = \parallel {\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)y_n-y_n\parallel + \parallel y_n-x_n\parallel \hfill \\ \hfill & = {\alpha }_n\parallel f\left(x_n\right)-y_n\parallel + \parallel y_n-x_n\parallel \to 0.\hfill \end{array}$$

(19)

Suppose that $\left\{x_{n_j}\right\}$ is a subsequence of $\left\{x_n\right\}$ such that $x_{n_j}\rightharpoonup {\omega }^{*}$. From (17) and (18), there exist subsequences of $\left\{z_n\right\}$ and $\left\{w_n\right\}$ satisfying $z_{n_j}\rightharpoonup {\omega }^{*}$ and $w_{n_j}\rightharpoonup {\omega }^{*}$, respectively. Since A is a bounded linear operator, then $A{z}_n\rightharpoonup A{\omega }^{*}$. Moreover, we know that $\parallel (J_{{\beta }_{i,n}}^{K_i}-I)A{z}_n\parallel \to 0$, which implies that $A{\omega }^{*}=J_{{\beta }_{i,n}}^{K_i}A{\omega }^{*}$, by Lemma 6, we get ${\omega }^{*}\in \Gamma$. From $\parallel S{w}_n-w_n\parallel \to 0$ and Lemma 3, we deduce ${\omega }^{*}\in Fix\left(S\right)$. Hence ${\omega }^{*}\in Fix\left(S\right)\bigcap \Gamma$. Then, it follows that

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim\; sup}⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n+1}-{\omega }^{†}⟩& =\underset{j\to \infty }{lim\; sup}⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{n_j+1}-{\omega }^{†}⟩\hfill \\ \hfill & =⟨f\left({\omega }^{†}\right)-{\omega }^{†},{\omega }^{*}-{\omega }^{†}⟩\le 0.\hfill \end{array}$$

Apply Lemma 2 to (10), we have $x_n\to {\omega }^{†}=P_{Fix\left(S\right)\bigcap \Gamma }f\left({\omega }^{†}\right)$.

Case 2: Suppose that the sequence $\{\parallel x_{n+1}-{\omega }^{†}\parallel \}$ is not monotonically decreasing. Then, there exists a subsequence $n_j$ such that

$$\begin{array}{c}\hfill \parallel x_{n_j}-{\omega }^{†}{\parallel }^2\le {\parallel x_{n_j+1}-{\omega }^{†}\parallel }^2, \forall j\in N.\end{array}$$

By Lemma 4, there exists a nondecreasing sequence $\left\{m_i\right\}\subset N$ such that $m_i\to \infty$:

$$\begin{array}{c}\hfill \parallel x_{m_i}-{\omega }^{†}{\parallel }^2 \le \parallel x_{m_i+1}-{\omega }^{†}{\parallel }^2, \parallel x_i-{\omega }^{†}{\parallel }^2 \le {\parallel x_{m_i+1}-{\omega }^{†}\parallel }^2.\end{array}$$

(20)

Similar to the proof in Case 1, we have

$$\begin{array}{cc}\hfill \parallel x_{m_i+1}-{\omega }^{†}{\parallel }^2& \le [1-{\alpha }_{m_i}(1-{\rho }^2)]{\parallel x_{m_i}-{\omega }^{†}\parallel }^2+2{\alpha }_{m_i}⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{m_i+1}-{\omega }^{†}⟩\hfill \\ \hfill & +{\alpha }_{m_i}(1-{\alpha }_{m_i})\frac{{\theta }_{m_i}}{{\alpha }_{m_i}}\parallel x_{m_i}-x_{m_i-1}\parallel M_3,\hfill \end{array}$$

and

$$\underset{n\to \infty }{lim\; sup}⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{m_i+1}-{\omega }^{†}⟩\le 0,$$

which implies

$$\begin{array}{cc}\hfill 0& \le \parallel x_{m_i+1}-{\omega }^{†}{\parallel }^2-{\parallel x_{m_i}-{\omega }^{†}\parallel }^2\hfill \\ \hfill & =[1-{\alpha }_{m_i}(1-{\rho }^2)]{\parallel x_{m_i}-{\omega }^{†}\parallel }^2+2{\alpha }_{m_i}⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{m_i+1}-{\omega }^{†}⟩\hfill \\ \hfill & +{\alpha }_{m_i}(1-{\alpha }_{m_i})\frac{{\theta }_{m_i}}{{\alpha }_{m_i}}\parallel x_{m_i}-x_{m_i-1}\parallel M_3-{\parallel x_{m_i}-{\omega }^{†}\parallel }^2,\hfill \end{array}$$

then using ${lim}_{n\to \infty }\frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel \to 0$, we get

$$\begin{array}{c}\hfill \parallel x_{m_i}-{\omega }^{†}{\parallel }^2\le \frac{2}{1-{\rho }^2}⟨f\left({\omega }^{†}\right)-{\omega }^{†},x_{m_i+1}-{\omega }^{†}⟩+\frac{1-{\alpha }_{m_i}}{1-{\rho }^2}\frac{{\theta }_{m_i}}{{\alpha }_{m_i}}\parallel x_{m_i}-x_{m_i-1}\parallel M_3\to 0.\end{array}$$

By (20), we obtain $\parallel x_{m_i+1}-{\omega }^{†}\parallel \to 0$. It follows from $\parallel x_i-{\omega }^{†}{\parallel }^2\le {\parallel x_{m_i+1}-{\omega }^{†}\parallel }^2$ for all $i\in N$ that $\parallel x_i-{\omega }^{†}{\parallel }^2\to 0$, by using Lemma 4, we deduce $x_i\to {\omega }^{†}$. Therefore, the sequence $x_n\to {\omega }^{†},n\to \infty$. This completes the proof. □

In Theorem 1, we put $f\left(x\right)=u$; then, we have the following result.

Corollary 1. 

Let ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ be two real Hilbert spaces. Let $A:{\mathcal{H}}_1\to {\mathcal{H}}_2$ be a bounded linear operator and $A^{*}$ be the adjoint operator of A. Suppose that $B_i:{\mathcal{H}}_1\to {\mathcal{H}}_1,K_i:{\mathcal{H}}_2\to {\mathcal{H}}_2$, $i=1,2,\dots ,N$ are two families of maximal monotone mappings. Let $u\in {\mathcal{H}}_1$ be fixed and $S:{\mathcal{H}}_1\to {\mathcal{H}}_1$ be a nonexpansive mapping such that $Fix\left(S\right)\bigcap \Gamma \ne \varnothing$. For $x_0,x_1\in {\mathcal{H}}_1$, the sequence $\left\{x_n\right\}$ defined by:

$$\left\{\begin{array}{cc}\hfill & z_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ \hfill & w_n={\Sigma }_{i=1}^N{\gamma }_{i,n}{J}_{{\beta }_{i,n}}^{B_i}[z_n-{\lambda }_{i,n}{A}^{*}(I-J_{{\beta }_{i,n}}^{K_i})A{z}_n],\hfill \\ \hfill & x_{n+1}={\alpha }_{n}u+(1-{\alpha }_n)[{\delta }_n{w}_n+(1-{\delta }_n)S{w}_n].\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\delta }_n\right\},\left\{{\gamma }_{i,n}\right\}\subset (0,1)$, $\left\{{\beta }_{i,n}\right\},\left\{{\lambda }_{i,n}\right\}$ are sequences of positive real numbers satisfying the following conditions:

(i) 

Let the parameter ${\theta }_n$ chosen as

$${\theta }_n=\left\{\begin{array}{cc}\hfill & min\{\theta ,\frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }\}\mathit{if}{x}_n\ne x_{n-1},\hfill \\ \hfill & \theta \mathit{otherwise},\hfill \end{array}\right.$$

where $\theta >0$, ${ϵ}_n$ is a positive real sequence such that ${ϵ}_n=o\left({\alpha }_n\right)$;

(ii) 

${lim}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$, ${\delta }_n\subset [a,b]\subset (0,1)$;

(iii) 

${\sum }_{i=1}^N{\gamma }_{i,n}=1$, ${\gamma }_{i,n}\subset [c,d]\subset (0,1)$, ${\lambda }_{i,n}\in (0,\frac{2}{{\parallel A\parallel }^2})$.

Then $\left\{x_n\right\}$ converges strongly to an element ${\omega }^{†}\in Fix\left(S\right)\bigcap \Gamma$, where ${\omega }^{†}=P_{Fix\left(S\right)\bigcap \Gamma }u$.

In Theorem 1, we set $B=B_1=B_2=\cdots =B_N,K=K_1=K_2=\cdots =K_N$. Then, we obtain the following result.

Corollary 2. 

Let ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ be two real Hilbert spaces. Let $A:{\mathcal{H}}_1\to {\mathcal{H}}_2$ be a bounded linear operator and $A^{*}$ be the adjoint operator of A. Suppose that $B:{\mathcal{H}}_1\to {\mathcal{H}}_1,K:{\mathcal{H}}_2\to {\mathcal{H}}_2$ are two maximal monotone mappings. Let $f:{\mathcal{H}}_1\to {\mathcal{H}}_1$ be a contraction with coefficient $\rho \in (0,1)$ and $S:{\mathcal{H}}_1\to {\mathcal{H}}_1$ be a nonexpansive mapping such that $Fix\left(S\right)\bigcap \Gamma \ne \varnothing$. For $x_0,x_1\in {\mathcal{H}}_1$, the sequence $\left\{x_n\right\}$ defined by:

$$\left\{\begin{array}{cc}\hfill & z_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ \hfill & w_n=J_{{\beta }_n}^B[z_n-{\lambda }_n{A}^{*}(I-J_{{\beta }_n}^K)A{z}_n],\hfill \\ \hfill & x_{n+1}={\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)[{\delta }_n{w}_n+(1-{\delta }_n)S{w}_n].\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\delta }_n\right\}\subset (0,1)$, $\left\{{\beta }_n\right\},\left\{{\lambda }_n\right\}$ are sequences of positive real numbers satisfying the following conditions:

(i) 

Let the parameter ${\theta }_n$ chosen as

$${\theta }_n=\left\{\begin{array}{cc}\hfill & min\{\theta ,\frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }\}\mathit{if}{x}_n\ne x_{n-1},\hfill \\ \hfill & \theta \mathit{otherwise},\hfill \end{array}\right.$$

where $\theta >0$, ${ϵ}_n$ is a positive real sequence such that ${ϵ}_n=o\left({\alpha }_n\right)$;

(ii) 

${lim}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$, ${\delta }_n\subset [a,b]\subset (0,1)$;

(iii) 

${\lambda }_n\in (0,\frac{2}{{\parallel A\parallel }^2})$.

Then, $\left\{x_n\right\}$ converges strongly to an element ${\omega }^{†}\in Fix\left(S\right)\bigcap \Gamma$, where ${\omega }^{†}=P_{Fix\left(S\right)\bigcap \Gamma }f\left({\omega }^{†}\right)$.

Let $\mathcal{C}\in {\mathcal{H}}_1$ and $\mathcal{Q}\in {\mathcal{H}}_2$ be two nonempty closed convex subsets. Now, we recall that the following split feasibility problem is to find

$$x\in \mathcal{C}, \mathrm{such}\mathrm{that} Ax\in \mathcal{Q}.$$

The solution set of the split feasibility problem is denoted by ${\Omega }^{†}$. In Corollary 2, if $J_{{\beta }_n}^B=P_{\mathcal{C}}$ and $J_{{\beta }_n}^K=P_{\mathcal{Q}}$, we obtain the following result.

Corollary 3. 

Let $\mathcal{C}$ and $\mathcal{Q}$ be nonempty closed convex subsets of Hilbert spaces ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$, respectively. Let $A:{\mathcal{H}}_1\to {\mathcal{H}}_2$ be a bounded linear operator and $A^{*}$ be the adjoint operator of A. Let $f:{\mathcal{H}}_1\to {\mathcal{H}}_1$ be a contraction with coefficient $\rho \in (0,1)$ and $S:{\mathcal{H}}_1\to {\mathcal{H}}_1$ be a nonexpansive mapping such that $Fix\left(S\right)\bigcap {\Omega }^{†}\ne \varnothing$. For $x_0,x_1\in {\mathcal{H}}_1$, the sequence $\left\{x_n\right\}$ defined by:

$$\left\{\begin{array}{cc}\hfill & z_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ \hfill & w_n=P_{\mathcal{C}}[z_n-{\lambda }_n{A}^{*}(I-P_{\mathcal{Q}})A{z}_n],\hfill \\ \hfill & x_{n+1}={\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)[{\delta }_n{w}_n+(1-{\delta }_n)S{w}_n].\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\delta }_n\right\}\subset (0,1)$, $\left\{{\lambda }_n\right\}$ are sequences of positive real numbers satisfying the following conditions:

(i) 

Let the parameter ${\theta }_n$ chosen as

$${\theta }_n=\left\{\begin{array}{cc}\hfill & min\{\theta ,\frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }\}\mathit{if}{x}_n\ne x_{n-1},\hfill \\ \hfill & \theta \mathit{otherwise},\hfill \end{array}\right.$$

where $\theta >0$, ${ϵ}_n$ is a positive real sequence such that ${ϵ}_n=o\left({\alpha }_n\right)$;

(ii) 

${lim}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$, ${\delta }_n\subset [a,b]\subset (0,1)$;

(iii) 

${\lambda }_n\in (0,\frac{2}{{\parallel A\parallel }^2})$.

Then, $\left\{x_n\right\}$ converges strongly to an element ${\omega }^{†}\in Fix\left(S\right)\bigcap {\Omega }^{†}$, where ${\omega }^{†}=P_{Fix\left(S\right)\bigcap {\Omega }^{†}}f\left({\omega }^{†}\right)$.

Let $f:{\mathcal{H}}_1\to R$ and $g:{\mathcal{H}}_2\to R$ be proper lower semicontinuous convex functions. The split minimization problem is to find

$$x\in {\mathcal{H}}_1\mathrm{such}\mathrm{that}x\in arg\underset{x\in {\mathcal{H}}_1}{min}f\left(x\right),Ax\in arg\underset{y\in {\mathcal{H}}_2}{min}g\left(y\right).$$

The solution set of the split minimization problem is denoted by ${\rm Y}$. It is well known that the subdifferential $\partial f$ is maximal monotone and $J_{\partial f}\left(x\right)=(I+\lambda \partial f)$ is firmly nonexpansive. In Corollary 2, if $J_{{\beta }_n}^B=J_{\partial f}\left(x\right)$ and $J_{{\beta }_n}^K=J_{\partial g}\left(x\right)$, we obtain the following result.

Corollary 4. 

Let ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ be Hilbert spaces and $f:{\mathcal{H}}_1\to R$, $g:{\mathcal{H}}_2\to R$ be proper lower semicontinuous convex functions. Let $A:{\mathcal{H}}_1\to {\mathcal{H}}_2$ be a bounded linear operator and $A^{*}$ be the adjoint operator of A. Let $f:{\mathcal{H}}_1\to {\mathcal{H}}_1$ be a contraction with coefficient $\rho \in (0,1)$ and $S:{\mathcal{H}}_1\to {\mathcal{H}}_1$ be a nonexpansive mapping such that $Fix\left(S\right)\bigcap {\rm Y}\ne \varnothing$. For $x_0,x_1\in {\mathcal{H}}_1$, the sequence $\left\{x_n\right\}$ defined by:

$$\left\{\begin{array}{cc}\hfill & z_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ \hfill & w_n=J_{\partial f}\left(x\right)[z_n-{\lambda }_n{A}^{*}(I-J_{\partial g}\left(x\right))A{z}_n],\hfill \\ \hfill & x_{n+1}={\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)[{\delta }_n{w}_n+(1-{\delta }_n)S{w}_n].\hfill \end{array}\right.$$

where $\left\{{\alpha }_n\right\},\left\{{\delta }_n\right\}\subset (0,1)$, $\left\{{\lambda }_n\right\}$ are sequences of positive real numbers satisfying the following conditions:

(i) 

Let the parameter ${\theta }_n$ chosen as

$${\theta }_n=\left\{\begin{array}{cc}\hfill & min\{\theta ,\frac{{ϵ}_n}{\parallel x_n-x_{n-1}\parallel }\}\mathit{if}{x}_n\ne x_{n-1},\hfill \\ \hfill & \theta \mathit{otherwise},\hfill \end{array}\right.$$

where $\theta >0$, ${ϵ}_n$ is a positive real sequence such that ${ϵ}_n=o\left({\alpha }_n\right)$;

(ii) 

${lim}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$, ${\delta }_n\subset [a,b]\subset (0,1)$;

(iii) 

${\lambda }_n\in (0,\frac{2}{{\parallel A\parallel }^2})$.

Then, $\left\{x_n\right\}$ converges strongly to an element ${\omega }^{†}\in Fix\left(S\right)\bigcap {\rm Y}$, where ${\omega }^{†}=P_{Fix\left(S\right)\bigcap {\rm Y}}f\left({\omega }^{†}\right)$.

4. Numerical Examples

In this section, we give some numerical experiments to illustrate the feasibility and effectiveness of our proposed algorithm and the main result. All the codes are written in Python 3.7.

Example 1. 

Let ${\mathcal{H}}_1={\mathcal{H}}_2=R^2$, and $A=\left[\begin{array}{cc}4& 6\\ 3& 2\end{array}\right]$. Let $B_1,B_2,K_1,K_2:R^2\to R^2$ be defined by $B_1=\left[\begin{array}{cc}4& 0\\ 0& 2\end{array}\right]$, $B_2=\left[\begin{array}{cc}6& 0\\ 0& 4\end{array}\right]$, $K_1=\left[\begin{array}{cc}5& 0\\ 0& 3\end{array}\right]$ and $K_2=\left[\begin{array}{cc}7& 0\\ 0& 5\end{array}\right]$. We put ${\beta }_{i,n}=\frac{1}{3}$, then we can get the resolvent mappings associated with $B_1, B_2, K_1$ and $K_2$. Let ${\gamma }_{i,n}=\frac{1}{2}$, ${\delta }_n=\frac{1}{4}$, ${\alpha }_n=\frac{1}{3n}$, and ${\lambda }_{i,n}=\frac{1}{{2\parallel A\parallel }^2}$ for all $n\in N$. We take

$${\theta }_n=\left\{\begin{array}{cc}\hfill & min\{0.5,\frac{1}{n^2\parallel x_n-x_{n-1}\parallel }\}\mathit{if}{x}_n\ne x_{n-1},\hfill \\ \hfill & 0.5\mathit{otherwise},\hfill \end{array}\right.$$

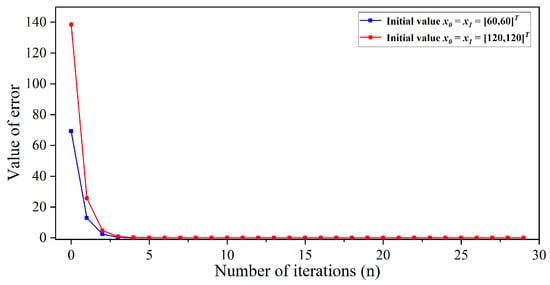
Let S and f be defined by $Sx=\frac{1}{6}x$, $f\left(x\right)=\frac{1}{5}x$. This implies that $\rho =\frac{1}{5}$. Starting the initial values $x_0=x_1=\left[\begin{array}{c}60\\ 60\end{array}\right]$ and $x_0=x_1=\left[\begin{array}{c}120\\ 120\end{array}\right]$ in (1), respectively. The numerical results have been shown in Table 1 and Figure 1. We test the convergence behavior of this algorithm under different stopping conditions. The results are shown in Table 2.

Table 1. The values of error $\parallel x_{n+1}-x_n\parallel$.

n	${\mathit{x}}_0={\mathit{x}}_1=\left[\begin{array}{c}60\\ 60\end{array}\right]$	${\mathit{x}}_0={\mathit{x}}_1=\left[\begin{array}{c}120\\ 120\end{array}\right]$
1	$69.238$	$138.476$
2	$12.854$	$25.671$
3	$2.36772$	$4.74734$
4	$0.44423$	$0.89771$
5	$0.08335$	$0.17194$
…	$\dots$	$\dots$
27	$2.47\times {10}^{-13}$	$8.43\times {10}^{-13}$
28	$9.84\times {10}^{-14}$	$2.33\times {10}^{-15}$
29	$5.49\times {10}^{-14}$	$8.47\times {10}^{-14}$
30	$6.81\times {10}^{-15}$	$2.59\times {10}^{-14}$

Figure 1. Numerical results for Example 1.

Table 2. The number of termination iterations and execution time with different stopping conditions.

$\parallel {\mathit{x}}_{\mathit{n}+1}-{\mathit{x}}_{\mathit{n}}\parallel <{\mathit{\epsilon }}_{\mathit{n}}$	${\mathit{x}}_0={\mathit{x}}_1=\left[\begin{array}{c}60\\ 60\end{array}\right]$		${\mathit{x}}_0={\mathit{x}}_1=\left[\begin{array}{c}120\\ 120\end{array}\right]$
${\epsilon }_{\mathbf{n}}$	Iter.	Times (ms)	Iter.	Times (ms)
${10}^{-4}$	6	$0.75$	8	$0.75$
${10}^{-5}$	9	$0.90$	10	$1.11$
${10}^{-6}$	12	$0.97$	12	$1.17$
${10}^{-7}$	14	$1.03$	14	$1.31$

Remark 1. 

The parameters we select satisfy the conditions (i)–(iii) in Theorem 1. We randomly selected initial values to study the convergence of the algorithm. The numerical results we obtained verify the effectiveness and feasibility of our proposed iterative algorithm. In addition, we can observe the convergence rate of the iterative algorithm. The most important thing is that the method we provide converges very quickly in terms of the number of iterations and execution time, and these results are not significantly related to the choice of initial values.

5. Conclusions

In this paper, we have presented and analyzed an inertial viscosity iterative algorithm for general split variational inclusion problems and fixed point problems in Hilbert spaces. The strong convergence of the proposed algorithms is demonstrated, and the numerical experiments are given to illustrate the efficiency of Theorem 1. We give an extension of the inertial viscosity approximation and the common fixed point problems in Hilbert spaces, and we generalize the split variational inclusion problems to the general split variational inclusion problems of Cholamjiak et al. [20] and Chuang [23]. In Corollary 2, if $f=S=I$, it is the main result of Pham et al. [24]. In addition, the methods and results also extend and improve some corresponding recent results of [12,13,14,22] as special cases.