Visco-Elastic Interface Effect on the Dynamic Stress of Symmetrical Tunnel Embedded in a Half-Plane Subjected to P Waves
Abstract
1. Introduction
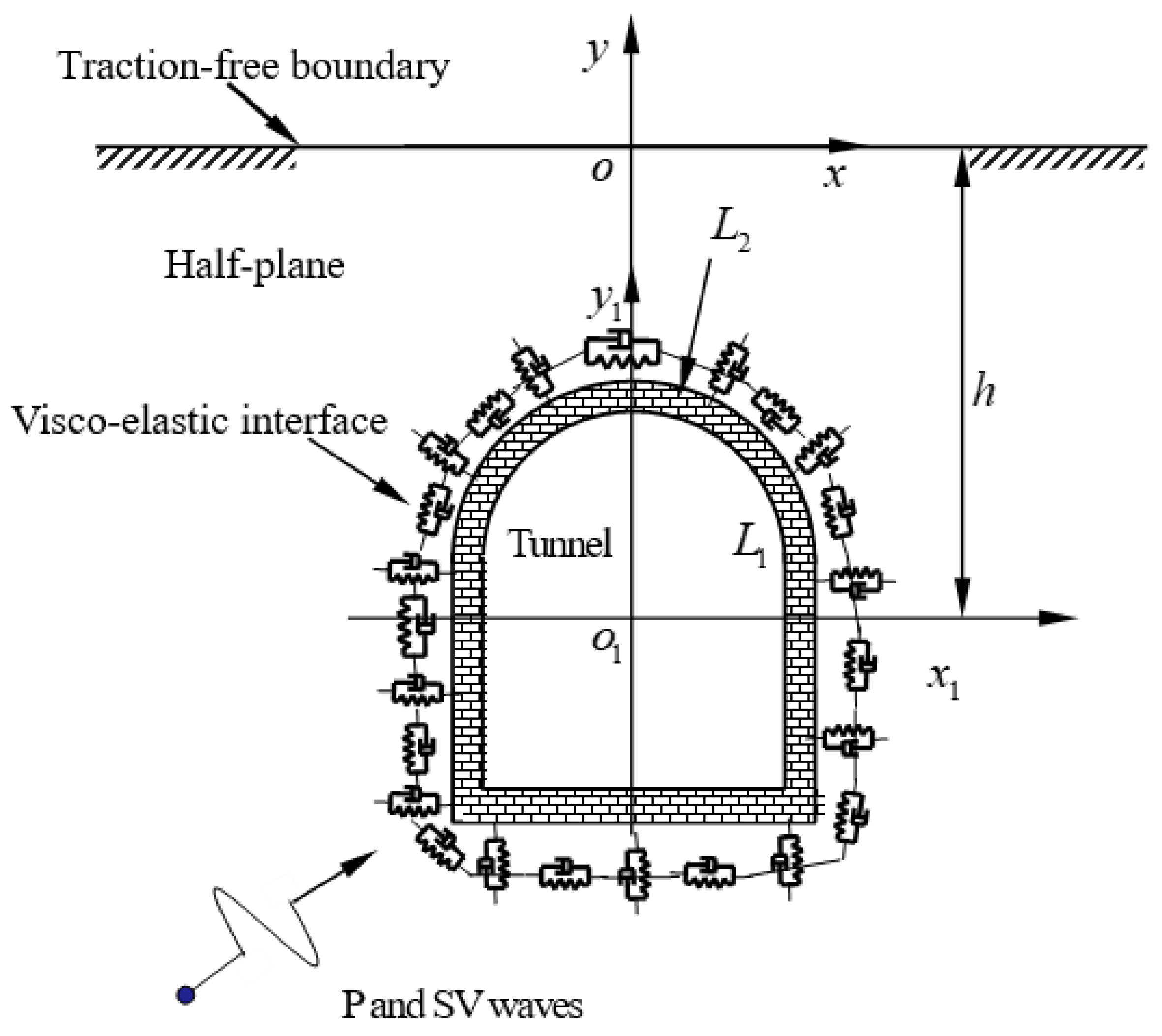
2. Problem Formulation and Basis Solutions
3. Wave Fields in the Rock Mass and Concrete Lining
3.1. The Incident Waves
3.2. The Scattered Field in the Half-Plane
3.3. The Reflected Field in the Tunnel Lining
3.4. The Refracted Field Inside the Tunnel Lining
3.5. The Wave Fields from the Half-Plane
3.6. The Total Displacement Potential in the Half-Plane and Concrete Tunnel
4. Boundary Conditions and Solving the Expanded Coefficients
5. Numerical Examples and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Huang, L.; Liu, Z.; Wu, C.; Liang, J. Interaction between a tunnel and alluvial valley under plane SV waves of earthquakes by IBIEM. Eur. J. Environ. Civ. Eng. 2021, 25, 2217–2235. [Google Scholar] [CrossRef]
- Jin, H.-X.; Fang, X.-Q.; Wang, Y.; Wang, B.-L. Interaction of two shallow non-circular tunnels with imperfect interfaces subjected to shear waves. Eur. J. Environ. Civ. Eng. 2018, 22, 546–561. [Google Scholar] [CrossRef]
- Yi, C.; Zhang, P.; Johansson, D.; Nyberg, U. Dynamic response of a circular lined tunnel with an imperfect interface subjected to cylindrical P-waves. Comput. Geotech. 2014, 55, 165–171. [Google Scholar] [CrossRef]
- Pao, Y.-H.; Mow, C.-C.; Achenbach, J.D. Diffraction of Elastic Waves and Dynamic Stress Concentrations. J. Appl. Mech. 1973, 40, 872. [Google Scholar] [CrossRef]
- Liu, D.; Gai, B.; Tao, G. Applications of the method of complex functions to dynamic stress concentrations. Wave Motion 1982, 4, 293–304. [Google Scholar] [CrossRef]
- Zhou, C.; Hu, C.; Ma, F.; Liu, D. Elastic wave scattering and dynamic stress concentrations in exponential graded materials with two elliptic holes. Wave Motion 2014, 51, 466–475. [Google Scholar] [CrossRef]
- Sancar, S.; Pao, Y. Spectral analysis of elastic pulses backscattered from two cylindrical cavities in a solid. Part I. J. Acoust. Soc. Am. 1981, 69, 1591–1596. [Google Scholar] [CrossRef]
- Moore, I.D.; Guan, F. Three-dimensional dynamic response of lined tunnels due to incident seismic waves. Earthq. Eng. Struct. Dyn. 2015, 25, 357–369. [Google Scholar] [CrossRef]
- Mohsen, K.; Mohammad, A.; Hamid, A. Seismic ground amplification by unlined tunnels subjected to vertically propagating SV and P waves using BEM. Soil Dyn. Earthq. Eng. 2015, 71, 63–79. [Google Scholar]
- Wang, T.-T.; Hsu, J.-T.; Chen, C.-H.; Huang, T.-H. Response of a tunnel in double-layer rocks subjected to harmonic P- and S-waves. Int. J. Rock Mech. Min. Sci. 2014, 70, 435–443. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, R. Dynamic response of twin closely-spaced circular tunnels to harmonic plane waves in a full space. Tunn. Undergr. Space Technol. 2012, 32, 212–220. [Google Scholar] [CrossRef]
- Krutin, V.; Markov, M.; Yumatov, A. Normal waves in a fluid-filled cylindrical cavity located in a saturated porous medium. J. Appl. Math. Mech. 1988, 52, 67–74. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, X.; Lu, J. Dynamic stress concentration around elliptic cavities in saturated poroelastic soil under harmonic plane waves. Int. J. Solids Struct. 2005, 42, 4295–4310. [Google Scholar] [CrossRef]
- Chris, Z. Scattering of plane compressional waves by spherical inclusions in a poroelastic medium. J. Acoust. Soc. Am. 1993, 94, 527–536. [Google Scholar]
- Kattis, S.E.; Beskos, D.E.; Cheng, A.H.D. 2D dynamic response of unlined and lined tunnels in poroelastic soil to harmonic body waves. Earthq. Eng. Struct. Dyn. 2003, 32, 97–110. [Google Scholar] [CrossRef]
- Sedarat, H.; Kozak, A.; Hashash, Y.; Shamsabadi, A.; Krimotat, A. Contact interface in seismic analysis of circular tunnels. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2009, 24, 482–490. [Google Scholar] [CrossRef]
- Lu, A.Z.; Zhang, L.Q. Complex Function Method on Mechanical Analysis of Underground Tunnel; Science Press: Beijing, China, 2007. [Google Scholar]
- Liu, Q.; Zhao, M.; Wang, L. Scattering of plane P, SV or Rayleigh waves by a shallow lined tunnel in an elastic half space. Soil Dyn. Earthq. Eng. 2013, 49, 52–63. [Google Scholar] [CrossRef]
- Ivanov, Y.A. Diffraction of Electromagnetic Waves on Two Bodies; National Aeronautics and Space Administration: Washington, DC, USA, 1970. [Google Scholar]
- Kargar, A.; Rahmannejad, R.; Hajabasi, M. A semi-analytical elastic solution for stress field of lined non-circular tunnels at great depth using complex variable method. Int. J. Solids Struct. 2014, 51, 1475–1482. [Google Scholar] [CrossRef]








| Elastic Properties of Rock Mass | Elastic Properties of Concrete Lining | ||||
|---|---|---|---|---|---|
| 35 | 2.73 | 0.3 | 30 | 2.5 | 0.25 |
| R | |||||
|---|---|---|---|---|---|
| 4.33 | 0.93 | –0.0246 | –0.0834 | –0.0521 | –0.0418 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, H.; Liu, X.; Zhou, J. Visco-Elastic Interface Effect on the Dynamic Stress of Symmetrical Tunnel Embedded in a Half-Plane Subjected to P Waves. Symmetry 2023, 15, 1434. https://doi.org/10.3390/sym15071434
Jin H, Liu X, Zhou J. Visco-Elastic Interface Effect on the Dynamic Stress of Symmetrical Tunnel Embedded in a Half-Plane Subjected to P Waves. Symmetry. 2023; 15(7):1434. https://doi.org/10.3390/sym15071434
Chicago/Turabian StyleJin, Hexin, Xiaomin Liu, and Junlong Zhou. 2023. "Visco-Elastic Interface Effect on the Dynamic Stress of Symmetrical Tunnel Embedded in a Half-Plane Subjected to P Waves" Symmetry 15, no. 7: 1434. https://doi.org/10.3390/sym15071434
APA StyleJin, H., Liu, X., & Zhou, J. (2023). Visco-Elastic Interface Effect on the Dynamic Stress of Symmetrical Tunnel Embedded in a Half-Plane Subjected to P Waves. Symmetry, 15(7), 1434. https://doi.org/10.3390/sym15071434






