Abstract
The variational quantum eigensolver is one of the most promising algorithms for near-term quantum computers. It has the potential to solve quantum chemistry problems involving strongly correlated electrons with relatively low-depth circuits, which are otherwise difficult to solve on classical computers. The variational eigenstate is constructed from a number of factorized unitary coupled-cluster terms applied onto an initial (single-reference) state. Current algorithms for applying one of these operators to a quantum state require a number of operations that scale exponentially with the rank of the operator. We exploit a hidden SU(2) symmetry to allow us to employ the linear combination of unitaries approach, Our Prepare subroutine uses ancilla qubits for a rank-n operator. Our Select() scheme uses Cnot gates. This results in a full algorithm that scales like the cube of the rank of the operator , a significant reduction in complexity for rank five or higher operators. This approach, when combined with other algorithms for lower-rank operators (when compared to the standard implementation), will make the factorized form of the unitary coupled-cluster approach much more efficient to implement on all types of quantum computers.
1. Introduction
One of the important motivations for developing quantum computers is their potential to simulate strongly correlated many-body systems efficiently [1,2]. Algorithms that exactly diagonalize the electronic Hamiltonian, known as the full configuration interaction approach, scale exponentially with the size of the Hilbert space, making it applicable to very few cases [3] on classical computers. The configuration interaction (CI) method offers an approximate solution by truncating the Hilbert space to only include the most important basis states. However, the energy calculated by the CI method does not scale properly with the size of the system when used on molecules with varying sizes, nor does it predict the dissociation energy correctly because it cannot produce factorized atomic states. The coupled-cluster (CC) method addresses these issues by being both size consistent and size extensive. Size consistency means that the method would yield the same energy of two particles separated by an infinite distance as the sum of the energies calculated individually. Size extensivity means the energy scales linearly with the number of particles for a homogeneous system [4]. The CC method is also memory efficient because it does not explicitly construct the energy eigenstate. Instead, the set of amplitudes for the CC ansatz is calculated iteratively by the so-called amplitude equations [4,5,6], which correspond to zeroing out the row (or column) of the similarity-transformed Hamiltonian matrix that corresponds to the initial single-reference state. The CC method with single, double and (perturbative) triple excitations is regarded as the “gold standard” for computational chemistry [7].
Quantum computers have been proposed as being capable of solving a set of quantum chemistry problems that are otherwise difficult or very challenging on classical machines: namely, molecules that contain both weakly and strongly correlated electrons. One of the most promising algorithms for the noisy intermediate-scale quantum (NISQ) era is the variational quantum eigensolver (VQE), where the trial wave function is prepared on the quantum hardware and the expectation value of the Hamiltonian is measured there as well; the parameters in the eigenstate are optimized variationally on classical machines [8,9]. The conventional coupled-cluster ansatz is given as , where is a trial wave function (often chosen to be the single-reference Hartree–Fock state), and is the cluster operator consisting of up to rank-n excitations (n electrons are removed from the Hartree–Fock state and replaced by n electrons in virtual orbitals). The excitation operator is given as
and , where is the creation operator acting on virtual orbital a and is the annihilation operator acting on occupied orbital i. Traditionally, the CC method employs a similarity-transformed Hamiltonian to obtain a set of equations to determine the amplitudes t:
where , and is a set of states that covers the entire space generated by acting on the reference state [5,10]. In practice, this set of amplitude equations is solved iteratively, which yields the energy without needing to construct the energy eigenstate. The total number of amplitude equations is given by the number of amplitudes in the expansion of the operator, which is much smaller than the total number of Slater determinants in the (which is typically exponentially larger). The properties of size consistency and size extensivity for the CC ansatz stem from the facts that the similarity-transformed Hamiltonian is additively separable and the term is multiplicatively separable. Notice that the electronic Hamiltonian for the molecule (in second quantization) is given by
where are the one-electron integrals and are the two-electron integrals:
Here, M is the number of atoms in the system, are their atomic numbers, , , and are the single-particle optimized orbitals from the HF solution [11,12]. In order to solve the amplitude Equations (2) and (3), we need to explicitly compute the similarity-transformed Hamiltonian. Using the Hadamard lemma (also called the Baker–Campbell–Hausdorff expansion or the Baker–Campbell formula), we can rewrite the transformed Hamiltonian as
Conveniently, the series truncates at the fourth order due to the Hamiltonian having only one- and two-body interaction terms [5,13] and the excitations always being from real to virtual orbitals. Traditionally, this projective method to determine the CC amplitudes is preferred over variational methods due to the non-unitarity of the operator [5,7].
Despite its success, the lack of unitarity prevents the CC operators from being implemented on quantum computers. This suggests using the unitary coupled-cluster ansatz (UCC), whose cluster operator now includes the excitation minus the de-excitation operator [14,15]. Similar to the CC approximation, only the low-rank cluster operators such as singles and doubles are usually selected for the variational eigenstate ansatz, but for more strongly correlated systems, one expects that higher-rank factors will also be needed. In practice, a projective method like the one used in the CC calculation does not work with the UCC ansatz because the similarity-transformed Hamiltonian no longer truncates after the fourth term. Common strategies for carrying it out on classical computers include truncating the Hadamard lemma series at a fixed order [14], expanding the exponential operator in a power series and then truncating it when the higher-rank terms no longer change the eigenfunction [16], and using an exact operator identity of the factorized form of the UCC to allow the wavefunction to be constructed in a tree structure [17]. But, there exists no simple method to work directly with the UCC ansatz in its original form. Since we are working with non-commuting fermionic operators in the exponent, one common way to decompose such a function is to adopt a Trotter product formula:
Another useful method is to express the ansatz in a factorized form, given by
which corresponds to the first-order approximation of the Trotter product formula in Equation (8). The benefit of only using the extreme case is two-fold: the quantum resources required to prepare the factorized UCC ansatz are much smaller than higher-order approximations and the Trotter errors of the first-order approximation can be ameliorated by the fact that the calculation is variational [18,19]. Within the classical computational chemistry framework, work by Chen et al. [17] created an algorithm using the factorized form of the UCC that produces significantly better results for strongly correlated systems and comparable results in terms of accuracy for weakly correlated systems. In this work, we show how one can create efficient implementation of these UCC factors using the linear combination of unitaries approach. For high-rank factors, this approach is preferable.
To implement the factorized UCC ansatz on quantum computers, one needs to transform the cluster operators expressed in the fermionic language into a spin language (via the Jordan–Wigner transformation, or other fermionic encodings). A common realization of this approach is to exactly simulate the individual exponentials of Pauli strings found after the JW transformation of [18,19]. For example, a Jordan-Wigner transformed rank-2 UCC factor is given as
Such a UCC factor can be rewritten as a product of exponentials of Pauli strings because the Pauli strings in the exponentials all commute [18,20]. A common strategy for creating circuits of the form is to use basis transformations where one starts with the circuit for evaluating and then apply basis transformations to evaluate the exponential of any Pauli string [21]. In order to evaluate a generic Pauli string, a basis transformation can be applied before the CNOT cascades such that the effective Pauli string is that of only Z’s. If the ith gate in the Pauli string is an X, a Hadamard gate is sandwiched around the CNOT cascade on the ith qubit. This leads to the effective exponential containing a Z since . Figure 1 shows an example circuit to apply . Similarly, if an exponentiated Y gate is applied, a gate is sandwiched around the CNOT cascade. Figure 2 shows an example circuit to apply Equation (10). In applying the UCC ansatz, circuits such as Figure 2 must be re-run times after applying all of the different basis transformations [18]. A general factorized doubles UCC operator can be rewritten as Equation (10) and implemented exactly by the circuit shown in Figure 2.
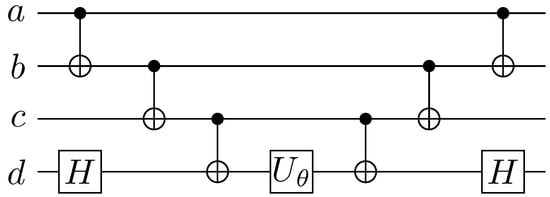
Figure 1.
Example of a circuit implementing for four qubits. To apply the X on a different qubit, Hadamard gates can be sandwiched around the respective qubits.
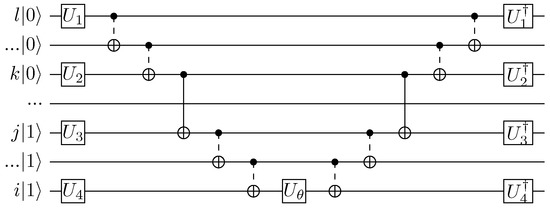
Figure 2.
Doubles UCC circuit as discussed in Refs. [18,19]. For a general doubles operator, the circuit must be applied eight times, with different combinations of U gates each time. The U-gate choices are summarized in Table 1. The dashed CNOT gates are part of a CNOT cascade.

Table 1.
Eight different subcircuits run sequentially to apply a UCC doubles factor to a wavefunction. Since the relevant operators all commute, the subcircuits can be run in any order, but all eight need to appear exactly once to complete the full circuit.
This is possible because the different Pauli strings (for a rank-n UCC factor) commute with each other. In our previous work, we found a way of reducing the number of control-NOT (Cnot) gates in quantum circuits for the factorized UCC ansatz by introducing extra ancilla qubits [20], with the largest reductions for the higher-rank factors. Alternatively, a factorization method introduced in Ref. [22] uses a two-step low-rank factorization to approximate the UCC operator. Circuits that implement the Select() subroutine for more general Jordan–Wigner strings with linear scaling have also been developed [23]. Another framework developed in Ref. [24] optimizes the two-qubit gates by bootstrapping the VQE iterations towards the convergence of the systems ground state energy. A quantum software developed in Ref. [25] optimizes the number of two-qubit gates systematically by compressing adjacent and Pauli operators using a set of rules from the -calculus. Other works have proposed different efficient methods to simulate the UCC factors [26], whose main idea is to directly implement the SU(2) identity of the UCC factors presented in Equation (22) by exchanging coefficients between the two active states. In this work, we introduce a method to directly simulate the sum of terms obtained from a hidden SU(2) symmetry of the first-order Trotter product that greatly reduces the number of multi-qubit entanglement gates of factorized UCC circuits.
2. Background
2.1. SU(2) Identity for Individual UCC Factors
Recall the rank-n cluster operator is defined as
The first two ranks are
where is the fermionic creation operator on the virtual orbital a and is the fermionic annihilation operator on the occupied orbital i, and they obey the standard anticommutation relations given by
where and is the Kronecker delta function. First, we note that because and are disjoint sets, , so the squared term becomes
where is the number operator for spin-orbital . The cubed term then becomes
because the projection operators and evaluate to one when they act on the corresponding fermionic operators. For any UCC factor, the power series expansion is given as
Combining with Equations (15) and (16), we can then exactly write the sum as
for any given set of occupied orbitals and virtual orbitals of rank n [17,27,28]. This identity gives a clear picture of what is happening after a UCC factor is applied to a state. If the state is neither excited by nor de-excited by , the state is unchanged by the UCC factor. Otherwise, the UCC factor acting on the state is equivalent to a cosine multiplied by the original state plus a sine multiplied by the excited (or de-excited) state, just as we would expect from a rotation in the many-body configuration space.
2.2. Jordan–Wigner Transformation of the SU(2) Identity
Hamiltonians written in fermionic terms need to be re-expressed in terms of spin operators in order to be implemented by quantum computers. In this work, we choose to work with the JW transformation for the fermionic encoding. This transformation is given by
where X, Y, and Z are the standard Pauli matrices, and , for the N qubits that describe the molecule. The qubit state has no electrons and has one electron. The SU(2) identity for a UCC factor, as shown in Equation (18), can be re-expressed in terms of the Pauli operators using Equations (19)–(21). For a factorized UCC double (UCCD) operator, the transformation is as follows:
Note that the JW strings simplify because for all cases where two strings overlap. This expression is a unitary operator, but it is also here expressed as a sum over unitary operators because Pauli strings are both Hermitian and unitary.
2.3. Linear Combination of Unitaries
To simulate the sum in Equation (22) on a quantum computer, we use the linear combination of unitaries (LCU) query model [29,30]. Given an input operator represented by a sum of unitaries , with coefficients for each unitary operator , the LCU technique will create a circuit to evaluate this operator acting on a state. It first prepares an ancilla bank with coefficients based on the coefficients in the linear combination:
Here, is a normalization factor, is the initial state of the ancilla bank, and is the product state that will later encode the unitaries in the LCU procedure. The operator Select() is then used to create entanglement between the ancilla bank and system states
One of the hallmarks of the LCU approach is that if the original operator is unitary and , then a single step of oblivious amplitude amplification is able to exactly apply the to the state [29]. Note that in our case the UCC factor, given in Equation (22) is unitary and for all , so it always satisfies this criteria. Hence, the LCU treatment of the sum is exact. The oblivious amplitude amplification is given by
where the and operators are defined as
The main source of circuit complexity of the LCU query model comes from the unitary transformation because it involves applying Select(), which itself can contain a substantial number of multi-qubit gates and quickly outgrows the capability of near-term hardware. One efficient circuit implementation of the Select() subroutine for a generic fermionic Hamiltonian uses Clifford and T gates, with Clifford gates running in layers and T gates in layers. Here, is the number of spin orbitals [23]. The ancilla preparation operator is often implemented by rotations and controlled rotations on the target qubits, followed by gates that create the required entanglement state for the ancilla bank.
Select(U)|n⟩ ⊗ | ψ⟩ = |n⟩ ⊗ Un|ψ⟩
3. Circuit Construction
We begin by illustrating the circuit implementation of the Prepare and Select() subroutines present in the LCU adaptation of the UCC factors for doubles. The doubles are the most ubiquitous terms in the low-rank representation of a UCC ansatz. Later in this section, we will show that UCC factors of arbitrary rank-n can be implemented via a similar algorithm. High-rank factors are necessary to generate an accurate correlation energy in strongly correlated systems.
3.1. Prepare Subroutine
The unitary transformation is used to generate the required entangled state in the ancilla bank, shown in Equation (23). The operator in Equation (22) lends itself to a binary encoding, where we create the linear combination of states multiplied by amplitudes, that is, the sum of . Because there are only three distinct coefficients present in the UCC factor regardless of the rank, the binary encoding allows us to reduce the size of the ancilla bank logarithmically so that it grows with the rank not with the exponential of the rank.
A Prepare circuit for the doubles factor is shown in the Figure 3. The H gates are Hadamard operators, and the and gates are rotations by an angle along the X and Y axis, respectively. For a UCC doubles operator, , and there are three distinct coefficients: eight terms with , seven terms with , and one term with . The four angles used in the circuit shown in Figure 3 can be found analytically:
And the magnitudes of these four angles are shown in Figure 4. The Prepare subroutine is implemented by encoding the amplitudes and in states that always have one different binary digit than those encoding the amplitude . For example, in the doubles circuit, we encode the amplitudes and in states and and encode the amplitude in states .
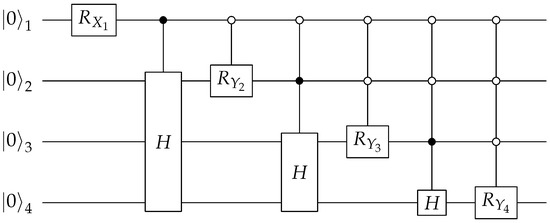
Figure 3.
Quantum circuit for preparing the ancilla bank of the LCU query for a rank-2 UCC factor (so-called doubles).
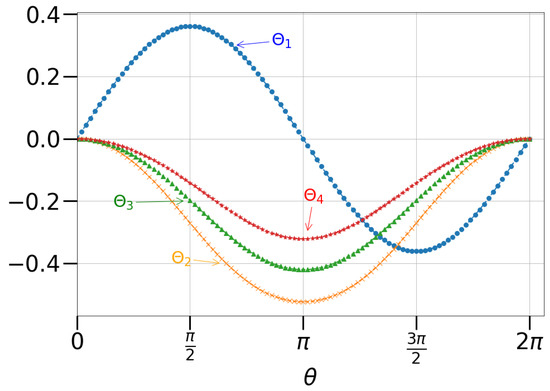
Figure 4.
The four angles used in the Prepare subroutine for a UCC doubles factor with an amplitude given by .
The Prepare circuit for a doubles UCC factor can be straightforwardly generalized to one for a rank-n operator. In this case, we require ancilla qubits, where there are subterms with coefficients , subterms with coefficients , and one term with coefficient . The hierarchical structure of the circuit is a simple generalization of the doubles circuit to higher rank, where the first element, which sets the sin terms is the same, while the remaining factors are created by extending the hierarchy with multiple controlled Hadamards followed by multiply controlled rotations. The angles for each rotation in the algorithm are
for .
Most of the quantum computing costs on near-term quantum computers come from the Cnot circuit elements; thus, we focus on counting the number of these gates to estimate the total cost of the circuits. The controlled-H gate, CH, is implemented by one Cnot sandwiched by one gate and one gate. The controlled- operator is employed by two Cnot gates and two half rotations. We use the linear-depth method proposed in Ref. [31] to decompose the multi-qubit control operators into standard Cnot and one-qubit gates. The Cnot cost of an n-qubit controlled operator is for all . The circuit needs Cnot gates for each k-qubit controlled operation. For , the Cnot cost is . To implement the circuit for an arbitrary rank-n, we need to employ the modular sub-circuit shown in Figure 5 and Figure 6 on ancilla qubits. The upper bound for the number of control qubits used in any module is . The total cost of running the Prepare subroutine is then , which can be further simplified to . Hence, the cost scales like the cube of the rank.
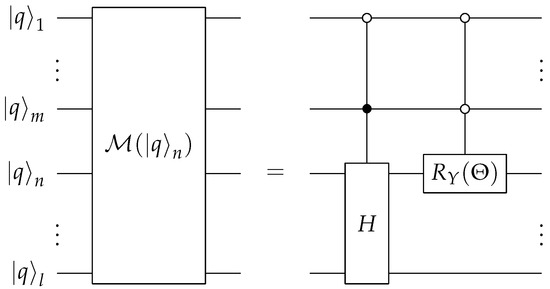
Figure 5.
Quantum circuit for the modules of qubit- used in the Prepare subroutine. The Hadamard operator is anticontrolled by the qubits between and and controlled by the qubit . The operator acting on the n-th input is anticontrolled by qubits to . The circuit on the right defines the circuit block on the left.
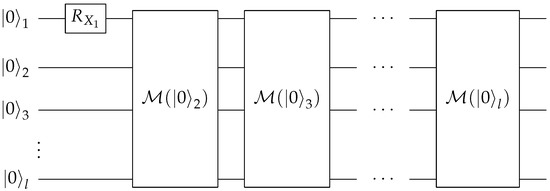
Figure 6.
Quantum circuit for the Prepare subroutine of arbitrary rank with modules introduced in Figure 5.
3.2. Select() Subroutine for Rank-2 Factors
In this section, we introduce a quantum circuit for implementing the operation, illustrated in Equation (24), for the UCCD factors, where the unitary is the operator given in Equation (22). The first step of the Select() circuit is to create one of the Pauli strings from the pool of the excitation operators ( strings) and one of the Pauli strings from the projection pool ( strings). In this example, we opt to create the and strings as shown in Figure 7; however, any arbitrary Pauli string can be the candidate for this step. It is important to note that we use control operations for the terms, whereas we use anticontrol operations for the terms. This is because we are partitioning the ancilla bank into two sectors, one part for the strings, and one part for the strings. In this case, ancilla-bank states to are used to create the strings, and ancilla-bank states to are used to create the strings. The resulting state, omitting the corresponding coefficients, which are prepared in the previous step, becomes
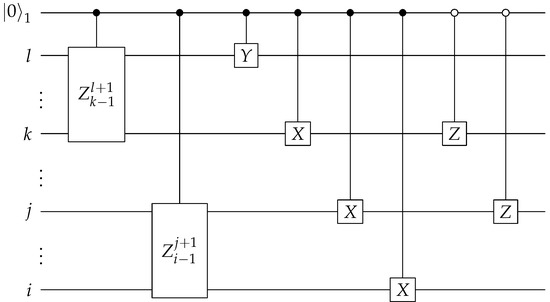
Figure 7.
Circuit to create and . denotes the first qubit of the ancilla bank. The first two circuit components are the controlled Pauli Z gates applied on qubits between (exclusively) indices l and k, and between indices j and i.
The construction of the controlled Pauli Z gates shown in Figure 7 is described next. With the starting reference states prepared, we can then create the entire state exactly. The first step is to apply a single-qubit controlled Pauli Z operator on qubits l and k, where the control is to be conditioned on the last qubit of the ancilla bank. The second step is similar, in that a single-qubit controlled Pauli Z operator is applied on qubits j and i. The control qubit of the second step is the second to last qubit of the ancilla bank. The final step is to apply the single-qubit controlled Pauli Z on qubits k and j, with the control qubit being the second qubit of the ancilla bank. The circuit diagram is illustrated in Figure 8. The Pauli strings and their corresponding states in the ancilla bank are shown in Table 2. The qubits on which the control operations are conditioned are chosen specifically for this table. In practice, when applying this algorithm, one needs to predetermine a table similar to Table 2 for all the binary encodings and their corresponding Pauli substrings, and choose accordingly the starting reference states and the control qubits to be used in the approach illustrated shown in Figure 7, Figure 8 and Figure 9.
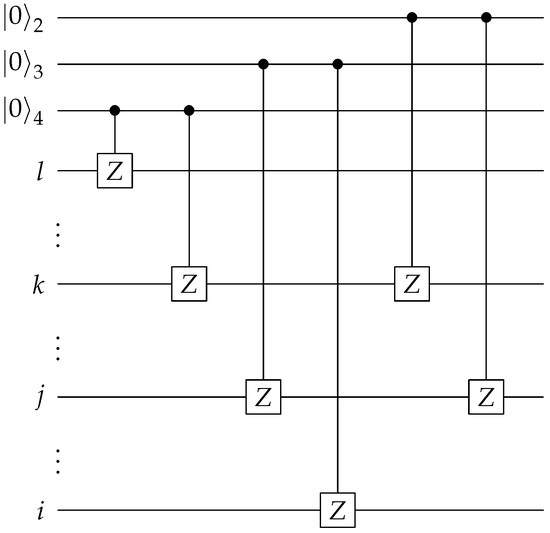
Figure 8.
Circuit to create the state shown in Equation (22). denotes the ith qubit of the ancilla bank.

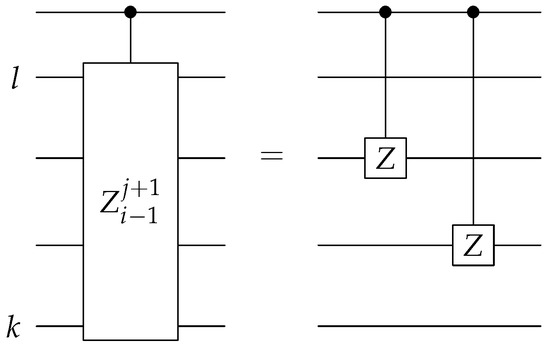
Figure 9.
The circuit for implementing the boxed controlled Pauli Z operators shown in Figure 7. The Pauli Z operators are being applied to the qubits to .
3.3. Select() for Arbitrary Rank-n
In this section, we demonstrate the algorithm for the rank-n UCC factor buy generalizing the algorithms shown in Section 3.1 and Section 3.2. First, let us re-examine the case for rank-2; that is, the doubles. Define groups and , with elements , where and are two different Pauli operators acting on different qubits. Additionally, the group elements have the following identities
where is the Pauli Z operator being applied on qubit . It should be clear that the expression in Equation (22) is of the schematic form , omitting the coefficients, where the groups contain subterms and the contain subterms. In the example shown in the Section 3.1 and Section 3.2, the corresponding groups are , , , and . There are in total three steps needed to create the eigenfunction; hence, we opted to use three digits for the binary encoding in the ancilla bank. The Select() subroutines are summarized in Table 3 and Table 4.

Table 3.
Matrix that shows the scheme for the subterms presented in Section 3.2. The entry colored in blue, , is the initial reference state. After the first step, the yellow entry is created. The pink entries are created after the second step. The first two steps use the identities in Equations (34) and (36). The final step is to use the identities in Equations (35) and (37) to create the green block.

Table 4.
Matrix that shows the scheme for the subterms presented in Section 3.2. The entry colored in blue, , is chosen to be the starting reference state. After the first step, the yellow entry is created. The pink entries result after the second step. The first two steps use the identities in Equations (34) and (36). The final step is to use the identities in Equations (35) and (37) to create the entire green block.
Similar to the way we define for the rank-2 factors, for rank-3, we define groups and ; therefore, the wavefunction for the UCC triples factors after the JW transformation take the form . The set of identities for rank-3 is
As shown in the Table 5 and Table 6, there are in total five steps needed to create the exact JW-transformed unitary, and thus we use five out of six digits for the binary encoding in the ancilla bank. Table 7 shows that the total number of steps needed to fully create the unitary is seven.

Table 5.
Matrix illustrating the scheme for constructing substrings in the JW-transformed unitary of the UCCT factors. The blue entry is chosen to be the starting reference state. After the first step using identity (38), grey entry is created. Using the identities in Equations (39) and (40), the yellow entries are created after the second step. The orange and pink columns are created after the next two steps via the identities in Equations (41) through (44). The final step is to apply the identities in Equations (46) through (49) to create the entire green block.

Table 6.
Matrix illustrating the scheme for constructing substrings in the JW-transformed unitary of the UCCT factors. The blue entry is the starting reference state. After the first step using the identity in Equation (38), the grey entry is created. Using the identities in Equations (39) and (40), the yellow entries are created after the second step. The orange and pink columns are created after the next two steps via the identities in Equations (41) through (44). The final step is to apply the identities in Equations (46) through (49) to create the entire green block.

Table 7.
Off-diagonal block of a matrix illustrating the scheme for constructing substrings in the JW-transformed unitary of the UCCQ factors. The blue entry of the first column is chosen to be the starting reference state. The grey entry is created after the first step, followed by the green entries in the second step and the yellow entries in the third step. The pink entries of the last column are created after the fourth step, followed by the orange columns in the fifth step and purple columns in the sixth step.
For a UCC factor with arbitrary rank n, a total number of transformations are required to complete the first column of the matrix. An additional transformations are then required to complete the rest of the diagonal or off-diagonal block, depending on whether the subterms are strings or strings. The final step is to perform the ’flip’ transformation to make the entire matrix. Therefore, for any UCC factor of rank n, a total number of steps are needed to construct the JW-transformed unitary operator.
3.4. Gate Counts
The LCU framework for rank-n UCC factors is given by a simple circuit implementation of the JW-transformed unitary in the form of
where each group contains elements that commute with every other element in the same group but anticommute with elements in the other group. The total number of steps in the Select() subroutine is for rank-n factors. Within each step of the Select() subroutine, two single-qubit controlled Pauli Z operators are needed, making the total number of Cnot gates . In addition, Cnot gates are needed for initializing the reference Jordan–Wigner strings. Here, is the number of qubits between the ith pair of the active orbitals. In the case of a UCCD factor discussed in Section 3.1 and Section 3.2, is the number of qubits between qubits k and l and is the number of qubits between qubits j and i. The circuit for preparing the ancilla bank hosts the majority of the complexity, where the total Cnot cost is . The total number of Cnot gates used in the LCU circuit for preparing the JW-transformed unitary is then , which can be further simplified to . Note that this has a large prefactor in the scaling with the rank. The total number of ancilla qubits required for this framework is . For a UCC factor with an arbitrary set of active orbitals, the Cnot cost of the circuits proposed in our work eventually becomes favorable compared with other existing methods when the rank becomes large (), including the one proposed in the authors’ previous work [20], although for low-rank factors, the fermionic-excitation-based (FEB) algorithm proposed by Ref. [26] is more efficient, which is shown in Figure 10.
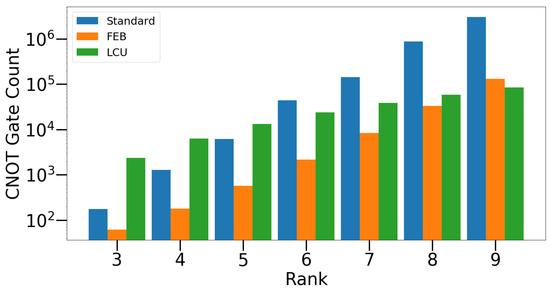
Figure 10.
Cnot gate counts for three different algorithms, the standard Cnot cascading circuits, the FEB circuits [26], and the linear-combination-of-unitary query circuits introduced in this work.
4. Discussion
In summary, we have introduced an application of the LCU query model that efficiently simulates the factorized UCC ansatze with a scaling that goes like the cube of the rank. We have demonstrated the quantum circuits for the Prepare and the Select() subroutines, whose Cnot counts scale linearly with the rank of the UCC ansatze and the number of active spin-orbitals. The Prepare operator employs a quantum circuit that scales as the cube of the rank of the UCC factor and requires a linear number of ancilla. The proposed LCU framework greatly reduces the number of two-qubit gates for high-rank UCC factors, which are needed for simulating strongly correlated systems on NISQ devices and future fault-tolerant quantum computers [28]. Although the UCC ansatzes that contain only singles and doubles with some triples treated perturbatively are considered the golden standard in quantum chemistry calculations, Refs. [32,33] demonstrated that rank-17 excitations are needed to obtain accurate results for systems such as the chromium dimer. Further, it is expected that strongly correlated systems will require higher rank terms and these are precisely the problems proposed for quantum computers.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/sym15071429/s1.
Author Contributions
Conceptualization, L.X. and J.K.F.; methodology, L.X.; validation, L.X. and J.K.F.; formal analysis, L.X. and J.K.F.; investigation, L.X. and J.K.F.; resources, J.K.F.; data curation, L.X.; writing—original draft preparation, L.X. and J.K.F.; writing—review and editing, L.X. and J.K.F.; visualization, L.X.; supervision, J.K.F.; project administration, J.K.F.; funding acquisition, J.K.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the U. S. Department of Energy grant number ERKJ347.
Data Availability Statement
The data presented in this study are openly available in Supplementary Materials.
Acknowledgments
We acknowledge helpful discussions with Joseph T. Lee, L. Xu, and J. K. Freericks were supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research (ASCR), Quantum Computing Application Teams (QCATS) program, under field work proposal number ERKJ347. J. K. Freericks was also supported by the McDevitt bequest at Georgetown University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aspuru-Guzik, A. Simulated Quantum Computation of Molecular Energies. Science 2005, 309, 1704–1707. [Google Scholar] [CrossRef]
- Whitfield, J.D.; Biamonte, J.; Aspuru-Guzik, A. Simulation of electronic structure Hamiltonians using Quantum Computers. Mol. Phys. 2011, 109, 735–750. [Google Scholar] [CrossRef]
- Sherrill, C.D.; Schaefer, H.F. The Configuration Interaction Method: Advances in Highly Correlated Approaches. Adv. Quantum Chem. 1999, 34, 143–269. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Purvis, G.D. Many-body perturbation theory, coupled-pair many-electron theory, and the importance of quadruple excitations for the correlation problem. Int. J. Quantum Chem. 1978, 14, 561–581. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Purvis, G.D.; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Anand, A.; Schleich, P.; Alperin-Lea, S.; Jensen, P.W.; Sim, S.; Díaz-Tinoco, M.; Kottmann, J.S.; Degroote, M.; Izmaylov, A.F.; Aspuru-Guzik, A.; et al. A quantum computing view on unitary coupled cluster theory. Chem. Soc. Rev. 2022, 51, 1659–1684. [Google Scholar] [CrossRef]
- Peruzzo, A.; Mcclean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Helgaker, T.J. Molecular Electronic-Structure Theory; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Szabo, A.; Ostlund, N.S. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory; Dover Publications: Mineola, NY, USA, 2006. [Google Scholar]
- Taketa, H.; Huzinaga, S.; O-Ohata, K. Gaussian-Expansion Methods for Molecular Integrals. J. Phys. Soc. Jpn. 1966, 21, 2313–2324. [Google Scholar] [CrossRef]
- Shavitt, I.; Bartlett, R.J. Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory; Cambridge University Press: Cambridge, MA, USA, 2009. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Kucharski, S.A.; Noga, J. Alternative coupled-cluster ansätze II. The unitary coupled-cluster method. Chem. Phys. Lett. 1989, 155, 133–140. [Google Scholar] [CrossRef]
- Schaefer, H.F. Methods of Electronic Structure Theory; Springer Science Business Media, LLC: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Cooper, B.; Knowles, P.J. Benchmark studies of variational, unitary and extended coupled cluster methods. J. Chem. Phys. 2010, 133, 234102. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Cheng, H.P.; Freericks, J.K. Quantum-Inspired Algorithm for the Factorized Form of Unitary Coupled Cluster Theory. J. Chem. Theory Comput. 2021, 17, 841–847. [Google Scholar] [CrossRef]
- Romero, J.; Babbush, R.; Mcclean, J.R.; Hempel, C.; Love, P.J.; Aspuru-Guzik, A. Strategies for quantum computing molecular energies using the unitary coupled cluster ansatz. Quantum Sci. Technol. 2018, 4, 014008. [Google Scholar] [CrossRef]
- Barkoutsos, P.K.; Gonthier, J.F.; Sokolov, I.; Moll, N.; Salis, G.; Fuhrer, A.; Ganzhorn, M.; Egger, D.J.; Troyer, M.; Mezzacapo, A.; et al. Quantum algorithms for electronic structure calculations: Particle-hole Hamiltonian and optimized wave-function expansions. Phys. Rev. A 2018, 98, 022322. [Google Scholar] [CrossRef]
- Xu, L.; Lee, J.T.; Freericks, J.K. Decomposition of high-rank factorized unitary coupled-cluster operators using ancilla and multiqubit controlled low-rank counterparts. Phys. Rev. A 2022, 105. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Motta, M.; Ye, E.; McClean, J.R.; Li, Z.; Minnich, A.J.; Babbush, R.; Chan, G.K.L. Low rank representations for quantum simulation of electronic structure. NPJ Quantum Inf. 2021, 7, 83. [Google Scholar] [CrossRef]
- Wan, K. Exponentially faster implementations of select(h) for Fermionic Hamiltonians. Quantum 2021, 5, 380. [Google Scholar] [CrossRef]
- Wang, Q.; Li, M.; Monroe, C.; Nam, Y. Resource-optimized fermionic local-Hamiltonian simulation on a quantum computer for Quantum Chemistry. Quantum 2021, 5, 509. [Google Scholar] [CrossRef]
- Cowtan, A.; Dilkes, S.; Duncan, R.; Simmons, W.; Sivarajah, S. Phase gadget synthesis for shallow circuits. Electron. Proc. Theor. Comput. Sci. 2020, 318, 213–228. [Google Scholar] [CrossRef]
- Magoulas, I.; Evangelista, F.A. CNOT-efficient circuits for arbitrary rank many-body fermionic and qubit excitations. J. Chem. Theory Comput. 2023, 19, 822–836. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Lee, J.T.; Freericks, J.K. Test of the unitary coupled-cluster variational quantum eigensolver for a simple strongly correlated condensed-matter system. Mod. Phys. Lett. B 2020, 34, 2040049. [Google Scholar] [CrossRef]
- Freericks, J.K. Operator relationship between conventional coupled cluster and unitary coupled cluster. Symmetry 2022, 14, 494. [Google Scholar] [CrossRef]
- Childs, A.M.; Wiebe, N. Hamiltonian simulation using linear combinations of unitary operations. Quantum Inf. Comput. 2012, 12, 901–924. [Google Scholar] [CrossRef]
- Berry, D.W.; Childs, A.M.; Cleve, R.; Kothari, R.; Somma, R.D. Simulating Hamiltonian dynamics with a truncated Taylor series. Phys. Rev. Lett. 2015, 114, 090502. [Google Scholar] [CrossRef]
- da Silva, A.J.; Park, D.K. Linear-depth quantum circuits for multiqubit controlled gates. Phys. Rev. A 2022, 106, 042602. [Google Scholar] [CrossRef]
- Li, J.; Yao, Y.; Holmes, A.A.; Otten, M.; Sun, Q.; Sharma, S.; Umrigar, C.J. Accurate many-body electronic structure near the basis set limit: Application to the chromium dimer. Phys. Rev. Res. 2020, 2, 012015. [Google Scholar] [CrossRef]
- Larsson, H.R.; Zhai, H.; Umrigar, C.J.; Chan, G.K.L. The chromium dimer: Closing a chapter of Quantum Chemistry. J. Am. Chem. Soc. 2022, 144, 15932–15937. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).