Symmetric and Asymmetric Crisscross Augmented Ladder Multilevel Inverter with Fuzzy Logic Controller Optimization
Abstract
1. Introduction
2. Proposed CCAL Topology
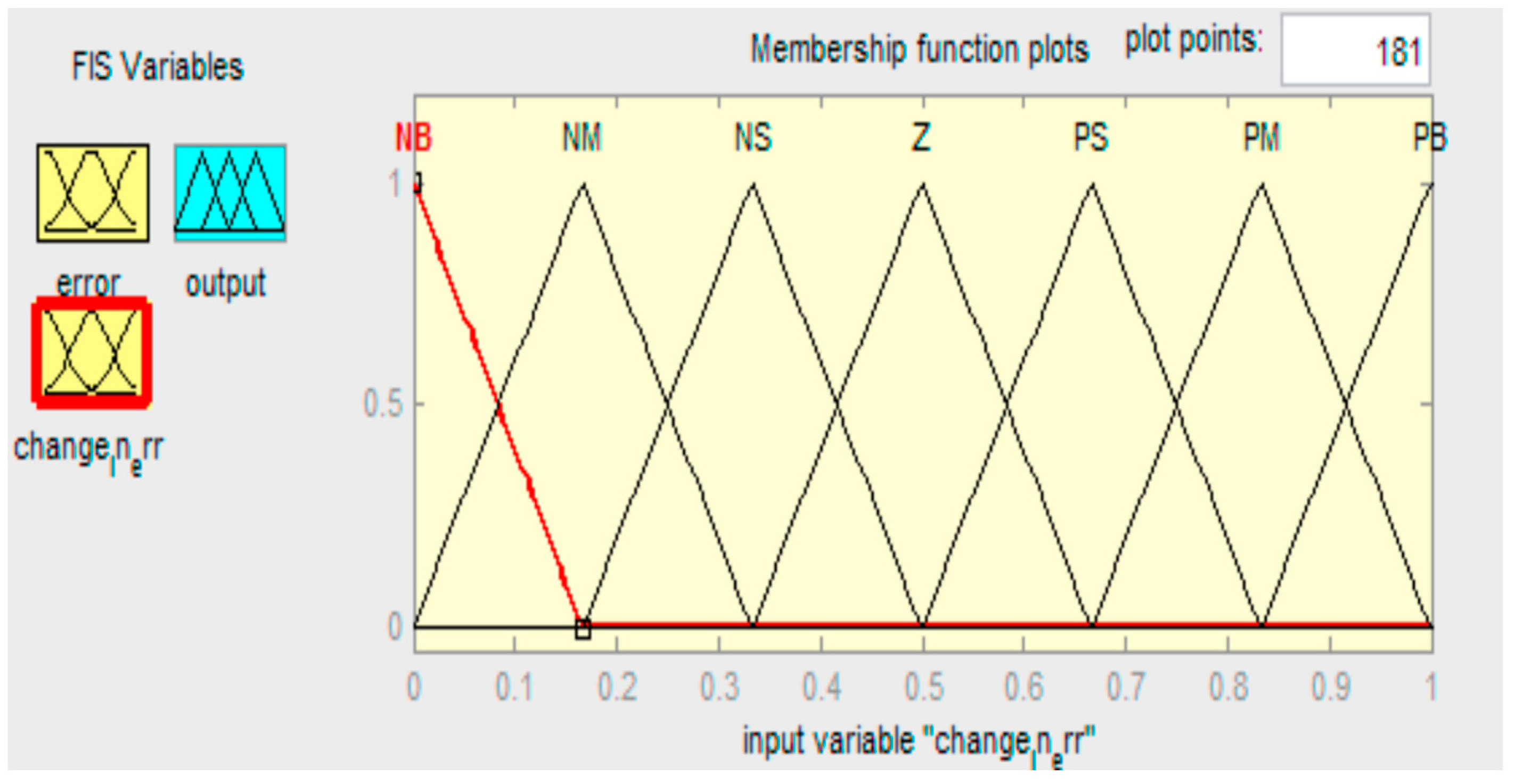
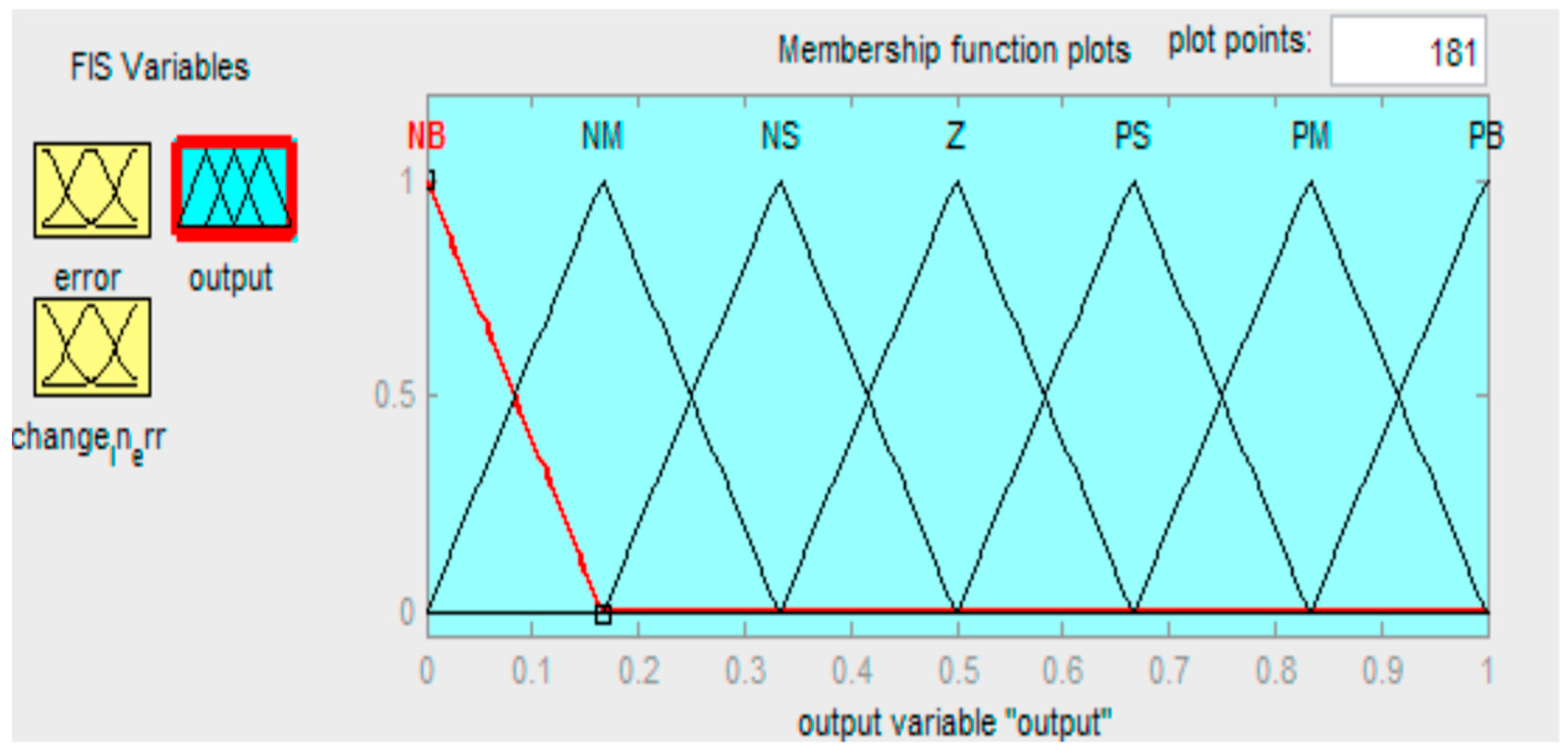
3. Modulation and Control Strategy
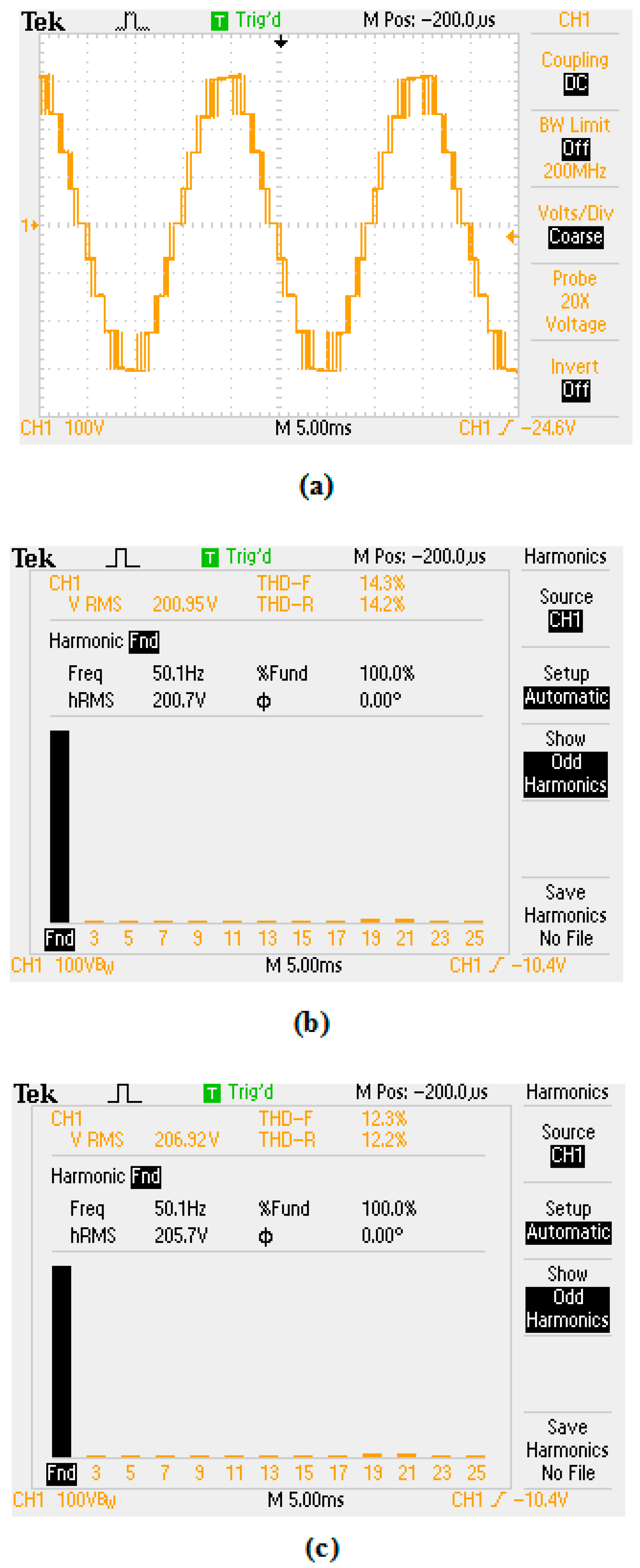
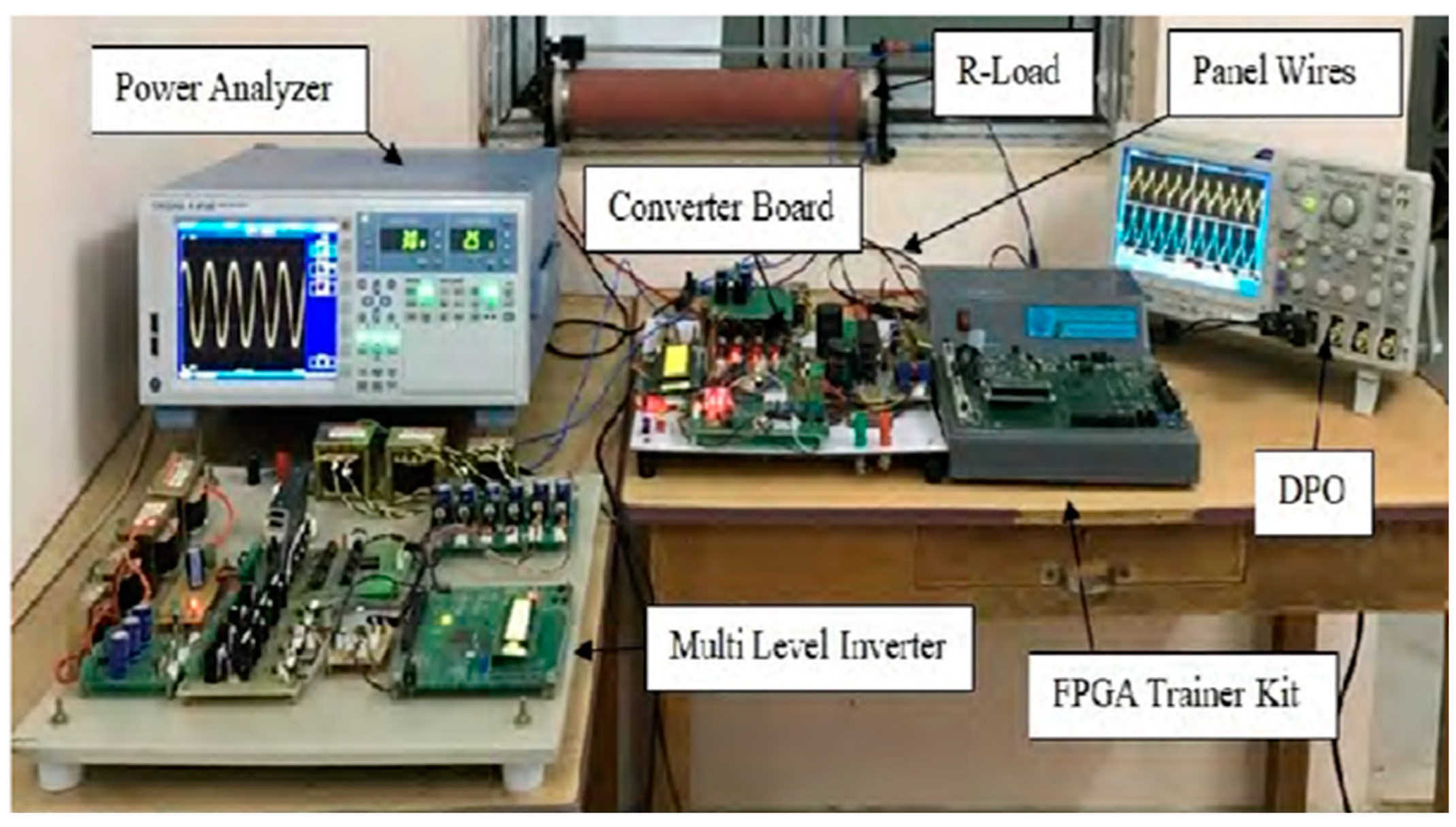
4. Simulation and Experimental Investigations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hota, A.; Jain, S.; Agarwal, V. An Improved Three Phase Five-level Inverter Topology with Reduced Number of Switching Power Devices. IEEE Trans. Ind. Electron. 2018, 65, 3296–3305. [Google Scholar] [CrossRef]
- Su, G.-J. Multilevel DC-Link Inverter. IEEE Trans. Ind. Appl. 2005, 41, 848–854. [Google Scholar] [CrossRef]
- Mondal, G.; Gopakumar, K.; Tekwani, P.N.; Levi, E. A Reduced-Switch-Count Five-Level Inverter with Common-Mode Voltage Elimination for an Open-End Winding Induction Motor Drive. IEEE Trans. Ind. Electron. 2007, 54, 2344–2351. [Google Scholar] [CrossRef]
- Ebrahimi, J.; Babaei, E.; Gharehpetian, G.B. A New Topology of Cascaded Multilevel Converters with Reduced Number of Components for High-Voltage Applications. IEEE Trans. Power Electron. 2011, 26, 3109–3118. [Google Scholar] [CrossRef]
- Nami, A.; Zare, F.; Ghosh, A.; Blaabjerg, F. A Hybrid Cascade Converter Topology with Series-Connected Symmetrical and Asymmetrical Diode-Clamped H-Bridge Cells. IEEE Trans. Power Electron. 2011, 26, 51–65. [Google Scholar] [CrossRef]
- Ramkumar, S.; Kamaraj, V.; Thamizharasan, S.; Jeevananthan, S. A new series parallel switched multilevel dc-link inverter topology. Int. J. Electr. Power Energy Syst. 2012, 36, 93–99. [Google Scholar] [CrossRef]
- Gupta, K.K.; Jain, S. Topology for multilevel inverters to attain maximum number of levels from given DC sources. IET Power Electron. 2012, 5, 435–446. [Google Scholar] [CrossRef]
- Babaei, E.; Kangarlu, M.F.; Mazgar, F.N. Symmetric and asymmetric multilevel inverter topologies with reduced switching devices. Electr. Power Syst. Res. 2012, 86, 122–130. [Google Scholar] [CrossRef]
- Lu, X.; Ge, B.; Peng, F.Z. Minimizing DC Capacitance Requirement of Cascadeded H-Bridge Multilevel Inverters for Photovoltaic Systems by 3rd Harmonic Injection. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 240–245. [Google Scholar] [CrossRef]
- Ajami, A.; Oskuee, M.R.J.; Khosroshahi, M.T.; Mokhberdoran, A. Cascade-multi-cell multilevel converter with reduced number of switches. IET Power Electron. 2014, 7, 552–555. [Google Scholar] [CrossRef]
- Gupta, K.K.; Ranjan, A.; Bhatnagar, P.; Sahu, L.K.; Jain, S. Multilevel Inverter Topologies with Reduced Device Count: A Review. IEEE Trans. Power Electron. 2016, 31, 135–151. [Google Scholar] [CrossRef]
- Roy, T.; Sadhu, P.K.; Dasgupta, A. Cross-Switched Multilevel Inverter using Novel Switched Capacitor Converters. IEEE Trans. Ind. Electron. 2019, 66, 8521–8532. [Google Scholar] [CrossRef]
- Arun, N.; Noel, M.M. Crisscross switched multilevel inverter using cascaded semi-half-bridge cells. IET Power Electron. 2018, 11, 23–32. [Google Scholar] [CrossRef]
- Farhadi-Kangarlu, M.; Torshakaan, M.B.; Neyshabouri, Y. A Transformerless DSTATCOM Based on Cross-Switched Multilevel Inverter for Grid Voltage Regulation. Int. J. Electr. Eng. Inform. 2020, 12, 398–417. [Google Scholar]
- Kangarlu, M.F.; Babaei, E. Cross-switched multilevel inverter: An innovative Topology. IET Power Electron. 2013, 6, 642–651. [Google Scholar] [CrossRef]
- Khosroshahi, M.T. Crisscross cascade multilevel inverter with reduction in number of components. IET Power Electron. 2014, 7, 2914–2924. [Google Scholar] [CrossRef]
- Titus, S. A Stipulation Based Sources Insertion Multilevel Inverter (SBSIMLI) for Waning the Component Count and Separate DC Sources. J. Electr. Eng. Technol. 2017, 12, 1519–1528. [Google Scholar]
- Kannan, C.; Mohanty, N.K.; Selvarasu, R. A new topology for cascaded H-bridge multilevel inverter with PI and Fuzzy control. Energy Procedia 2017, 117, 917–926. [Google Scholar] [CrossRef]
- Samadaei, E.; Gholamian, S.A.; Sheikholeslami, A.; Adabi, J. An envelope type (E-Type) module: Asymmetric multilevel inverters with rreduced components. IEEE Trans. Ind. Electron. 2016, 63, 7148–7156. [Google Scholar] [CrossRef]
- Jose, S.E.; Titus, S. A Level Dependent Source Concoction Multilevel Inverter Topology with a Reduced Number of Power Switches. J. Power Electron. 2016, 16, 1316–1323. [Google Scholar] [CrossRef]
- Khosroshahi, M.T.; Ajami, A.; Mokhberdoran, A.O.; OsKuee, M.J. Multilevel hybrid cascade-stack inverter with substantial reduction in switches number and power losses. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 987–1000. [Google Scholar] [CrossRef]
- Dhanamjayulu, C.; Prasad, D.; Padmanaban, S.; Maroti, P.K.; Holm-Nielsen, J.B.; Blaabjerg, F. Design and Implementation of Seventeen Level Inverter with Reduced Components. IEEE Access 2021, 9, 16746–16760. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekhilef, S.; Rawa, M.; Wahyudie, A.; Chokaev, B.; Salamov, I. Extended Multilevel Inverter Topology with Reduced switch Count and Voltage stress. IEEE Access 2020, 8, 201835–201846. [Google Scholar] [CrossRef]
- Arif, M.S.B.; Mustafa, U.; Ayob, S.B.M.; Rodriguez, J.; Nadeem, A.; Abdelrahem, M. Asymmetrical 17-Level Inverter Topology with Reduced Total Standing Voltage and Device Count. IEEE Access 2021, 9, 69710–69723. [Google Scholar] [CrossRef]
- Siddique, M.D.; Iqbal, A.; Memon, M.A.; Mekhilef, S. A New Configurable Topology for Multilevel Inverter with Reduced Switching Components. IEEE Access 2020, 8, 188726–188741. [Google Scholar] [CrossRef]
- Zolfaghar, M.; Najafi, E.; Hasanzadeh, S. A modified diode clamped inverter with reduced number of switches. In Proceedings of the 2018 9th Annual Power Electronics, Drives Systems and Technologies Conference (PEDSTC), Tehran, Iran, 13–15 February 2018; pp. 53–58. [Google Scholar]
- Bouafassa, A.; Rahmani, L.; Kessal, A.; Babes, B. Unity power factor Converter based on a Fuzzy controller and Predictive Input Current. ISA Trans. 2014, 53, 1817–1821. [Google Scholar] [CrossRef]
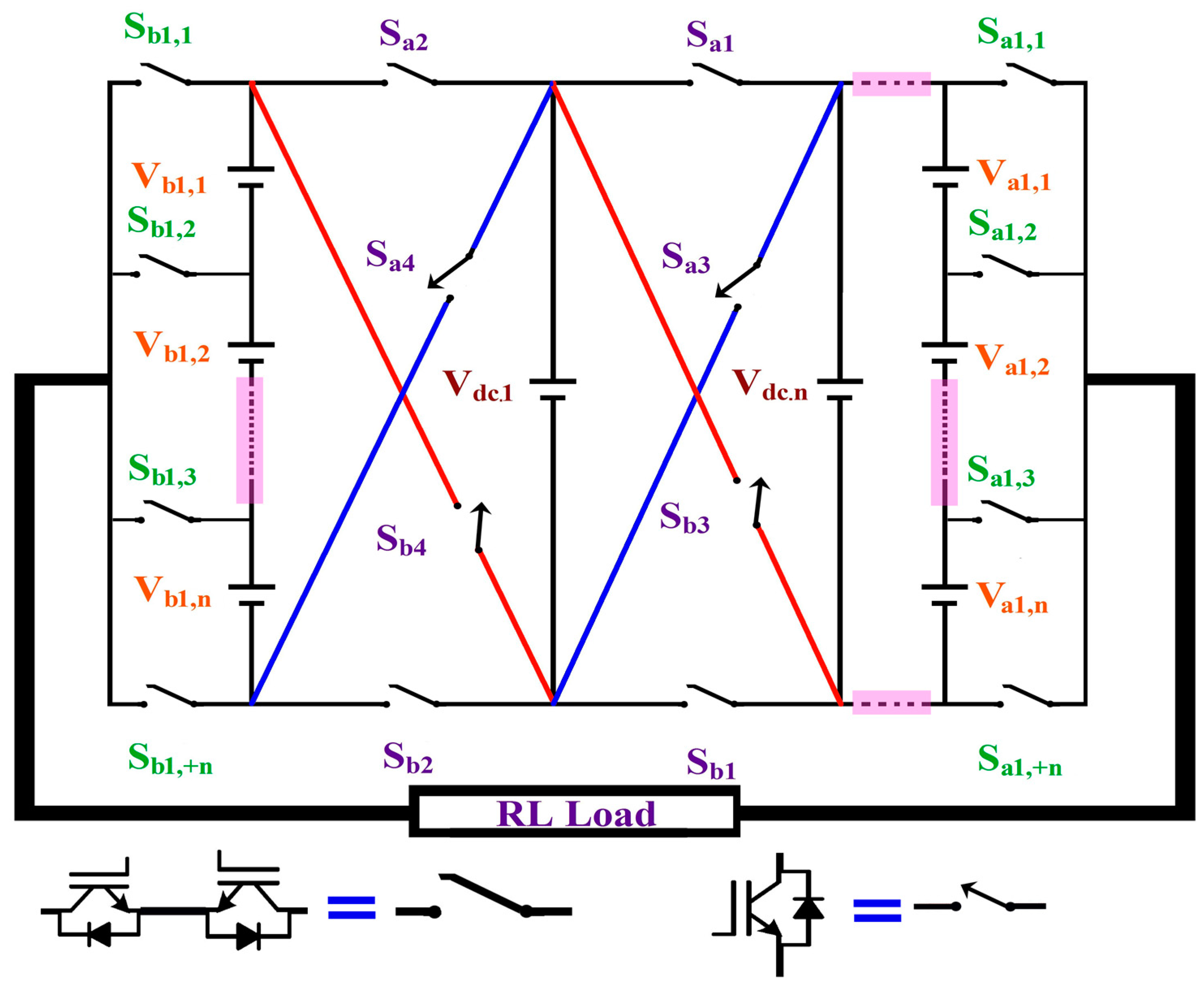
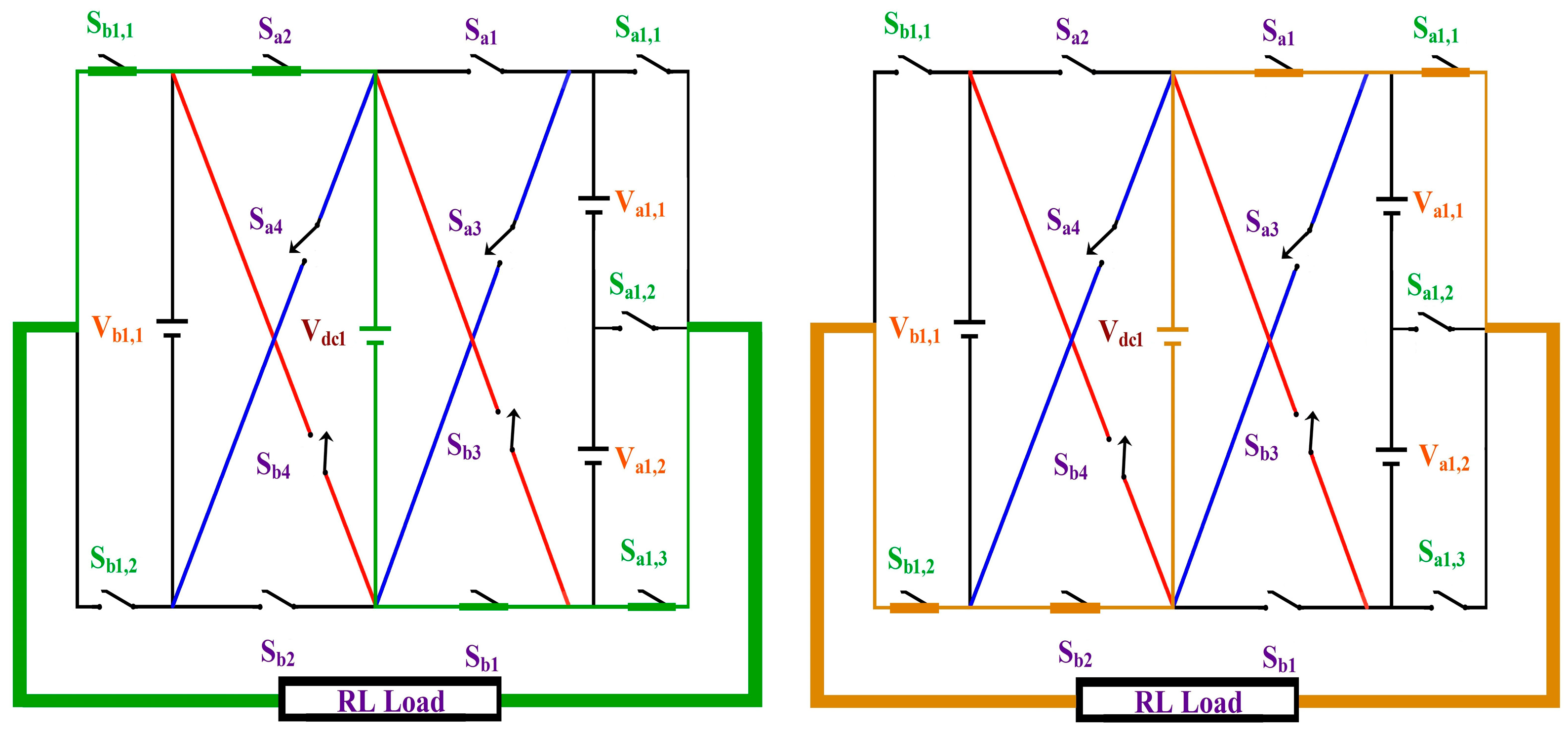

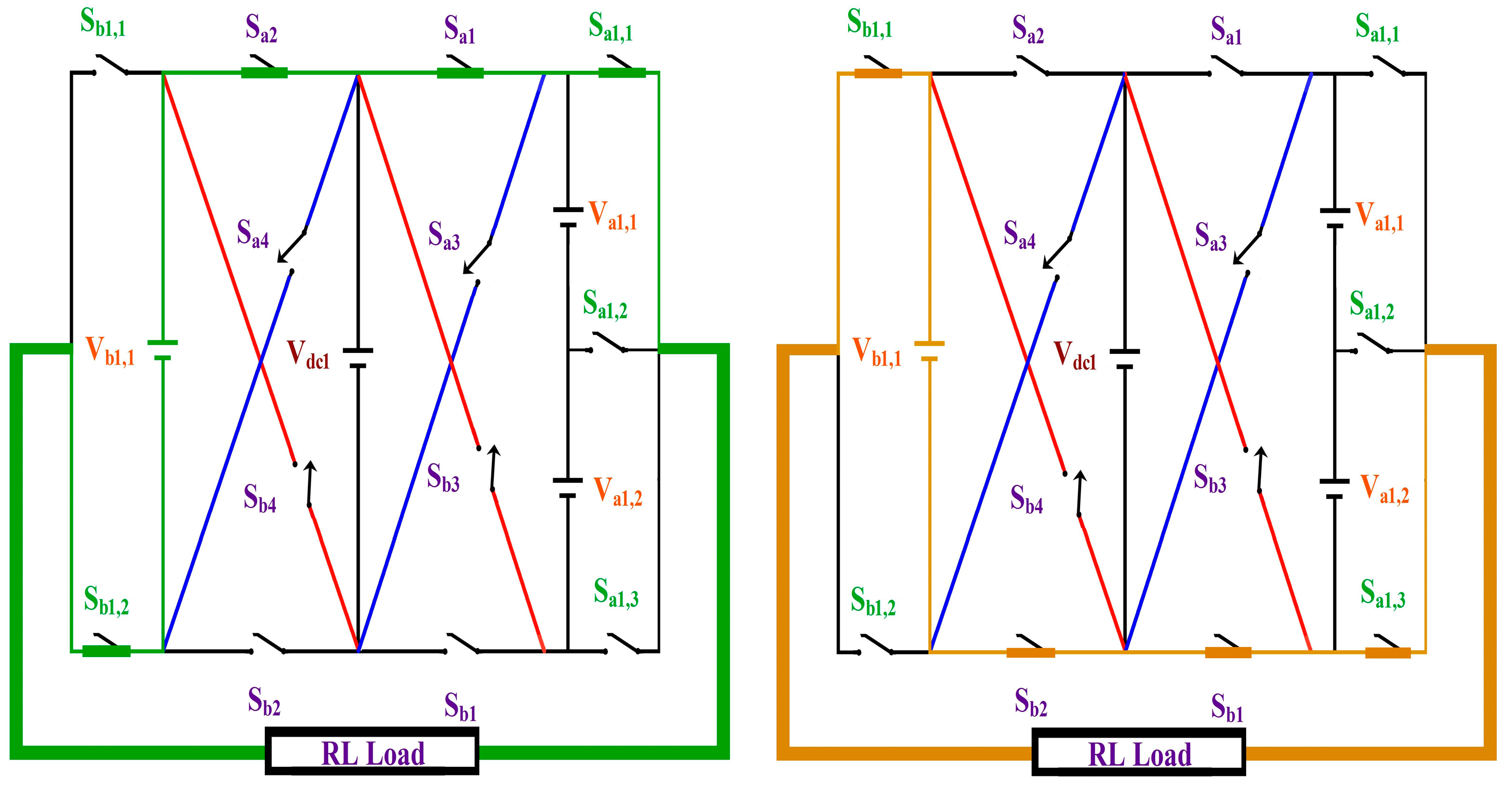

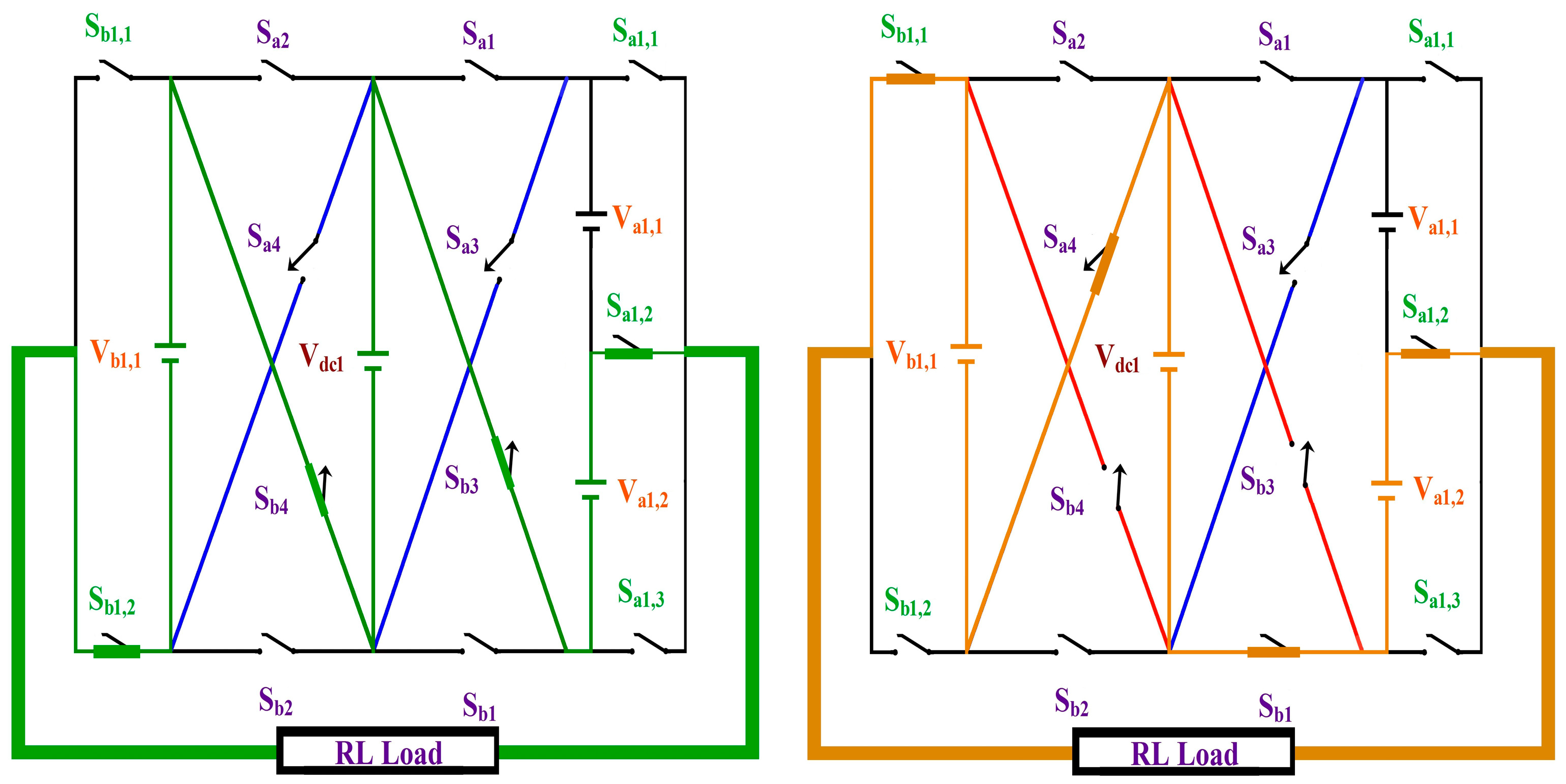
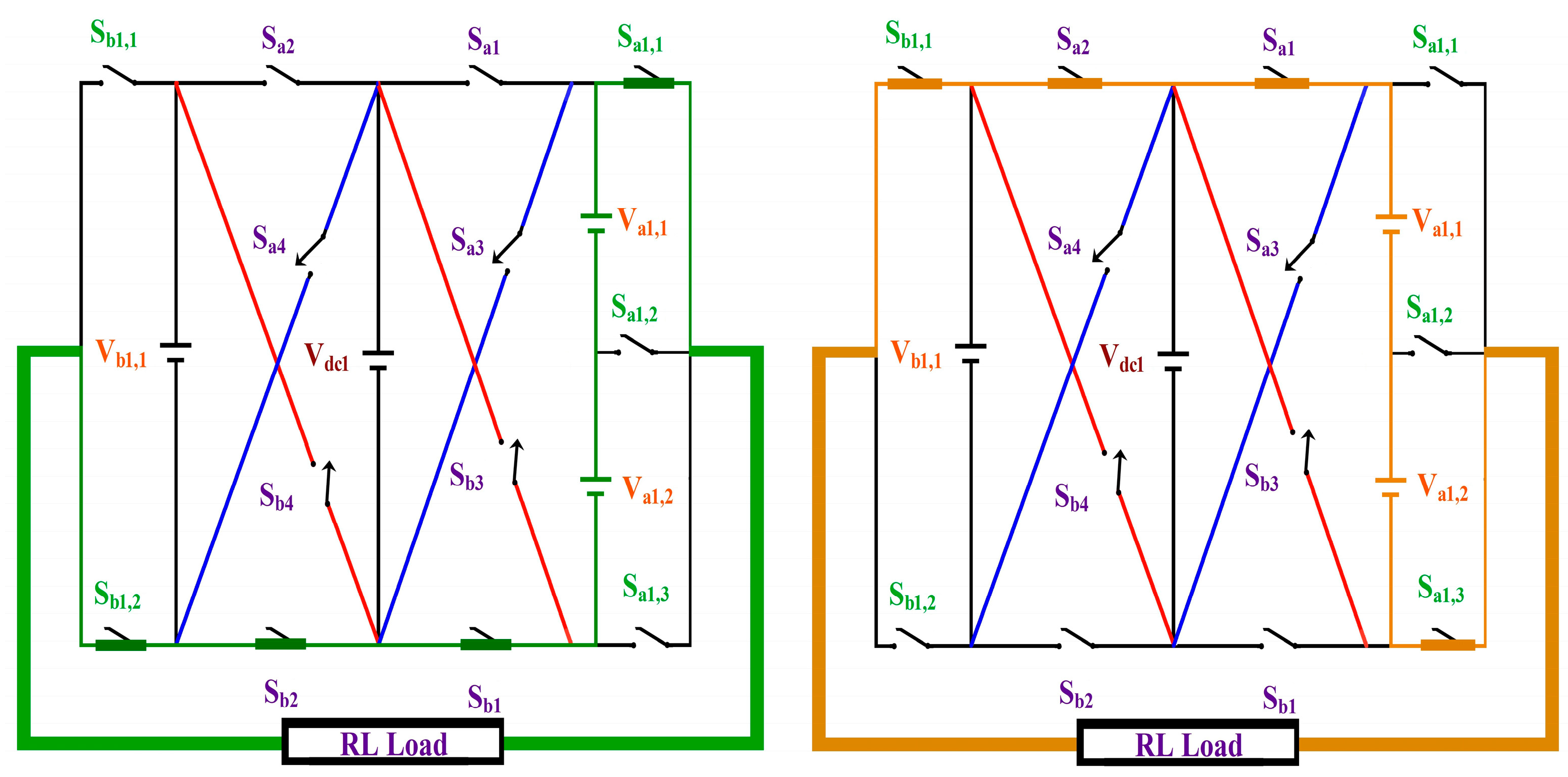
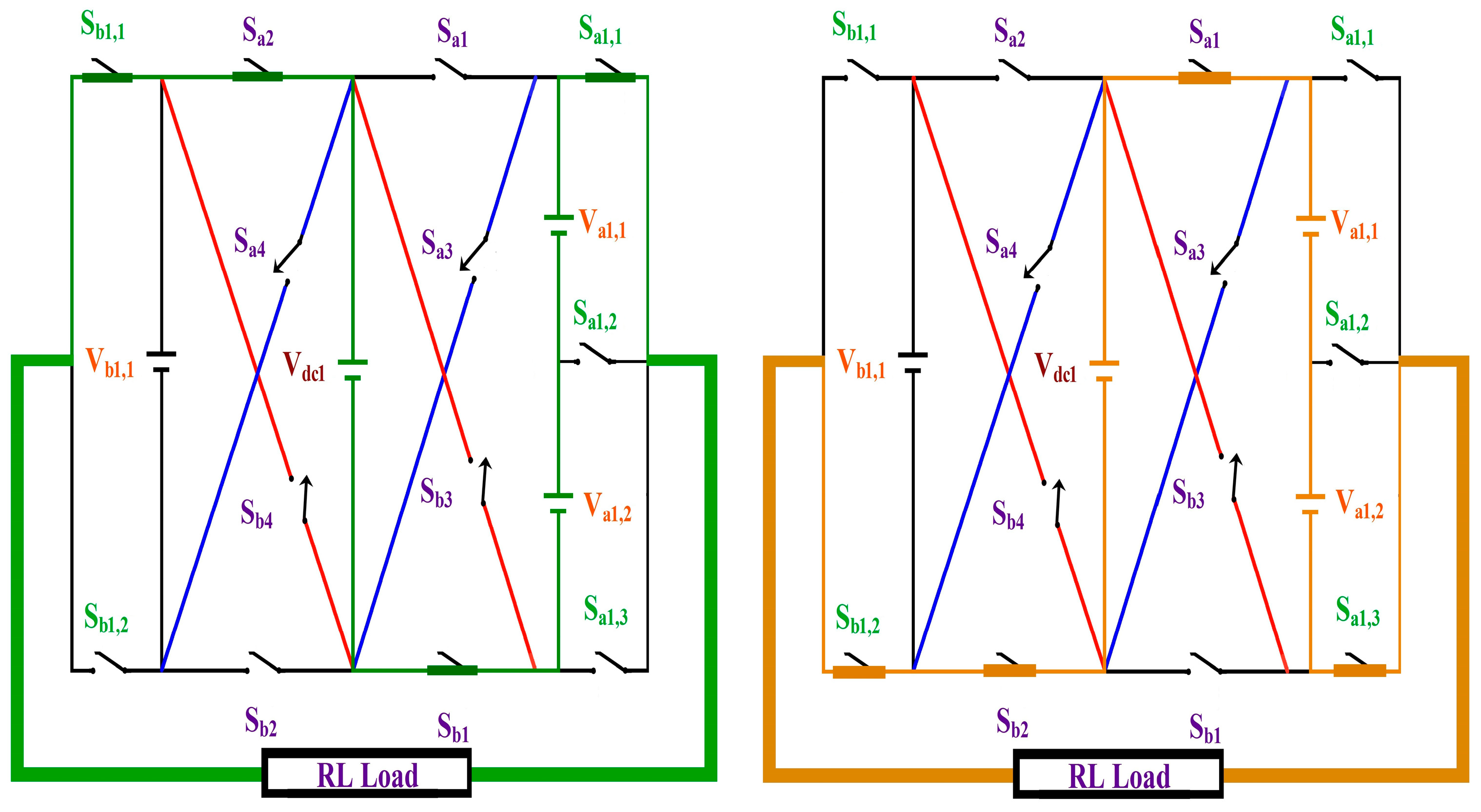
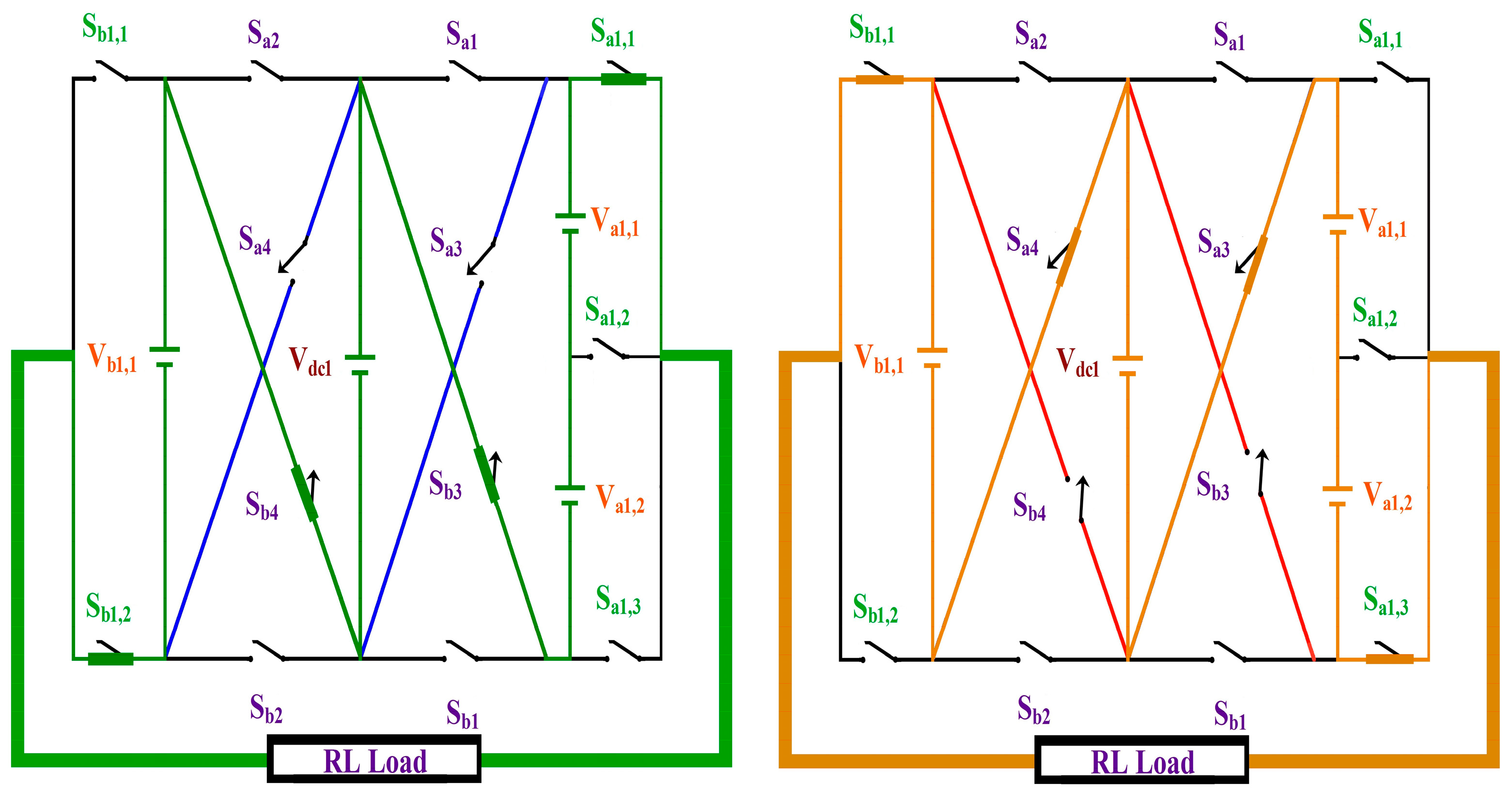
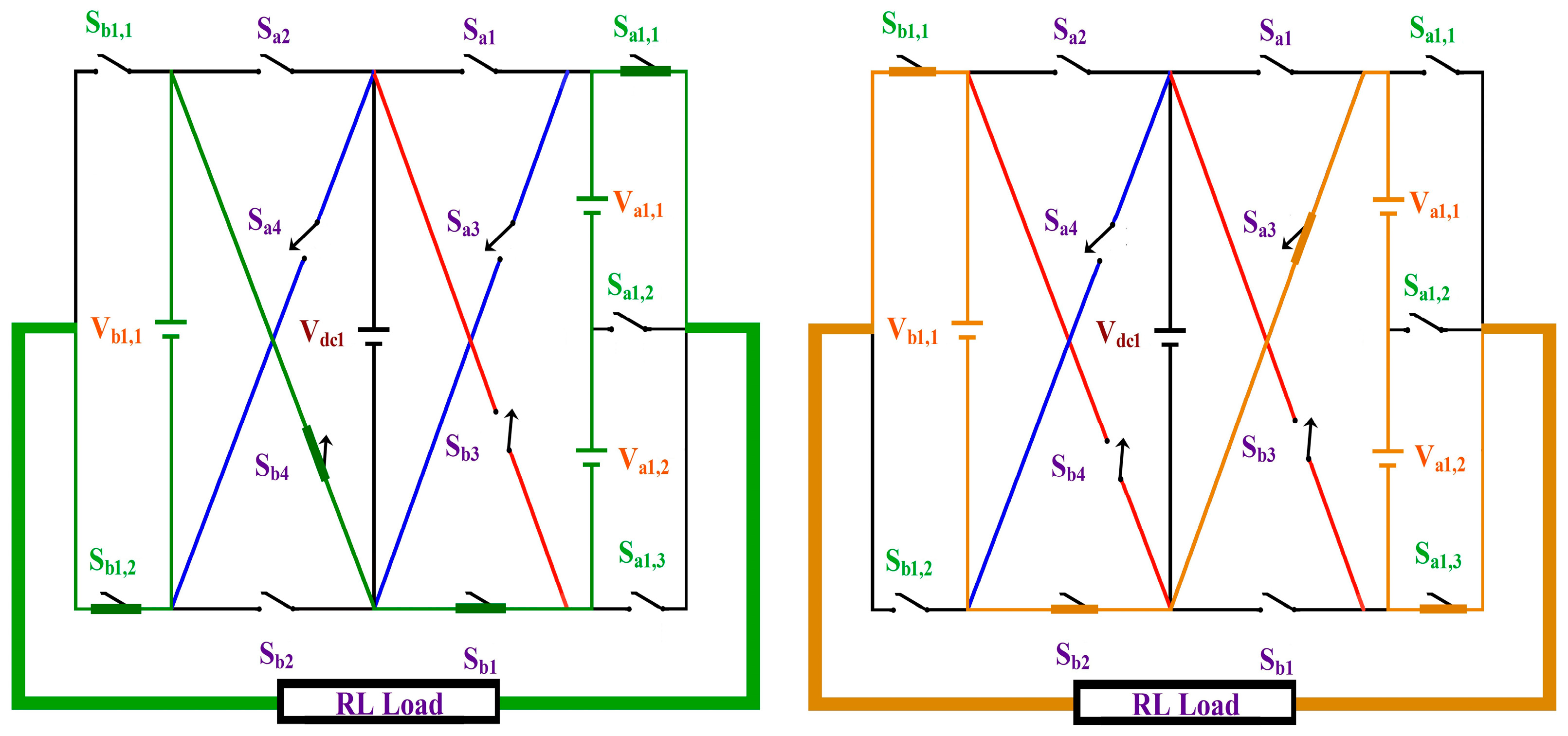
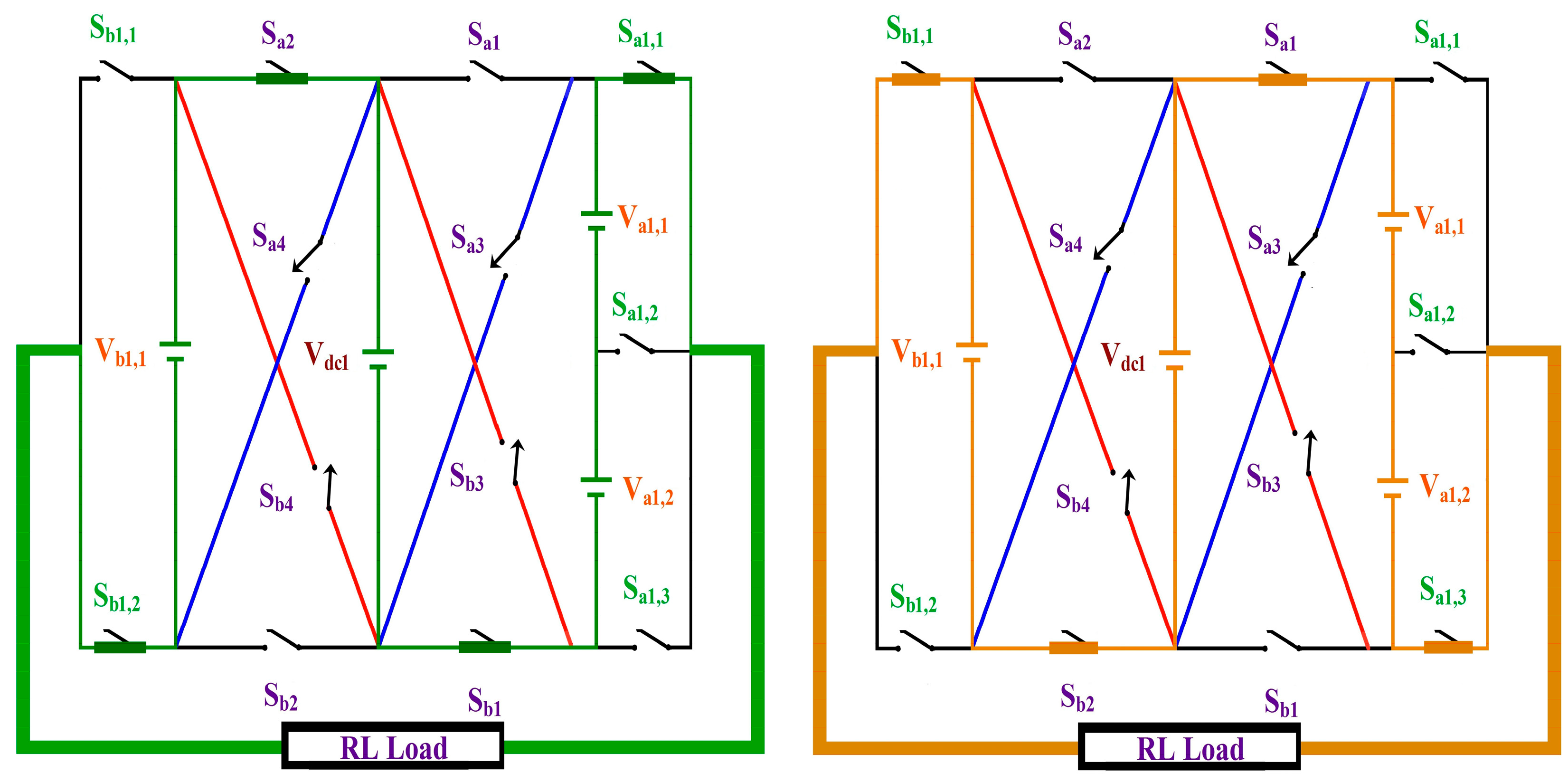







| SDCs | Conducting Switches | ‘m’ Level | Conducting Switches | SDCs | |
|---|---|---|---|---|---|
| Va1,1 + Va1,2 + Vb1,1 + Vdc1 | Sb1, Sa1,1, Sb1,2, Sa2 | +10 | −10 | Sa1, Sa1,3, Sb1,1, Sb2 | −(Va1,1 + Va1,2 + Vb1,1 + Vdc,1) |
| Va1,1 + Va1,2 + Vb1,1 | Sb1, Sa1,1, Sb1,2, Sb4 | +9 | −9 | Sa3, Sa1,3, Sb1,1, Sb2 | −(Va1,1 + Va1,2 + Vb1,1) |
| Va1,1 + Va1,2 + Vb1,1 − Vdc,1 | Sb4, Sa1,1, Sb1,2, Sb3 | +8 | −8 | Sa4, Sa1,3, Sb1,1, Sa3 | −(Va1,1 + Va1,2 + Vb1,1 − Vdc,1) |
| Va1,1 + Va1,2 + Vdc,1 | Sb1, Sa1,1, Sb1,1, Sa2 | +7 | −7 | Sa1, Sa1,3, Sb1,2, Sb2 | −(Va1,1 + Va1,2 + Vdc,1) |
| Va1,1 + Va1,2 | Sb1, Sa1,1, Sb1,2, Sb2 | +6 | −6 | Sa1, Sb1,1, Sa1,3, Sa2 | −(Va1,1 + Va1,2) |
| Va1,2 + Vb1,1 − Vdc,1 | Sb4, Sa1,2, Sb1,2, Sb3 | +5 | −5 | Sb1,1, Sa4, Sb1, Sa1,2 | −(Va1,2 + Vb1,1 − Vdc,1) |
| Vb1,1 + Vdc,1 | Sb1, Sa1,3, Sb1,2, Sa2 | +4 | −4 | Sb2, Sa1,1, Sb1,1, Sa1 | −(Vb1,1 + Vdc,1) |
| Vb1,1 | Sa2, Sa1,1, Sb1,2, Sa1 | +3 | −3 | Sb2, Sb1,1, Sa1,3, Sb1 | −Vb1,1 |
| Vb1,1 − Vdc,1 | Sb4, Sa1,1, Sb1,2, Sa1 | +2 | −2 | Sa3, Sa1,2, Sb1,1, Sa2 | −(Va1,1-Vdc,1) |
| Vdc,1 | Sb1, Sa1,3, Sb1,1, Sa2 | +1 | −1 | Sa1, Sa1,1, Sb1,2, Sb2 | −Vdc,1 |
| Sa1, Sa1,1, Sb1,1, Sa2 | 0 | Sa1, Sa1,1, Sb1,1, Sa2 | |||
| MLI Structure | Cascaded H Bridge MLI Structure | Diode Clamped MLI Structure | Capacitor Clamped MLI Structure | Proposed Crisscross MLI Structure |
|---|---|---|---|---|
| Active power Switches | 2(m − 1) | 2(m − 1) | 2(m − 1) | (m + 17)/2 |
| Passing diodes | - | |||
| Coupling diodes | 2(m − 3) | |||
| Voltage splitting capacitors | (m − 1)/2 | (m − 1)/2 | ||
| Coupling capacitors | (2m − 6)/2 | |||
| Number of sources | (m − 1)/2 | 1 | 1 | (m − 1)/2 |
| e | ∆e | ||||||
|---|---|---|---|---|---|---|---|
| nb | nm | ns | zr | ps | pm | pb | |
| nb | nb | nb | nb | nm | nm | ns | zr |
| nm | nb | nb | nm | nm | ns | zr | ps |
| ns | nb | nm | nm | ns | zr | ps | pm |
| zr | nm | nm | ns | zr | ps | pm | pm |
| ps | nm | ns | zr | ps | pm | pm | pb |
| pm | ns | zr | ps | pm | pm | pb | pb |
| pb | zr | ps | pm | pm | pb | pb | pb |
| FLC Algorithm | Voltage Source Magnitude | Vmax | ‘m’ |
|---|---|---|---|
| Algorithm 1 | j = 2, 3, …, k | ||
| Algorithm 2 | j = 2, 3, …, k | ||
| Algorithm 3 | j = 2, 3, …, k |
| Operating Mode | Simulated Result | Voltage Levels | |||||
|---|---|---|---|---|---|---|---|
| Voltage | Current | Fundamental RMS | Voltage THD | Current THD | |||
| Symmetric voltage ratio (1:1:1:1) | Without FLC | 295.7 | 3.14 | 209.09 | 12.85% | 3.45% | 9 |
| With FLC | 298.5 | 2.98 | 211.07 | 9.28% | 3.15% | ||
| Asymmetric voltage ratio Binary (1:2:2:2) | Without FLC | 296.4 | 2.94 | 209.58 | 8.34% | 3.03% | 15 |
| With FLC | 298.5 | 2.98 | 211.07 | 7.14% | 2.58% | ||
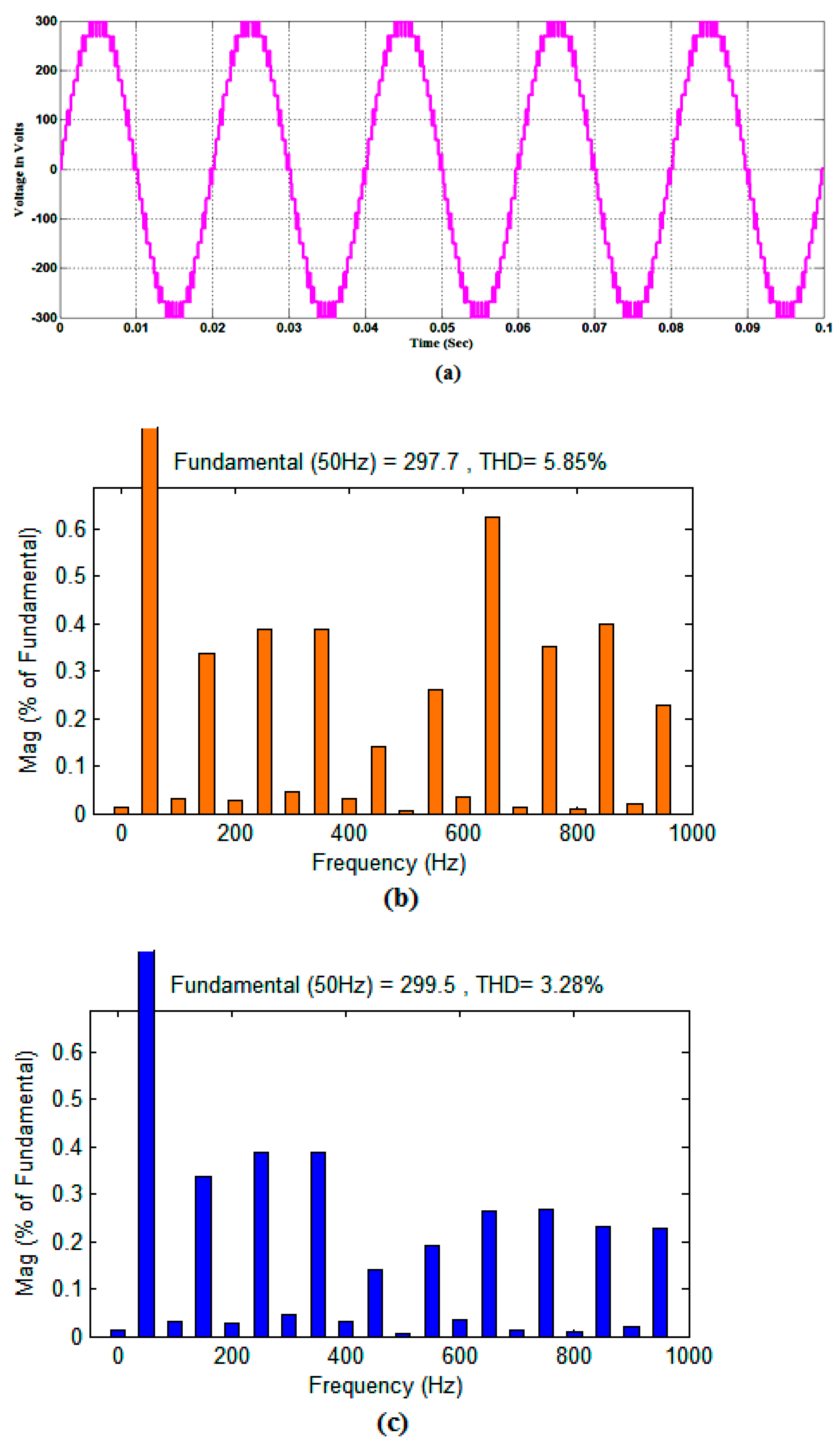
| Asymmetric voltage ratio Ternary (1:3:3:3) | Without FLC | 297.7 | 3.04 | 210.05 | 5.85% | 3.35% | 21 |
| With FLC | 299.5 | 2.86 | 211.77 | 3.28% | 2.35% | ||
| Operating Mode | Hardware Result | Voltage Levels | |||||
|---|---|---|---|---|---|---|---|
| Voltage | Current | Fundamental RMS | Voltage THD | Current THD | |||
| Symmetric voltage ratio (1:1:1:1) | Without FLC | 284.2 | 3.14 | 200.95 | 14.38% | 3.05% | 9 |
| With FLC | 292.5 | 2.98 | 206.92 | 12.58% | 2.95% | ||
| Asymmetric voltage ratio Binary (1:2:2:2) | Without FLC | 289.3 | 2.94 | 204.59 | 9.64% | 3.13% | 15 |
| With FLC | 294.5 | 2.98 | 208.24 | 8.14% | 3.08% | ||
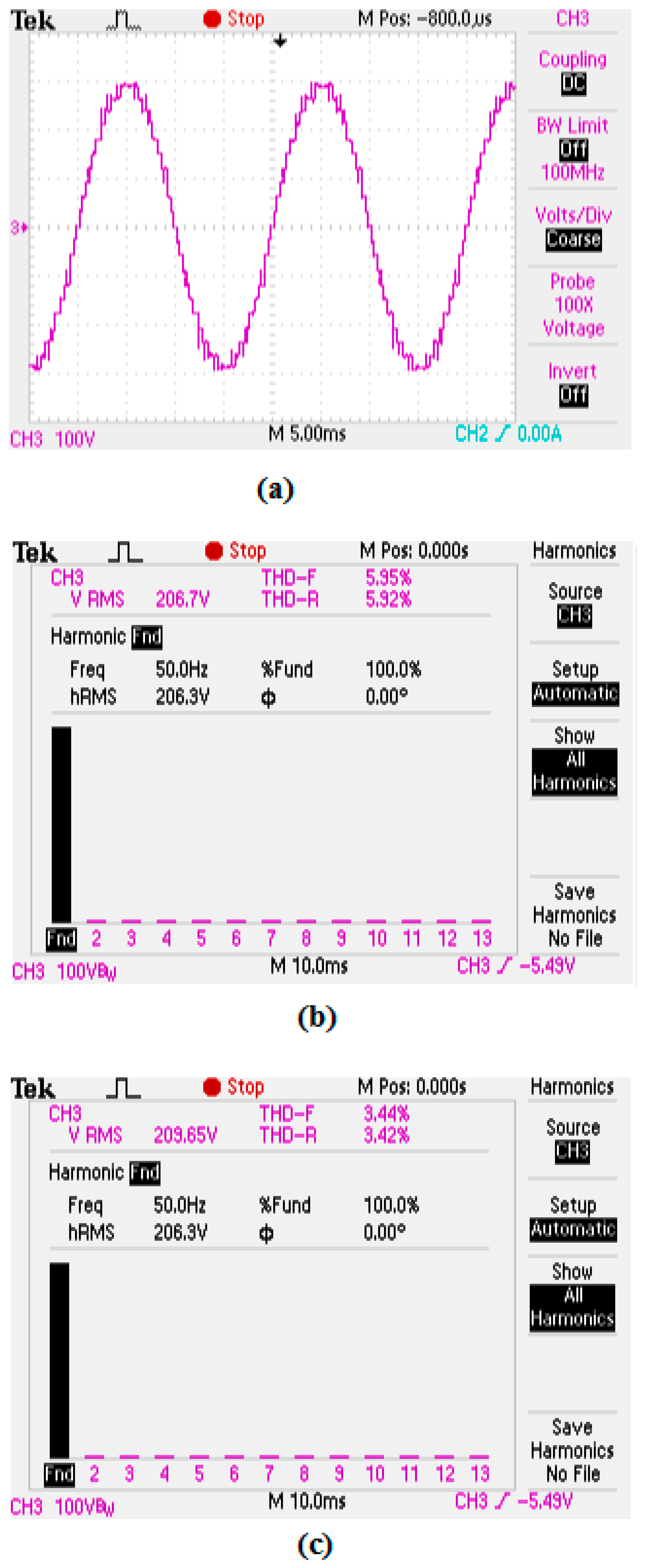
| Asymmetric voltage ratio Ternary (1:3:3:3) | Without FLC | 291.7 | 3.04 | 206.26 | 5.95% | 3.05% | 21 |
| With FLC | 296.5 | 2.86 | 209.65 | 3.44% | 2.25% | ||
| Voltage Levels | Cascaded H Bridge MLI | Diode Clamped MLI | Flying Capacitor MLI | CHB-MLDCLI | DC- MLDCLI | CC- MLDCLI | Proposed CCAL MLI |
|---|---|---|---|---|---|---|---|
| 9 | 8 | 8 | 8 | 6 | 6 | 6 | 4 |
| 15 | 14 | 14 | 14 | 9 | 9 | 9 | 4 |
| 21 | 20 | 20 | 20 | 12 | 12 | 12 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arumugam, P.; Subbaraman, S.; Chandrasekaran, K. Symmetric and Asymmetric Crisscross Augmented Ladder Multilevel Inverter with Fuzzy Logic Controller Optimization. Symmetry 2023, 15, 1366. https://doi.org/10.3390/sym15071366
Arumugam P, Subbaraman S, Chandrasekaran K. Symmetric and Asymmetric Crisscross Augmented Ladder Multilevel Inverter with Fuzzy Logic Controller Optimization. Symmetry. 2023; 15(7):1366. https://doi.org/10.3390/sym15071366
Chicago/Turabian StyleArumugam, Parimala, Srinath Subbaraman, and Kannan Chandrasekaran. 2023. "Symmetric and Asymmetric Crisscross Augmented Ladder Multilevel Inverter with Fuzzy Logic Controller Optimization" Symmetry 15, no. 7: 1366. https://doi.org/10.3390/sym15071366
APA StyleArumugam, P., Subbaraman, S., & Chandrasekaran, K. (2023). Symmetric and Asymmetric Crisscross Augmented Ladder Multilevel Inverter with Fuzzy Logic Controller Optimization. Symmetry, 15(7), 1366. https://doi.org/10.3390/sym15071366






