Molecular Dynamics Simulation from Symmetry Breaking Changing to Asymmetrical Phospholipid Membranes Due to Variable Capacitors during Resonance with Helical Proteins
Abstract
1. Introduction
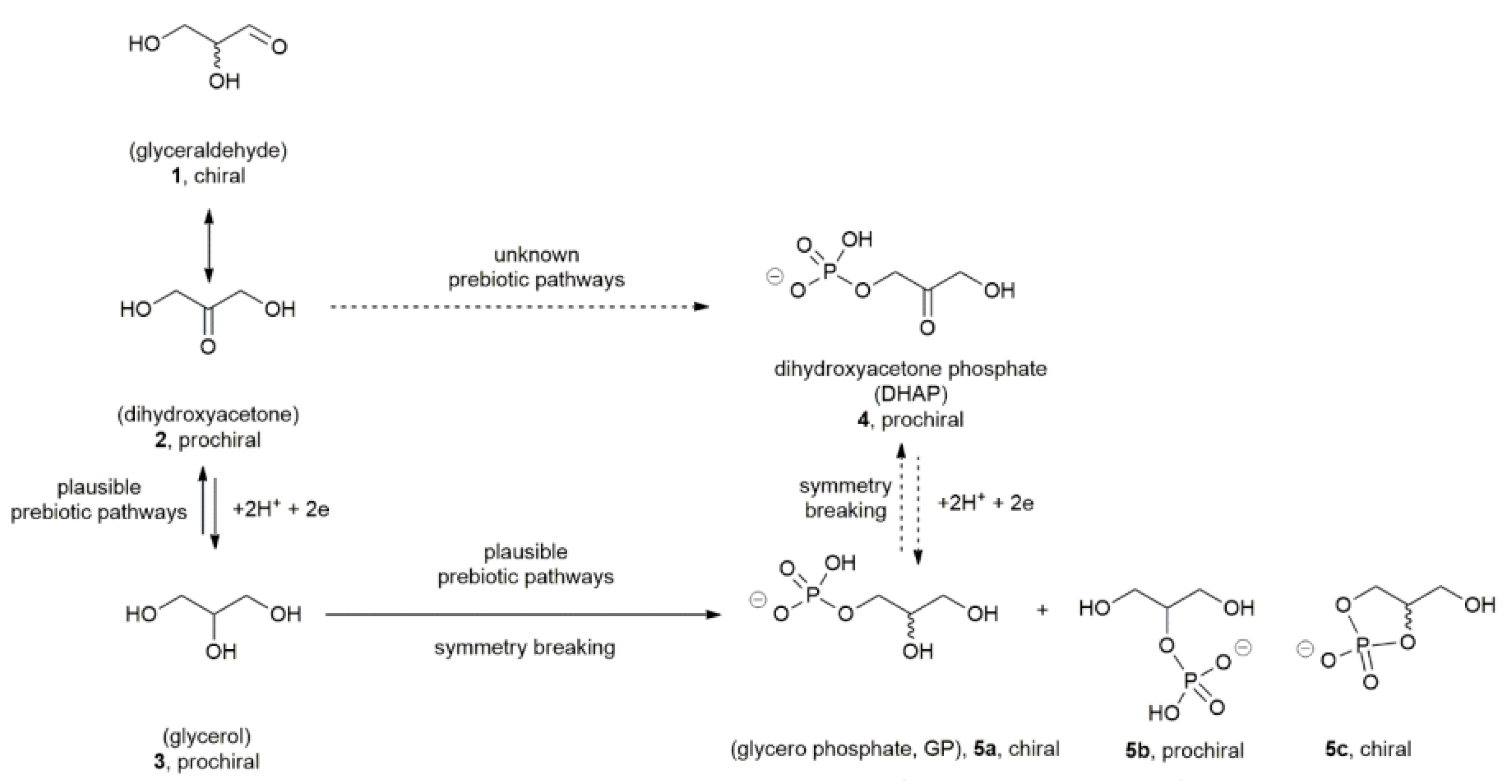
1.1. Prebiotic Approaches for the Asymmetry of Phospholipids Structures
1.2. Achiral and Racemic Amphiphiles
2. Materials and Methods
2.1. Lipid Membrane Simulations
2.2. Computational Details
3. Results and Discussion
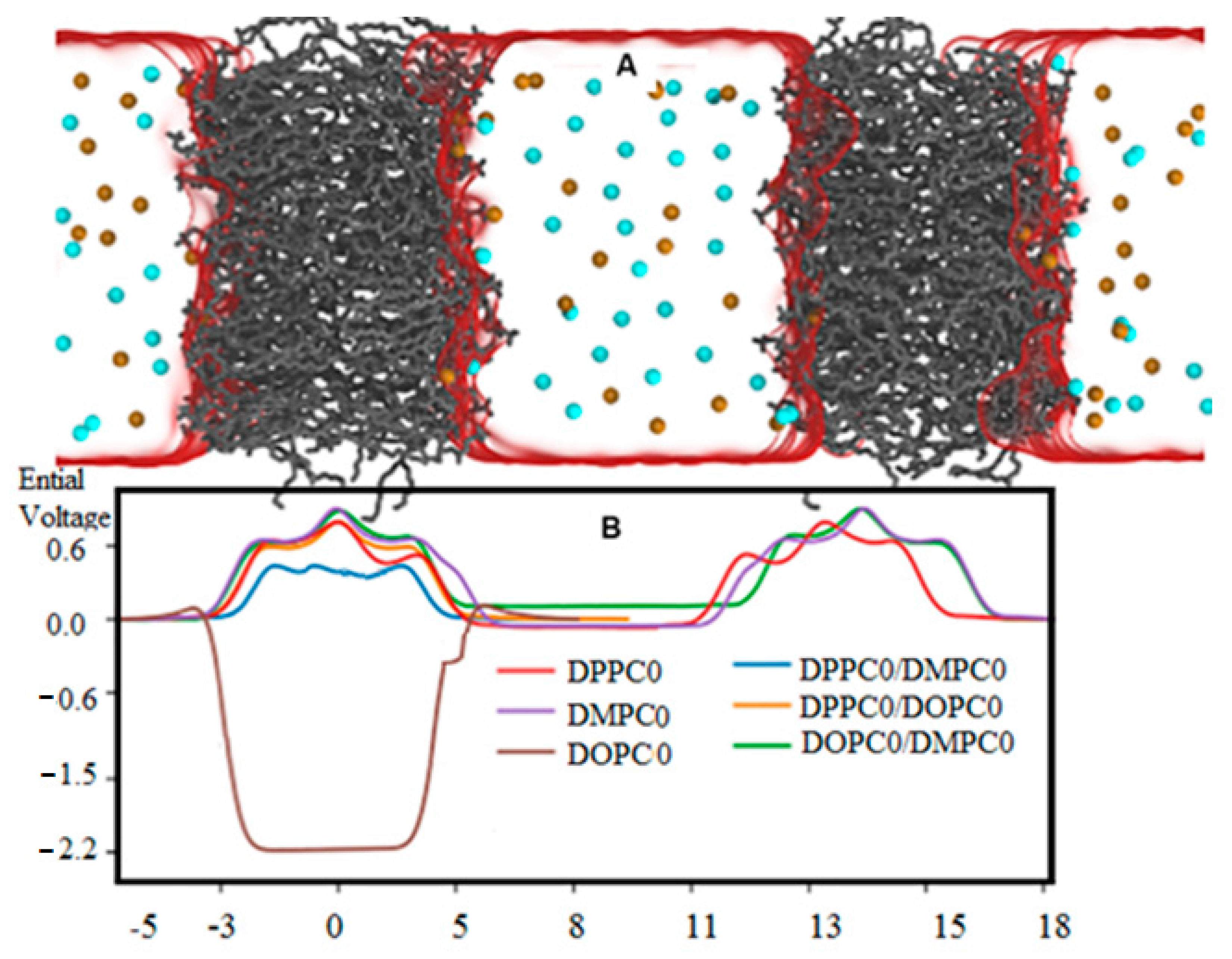
3.1. Asymmetry with Fewer Lipids
3.2. Membrane Asymmetry
3.3. Electrostatic of Symmetry Breaking in Bilayers
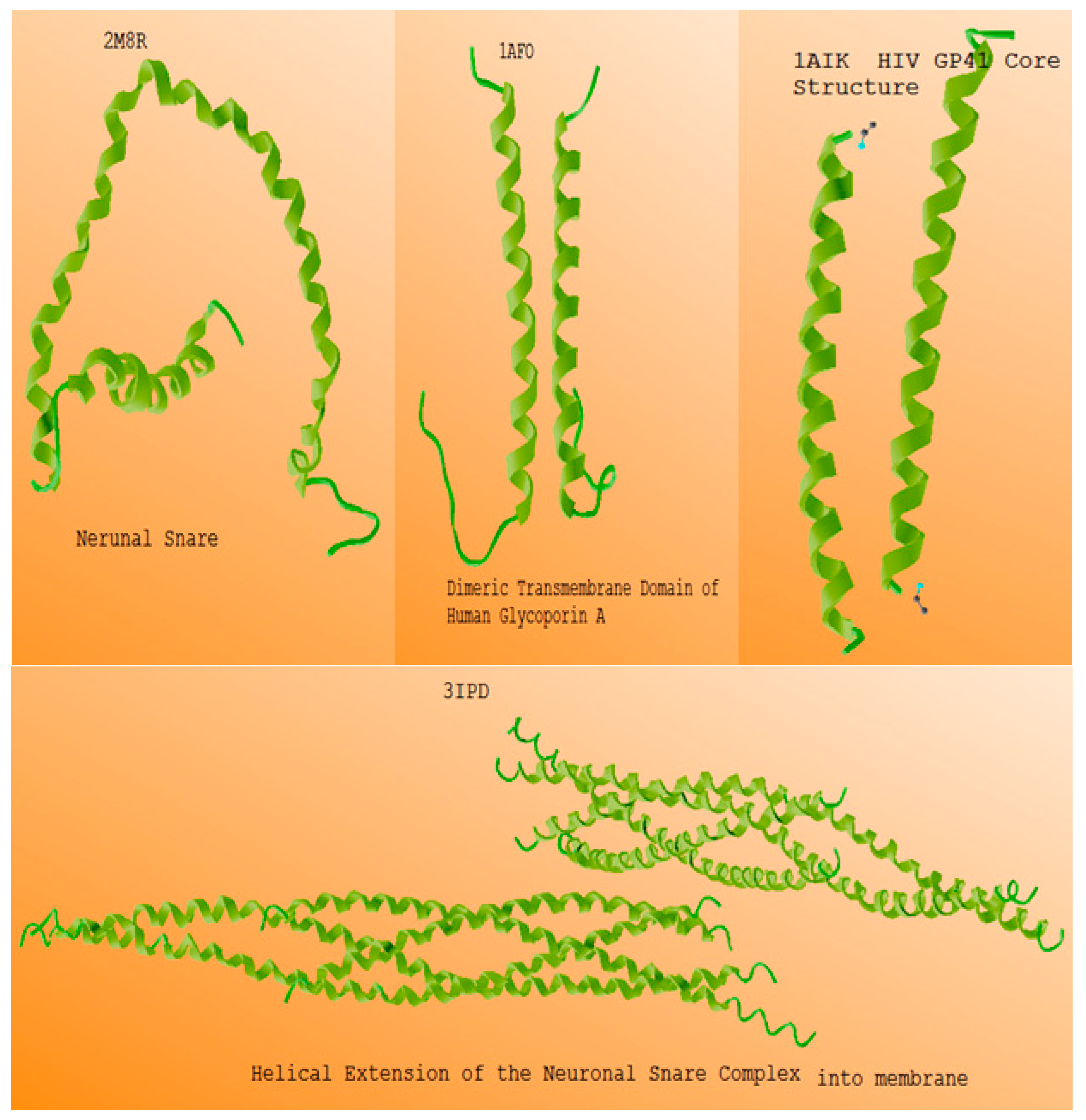
3.4. Membrane Capacitor Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, R.; Bowerman, B. Symmetry breaking in biology. Cold Spring Harb. Perspect. Biol. 2010, 2, a003475. [Google Scholar] [CrossRef]
- Wodarz, A. Establishing cell polarity in development. Nat. Cell Biol. 2002, 4, E39–E44. [Google Scholar] [CrossRef]
- Li, R.; Gundersen, G.G. Beyond polymer polarity: How the cytoskeleton builds a polarized cell. Nat. Rev. Mol. Cell Biol. 2008, 9, 860–873. [Google Scholar] [CrossRef]
- Munro, E.; Nance, J.; Priess, J.R. Cortical flows powered by asymmetrical contraction transport PAR proteins to establish and maintain anterior-posterior polarity in the early C. elegans embryo. Dev. Cell 2004, 7, 413–424. [Google Scholar] [CrossRef] [PubMed]
- Borovina, A.; Superina, S.; Voskas, D.; Ciruna, B. Vangl2 directs the posterior tilting and asymmetric localization of motile primary cilia. Nat. Cell Biol. 2010, 12, 407–412. [Google Scholar] [CrossRef]
- Van der Gucht, J.; Sykes, C. Physical model of cellular symmetry breaking. Cold Spring Harb. Perspect. Biol. 2009, 1, a001909. [Google Scholar] [CrossRef]
- Motegi, F.; Seydoux, G. The PAR network: Redundancy and robustness in a symmetry-breaking system. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013, 368, 20130010. [Google Scholar] [CrossRef] [PubMed]
- Padinhateeri, R.; Kolomeisky, A.B.; Lacoste, D. Random hydrolysis controls the dynamic instability of microtubules. Biophys. J. 2012, 102, 1274–1283. [Google Scholar] [CrossRef]
- Callan-Jones, A.; Sorre, B.; Bassereau, P. Curvature-driven lipid sorting in biomembranes. Cold Spring Harb. Perspect. Biol. 2011, 3, a004648. [Google Scholar] [CrossRef] [PubMed]
- Skotland, T.; Sandvig, K.; Llorente, A. Lipids in exosomes: Current knowledge and the way forward. Prog. Lipid Res. 2017, 66, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Gruenberg, J. Life in the lumen: The multivesicular endosome. Traffic 2020, 21, 76–93. [Google Scholar] [CrossRef]
- Van Meer, G.; Voelker, D.R.; Feigenson, G.W. Membrane lipids: Where they are and how they behave. Nat. Rev. Mol. Cell Biol. 2008, 9, 112–124. [Google Scholar] [CrossRef]
- Lorent, J.H.; Levental, K.R.; Ganesan, L.; Rivera-Longsworth, G.; Sezgin, E.; Doktorova, M.; Levental, I. Plasma membranes are asymmetric in lipid unsaturation, packing and protein shape. Nat. Chem. Biol. 2020, 16, 710. [Google Scholar] [CrossRef]
- Collins, M.D.; Keller, S.L. Tuning lipid mixtures to induce or suppress domain formation across leaflets of unsupported asymmetric bilayers. Proc. Natl. Acad. Sci. USA 2008, 105, 124–128. [Google Scholar] [CrossRef]
- Perlmutter, J.D.; Sachs, J.N. Interleaflet interaction and asymmetry in phase separated lipid bilayers: Molecular dynamics simulations. J. Am. Chem. Soc. 2011, 133, 6563–6577. [Google Scholar] [CrossRef]
- Becker, S.; Feldmann, J.; Wiedemann, S.; Okamura, H.; Schneider, C.; Iwan, K.; Crisp, A.; Rossa, M.; Amatov, T.; Carell, T. Unified prebiotically plausible synthesis of pyrimidine and purine RNA ribonucleotides. Science 2019, 366, 76–82. [Google Scholar] [CrossRef]
- Eghiaian, F.; Rico, F.; Colom, A.; Casuso, I.; Scheuring, S. High-speed atomic force microscopy: Imaging and force spectroscopy. FEBS Lett. 2014, 588, 3631–3638. [Google Scholar] [CrossRef] [PubMed]
- Böhm, C.; Möhwald, H.; Leiserowitz, L.; Als-Nielsen, J.; Kjaer, K. Influence of chirality on the structure of phospholipid monolayers. Biophys. J. 1993, 64, 553–559. [Google Scholar] [CrossRef] [PubMed]
- Eschenmoser, A.; Loewenthal, E. Chemistry of potentially prebiological natural products. Chem. Soc. Rev. 1992, 21, 1. [Google Scholar] [CrossRef]
- Subramanian, H.; Gatenby, R.A. Evolutionary advantage of directional symmetry breaking in self-replicating polymers. J. Theor. Biol. 2018, 446, 128–136. [Google Scholar] [CrossRef]
- Altamura, E.; Comte, A.; D’Onofrio, A.; Roussillon, C.; Fayolle, D.; Buchet, R.; Mavelli, F.; Stano, P.; Fiore, M.; Strazewski, P. Racemic Phospholipids for Origin of Life Studies. Symmetry 2020, 12, 1108. [Google Scholar] [CrossRef]
- Schreiber, A.; Huber, M.C.; Schiller, S.M. Prebiotic Protocell Model Based on Dynamic Protein Membranes Accommodating Anabolic Reactions. Langmuir 2019, 35, 9593–9610. [Google Scholar] [CrossRef] [PubMed]
- Koga, Y.; Kyuragi, T.; Nishihara, M.; Sone, N. Did Archaeal and Bacterial Cells Arise Independently from Noncellular Precursors? A Hypothesis Stating that the Advent of Membrane Phospholipid with Enantiomeric Glycerophosphate Backbones Caused the Separation of the Two Lines of Descent. J. Mol. Evol. 1998, 46, 54–63. [Google Scholar] [CrossRef] [PubMed]
- Yokobori, S.; Nakajima, Y.; Akanuma, S.; Yamagishi, A. Birth of Archaeal Cells: Molecular Phylogenetic Analyses of G1P Dehydrogenase, G3P Dehydrogenases, and Glycerol Kinase Suggest Derived Features of Archaeal Membranes Having G1P Polar Lipids. Archaea 2016, 2016, 1802675. [Google Scholar] [CrossRef] [PubMed]
- Koga, S.; Williams, D.S.; Perriman, A.W.; Mann, S. Peptide-nucleotide microdroplets as a step towards a membrane-free protocell model. Nat. Chem. 2011, 3, 720–724. [Google Scholar] [CrossRef]
- Tahan, A.; Mollaamin, F.; Monajjemi, M. Thermochemistry and NBO analysis of peptide bond: Investigation of basis sets and binding energy. Russ. J. Phys. Chem. A 2009, 83, 587–597. [Google Scholar] [CrossRef]
- Khalili Hadad, B.; Mollaamin, F.; Monajjemi, M. Biophysical chemistry of macrocycles for drug delivery: A theoretical study. Russ. Chem. Bull. 2011, 60, 238–241. [Google Scholar] [CrossRef]
- Zadeh, M.A.A.; Lari, H.; Kharghanian, L.; Balali, E.; Khadivi, R.; Yahyaei, H.; Mollaamin, F.; Monajjemi, M. Density functional theory study and anti-cancer properties of shyshaq plant: In view point of nano biotechnology. J. Comput. Theor. Nanosci. 2015, 12, 4358–4367. [Google Scholar] [CrossRef]
- Peretó, J.; López-García, P.; Moreira, D. Ancestral lipid biosynthesis and early membrane evolution. Trends Biochem. Sci. 2004, 29, 469–477. [Google Scholar] [CrossRef]
- Lopez, A.; Fiore, M. Investigating prebiotic protocells for a comprehensive understanding of the origins of life: A prebiotic systems chemistry perspective. Life 2019, 9, 49. [Google Scholar] [CrossRef]
- Stano, P.; Altamura, E.; Mavelli, F. Novel directions in molecular systems design: The case of light-transducing synthetic cells. Commun. Integr. Biol. 2017, 10, e1365993. [Google Scholar] [CrossRef] [PubMed]
- Altamura, E.; Milano, F.; Tangorra, R.R.; Trotta, M.; Omar, O.H.; Stano, P.; Mavelli, F. Highly oriented photosynthetic reaction centers generate a proton gradient in synthetic protocells. Proc. Natl. Acad. Sci. USA 2017, 114, 3837–3842. [Google Scholar] [CrossRef] [PubMed]
- Altamura, E.; Albanese, P.; Marotta, R.; Milano, F.; Fiore, M.; Trotta, M.; Stano, P.; Mavelli, F. Light-driven ATP production promotes mRNA biosynthesis inside hybrid multi-compartment artificial protocells. bioRxiv 2020, 1–24. [Google Scholar] [CrossRef]
- Pasek, M.A. Thermodynamics of Prebiotic Phosphorylation. Chem. Rev. 2019, 120, 4690–4706. [Google Scholar] [CrossRef]
- Walde, P. Surfactant Assemblies and Their Various Possible Roles for the Origin(s) of Life. Orig. Life Evol. Biosph. 2006, 36, 109–150. [Google Scholar] [CrossRef]
- Douliez, J.-P.; Gaillard, C. Self-assembly of fatty acids: From foams to protocell vesicles. New J. Chem. 2014, 38, 5142–5148. [Google Scholar] [CrossRef]
- Fiore, M.; Strazewski, P. Prebiotic lipidic amphiphiles and condensing agents on the early earth. Life 2016, 6, 17. [Google Scholar] [CrossRef]
- Hargreaves, W.R.; Deamer, D.W. Liposomes from Ionic, Single-Chain Amphiphiles. Biochemistry 1978, 17, 3759–3768. [Google Scholar] [CrossRef]
- Fayolle, D.; Altamura, E.; D’Onofrio, A.; Madanamothoo, W.; Fenet, B.; Mavelli, F.; Buchet, R.; Stano, P.; Fiore, M.; Strazewski, P. Crude phosphorylation mixtures containing racemic lipid amphiphiles self-assemble to give stable primitive compartments. Sci. Rep. 2017, 7, 18106. [Google Scholar] [CrossRef]
- Ourisson, G.; Nakatani, Y. The terpenoid theory of the origin of cellular life: The evolution of terpenoids to cholesterol. Chem. Biol. 1994, 1, 11–23. [Google Scholar] [CrossRef]
- Jordan, S.F.; Rammu, H.; Zheludev, I.N.; Hartley, A.M.; Maréchal, A.; Lane, N. Promotion of protocell self-assembly from mixed amphiphiles at the origin of life. Nat. Ecol. Evol. 2019, 3, 1705–1714. [Google Scholar] [CrossRef]
- Hargreaves, W.R.; Mulvihill, S.J.; Deamer, D.W. Synthesis of phospholipids and membranes in prebiotic conditions. Nature 1977, 266, 78–80. [Google Scholar] [CrossRef] [PubMed]
- Epps, D.E.; Sherwood, E.; Eichberg, J.; Oró, J. Cyanamide mediated syntheses under plausible primitive earth conditions. J. Mol. Evol. 1978, 11, 279–292. [Google Scholar] [CrossRef]
- Rao, M.; Eichberg, J.; Oró, J. Synthesis of phosphatidylcholine under possible primitive Earth conditions. J. Mol. Evol. 1982, 18, 196–202. [Google Scholar] [CrossRef]
- Rao, M.; Eichberg, J.; Oró, J. Synthesis of phosphatidylethanolamine under possible primitive earth conditions. J. Mol. Evol. 1987, 25, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Rushdi, A.I.; Simoneit, B.R.T.T. Abiotic condensation synthesis of glyceride lipids and wax esters under simulated hydrothermal conditions. Orig. Life Evol. Biosph. 2006, 36, 93–108. [Google Scholar] [CrossRef]
- Maheen, G.; Tian, G.; Wang, Y.; He, C.; Shi, Z.; Yuan, H.; Feng, S. Resolving the enigma of prebiotic C-O-P bond formation: Prebiotic hydrothermal synthesis of important biological phosphate esters. Heteroat. Chem. 2010, 21, 161–167. [Google Scholar] [CrossRef]
- Bonfio, C.; Caumes, C.; Duffy, C.D.; Patel, B.H.; Percivalle, C.; Tsanakopoulou, M.; Sutherland, J.D. Length-Selective Synthesis of Acylglycerol-Phosphates through Energy-Dissipative Cycling. J. Am. Chem. Soc. 2019, 141, 3934–3939. [Google Scholar] [CrossRef]
- Pasek, M.A.; Gull, M.; Herschy, B. Phosphorylation on the early earth. Chem. Geol. 2017, 475, 149–170. [Google Scholar] [CrossRef]
- Xu, J.; Green, N.J.; Gibard, C.; Krishnamurthy, R.; Sutherland, J.D. Prebiotic phosphorylation of 2-thiouridineprovides either nucleotides or DNA building blocks via photoreduction. Nat. Chem. 2019, 11, 457–462. [Google Scholar] [CrossRef] [PubMed]
- Pross, A. Toward a general theory of evolution: Extending Darwinian theory to inanimate matter. J. Syst. Chem. 2011, 2, 1. [Google Scholar] [CrossRef]
- Toparlak, D.; Karki, M.; Ortuno, V.E.; Krishnamurthy, R.; Mansy, S.S. Cyclophospholipids Increase Protocellular Stability to Metal Ions. Small 2020, 16, 1903381. [Google Scholar] [CrossRef]
- Gibard, C.; Bhowmik, S.; Karki, M.; Kim, E.-K.K.; Krishnamurthy, R. Phosphorylation, oligomerization and self-assembly in water under potential prebiotic conditions. Nat. Chem. 2018, 10, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Wassenaar, T.A.; Ingólfsson, H.I.; Böckmann, R.A.; Tieleman, D.P.; Marrink, S.J. Computational lipidomics with insane: A versatile tool for generating custom membranes for molecular simulations. J. Chem. Theory Comput. 2015, 11, 2144–2155. [Google Scholar] [CrossRef]
- Wassenaar, T.A.; Pluhackova, K.; Böckmann, R.A.; Marrink, S.J.; Tieleman, D. Going backward: A flexible geometric approach to reverse transformation from coarse grained to atomistic models. J. Chem. Theory Comput. 2014, 10, 676–690. [Google Scholar] [CrossRef] [PubMed]
- KKlauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D., Jr.; Pastor, R.W. Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multilevel parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Monajjemi, M.; Farahani, N.; Mollaamin, F. Thermodynamic study of solvent effects on nanostructures: Phosphatidylserine and phosphatidylinositol membranes. Phys. Chem. Liq. 2012, 50, 161–172. [Google Scholar] [CrossRef]
- Mollaamin, F.; Ilkhani, A.R.; Sakhaei, N.; Bonsakhteh, B.; Faridchehr, A.; Tohidi, S.; Monajjemi, M. Thermodynamic and solvent effect on dynamic structures of nano bilayer-cell membrane: Hydrogen bonding study. J. Comput. Theor. Nanosci. 2015, 12, 3148–3154. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log (N) method for Ewald sums in large systems. J. Chem. Phys. 1983, 98, 10089–10092. [Google Scholar] [CrossRef]
- Tieleman, D.P.; Marrink, S.J.; Berendsen, H.J. A computer perspective of membranes: Molecular dynamics studies of lipid bilayer systems. Biochim. Biophys. Acta 1997, 1331, 235–270. [Google Scholar] [CrossRef]
- Feller, S.E.; Pastor, R.W.; Rojnickarin, A.; Bogusz, S.; Brooks, B.R. Effect of electrostatic force truncation on interfacial and transport properties of water. J. Phys. Chem. 1996, 100, 17011. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Zakrzewski, V.G.; Montgomery, J.A., Jr.; Stratmann, R.E.; Burant, J.C.; et al. Gaussian 98; Gaussian, Inc.: Pittsburgh, PA, USA, 1998. [Google Scholar]
- Monajjemi, M. Liquid-phase exfoliation (LPE) of graphite towards graphene: An ab initio study. J. Mol. Liq. 2017, 230, 461–472. [Google Scholar] [CrossRef]
- Jalilian, H.; Monajjemi, M. Capacitor simulation including of X-doped graphene (X = Li, Be, B) as two electrodes and (h-BN)m (m = 1–4) as the insulator. Jpn. J. Appl. Phys. 2015, 54, 085101. [Google Scholar] [CrossRef]
- Monajjemi, M. Non-covalent attraction of B2N(−, 0) and repulsion of B2N(+) in the BnNnring: A quantum rotatory due to an external field. Theor. Chem. Acc. 2015, 134, 77. [Google Scholar] [CrossRef]
- Monajjemi, M.; Lee, V.S.; Khaleghian, M.; Honarparvar, B.; Mollaamin, F. Theoretical Description of Electromagnetic Nonbonded Interactions of Radical, Cationic, and Anionic NH2BHNBHNH2 Inside of the B18N18 Nanoring. J. Phys. Chem. C 2010, 114, 15315–15330. [Google Scholar] [CrossRef]
- Monajjemi, M.; Boggs, J.E. A New Generation of BnNn Rings as a Supplement to Boron Nitride Tubes and Cages. J. Phys. Chem. A 2013, 117, 1670–1684. [Google Scholar] [CrossRef] [PubMed]
- Monajjemi, M. Non bonded interaction between BnNn (stator) and BN(−, 0, +)B (rotor) systems: A quantum rotation in IR region. Chem. Phys. 2013, 425, 29–45. [Google Scholar] [CrossRef]
- Monajjemi, M. Metal-doped graphene layers composed with boron nitride–graphene as an insulator: A nano-capacitor. J. Mol. Model. 2014, 20, 2507. [Google Scholar] [CrossRef] [PubMed]
- Mollaamin, F.; Monajjemi, M.; Salemi, S.; Baei, M.T. A Dielectric Effect on Normal Mode Analysis and Symmetry of BNNT Nanotube. Full. Nanotub. Carbon Nanostructures 2011, 19, 182–196. [Google Scholar] [CrossRef]
- Mahdavian, L.; Monajjemi, M. Alcohol sensors based on SWNT as chemical sensors: Monte Carlo and Langevin dynamics simulation. Microelectron. J. 2010, 41, 142–149. [Google Scholar] [CrossRef]
- Bennett, W.F.D.; MacCallum, J.L.; Hinner, M.J.; Marrink, S.J.; Tieleman, D.P. Molecular view of cholesterol flip-flop and chemical potential in different membrane environments. J. Am. Chem. Soc. 2009, 131, 12714–12720. [Google Scholar] [CrossRef]
- Bennett, W.F.D.; MacCallum, J.L.; Tieleman, D.P. Thermodynamic analysis of the effect of cholesterol on dipalmitoylphosphatidylcholine lipid membranes. J. Am. Chem. Soc. 2009, 131, 1972–1978. [Google Scholar] [CrossRef] [PubMed]
- Bennett, W.F.D.; Sapay, N.; Tieleman, D.P. Atomistic simulations of pore formation and closure in lipid bilayers. Biophys. J. 2014, 106, 210–219. [Google Scholar] [CrossRef]
- Bennett, W.F.D.; Tieleman, D.P. Molecular simulation of rapid translocation of cholesterol, diacylglycerol, and ceramide in model raft and nonraft membranes. J. Lipid Res. 2012, 53, 421–429. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; De Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef]
- Klein, D.L.; Roth, R.; Lim, A.K.L.; Alivisatos, A.P.; McEuen, P.L. A single-electron transistor made from a cadmium selenide nanocrystal. Nature 1997, 389, 699. [Google Scholar] [CrossRef]
- Liu, Z.; Song, L.; Zhao, S.Z.; Huang, J.Q.; Ma, L.L.; Zhang, J.N.; Lou, J.; Ajayan, P.M. Direct Growth of Graphene/Hexagonal Boron Nitride Stacked Layers. Nano Lett. 2011, 11, 2032–2037. [Google Scholar] [CrossRef]
- Liu, Z.; Zhan, Y.J.; Shi, G.; Moldovan, S.; Gharbi, M.; Song, L.; Ma, L.L.; Gao, W.; Huang, J.Q.; Vajtai, R.; et al. Anomalous high capacitance in a coaxial single nanowire capacitor. Nat. Commun. 2012, 3, 879. [Google Scholar] [CrossRef]
- Macucci, M.; Hess, K.; Iafrate, G.J. Electronic energy spectrum and the concept of capacitance in quantum dots. Phys. Rev. B 1993, 48, 17354–17363. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Zhao, X.; Wang, J.; Guo, H. Nonlinear quantum capacitance. Appl. Phys. Lett. 1999, 74, 2887–2889. [Google Scholar] [CrossRef]
- Monajjemi, M. Cell membrane causes the lipid bilayers to behave as variable capacitors: A resonance with self-induction of helical proteins. Biophys. Chem. 2015, 207, 114–127. [Google Scholar] [CrossRef]
- Monajjemi, M.; Mollaamin, F. Intermolecular simulation of nanobiological structures in point of potential energy and second virial coefficient. J. Comput. Theor. Nanosci. 2012, 9, 2208–2214. [Google Scholar] [CrossRef]
- Monajjemi, M.; Baheri, H.; Mollaamin, F. A percolation model for carbon nanotube-polymer composites using the Mandelbrot-Given curve. J. Struct. Chem. 2011, 52, 54–59. [Google Scholar] [CrossRef]
- Monajjemi, M.M.; Bagheri, S.; Moosavi, M.S.; Moradiyeh, N.; Zakeri, M.; Attarikhasraghi, N.; Saghayimarouf, N.; Niyatzadeh, G.; Shekarkhand, M.; Khalilimofrad, M.S.; et al. Symmetry Breaking of B2N(−, 0, +): An Aspect of the Electric Potential and Atomic Charges. Molecules 2015, 20, 21636–21657. [Google Scholar] [CrossRef]





| Item | Polarizing Cue | Physical Effect | Effect Molecular |
|---|---|---|---|
| S. cerevisiaes | Cdc42 activation | Transportation of plasma | F-actin |
| D. meleanogaster | Toll | Planar polarization | Non-muscle tissues |
| C. elegans | Sperms entry | A/P polarization | |
| Node of Ranvier | Canonical and non-canonical of Wnt | Parkinson | Nodal cilia structure |
| Danio rerio | Fluctuating adhesion | Large actin disassembly | Cortical-actomyosin |
| Phospholipids | Model 1 40 mol% Cholesterol | Model 2 40 mol% Cholesterol | Model 2 40 mol% Cholesterol | |||
|---|---|---|---|---|---|---|
| Mol Ratio (Lower) | Mol Ratio (Upper) | Mol Ratio (Lower) | Mol Ratio (Upper) | Mol Ratio (Lower) | Mol Ratio (Upper) | |
| DPPC | 20 | 30 | 20 | 30 | ||
| DOPC | 60 | 40 | 20 | 30 | ||
| DMPC | 20 | 30 | 60 | 40 | 60 | 40 |
| PAPE | 20 | 30 | 20 | 30 | ||
| Phospholipids | Mol% | DPCC (Lower) | DPCC (Upper) | DMPC (Lower) | DMPC (Upper) |
|---|---|---|---|---|---|
| DPPC0 | 0 | 0.655 | 0.655 | ||
| DPCC5 | 0 | 0.620 | 0.665 | ||
| DPCC10 | 0 | 0.715 | 0.763 | ||
| DMPC0 | 0 | 0.534 | 0.564 | ||
| DMPC5 | 0 | 0.555 | 0.532 | ||
| DMPC10 | 0 | 0.543 | 0.454 | ||
| DMPC/DPPC | 0 | 0.333 | 0.438 | ||
| DMPC/POPC | 0 | 0.435 | 0.432 | ||
| DPPC/POPC | 0 | 0.435 | 0.549 |
| DPPC& Number of Atoms |
Expectation of Dielectric Thickness | Dielectric Constant | |||
|---|---|---|---|---|---|
| (N = 50) | - | - | - | - | - |
| (N = 100) | 5.34 | 1.43 | 32.43 | 2.6 | 8.35 |
| (N = 200) | 4.12 | 1.76 | 36.35 | 4.55 | 5.44 |
| (N = 400) | 8.44 | 1.34 | 33.43 | 3.11 | 3.65 |
| (N = 500) | 12.43 | 1.55 | 32.44 | 5.22 | 4.33 |
| (N = 600) | 17.33 | 1.43 | 36.5 | 1.98 | 7.42 |
| (N = 3000) | 14.75 | 1.08 | 38.43 | 1.34 | 3.54 |
| DPPC& Number of Atoms | ||||
|---|---|---|---|---|
| ESP | Mulliken | ESP | Mulliken | |
| (N = 500) | 1.16 | 1.36 | 1.45 | 1.32 |
| (N = 600) | 1.38 | 1.98 | 0.91 | 0.96 |
| (N = 2000) | 1.76 | 1.23 | 1.09 | 1.25 |
| (N = 3000 | 1.64 | 1.77 | 0.98 | 0.99 |
| Helical Proteins | Number of Coils | Millimeter Waves | Self Induction Per coil |
|---|---|---|---|
| 1AFO | 16 | 65 GHZ | 43.55 |
| 1AIK | 27 | 55GHZ | 27.6 |
| 2M8R | 32 | 70 GHZ | 11.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thi Dang, D.M.; Monajjemi, M.; Mollaamin, F.; Dang, C.M. Molecular Dynamics Simulation from Symmetry Breaking Changing to Asymmetrical Phospholipid Membranes Due to Variable Capacitors during Resonance with Helical Proteins. Symmetry 2023, 15, 1259. https://doi.org/10.3390/sym15061259
Thi Dang DM, Monajjemi M, Mollaamin F, Dang CM. Molecular Dynamics Simulation from Symmetry Breaking Changing to Asymmetrical Phospholipid Membranes Due to Variable Capacitors during Resonance with Helical Proteins. Symmetry. 2023; 15(6):1259. https://doi.org/10.3390/sym15061259
Chicago/Turabian StyleThi Dang, Dung My, Majid Monajjemi, Fatemeh Mollaamin, and Chien Mau Dang. 2023. "Molecular Dynamics Simulation from Symmetry Breaking Changing to Asymmetrical Phospholipid Membranes Due to Variable Capacitors during Resonance with Helical Proteins" Symmetry 15, no. 6: 1259. https://doi.org/10.3390/sym15061259
APA StyleThi Dang, D. M., Monajjemi, M., Mollaamin, F., & Dang, C. M. (2023). Molecular Dynamics Simulation from Symmetry Breaking Changing to Asymmetrical Phospholipid Membranes Due to Variable Capacitors during Resonance with Helical Proteins. Symmetry, 15(6), 1259. https://doi.org/10.3390/sym15061259








