Abstract
The monomiality principle is based on an abstract definition of the concept of derivative and multiplicative operators. This allows to treat different families of special polynomials as ordinary monomials. The procedure underlines a generalization of the Heisenberg–Weyl group, along with the relevant technicalities and symmetry properties. In this article, we go deeply into the formulation and meaning of the monomiality principle and employ it to study the properties of a set of polynomials, which, asymptotically, reduce to the ordinary two-variable Kampè dè Fèrièt family. We derive the relevant differential equations and discuss the associated orthogonality properties, along with the relevant generalized forms.
1. Introduction
Significant efforts have been made in the past to provide a more efficient view to the theoretical foundations of special functions and polynomials. Most of the proposed methods trace back to the Lie algebraic technicalities, summarized in the Wigner Princeton lectures (see Refs. [1,2,3]). In this article we describe more recent developments, which yield interesting results worth being underscored.
The Heisenberg–Weyl group (HWG) has played a central role in the development of quantum mechanics (QM) [4,5,6], which represents a fairly direct way of embedding position and momentum operators to disclose invariance properties associated with the specific problems under study. At a more fundamental level, the HWG provides quite a natural environment to place questions related to the connection between QM and Fourier analysis [7,8,9]. The wealth of their properties allows the understanding of the transition from a classical to quantum mechanics phase space evolution [10], along with the relevant formulation in terms of Liouville or Von Neumann Equations [11]. Furthermore a non-secondary role is played in the study of special functions, and indeed the Hermite polynomials, and the associated orthogonal functions as well are directly associated with the HWG generators and the relevant exponentiation [12,13,14,15,16]. For a deeper insight on the previous points, see the recent papers reported in [17,18], where the interplay between HWGs and generalized Hermite functions has been studied in depth.
The differential realization of the HWG may occur through the use of operators not straightforwardly recognized as the ordinary position and momentum. The search for generalized forms of HWG generators has offered the possibility of exploiting new tools to construct families of orthogonal polynomials and study their properties to solve integro-differential equations, useful for the study of problems in optics, electromagnetism, and astrophysics [19].
The key element to accomplish this research program has been the formulation of the monomiality principle [19,20,21] and a revisitation of the umbral calculus [22] originally developed in [23,24,25,26]. Monomiality and umbrality are, within certain limits, complementary. The former can be viewed as an abstract theory of the Heisenberg commutation bracket through non-trivial realizations of the derivative and position operators.
This point of view has been the main motivation in Ref. [19] and of the study of the Appèll/Sheffer polynomials [27] as images of ordinary monomials [28,29]. Monomiality is a modern formulation of a point of view, not only tracing back to Steffensen [30,31,32] but even to older studies by Jeffery (for a recent account see Ref. [33]), Boole [34], and other speculations developed almost two hundred years ago. These studies deepened their roots into the calculus of differences [35], and were the first to be recognized as amenable for a symbolic interpretation. The rules underlying monomiality are fairly simple and can be formulated as reported below [28,29,36,37].
The purpose of this article is to go through the theory of quasi-monomiality and exploit the associated formalism to construct derivative and multiplicative operators, which are used to define a new family of orthogonal Hermite-like operators.
Properties 1.
, if a couple of operators are such that:
- (a)
- They do exist along with a differential realization [38,39];
- (b)
- They can be embedded to form Weyl algebra [15,38,40], namely, if the commutator is such that ;
- (c)
- It is possible to univocally define a polynomial set such that:then it follows that
- (d)
- (e)
- and the polynomials are said quasi-monomials.
Proof.
Remark 1.
The important point we like to convey is that the essence of the discussion on monomiality is the existence of the operators (multiplicative), which univocally define the set of polynomials (not vice versa), and acting on the polynomials, as an ordinary derivative.
According to the above statement, polynomial sets such as Appéll, Sheffer [42], and Boas Buck [43] can be ascribed to the monomial family, while others, e.g., Legendre, Chebyshev, and Jacobi [39,44], are not yet framed within such a context.
After these remarks, aimed at clarifying the environment in which we are going to develop our speculations, we remind that the and operators that define the Appèll family are specified by
where is assumed to be an analytic function.
According to our introductory remarks, the explicit form of the Appéll polynomials is obtained from the identity (property of Equation (1))
The use of standard operational rules allows us to cast Equation (7) in a more convenient form.
Corollary 1.
We note that [45,46]
and noting that
we can write, by iteration
According to Equation (10), the generating function of Appèl polynomials reads
It is evident that it consists of two contributions: the exponential term and , which will be defined as the “amplitude”.
Corollary 2.
In the case of the two variable Hermite polynomials (), we have that the amplitude is specified by
with the multiplicative operator being explicitly specified as
The associated polynomial family is, accordingly, provided by [22]
The use of the Crofton identity [47]
(or of identities (10) and (11) as well) allows to cast Equation (14) in the form
The expansion of the exponential operator in Equation (16), along with the relevant action on the monomial , yields the explicit form of the two variable Hermite Kampè dè Fèrièt polynomials [27,38], namely,
The operational identity in Equation (16) is particularly pregnant from the mathematical point of view. It states that the two variable Hermites (17) are solutions of the heat equation and can be used as a pivotal tool to prove the orthogonal properties of this polynomial family [22,38].
In this article we consider the polynomial family generated by
study the relevant properties, and look at the possibility of defining an associated orthogonal set.
2. Quasi-Hermite and Appéll Sequences
In this section, we exploit the general properties of the Appéll polynomials, discussed in the introductory remarks, to state the properties of the associated polynomials.
Definition 1.
Appéll polynomials with amplitude (18) are explicitly defined through the identity
and they will be called quasi-Hermite polynomials ().
(Remark: According to the discussion of the previous section, it should be noted that)
Properties 2.
The relevant recurrences of are obtained after noting that, for this specific case, we obtain
so
Proof.
Properties and are obtained from the realization of the derivative and multiplicative operators given in Equation (6), and the third one is the result of some algebraic steps (we simplify the writing for brevity by omitting the Hermite arguments):
- (i)
- From property , we writewhich provides, from property ,
- (ii)
- and finally
- (iii)
□
Proposition 1.
The explicit form of the is inferred from Equation (19), which yields
and the relevant differential equation is
Proof.
(a) , we use binomial Newton to write
(b) The relevant differential equation is easily obtained by applying Equation (21) in Properties 2. □
Corollary 3.
After a few algebraic manipulations, Equation (23) can be reduced to the following third-order
which evidently tends to the ordinary (two variables) Hermite equation, producing large N values.
Proof.
By starting from Equation (23), we proceed as outlined below
□
Corollary 4.
The satisfied by the (expected to be an extension of the heat equation) is obtained by keeping the partial derivative with respect to y of both sides of Equation (19), namely,
Example 1.
Equation (25) can eventually be written as
The relevant (formal) solution can be obtained as
where is a kind of evolution operator. To be eventually written as in Equation (19), after explicitly working out the integral in the exponent of Equation (27), we find
According to the previous definition, the satisfies the composition rule
Therefore, unlike the two variable specified by an amplitude that is an exponential, the composition property does not hold; therefore,
An important (albeit naive) consequence of Equation (29) is the following composition rule
which suggests the necessity of a suitable extension of , possibly involving higher-order forms, as discussed in the forthcoming section.
Observation 1.
The non exponential nature of the amplitude determines the further worth to be noted as a consequence
where the r.h.s. has been obtained after exploiting standard Laplace transform methods.
We will see in the following that Equation (32) is of pivotal importance for the definition of the orthogonal properties of the .
Observation 2.
Before closing this section, we notice that Equation (23) can be generalized such that
and by following the same procedure provided in Corollary 3, it is possible to deduce the relative differential equation.
3. Multivariable QHP
Higher-order Hermite polynomials (also called Lacunary HP) are defined through the operational rule [38,47]
and, in analogy, the higher-order s are specified by and the notation ; however, we drop the superscript for and add it whenever ambiguities arise.)
Example 2.
Example 3.
Before going further, we consider the definition of the of order one, which will be referred to as quasi-binomial polynomials (), namely,
For large N, they reduce to , hence the name. The explicit form of this family of polynomials can be written as
The same strategy adopted in Corollary 3, by exploiting Equation (33), yields for the , the
and the
The last identity can also be cast in the integro-differential form
where the Laplace transform provides the integral representation
which when inserted into Equation (41) yields
and after exploiting the shift operator identity [38], we obtain Equation (42).
Example 4.
We can combine the various definitions given before to introduce three variables as
Further generalizations can easily be obtained. For example, the m-th variable extension reads
The examples we have just touched on in this section yield an idea of the possible extensions of this family of polynomials, which will be more carefully discussed in forthcoming research.
4. Final Comments
We have already mentioned the possible orthogonal nature of the , and in this section we address the problem by the use of the techniques developed in Refs. [48,49].
Proposition 2.
We assume that a given function can be expanded in terms of , according to the identity
which can be inverted, thus yielding
(Note: The reasons of “” will be clarified below.)
Corollary 5.
Equation (49) can be further elaborated:
- 1.
- We apply the Gauss–Weierstrass transform [22] to writeIt holds for (hence the choice of the sign in the expansion (47)).
- 2.
- We use the two variable Hermite-generating functions (we have ) [38] to write
- 3.
According to the above results, the expansion holds only if the integrals appearing in Equation (52) are converging. In order to provide an example we consider the generalization of the Glaisher formula [47]. Namely, Equation (48) for becomes
For very large N, reduces to the ordinary Glaisher identity
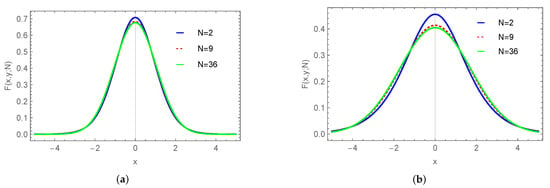
In Figure 1, we have reported vs. x for different values of N and y.

Figure 1.
vs. x for different values of N and y. (a) , (b) .
The definition of higher-order s is not unique, and another possibility is offered by the relation
where are relatively prime integers. The definition in Equation (55) allows to write the composition identity (29) as
In this article we have looked at the properties of polynomials using the monomiality principle and the classification in terms of Appèll/Sheffer polynomials [42,50,51,52]. In this respect, Laguerre polynomials cannot be considered members of this family, and notwithstanding that they can be treated using the formalism of quasi-monomials, the associated derivative and multiplicative operators are realized in terms of differential and integral operators [29], namely,
where is an integral operator such that
As easily checked, the operators (57) and (58) realize the generators of the HWG, and what is remarkable is that it allows the generalization of new families of Hermite polynomials and of Hermite functions defined no longer by ordinary differential equations, with non-constant coefficients, but by integral Equations [53].
In a forthcoming investigation we will reconsider the concepts associated with the monomiality realization in terms of integral operators to provide a new generalization of the HWG and draw further consequences on new families of Laguerre-type polynomials.
Author Contributions
Authors contributed to the paper equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The work of S. Licciardi was supported under the auspices of INDAM’s GNFM (Italy) and by the following funders: Project funded under the National Recovery and Resilience Plan (NRRP), Mission 4 Component 2 Investment 1.3—Call for tender No. 1561 of 11 October 2022 of Ministero dell’Università e della Ricerca (MUR); funded by the European Union—NextGenerationEU. Award Number: Project code PE0000021, Concession Decree No. 1561 of 11 October 2022 adopted by Ministero dell’Università e della Ricerca (MUR), CUP—B73C220012800006, according to attachment E of Decree No. 1561/2022, Project title “Network 4 Energy Sustainable Transition—NEST”. Spoke 7 ‘Smart sector integration’.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wigner, E.P. Application of Group Theory to the Special Functions of Mathematical Physics; Lecture Notes; Princeton University: Princeton, NJ, USA, 1955. [Google Scholar]
- Vilenkin, N.J. Special Functions and the Theory of Group Representation; American Mathematical Society: Providence, RI, USA, 1968. [Google Scholar]
- Cartan, E. Sur la détermination d’un système orthogonal complet dans un espace de riemann symétrique clos. Rend. Circ. Matem. Palermo 1929, 53, 217–252. [Google Scholar] [CrossRef]
- Heisenberg, W. Erinnerungen and die Zeit der Entwicklung der Quantenmechanik. In Theoretical Physics in the Twentieth Century; A Memorial Volum to Wolfgang Pauli; Interscience: New York, NY, USA, 1960. [Google Scholar]
- Weyl, H. The Theory of Groups and Quantum Mechanics; Dover: New York, NY, USA, 1950. [Google Scholar]
- Wolf, K.B. The Heisenberg-Weyl ring in Quantum Mechanics. In Group Theory and Its Applications; Loebl, E.M., Ed.; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Thangavelu, S. Lectures on Hermite and Laguerre Expansions; Mathematical Notes; Princeton Univ. Press: Princeton, NJ, USA, 1993; Volume 42. [Google Scholar]
- Thangavelu, S. Harmonic Analysis on the Heisenberg Group; Birkhauser: Boston, MA, USA, 1998. [Google Scholar]
- Dattoli, G.; Torre, A.; Mazzacurati, G. An Alternative point of view to the theory of Fractional Fourier Transform. IMA J. Appl. Math. 1998, 60, 215–224. [Google Scholar] [CrossRef]
- Kim, Y.S.; Noz, M.E. Phase Space Picture of Quantum Mechanics: Group Theoretical Approach; World Scientific Lecture Notes in Physics; World Scientific: Singapore, 1991. [Google Scholar]
- Bogolubov, N.N.; Bogolubov, N.N., Jr. Introduction to Quantum Statistical Mechanics; World Scientific: Singapore, 1982. [Google Scholar] [CrossRef]
- Wilcox, R.M. Exponential Operators and Parameter Differentiation in Quantum Physics. J. Math. Phys. 1967, 8, 962–982. [Google Scholar] [CrossRef]
- Talman, J.D. Special Functions, a Group Theoretic Approach; Benjamin: New York, NY, USA, 1968. [Google Scholar]
- Eriksen, E. Properties of Higher-Order Commutator Products and the Baker-Campbell-Hausdorf formula. J. Math. Phys. 1968, 9, 790–796. [Google Scholar] [CrossRef]
- Dattoli, G.; Gallardo, J.C.; Torre, A. An algebraic view to the operatorial ordering and its applications to optics. Riv. Del Nuovo Cim. 1988, 11, 1–79. [Google Scholar] [CrossRef]
- Dattoli, G.; Loreto, V.; Mari, C.; Richetta, M.; Torre, A. Biunitary Transformations and Ordinary differential Equations. Nuovo Cim. 1991, 106B, 1357–1374. [Google Scholar] [CrossRef]
- Celeghini, E.; Gadella, M.; Dell’Olmo, M.A. Generalized Heisenberg-Weyl Groups and Hermite Functions. Symmetry 2021, 13, 1060. [Google Scholar] [CrossRef]
- Celeghini, E.; Gadella, M.; Dell’Olmo, M.A. Symmetry Groups, Quantum Mechanics and Generalized Hermite Functions. Mathematics 2022, 10, 1448. [Google Scholar] [CrossRef]
- Dattoli, G.; Levi, D.; Winternitz, P. Heisenberg algebra, umbral calculus and orthogonal polynomials. J. Math. Phys. 2008, 49, 053509. [Google Scholar] [CrossRef]
- Dattoli, G.; Torre, A.; Mazzacurati, G. Quasi Monomials and Isospectral Problems. Nuovo Cim. 1997, 112B, 133–138. [Google Scholar]
- Smirnov, Y.; Turbiner, A. Lie algebraic discretization of differential equations. Mod. Phys. Lett. A 1995, 10, 1795–1802. [Google Scholar] [CrossRef]
- Licciardi, S.; Dattoli, G. Guide to the Umbral Calculus, a Different Mathematical Language; World Scientific: Singapore, 2022. [Google Scholar]
- Roman, S.; Rota, G.C. The umbral calculus. Adv. Math. 1978, 27, 95–188. [Google Scholar] [CrossRef]
- Roman, S. The Umbral Calculus; Academic: New York, NY, USA, 1984. [Google Scholar]
- Rota, G.C. Finite Operator Calculus; Academic: New York, NY, USA, 1975. [Google Scholar]
- Di Bucchianico, A.; Loeb, D. A Selected Survey of Umbral Calculus. Electron. J. Comb. 2000, 2, 28. [Google Scholar]
- Appéll, P.; Kampé de Fériét, J. Fonctions Hypergeometriques and Hyperspheriques. Polynomes d’Hermite; Gauthiers-Villars: Paris, France, 1926. [Google Scholar]
- Bell, E.T. The History of Blissard’s Symbolic Method, with a Sketch of its Inventor’s Life. Am. Math. Mon. 1938, 45, 414–421. [Google Scholar] [CrossRef]
- Dattoli, G. Generalized polynomials, operational identities and their applications. J. Comput. Appl. Math. 2000, 118, 111–123. [Google Scholar] [CrossRef]
- Steffensen, J.F. Interpolation; The Williams & Wilkins Company: Baltimore, MD, USA, 1927. [Google Scholar]
- Steffensen, J.F. On the definition of the central factorial. J. Inst. Actuar. 1933, 64, 165–168. [Google Scholar] [CrossRef]
- Steffensen, J.F. The Poweroid, an Extension of the Mathematical Notion of Power. Acta Math. 1941, 73, 333–366. [Google Scholar] [CrossRef]
- Dowker, J.S. Poweroids revisited—An old symbolic approach. arXiv 2013, arXiv:1307.3150. [Google Scholar]
- Boole, G. Calculus of Finite Differences, 2nd ed.; MacMillan: Cambridge, MA, USA, 1872. [Google Scholar]
- Jordan, C. Calculus of Finite Differences, 3rd ed.; AMS Chelsea: New York, NY, USA, 1965. [Google Scholar]
- Dattoli, G. Hermite-Bessel and Laguerre-Bessel functions: A by-product of the monomiality principle. In Advanced Special Functions and Applications, Proceedings of the Melfi School on Advanced Topics in Mathematics and Physics, Melfi, Italy, 9–12 May 1999; Cocolicchio, D., Dattoli, G., Srivastava, H.M., Eds.; Aracne Editrice: Rome, Italy, 2000; pp. 147–164. [Google Scholar]
- Dattoli, G. Laguerre and generalized Hermite polynomials: The point of view of the operational method. Int. Trans. Spec. Funct. 2004, 15, 93–99. [Google Scholar] [CrossRef]
- Babusci, D.; Dattoli, G.; Licciardi, S.; Sabia, E. Mathematical Methods for Physics; World Scientific: Singapore, 2019. [Google Scholar]
- Abramovitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, 9th ed.; Dover: New York, NY, USA, 1972. [Google Scholar]
- Dattoli, G.; Ottaviani, P.L.; Torre, A.; Vazquez, L. Evolution operator equations: Integration with algebraic and finitedifference methods. applications to physical problems in classical and quantum mechanics and quantum field theory. Riv. Nuovo Cim. 1997, 20, 3–133. [Google Scholar] [CrossRef]
- Louisell, W.H. Quantum Statistical Properties of Radiation; John Wiley and Sons: Hoboken, NJ, USA, 1973; Chapter 2. [Google Scholar]
- Sheffer, I.M. Some Properties of Polynomial Sets of Type Zero. Duke Math. J. 1939, 5, 590–622. [Google Scholar] [CrossRef]
- Boas, R.P.; Buck, R.C. Polynomial Expansions of Analytic Functions; Ergebnisse der Mathematik und ihrer Grenzgebiete. Neue Folge, 19; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1958. [Google Scholar]
- Andrews, L.C. Special Functions For Engeneers and Applied Mathematicians; Mc Millan: New York, NY, USA, 1985. [Google Scholar]
- Dattoli, G.; Germano, B.; Martinelli, M.R.; Ricci, P.E. Sheffer and Non-Sheffer Polynomial Families. Int. J. Math. Math. Sci. 2012, 2012, 323725. [Google Scholar] [CrossRef]
- Dattoli, G.; Zhukovsky, K. Appél Polynomial Series Expansions. Intern. Mathem. Forum 2010, 5, 649–662. [Google Scholar]
- Dattoli, G.; Khan, S.; Ricci, P.E. On Crofton-Glaisher type relations and derivation of generating functions for Hermite polynomials including the multi-index case. Int. Transf. Spec. Funct. 2008, 19, 1–9. [Google Scholar] [CrossRef]
- Dattoli, G.; Germano, B.; Ricci, P.E. Comments on monomiality, ordinary polynomials and associated bi-orthogonal functions. Appl. Math. Comput. 2004, 154, 219–227. [Google Scholar] [CrossRef]
- Dattoli, G.; Germano, B.; Ricci, P.E. Hermite polynomials with more than two variables and associated bi-orthogonal functions. Integr. Transf. Spec. Funct. 2009, 20, 17–22. [Google Scholar] [CrossRef]
- Appell, P. Sur une classe de polynômes. Ann. Sci. Éc. Norm. Supéer 1880, 9, 119–144. [Google Scholar] [CrossRef]
- Costabile, F.A.; Gualtieri, M.I.; Napoli, A. Towards the Centenary of Sheffer Polynomial Sequences: Old and Recent Results. Mathematics 2022, 10, 4435. [Google Scholar] [CrossRef]
- Dattoli, G.; Migliorati, M.; Srivastava, H. Sheffer polynomials, monomiality principle, algebraic methods and the theory of classical polynomials. Math. Comput. Model. 2007, 45, 1033–1041. [Google Scholar] [CrossRef]
- Dattoli, G.; Arena, A.; Ricci, P.E. The Laguerrian Derivative and Wright functions. Math. Comput. Model. 2004, 40, 877–881. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).