Iterative Solutions for the Nonlinear Heat Transfer Equation of a Convective-Radiative Annular Fin with Power Law Temperature-Dependent Thermal Properties

Abstract

The temperature distribution in a conductive-radiative rectangular profiled annular fin with internal heat generation is scrutinized in the present investigation. The nonlinear variation of thermal conductivity and heat transfer coefficient governed by the power law is considered. The analytical approximation for the non-dimensional temperature profile is obtained using the differential transform method (DTM)-Pade approximant. The nondimensionalization of the governing energy equation using dimensionless terms yields a nonlinear ordinary differential equation (ODE) with corresponding boundary conditions. The resulting ODE is analytically solved with the assistance of the DTM-Pade approximant procedure. Furthermore, the impact of thermal parameters on the temperature field and thermal stress is elaborated with graphs. The important results of the report divulge that temperature distribution greatly enhances with an augmentation of the heat generation parameter, but it gradually reduces with an increment in the magnitude of the thermogeometric and radiative-conductive parameter.

1. Introduction

Heat transfer science is among the most significant and widely used engineering subjects. Enhancing this process to achieve a higher heat transmission rate has become one of the most important factors necessary for the substantial advancement of modern technology. Heat transfer fluids (HTF), namely nanofluids, and hybrid nanofluids, may be used in manufacturing processes to achieve the maximum heat transfer rate. This is one of the well-known methods used to improve heat transfer. Many investigators have researched heat transmission’s physical and chemical mechanisms in the flow of various liquids through diverse geometries. Numerous researchers have addressed heat transfer involving nanofluids, hybrid nanofluids, and non-Newtonian fluid flow. Rashid et al. [1] addressed the transfer mechanism of heat in the flow of nanoliquid past a cylinder. By considering the inclined effect of the magnetic field, Abbas et al. [2] described the transfer of heat on hybrid nanoliquid stream in cylindrical geometry. Kumar et al. [3] probed the characteristic of heat transfer on the flow behavior of carbon nanotubes. Bilal et al. [4] considered the chemical effect for investigating heat transfer features on a nanoliquid stream through a parallel plate. Alharbi et al. [5] studied the impact of induction on the heat transfer of nanoliquid incorporating tri-nanoparticles. With the consideration of entropy production, Rasool et al. [6] illustrated the transfer of heat on the flow of nanoliquid including carbon nanotubes in a cavity. The radiative mode of heat transmission was studied by Rasool et al. [7] in the presence of rate-type nanoliquid. The studies described above show that the major use of nanofluids is to accomplish heat transfer rates by modifying the thermal conductivity.

On the other side, excessive air-side thermal resistance must be reduced to augment the thermal performance of air-cooled heat exchangers. As a result, extended surfaces are extensively used in air-side heat exchangers and greatly develop the heat transmission rate by expanding the surface area and promoting turbulent airflow mixing. Consequently, to accurately separate the development of the temperature interface layer from the leading edge, highly interrupted surfaces are frequently encountered in enhanced surfaces. Fins are extended surfaces utilized in a wide range of engineering systems to increase the heat transmission rate. As a result, many researchers have proposed analytical and numerical approaches to the heat transfer phenomenon in extended surfaces/fins. Recently, the transport of heat and temperature distribution through differently structured fins has been examined. Gouran et al. [8] described the production of internal heat and the convective transfer of heat in the straight fin. They concluded that fin cooling performance improves in the presence of radiative heat transport. With the application of the spectral collocation technique, Weera et al. [9] explored the nature of thermal dispersion in the permeable dovetail extended surface. They noticed that using fins with a non-uniform cross-sectional area and convective heat transfer at the fin tip is effective for enhanced heat transmission. Din et al. [10] inspected the impact of entropy and scrutinized the transmission of heat through the permeable exponential profiled extended surface. Their finding indicates that radiation has a greater influence on heat transmission in the fin. Kumar et al. [11] performed a simulation calculation to debrief the thermal discrepancy in the straight fin. Their foremost results emphasized the significance of nonlinear temperature-dependent thermal conductivity in analyzing thermal dispersion in the fin. Abdulrahman et al. [12] investigated the heat transport mechanism in a permeable exponential fin wetted with hybrid nanoliquid. In their research, they revealed that the wet surface condition with hybrid nanoliquid would effectively impact the temperature dispersion and rate of heat transmission.

Thermal equipment generally requires an efficient transfer of heat from one form of energy to another. Fins are expanded surfaces that strengthen heat transmission between a solid and an adjacent fluid. Because of their compactness and significant thermal performance, annular fins with constant thickness are widely used in numerous engineering fields. Electronic cooling, aerospace industries, vehicle radiators, internal combustion engines, compact heat exchangers, electrical components, and so on are their common applications. As a result, one of the most considerable purposes is to explore heat transmission through an annular fin (AF). In several circumstances, engineers neglected the coupled thermomechanical consequences developed throughout heat transfer provoked by an inhomogeneous temperature gradient. In this perspective, thermal stresses play a prominent part in various mechanical phenomena, such as crack propagation, creep, and fatigue, which can shorten a material’s life expectancy. As a consequence, taking into account thermal stresses is critical for avoiding material degradation, and it is something that ought not to be neglected while designing. Many researchers have examined thermal stress and temperature dispersal through AN in view of these considerations. The thermal stress aspects and the temperature response of an annular fin were examined by Mallick and Das [13]. They observed that the Biot number affects the stress and temperature distributions. Using the pseudospectral technique, Darvishi et al. [14] probed the energy transfer of a hyperbolic profiled annular fin. Their research has shown that thermal conductivity rises with temperature, which improves both the fin’s temperature distribution and efficiency. Kundu and Lee [15] explicated the radiation phenomenon and the impact of internal heat production in an annular stepped fin by employing the differential transform method (DTM). Their study reveals that porous fins better transfer heat than solid fins. Using the homotopy perturbation method (HPM), the thermal stress behavior and temperature dispersal in an annular fin were reviewed by Mallick et al. [16]. Their study did not discuss the radiative impact on stress and temperature distribution. The thermal stress aspects and behavior of temperature attributes of a rectangular profiled annular fin with temperature-dependent thermal properties were scrutinized by Kumar et al. [17]. They observed that the impact of the discussed thermal parameters on fin efficiency varies greatly in multi-boiling heat transfer instances. Various thermophysical properties, such as the material’s thermal conductivity, heat transfer coefficient, geometry, and so on, influence the temperature distribution within the fin. The concept of constant thermophysical parameters has been used in most fin analytical investigations. This consideration greatly reduces the mathematical difficulties of solving the heat transfer issue, providing a simpler explicit analytical solution. The thermal conductivity, however, differs from the local temperature difference in reality. Since variable thermal conductivity is considered, the governing heat transfer equation has quite strong nonlinearity. Several researchers have explored these equations’ numerical and semi-analytical solutions by considering the power law thermal properties. Mosayebidorcheh et al. [18] researched the thermal attribute of a fin with power law temperature-dependent thermal properties and solved the energy equation by employing the DTM scheme. Kader et al. [19] considered the nonlinear thermal properties for scrutinizing a straight fin’s heat transmission and efficacy. Using the variational iteration method (VIM), the energy transference in an extended surface having diverse profiles was debriefed by Ndlovu and Moitsheki [20] with the consideration of nonlinearly varying thermal conductivity. Sun and Li [21] examined the convective heat transfer phenomenon within a straight longitudinal fin by ignoring the radiation mode of heat transfer. They used the generalized power law thermal conductivity and discussed heat dissipation for various special cases.

A powerful semi-exact method is the differential transform method (DTM), which is notable for its ease of use and functionality in solving nonlinear differential equations. This technique differs significantly from the conventional higher-order Taylor series methodology. The Taylor series procedure is computationally complex for higher orders. The DTM is an alternative algorithm for detecting an analytic Taylor series solution to nonlinear equations. This technique can be implemented directly to nonlinear differential equations without the requirement for discretization, so it is unaffected by discretization inconsistencies. Kundu et al. [22] utilized the procedure of DTM to predict thermal dispersal through an exponential profiled fin and conferred the effect of parameters on fin efficiency. Lin and Chen [23] employed the DTM technique to obtain the analytical approximation for the annular fin of the hyperbolic profile. They compared the result of DTM with the double-decomposition method (DDM) and concluded that DTM gives more accurate results than DDM without any linearization. The closed-form solution for an annular disc extended surface in the presence of heat production was probed by Kundu [24] using the DTM approach. The closed-form-based series solutions for the velocity and temperature profile of the hybrid nanofluid flow were presented by Christopher et al. [25] via the DTM procedure. Alhejaili et al. [26] inspected heat transference features of a radiant longitudinal fin using the DTM algorithm.

As disclosed in the above-mentioned literature, many researchers performed an investigation of heat transfer through the different profiled fins using analytical techniques to solve the heat equation. Since heat loss from the fin surface to the environment via convection and radiation impacts local temperature variations, numerous studies have been published to assess the thermal dispersal through a fin of various profiles in the involvement of these phenomena. However, very few investigations can be found in examining the convection and radiation phenomena and the distribution of temperature variance in an annular fin. In this context, the thermal stresses and temperature dispersal in a conductive-radiative annular fin are examined by considering the nonlinear temperature-dependent thermal conductivity and heat transfer coefficient. Also, the proposed study fills the research gap of deriving the analytical solutions for several cases of power index of thermal conductivity and heat transfer coefficient using the DTM-Pade approximant method. Furthermore, the variations in the temperature field are expounded graphically for the impact of several non-dimensional parameters and the power index of thermal conductivity. The novelty of the current thermal analysis can be summarized as follows:

• Thermal distribution through an AF with radiation impact using nonlinear thermal conductivity and coefficient of heat transfer.
• Analysis of thermal stress in the AF with radiative and convective heat transfer mechanisms.
• Presenting the analytical solution for the nonlinear equation of the considered AF problem.
• A simulation approach for thermal distribution and stress analysis using ANSYS software.

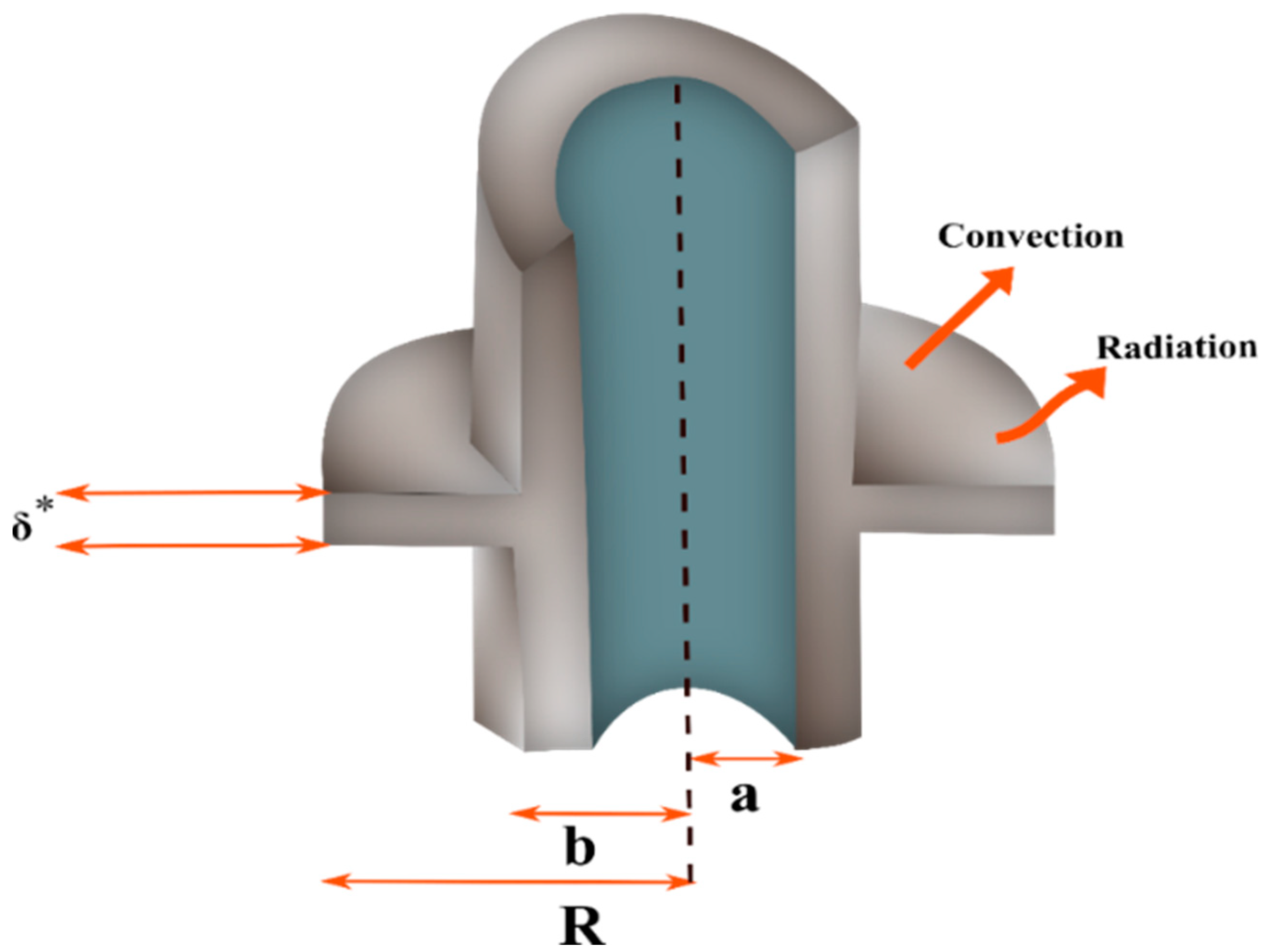
2. Formulation of the Problem

Consider an axisymmetric thin AF constructed of a homogenous isotropic substance with an inner radius $r_i$, outer radius $r_0$, and uniform thickness ${\delta }^{*}$, as shown in Figure 1. For designing the governing equations of an annular fin, the following conventions are assumed:

• The fin is positioned on a cylinder-shaped prime surface with temperature $T_b$, and $T_{\infty }$ denotes the surrounding fluid temperature during the heat dissipation.
• The fin’s tip is presumed to be insulated, so the heat dissipation is inconsequential at its tip.
• The thermal properties of the fin are taken to be temperature-dependent nonlinearities.
• Heat is transferred from AF to its surroundings by convection and radiation.
• Since the fin’s thickness is assumed to be much less than other dimensions, the heat conduction arises only in the radial direction.
• Since the fin is considered to be thin, the temperature dispersal within the fin does not depend on the axial direction.
• It is presumed that the coefficient of convective heat transfer varies with temperature.

The governing differential equation for one-dimensional heat transference with convection and radiation is specified as (see Ranjan et al. [27]):

$$q_r-q_{r+dr}=2\pi h^{*}r\left(T-T_{\infty }\right)dr-2\pi q^{*}\left(T\right){\delta }^{*}rdr+2\pi {\epsilon }_{rad}{\sigma }_{st}r\left(T^4-T_{\infty }^4\right)dr$$

(1)

where the surface emissivity ${\epsilon }_{rad}$ is presumed to be constant.

Equation (1) can be written as:

$$-\frac{dq}{dr}-2\pi h^{*}r\left(T-T_{\infty }\right)+2\pi q^{*}\left(T\right){\delta }^{*}r-2\pi {\epsilon }_{rad}{\sigma }_{st}r\left(T^4-T_{\infty }^4\right)=0$$

(2)

The $q$ is addressed using Fourier’s conduction law as follows:

$$q=-k^{*}(T)A_c\frac{dT}{dr} \mathrm{and} A_c=2\pi {\delta }^{*}r$$

(3)

$k^{*}\left(T\right)$ and $h^{*}\left(T\right)$ are the power functions, whereas $q^{*}\left(T\right)$ is linearly dependent on temperature and are given as:

$$\left.\begin{array}{l}{k}^{*}(T)=k_0{\left[\frac{T-T_{\infty }}{T_b-T_{\infty }}\right]}^m,\\ q^{*}(T)=q_0\left[1+c\left(T-T_{\infty }\right)\right],\\ h^{*}(T)=h_0{\left[\frac{T-T_{\infty }}{T_b-T_{\infty }}\right]}^n.\end{array}\right\}$$

(4)

The power index $m$ of $k^{*}(T)$ elucidates the variance of $k^{*}(T)$ as a function of temperature. For example, if $m=0$, $k^{*}(T)$ is constant, while if $m=1$, $k^{*}(T)$ fluctuates as a linear function of temperature, and when $m=2$, $k^{*}(T)$ has a parabolic or nonlinear dependency on temperature. On the other side, the constant $n$ depends on the heat transfer mechanism and may fluctuate between −6.6 and 5. For instance, $n=-3$ indicates the transition boiling. Film boiling and convection occur for $n=0$ and $n=1$. $n=2$ and $n=3$ signify the nucleate boiling and radiation mode of heat transference, respectively.

The subsequent energy balance equation is derived by substituting Equation (3) into Equation (2):

$${\delta }^{*}\frac{d}{dr}\left[k^{*}2\pi r\frac{dT}{dr}\right]-2\pi h^{*}r\left(T-T_{\infty }\right)+2\pi q^{*}{\delta }^{*}r-2\pi r{\epsilon }_{rad}{\sigma }_{st}\left(T^4-T_{\infty }^4\right)=0$$

(5)

The corresponding boundary conditions (BCs) for Equation (5) are:

$$\hspace{0.17em}\left.\begin{array}{ll}r=a:& T=T_b,\\ r=b:& \frac{dT}{dr}=0.\end{array}\right\}$$

(6)

For simplification, the non-dimensional variables mentioned below are presented:

$$\left.\begin{array}{l}R=\frac{b}{a},\hspace{0.17em}\theta =\frac{T-T_{\infty }}{T_b-T_{\infty }},\hspace{0.33em}\gamma =c\left(T_b-T_{\infty }\right),\hspace{0.33em}Nt=\frac{T_{\infty }}{T_b-T_{\infty }},\hspace{0.17em}\xi =\frac{r-a}{a},\\ {\psi }^2=\frac{h_0{a}^2}{k_0{\delta }^{*}},\hspace{0.33em}Nr=\frac{{\epsilon }_{rad}{\sigma }_{st}{a}^2{\left(T_b-T_{\infty }\right)}^3}{k_0{\delta }^{*}},\hspace{0.33em}\mu =\frac{q_0{a}^2}{k_0\left(T_b-T_{\infty }\right)}.\end{array}\right\}$$

(7)

Equation (4) is substituted in Equation (5), and the resulting equation is reduced to a dimensionless form by using Equation (7), which is given as:

$${\theta }^m\frac{d^2\theta }{d{\xi }^2}+\frac{{\theta }^m}{\left(1+\xi \right)}\frac{d\theta }{d\xi }+m{\theta }^{m-1}{\left(\frac{d\theta }{d\xi }\right)}^2-{\psi }^2{\theta }^{n+1}+\mu \left(1+\gamma \theta \right)-Nr\left({\left(Nt+\theta \right)}^4-N{t}^4\right)=0$$

(8)

Also, Equation (6) takes the below dimensionless form:

$$\left.\begin{array}{cc}\xi =0:\hfill & \hfill \theta =1,\\ \xi =R-1:\hfill & \hfill {\theta }^{\prime }=0.\end{array}\right\}$$

(9)

If $m\ne 0$, Equation (8) exhibits nonlinear behavior, and when both $m\ne 0$ and $n\ne 0$, the problem indicates multi-nonlinearity. The linear relationship is interpreted in Equation (8) for $m=n=0$. In this investigation, the exponent index of $k^{*}(T)$ and $h^{*}(T)$ is taken to be $m>0$ and $n>0$ because $k^{*}(T)$ is supposed to be positive in most practical situations. Heat transport attributes are examined in several investigations with constant and linear temperature variance $k^{*}(T)$. The nonlinear function of thermal conductivity is presented in Vitanov et al. [28], Mhlongo et al. [29], and Abbasbandy and Shivanian [30].

3. Preliminary Results of DTM

Taylor’s series can be denoted as (see Kundu et al. [22]):

$$f(l)={{\displaystyle \sum _{\vartheta =0}^{\infty }\frac{{\left(\varsigma -{\varsigma }_0\right)}^{\vartheta }}{\vartheta !}\left[\frac{d^{\vartheta }f(\varsigma )}{d{x}^{\vartheta }}\right]}}_{\varsigma ={\varsigma }_0}$$

(10)

The differential transformation of the $\vartheta \mathrm{th}$ derivative of a function $f(\varsigma )$ is defined by (see Wang et al. [31]):

$$F\left(\vartheta \right)=\frac{1}{\vartheta !}{\left[\frac{d^{\vartheta }f(\varsigma )}{d{x}^{\vartheta }}\right]}_{\varsigma ={\varsigma }_0}$$

(11)

and the inverse differential transformation is signified as:

$$f(\varsigma )={\displaystyle \sum _{\vartheta =0}^{\infty }F\left(\vartheta \right){\left(\varsigma -{\varsigma }_0\right)}^{\vartheta }}$$

(12)

Pade approximant is an effective strategy for approximating a polynomial function in terms of rational polynomial functions of a particular order. The fundamental properties of this methodology are mentioned in Dogonchi et al. [32] and Sowmya et al. [33]. The major fundamentals of DTM are specified in

Table 1. Properties of DTM.

Original Function	Transformed Function
$\phi \left(u\right)=z_1\left(u\right)\pm z_2\left(u\right)$	$\mathrm{\Phi }\left(\vartheta \right)=Z_1\left(\vartheta \right)\pm Z_2\left(\vartheta \right)$
$\phi \left(u\right)=i z\left(u\right)$	$\mathrm{\Phi }\left(\vartheta \right)=iZ\left(\vartheta \right)$, where $i$ is the constant.
$\phi \left(u\right)=\frac{d z\left(u\right)}{du}$	$\mathrm{\Phi }\left(\vartheta \right)=\left(\vartheta +1\right)Z\left(\vartheta +1\right)$
$\phi \left(u\right)=\frac{d{ }^{p}z\left(u\right)}{du}$	$\mathrm{\Phi }\left(\vartheta \right)=\left(\vartheta +1\right)\left(\vartheta +2\right)\dots \left(\vartheta +n\right)Z\left(\vartheta +p\right)$
$\phi \left(u\right)=u^i$	$\mathrm{\Phi }\left(\vartheta \right)=\delta \left(\vartheta -i\right)=\left\{\begin{array}{l}1,\vartheta =i\\ 0,\hspace{0.17em}\vartheta \ne i\end{array}\right\}$
$\phi \left(u\right)=z_1\left(u\right)z_2\left(u\right)$	$\mathrm{\Phi }\left(\vartheta \right)={\displaystyle \sum _{r=0}^{\vartheta }{Z}_1\left(r\right)Z_2\left(\vartheta -r\right)}$
$\begin{array}{l}\phi \left(u\right)=z_1\left(u\right)z_2\left(u\right)\dots .\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\dots \dots z_{s-1}\left(u\right)z_s\left(u\right)\end{array}$	$\mathrm{\Phi }\left(\vartheta \right)={\displaystyle \sum _{{\vartheta }_{s-1}=0}^{\vartheta }{\displaystyle \sum _{{\vartheta }_{s-2}=0}^{{\vartheta }_{s-1}=0}\dots .{\displaystyle \sum _{{\vartheta }_2=0}^{{\vartheta }_3}{\displaystyle \sum _{{\vartheta }_1=0}^{{\vartheta }_2}{Z}_1\left({\vartheta }_1\right)}}}\hspace{0.17em}{Z}_2\left({\vartheta }_2-{\vartheta }_1\right)\dots Z_{s-1}\left({\vartheta }_{s-1}-{\vartheta }_{s-2}\right)}{Z}_s\left(\vartheta -{\vartheta }_{s-1}\right)$

.

4. Applications of DTM-Pade Method

Case 1: Linear thermal conductivity with nucleate boiling mode of heat transfer (m = 1 and n = 2).

Taking the differential transform of Equations (8) and (9), we obtain:

$$\left.\begin{array}{l}{\displaystyle \sum _{\omega =0}^u}\hspace{0.17em}\mathrm{\Theta }\left[u-\omega \right]\left(\omega +1\right)\left(\omega +2\right)\mathrm{\Theta }\left[\omega +2\right]+\frac{1}{1+\delta \left[s-1\right]}{\displaystyle \sum _{\omega =0}^u}\left(u-\omega +1\right)\mathrm{\Theta }\left[u-\omega +1\right]\hspace{0.17em}{\displaystyle \sum _{s=0}^{\omega }}\mathrm{\Theta }\left[\omega -s\right]+\\ \\ {\displaystyle \sum _{\omega =0}^u}\left(u-\omega +1\right)\mathrm{\Theta }\left[u-\omega +1\right]\left(\omega +1\right)\mathrm{\Theta }\left[\omega +1\right]-{\psi }^2{\displaystyle \sum _{\omega =0}^u}\hspace{0.17em}{\displaystyle \sum _{s=0}^{\omega }}\mathrm{\Theta }\left[s\right]\mathrm{\Theta }\left[\omega -s\right]\mathrm{\Theta }\left[u-\omega \right]-\\ \\ Nr\left(\begin{array}{l}4N{t}^3\mathrm{\Theta }\left[u\right]+6N{t}^2{\displaystyle \sum _{\omega =0}^u}\mathrm{\Theta }\left[\omega \right]\mathrm{\Theta }\left[u-\omega \right]+4Nt{\displaystyle \sum _{\omega =0}^u}\mathrm{\Theta }\left[u-\omega \right]\hspace{0.17em}{\displaystyle \sum _{s=0}^{\omega }}\mathrm{\Theta }\left[s\right]\hspace{0.17em}\mathrm{\Theta }\left[\omega -s\right]+\\ \\ {\displaystyle \sum _{\omega =0}^u}\hspace{0.17em}{\displaystyle \sum _{s=0}^{\omega }}\hspace{0.17em}{\displaystyle \sum _{w=0}^s}\mathrm{\Theta }\left[w\right]\hspace{0.17em}\mathrm{\Theta }\left[s-w\right]\hspace{0.17em}\mathrm{\Theta }\left[\omega -s\right]\mathrm{\Theta }\left[u-\omega \right]\end{array}\right)\\ \\ +\mu \delta \left[u\right]+\gamma \mu \hspace{0.17em}\mathrm{\Theta }\left[u\right]=0\end{array}\right\}$$

(13)

$$\left.\begin{array}{l}\mathrm{\Theta }\left[0\right]=1,\\ \mathrm{\Theta }\left[1\right]=\mathsf{B},\end{array}\right\}$$

(14)

where $\mathrm{\Theta }\left[u\right]$ is the differential transform of $\theta \left(\xi \right)$.

Recursively evaluating the $\mathrm{\Theta }\left[u\right]$ from Equation (13) yields the following series solution:

$$\theta \left(\xi \right)=\mathrm{\Theta }\left[0\right]+\mathrm{\Theta }\left[1\right]\xi +\mathrm{\Theta }\left[2\right]{\xi }^2+\mathrm{\Theta }\left[3\right]{\xi }^3+\mathrm{\Theta }\left[4\right]{\xi }^4$$

(15)

where $\mathrm{\Theta }\left[i\right],i=1,2,3,4$, have the forms:

$$\mathrm{\Theta }\left[2\right]=2NrN{t}^3+3NrN{t}^2-\frac{1}{2}{\mathsf{B}}^2+2NrNt-\frac{1}{2}\gamma \mu +\frac{1}{2}{\psi }^2-\frac{1}{2}\mathsf{B}+\frac{1}{2}Nr-\frac{1}{2}\mu ,$$

(16)

$$\left.\begin{array}{l}\mathrm{\Theta }\left[3\right]=-\frac{4}{3}\mathsf{B}NrN{t}^3-\mathsf{B}NrN{t}^2+\frac{1}{2}{\mathsf{B}}^3\frac{1}{3}\gamma \mu \mathsf{B}+\frac{1}{2}{\mathsf{B}}^2+\frac{1}{6}Nr\mathsf{B}+\frac{1}{2}\mathsf{B}\mu +\frac{1}{6}\gamma \mu -\frac{2}{3}NrN{t}^3-NrN{t}^2-\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{2}{3}NrNt+\frac{1}{6}\mu -\frac{1}{6}{\psi }^2+\frac{1}{12}\mathsf{B}-\frac{1}{6}Nr,\end{array}\right\}$$

(17)

$$\left.\begin{array}{l}\mathrm{\Theta }\left[4\right]=\frac{3}{8}{\mathsf{B}}^2{\psi }^2+\frac{5}{12}{\mathsf{B}}^{2}Nr-\frac{3}{4}{\mathsf{B}}^2\mu +\frac{1}{6}N{r}^{2}Nt+\frac{1}{6}{\psi }^2\mathsf{B}+\frac{1}{24}{\psi }^{2}Nr+\frac{1}{8}{\psi }^2\mu +\frac{1}{12}\mathsf{B}Nr-\frac{5}{12}\mathsf{B}\mu +\frac{1}{24}N{r}^2+\frac{1}{12}Nr\mu -\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{1}{8}{\mu }^2-\frac{4}{3}N{r}^{2}N{t}^6-3N{r}^{2}N{t}^5-\frac{17}{6}N{r}^{2}N{t}^4-\hspace{0.17em}\frac{7}{6}N{r}^{2}N{t}^3-\frac{1}{8}{\mathsf{B}}^4-\frac{5}{8}{\mathsf{B}}^3-\frac{5}{24}{\mathsf{B}}^2-\frac{1}{16}\mathsf{B}-\frac{1}{12}{\gamma }^2{\mu }^2-\frac{5}{24}\gamma {\mu }^2-\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em} \frac{1}{6}{\mathsf{B}}^5\gamma \mu -\frac{5}{24}{\mathsf{B}}^2\gamma \mu +\frac{1}{12}\gamma \mu {\psi }^2-\frac{1}{4}\gamma \mu \mathsf{B}+\frac{1}{24}\gamma \mu Nr+\frac{2}{3}NrN{t}^3\gamma \mu +\frac{3}{4}NrN{t}^2\gamma \mu +\frac{1}{3}NrNt\gamma \mu -\frac{1}{24}{\mathsf{B}}^4\gamma \mu +\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{13}{6}NrN{t}^3{\mathsf{B}}^2-\frac{1}{3}NrN{t}^3{\psi }^2+\frac{4}{3}NrN{t}^3\mathsf{B}+\hspace{0.17em}\frac{5}{6}NrN{t}^3\mu +\frac{5}{2}NrN{t}^2{\mathsf{B}}^2-\frac{1}{4}NrN{t}^2{\psi }^2+\frac{3}{2}NrN{t}^2\mathsf{B}+NrN{t}^2\mu +\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{3}{2}{\mathsf{B}}^{2}NrNt+\frac{2}{3}NrNt\mathsf{B}+\frac{1}{2}NrNt\mu .\\ \end{array}\right\}$$

(18)

and so on. where $\mathsf{B}$ is the constant to be determined using Equation (9).

For determining the $\mathsf{B}$ value, the Pade approximant is implemented into Equation (18). For $\psi = 0.1$, $\mu = 0.1$, $Nt=0.1$, $Nr=0.1$, $\gamma =1$, we have found $\mathsf{B}=-0.27478$. So, the solution of Equation (8) is:

$$\begin{array}{l}\theta \left(\xi \right)=\hspace{0.17em}\hspace{0.17em}1-0.2747898495\hspace{0.17em}\xi +0.07784019410\hspace{0.17em}{\xi }^2+0.00420937640\hspace{0.17em}{\xi }^3+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}0.02344500766\hspace{0.17em}{\xi }^4+\dots \dots .,\end{array}$$

(19)

Case 2: Nonlinear thermal conductivity with radiation mode of heat transfer (m = 2 and n = 3).

The analytical solution for nonlinear thermal conductivity with radiation mode of heat transfer (m = 2 and n = 3) is derived.

Taking the differential transform of Equation (8), we obtain:

$$\left.\begin{array}{l}{\displaystyle \sum _{\omega =0}^u}\hspace{0.17em}\mathrm{\Theta }\left[u-\omega \right]{\displaystyle \sum _{s=0}^{\omega }}\hspace{0.17em}\left(s+1\right)\left(s+2\right)\mathrm{\Theta }\left[s+2\right]\mathrm{\Theta }\left[\omega -s\right]+\frac{1}{1+\delta \left[w-1\right]}{\displaystyle \sum _{\omega =0}^u}\left(u-\omega +1\right)\mathrm{\Theta }\left[u-\omega +1\right]\hspace{0.17em}{\displaystyle \sum _{s=0}^{\omega }}\mathrm{\Theta }\left[\omega -s\right]\hspace{0.17em}{\displaystyle \sum _{w=0}^s}\mathrm{\Theta }\left[s-w\right]+\\ \\ 2\hspace{0.17em}{\displaystyle \sum _{\omega =0}^u}\mathrm{\Theta }\left[u-\omega \right]\hspace{0.17em}{\displaystyle \sum _{s=0}^{\omega }}\hspace{0.17em}\left(s+1\right)\mathrm{\Theta }\left[s+1\right]\left(\omega -s+1\right)\mathrm{\Theta }\left[\omega -s+1\right]-{\psi }^2{\displaystyle \sum _{\omega =0}^u}\mathrm{\Theta }\left[u-\omega \right]\hspace{0.17em}{\displaystyle \sum _{s=0}^{\omega }}\hspace{0.17em}{\displaystyle \sum _{w=0}^s}\mathrm{\Theta }\left[w\right]\hspace{0.17em}\mathrm{\Theta }\left[s-w\right]\hspace{0.17em}\mathrm{\Theta }\left[\omega -s\right]-\\ \\ Nr\left(\begin{array}{l}4N{t}^3\mathrm{\Theta }\left[u\right]+6N{t}^2{\displaystyle \sum _{\omega =0}^u}\mathrm{\Theta }\left[\omega \right]\mathrm{\Theta }\left[u-\omega \right]+4Nt{\displaystyle \sum _{\omega =0}^u}\mathrm{\Theta }\left[u-\omega \right]\hspace{0.17em}{\displaystyle \sum _{s=0}^{\omega }}\mathrm{\Theta }\left[s\right]\hspace{0.17em}\mathrm{\Theta }\left[\omega -s\right]+\\ \\ {\displaystyle \sum _{\omega =0}^u}\hspace{0.17em}{\displaystyle \sum _{s=0}^{\omega }}\hspace{0.17em}{\displaystyle \sum _{w=0}^s}\mathrm{\Theta }\left[w\right]\hspace{0.17em}\mathrm{\Theta }\left[s-w\right]\hspace{0.17em}\mathrm{\Theta }\left[\omega -s\right]\mathrm{\Theta }\left[u-\omega \right]\end{array}\right)\\ \\ +\mu \delta \left[u\right]+\gamma \mu \hspace{0.17em}\mathrm{\Theta }\left[u\right]=0,\end{array}\right\}$$

(20)

Recursively evaluating the $\mathrm{\Theta }\left[u\right]$ from Equation (20) yields the following series solution:

$$\theta \left(\xi \right)=\mathrm{\Theta }\left[0\right]+\mathrm{\Theta }\left[1\right]\xi +\mathrm{\Theta }\left[2\right]{\xi }^2+\mathrm{\Theta }\left[3\right]{\xi }^3+\mathrm{\Theta }\left[4\right]{\xi }^4$$

(21)

where $\mathrm{\Theta }\left[i\right],i=1,2,3,4$, have the forms:

$$\mathrm{\Theta }\left[2\right]=2NrN{t}^3+3NrN{t}^2-{\mathsf{B}}^2+2NrNt-\frac{1}{2}\gamma \mu +\frac{1}{2}{\psi }^2-\frac{1}{2}\mathsf{B}+\frac{1}{2}Nr-\frac{1}{2}\mu ,$$

(22)

$$\left.\begin{array}{l}\mathrm{\Theta }\left[3\right]=-\frac{10}{3}\mathsf{B}NrN{t}^3-4\mathsf{B}NrN{t}^2+\frac{5}{3}{\mathsf{B}}^3-2\mathsf{B}NrNt+\frac{5}{6}\gamma \mu \mathsf{B}-\frac{1}{3}{\psi }^2\mathsf{B}+{\mathsf{B}}^2-\frac{1}{3}\mathsf{B}Nr+\mathsf{B}\mu +\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{1}{6}\gamma \mu -\frac{2}{3}NrN{t}^3-NrN{t}^2-\frac{2}{3}NrNt+\frac{1}{6}\mu -\frac{1}{6}{\psi }^2+\frac{1}{12}\mathsf{B}-\frac{1}{6}Nr\end{array}\right\}$$

(23)

$$\left.\begin{array}{l}\mathrm{\Theta }\left[4\right]=\frac{5}{3}NrN{t}^3\gamma \mu +\frac{9}{4}NrN{t}^2\gamma \mu +\frac{4}{3}NrNt\gamma \mu -\frac{10}{3}{\mathsf{B}}^4-\frac{1}{12}{\psi }^4-\frac{25}{12}{\mathsf{B}}^2\gamma \mu +\frac{7}{24}\gamma \mu {\psi }^2+\frac{7}{24}\gamma \mu Nr+\frac{1}{2}\mathsf{B}Nr+\frac{1}{2}{\psi }^2\mathsf{B}-\frac{5}{6}\mathsf{B}\mu -\\ \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{5}{24}{\gamma }^2{\mu }^2-\frac{11}{24}\gamma {\mu }^2-\frac{5}{2}{\mathsf{B}}^3-\frac{5}{12}{\mathsf{B}}^2-\frac{1}{16}\mathsf{B}+3\mathsf{B}NrN{t}^3+4\mathsf{B}NrN{t}^2+\frac{7}{3}\mathsf{B}NrNt-\frac{3}{4}\gamma \mu \mathsf{B}-\frac{10}{3}N{r}^{2}N{t}^6-9N{r}^{2}N{t}^5-\frac{34}{3}N{r}^{2}N{t}^4-\\ \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{49}{6}N{r}^{2}N{t}^3-\frac{7}{2}N{r}^{2}N{t}^2+\frac{4}{3}{\mathsf{B}}^2{\psi }^2+\frac{4}{3}{\mathsf{B}}^{2}Nr-\frac{5}{2}{\mathsf{B}}^2\mu -\frac{5}{6}N{r}^{2}Nt-\frac{1}{6}{\psi }^{2}Nr+\frac{1}{3}{\psi }^2\mu -\frac{1}{12}N{r}^2+\frac{1}{3}Nr\mu -\frac{1}{4}{\mu }^2+\frac{25}{3}NrN{t}^3{\mathsf{B}}^2-\\ \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{7}{6}NrN{t}^3{\psi }^2+\frac{11}{6}NrN{t}^3\mu +\frac{21}{2}NrN{t}^2{\mathsf{B}}^2-\frac{3}{2}NrN{t}^2{\psi }^2+\frac{5}{2}NrN{t}^2\mu +6{\mathsf{B}}^{2}NrNt-\frac{5}{6}NrNt{\psi }^2+\frac{3}{2}NrNt\mu \\ \end{array}\right\}$$

(24)

and so on.

For determining the $\mathsf{B}$ value, apply Pade approximant to Equation (24). For $\hspace{0.17em}\psi = 0.1$, $\mu = 0.1$, $Nt=0.1$, $Nr=0.1$, $\gamma =1$, we have found $\mathsf{B}=-0.54053$. So, the solution of Equation (8) is

$$\begin{array}{cc}\theta \left(\xi \right)=1& -\hspace{0.17em}0.5405345009\xi -0.0437102963\hspace{0.17em}{\xi }^2-0.07494578964\hspace{0.17em}{\xi }^3\hfill \\ & -\hspace{0.17em}0.0083211651\hspace{0.17em}{\xi }^4+\dots \dots .\hfill \end{array}$$

(25)

5. Thermal Stress Formulation

A comprehensive thermal stress investigation is essential for effectively modeling a fin and selecting a suitable material to strengthen its performance and life span. In regard to this, numerous investigators have examined the stress behavior of an annular fin using the classical theory of elasticity. Mallick and Das [13] and Mallick et al. [16] explain the fundamentals of the thermal stress of a convective annular fin. Motivated by these works, the thermal stress variation for a radiative annular fin has been examined in this inspection. Therefore, the fundamental properties of thermal stress are not necessary to describe here. The solutions to the closed-form stress fields are given in the aforementioned studies i.e.,

$${\sigma }_r=-\frac{{\alpha }^{*}E}{r^2}{\displaystyle \underset{a}{\overset{r}{\int }}\left(T-T_{\infty }\right)}\hspace{0.17em}\xi \hspace{0.17em}d\xi +\frac{{\alpha }^{*}E}{b^2-a^2}\left(1-\frac{a^2}{r^2}\right){\displaystyle \underset{a}{\overset{b}{\int }}\left(T-T_{\infty }\right)}\hspace{0.17em}\xi \hspace{0.17em}d\xi$$

(26)

and

$${\sigma }_{\varphi }=-{\alpha }^{*}E\left(T-T_{\infty }\right)+\frac{{\alpha }^{*}E}{r^2}{\displaystyle \underset{a}{\overset{r}{\int }}\left(T-T_{\infty }\right)}\hspace{0.17em}\xi \hspace{0.17em}d\xi +\frac{{\alpha }^{*}E}{b^2-a^2}\left(1+\frac{a^2}{r^2}\right){\displaystyle \underset{a}{\overset{b}{\int }}\left(T-T_{\infty }\right)}\hspace{0.17em}\xi \hspace{0.17em}d\xi$$

(27)

These expressions are reduced to their non-dimensional form as:

$${\sigma }_r{}^{*}=-\frac{{\alpha }^{*}}{{\xi }_1{}^2{a}^2}\left(T_b-T_{\infty }\right){\displaystyle \underset{1}{\overset{{\xi }_1}{\int }}\theta a}{\xi }_{1}ad{\xi }_1+\frac{{\alpha }^{*}}{b^2-a^2}\left(T_b-T_{\infty }\right)\left(1-\frac{1}{{\xi }_1{}^2}\right){\displaystyle \underset{1}{\overset{R}{\int }}\theta a}{\xi }_{1}ad{\xi }_1$$

(28)

and

$${\sigma }_{\varphi }{}^{*}=-{\alpha }^{*}\left(T_b-T_{\infty }\right)\theta +\frac{{\alpha }^{*}}{{\xi }_1{}^2{a}^2}\left(T_b-T_{\infty }\right){\displaystyle \underset{1}{\overset{{\xi }_1}{\int }}\theta a}{\xi }_{1}ad{\xi }_1+\frac{{\alpha }^{*}}{b^2-a^2}\left(T_b-T_{\infty }\right)\left(1+\frac{1}{{\xi }_1{}^2}\right){\displaystyle \underset{1}{\overset{R}{\int }}\theta a}{\xi }_{1}ad{\xi }_1$$

(29)

With the aid of dimensionless parameters (Sowmya et al. [34]):

$${\sigma }_r{}^{*}=\frac{{\sigma }_r}{E},\hspace{0.33em}{\sigma }_{\varphi }{}^{*}=\frac{{\sigma }_{\varphi }}{E},\hspace{0.33em}{\xi }_1=\frac{r}{a},\hspace{0.33em}R=\frac{b}{a},\hspace{0.33em}\theta =\frac{T-T_{\infty }}{T_b-T_{\infty }}\hspace{0.33em}\mathrm{and}\hspace{0.33em}\chi ={\alpha }^{*}\left(T_b-T_{\infty }\right)$$

(30)

Using $\chi$ and $R$, Equations (28) and (29) are denoted as:

$${\sigma }_r{}^{*}=-\frac{\chi }{{\xi }_1{}^2}{\displaystyle \underset{1}{\overset{{\xi }_1}{\int }}\theta \hspace{0.17em}}{\xi }_{1}d{\xi }_1+\frac{\chi \left({\xi }_1{}^2-1\right)}{\left(R^2-1\right){\xi }_1{}^2}{\displaystyle \underset{1}{\overset{R}{\int }}\theta }\hspace{0.17em}{\xi }_{1}d{\xi }_1$$

(31)

and

$${\sigma }_{\varphi }{}^{*}=-\chi \theta +\frac{\chi }{{\xi }_1{}^2}{\displaystyle \underset{1}{\overset{{\xi }_1}{\int }}\theta \hspace{0.17em}}{\xi }_{1}d{\xi }_1+\frac{\chi \left({\xi }_1{}^2+1\right)}{\left(R^2-1\right){\xi }_1{}^2}{\displaystyle \underset{1}{\overset{R}{\int }}\theta }\hspace{0.17em}{\xi }_{1}d{\xi }_1$$

(32)

The $\xi$ and ${\xi }_1$ are related as ${\xi }_1=\xi +1$ and, thus, yields:

$${\sigma }_r{}^{*}=-\frac{\chi }{{\left(\xi +1\right)}^2}{\displaystyle \underset{0}{\overset{\xi }{\int }}\theta \hspace{0.17em}}\left(\xi +1\right)d\xi +\frac{\chi \left({\xi }^2+2\xi \right)}{\left(R^2-1\right){\left(\xi +1\right)}^2}{\displaystyle \underset{0}{\overset{R-1}{\int }}\theta }\hspace{0.17em}\left(\xi +1\right)d\xi$$

(33)

$${\sigma }_{\varphi }{}^{*}=-\chi \theta +\frac{\chi }{{\left(\xi +1\right)}^2}{\displaystyle \underset{0}{\overset{\xi }{\int }}\theta \hspace{0.17em}}\left(\xi +1\right)d\xi +\frac{\chi \left({\xi }^2+2\xi +2\right)}{\left(R^2-1\right){\left(\xi +1\right)}^2}{\displaystyle \underset{0}{\overset{R-1}{\int }}\theta }\hspace{0.17em}\left(\xi +1\right)d\xi$$

(34)

6. Numerical Procedure

Many investigations have focused on the numerical and analytical solutions to the thermal modeling of the fins under several operational conditions. However, the majority of the solutions that have been developed are centered around the presumption of constant thermal properties. Also, the heat transmission coefficients change with temperature. As the heat transfer coefficient varies as a function of temperature, a power law is generally responsible for this change. Furthermore, the thermal conductivity of the fin is temperature-dependent. In this case, the differential equations describing the thermal changes of the fin under diverse situations become strictly nonlinear. The existing literature has numerous techniques for tackling the nonlinear fin problem. The techniques used include HPM [16], DTM [23], the collocation method [35], the Adomian decomposition method [36], the Akbari-Ganji method [37], the Legendre wavelet collocation method (LWCM), the least square method (LSM) and the moment method (MM) [38]. In the present investigation, numerical calculations are performed using the Runge-Kutta Fehlberg fourth-fifth order (RKF-45) technique. This method numerically solves Equations (8) and (9). The resulting equations have a two-point boundary and are higher-order. This is accomplished by transforming the provided ODEs and BCs into a first-order initial value problem, as shown below:

$$\theta =\mathrm{H},\hspace{0.17em}\hspace{0.17em}{\theta }^{\prime }={\mathrm{H}}^{*},\hspace{0.17em}\hspace{0.17em}{\theta }^{″}={\mathrm{H}}^{\prime }={\mathrm{H}}^{**}$$

(35)

$${\mathrm{H}}^{**}=-\frac{1}{\left({\mathrm{H}}^m\right)}\left[\begin{array}{l}-\frac{{\mathrm{H}}^m}{\left(1+\xi \right)}{\mathrm{H}}^{*}-m\hspace{0.17em}{\mathrm{H}}^{\hspace{0.17em}m-1}{\left({\mathrm{H}}^{*}\right)}^2+{\psi }^2{\mathrm{H}}^{n+1}-\\ \mu \left(1+\gamma \hspace{0.17em}\mathrm{H}\right)+Nr\left({\left(Nt+\mathrm{H}\right)}^4-N{t}^4\right)\end{array}\right]$$

(36)

and reduced boundary conditions are:

$$\mathrm{H}\left(0\right)=1, {\mathrm{H}}^{*}\left(1\right)=0$$

(37)

A detailed description of this scheme is as follows:

$${\beta }_1=hG(x_{\beta },y_{\beta })$$

(38)

$${\beta }_2=hG(x_{\beta }+\frac{1}{4}h, y_{\beta }+\frac{1}{4}{\beta }_1),$$

(39)

$${\beta }_3=hG(x_{\beta }+\frac{3}{8}h, y_{\beta }+\frac{3}{32}{\beta }_1+\frac{9}{32}{\beta }_2),$$

(40)

$${\beta }_4=hG(x_{\beta }+\frac{12}{13}h,{ y}_{\beta }+\frac{1932}{2197}{\beta }_1-\frac{7200}{2197}{\beta }_2+\frac{7296}{2197}{\beta }_3),$$

(41)

$${\beta }_5=hG(x_{\beta }+h, y_{\beta }+\frac{439}{216}{\beta }_1-8{\beta }_2+\frac{3680}{513}{\beta }_3-\frac{845}{4104}{\beta }_4),$$

(42)

$${\beta }_6=hG (x_{\beta }+\frac{1}{2}h, y_{\beta }-\frac{8}{27}{\beta }_1+2{\beta }_2-\frac{3544}{2565}{\beta }_3+\frac{1859}{4104}{\beta }_4-\frac{11}{40}\beta -5).$$

(43)

The Runge-Kutta fourth-order approach has been utilized to determine an approximate solution:

$$y_{\beta +1}=y_{\beta }+\frac{25}{216}{\beta }_1+\frac{1408}{2565}{\beta }_3+\frac{2197}{4101}{\beta }_4-\frac{1}{5}{\beta }_5.$$

(44)

Employing the Runge-Kutta fifth-order technique, the value of the solution is improved:

$$z_{\beta +1}=y_{\beta }+\frac{16}{135}{\beta }_1+\frac{6656}{12825}{\beta }_3+\frac{28561}{56430}{\beta }_4-\frac{9}{50}{\beta }_5+\frac{2}{55}{\beta }_6.$$

(45)

For calculations, a step size of 0.1 is chosen, with a 10⁻⁶ error tolerance and the solution we obtain is more credible, and this technique has a quicker convergence rate of about 10⁻⁶.

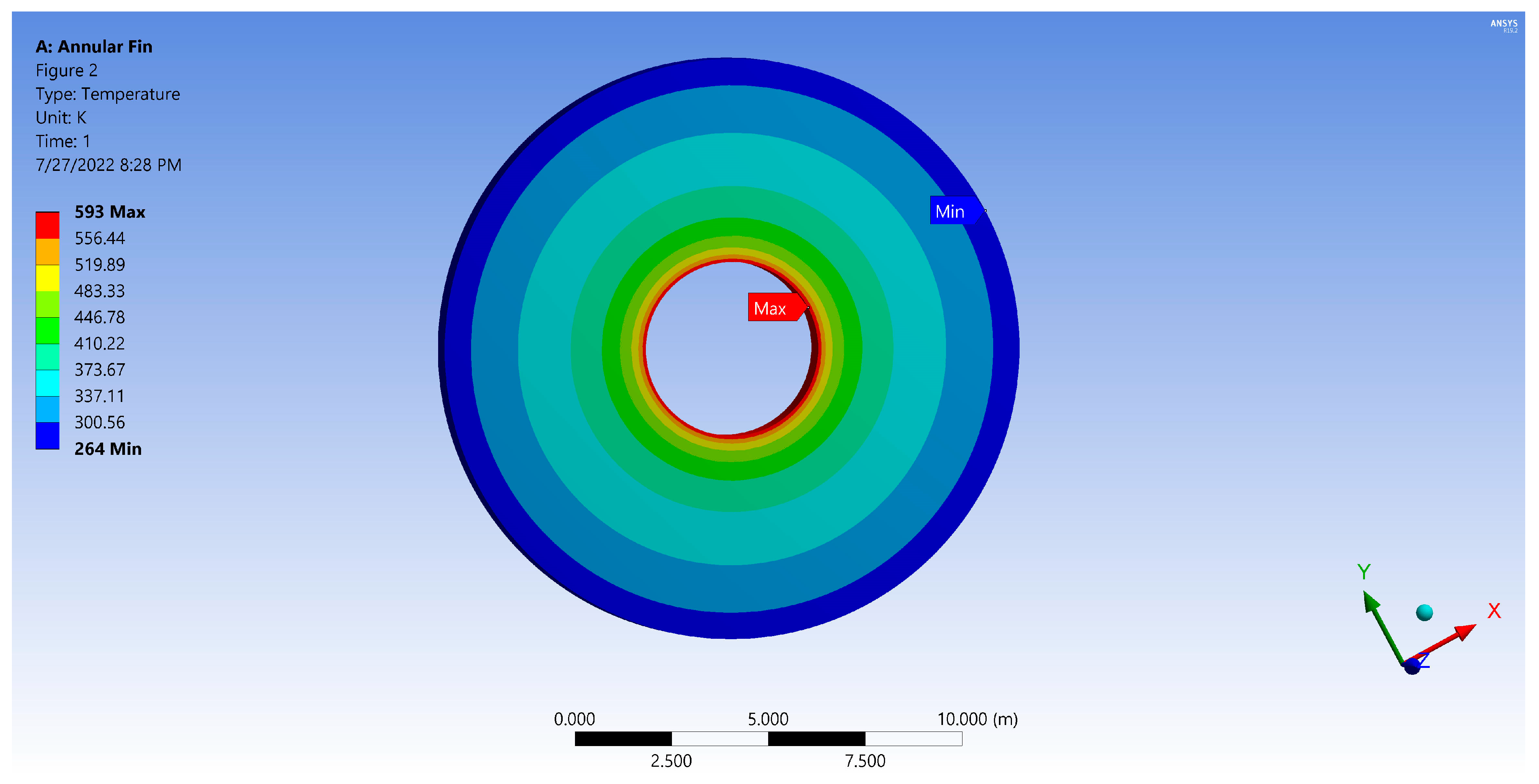
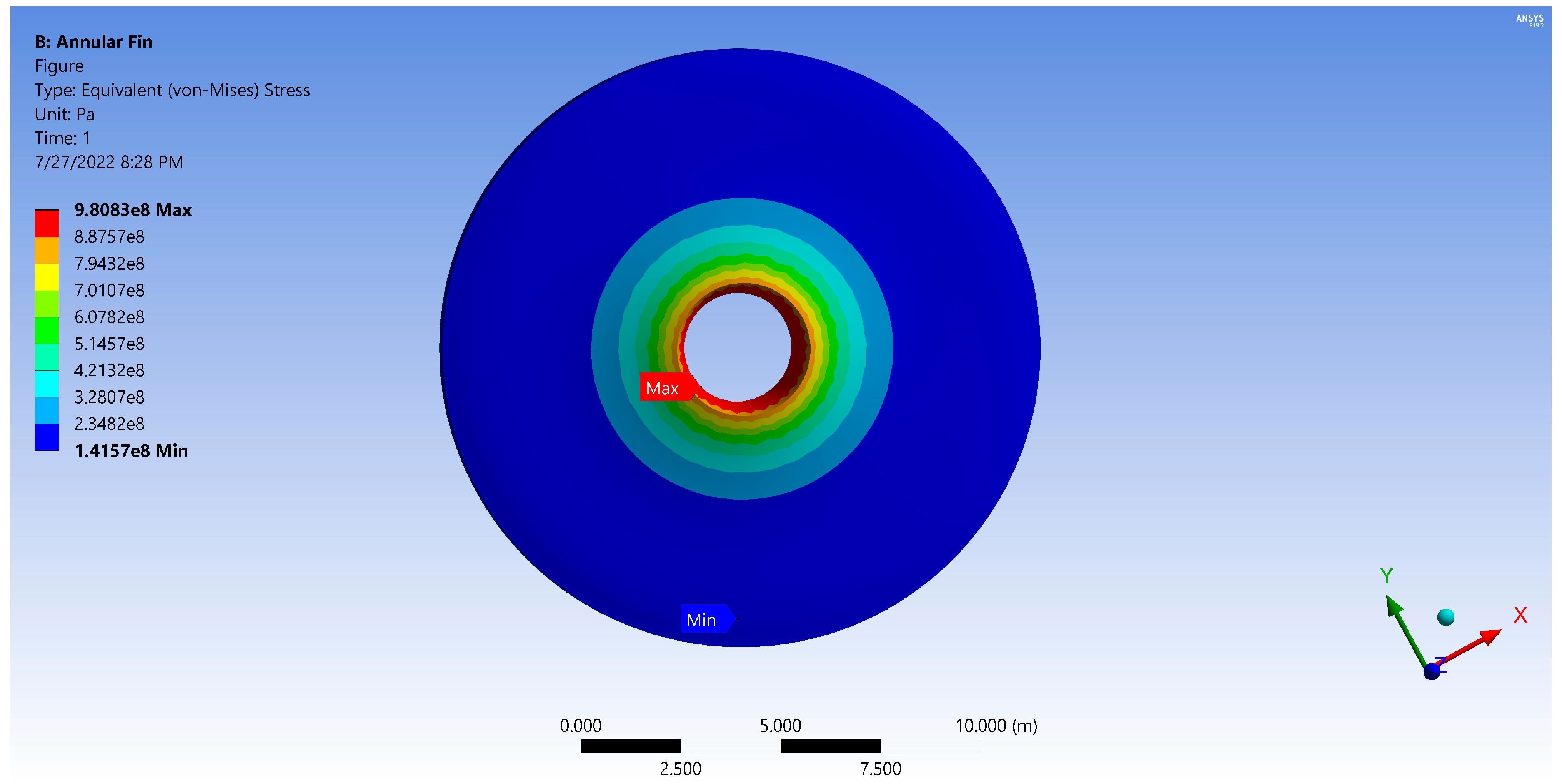
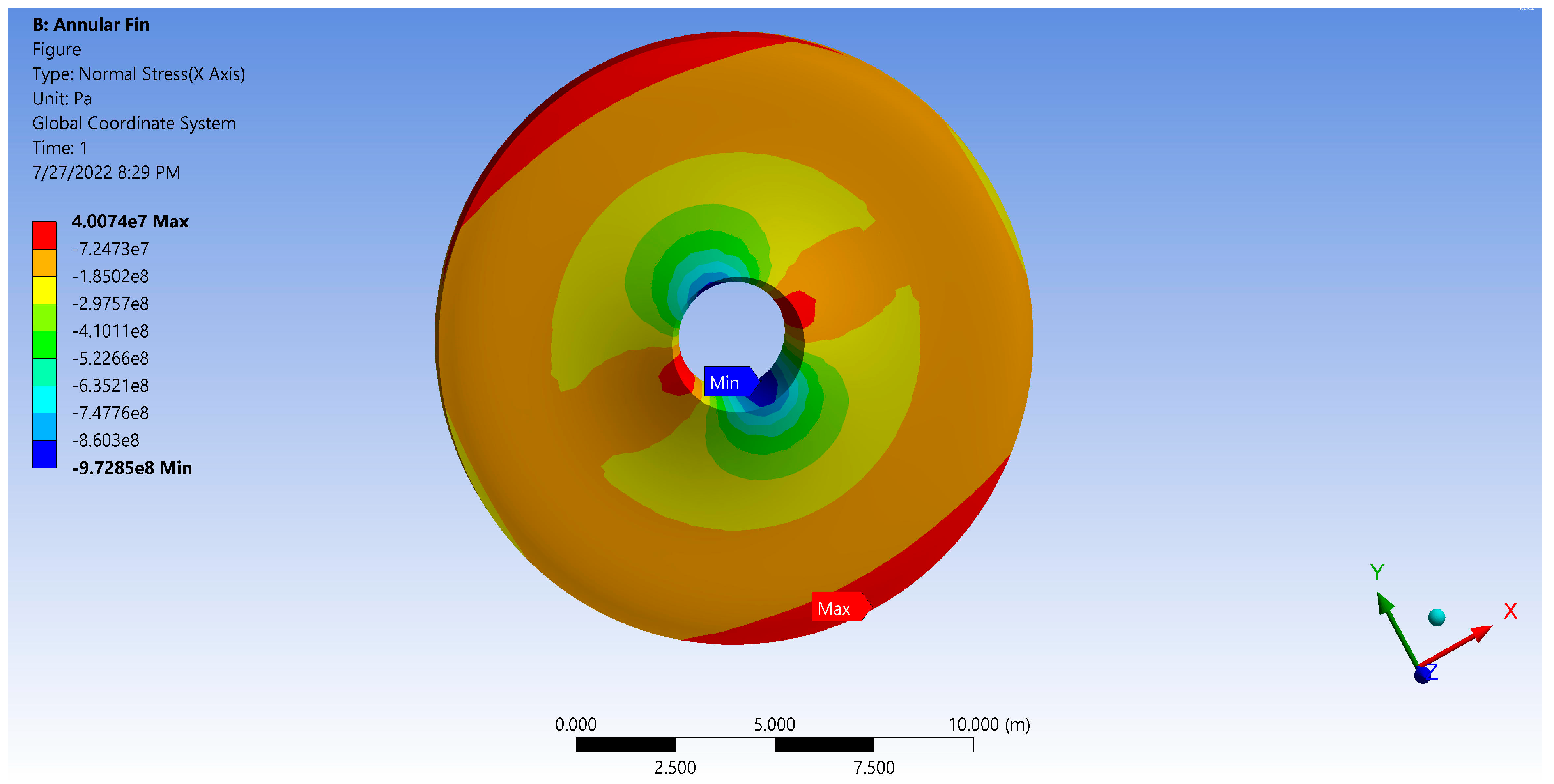
7. Simulation of Thermal Distribution and Stress Analysis

The thermal analysis in an AF is performed using ANSYS WORKBENCH with a steady-state thermal module, which can execute a wide range of engineering modeling scenarios, such as stress, vibration, thermo-electric, and thermal simulations. ANSYS R19.2 has been used to analyze the system with 17,392 nodes and 3342 elements. ANSYS is a low-cost way to examine the effectiveness of products or operations in a simulated environment. An annular fin fitted to a cylindrical surface is considered with dimensions of inner radius 4.5 m, outer radius 16 m, and thickness 1.2 m. Some fundamental presumptions are outlined below for analyzing the fin temperature distribution.

• In the x-direction, one-dimensional heat conduction is considered, and stress is caused by the temperature gradient.
• Over the entire fin surface, the coefficient of convective heat transfer is constant and homogeneous, which is taken as 35 $\mathrm{W}{\mathrm{m}}^{-1} {\mathrm{K}}^{-1}$.
• Radiation from the fin surface is considered with an emissivity of 0.83.
• The ambient temperature is taken as 298.15 K.
• Heat generation of 1853 $\mathrm{W}{\mathrm{m}}^{-3}$ is taken in the fin.

8. Results and Discussions

The heat transfer equation (Equation (1)) is formulated by taking into account heat generation and surface emissivity. The power law $k^{*}\left(T\right)$ and $h^{*}\left(T\right)$ are considered in this inspection, and the heat equation is non-dimensionalized using suitable non-dimensional variables as explained in Section 2. Using the preliminary results of DTM (see Section 3), the analytical solutions for various values of power-index thermal properties are presented in Section 4. In Section 5, the non-dimensional representation of the stress field components is derived with the help of dimensionless terms. In this section, the non-dimensional temperature gradient $\left(\theta \right)$ variation and the behavior of thermal stress components (${\sigma }_r{}^{*}$ and ${\sigma }_{\varphi }{}^{*}$) with the upshot of several non-dimensional parameters, namely heat generation $\mu$, radiative-conductive $Nr$, thermogeometric $\psi$, and temperature ratio $Nt$ are elucidated with the aid of graphs. Maple 17 (version: 813486) software is used to plot the graphs by setting the physical parameters values as $\mu =0.8$, $\gamma =0.1$, $\psi =0.5$, $n=2\hspace{0.17em}\mathrm{or}\hspace{0.17em}3$, $m=1\hspace{0.17em}\mathrm{or}\hspace{0.17em}2$, $Nt=0.1$, and $Nr=0.5$. The upshot of each thermal parameter on the thermal profile is illustrated via figures by varying the associated parameter while retaining the values of the other parameters. Furthermore, the graphs drawn for the solutions obtained by the DTM-Pade display the closer convergence with the numerical method (NM), and this confirms the validation of the obtained results. The solid lines in the graph indicate the solution of DTM-Pade approximant, whereas the dotted lines are for the numerical method. Validation of the current result with NM is examined in Figure 2. The proposed DTM approach shows closer convergence with NM, and these two methods differ by an absolute maximum error of 0.02 %. Also,

Table 2. Comparison of $\theta (\xi )$ for available literature and present DTM-Pade approximant when $\mu \hspace{0.17em} = 0$, $\gamma =0$, $\psi \hspace{0.17em}=0 .3$, $Nt=0$, $Nr=0$, $n=0$ and $m=0$.

Non-Dimensional Radius $\mathit{\xi }$	Mallick et al. HPM [39] $\left(\mathit{\beta } = 0\right)$	Present DTM-Pade	$\mathbf{Error} = \left|{\mathsf{\theta }}_{\mathbf{DTM}}-{\mathsf{\theta }}_{\mathbf{HPM}}\right|$
0	1.0000	1.0000	0
0.1	0.9355	0.9449	0.0094
0.2	0.8820	0.8962	0.0142
0.3	0.8379	0.8536	0.0157
0.4	0.8018	0.8168	0.0151

is constructed for validating the present DTM-Pade approximant results of an annular fin temperature profile with available literature when $\mu =0$, $\gamma =0$, $\psi \hspace{0.17em}=0.3$, $Nt=0$, $Nr=0$, $n=0$ and $m=0$. The computational error is determined by using $\mathrm{Error}\hspace{0.17em}=\left|{\mathsf{\theta }}_{\mathrm{DTM}}-{\mathsf{\theta }}_{\mathrm{num}}\right|$. The variations in $\theta$ of an annular fin for the various values of power exponent of $k^{*}\left(T\right)$ and $h^{*}\left(T\right)$ are revealed in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. The values of the power exponent are taken to be $m=1$, $n=2$ (linear thermal conductivity with nucleate boiling) in the first case and $m=2$, $n=3$ (nonlinear thermal conductivity with radiation) in the second case. To scrutinize the thermal deviations with the implications of non-dimensional physical parameters for the particular case, the graphs are plotted and assembled separately. In particular, the labels (a) and (b) followed by the label Figure represent the graphs for both cases i.e., $m=1$, $n=2$ and $m=2$, $n=3$ respectively.

The thermogeometric parameter has its influence on $\theta$ of a convective-radiative AN and is shown in Figure 3. The nature of $\theta$ with the upshot of thermogeometric parameter for the case $m=1$ and $n=2$ is displayed in Figure 3a, whereas Figure 3b is for the case $m=2$ and $n=3$. In both cases, $\theta$ varies decreasingly for a higher magnitude of the thermogeometric parameter. This Figure manifests that the convective heat transmission rate through the fin intensifies as the thermogeometric variable rises, due to which the temperature in the fin diminishes. The result indicates that the ratio of convective to conductive heat transmission at the fin’s base has a significant impact on temperature variation. Figure 4a,b reveal the impact of the radiation-conduction parameter on $\theta$ of an AF for each case of the power index of $k^{*}\left(T\right)$ and $h^{*}\left(T\right)$, respectively. The existence of the radiation process provokes energy loss from the fin to the surrounding environment, and cooling occurs as a result of the heat loss. As a consequence, increasing the radiative-conductive parameter strengthens the cooling process, causing the temperature to significantly drop.

The dimensionless temperature ratio parameter perceived in the non-dimensional heat equation (Equation (7)) is also accountable for the variations of heat transmission, and the impact of this parameter on $\theta$ of the AF is demonstrated in Figure 5a,b with the consideration of both the cases. In particular, Figure 5a is for the case $m=1$ and $n=2$, in which the temperature field decreases with an improvement in the scale of $Nt$. Similar behavior of temperature profile is perceived for the case $m=2$ and $n=3$, as revealed in Figure 5b. Figure 6a,b are designed to analyze the impact of $\mu$ on $\theta$ for each case. The temperature profile of the fin augments with an improvement in heat generation number in both cases. The variation in the thermal response of an annular fin for heat generation variable $\gamma$ is explicated in Figure 7a,b by considering the different power index values of $k^{*}\left(T\right)$ and $h^{*}\left(T\right)$. Both the Figures signify that enhancement in the magnitude of $\gamma$ leads to the increase of $\theta$. By increasing the magnitude of this parameter, the heat generation within the fin is significantly enhanced. The temperature profile increases as the heat generation develops because the fin must disseminate greater heat to the surrounding environment. Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show changes in ${\sigma }_r{}^{*}$ and ${\sigma }_{\varphi }{}^{*}$ as a result of various thermophysical parameters. Figure 8a,b indicate the deviance in ${\sigma }_r{}^{*}$ and ${\sigma }_{\varphi }{}^{*}$ for the different magnitudes of $m$. Here, ${\sigma }_r{}^{*}$ drops as the power index of thermal conductivity improves, whereas ${\sigma }_{\varphi }{}^{*}$ is considerably less near the base and is sharp at the fin’s tip. Figure 9a,b highlight the consequence of the thermogeometric parameter on ${\sigma }_r{}^{*}$ and ${\sigma }_{\varphi }{}^{*}$, respectively. As the magnitude of thermogeometric parameter rises, ${\sigma }_r{}^{*}$ decreases, while ${\sigma }_{\varphi }{}^{*}$ drops significantly at the base and improves at the fin’s tip. In the stress distribution components, the same pattern can be noticed as a consequence of $Nr$ and $Nt$, as exemplified in Figure 10a,b and Figure 11a,b. Figure 12a,b indicate the consequence of $\mu$ on the radial and tangential stress, correspondingly. ${\sigma }_r{}^{*}$ varies considerably according to the scale of $\mu$, and stronger radial stress is associated with a lesser $\mu$ value. ${\sigma }_{\varphi }{}^{*}$ is greater at the initial stage and then declines after it reaches zero as a result of an increase in $\mu$. Similar behavior is perceived for higher values of the heat generation parameter, as indicated in Figure 13a,b.

Simulated computational analyses have been used to achieve the temperature distribution along the AF. The inner radius of 4.5 m, the outer radius of 16 m, and the thickness of 1.2 m are the values selected for this calculation. The base’s temperature is kept at T_b = 593 K and $h^{*}=35\hspace{0.17em}\mathrm{W}{\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$. With an emissivity of 0.83, radiation from the fin surface is taken into account. The heat is expelled to the surrounding environment, which is at $T_{\infty }=298.15\hspace{0.17em}\mathrm{K}$. The tip temperature is taken as $T_{tip}=264\hspace{0.17em}\mathrm{K}$. In determining the temperature distribution and the thermal stresses affected, the material property is essential.

Table 3. Material properties of structural steel.

Density	$7850 \mathbf{kg} {\mathbf{m}}^{-3}$
Thermal Conductivity	$45 \mathrm{W}{\mathrm{m}}^{-1}\hspace{0.17em}{\mathrm{K}}^{-1}$
Young’s Modulus Pa	$2\times {10}^{11}$
Poisson’s Ratio	0.3

lists the properties of the material used in this analysis. The temperature distribution of the AF can be calculated using ANSYS. Figure 14, Figure 15 and Figure 16 show the temperature changes of the AN under the specified operating settings. The inner radius temperature is assumed to be T_b = 593 K, and the fin’s tip is supposed to be insulated. The maximum temperature will be 593 K at the fin base, and the minimum temperature occurs at the fin’s tip is given by 264 K, whereas the average thermal value is 380.28 K. This indicates that the fin’s thermal distribution takes place in the decreasing behavior from fin base to tip, as seen in Figure 14. The variation in the von-Mises stress (VMS) by imposing the obtained thermal conditions of Figure 14 is denoted in Figure 15. By this analysis, it is noted that a maximum VMS value of $9.8083\times {10}^8$ Pa is observed at the base and minimum VMS is $1.4157\times {10}^8$ Pa at the surface, while the average VMS value is given as $2.6386\times {10}^8$ Pa. Similarly, the normal stress is discussed for the annular fin via Figure 16. The maximum stress has occurred at the fin’s tip with $4.0074\times {10}^7$ Pa, whereas the minimum stress value of −$9.7258\times {10}^8$ Pa is at the fixed support of the fin. The average stress is given by the value −$2.1542\times {10}^8$ Pa. Furthermore, the grid independence test is performed for unequally spaced grids, as shown in

Table 4. Grid independence verification.

Grid Points	Temperature	% abs Change
1072	372.64	0.584888
2334	378.91	0.058697
3342	380.28	-

, in which the grid elements are ranged from 1072 to 3342, and the average temperature and percentage difference are also calculated. This tabulated information illustrates that the temperature is increasing steadily while the percentage change in absolute value is reducing for considered grid elements.

9. Conclusions

The current assessment elucidates the temperature dispersal in an annular extended surface with convective and radiative influence utilizing the DTM-Pade. Consequently, the proposed scheme yields an analytical approximant for the considered fin problem. This examination reveals that the DTM-Pade treatment is the easiest strategy for handling extremely nonlinear ODEs and provides very precise results. The following are the main insights derived from this research:

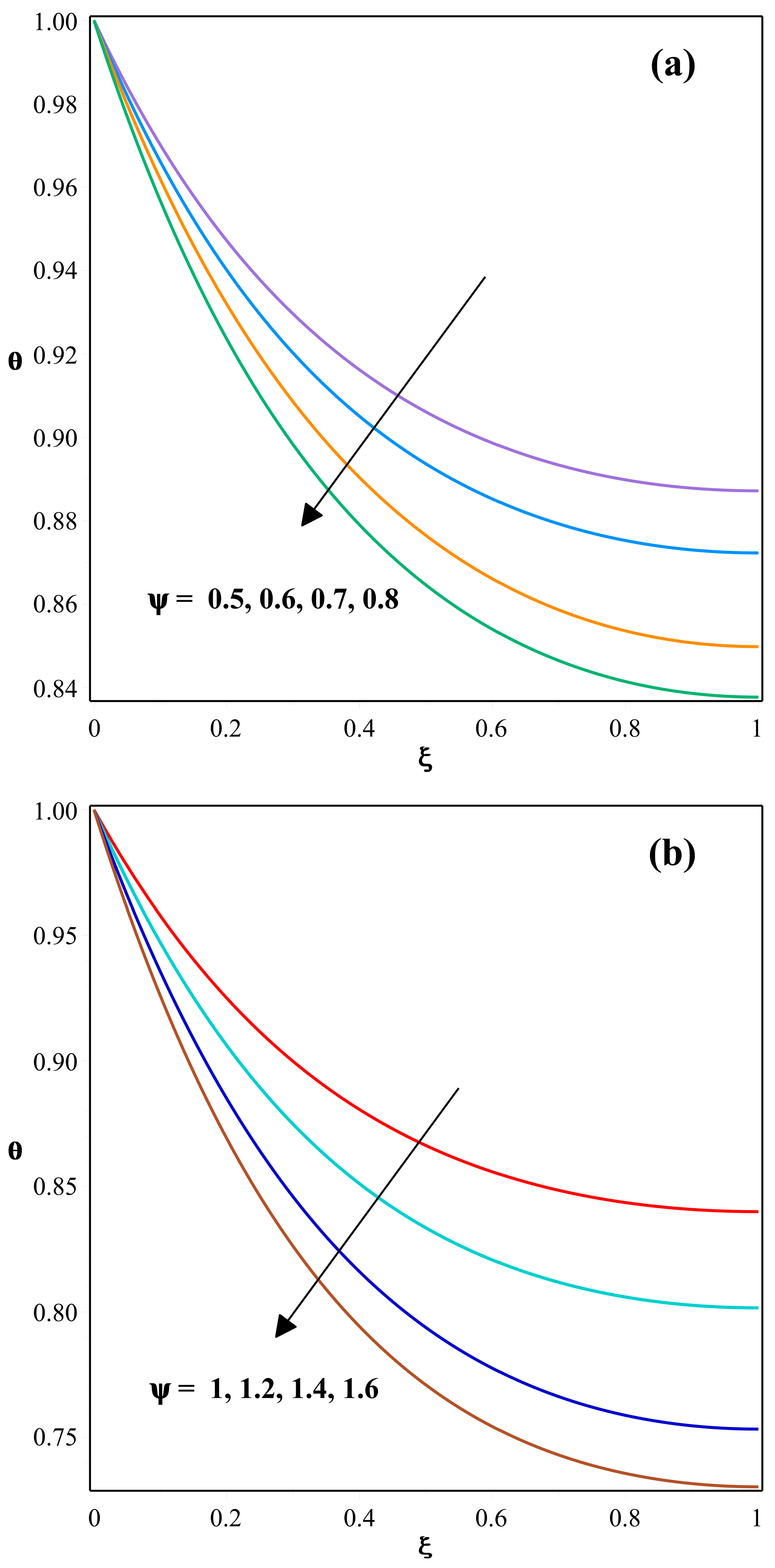
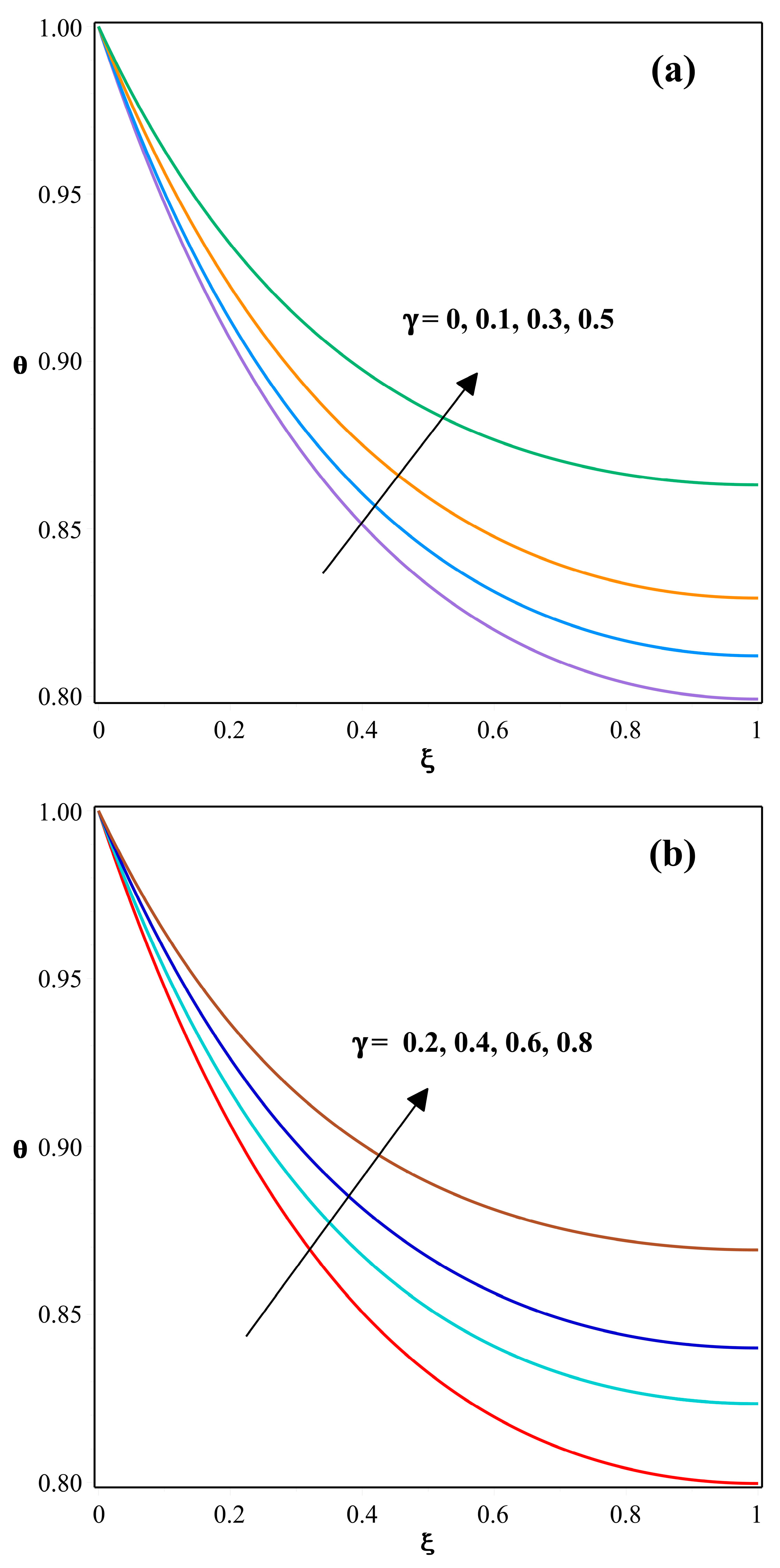
• Increased thermogeometric parameter values result in a decreased thermal distribution.
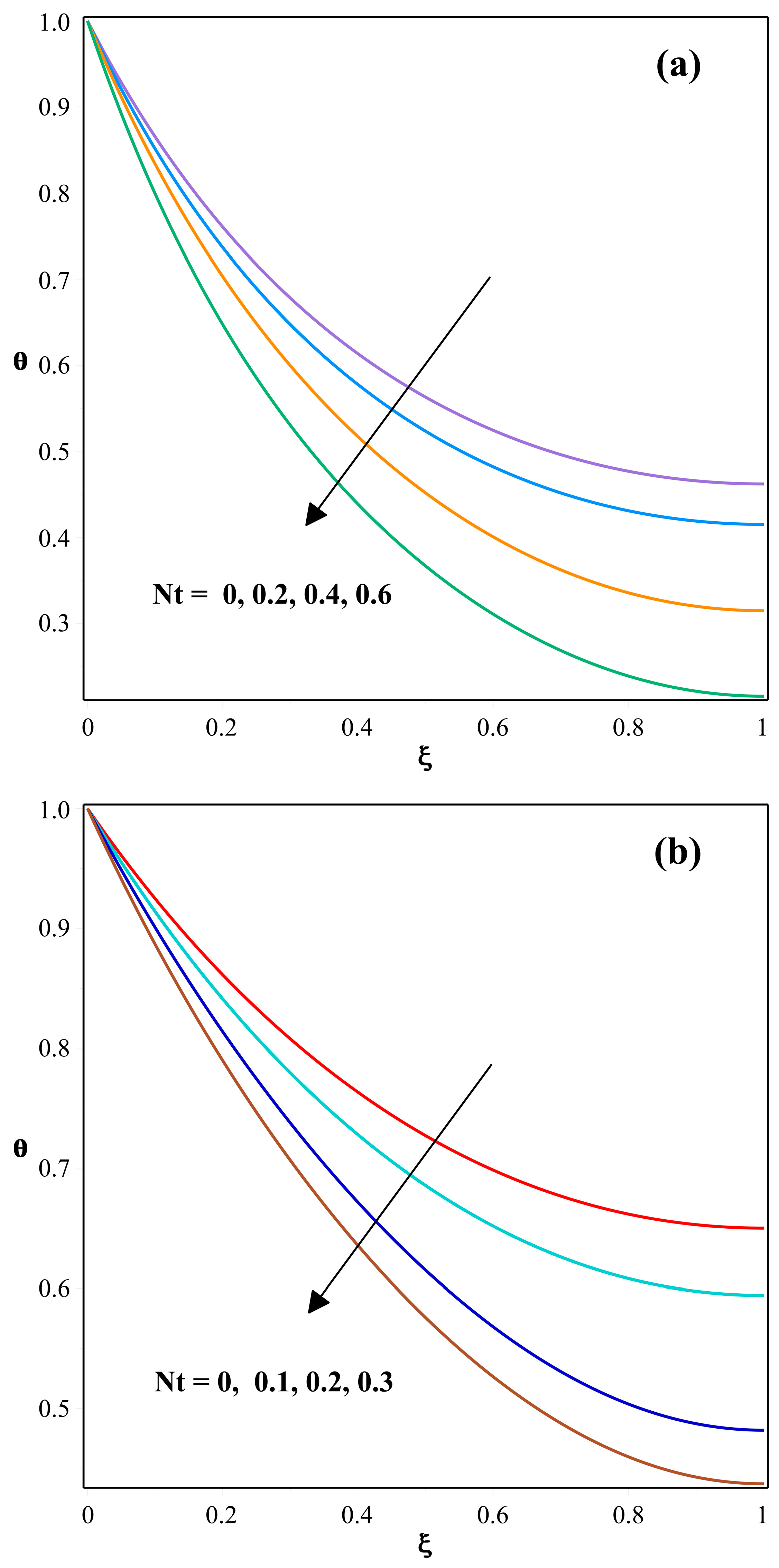
• As the magnitude of a non-dimensional radiation-conduction parameter is increased, the temperature distribution within the fin decreases. Also, the temperature dispersion within the fin declines as the non-dimensional temperature ratio parameter is raised.
• The thermal dispersal within the fin enhances for augmented values of $\mu$.
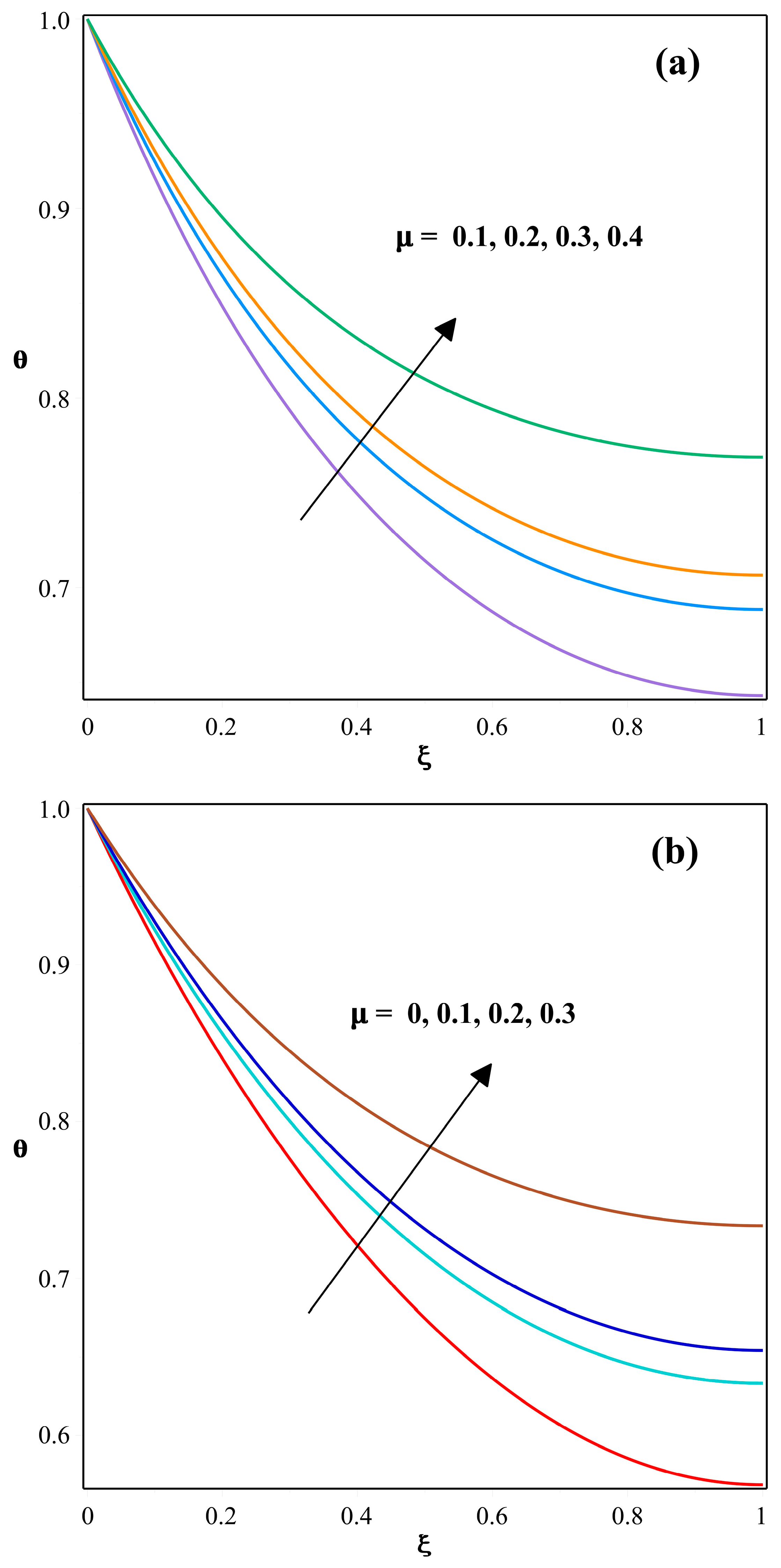
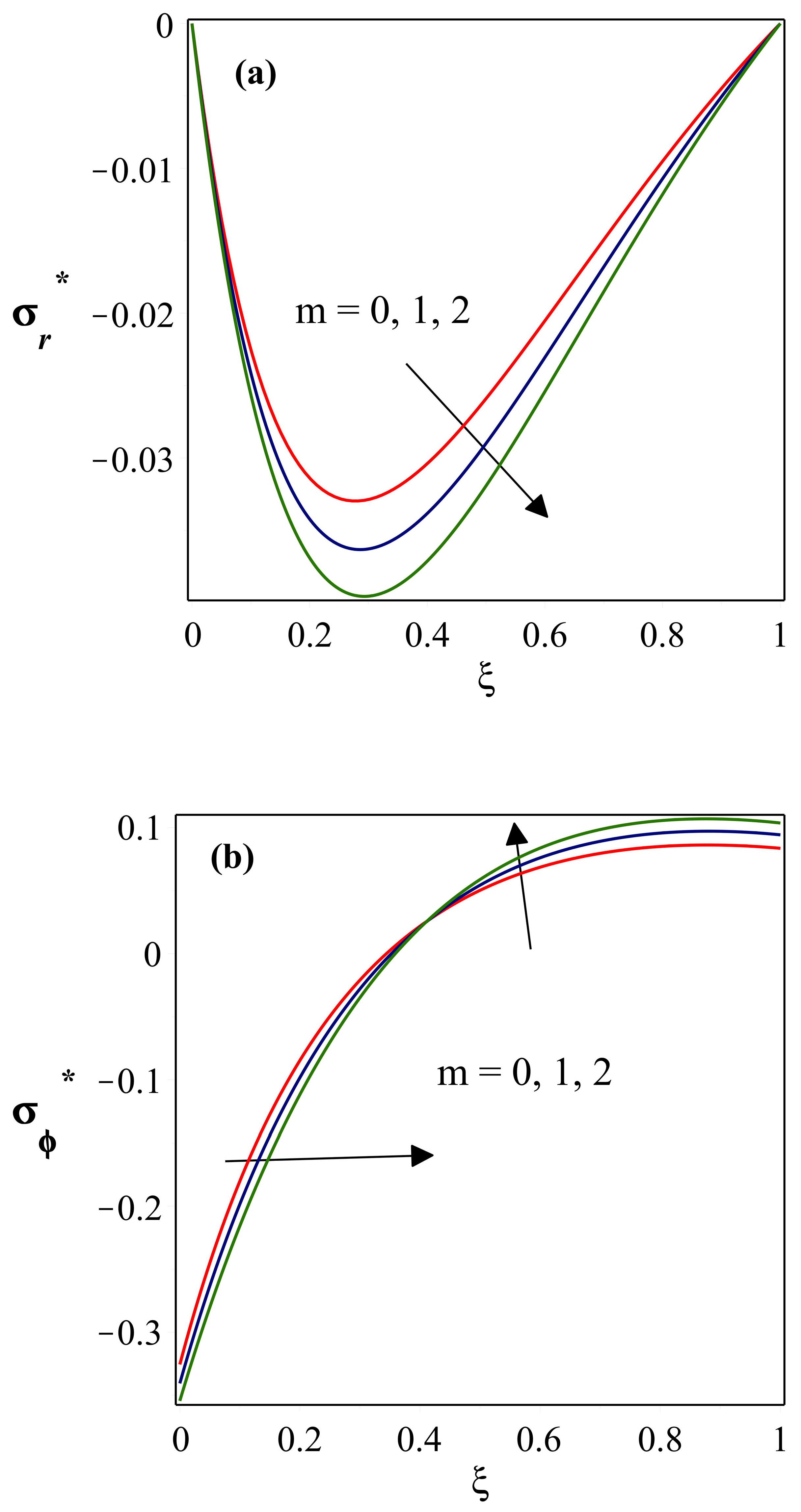
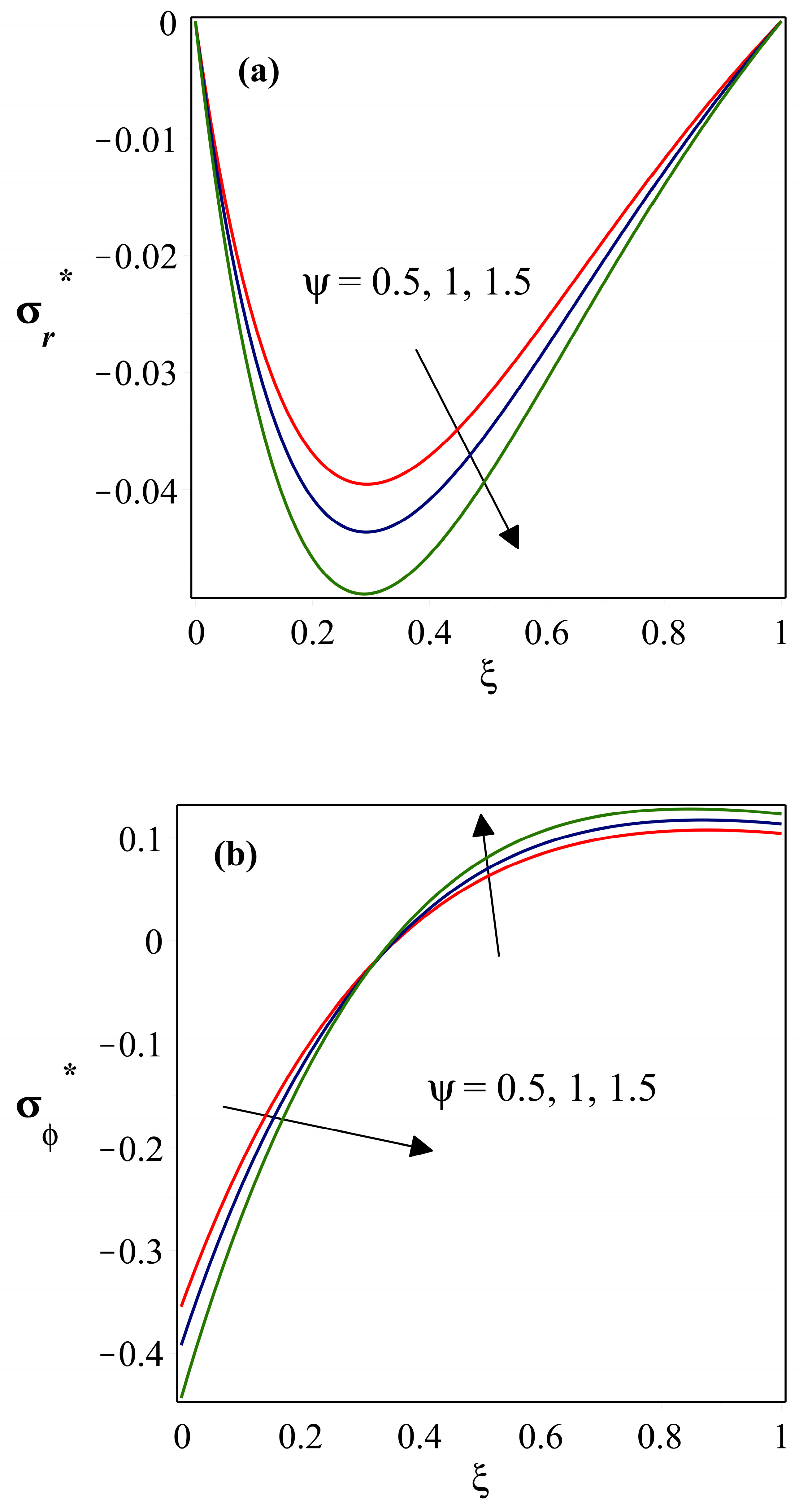
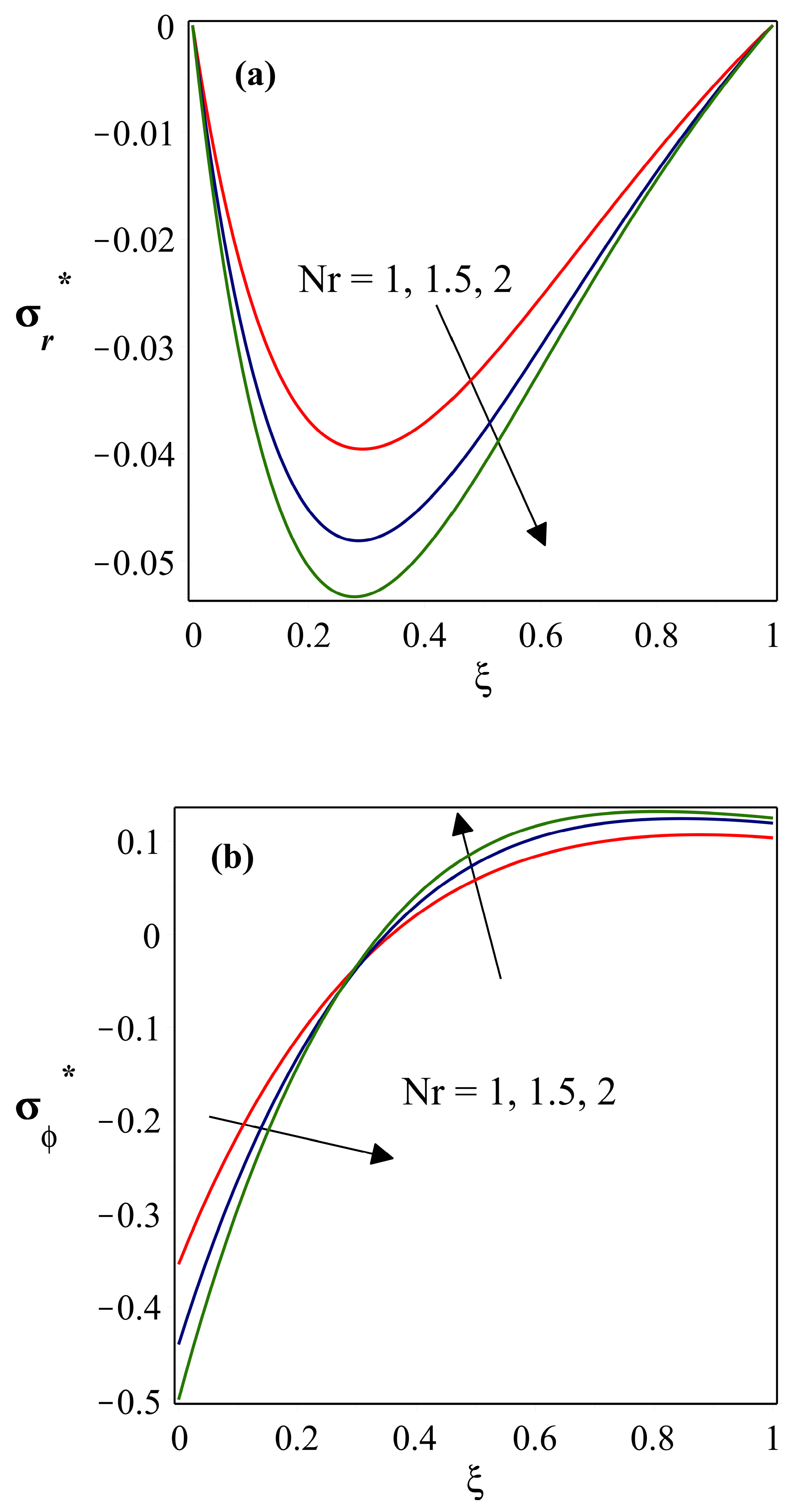
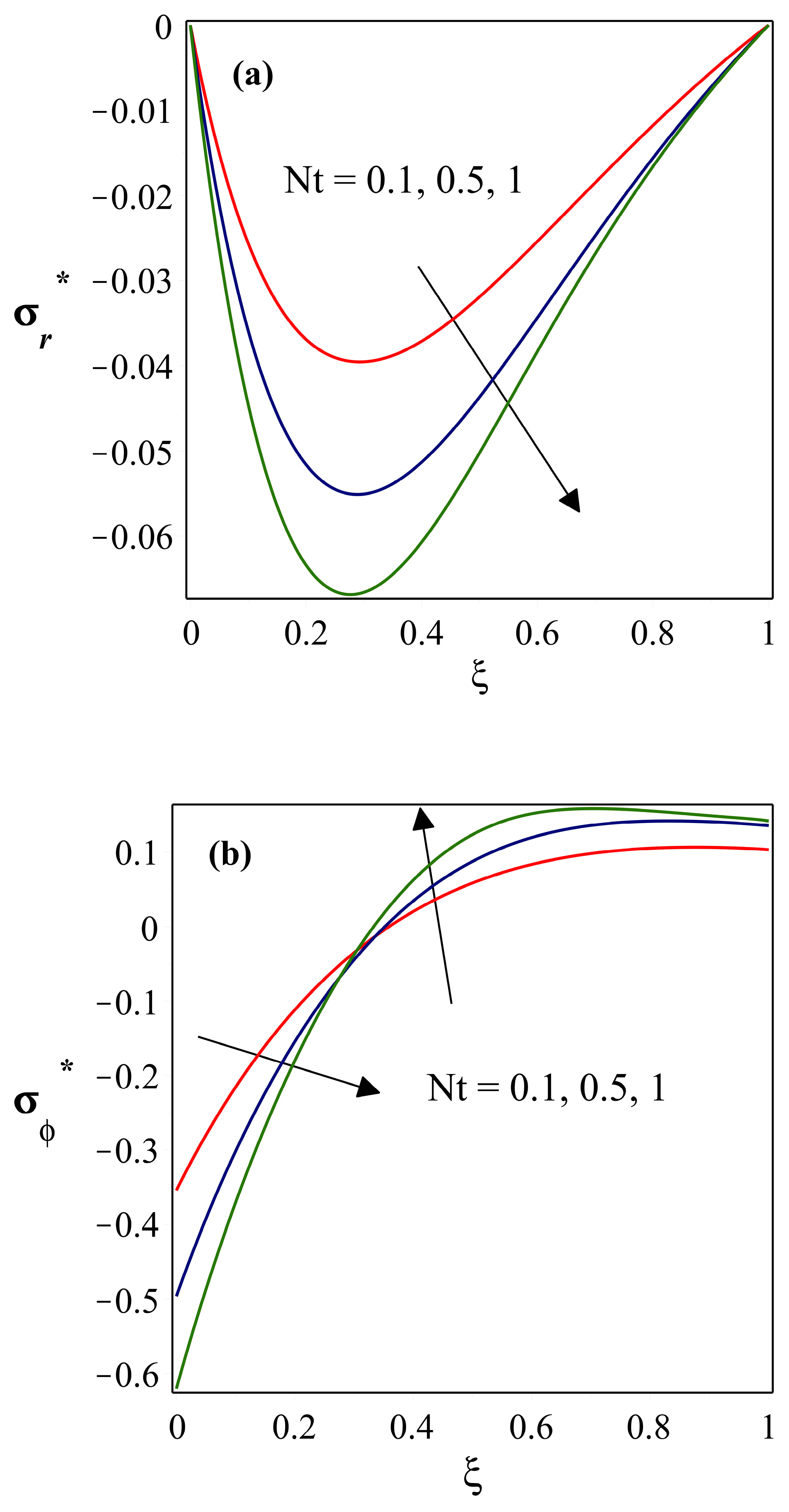
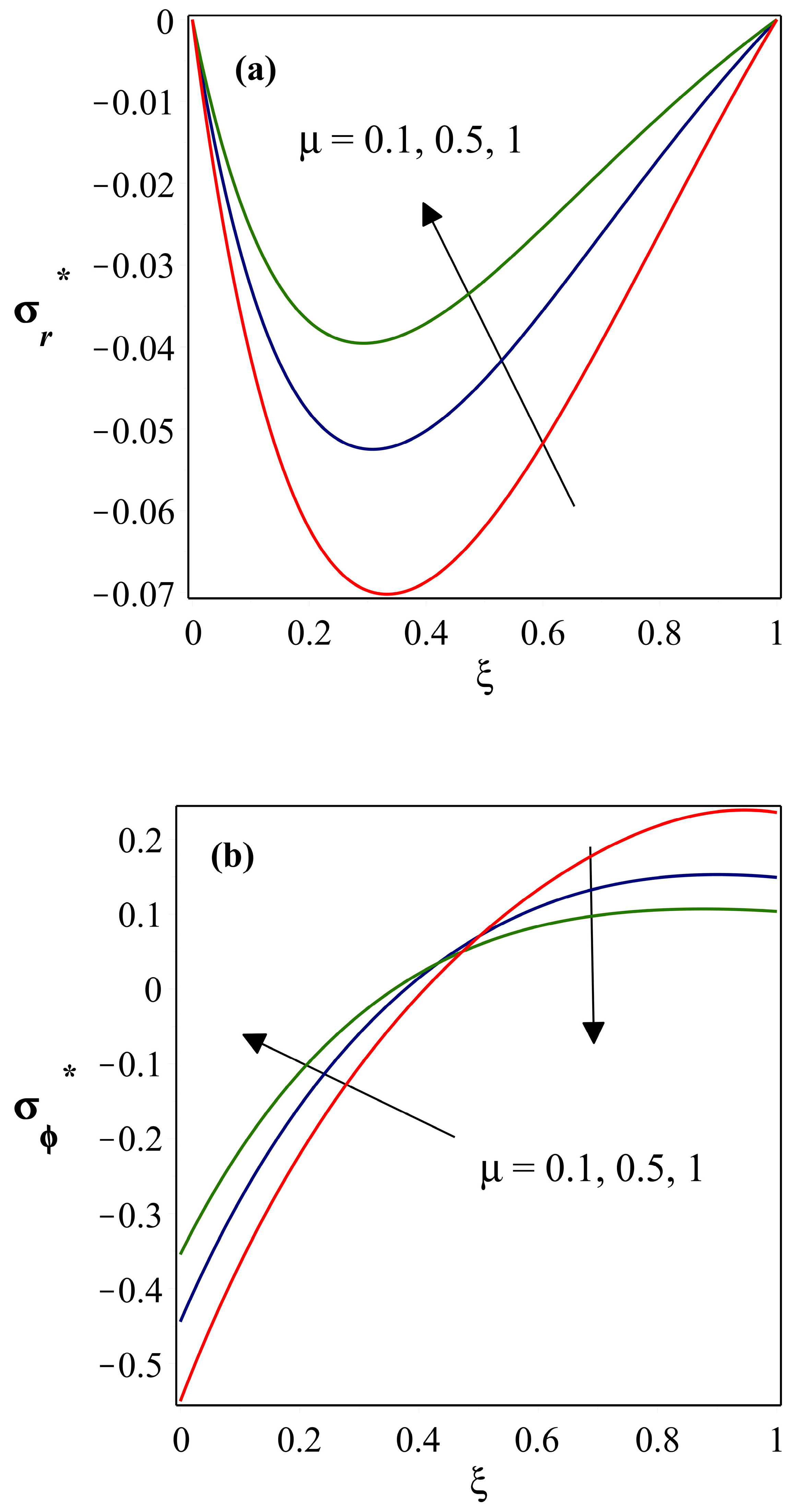
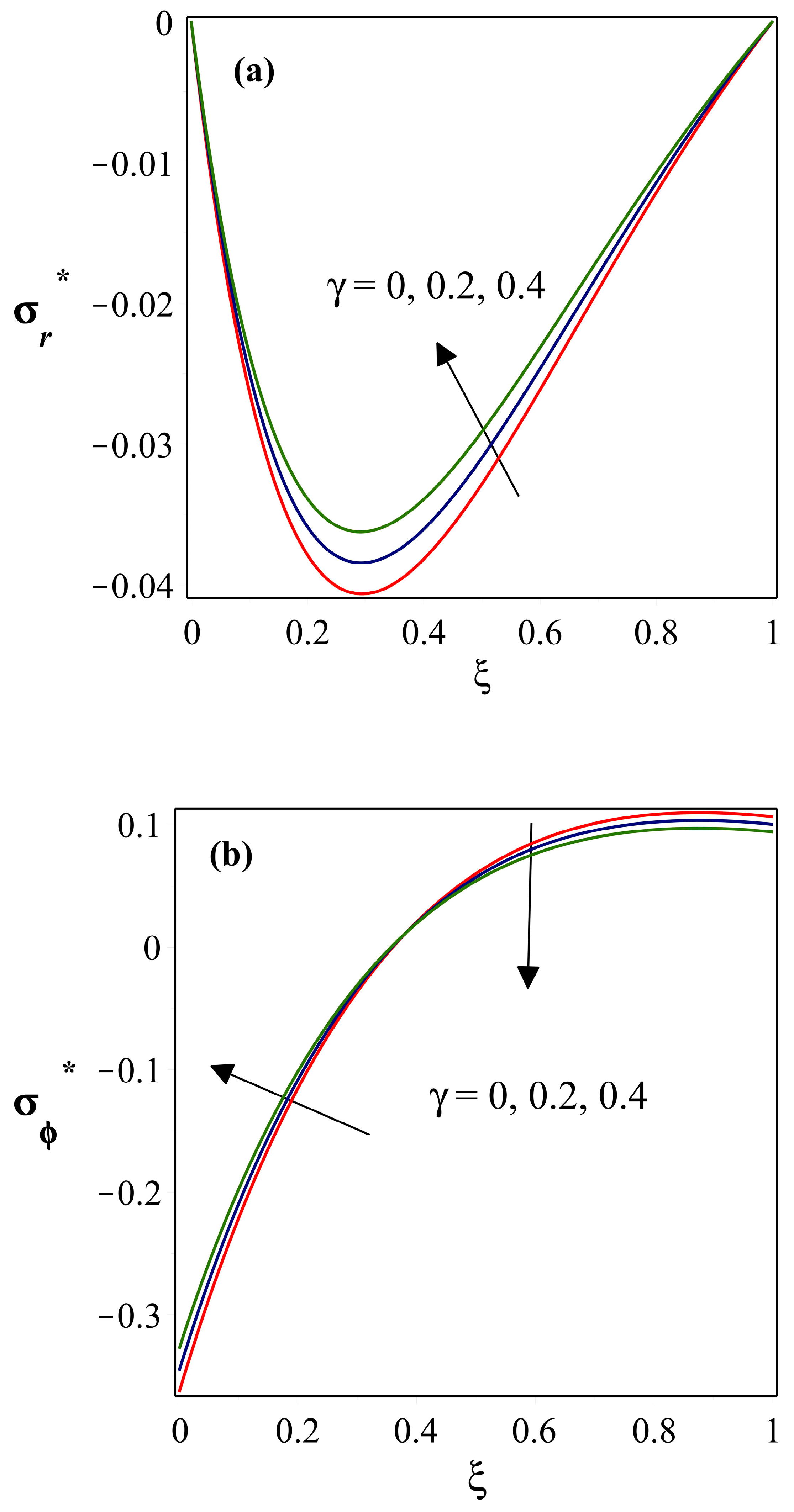
• ${\sigma }_r{}^{*}$ drops as the power index of thermal conductivity heightens, whereas ${\sigma }_{\varphi }{}^{*}$ is considerably less near the base and more at the fin’s tip. The magnitude of $\psi$, $Nr$, and $Nt$ parameters all exhibit a similar trend in the stress distribution fields.
• ${\sigma }_r{}^{*}$ varies significantly with the impact of $\mu$, and stronger ${\sigma }_r{}^{*}$ is related to a lower $\mu$ value. With an increase in this parameter, the ${\sigma }_{\varphi }{}^{*}$ is initially high, then diminishes after it reaches zero.
• The stress variation caused by thermal loading for an annular fin is addressed in this article by providing the analytical and simulation approach, in addition to the thermal distribution in the fin. The analytical solution is achieved using DTM, and the simulation is carried out using ANSYS software. According to the simulation approach, the maximum temperature is seen at the base of the fin, while the minimum temperature is spotted at the tip of the fin. The same temperature behavior can be observed in the discussed Figures obtained through numerical and analytical techniques. Thermal stress behaves similarly; thus, the current research establishes scientific importance.
• Annular fins have a wide range of uses, including compact heat exchangers, air-cooled motorcycle engines, double-pipe heat exchangers, refrigeration equipment, and electrical cooling apparatus. Since the proposed study focuses on the convective-conductive-radiative heat transfer mechanism through an annular fin, it is more advantageous in the realm of the aforementioned application sector.