Abstract
While superluminal phenomena are not empirically substantiated, they present an intriguing hypothetical case. For this speculative framework, the Lorentz transformations would necessitate a revision: instead of the standard , the absolute value of ought to be expressed as , because if v were to exceed c, then the interval traversed by the superluminal frame would surpass the distance covered by light. Under the postulates of relativity, the subluminal scenario leads to the conventional Lorentz factor. Meanwhile, the superluminal scenario introduces an alternative transformation factor that accounts for the presence of the speed of light (c) barrier. This factor is also invariant within Minkowski spacetime, meaning it symmetrically preserves spacetime intervals. The details of this derivation become more evident when using a reverse coordinate system. This result is not, per se, evidence for the existence of superluminal phenomena, but it does allow us to speculate with a new argument about the possibility of their existence.
1. Introduction
1.1. On the Evasive Tachyons
Fanchi [1] categorized particles based on their velocities. First, bradyons are particles with subluminal velocities and real rest mass, such as protons. Second, luxons are massless particles that travel at the speed of light, exemplified by photons. These two groups form part of the standard model and have considerable empirical support.
The third group, tachyons, travel at superluminal speeds and exhibit imaginary mass. As they lack empirical evidence, they remain hypothetical, and many researchers regard them as improbable, due to the violation of fundamental physical principles their existence would entail.
A lack of empirical evidence and the mathematical implications of the Lorentz factor (LF) have directly or indirectly influenced mainstream physics to pay little attention to what we know as tachyons. However, six decades ago, Bilaniuk et al. (1962) argued the possibility of the existence of particles that exceed the speed of light, as long as they were created with that velocity, thus avoiding a conflict with the special theory of relativity (STR) [2]. Five years later (1967), Gerald Feinberg [3] coined the term tachyon for these particles, which could be made from excitations of a quantum field with imaginary mass [2]. Five years later, Cawley suggested that neutrinos might be these tachyons [4]. In 1985, Chodos et al. [5] discussed a theoretical framework for these theoretical particles.
The existence of these superluminal particles is still a matter of debate in the physics community, although their existence is not forbidden by the STR [1,6]. Some authors argue that tachyons could violate the principle of macroscopic causality [7], whereas others believe they may not [8,9].
1.2. On Imaginary Mass
One of the major challenges associated with tachyons is their predicted imaginary rest mass [3,7], which would violate causality and lead to paradoxes. However, other theorists [1,7,10] have argued that their rest mass is a real value, for which they proposed various explanations. For instance, Caligiuri [7] has developed a novel relativistic quantum model that does not require an imaginary value for the mass, while Chodos [11] has suggested a new symmetry principle.
There is generally a consensus that there is no empirical evidence for anything traveling faster than the speed of light. This view is a consequence of the ambiguous results obtained from searches for tachyons [6]. Out of 13 experiments conducted between 1990 and 2021 to measure the effective mass of neutrinos, only one (the KATRIN experiment) reported detecting evidence of a mass with values of [12].
However, some physicists consider that tachyons are a possibility that deserves attention [6]. For instance, several authors considered the possibility that neutrinos are tachyons [5,13,14,15]. Additionally, some authors [16,17,18] have considered tachyons a good candidate for dark energy [12].
Ehrlich [12] believes that these superluminal particles may have been evasive because we have been looking for them “in the wrong way or in the wrong places”, although we may also be searching with inadequate theoretical resources.Therefore, a modification of the search strategy may be required [10]. In our study, we delve into the very beginnings of the theory: into the derivation of the Lorentz factor mathematical expression included in our results.
1.3. Definition of Tachyon
Schwartz [6] summarized the theories of tachyons into two categories: In the first, tachyons are particles resulting from a wave equation, where the mass parameter is replaced by an imaginary number. In the second, tachyons are particles or fields that always travel outside of the Minkowski light cone (MLC); that is, with . In our case, similarly to Schwartz, we fall within the second concept.
In this context, authors frequently propose replacing the Lorentz factor with Equation (1) [3], sometimes without the imaginary unit [6,10], perhaps due to practical considerations or by reinterpreting the value of the imaginary unit [19].
Tachyons have certain long-debated characteristics, but in this article, we focus on their faster-than-light motion—their fundamental attribute—analyzing this from the postulates of the special theory of relativity (STR).
1.4. The Lorentz Transformations
Although the initial study of the STR (1905) did not rely on the concept of Minkowski spacetime (MST) (1908), this resource has allowed for a more extensive and profound analysis of the theory in later times.
In addition to Euclidean 3D space, the MST introduces the time axis CT as an additional coordinate. In this context, a Minkowski light cone (MLC) is a geometric representation in spacetime that illustrates the path of light emanating from an event.
The Lorentz transformations (LT) define the relationship between events in frame S and in frame S’, assuming their axes are aligned. Frame S’ moves away from the stationary frame S at a constant velocity v along the X axis, and both frames have aligned axes. The origins of frames S and S’ are assumed to coincide at .
As is commonly known in the literature on the STR, every event will occur within the MLC, since nothing can travel faster than light, including the worldline of the inertial frame S’.
The LT, in its matrix form is (2)
where is the Lorentz factor (3) and is the relative speed with respect to light (4).
The transformation matrix is also referred to as an X-boost. In this context, according to Minkowski, Equation (5) is Lorentz-invariant.
As we can see, the domain (real numbers) of the LF (3) is . Two situations arise for the indicated domain:
- If , we must deal with imaginary numbers.
- If , mathematically, this implies . This singularity constitutes a barrier with various implications; for example, the need for infinite energy for a massive particle to reach a speed of c.
In this study, we specifically address the first situation.
1.5. On the Mathematical Domain of the Lorentz Factor
Any new analysis intended to contribute to the ongoing discussion of hypothetical superluminal phenomena must consider the notable absence of empirical evidence, and as such, it inherently possesses a speculative nature. Nevertheless, any such proposal should be cautious not to present predictive conflicts with the abundant empirical evidence in subluminal and luminal contexts and supporting canonical theories, and, if possible, even provide explanations for counterexamples or discrepancies observed in previous theories [20].
In this study, based on the two postulates of special relativity, we argue that the emergence of imaginary values in superluminal velocities arises from an implicit assumption in the equations initially used to derive the Lorentz transformations. In other words, these equations are formulated in such a way that they implicitly assume the velocity of the inertial frame S’ is slower than the speed of light; that is, .
Considering this, the Lorentz factor’s domain is restricted to the subluminal velocities. To tackle superluminal phenomena while relying on the same special relativity postulates, an alternative transformation factor is derived. This factor, however, does not imply a validation of the reality of superluminal phenomena. Instead, it serves as a mathematical expression subject to later examination for logical consistencies or inconsistencies, either opening or closing possibilities in the superluminal domain and possibly aiding in the development of experimental proposals for such conjectural phenomena. While these aspects fall beyond the scope of this study, we will offer some peripheral references.
2. Methods
Many laws of physics are only valid within a limited domain, implying that they function effectively under specific conditions but fail to explain or predict phenomena beyond those conditions. For instance, Boyle’s law, which relates gas volume and pressure at a constant temperature, becomes less accurate for real gases at high pressures and low temperatures. In our argument, we propose the possibility that the Lorentz factor, despite its empirically supported efficiency in the subluminal domain, may not adequately explain superluminal phenomena, should they exist.
Our research question is grounded in the fact that, in a subluminal scenario, an inertial frame S’ (a bradyon) moving with a velocity slower than that of a light pulse P, will cover a shorter distance than the light pulse itself, represented as . This scenario is commonly encountered during the derivation of Lorentz transformations. However, in a superluminal scenario, frame S’ (a tachyon) has a velocity greater than c, implying that it will have covered a greater distance than that covered by P; that is, .
The mathematization of these two scenarios, under Galilean relativity, leads to algebraically equivalent equations. However, from the perspective of STR, contrary to the possible mathematical intuition, these two scenarios separated by the speed of light lead to different outcomes.
To explain this difference, we employ a common thought experiment in STR studies [21] and provide a detailed derivation to support our argument (The included derivations may be more detailed than usual, but they were included because they allowed for greater clarity in the revisions made by our collaborators). Additionally, we utilize a reversed coordinate system to emphasize our points. Furthermore, it is important to note that our study is constrained to the context of the STR in Minkowski spacetime (i.e., without gravity).
Reverse Coordinates on the X Axis
In its usual form, the derivation of Lorentz transformations employs coordinate systems aligned in all three of their axes: X, Y, and Z. To facilitate our analysis and highlight important details, we use reference frames with reversed coordinates along their X axes, following the approach suggested by Friedman and Scarr [22]. Specifically, the positive side of the X axis points to the right, while the positive side of the X’ axis points to the left (Figure 1). We used this method in our prior work [23], from which we will take some of the derivations that we expanded upon, and especially those for which we provided a broader interpretation.
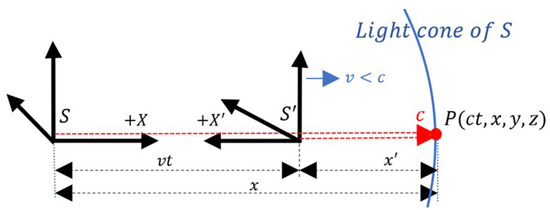
Figure 1.
Reverse frames. Location of an event P in the Minkowski light cone. MST where .
As noted by Friedman and Scarr [22], using aligned coordinate systems breaks the symmetry in the relative motion of frames, since frame S moves in a negative direction with respect to frame S’, leading to a difference in the structure of the transformation equations and their reverses [24], which differ by the sign of v. Although the choice of a particular type of coordinate does not affect the results, using reversed coordinates can help highlight certain features, such as those related to symmetry.
An MST diagram that corresponds to reversed coordinates only needs to substitute the positive X’ axis with its negative counterpart, -X’.
Subsequently, we derive the Lorentz factor for reversed frames by mathematically formalizing the two postulates of the STR: the relativity of motion, and the constancy of the speed of light [25].
According to theory, the light cone (blue) of frame S contains the worldline of frame S’ inside it (Figure 1). In this case, an event P of light from this cone corresponds to a light pulse that moves in the positive direction of the X axis but in the negative direction of the X’ axis, which is the only difference from the usual thought experiment used to derive the Lorentz transformations. Event P is located on the positive X axis of frame S and corresponds to the negative X’ axis in frame S’.
In this way, as explained by Friedman and Scarr [22], in Galilean transformations, the relationship between x and within an aligned coordinate system is determined by . To apply the same conversion in a reversed coordinate system, we must reverse the axis [23], resulting in:
Within aligned coordinates, the reverse transformation from x to is determined by . If the same substitution is applied for reversed coordinates, we have
In this case, the vectors , i.e., observers within both frames S and S’, see the other frame moving away along its positive X axis and positive X’ axis, respectively. Equations (7) and (9) share the same symmetric mathematical structure, and together they comprise the Galilean transformations in reverse frames.
According to the postulates of the STR, the speed of light is constant and time is not absolute (). Additionally, the transformation factor must be the same for both frames, in accordance with the second postulate of the STR. Therefore,
On the other hand, within frame S (Figure 1), the light pulse will have traveled a distance along the X axis, such that
While in frame S’,
The light pulse P moves along the positive X axis in frame S but along the negative X’ axis in frame S’ (Figure 1), so
Substituting this into (15),
As expected, the same Lorentz factor is obtained for the reverse coordinates. To convert the Lorentz transformations from reverse coordinates, that is, Equations (10) and (11) into aligned coordinates, we must consider that , , , , , and , although the fourth and sixth equivalences are not included in the equations. Using these equivalences, we obtain the usual Lorentz transformations. Additionally, it is important to note that this factor applies to four-dimensional physics, and there is no relative movement in the Y and Z axis directions. The Lorentz transformations can be expressed in matrix form (2) and in their inverse form (23).
It is expected that a change of coordinate system does not alter the Lorentz factor, so this result is not surprising. However, let us analyze the interpretation of the assumptions in this derivation from both a geometric and mathematical perspective.
As is common in the relativistic literature, we can see that the light cone encompasses the worldline of frame S’ within it [6] (Figure 1). This occurs because the light cone moves away from the origin of S with greater velocity than that of frame S’. Thus, the assumption that is a starting point. However, as mentioned earlier, in the case of Galilean transformations, this assumption does not lead to different results if we initially assume that , since c does not have any particular condition that distinguishes it from any other velocity. However, in the STR, such a condition exists as a postulate.
3. Derivation of the Transformation Factor Assuming That
As previously stated, tachyons have no empirical support, but we can speculate about a hypothetical scenario in which they existed. In this context, let us start with the assumption that and, as occurs in Galilean transformations, test whether the transformation factor we derive matches that of Lorentz.
In this case, according to Schwartz [6], the worldline of the tachyonic frame S’ should be located outside the light cone of frame S (Figure 2), since its velocity would be greater (), and therefore it would have traveled a greater distance than that of the light cone ().
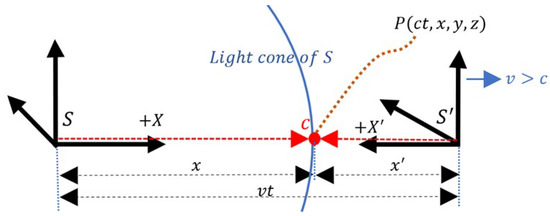
Figure 2.
Reverse frames. Location of a point (event) outside of the Minkowski light cone, where .
Thus, this superluminal phenomenon, in a Galilean spacetime using reversed coordinates (Figure 2), would have its transformations determined by and its reverse , equations, which are symmetric in form. The two reverse reference frames are moving away from each other along the positive X and X’ axes, respectively, which implies that . The light-like pulse P is moving away from the origins of these two frames along the same positive sides of the X and X’ axes, with relative velocities , i.e., both velocities are positive but have different magnitudes.
In a relativistic context, the light-like pulse P is similarly moving away from the origins of these two frames along the same positive sides of the X and X’ axes, but in this scenario with a constant velocity , in accordance with the second postulate of the STR. Due to the symmetry in this case, the transformations are
Symmetric equations in their form under reversed coordinates, as suggested by Friedman and Scarr [22].
The distance traveled by a light pulse along the X axis in frame S (Figure 2) is denoted as
While in frame S’,
In this context, it is essential to take into account that light pulse P moves along the positive X axis in frame S and, similarly, in frame S’ it moves along the positive X’ axis, so
Substituting into (29),
We obtain a transformation factor in reverse coordinates, , for superluminal motion that differs from the Lorentz factor. Corresponding transformations from reverse coordinates to aligned coordinates can be obtained by considering the aforementioned conditions, resulting in the same matrix (2) as mentioned above, but with a different transformation factor (36).
An important characteristic of this superluminal transformation factor is that , since and . Thus, (36) can be expressed as
In summary, the factor replaces the imaginary domain of the LF in superluminal motion with real values, resulting in a kind of extended transformation factor (ETF) that can be defined by a piecewise function:
In Figure 3, the functional values of the two transformation factors (38) are shown. It can be observed that between the two domains, the velocity c represents a sort of barrier between sub- and superluminal worlds.
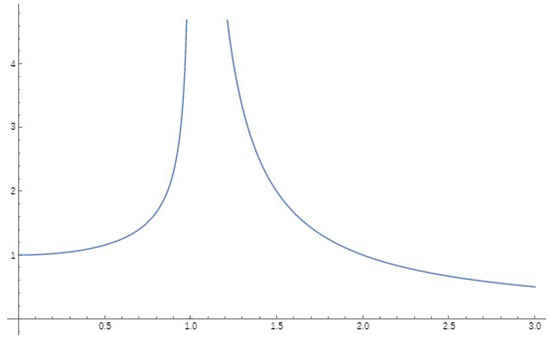
Figure 3.
Extended TF as a function of c.
It can be observed that the MST intervals are also invariant under the new superluminal transformation factor (36):
Given ,
This is equal to the LHS of the MST interval in frame S:
As a result, the intervals in the context of the MST are also invariant in the realm of tachyons.
3.1. Alternative Extended Transformation Factor
The ETF (38) includes two equations corresponding to each of the sub- and superluminal domains, respectively. Next, we derive an alternative extended transformation factor (AETF) using a single function and from a different perspective.
To derive the LT, it should not matter which event P on the MLC (isotropy) is used, i.e., any incidence angle (Figure 4). Similarly, any group of three points on a circle will result in the same equation. While it is true that some derivations of the LT start from more general scenarios, it is common to simplify the derivation by assuming no movement on the Y and Z axes, which indirectly leads to the particular case of . Now, we will perform the derivation using a pulse P on the MLC with an angle greater than zero ().
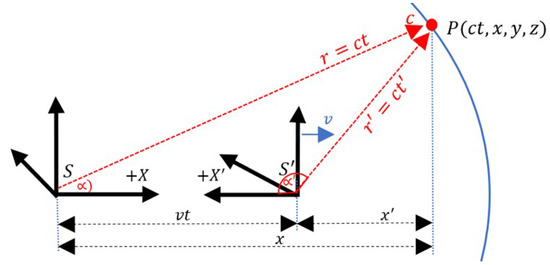
Figure 4.
Event P is not aligned with the X or X’ axis. Subluminal motion.
Our next step involves explicitly introducing a variable that was previously represented implicitly by the coefficient of 1 for velocity c and that corresponds to the cosine of the angle between the light pulse’s trajectory and the X axis.
In a thought experiment, this angle can represent a light pulse emitted in that direction (trajectory), or in the particle world, it could be related to the angle at which a photon separates from an electron in neutron decay [26]. In the macrocosmic world, this could be associated with the angle of incidence in the relativistic aberration of light.
In its reverse form,
In this case, the vectors , i.e., both frames S and S’, see the other frame moving away along its positive X axis and positive X’ axis, respectively. Equations (47) and (49) share the same symmetric mathematical structure,
Based on the description of the event P (Figure 4), and in accordance with the second postulate of the STR, the following equations are proposed:
It is worth noting that the vector r is greater than ; hence, is greater than . Since the speed of light c is constant, this geometrically suggests that the time t is greater than . Employing vector notation, the components of the speed of light c in frame S are expressed as , while in frame S’, they are represented by .
In this context, the distance x corresponds to the component of r in the X axis, and analogously for . The X components of vectors r and in angular notation are
In this general case, , as the magnitude and sign of the coefficient will be determined by the cosines of and . Substituting into Equation (61), we obtain an alternative extended transformation factor (AETF) for any angle of incidence (in the second parenthesis of the denominator of Equation (62), it does not correspond to one of the previously mentioned components, as it combines angle from frame S’ with the speed of light c from frame S):
This transformation factor is a general mathematical expression that includes both the LF and the ETF, as a function of the angle , as analyzed below.
3.2. The Special Case of AETF When and
The AETF (62) appears to differ from the LF. However, in the case where (subluminal motion) and, if (Figure 4), we have in frame S, which corresponds to the angle and thus in frame S’. Substituting these cosines into Equation (62),
Equation (65) for reverse coordinates yields the same Lorentz factor as that found in the relativistic literature for aligned coordinates. However, it should be noted that this is only possible if , which is a necessary condition. As can be seen in Figure 4, this is because event P is located on the negative X’ axis and, therefore, its component is negative. In summary, the (initial) condition that is not a consequence but, rather, an implicit assumption of its derivation.
3.3. Special Case of AETF When and
The general case is where the frame S’ has a superluminal velocity, i.e., , and the angle of the trajectory of P does not coincide with the trajectory of S’ (Figure 5). However, if in this case the trajectories were to coincide, then the angles and would be ; therefore, the value of their cosine is equal to 1 in both cases. This situation corresponds to that presented in Figure 2.
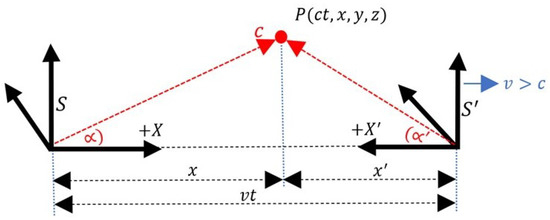
Figure 5.
Event P is not aligned with the X or X’ axis. Superluminal motion.
In this way, we obtain the same transformation factor (36) for the assumption that .
3.4. The Transformation between the Angles and
As previously mentioned, the special case of is just one of the events on the MLC of frame S. The isotropic principle of space implies that the results should be the same for any angle . In order to apply the AETF (62), we need a transformation equation between the angles and , which is given by
This Equation (68) is remarkably similar to the standard function for the relativistic aberration of light [27,28] but with the AETF applied. Furthermore, (68) is similar to the relation between the angle at which a particle is emitted in the laboratory frame and the angle at which it is emitted in the center-of-momentum frame.
3.5. Special Case of AETF When and
The Lorentz factor (65) yields the same results as the AETF (62), even though the latter depends on the incidence angles of the selected events P. For example, if the velocity of the frame S is and the angle , we can substitute these values into Equations (62), (65), and (68), as shown in Figure 5.
LF:
AETF:
Equation (72) has a solution of angle , which corresponds to a factor , coinciding with the result of LF. The relationship between the angles and is the same as that established by the phenomenon of relativistic aberration within the MST. While both transformation factors yield the same results, only the AETF allows for real values for superluminal motion.
3.6. Special Case When and
Faster-than-light motion is not a new concept in the literature regarding the STR, general relativity, or quantum physics [29,30]. This is particularly relevant when discussing the case of neutrinos, which may be tachyons [18,31]. It should be noted that we were able to calculate a transformation factor for faster-than-light motion using Equation (36), assuming an event P on the positive X’ axis, i.e., . However, if we apply the AETF (62) with the frame S’ moving at a superluminal velocity of and the angle , we can obtain a real value.
4. Discussion and Conclusions
In agreement with Friedman and Scarr [22], the use of reverse coordinates allows the transformation equations and their reversals to share the same mathematical structure, effectively highlighting symmetry-related aspects. In our case, these reverse coordinates have facilitated the explanation of certain details in our argumentation that were challenging to address using conventional aligned coordinates. In this regard, it may be advisable to analyze other symmetry-related aspects using both coordinate systems. However, we emphasize that the results will be the same in either of the two cases.
As we mentioned earlier, superluminal phenomena are not supported by empirical evidence. However, assuming their existence, we employed a reverse coordinate system to facilitate our argumentation, and based on the postulates of special relativity, we derived the transformation factor as if the inertial reference system were superluminal.
In the subluminal domain, this transformation factor aligns with the Lorentz factor, thus being consistent with its own empirical evidence. However, in the superluminal domain, this factor diverges, despite employing the same postulates and mathematical procedures. Unfortunately, in this domain, we lack empirical evidence to verify its validity, which limits us to mathematical argumentation.
It is worth highlighting the fact that this factor, per se, does not imply evidence for the existence of superluminal phenomena; rather, it is the mathematical expression that may allow for future speculation regarding the existence or nonexistence of hypothetical superluminal phenomena. It is this factor that should be analyzed for the consistency or inconsistency of its predictions, and if positive, it may prove useful in planning potential experimental proposals aimed at detecting these hypothetical particles.
Currently, when analyzing superluminal motion, the most commonly used transformation factor is , which corresponds to the Lorentz factor, including an imaginary unit due to v being greater than c [32]. This factor also implies a negative squared mass () [10]. In the case of the proposed alternative factor, this overcomes the difficulty of the imaginary value or negative squared mass. However, both transformation factors mathematically demonstrate an apparently insurmountable barrier between subluminal and superluminal domains, with particles confined to remain in the domain in which they were generated [6,10]. Nevertheless, perhaps with this alternative factor, we can also attempt to find some kind of “tunneling effect” between two domains of real numbers, rather than one of them being of imaginary nature.
On the other hand, the two factors exhibit differences in the resulting values. Due to the absence of empirical verification, it is necessary to confine the discussion to mathematical argumentation. From our perspective, the new factor is underpinned by more robust arguments.
Nowadays, the mainstream physics community is hesitant to accept studies on superluminal phenomena; however, that has not prevented theoretical discussions on the topic [7,33,34,35,36]. Our study begins with the hypothesis that the derivation of the Lorentz factor implicitly assumes that the velocity of the inertial frame S’ is subluminal (), which leads to the domain of this equation being the same as the initial assumption. This implicit assumption is concretized in the mathematical formalization of the initial equations. If this is the case, then assuming as a starting point that the frame S’ is superluminal () would not yield the same transformation factor as expected, as in the case of Galilean transformations. For our analysis, we used a reverse coordinate system to highlight some important points.
On the other hand, the new transformation factor (36) leaves the Minkowski spacetime interval invariant and has its domain in the set of real numbers. These results, which partially coincide with Jin and Lazar [30], allow us to speculate further about the possibility of faster-than-light phenomena. One of these cases that holds great interest is precisely the hypothetical tachyons [2], which are approached in different ways, including their possible relation with dark energy and dark matter using low-energy neutrinos [18,31].
Furthermore, we have argued that, due to the isotropy of space, the results should be the same regardless of which angle of the event P on the light cone is selected. Under this assumption, we have derived an alternative extended transformation factor (AETF) that includes both the subluminal Lorentz factor and the superluminal transformation factor. It is worth emphasizing that, with respect to subluminal phenomena, regardless of the angle of the event P’s location on the light cone, this alternative factor yields the same results as the Lorentz factor, and therefore does not present conflicts with the relativistic isotropy.
Although there is no empirical evidence supporting faster-than-light phenomena, it is still too early to dismiss the possibility. In fact, other proposals such as the breaking of fundamental symmetries also lack empirical support, yet they have stimulated numerous experiments at CERN searching for that elusive evidence [37,38].
If tachyons exist, how might they be detected? Ehrlich [12] cautions that superluminal phenomena have been elusive possibly because we have been searching for them “in the wrong way or in the wrong places”, or in other words, we may be applying theoretical foundations that are not appropriate for this domain. We hope that the predictions provided by the alternative factor align with “the correct way or the correct place”, that is, they should offer new experimental possibilities and even fresh perspectives on previously failed experiments. Therefore, it could be an insightful exercise to analyze the experimental proposals suggested by various authors such as Schwartz [6] and Ehrlich [12] from the viewpoint of this alternative factor.
In any case, the fact that the AETF does not contradict subluminal empirical evidence allows us to speculate about the possibility that the same may hold true for superluminal phenomena, if they exist. It is very likely that with the appropriate perspective, we may find many new tachyonic particles, and even dark matter and energy, living to the north of the light barrier [10].
The AETF, like any theoretical proposal, can evolve through the identification and overcoming of contradictions and difficulties. However, as happens with canonical theories today, empirical evidence will be the ultimate judge, which can even turn seemingly absurd predictions into paradoxical predictions.
In fact, even though the extended transformation factor is better aligned with the postulates of relativity, it does not eliminate other potential difficulties that need to be resolved. For instance, it is noteworthy that the factor becomes one at twice the speed of light. Nevertheless, this factor represents a significant advancement, as it overcomes other obstacles that were previously encountered. The extended transformation factor seemingly enables tachyons to overcome theoretical obstacles, such as negative and imaginary mass, causality problems, and tachyon condensation, which are linked to and result from the utilization of the Lorentz factor beyond its subluminal domain.
In closing, we would like to add a comment that may not be strictly necessary. Our initial expectation was to obtain a factor similar to that in Equation (1), albeit without the presence of the imaginary unit. Instead, we derived the “not so aesthetically pleasing” mathematical expression (37), which may have caused others to abandon it. Nonetheless, we have opted to retain it in our analysis. Our main contribution is demonstrating that the Lorentz factor applies exclusively to subluminal motion. In contrast, superluminal motion requires a distinct transformation factor, which we have proposed herein and opened to discussion. We would like to point out that we have also derived a different factor through another approach. However, we have omitted this, since the current proposal seems to be the most compelling at this time.
Author Contributions
Conceptualization, D.R.; formal analysis, F.R.-A. and D.R.; investigation, F.R.-A. and D.R.; visualization, F.R.-A. and D.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We are especially indebted to Esteban Samaniego for his valuable comments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AETF | alternative extended transformation factor |
| ETF | extended transformation factor |
| LT | Lorentz transformations |
| MLC | Minkowski light cone |
| MST | Minkowski spacetime |
| STR | special theory of relativity |
References
- Fanchi, J. Tachyon Behavior Due to Mass-State Transitions at Scattering Vertices. Physics 2022, 4, 217–228. [Google Scholar] [CrossRef]
- Ehrlich, R. Faster-than-light speeds, tachyons, and the possibility of tachyonic neutrinos. Am. J. Phys. 2003, 71, 1109–1114. [Google Scholar] [CrossRef]
- Feinberg, G. Possibility of faster-than-light particles. Phys. Rev. 1967, 159, 1089–1105. [Google Scholar] [CrossRef]
- Cawley, R. Neutrino mass bounds. Lett. Nuovo 1972, 3, 523–525. [Google Scholar] [CrossRef]
- Chodos, A.; Hauser, A.; Kostelecký, V. The neutrino as a tachyon. Phys. Lett. B 1985, 150B, 431–435. [Google Scholar] [CrossRef]
- Schwartz, C. A Consistent Theory of Tachyons with Interesting Physics for Neutrinos. Symmetry 2022, 14, 1172. [Google Scholar] [CrossRef]
- Caligiuri, L.M. A new quantum—Relativistic model of tachyons. J. Phys. Conf. Ser. 2019, 1251, 012009. [Google Scholar] [CrossRef]
- Rembieliński, J. Tachyons and Preferred Frames. Int. J. Mod. Phys. A 1997, 12, 1677–1709. [Google Scholar] [CrossRef]
- Radzikowski, M. A quantum field model for tachyonic neutrinos with Lorentz symmetry breaking. In CPT Lorentz Symmetry; World Scientific: Singapore, 2010; pp. 224–228. [Google Scholar] [CrossRef]
- Chashchina, O.; Silagadze, Z. Relativity 4-ever? Physics 2022, 4, 421–439. [Google Scholar] [CrossRef]
- Chodos, A. Light Cone Reflection and the Spectrum of Neutrinos. arXiv 2018, arXiv:1206.5974v2. [Google Scholar]
- Ehrlich, R. A Review of Searches for Evidence of Tachyons. Symmetry 2022, 14, 1198. [Google Scholar] [CrossRef]
- Jentschura, U.D.; Wundt, B.J. Localizability of tachyonic particles and neutrinoless double beta decay. Eur. Phys. J. C 2012, 72, 1894. [Google Scholar] [CrossRef]
- Rembieliński, J.; Caban, P.; Ciborowski, J. Quantum field theory of space-like neutrino. Eur. Phys. J. C 2021, 81, 716. [Google Scholar] [CrossRef]
- Schwartz, C. Tachyon Interactions. Symmetry 2023, 15, 209. [Google Scholar] [CrossRef]
- Davies, P.; Moss, I.G. Cosmological bounds on tachyonic neutrinos. Astropart. Phys. 2012, 35, 679–680. [Google Scholar] [CrossRef]
- Jentschura, U.; Wundt, B. From Generalized Dirac Equations to a Candidate for Dark Energy. Int. Sch. Res. Not. 2013, 2013, 21. [Google Scholar] [CrossRef]
- Schwartz, C. Tachyon dynamics for neutrinos? Int. J. Mod. Phys. A 2018, 33, 1850056. [Google Scholar] [CrossRef]
- Maccarrone, G.; Recami, E. The Introduction of Superluminal Lorentz Transformations: A Revisitation. Found. Phys. 1987, 14, 367–407. [Google Scholar] [CrossRef]
- Lakatos, I. Falsification and the Methodology of Scientific Research Programmes. In Criticism and the Growth of Knowledge; Cambridge University Press: Cambridge, UK, 1970; pp. 91–196. [Google Scholar] [CrossRef]
- Alstein, P.; Krijtenburg-Lewerissa, K.; van Joolingen, W.R. Teaching and learning special relativity theory in secondary and lower undergraduate education: A literature review. Phys. Rev. Phys. Educ. Res. 2021, 17, 023101. [Google Scholar] [CrossRef]
- Friedman, Y.; Scarr, T. Symmetry and Special Relativity. Symmetry 2019, 11, 1235. [Google Scholar] [CrossRef]
- Roldán, D.; Sempértegui, R.; Roldán-Aráuz, F. The Lorentz factor in a reverse coordinate system. arXiv 2022, arXiv:2203.13191. [Google Scholar] [CrossRef]
- Kichenassamy, S. Hot Spots in the Weak Detonation Problem and Special Relativity. Axioms 2021, 10, 311. [Google Scholar] [CrossRef]
- Mathews, W.N. Seven formulations of the kinematics of special relativity. Am. J. Phys. 2020, 88, 269–278. [Google Scholar] [CrossRef]
- Strumia, A. Dark Matter interpretation of the neutron decay anomaly. J. High Energy Phys. 2022, 22, 67. [Google Scholar] [CrossRef]
- Jarabo, A.; Masia, B.; Velten, A.; Barsi, C.; Raskar, R.; Gutierrez, D. Relativistic Effects for Time-Resolved Light Transport. Comput. Graph. Forum 2015, 34, 12604. [Google Scholar] [CrossRef]
- Van Acoleyen, K.; Van Doorsselaere, J. Captain Einstein: A VR experience of relativity. Am. J. Phys. 2020, 88, 801–813. [Google Scholar] [CrossRef]
- Hill, J.M.; Cox, B.J. Einstein’s special relativity beyond the speed of light. Proc. R. Soc. A 2012, 468, 4174–4192. [Google Scholar] [CrossRef]
- Jin, C.; Lazar, M. A note on Lorentz-like transformations and superluminal motion. J. Appl. Math. Mech. 2015, 95, 690–694. [Google Scholar] [CrossRef]
- Schwartz, C. An approach for modeling tachyons with gravitation. Int. J. Mod. Phys. A 2019, 34, 19501033. [Google Scholar] [CrossRef]
- Nanni, L. Production of tachyonic neutrino in matter. J. Phys. Commun. 2020, 4, 025003. [Google Scholar] [CrossRef]
- Kostelecký, V.A.; Samuel, S. Spontaneous breaking of Lorentz symmetry in string theory. Phys. Rev. D 1989, 39, 683–685. [Google Scholar] [CrossRef] [PubMed]
- Lentz, E. Breaking the warp barrier: Hyper-fast solitons in Einstein—Maxwell-plasma theory. Class. Quantum Gravity 2021, 38, 075015. [Google Scholar] [CrossRef]
- Ruan, X. Information wave and the theory of o bservational relativity. viXra 2017, viXra:1707.0379. [Google Scholar]
- Ruan, X. Observation and Relativity: Why is the Speed of Light Invariant in Einstein’s Special Relativity? J. Beijing Univ. Technol. 2020, 46, 82–105. [Google Scholar] [CrossRef]
- Lehnert, R. Testing Times for Space—Time Symmetry. Available online: https://cerncourier.com/a/testing-times-for-space-time-symmetry/ (accessed on 11 November 2016).
- Russell, N. Framing Lorentz Symmetry. Available online: https://cerncourier.com/a/framing-lorentz-symmetry/ (accessed on 24 November 2016).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).