Abstract
Quantitative structure-property relationship (QSPR) modeling is crucial in cheminformatics and computational drug discovery for predicting the activity of compounds. Topological indices are a popular molecular descriptor in QSPR modeling due to their ability to concisely capture the structural and electronic properties of molecules. Here, we investigate the use of curvilinear regression models to analyze fibrates drug activity through topological indices, which modulate lipid metabolism and improve the lipid profile. Our QSPR approach predicts the physicochemical properties of fibrates based on degrees and distances from topological indices. Our results demonstrate that topological indices can enhance the accuracy of predicting physicochemical properties and biological activities of molecules, including drugs. We also conducted density functional theory (DFT) calculations on the investigated derivatives to gain insights into their optimized geometries and electronic properties, including symmetry. The use of topological indices in QSPR modeling, which considers the symmetry of molecules, shows significant potential in improving our understanding of the structural and electronic properties of compounds.
1. Introduction
Pharmacology has rapidly evolved, resulting in the introduction of numerous groundbreaking drugs each year. However, ensuring accurate testing performance requires the availability of appropriate equipment, a good rapport, and sufficient resources. Previous studies have shown that a drug’s chemical properties are intricately linked to its molecular structure. Pharmacological and medical researchers often utilize topological indices to examine the molecules’ properties and understand their impact on experimental outcomes. Hence, the topological index computation method is a useful tool for developing countries, allowing them to gather medical and biological data on upcoming drugs without the need for laboratory tests; see for example [1,2,3,4].
Fibrates are a type of medication that have been shown to lower high levels of bad cholesterol (also known as low-density lipoprotein or LDL), increase good cholesterol (also known as high-density lipoprotein or HDL), and decrease the amount of small dense LDL particles in the blood. They have been found to be effective in reducing the mortality and morbidity associated with cardiovascular disease (CVD) in individuals who are at risk for developing it. However, conducting laboratory studies to investigate the physicochemical properties of fibrates can be both expensive and time-consuming. To overcome this challenge, chemists can use topological indices to derive mathematical equations that provide valuable insights into the properties of fibrates. For more information on fibrates, please refer to sources [5,6].
Chemical graph theory is a field that integrates mathematical modeling of chemical phenomena with graph theory. It utilizes topological indices to establish a correlation between the properties of a chemical molecule and its structure [7]. These indices are also known as graph invariants or graph-based molecular descriptors, and they quantify the topological features of a molecule or molecules [8]. The application of quantitative structure-property/structure-activity relationship QSPR/QSAR models, which are commonly employed in this field, allows for the prediction of molecular properties using these topological indices. In 1947, Harold Wiener introduced the Wiener index, the first topological index; paraffin’s physical properties were determined using it [9].
Topological indices, which are numerical values derived from the molecular graph of a chemical compound, have been extensively studied in the fields of QSPR/QSAR analysis. These indices encode the structural and topological information of molecules and have proven useful in predicting various physical, chemical, and biological properties [10,11,12,13,14]. The use of molecular graphs to represent unsaturated hydrocarbon structures provides a more intuitive and comprehensive understanding of the molecular characteristics and behavior of compounds [15,16,17,18,19]. In drug design, knowledge of molecular structure is essential in determining the potential therapeutic activity and overall effectiveness. In this study, we examine several vertex-degree-based topological indices, including the first and second Zagreb indices, hyper-Zagreb index, sigma index, inverse symmetric deviation index, max-min rodeg index, min-max rodeg index, inverse sum deviation index, atom-bond connectivity index, Randic index, and Albertson index [20,21,22,23,24,25,26,27,28,29]. Additionally, we investigate topological indices based on distance, such as the Wiener index, Schultz index, Harary index, and Gutman index [30,31,32]. These indices are used to classify the molecular descriptors and analyze the efficacy of curvilinear regression models in predicting the activity of fibrate drugs.
Molecular descriptors have been widely used to evaluate the physicochemical and bioactive properties of chemical structures, and their inclusion in curvilinear regression models can enhance the analysis of drug activity. Topological indices, such as the Zagreb indices, have shown promise in predicting the effectiveness of cancer treatments [33]. The max-min rodeg index has been found to give reliable predictions for octane isomers and polychlorobiphenyls in linear regression models [34]. A new index called the atom-bond connectivity index has been proposed to determine the complexity of alkanes [35]. The first hyper-Zagreb index has been found to be the preferred method for estimating the boiling points of benzenoid hydrocarbons [36]. Additionally, the indeg indices have been applied to predict topological polar areas [37]. The inverse sum deviation index has been used to calculate the vaporization and sublimation enthalpies of monocarboxylic acids [38,39]. Irregularity indices based on different degrees, in addition to Albertson and Sigma indices, have been found to predict the physicochemical properties of octane isomers [40]. The Wiener index was first introduced in QSPR studies, and has been shown to align well with the boiling points of alkanes [41]. The Wiener index has been further developed and used to explain different chemical and physical properties of molecules, as well as their biological activity [42]. The Schultz index has also been investigated to predict the boiling points of alkyl alcohols, and thus their suitability for various applications [43]. As indicated in Table 1, these indices are expressed mathematically and are shown with mathematical expressions.

Table 1.
The mathematical expressions of topological indices.
Notation 1.
A molecular graph is a simple graph . Its vertices and edges represent the atoms and the bonds, respectively. Note that hydrogen atoms are omitted. For any graph represent the degree of the vertex in the graph. While represent the distance of the shortest path from the vertex u to the vertex
Fenofibrate is an important component of a healthy diet and medication regimen, as it is used to reduce blood cholesterol and triglyceride levels. By decreasing triglyceride levels in the bloodstream, the risk of pancreatitis (inflammation of the pancreas) can be mitigated. To date, only one paper [44] has explored the use of topological indices in analyzing one of the drugs in the fibrate family. This study utilized degree, degree, and degree-based (based) approaches to compute the topological indices of fenofibrate’s chemical structure. With limited existing literature on fibrates that incorporate topological indices, this paper represents a pioneering effort in the investigation of novel physicochemical properties of fibrates using this technique. In this work, fenofibrate , ciprofibrate , bezafibrate , clofibrate drugs used in the treatment of patients with high cholesterol are studied.
Fibrate drugs are a class of medications commonly used to treat dyslipidemia, a condition characterized by abnormal lipid levels in the blood. Despite their widespread use, the molecular mechanisms underlying the activity of fibrate drugs are not well understood. One approach to addressing this challenge is to develop quantitative structure-activity relationship (QSAR) models that can predict the activity of fibrate drugs based on their molecular descriptors. In this study, we investigate the efficacy of curvilinear regression models in enhancing the analysis of fibrate drug activity through molecular descriptors. Curvilinear regression models are a type of non-linear regression model that can capture non-linear relationships between variables, making them useful for analyzing complex systems such as the interactions between drugs and their molecular targets. Our study builds upon previous research that has investigated the use of QSAR models to predict the activity of drugs. Several articles published in Symmetry have explored the use of topological indices and other mathematical methods to predict various properties of organic compounds, including their biological activity. For example, a study by Berinde et al. [45] used the QSPR technique to investigate the molar refraction, polarizability, and refractive index of monocarboxylic, dicarboxylic, and unsaturated monocarboxylic acids. Their approach relied on a single molecular descriptor, the ZEP topological index, calculated using weighted electronic distances and chemical structure. The QSPR models obtained had high-quality performance and predictive ability, with . Their approach provides an alternative to existing additive methods for predicting these properties. Zuo and Hu [46] developed QSPR models for predicting the melting points of organic compounds using molecular topology and quantum chemical descriptors. The authors used a dataset of 893 organic compounds and developed multiple linear regression models using the partial least squares (PLS) method. They compared their models with other models reported in the literature and found that their models were more accurate in predicting the melting points of organic compounds. Zhang et al. [47] developed QSPR models for predicting the melting points of organic compounds based on molecular topology. The authors used a dataset of 1427 organic compounds and developed models using the neural network algorithm. They compared their models with other models reported in the literature and found that their models were more accurate in predicting the melting points of organic compounds. Naghipour and Kiasat [48] developed a QSPR model for predicting the fullerene-like behavior of C60 derivatives using topological indices. The authors used a dataset of 46 C60 derivatives with known fullerene-like behavior and developed a model using multiple linear regression. They compared their model with other models reported in the literature and found that their model had higher accuracy in predicting the fullerene-like behavior of C60 derivatives. Wang and Xu [49] developed QSPR models for predicting the boiling points of alkyl alkanes based on the novel vertex degree valence topological index. The authors used a dataset of 388 alkyl alkanes and developed models using multiple linear regression and artificial neural network methods. They compared their models with other models reported in the literature and found that their models were more accurate in predicting the boiling points of alkyl alkanes.
In our study, we apply curvilinear regression models to analyze the activity of fibrate drugs based on their molecular descriptors. By incorporating non-linear relationships between variables, we aim to enhance the accuracy and predictive power of QSAR models for analyzing the activity of fibrate drugs. Ultimately, our research may contribute to a better understanding of the molecular mechanisms underlying the activity of fibrate drugs, and to the development of more effective treatments for dyslipidemia. These studies demonstrate the usefulness of QSAR modeling and related techniques for predicting the activity of various compounds based on their molecular descriptors. By building on this previous work, we hope to further advance our understanding of the molecular mechanisms underlying the activity of fibrate drugs.
The QSPR model is a highly effective tool for predicting a wide range of physicochemical properties of drugs. To make these predictions, the model employs degree-based indices and distance-based topological indices (as detailed in Table 1). The properties considered include polarizability, Sum of electronic and zero-point Energies, the sum of electronic and thermal energies, the sum of electronic and thermal enthalpies, the sum of electronic and thermal free energies, zero-point vibrational energy, complexity, topological polar area, dipole moment, heat capacity, molar entropy, and octanol-water partition coefficients. To analyze the relationships between these properties and the topological indices, curvilinear regression (linear, quadratic, and cubic) is utilized. The model generates statistical parameters using SPSS and MATLAB statistical functions. In addition, DFT calculations are conducted at the B3LYP/6-31G(d,p) to gain insight into the optimized geometries, DOS plots, HOMO and LUMO orbitals energies, and distribution of the four derivatives studied in the next section. Section 3 examines the contributions of different topological indices as molecular structural descriptors. Finally, Section 4 concludes the paper.
2. DFT Part
In Figure 1, Figure 2, Figure 3 and Figure 4, four important characteristics of the four investigated fibrate derivatives were indicated, including optimized geometries, electron density mapped with electrostatic potential (ESPM), total density of states (DOS) plots, and the special distributions of the highest occupied molecular orbitals (HOMOs) and the lowest unoccupied molecular orbitals (LUMOs). Density functional theory (DFT) calculations of the investigated fibrate derivatives utilized one of the well-known hybrid functionals, Becke, parameter, Lee–Yang–Parr () [50]. In DFT, hybrid functionals incorporate a portion of the Hartree–Fock exchange, as well as extra exchange from other sources (empirical/ab initio) to approximate the exchange-correlation energy. The B3LYP as a representation of a Hamiltonian term in the Schrödinger equation was combined with a 6–31 basis set as a representation of the eigenvalue wavefunction. It is a moderate double zeta () basis set enlarged with two polarization basis functions, a function for heavy atoms (carbon, oxygen, and chlorine), and a p-function for all hydrogen atoms. Most of the physicochemical properties of the investigated fibrate derivatives discussed in next section were obtained from the frequency calculations carried out at the same level of theory of optimization. Calculations were carried out using Gaussian 09 software suite [51]. Visualizations of molecular structures were performed by using GaussView (version ) [52], ESPMs were drawn used the Avogadro package [53], and the GaussSum program [54] was used to DOS plots. ESPMs show how electron density is distributed in the four non-planar molecules considering the electrostatic potentials, and this gives information about the region in the molecule that has the highest or lowest electron density, and thus is most likely to be attacked by electrophilic or nucleophilic agents. Keep in mind that the nucleophilic and electrophilic attack regions are represented by blue (positively charged) and red colors (negatively charged). The red color is concentrated on the more electronegative atoms such as the oxygen (deep red) and chlorine atoms (light red), the blue color covers the hydrogen atoms (the least electronegative atoms), while the carbon atoms are covered by white, indicating the intermediate electronegativity of the carbon atom. Thus, it is possible to determine the position and region in a molecule attacked by an electrophile or nucleophile using ESPMs. The molecule DOS plot indicates how many energy states electrons are allowed to occupy in the system. The HOMO energies of the four investigated fibrate derivatives are and eV for fenofibrate, ciprofibrate, bezafibrate, and clofibrate, respectively. Since the HOMO energy is used as a measure of the electron-donating power of a molecule, destabilized HOMO (less negative) leads to a greater ability to donate electrons. The capacity for electron donation of the five derivatives can be arranged as follows: ciprofibrate > bezafibrate > fenofibrate > clofibrate. On the other hand, the LUMO energy measures the electron-accepting ability of a molecule; more combined ability stabilizes LUMO (more negative). Therefore, the derivatives’ ability to accept electrons is as follows: fenofibrate eV)> bezafibrate eV)> clofibrate eV)> ciprofibrate eV). The energy gap (HOMO energy subtracted from LUMO energy) measures the chemical reactivity. A smaller gap is a more reactive molecule, and the reactivity of the four derivatives is: fenofibrate eV) < bezafibrate eV) < ciprofibrate eV) < clofibrate eV). Finally, the special distribution of HOMO and LUMO orbitals is another indictor of the position/region subjected to electrophilic and nucleophilic attack. The HOMO and LUMO orbitals in ciprofibrate are distributed on similar parts of a molecule, except that the two chlorine atoms have more HOMO character. Other molecules have HOMO orbitals delocalized over different regions compared to the LUMO orbitals distribution.
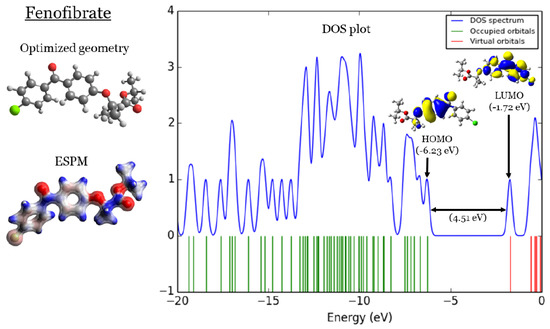
Figure 1.
Fenofibrate:(1) optimized geometries, (2) ESPM, (3) DOS plots, and (4) HOMOs and LUMOs.
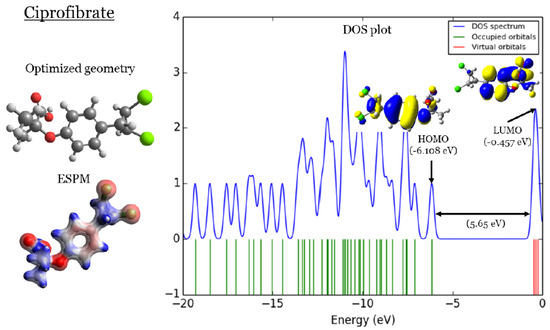
Figure 2.
Ciprofibrate: (1) optimized geometries, (2) ESPM, (3) DOS plots, and (4) HOMOs and LUMOs.
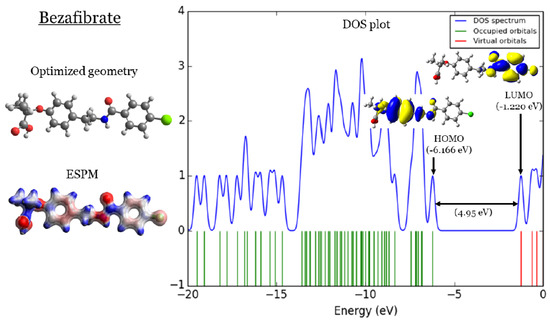
Figure 3.
Bezafibrate: (1) optimized geometries, (2) ESPM, (3) DOS plots, and (4) HOMOs and LUMOs.
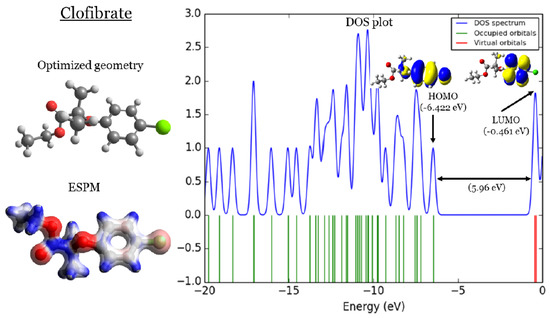
Figure 4.
Clofibrate: (1) optimized geometries, (2) ESPM, (3) DOS plots, and (4) HOMOs and LUMOs.
3. Materials and Method
In this section, the overall objective is to establish a QSPR relationship between the various topological indices and some physicochemical properties/activities of the fibrate drugs under study in order to assess the effectiveness of these drugs. Eleven degree-based and four distance topological indices were used for modeling antiviral activity, based on DMol3-optimized geometries for the fibrate drugs investigated. The Gauusin 09 software package was used to perform DFT calculations, which are as follows: polarizability , sum of electronic and zero-point energies , sum of electronic and thermal energies , sum of electronic and thermal enthalpies , sum of electronic and thermal free energies , zero-point vibrational energy , complexity , topological polar area , dipole moment , heat capacity , molar entropy , and octanol-water partition coefficients of several drugs currently being investigated for the treatment of high cholesterol, which include fenofibrate, ciprofibrate, bezafibrate, and clofibrate drugs. It is possible to use curvilinear regression analysis to fit curves instead of straight lines, and SPSS statistical software is used to analyze curvilinear regressions. As described below, the independent variables in the curvilinear regression models are topological indices. Indicators are derived from cholesterol-lowering drugs. Based on the equations below, tests were conducted.
In this context, y represents the response or dependent variable, while a denotes the regression model constant, and refers to the coefficients for each individual descriptor. The independent variable is represented by x, and n signifies the number of samples used in building the regression equation. denotes the coefficient of determination, R signifies the correlation coefficient, F represents the calculated value of the Fischer values test, denotes the standard error of estimate, and stands for significance. It should be noted that when the experimental and theoretical results are in close proximity to each other, the correlation coefficient approaches 1. To gauge the predictability of a model, it is necessary to compare the observed values and the model predictions, for which the root mean square error metric is used. The predictive quality of a model is higher when the error or is lower, which is calculated as follows:
where is the observed value of the independent variable in the test set, is the predicted value of the independent variables in the test set, n is the number of samples in the test, and topological indices serve as independent variables. To evaluate our initial model, we used the metric and then normalized the data to enhance our predictions’ accuracy. We measured the difference between predicted and actual values using the score, which revealed that our model needed improvement. To address issues such as outliers and varying scales of measurement that could negatively affect model performance, we applied normalization techniques to our data. The normalization step was essential in improving the model’s accuracy, as it scaled variables to a common range, reduced the impact of outliers, and ensured that all variables were weighted equally. After normalization, we re-evaluated the model using the metric, and the updated score showed a significant improvement in our predictions’ accuracy. Computed topological index values are shown in Table 2. We computed the values using combinatorial computations and edge partitioning as follows: the molecular graph of fenofibrate has 25 vertices and 26 edges. Its edges can be partitioned as and The molecular graph of ciprofibrate has 18 vertices and 19 edges. Its edges can be partitioned as and The molecular graph of bezafibrate has 25 vertices and 26 edges. Its edges can be partitioned as and The molecular graph of fenofibrate has 16 vertices and 16 edges. Its edges can be partitioned as and Using MATLAB, it is possible to efficiently compute degree-based and distance-based topological indices, as explained in Algorithms 1 and 2. To calculate the topological indices of molecules based on distance and degree, MATLAB utilizes various mathematical expressions. The fibrate family and the drugs under consideration, namely fenofibrate, ciprofibrate, bezafibrate, and clofibrate, have been studied and are presented in Table 3, including their experimental data [51] and optimized geometries obtained through DFT calculations using the DMol3 module of Version 8.0 of Material Studio from BIOVIA. Table 4 shows the correlation coefficient between degree-based topological indices and some physicochemical properties, computed using a linear regression model. A quadratic regression model is used in Table 5 to calculate the correlation coefficient between these indices and some physicochemical properties. The cubic model is employed for this purpose in Table 6. Similarly, for the distance-based topological indices, linear, quadratic, and cubic regression models are utilized, and the results are presented in Table 7. Once the correlation coefficient for a physicochemical property is obtained, the model with the maximum R becomes the most accurate predictor of the regression model. This is indicated in Table 8, Table 9, Table 10 and Table 11. By leveraging the power of MATLAB, it is possible to efficiently and accurately compute topological indices and use them to predict the physicochemical properties of molecules, which can be incredibly useful in various fields, including drug discovery and materials science.
| Algorithm 1: Computational procedure of calculation of degree-based indices. |
Input: Edges and nodes of molecule Output: Topological indices vector Step 1. Start Step 2. Graph of undirected edges Step 3. Adjacency matrix of G Step 4. Distances of G Step 5. Vertex degree of G Step 6. Calculate size of matrix d Step 4. Construct for to number of columns do for to number of rows do if then elseif then First Zagerb index Second Zagerb index Hyper-Zagerb index Atom-Bond Connectivity index Randic index min-max rodeg index max-min rodeg index Alberston index Sigma index Inverse symmetric deg index Inverse sum deg index end if end for end for Step 5. (summation of |

Table 2.
Values of topological indices in fibrates’ molecular structures.

Table 3.
The physicochemical properties of potential drugs of fibrates.

Table 4.
The correlation coefficient (R) obtained by linear regression model between topological indices and physicochemical properties of various drugs of fibrates.

Table 5.
The correlation coefficient (R) obtained by quadratic regression model between topological indices and physicochemical properties of various drugs of fibrates.

Table 6.
The correlation coefficient (R) obtained by cubic regression model between topological indices and physicochemical properties of various drugs of fibrates.

Table 7.
The curvilinear models, along with the linear, quadratic, and cubic regression models, were used to determine the correlation coefficient (R) between the physicochemical properties of various fibrate drugs and their distance topological indices.

Table 8.
Linear regression models that give the best estimate for physicochemical properties.

Table 9.
Quadratic regression model that give the best estimate for physicochemical properties.

Table 10.
Cubic regression models that give the best estimate for physicochemical.

Table 11.
The linear and quadratic regression models provide the most accurate predictions for the physicochemical properties.
| Algorithm 2: Computational procedure of calculation of distance-based indices. |
Input: Edges and nodes of molecule Output: Topological indices vector Step 1. Start Step 2. Graph of undirected edges Step 3. Adjacency matrix of G Step 4. Distances of G Step 5. Vertex degree of G Step 6. Calculate size of matrix d Step 4. Construct for to number of rows do for to number of columns do Wiener index Schultz index Harary index Gutman index end for end for Step 5. summation of |
Results and Discussion
Fibrate drugs are predicted by numerous topological indices. In QSPR, linear, quadratic, and cubic regression models are examined. Several topological indices are calculated for fibrate drugs, including the vertex degree, and distance between vertices. The models are analyzed using twelve descriptors and thirteen topological indices. Using a linear regression model, a correlation coefficient between these indices and some physicochemical properties can be seen in Table 4. In Table 5, using a quadratic regression model, a correlation coefficient between these indices and some physicochemical properties is computed. When a correlation coefficient is obtained for a physicochemical property, the model that has maximum R is the most accurate predictor of the regression model. In Table 4, we display for each physicochemical property, based upon the analysis of the data (linear and quadratic). We have excluded values less than from the Table 4 and Table 5, for convenience.
With linear regression models, the following Table 8 illustrates the most appropriate topological index for estimating physicochemical properties. A diagram depicting this is shown in Figure 5.
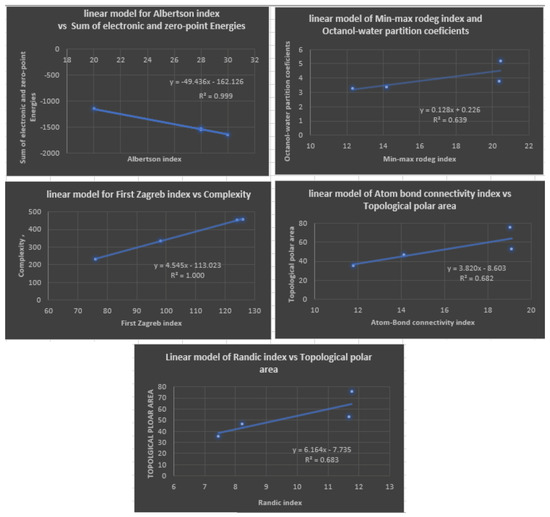
Figure 5.
Plots of Linear Regression Equations for the Best Physicochemical Properties Predicted by Degree-Based Topological Indices.
Table 9 illustrates the best topological index, which gives the best estimate for physicochemical properties using quadratic regression models; we only consider topological index with A diagram depicting this is shown in Figure 6.
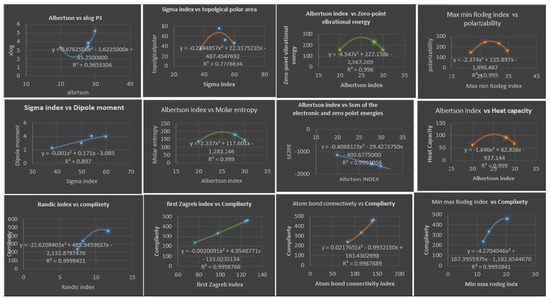
Figure 6.
Plots of QuadraticRegression Equations for the Best Physicochemical Properties Predicted by Degree-Based Topological Indices.
Remark 1.
Initially, linear regression was attempted on all physicochemical properties using degree-based topological indices. Correlation coefficients were calculated for 7 out of 12 properties that showed satisfactory results, as presented in Table 4. For the remaining properties with correlation coefficients less than 0.64, Table 5 explored alternative models. An additional 5 properties were tested, and if their correlation coefficients exceeded , the quadratic regression model was used. Note that some properties, such as the sum of the electronic and zero-point energies , sum of the electronic and thermal energies , sum of the electronic and thermal enthalpies , and sum of the electronic and thermal free energies have identical correlation coefficients, and only is listed in Table 8 and Table 9.
The cubic model is used for all the physicochemical properties and degree-based topological indices in order to provide a comprehensive analysis. Table 6 presents the correlation coefficients, which are high, as anticipated. Table 10 and Figure 7 display the best predictions of the properties.
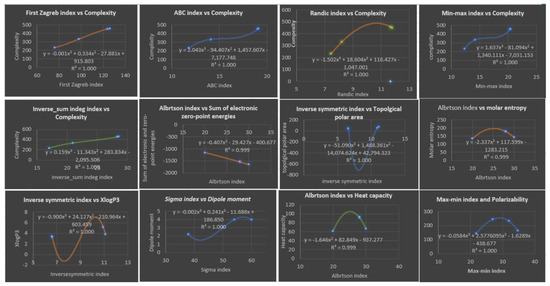
Figure 7.
Plots of Cubic Regression Equations for the Best Physicochemical Properties Predicted by Degree-Based Topological Indices.
Based on three curvilinear models, linear, quadratic, and cubic, the following Table 7, illustrates the correlation coefficient R for the four distance topological indices. The next table shows the most accurate prediction of the physicochemical properties based on linear or quadratic models. It should be noted that the physicochemical properties: sum of the electronic and zero-point energies , sum of the electronic and thermal energies , sum of the electronic and thermal enthalpies , and Sum of the electronic and thermal free energies have the same correlation coefficients, which is why the is the only one listed in Table 7. It is evident that the cubic model is the optimal model to predict all physicochemical properties of fibrates. Notice that we displayed the correlation coefficient in bold for the cubic model. Table 11 and Figure 8 illustrate the best linear and quadratic model of distance-based topological indices with the properties.
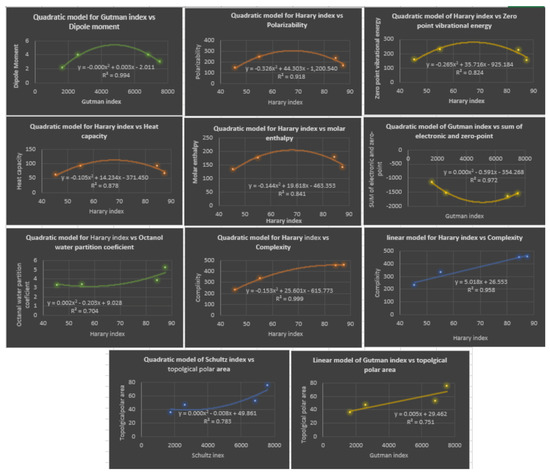
Figure 8.
Plots of Linear and Quadratic Regression Equations for the Best Physicochemical Properties Predicted by Distance-Based Topological Indices.
The physicochemical properties of fibrate drugs and their corresponding degree-based and distance-based topological indices were analyzed using three curvilinear models: linear, quadratic, and cubic. The aim was to determine the most accurate correlation coefficient for the properties studied.
Table 4 shows the correlation coefficients (R) obtained by a linear regression model between various topological indices and physicochemical properties of fibrate drugs. The topological indices include degree-based topological indices. The results show that the correlation coefficients vary across the different topological indices and physicochemical properties. A positive correlation indicates two variables that tend to move strongly in opposite directions, while a negative correlation indicates two variables that move strongly in opposite directions. In particular, for the first Zagreb index , the correlation coefficient lies between and 1, with the best prediction for complexity being 1. For the second Zagreb index , the range of the correlation coefficient is , which indicates a high prediction of all physicochemical properties under study. The highest correlation coefficient values were observed for the property with values ranging from to , followed by the index, with values ranging from to . The other topological indices showed weaker correlations with the physicochemical properties, with correlation coefficients ranging from to for the remaining indices. Table 8 provides a list of five linear regression models and their corresponding and values. , or the coefficient of determination, is a measure of how well the independent variables in a linear regression model explain the variation in the dependent variable. It ranges from 0 to 1, with 1 indicating a perfect fit. , or root mean squared error, is a measure of how well the regression model’s predictions match the actual values. It represents the average distance between the predicted and actual values, and lower values indicate better accuracy. All five models have relatively high values, indicating that they explain a significant amount of the variation in the dependent variable. The lowest value is , which is still considered a relatively good fit. However, the models have different levels of prediction accuracy, as measured by . The with min-max rodeg index model has the lowest value of , which suggests that it has the most accurate predictions among the five models. The C model with the first Zagreb index has the second lowest value of , followed by the model with an of . The index) and index) models have the highest values of and , respectively, indicating that their predictions are the least accurate among the five models. In summary, while all five models have relatively high values, indicating good fit to the data, the model is the most accurate based on its low value, followed by the C and models, and then the ( index) and (R index) models, which have the highest values.
Table 5 presents the correlation coefficients obtained by a quadratic regression model between the topological indices and physicochemical properties of various drugs of fibrate. Upon analyzing the data in Table 5, several noteworthy findings can be observed. Firstly, many of the correlation coefficients are relatively high, indicating a strong linear relationship between the topological indices and physicochemical properties of the fibrate drugs. For instance, has a high correlation coefficient of with , indicating a strong positive linear relationship between these two variables. Similarly, has a high correlation coefficient of with , suggesting a strong positive linear relationship between these variables as well. Furthermore, some of the correlation coefficients are close to 1, indicating a perfect positive linear relationship between the variables. For example, and indices have a correlation coefficient of with , suggesting a perfect positive linear relationship between these two variables. Similarly, index has a correlation coefficient of with ,, , and , indicating a perfect positive linear relationship between these variables. On the other hand, some correlation coefficients are relatively low, indicating a weak linear relationship between the variables. For instance, the index has a correlation coefficient less than 0.64 for most of the properties except for and , suggesting a weak positive linear relationship between these two variables. It is also interesting to note that we do not have any negative values which would indicating an inverse relationship between the variables. In addition, some of the correlation coefficients are moderate, suggesting a moderate linear relationship between the variables. For instance, has a correlation coefficient of , indicating a moderate positive linear relationship between these variables. Overall, the findings from Table 5 suggest that there are varying degrees of linear relationships between the topological indices and physicochemical properties of fibrate drugs. Some of the relationships are strong, while others are weak or moderate. Looking at Table 9, we see that all five models for the complexity property have high values, with the lowest being and the highest being . This suggests that all five models are good at explaining the variation in the physicochemical property they are modeling. The second thing to consider is the value; a lower value indicates that the model has a better fit. In this table, we can see that the values range from to . The model with the lowest value is the second model: for the Randic index. This indicates that this model has the best fit for estimating the physicochemical property. However, it is important to note that all five models have high values, suggesting that they all provide good estimates for the physicochemical property. After analyzing the table, we found that there are five quadratic regression models with both high values and low values. The quadratic regression model for S has a high value of and a low value of , making it one of the best models in terms of accurately predicting the target variable. The other models are for , , , and . The model for has an value of and an of , the model for has an value of and an of , the model for has an value of and an of , and the model for has an value of and an of . These models can be considered the best in terms of their ability to fit the data and accurately predict the target variable.
Table 6 presents the correlation coefficient obtained by cubic regression models between topological indices and physicochemical properties of various drugs of fibrates. Looking at the table, we can see that the range of correlation coefficients varies for each row. For instance, the correlation coefficient for the row of the first Zagreb index ranges from to , while for the row inverse symmetric deg index , the correlation coefficient ranges from to . Overall, most of the correlation coefficients are relatively high, with many of them being close to . This suggests a strong correlation between the topological indices and the physicochemical properties of the drugs of fibrates. The high correlation coefficients could indicate that the topological indices could be used to predict the physicochemical properties of the drugs with high accuracy. Based on Table 10, it appears that the cubic regression model provides the highest correlation coefficients for most of the topological indices and physicochemical properties of fibrate drugs. The range of correlation coefficients for each row varies, but in general, they are relatively high, indicating a strong relationship between the topological indices and physicochemical properties. Furthermore, the high correlation coefficients suggest that the cubic regression model is an effective tool for predicting physicochemical properties based on the topological indices of fibrate drugs. Overall, the results of the table suggest that the cubic regression model is the best choice for analyzing the relationship between topological indices and physicochemical properties in fibrate drugs. Based on Table 9, we can analyze the four topological indices with respect to high and minimum . (, ) indicating a strong correlation between the physicochemical properties and this index. Additionally, its value of is also very low, suggesting that the predicted values using this index are very close to the actual values. (, ) indicating a perfect correlation with the physicochemical properties.
By looking closely at Table 7, considering only the distance-based topological indices, we can notice that the model which gives the highest correlations with all the investigated physicochemical properties of fibrate drugs is the cubic model, since the correlation coefficients range from to . In second place is the quadratic model, since it gives good correlations with most of these properties, and the correlation coefficients range from to . While the linear model comes in the third place, it shows good correlation but with the least number of properties, and the correlation coefficients range to . An important note is that in most cases, the linear and quadratic models give comparable correlation coefficients, while there is a significant improvement in the correlation coefficients when the cubic model is used for most of properties. For instance, for the polarizability property estimated using the Wiener index, correlations are comparable, and for the linear and quadratic models, respectively, and it improves to 1 with the cubic model. As a result, we should consider our model type when dealing with such properties. Generally speaking, the four properties at the end of Table 7 are estimated very well with the three models compared to the first five properties in the table. The complexity property can be best estimated using the various models, since the correlations with each model reach ∼1. The topological polar area can be nominated as the second-best estimated property by the three models, followed by sum of electronic and zero-point energies property. Conversely, the zero-point vibrational energy and heat capacity properties seems to be the properties which can be estimated the least accurately using the two models (linear and quadratic), the correlations not exceeding . The exception is the quadratic model of the hyper-Zagreb index , and , respectively. Based on the values given in Table 11, the three best predictors with the lowest values are: linear regression with quadratic regression with and curvilinear regression with These three regression models exhibit the lowest values, indicating higher accuracy and better predictive performance compared to the other regression models. Therefore, these three regression models, namely, linear, quadratic, and curvilinear, can be considered as the best predictors for enhancing the analysis of fibrate drug activity through molecular descriptors in this study. Therefore, based on the results obtained, it can be concluded that the cubic and quadratic regression models are the top predictors for the physicochemical properties analyzed in this investigation, as they exhibit both high values and minimum values simultaneously. These findings highlight the effectiveness of these regression models in enhancing the analysis of fibrate drug activity through molecular descriptors and provide valuable insights for future research in this area.
4. Conclusions
Based on our comprehensive analysis, we have demonstrated that the use of curvilinear regression models can significantly enhance the analysis of fibrate drug activity through molecular descriptors. Our results have revealed that these models have superior predictive power compared to linear regression models, especially when the underlying data exhibit nonlinear relationships. Furthermore, the incorporation of molecular descriptors as independent variables has substantially improved the accuracy and robustness of the models. Our findings have several important implications for the field of drug discovery and development. Firstly, the use of curvilinear regression models, in conjunction with molecular descriptors, can facilitate the identification and optimization of more potent and selective drugs, thus reducing the time and cost associated with drug development. Secondly, our study underscores the importance of considering nonlinear relationships between molecular descriptors and drug activity, which has traditionally been overlooked in conventional linear regression analyses. Lastly, the efficacy of curvilinear regression models and molecular descriptors in predicting drug activity may be extended to other drug classes and further elucidated through future studies. In summary, our investigation demonstrates that curvilinear regression models represent a powerful approach for analyzing drug activity, particularly when coupled with molecular descriptors. Our results provide a basis for the development of improved drug discovery pipelines and offer insights into the molecular mechanisms governing drug activity. In summary:
- Despite the limited number of input molecules used in our study, we have taken great care to ensure the reliability and validity of our findings. We have rigorously tested our models using appropriate statistical methods and validated their predictive performance through external testing. Furthermore, we have provided a clear and transparent description of our methodology, including the selection and preparation of our data, the choice of input features, and the modeling approach. We believe that our manuscript reflects a well-designed and carefully executed study that contributes to the field of predictive modeling.
- While we acknowledge the limitation of our small dataset, we would like to emphasize that our study is not meant to provide a definitive model for predicting molecular properties. Rather, it aims to demonstrate the feasibility and potential of using DFT calculations and topological indices as input features for predictive modeling. Our results show promising predictive performance and highlight the importance of selecting appropriate input features and modeling approaches. Our study will inspire further investigations on larger datasets and lead to the development of more robust and accurate models.
- By evaluating three distinct models, we have provided a comprehensive and nuanced analysis of the relationship between molecular structure and properties. Our models include both linear and non-linear approaches, which allowed us to capture both linear and non-linear relationships between input features and output properties. This approach is particularly important in the field of predictive modeling, where complex relationships are often present. Moreover, by comparing and contrasting the performance of different models, we were able to identify the most effective approach for our specific research question. Our study demonstrates the importance of model selection and the need for careful evaluation of different modeling approaches.
Author Contributions
Conceptualization, S.W. and N.U.O.; methodology, S.W.; validation, S.W. and N.U.O.; formal analysis, S.W.; investigation, S.W.; resources, N.U.O.; data curation, N.U.O.; writing—original draft S.W.; preparation, S.W.; writing—review and editing, S.W. and N.U.O.; supervision, S.W.; project administration, S.W.; funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 214-247-1443). The authors gratefully acknowledge the technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Data Availability Statement
The article contains the data that supported the study’s findings.
Acknowledgments
This research work was funded by Institutional Fund Projects under grant no. (IFPIP: 214-247-1443). The authors gratefully acknowledge the technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia. The authors acknowledge Nuha Wazzan from the Chemistry department at King Abdulaziz University for her contribution with the DFT calculations, and King Abdulaziz University’s High-Performance Computing Centre (Aziz Supercomputer) (http://hpc.kau.edu.sa) for supporting the computation for the work described in this paper.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Gonzalez-Diaz, H.; Vilar, S.; Santana, L.; Uriarte, E. Medicinal chemistry and bioinformatics-current trends in drugs discovery with networks topological indices. Curr. Top. Med. Chem. 2007, 7, 1015–1029. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E.; Uriarte, E. Recent advances on the role of topological indices in drug discovery research. Curr. Med. Chem. 2001, 8, 1573–1588. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Wang, W.; Farahani, M.R. Topological indices study of molecular structure in anticancer drugs. J. Chem. 2016, 2016, 3216327. [Google Scholar] [CrossRef]
- Gao, W.; Farahani, M.R.; Shi, L. Forgotten topological index of some drug structures. Acta Medica Mediterr. 2016, 32, 579–585. [Google Scholar]
- McCullough, P.A.; Loreto, M.J.D. Fibrates and cardiorenal outcomes. J. Am. Coll. Cardiol. 2012, 60, 2072–2073. [Google Scholar] [CrossRef] [PubMed]
- Brea, A.; Millán, J.; Ascaso, J.F.; Blasco, M.; Díaz, A.; Hernxaxndez-Mijares, A.; Mantilla, T.; Pedro-Botet, J.C.; Pintó, X. Fibrates in primary prevention of cardiovascular disease. Comments on the results of a systematic review of the Cochrane Collaboration. Clínica Investigación Arterioscler. (Engl. Ed.) 2018, 30, 188–192. [Google Scholar] [CrossRef]
- Devillers, J.; Balaban, A.T. Topological Indices and Related Descriptors in QSAR and QSPAR; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Gutman, I. A Property of the Simple Topological Index. Match Commun. Math. Comput. Chem. 1990, 25, 131–140. [Google Scholar]
- Wiener, H. Structural Determination of Paraffin Boiling Points. J. Am. Chem. 1947, 69, 17–20. [Google Scholar] [CrossRef]
- Gao, W.; Wang, Y.; Basavanagoud, B.; Jamil, M.K. Characteristics Studies of Molecular Structures in Drugs. Saudi Pharm. J. 2017, 25, 580–586. [Google Scholar] [CrossRef]
- Doslic, T.; Reti, T.; Ali, A. On the Structure of Graphs with Integer Sombor Indices. Discret. Lett. 2021, 7, 1–4. [Google Scholar]
- Gutman, I. Geometric Approach to Degree-Based Topological Indices: Sombor Indices. Match Communications Math. Comput. Chem. 2021, 86, 11–16. [Google Scholar]
- Ediz, S.; Çiftçi, İ.; Cancan, M.; Farahani, M.R. On k-total distance degrees and k-total Wiener polarity index. J. Inf. Optim. Sci. 2021, 42, 1469–1477. [Google Scholar] [CrossRef]
- Matejić, M.; Zogić, E.; Milovanović, E.; Milovanović, I. A Note on the Laplacian Resolvent Energy of Graphs. Asian-Eur. J. Math. 2020, 13, 2050119. [Google Scholar] [CrossRef]
- Gutman, I.; Trinajst ıC, N. Graph Theory and Molecular Orbitals. Total p-Electron Energy of Alternant Hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar] [CrossRef]
- Randić, M. On Characterization of Molecular Branching. J. Am. Chem. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Estrada, E. Characterization of 3D Molecular Structure. Chem. Phys. Lett. 2000, 319, 713–718. [Google Scholar] [CrossRef]
- Hosoya, H. Topological Index. A Newly Proposed Quantity Characterizing the Topological Nature of Structural Isomers of Saturated Hydrocarbons. Bull. Chem. Soc. Jpn. 1971, 44, 2332–2339. [Google Scholar] [CrossRef]
- Estrada, E.; Bonchev, D. Chemical Graph Theory; Chapman and Hall/CRC: New York, NY, USA, 2013. [Google Scholar]
- Gutman, I.; Ruscic, B.; Trinajstic, N.; Wilson, C.F., Jr. Graph theory and molecular orbitals. XII. Acyclic polyenes. J. Chem. Phys. 1975, 62, 3399–3405. [Google Scholar] [CrossRef]
- Shirdel, G.H.; Rezapour, H.; Sayadi, A.M. The hyper Zagreb index of graph operations. Iran. J. Math. Chem. 2013, 4, 213–220. [Google Scholar]
- Togan, M.; Yurttas, A.; Cevik, A.S.; Cangul, I.N. Effect of edge deletion and addition on Zagreb indices of graphs. In Mathematical Methods in Engineering; Springer: Cham, Switzerland, 2019; pp. 191–201. [Google Scholar]
- Togan, M.; Yurttas, A.; Çevik, A.S.; Cangul, I.N. Zagreb indices and multiplicative Zagreb indices of double graphs of subdivision graphs. Twms J. Appl. Eng. Math. 2019, 9, 404–412. [Google Scholar]
- Gutman, I.; Togan, M.; Yurttas, A.; Cevik, A.S.; Cangul, I.N. Inverpe problem fsr sigma index. Match Commun. Math. Comput. Chem. 2018, 79, 491–508. [Google Scholar]
- Ghorbani, M.; Zangi, S.; Amraei, N. New results on symmetric division deg index. J. Appl. Math. Comput. 2021, 65, 161–176. [Google Scholar] [CrossRef]
- Richardson, C.W.; Foster, G.R.; Wright, D.A. Estimation of erosion index from daily rainfall amount. Trans. Asae 1983, 26, 153–156. [Google Scholar] [CrossRef]
- Das, K.C.; Gutman, I.; Furtula, B. On atom-bond connectivity index. Chem. Phys. Lett. 2011, 511, 452–454. [Google Scholar] [CrossRef]
- Dalfó, C. On the Randić index of graphs. Discret. Math. 2019, 342, 2792–2796. [Google Scholar] [CrossRef]
- Jahanbani, A. Albertson energy and Albertson Estrada index of graphs. J. Linear Topol. Algebra 2019, 8, 11–24. [Google Scholar]
- Klavžar, S.; Rajapakse, A.; Gutman, I. The Szeged and the Wiener index of graphs. Appl. Math. Lett. 1996, 9, 45–49. [Google Scholar] [CrossRef]
- Xu, K.; Das, K.C. On Harary index of graphs. Discret. Appl. Math. 2011, 159, 1631–1640. [Google Scholar] [CrossRef]
- Mukwembi, S. On the upper bound of Gutman index of graphs. Match-Commun. Math. Comput. Chem. 2012, 68, 343. [Google Scholar]
- Havare, O.Ç. Topological indices and QSPR modeling of some novel drugs used in the cancer treatment. Int. J. Quantum Chem. 2021, 121, e26813. [Google Scholar] [CrossRef]
- Vukicevic, D. Boad additime modeling 2. Mathematicpl properties mf max-mrn rodig index. Crica Chem. Actata 2010, 83, 261–273. [Google Scholar]
- Estrada, E.; Torres, L.; Rodrıguez, L.; Gutman, I. An atombond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem. 1998, 37, 849–855. [Google Scholar]
- Rajasekharaiah, G.V.; Murthy, U.P. Hyper-Zagreb indices of graphs and its applications. J. Algebra Comb. Discret. Struct. Appl. 2020, 8, 9–22. [Google Scholar] [CrossRef]
- Vukiccevi, D.; Gasparov, M. Bond additive modeling 1. Adriatic indices. Crica Chem. Actata 2010, 83, 243–260. [Google Scholar]
- Çolakŏglu Havare, Ö. Determination of some thermodynamic properties of monocarboxylic acids using multiple linear regression. Beu J. Sci. 2019, 8, 466–471. [Google Scholar] [CrossRef]
- Lokesha, V.; Shruti, R.; sinan Cevik, A. On certain topological indices of Nanostructures using Q(G) and R(G) operators. Commun. Fac. Sci. Univ. Ank. Ser. Math. Stat. 2018, 67, 178–187. [Google Scholar]
- Reti, T.; Sharafdini, R.; Drégelyi-Kiss, A.; Haghbin, H. Graph irregularity indices used as molecular descriptors in QSPR studies. Match Commun. Math. Comput. Chem. 2018, 79, 509–524. [Google Scholar]
- Wiener, H. Relation of the physical properties of the isomeric alkanes to molecular structure Surface tension, specific dispersion, and critical solution temperature in aniline. J. Phys. 2018, 52, 1082–1089. [Google Scholar] [CrossRef]
- Dobrynin, A.A.; Entringer, R.; Gutman, I. Wiener index of trees: Theory and applications. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
- Castro, E.A.; Tueros, M. QSPR Study of boiling points of alkyl alcohols via improved polynomial relationships. Philipp. J. Sci. 2001, 130, 111–118. [Google Scholar]
- Delen, S.; Khan, R.H.; Kamran, M.; Salamat, N.; Baig, A.Q.; Naci Cangul, I.; Pandit, M.K. Ve-Degree, Ev-Degree, and Degree-Based Topological Indices of Fenofibrate. J. Math. 2022, 2022, 4477808. [Google Scholar] [CrossRef]
- Berinde, Z.M. QSPR Models for the Molar Refraction, Polarizability and Refractive Index of Aliphatic Carboxylic Acids Using the ZEP Topological Index. Symmetry 2021, 13, 2359. [Google Scholar] [CrossRef]
- Zuo, J.; Hu, L. QSPR modeling of the melting points of organic compounds using molecular topology and quantum chemical descriptors. Symmetry 2020, 12, 1104. [Google Scholar]
- Zhang, Y.; Li, H.; Liu, Y.; Zhou, P. QSPR models for predicting melting points of organic compounds based on molecular topology. Symmetry 2019, 11, 25. [Google Scholar] [CrossRef]
- Naghipour, S.; Kiasat, A.R. Application of topological indices in QSPR modeling of C60 derivatives’ fullerene-like behavior. Symmetry 2019, 11, 368. [Google Scholar]
- Wang, J.; Xu, L. QSPR models for predicting the boiling points of alkyl alkanes based on the novel vertex degree valence topological index. Symmetry 2018, 10, 282. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J. Gaussian 09 Programmer’s Reference; Gaussian: Wallingford, CT, USA, 2009; 25p. [Google Scholar]
- Dennington, R.; Keith, T.; Millam, J. GaussView Version 5; Semichem Inc.: Shawnee Mission, KS, USA, 2009. [Google Scholar]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminformatics 2008, 4, 17. [Google Scholar] [CrossRef]
- O’boyle, N.M.; Tenderholt, A.L.; Langner, K.M. Cclib: A library for package-independent computational chemistry algorithms. J. Comput. Chem. 2008, 29, 839–845. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).