Abstract
Numerical and physical simulations of the magnetohydrodynamic mixed convective flow of electrically conducting fluid along avertical magnetized and symmetrically heated plate with slip velocity and thermal slip effects have been performed. The novelty of the present work is to evaluate heat transfer and magnetic flux along the symmetrically magnetized plate with thermal and velocity slip effects. For a smooth algorithm and integration, the linked partial differential equations of the existing fluid flow system are converted into coupled nonlinear ordinary differential equations with specified streaming features and similarity components. By employing the Keller Box strategy, the modified ordinary differential equations (ODEs) are again translated in a suitable format for numerical results. The MATLAB software is used to compute the numerical results, which are then displayed in graphical and tabular form. The influence of several governing parameters on velocity, temperature distribution and magnetic fields in addition to the friction quantity, magnetic flux and heat transfer quantity has been explored. Computational evaluation is performed along the symmetrically heated plate to evaluate the velocity, magnetic field, and temperature together with their gradients. The selection of the magnetic force element, the buoyancy factor , and the Prandtl parameter range were used to set the impacts of magnetic energy and diffusion, respectively. In the domains of magnetic resonance imaging (MRI), artificial heart wolves, interior heart cavities, and nanoburning systems, the present thermodynamic and magnetohydrodynamic issuesare significant.
1. Introduction and Literature Review
The effects of thermal slip and velocity slip on the mixed convective flow of electrically conducting fluid along the magnetized and symmetrically heated surface are the main focus of the present research. The most crucial symmetry for boundary layers is the one that results from wall-normal and stream-wise transformations of the leading edge. The magnetization that arises from the wall-normal and stream-wise modifications of the top edge, respectively, is especially significant for flow separation. The slip-flow process is the movement of fluid molecules without their interacting with the surface of a plate. It is generally known that the no-slip condition, a crucial characteristic for viscous fluid at a solid barrier, causes the velocity of the fluid to match the velocity of the solid boundary. However, there are some situations where the no-slip requirement is broken. This is a fundamentally intriguing subject in fluid mechanics, but there are still gaps in our knowledge and the experimental work does not fully address it. Modern technology uses fluid with slip-boundary for a variety of things, including polishing prosthetic heart valves and interior heart cavities. Due to its potential use in diverse manufacturing and technical industries, mixed convection flow in a vertical plate has been the subject of many previous studies. These include gas-cooled nuclear reactors, the heating of the Trombe wall system, and the cooling of electrical devices.
Prosthetic heart valves, inner heart cavities, nanoburning systems, geothermal reservoirs, drying of porous materials, heat resistance, improved extraction of oil, packed-bed catalyzed reactors, cooling of nuclear reactors, and basement energy transit are just a few engineering and geophysical applications of simultaneous heat transfer from various shapes with consequences for velocity slip and thermal slip. Convection and thermal forced flow across vertical surfaces are beneficial for geothermal energy, industrial purposes, mechanical, civil, and chemical engineering. The flow of helium in pebble-bed nuclear reactors, the subsurface removal of nuclear or nonnuclear waste, the preparation and food preservation, the filtration of crude oil, the flow in glaucoma patients’ eyes, and the flow via filter materials are additional significant examples of fluid flows in the induced magnetic field. The effects of the Lorentz force conferresistance on the liquid flow because a fluid’s viscosity differs from that of a magnetic field. In addition, the current problems have substantial implications for polymer industries, such as paper manufacturing, glass-fiber processing, liquid crystal densification, petroleum refining, fabrication of strange lubricants, suspension treatments, wire drawing, consistent cooling, fabric spinning, plastic film production, thermoplastic cover extraction, fault zones, petroleum resource restoration, catalyzed reactors, and the manufacture of electronic machines.
In the areas of metallurgy, polymerization, and nuclear technology, the current magnetic flux and thermal efficiency issue of mixed convective flow over a magnetic surface is significant for both research and practical use. In a variety of applications, including nuclear energy, geophysics, astronomy, and liquid metals, the magnetohydrodynamic and mixed convection processes are fundamentally important for engineers. The magnetohydrodynamic may additionally be utilized externally in a variety of circumstances to improve or enhance heat transport. Magnetohydrodynamics, which was invented by Maxwell for electromagnetism, is the dynamic study of electromagnetic fluid. As a result, in this branch of study, consolidation of the findings has taken precedence. The analysis of recent advances in the field of heat transfer in the presence of a magnetic field and the provision of a concise assessment of the situation are the study’s secondary goals. This is the basic notion underlying an electrically conducting fluid.
The analysis of the dynamics and magnetic characteristics of fluids with electrical conductivity is known as magnetohydrodynamics or hydromagnetics. These magnetic liquids include liquid materials, plasmas, electrolytes, and seawater, for instance. Hannes Alfven received the Nobel Prize in Physics in 1970 for his ground-breaking study of magnetohydrodynamics. In physics, astronomy, solar physics, space plasma physics, blood-pumping devices, cancer tumor therapy, and laboratory plasma investigations, magnetohydrodynamic is used extensively. Revnic et al. [1] addressed the mixed flow of convection towards an axially symmetric stagnation point on a circular channel numerically. They also analyzed the type of approach in the situation of the massive Prandtl number asymptotic limit. Chamkha [2] has quantitatively determined the general methodological issue by taking into account the consequences of viscous dissipation and heat flux. He accomplished this by using the implicitly finite-difference methodology. They summarized their findings for crucial characteristics including temperature. Using a control volume approach and the SIMPLE algorithm, free convective slipping rates inside an open-ended vertically plate with asymmetric and symmetric surface temperatures have been computationally explored in [3]. Due to the prevalence of frictional dissipation, the central pressure drops in the channel’s early portion. Zaidi [4] completed quantitative research on the MHD flow of theinviscid electrically charged fluid inside a vertical stream over asymmetric and symmetric wall heat regimes. They observed that as heat generation raises, the intensity of the process of heat transport on the isoflux flow path declines. By taking into account symmetrical heat along the adiabatic and heating surfaces, Habchi and Acharya [5] carried out a computational assessment on convective heat transport of air inside a vertical channel. They foundthat the axial velocity reveals a concavity around the axis inside the symmetrical heat situation and rises close towards the hot surfaces.
It is advantageous to utilize the combined effects of magnetohydrodynamics and heat sources to produce a final product with attractive characteristics. Such factors are crucial, particularly in the metallurgical processes that include the purifying of metallic materials from nonmetallic impurities and the cooling of consecutive strips and filaments dragged through a quiescent fluid. Due to its important impact in numerous fields, especially the mechanical, geomagnetic, and pesticide sciences, the research of heat transport in porous materials has recently attracted the attention of many scientists using vertical geometries by [6]. They found that a higher local Nusselt number increases the impact of viscous parameters over the surface. Singh and Makinde [7] depicted the presence of free stream over a free forced convective slip flow with heat transport along a rotating plate. They found that for higher slip effects and rates of heat transfer, the density of the thermal boundary decreases. Ashraf et al. [8] illustrated the analysis of mass-transfer with convective conditions over a free forced radiating flow of a three-dimensional nanoliquid across an inclined elastic sheet. They found that results of the local Nusselt number and local Sherwood number show an inverse relation. Raju et al. [9] studied nonlinear convection flow, which is not stable over a moving vertical geometry for non-Newtonian fluid passing in a magnetohydrodynamics sequence. They found that flow characteristics profiles as well as skin friction coefficients decrease as nonlinear temperature and concentration flow parameters increase. Mukhopadhyay and Mandal [10] illustrated free forced convective slip flows and thermal expansion over a vertical surface using boundary layer flow. They observed that as the suction parameter is increased, the surface temperature falls. The researchers [11,12] analyzed the comparable results by reducing magnetic force and thermal slip effects for various values of the magnetic Prandtl number in the presence of aligned magnetic impact past the vertical surface.
The use of the MHD concept is a necessary process for changing the structure of the flow separation in order to influence the flow pattern in the desired direction. Many artificial approaches have been specifically designed to regulate the behavior of flow separation. The usage of fluids with electrical conductivity in a variety of industrial settings under the influence of electromagnetic fields has sparked a resurgencein research into hydromagnetic flow and heat transfer in numerous geometries. Maneengam et al. [13] performed convective heat transport issue in a lid-driven shape filled with nanoliquid with a heating source. They observed that shear stress drops as the temperature increases, but it rises as the slip velocity rises. Atashafrooz and Nassab [14] represented laminar free forced convection recess flow including a heat transfer system. They found that increasing the values of radiation-conduction parameters have a greater positive impact than the total local Nusselt number along the walls of the heated ducts. Haq et al. [15] has carried out statistical predictions for the thermos-migration nanoliquid susceptible to radiant heat and porous materials. Hayat et al. [16] studied nonlinear free forced convective Darcy forchheimer flow by using an optimal homotopic analysis method. They observed that the lower thermal diffusivity is associated with a greater Prandtl number, which reduces the fluid temperature.
Due to its industrial uses and significant implications for advanced technical procedures, the analysis of hydrodynamic flow and the transfer of heat through extending spheres or flat plates have attracted a lot of attention. For the efficient working of pumps, turbines, and bearings, this assessment of MHD fluids became essential. Armaghani et al. [17] analyzed entropy transmission in free forced convection by using MHD effects in an open C-shaped hole. The findings reveal that a higher Hartmann number leads to increased entropy generation while increasing the aspect ratio of the cavity, promotingthe movement of heat. Khan et al. [18] illustrated thin revolutionary objects having free forced thermal conduction in porous material with generalized mixed small particles. They found that the velocity field of the type of nanofluid and flow over the various shape bodies is reduced. Saleem and Nadeem [19] numerically studied slip flows on a moving geometric figure with heat transfer impacts. They found that the fluid temperature graph is an increasing component of the Eckert number. The use of liquid is made more efficient by technologies with jet flow, which also improves the quantities of both heat and mass transmission by [20].For contributing grey substances in 2-D/3-D complicated geometric enclosures with constraints, a finite-volume radiated structure was developed in [21]. They noticed that with increased free forced convection, the momentum and the temperature increase. Uddin et al. [22] developed nonlinear absorption and numerical modeling of MHD convection nanofluid flow in porous material. They observedthat the heat flux is reduced by increasing slip effects.
The majority of the research previously listed resumed their discussions under the assumption of no slip boundary conditions. Under particular circumstances, a phenomenon known as velocity slip—the fluid’s non-adherence to a solid boundary—has been observed. Moreover, the macroscopic wall slip that is frequently seen in polymer materials is typically controlled by a non-linear and monotonic connection between slip velocity and traction. Das et al. [23] elaborated free forced convection slip flows involving variable viscosity and heat transfer MHD across an inclined vertical plate. They have seen that when the velocity ratio is increased, the velocity profile decreases. Jamil and Ahmed [24] analyzed the motions of fractionalized mixed convective elastic fluid by using two different slip flow effects. They found that the temperature gradients at the surface are proportional to the average velocity profile. Liu and Guo [25] further investigatedthe influence of slip with second order on a partial mixed convection flows. They noticed that when the slip factors are non-zero, the velocities and shear forces are decreased. In the context of slip velocity, stratification, and separable gravity, the oscillating hydro-magnetic procedure across the non-magnetized material has been depicted in [26,27,28,29]. In order to investigate the dynamics of the MHD convective hybrid nanofluid and nanofluid flow between the two spinning and shrinking discs with radiative heating and the magnetization, the heat transport procedure was carried out in [30]. By employing wavelets, Kumar and Murthy [31] modified the finite-difference approach to solve the equations illustrating the heat transport process in a heated regenerator. For the purpose of industrial optimization in thermal systems using air-water as the working fluid, Kumar [32] evaluated rotational packed beds (RPBs).The consequences of magnetization characteristics and flow slipping on convective heat transmission along non-magnetized configuration were evaluated by Ullah et al. [33]. The entropy generating mechanism was implemented by Kan et al. [34] for the imaging and qualitative examination of significant energy loss sections in order to explore the modification of heat losses throughout the transition phase of a bidirectional axial-flow pump. Using computational modeling, Kan et al. [35] used the entropy generating strategy to evaluate the impact of TLF on the PAT’s thermal performance. The consequences of chemical processes and numerous slip conditions on the computation of multiple inviscid hydromagnetic nanofluid through a stretchy cylinder containing microorganisms have been covered in [36]. Ullah et al. [37] have addressed the thermal study of heat transfer of viscous flow field with temperature slip and heat radiating effects along the vertically symmetrical plane surface immersed inside a permeable medium. Ali [38] reported on the Cattaneo–Christov characteristics and self-motivated bio-convective microorganisms submerged in the water-based nanofluid with excision/accretion of the leading edge. The importance of a nanoparticle’s radius was evaluated in [39] for the hydro-magnetic micropolar and tangential hyperbolic movement for water-based nanofluid above a stretched sheet. Rahman et al. [40] has implemented a quantitative two-phase flow framework that investigates the connection of Casson nanofluid and dust particles on a stretching sheet by employing MHD Darcy-Forchheimer and Fourier’s law via Cattaneo-Christov heating flux. The researcher [41] evaluated the fluid motion movements toward a vertically stretchy layer near the static pressure of an incompressible fluid involving vacuum, injector, and entropy generation influences. Tlili [42] conducted a study of the hydrodynamic g-Jitter-free convective boundary layer flow across an angled stretchy surface. Ullah et al. [43] used the similarity transformation for electrical conducting fluid along the vertical surface. Kumar et al. [44] evaluated the characteristics of heat and mass rate of Casson nanofluid through accelerating surface numerically.
The novelty of this research is to discuss the computational assessment of two-dimensional hydro-magnetic flow of electrically conducting fluid through heated plate in presence of thermal slip and velocity slip. The analytical expressions have been made simpler via scaling factor, and the simplified boundary value equations have been numerically solved using the Keller box methodology. The global matrix of mathematical equations is constructed using the Keller Box methodology (KBM), with adequate assumptions provided by the Newton–Raphson technique (NRT) and the finite difference procedure (FDP). The KBM has been implemented to tackle numerous nonlinear issues in science and technology since it requires no auxiliary element and quickly transforms approximations to optimum solution. The recent research is novel because it evaluates magnetic properties of the electrically charged flow along the heating vertical plate. To evaluate friction factor, heat transmission, and magnetic flux, the approximate solutions for the stable component are evaluated. Due to the magnetic fluid’s surface in the current assignment, which insulates heat during mechanism and eliminates excessive energy, the fluid becomes electrically conductive. The outcomes are outstanding and precise since they satisfy the boundary requirements that were specified.
2. The Flow Geometry and Mathematical Formulation
Computational algorithms for slip boundary assessments of the convective flow rate of heat through heated and magnetic shapes are the primary topic of the article. Using stream-function patterns, the basic problem will be reduced into a sequence of partial differential conditions, which will subsequently be changed into ordinary ones. The FDM approach will be coupled with the Keller Box procedure to address the present issue. The computational results for the physical characteristics under discussion will be provided in mathematical and qualitative order.
The terminologies and denotemagnetic and fluid velocity vectors, respectively, in the and directions in Figure 1, in which and are parallel and normal to the vertical plate. This is done by considering electrically conducting fluid that is steady and inviscidin two components. The thermal diffusivity of the fluids is denoted by , represents the magnetic intensity, the temperature is denoted by , the free stream temperature is denoted by , represents the heat capacity, and refer to the magnetization at the surface. The density of the fluid is denoted by , the magnetic moment is represented by , the kinetic viscosity of the fluid is denoted by , the volumetric temperature coefficient is represented , and the gravitational acceleration is denoted by . These are examples of how inclined electromagnetic field, heat, momentum, and continuity are expressed mathematically by the following [11,12]:
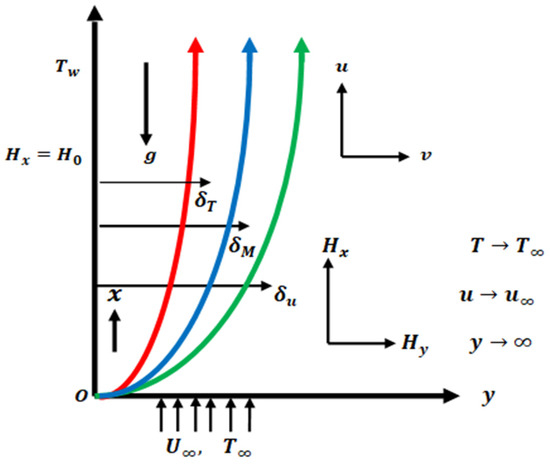
Figure 1.
Coordinate system and flow geometry.
The boundary conditions of the present model are,
The above-described boundary conditions pertain to magnetic, velocity and temperature conditions with the temperature-slip factor and the velocity components with the slip velocity. With being the initial value of velocity having some dimension of length, being the local Reynolds number , and being the free steam velocity, is the velocity slip factor, is the surface temperature and the constant temperature is denoted by across the electromagnetic vertical plate.
3. Stream Functions and Similarity Variables
To reduce partial differential formulas into ordinary differential equations, the essential non-dimensional similarities and streaming feature are provided by [43,44]:
By considering above similarities, Equations (1)–(6) are reduced into an ordinary differential format,
where the values of the parameters are Pr , , , , , , , , . Equation (6) in the form of ODEs is:
The slope of velocity is , slope of temperature is , and slope of the magnetic field is , where, , , and are defined as:
The formulas of skin friction, Nusselt number and magnetic flux are provided as,
4. Numerical Technique and Simulation
Using an adequate stream function approach, the associated mathematically dynamic PDEs system is changed into a similar ODEs framework having similarity elements. Equations (9)–(11) use the progressive Keller Box procedure to solve a related associated ODE system with provided boundary conditions (12). By employing expression (13), the newly established elements are provided by and ,
The above transformations in (13) are again reduced in the following manner,
The converted boundary conditions are:
Now consider the midpoint values with segment , with by using Equation (23):
The calculation in (24) modifies the aforementioned Formulas (14)–(22) using the averaged and central difference expressions,
and
along with boundary conditions
Furthermore, using the smoothing approach evaluated below along with the sequential Newton–Raphson procedure, the following expressions are obtained:
Calculations (25)–(29) are greatly simplified by the Newton–Raphson method by removing all repetitions of power higher than the initial power,
Again using Equations (35)–(39) in Equations (30)–(33), the equations in their condensed form are given below,
5. Matrix Form of Vector Equations
The above-mentioned difference coefficients’ matrix-based format is an essential subsequent stage. Improper implementation results in either zero outputs because of an individual matrix having zero Eigen-value, sub-matrix or extremely poor execution since the matrix has no observable pattern. Vector coefficients are expressed in matrix format as follows:
6. The Results and Discussions
The main focus of this research is to discuss the computational assessment of the two-dimensional hydro-magnetic flow of electrically conducting fluid through a heated plate in presence of thermal slip and velocity slip. The analytical expressions have been simplified via a scaling factor, and the simplified boundary value equations have been numerically solved using the Keller box methodology. The global matrix of mathematical equations is constructed using the Keller Box methodology (KBM), with adequate assumptions provided by the Newton–Raphson technique (NRT) and the finite difference procedure (FDP).The KBM has been implemented to tackle numerous nonlinear issues in science and technology since it does not require an auxiliary element and quickly transforms approximations into the optimal solution. The recent research is novel because it evaluates magnetic properties of the electrically charged flow along the heating vertical plate. To evaluate friction factor, heat transmission, and magnetic flux, the approximate solutions for the stable component are evaluated. The outcomes are outstanding and precise since they satisfy the boundary requirements that were specified. The impact of physical parameters such as the Prandtl factor Pr, temperature slip , velocity slip , buoyancy number , magnetic/force number , and magneto Prandtl element are evaluated scientifically.
The significance of the Prandtl number is shown in Figure 2a–c for distinct values of Pr = 0.1, 0.71, 3.0, and 7.0 along the heated and magnetized plate. By maintaining some constant variables, the fluid temperature, magnetic field, and velocity are acquired in order to examine the behavior of physical attributes. In Figure 2a, it is shown that the velocity improves when Pr is less than 0.1, but falls when Pr is more than 7.0. It should be observed that the desirable variations are obtained at each Pr value and then approach the specified boundary condition asymptotically. The electromagnetic effects in the fluid in Figure 2b are at their peak at a smaller Pr = 0.1, while minor quantities are seen at larger Pr = 7.0. The fluid’s magnetic profile showed good changes at each Pr value. The temperature distribution is maximal for a small value of Pr = 0.1, but is investigated at a bigger Pr =7.0 in a noticeable way, according to Figure 2c. The presence of = 1.6 causes the temperature changes to be very noticeable along with noticeable slip effects. The above reaction was anticipated since a rise in Pr is associated with higher temperature-dependent density variation, which enhances the buoyant force. When Pr grows, the thickness of the thermodynamic boundary layer diminishes. At each amount of Pr, the temperature plot demonstrates significant temperature slip with significant variance. The velocity field, magnetic plot, and temperature distribution for different quantities of = 0.1, 0.7, 1.5, and 2.5 along the surface of heated and magnetically chargedsurfacesare shown in Figure 3a–c.
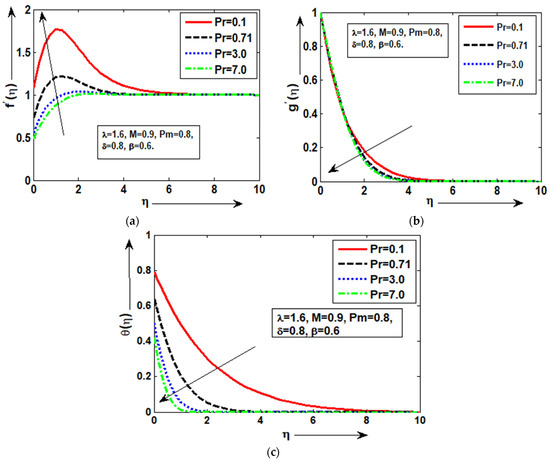
Figure 2.
(a–c): Physical sequence of temperature , magnetic/field for Pr.
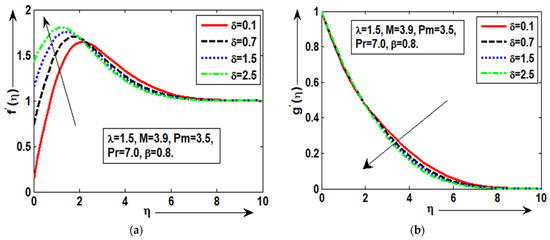
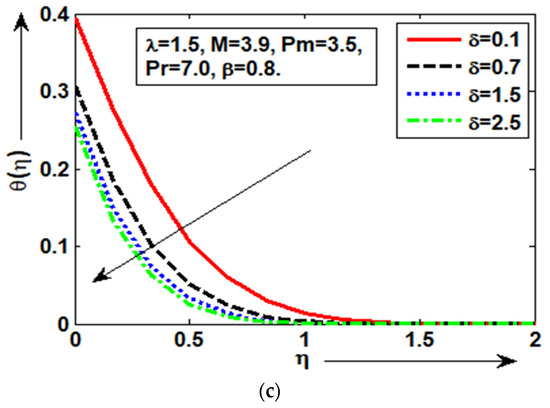
Figure 3.
(a–c): Physical sequence of temperature , magnetic/field for .
The velocity graph in Figure 3a reaches its highest value at a large value of = 2.5 and its minimum value at a small value of = 0.1 with noticeable slip, and it then approaches its supplied condition asymptotically. With good variations, it can be shown in Figure 3b that the magnetic profile improves at small values of = 0.1 and is minimal at large values of = 2.5. Figure 3c shows that, with better thermal slip, the temperature profile improves at lower values of = 0.1 but declines at higher values of = 2.5. The solutions are significantly affected by the magnetic parameter. It is evident that magnetization increases fluid restriction, restricting the fluid’s movement. The magnetization actually works against the transport processes. This happens due to the impact of the electromagnetic field’s Lorentz force, which grows with rising Pm and creates additional restriction of the transport mechanisms. In Figure 4a, when = 1.7, = 3.5, and = 1.3 are present along a polarized and heatingsurface, the highest velocity slip is obtained at bigger Pm = 3.5, and the minimum velocity slip is obtained at reduced Pm = 0.5. For each value of Pm, the magnetic plot in Figure 4b shows the major changes. Figure 4c shows the temperature response for each Pm to be similar. The velocity graph shows a good slip phenomenon that is both excellent and favorable. At each value of Pm, the flow velocity graph shows good changes, which then asymptotically approach the specified boundary condition. The viscosity of the fluid increases and the fluid thickens more as the electromagnetic Prandtl number grows; as a result, the thickness of the boundary layer diminishes. The electromagnetic Prandtl value, which measures the ratio of magnetic to kinetic energy, reveals that this conclusion was anticipated. The magnetic energy is thus enhanced while the kinetic energy is decreased by reducing the electromagnetic Prandtl value Pm.
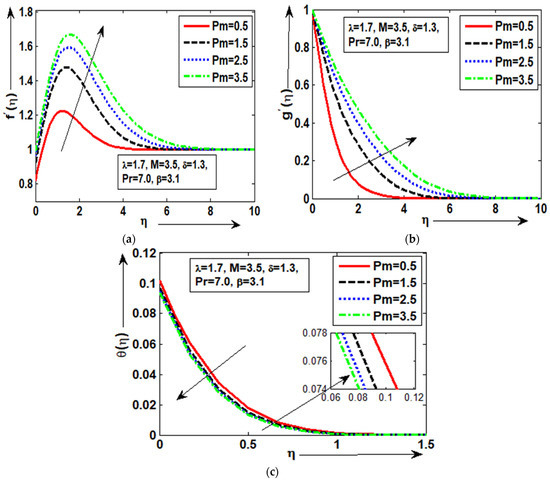
Figure 4.
(a–c): Physical sequence of temperature , magnetic/field for Pm.
Figure 5a–c illustrates the impact of the thermal slip parameter along a magnetically vertical surface at distinct values of = 0.1, 0.7, 1.5, and 2.5. In Figure 5a, it can be observed that velocity increases at lesser concentrations of a = 0.1 while it declines at higher quantities of a = 0.7. Additionally, it needs to be highlighted that in the presence of thermal slip, the velocity profile exhibits good slip effects along the vertical surface. In Figure 5b, the magneto profile rises when the thermal slip parameter is reduced ( = 0.1), but when it is larger ( = 0.7), a lower magnetic profile is achieved by maintaining some other factors constant ( = 7.3, = 5.1, and = 0.5). The above outcome was anticipated since an enhancement in magnetic force enhances the Lorentz forces that resist flow patterns and slow down fluid motion. At any value of the thermal-slip number, the same outcome is achieved. According to Figure 5c, the thermal-slip effects on fluid temperature are at their peak when the quantity is smaller than = 0.1 and smaller than = 0.7. Additionally, it should be highlighted that the presented phenomena yield a temperature distribution with outstanding thermal slip that asymptotically achieves the specified boundary conditions. It was expected because magneto diffusion, which is essential for the aforementioned processes, is diminished by increasing magnetic-Prandtl quantity. For the magnetic surface, Figure 6a–c show a comparison of the various values of the mixed convection parameter = 0.5, 1.0, 1.5, and 2.5.
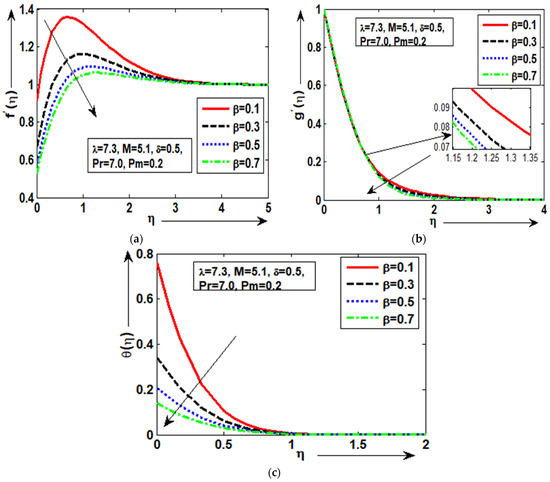
Figure 5.
(a–c): Physical sequence of temperature , magnetic/field for .
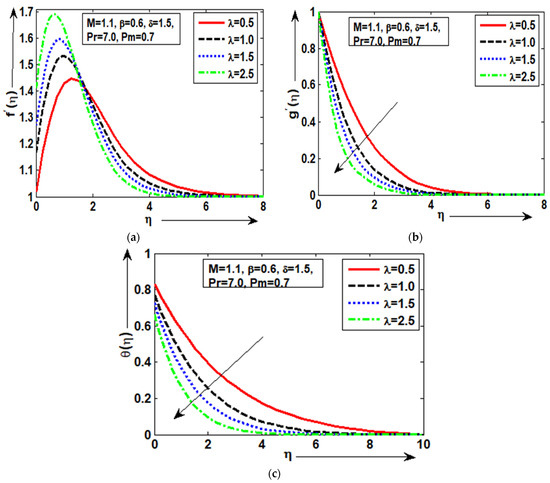
Figure 6.
(a–c): Physical sequence of temperature , magnetic/field for .
As seen in Figure 6a, the velocity is at its highest with a fair slip response at a mixed convection parameter value of = 2.5, but the quantity of is at its lowest at = 0.5. Additionally, it should be mentioned that the profile exhibits good behavior for surfaces of geometrical shape when mixed convection is present. The magnetic field profile in Figure 6b demonstrated good variances for each value of along the electromagnetic geometry and asymptotically achieves the specified boundary conditions. The Prandtl number indicates the connection between thermal and momentum diffusivity. Heat will escape from the surface more quickly from fluids with smaller Prandtl coefficients due to their greater thermal conductivity. By leaving the remaining parameters = 1.1, = 0.6, and = 1.5 in constant form, it can be determined from Figure 6c that the surface temperature along the field of the provided shape is maximal at the minimal value of = 0.5 and minimum at the larger value of = 2.5. At each value of, the temperature graph shows a good variety. Physically, it was anticipated since bigger values of related to higher forced convection, which improves the fluid flow’s acceleration. The magnetic effects are significantly detected exactly at the surface because of conducting processes, but they are zero for all values below the surface.
According to Table 1, under the impact of the buoyancy factor = 1.5, skin friction is increased for a small of 0.1 and concluded to be at its lowest for a larger of 2.5. With buoyancy component = 1.5, the heat rate is increased for a bigger of 2.0, and the minimal heat transfer is calculated for a smaller of 0.1.The lower = 0.1 has the highest magnetic energy, and the larger = 2.5 with a buoyancy factor of = 1.5 has the lowest magnetic energy. For physical features of and through the magnetic field including variables = 1.7, = 3.5, and = 1.3, Table 2 is given for the impact of factor with some selections = 0.5, 1.5, 2.0, and 3.5. For a maximal = 3.5, the friction is improved, and for minimal = 0.5, the skin-friction lowest value is evaluated. It is reported that raising the to 3.5 improves the heat and reducing the to 0.5 diminishes it. As can be observed, for a smaller value of = 0.5, the magnetic flux is boosted, whereas for a larger significance of = 3.5, the decreasing trend of magnetic flux is evaluated. In the presence of induced magnetic contact across the vertical surface, Table 3 evaluates skin friction as per the works of Mehmood et al. [11] and Ilyas et al. [12] for three characteristics of the magneto Prandtl number Pm = 1, 10, and 100. It is inferred that thermal slip consequences for every Pm are responsible for the substantial skin friction. Moreover, the present skin friction outcomes are consistent with the earlier findings.

Table 1.
The numerical outcomes of skin friction magneticflux and heat transfer with some choices of .

Table 2.
The numerical outcomes of skin friction magneticflux and heat transfer with some choices of .

Table 3.
The numerical outcomes of skin friction various choices of for at the leading edge.
7. Conclusions
The current work presents the computational assessment of two-dimensional hydro-magnetic flow of electrically conductive fluid through heated plate in presence of thermal slip and velocity slip. The analytical expressions have been made simpler via a scaling factor, and the simplified boundary value equations have been numerically solved using the Keller box methodology. The global matrix of mathematical equations is constructed using the Keller Box methodology (KBM), with adequate assumptions provided by the Newton–Raphson technique (NRT) and the finite difference procedure (FDP). The KBM has been implemented to tackle numerous nonlinear issues in science and technology since it does not require an auxiliary element and quickly transforms approximations to the optimal solution. The recent research is novel because it evaluates magnetic properties of the electrically charged flow along the vertical heating plate. To evaluate the friction factor, heat transmission, and magnetic flux, the approximate solutions for the stable component are evaluated. The outcomes are outstanding and precise since they satisfy the boundary requirements that were specified. The impact of physical parameters such as the Prandtl factor Pr, temperature slip , velocity slip , buoyancy number , magnetic/force number , and magneto Prandtl element Pm are evaluated scientifically. The main findings are provided as:
- At each level of Pr, the temperature plot demonstrates significant temperature slip with significant variance. The maximum slip effect is obtained for a small value of Pr. This is because slip effects increase as Pr decreases due to lower viscosity of the fluid in the presence of velocity slip and thermal slip.
- It is concluded that the magnetic profile is improved at small values of = 0.1 and is minimal at large values of = 2.5. The good slip effect in the temperature graph is observed at each value of Pm along the utilized shape with good agreement.
- It is determined that the Prandtl number indicates the connection between thermal and momentum diffusivity. The magnetic effects are significantly detected exactly at the surface because of conducting processes, but they are zero for all values below the surface.
- In the domains of magnetic resonance imaging (MRI) resonance patterns, artificial heart wolves, interior heart cavities, and nanoburning systems, the present thermodynamic and magnetohydrodynamic issues are significant.
Author Contributions
Writing—original draft preparation, Z.U.; supervision, Z.U.; software, Z.U.; validation, Z.U.; investigation, Z.U.; resources, K.A.M.A.; data curation, K.A.M.A.; writing—review& editing, K.A.M.A.; validation, K.A.M.A.; project administration, K.A.M.A.; supervision, K.A.M.A.; supervision, N.J.; funding acquisition, N.J.; validation, N.J.; analysis of data, M.A.; supervision, M.A.; validation, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (23UQU4310392DSR002).
Data Availability Statement
Not applicable..
Acknowledgments
The authors appreciate the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: (23UQU4310392DSR002).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Revnic, C.; Grosan, T.; Merkin, J.; Pop, I. Mixed convection flow near an axisymmetric stagnation point on a vertical cylinder. J. Eng. Math. 2009, 64, 1–13. [Google Scholar] [CrossRef]
- Chamkha, A.J. On laminar hydromagnetic mixed convection flow in a vertical channel with symmetric and asymmetric wall heating conditions. Int. J. Heat Mass Transf. 2002, 45, 2509–2525. [Google Scholar] [CrossRef]
- Niazmand, H.; Rahimi, B. Mixed convective rarefied flows with symmetric and asymmetric heated walls. Comput. Therm. Sci. Int. J. 2013, 5. [Google Scholar] [CrossRef]
- Zaidi, H.N. Effect of Induced Magnetic Field on Mixed Convection Flow in a Vertical Channel with Symmetric and Asymmetric Wall Heating Conditions. Appl. Appl. Math.Int. J. AAM 2020, 15, 27. [Google Scholar]
- Habchi, S.; Acharya, S. Laminar mixed convection in a symmetrically or asymmetrically heated vertical channel. Numer. Heat Transf. Part A Appl. 1986, 9, 605–618. [Google Scholar]
- Al-Harbi, S.M.; Ibrahim, F.S. Unsteady mixed convection boundary layer flow along a symmetric wedge with variable surface temperature embedded in a saturated porous medium. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1162–1175. [Google Scholar] [CrossRef]
- Singh, G.; Makinde, O.D. Mixed convection slip flow with temperature jump along a moving plate in presence of free stream. Therm. Sci. 2015, 19, 119–128. [Google Scholar] [CrossRef]
- Ashraf, M.B.; Hayat, T.; Shehzad, S.A.; Alsaedi, A. Mixed convection radiative flow of three dimensional Maxwell fluid over an inclined stretching sheet in presence of thermophoresis and convective condition. AIP Adv. 2015, 5, 027134. [Google Scholar] [CrossRef]
- Raju AM, M.; Raju GS, S.; Mallikarjuna, B. Unsteady nonlinear convective Darcy flow of a non-Newtonian fluid over a rotating vertical cone. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 263, p. 062001. [Google Scholar]
- Mukhopadhyay, S.; Mandal, I.C. Magnetohydrodynamic (MHD) mixed convection slip flow and heat transfer over a vertical porous plate. Eng. Sci. Technol. Int. J. 2015, 18, 98–105. [Google Scholar] [CrossRef]
- Mahmood, M.; Asghar, S.; Hossain, M.A. Hydromagnetic flow of viscous incompressible fluid past a wedge with permeable surface. J. Appl. Math. Mech. 2009, 89, 174–188. [Google Scholar] [CrossRef]
- Ilyas, A.; Ashraf, M.; Rashad, A.M. Periodical analysis of convective heat transfer along electrical conducting cone embedded in porous medium. Arab. J. Sci. Eng. 2022, 47, 8177–8188. [Google Scholar] [CrossRef]
- Maneengam, A.; Bouzennada, T.; Abderrahmane, A.; Guedri, K.; Weera, W.; Younis, O.; Bouallegue, B. Numerical study of lid-driven hybrid nanofluid flow in a corrugated porous cavity in the presence of magnetic field. Nanomaterials 2022, 12, 2390. [Google Scholar] [CrossRef] [PubMed]
- Atashafrooz, M.; Nassab, S.G. Simulation of laminar mixed convection recess flow combined with radiation heat transfer. Iran. J. Sci. Technol. Trans. Mech. Eng. 2013, 37, 71. [Google Scholar]
- Haq, E.U.; Khan, S.U.; Abbas, T.; Smida, K.; Hassan, Q.M.U.; Ahmad, B.; Khan, M.I.; Guedri, K.; Kumam, P.; Galal, A.M. Numerical aspects of thermo migrated radiative nanofluid flow towards a moving wedge with combined magnetic force and porous medium. Sci. Rep. 2022, 12, 10120. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Haider, F.; Alsaedi, A. Darcy-Forchheimer flow with nonlinear mixed convection. Appl. Math. Mech. 2020, 41, 1685–1696. [Google Scholar] [CrossRef]
- Armaghani, T.; Kasaeipoor, A.; Mohammadpoor, U. Entropy generation analysis of mixed convection with considering magnetohydrodynamic effects in an open C-shaped cavity. Therm. Sci. 2019, 23, 3455–3465. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Sheikholeslami, M.; Wakif, A.; Baleanu, D. Mixed convective radiative flow through a slender revolution bodies containing molybdenum-disulfide graphene oxide along with generalized hybrid nanoparticles in porous media. Crystals 2020, 10, 771. [Google Scholar] [CrossRef]
- Saleem, S.; Nadeem, S. Theoretical analysis of slip flow on a rotating cone with viscous dissipation effects. J. Hydrodyn. Ser. B 2015, 27, 616–623. [Google Scholar] [CrossRef]
- Puneeth, V.; Khan, M.I.; Jameel, M.; Geudri, K.; Galal, A.M. The convective heat transfer analysis of the casson nanofluid jet flow under the influence of the movement of gyrotactic microorganisms. J. Indian Chem. Soc. 2022, 99, 100612. [Google Scholar] [CrossRef]
- Guedri, K.; Ammar Abbassi, M.; NaceurBorjini, M.; Halouani, K.; Saïd, R. Application of the finite-volume method to study the effects of baffles on radiative heat transfer in complex enclosures. Numer. Heat Transf. Part A Appl. 2009, 55, 780–806. [Google Scholar] [CrossRef]
- Uddin, M.J.; Rana, P.; Bég, O.A.; Ismail, A.M. Finite element simulation of magnetohydrodynamic convective nanofluid slip flow in porous media with nonlinear radiation. Alex. Eng. J. 2016, 55, 1305–1319. [Google Scholar] [CrossRef]
- Das, S.; Jana, R.N.; Makinde, O.D. Magnetohydrodynamic mixed convective slip flow over an inclined porous plate with viscous dissipation and Joule heating. Alex. Eng. J. 2015, 54, 251–261. [Google Scholar] [CrossRef]
- Jamil, M.; Ahmed, I. Twice order slip on the flows of fractionalized MHD viscoelastic fluid. Eur. J. Pure Appl. Math. 2019, 12, 1018–1051. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, B. Effects of second-order slip on the flow of a fractional Maxwell MHD fluid. J. Assoc. Arab. Univ. Basic Appl. Sci. 2017, 24, 232–241. [Google Scholar] [CrossRef]
- Ullah, Z.; Ashraf, M.; Rashad, A. Magneto-thermo analysis of oscillatory flow around a non-conducting horizontal circular cylinder. J. Therm. Anal. Calorim. 2020, 142, 1567–1578. [Google Scholar] [CrossRef]
- Ullah, Z.; Ashraf, M.; Zia, S.; Ali, I. Surface temperature and free stream velocity oscillation effects on mixed convention slip flow from surface of a horizontal circular cylinder. Therm. Sci. 2020, 24, 13–23. [Google Scholar] [CrossRef]
- Ullah, Z.; Ashraf, M.; Zia, S.; Chu, Y.; Khan, I.; Nisar, K.S. Computational analysis of the oscillatory mixed convection flow along a horizontal circular cylinder in thermally stratified medium. CMC Comput. Mater. Contin. 2020, 65, 109–123. [Google Scholar] [CrossRef]
- Ullah, Z.; Ashraf, M.; Sarris, I.E.; Karakasidis, T.E. The Impact of Reduced Gravity on Oscillatory Mixed Convective Heat Transfer around a Non-Conducting Heated Circular Cylinder. Appl. Sci. 2022, 12, 5081. [Google Scholar] [CrossRef]
- Yaseen, M.; Rawat, S.K.; Kumar, M. Cattaneo–Christov heat flux model in Darcy–Forchheimer radiative flow of MoS2–SiO2/kerosene oil between two parallel rotating disks. J. Therm. Anal. Calorim. 2022, 147, 10865–10887. [Google Scholar] [CrossRef]
- Kumar, G.; Murthy, D.S. A multiresolution wavelet optimised finite-difference method for simulation of thermal regenerator. Therm. Sci. Eng. Progress 2020, 19, 100669. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, G.; Murthy, D.S. Experimental investigation on thermal performance characteristics of rotating packed bed. Exp. Heat Transf. 2022, 1–13. [Google Scholar] [CrossRef]
- Ullah, Z.; Ehsan, M.; Ahmad, H.; Ilyas, A. Combined effects of MHD and slip velocity on oscillatory mixed convective flow around a non-conducting circular cylinder embedded in a porous medium. Case Stud. Therm. Eng. 2022, 38, 102341. [Google Scholar] [CrossRef]
- Kan, K.; Xu, Z.; Chen, H.; Xu, H.; Zheng, Y.; Zhou, D.; Muhirwa, A.; Maxime, B. Energy loss mechanisms of transition from pump mode to turbine mode of an axial-flow pump under bidirectional conditions. Energy 2022, 257, 124630. [Google Scholar] [CrossRef]
- Kan, K.; Zhang, Q.; Xu, Z.; Zheng, Y.; Gao, Q.; Shen, L. Energy loss mechanism due to tip leakage flow of axial flow pump as turbine under various operating conditions. Energy 2022, 255, 124532. [Google Scholar] [CrossRef]
- Kumar, P.; Poonia, H.; Ali, L.; Shah, N.A.; Chung, J.D. Significance of Weissenberg Number, Soret Effect and Multiple Slips on the Dynamic of Biconvective Magnetohydrodynamic CarreauNanofuid Flow. Mathematics 2023, 11, 1685. [Google Scholar] [CrossRef]
- Ullah, Z.; Bilal, M.; Sarris, I.E.; Hussanan, A. MHD and Thermal Slip Effects on Viscous Fluid over Symmetrically Vertical Heated Plate in Porous Medium: Keller Box Analysis. Symmetry 2022, 14, 2421. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Ghori, M.B. Melting effect on Cattaneo–Christov and thermal radiation features for aligned MHD nanofluid flow comprising microorganisms to leading edge: FEM approach. Comput. Math. Appl. 2022, 109, 260–269. [Google Scholar] [CrossRef]
- Kumar, P.; Poonia, H.; Ali, L.; Areekara, S. The numerical simulation of nanoparticle size and thermal radiation with the magnetic field effect based on tangent hyperbolic nanofluid flow. Case Stud. Therm. Eng. 2022, 37, 102247. [Google Scholar] [CrossRef]
- Rehman, S.U.; Fatima, N.; Ali, B.; Imran, M.; Ali, L.; Shah, N.A.; Chung, J.D. The Casson dusty nanofluid: Significance of Darcy–forchheimer law, magnetic field, and non-Fourier heat flux model subject to stretch surface. Mathematics 2022, 10, 2877. [Google Scholar] [CrossRef]
- Muthukumaran, C.; Bathrinathan, K. Mathematical modeling of mixed convection boundary layer flows over a stretching sheet with viscous dissipation in presence of suction and injection. Symmetry 2020, 12, 1754. [Google Scholar] [CrossRef]
- Tlili, I. Effects MHD and heat generation on mixed convection flow of Jeffrey fluid in microgravity environment over an inclined stretching sheet. Symmetry 2019, 11, 438. [Google Scholar] [CrossRef]
- Ullah, Z.; Akkurt, N.; Alrihieli, H.F.; Eldin, S.M.; Alqahtani, A.M.; Hussanan, A.; Jabeen, M. Temperature-Dependent Density and Magnetohydrodynamic Effects on Mixed Convective Heat Transfer along Magnetized Heated Plate in Thermally Stratified Medium Using Keller Box Simulation. Appl. Sci. 2022, 12, 11461. [Google Scholar] [CrossRef]
- Suresh Kumar, Y.; Hussain, S.; Raghunath, K.; Ali, F.; Guedri, K.; Eldin, S.M.; Khan, M.I. Numerical analysis of magnetohydrodynamics Casson nanofluid flow with activation energy, Hall current and thermal radiation. Sci. Rep. 2023, 13, 4021. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).