Abstract
This paper investigates the stabilization of nonlinear systems with external disturbances, which are both bounded and unbounded. Firstly, the stabilization problem of the nominal nonlinear system is realized, and the corresponding stabilization controllers are designed. Then, three suitable filters are proposed and applied to asymptotically estimate the corresponding disturbances, and the disturbance estimators are presented and used to exactly eliminate the corresponding disturbances. Then, the disturbance estimator (DE)-based controllers are proposed to stabilize such nonlinear systems. It should be pointed out the unbounded disturbances are exactly estimated by suitable filters, which has advantages over the existing results. Finally, two illustrative examples, which have certain symmetrical properties, are taken, and the related numerical simulations are carried out to verify the effectiveness and correctness of the proposed results.
1. Introduction
Nonlinear systems have received extensive attention; not only in control engineering but also in biomedicine [1,2], the stability analysis and control design of nonlinear systems are hot topics of research. In the field of control, a fundamental problem that has been extensively studied by scholars is how to achieve the stability of a closed-loop system by designing a feedback controller [3,4,5]. There are two methods to realize the control goal; one is the input feedback, and the other is output feedback. Output feedback can maintain the controllability and observability of the system and only needs to use external signals, but the nonlinear system based on output feedback is a complex problem in terms of achieving global stability, and some state variables are not measurable, mainly because the nonlinear system has great instability and is susceptible to noise disturbances. Input feedback is often used in theoretical analysis. How to achieve the stabilization of nonlinear systems by input feedback has been the key to research in recent decades.
It is encouraging that some important results have been published for this problem, e.g., schemes of using output functions; if the nonlinear term depends only on the measurable signal, the unknown disturbance information can be filtered by special filters, such as high gain observers [6], K-filters [7], mt-filters [8], etc. In dealing with uncertain feedback systems with input saturation and output constraints, an adaptive fuzzy control method was proposed in [9], and in [10,11], the variable separation method was applied to the controller design of non-strict feedback systems. It is worth noting that with the development of modern control theory techniques, the decoupling problem has also gradually been applied to nonlinear systems [12], and the decoupling method for solving nonlinear systems is mainly based on the differential geometry method, which solves the key problems of nonlinear systems to a large extent. The Lyapunov direct method is an important tool to deal with the stability of nonlinear systems. In [13], the early fractional order Lyapunov class theory of fractional order systems was studied. In [14], the Mittag–Leffler stability and the generalized Mittag–Leffler stability were introduced to describe the fractional-order Lyapunov stability of fractional-order systems [15,16].
Usually, the established nonlinear system and the actual system will inevitably produce errors, such as parameter uncertainty [17,18], modeling errors, and unknown functions, which require the designed controller to have strong adaptivity and robustness, and an adaptive control method [19,20] was proposed in the early days to deal with the control problem of nonlinear systems with unknown parameters [21,22,23]. It is inevitable that the nonlinear system is subjected to disturbances that also significantly affect the behavior of the system, and it is more realistic to consider the control problem of nonlinear systems containing disturbances; for the disturbances containing some special forms of bounded forms currently given, results were given in Ref. [24]. Because the nonlinear characteristics are the cause of nonlinear phenomena, and in many control practices the characteristics of the system need to be preserved, the difficulty of this problem lies in how to preserve the nonlinearity while suppressing the unbounded external disturbances. Currently, some methods for suppressing the disturbances have been proposed, such as sliding mode control methods [25,26] and neural network methods [27,28], which are able to suppress the effects of nonlinearities and external disturbances. However, those methods compensate for the effects of nonlinearities while not taking into account the suppression of unbounded forms of disturbances; therefore, they do not apply to dealing with the problem of suppressing the nonlinear systems containing bounded as well as unbounded forms of disturbances considered in this paper. The uncertainty and disturbance estimation (UDE)-based control method [29] is an effective method for dealing with model uncertainty and external disturbances, which has the advantage of being operationally simpler and physically easier to implement when dealing with uncertainty and external disturbances in the system compared to the above methods. The core idea of the UDE-based control method is to consider the uncertainty and external disturbances in the system as a set total disturbance and then estimate the set total disturbance as a whole by designing a suitable filter and canceling it out by designing a corresponding controller to achieve the exact control goal. However, for some unbounded disturbances, such as , , where unknown constants, no suitable filter has been designed in [24,29] so far. It is noted that the uncertainty influences the asymptotic tracking effect of the filter. Thus, only the robust control objective is achieved by the UDE-based control method in most cases and not the asymptotic control objectives. Compared to the UDE-based control method, the advantage of our method is shown in Remark 4. It is both important and urgent to propose suitable filters to asymptotically estimate the external disturbances. Inspired by the UDE-based control method, this paper presents a DE-based control method which can asymptotically estimate both bounded and unbounded disturbances and can achieve the better control objective; thus, it can realize the problem of the stabilization of nonlinear systems with bounded and unbounded disturbances. The main contributions of this paper are summarized as follows
- (1).
- The stabilization of the controlled nominal nonlinear system is realized by the dynamic feedback control method and linear feedback control method;
- (2).
- Three suitable filters are proposed to asymptotically estimate the corresponding bounded and the unbounded disturbances, i.e., the periodic disturbance: , where and are unknown constants; the unbounded disturbances: e.g., , where is an unknown constant, and a is a small known constant; and , where and are unknown constants. Then, the corresponding disturbance estimators are presented;
- (3).
- Three DE-based controllers are designed and used to realize the stabilization of nonlinear systems.
The rest of this paper is organized as follows. Section 2 introduces some preliminary results, Section 3 presents the problem formation of this paper, Section 4 shows the main results and proofs, Section 5 provides the numerical simulation results, and Section 6 gives the conclusions and future prospects.
Some notations used in this paper are presented before ending this section. The Laplace transformation is expressed by “ℓ”, and “” stands for the inverse Laplace transformation, i.e.,
where s is a complex variable with , is a function which meets some appropriate conditions, and .
In addition, “✶” represents the convolution of two functions; that is,
where is a function that satisfies certain conditions.
2. Preliminary
For the sequel use, some preliminary results are presented in the following paragraphs.
Lemma 1
([30]). Consider the following system
where is the state, , , and u is the controller to be designed. If is controllable, then the stabilization controller u is
where and
Lemma 2
([31]). Consider the nonlinear system
If the system is exponentially asymptotically stable, and , where , and is sufficiently larger number, then .
3. Problem Formation
Consider the controlled nonlinear system with external disturbances
where is the state, is a continuous vector function, represents the disturbances, is a constant vector, and is the controller to be designed, where is used to stabilize the original system without the disturbance in the following form
which is usually called the controlled nominal system, and is the disturbance estimator, which meets the following performance:
The main goal of this paper is to design the DE-based controller u to achieve the following performance:
The DE-based controller u is presented by the following two steps: in the first step, the stabilization of the nominal system (6) is realized, and the stabilization controller is designed. The disturbance estimator is proposed in the second step. Thus, the DE-based controller is obtained, and the stabilization of system (5) is achieved.
4. Main Results
4.1. Stabilization of the Controlled Nominal System
In this section, the stabilization of nominal system (6) is investigated, and a conclusion is derived as follows.
Theorem 1.
Consider the controlled nominal system (6). If is controllable, the stabilization controller is designed as
where , and
Proof.
Since is controllable, the conclusion of this theorem is proved according to the dynamic feedback control method in Lemma 1. □
4.2. Suitable Filters Are Designed for the Corresponding External Disturbances
Filters are mainly composed of filter circuits consisting of inductors and capacitors, which are widely used in control systems to eliminate the effects of disturbances. The filter allows useful signals to pass through, and it has a large attenuation of high-frequency disturbance signals. Thus, it can improve the disturbance rejection performance of the investigated system by realizing the separation of useful signals from disturbance signals and eliminating the influence of the bounded and unbounded disturbances on such systems.
In this section, some appropriate filters are proposed for the bounded and unbounded disturbances.
Theorem 2.
For the periodically external disturbance: , where and are unknown constants, a suitable filter is presented as follows
where , and (t) is given by the inverse Laplace transform formula
which meets the following performance:
Proof.
We compute the following convolution, and it concludes
as .
Thus, the proof of above theorem is complete. □
Theorem 3.
For the unbounded exponentially increasing external disturbance: , where is an unknown constant, and a is a small known constant, a suitable filter is presented as follows
where and is given by the inverse Laplace transform formula
which meets the following performance:
Proof.
Computing the following convolution results in
as .
Thus, the proof of the above theorem is complete. □
Theorem 4.
For the unbounded external disturbance: , where and are unknown constants, a suitable filter is presented as follows
where = 1,000,000, = 23,600,000, = 23,600,000, = 247,116,000, = 389,656,100, = 100,000, = 3,150,000, = 35,530,000, = 165,951,000, = 295,331,250, = 384,771,519, , and is given by the inverse Laplace transform formula
which meets the following performance:
Proof.
Computing the following convolution, we obtain
as . Thus, the proof of above theorem is complete. □
Remark 1.
Compared with the existing results, not only is the bounded disturbance considered, such as the periodic disturbance: , where and are unknown constants, but the unbounded disturbances are also handled, e.g., , where is an unknown constant, and a is a small known constant, and , where and are unknown constants. Thus, the results in this paper have advantages over the existing ones.
4.3. The Disturbance Estimators Are Designed for the External Disturbances
Theorem 5.
5. Illustrative Examples and Numerical Simulations
In this section, two illustrative examples with numerical simulations are used to verify the feasibility of the proposed results.
The first example is the famous Lorenz system. It is one of the most classical low-dimensional chaos models, introduced by Lorenz as a finite approximation to the partial equations simulating convective motion in a fluid layer, which has attracted extensive research by scholars, and through the study of this system, it was found that the system has three equilibrium states, two of which are symmetric with the transformation . The trajectories of the system circulating around the two symmetric foci may form chaotic attractors, the famous butterfly effect. The other one is the Chen–Lee system, which also has a similar symmetrical property.
where is the state, and
has as the disturbance, i.e.,
Example 1.
The Lorenz system [32] with external disturbances
Case 1:
Case 2:
where and are unknown constants, and a is a known small constant.
There are two steps to obtain the controller . In the first step, is proposed and used to stabilize the controlled nominal system . The disturbance estimator with a suitable filter is presented in the second step.
Firstly, for the controlled nominal system , and it gives the following controller:
and the controlled nominal system is presented as
Thus, system (32) is globally asymptotically stable.
Secondly, the disturbance estimator with suitable filter is presented for the given disturbance.
Case 1: For the disturbance given in Equation (29), according to Theorem 5, the disturbance estimator is proposed as
where is given in Equation (11), and is given in Equation (32).
Remark 2.
Since is controllable, another stabilization controller and , according to Theorem 1. According to Theorem 5, another disturbance estimator is proposed as
where is given in Equation (11).
Case 2: For the disturbance given in Equation (30), according to Theorem 5, the disturbance estimator is proposed as
where is given in Equation (15).
Remark 3.
Since is controllable, another stabilization controller and , according to Theorem 1. According to Theorem 5, another disturbance estimator is proposed as
where is given in Equation (15).
Case 1: Numerical simulations were made with the initial condition of the Lorenz system (27): , and . The controller , where is given in Equation (31), and is given in Equation (35).
From Figure 1, it can be seen that the Lorenz system (27) is asymptotically stable under the DE-based controller u. Figure 2 shows tends to the disturbance as , which shows the disturbance can be estimated asymptotically and thus it can be eliminated exactly.
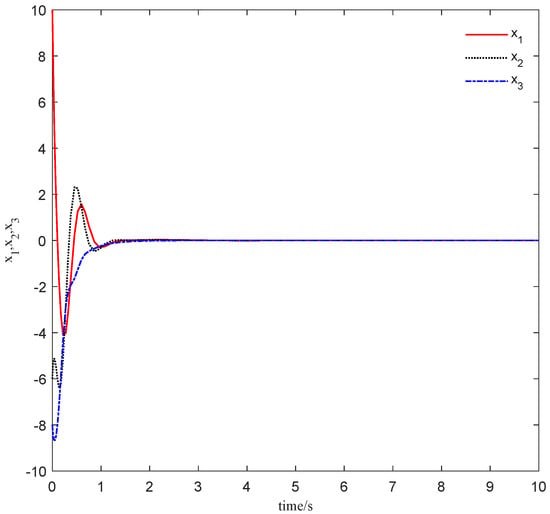
Figure 1.
The Lorenz system (27) is asymptotically stable.
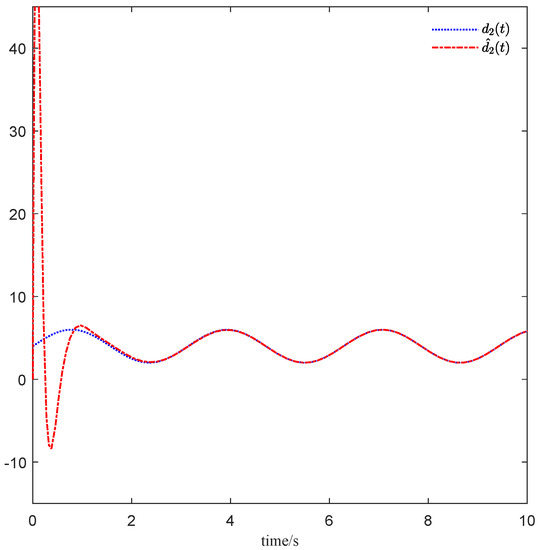
Figure 2.
Disturbance estimator tends to the disturbance as .
Remark 4.
For the disturbance , the proposed filter in Ref. [29] is given as follows
where w = 4π, = 10 w, and = 100 .
Let and ; the numerical simulation is carried out with , and the state of e is shown below.
From Figure 3, it can be seen that the proposed filter in Equation (39) only realizes the robust estimation of , but the designed filter in (12) can asymptotically estimate the . Therefore, the obtained result has advantages over the existing ones.
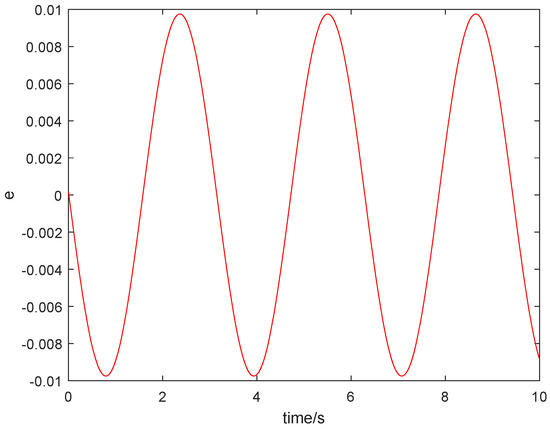
Figure 3.
The state of e.
Case 2: Numerical simulations were carried out with the initial condition of the Lorenz system (27): , and . The controller , where is given in Equation (31), and is given in Equation (35).
It can be seen from Figure 4 that the Lorenz system (27) is asymptotically stable under the DE-based controller u. Figure 5 illustrates that converges to the disturbance as , which shows the disturbance can be estimated asymptotically and thus it can be eliminated exactly.
where is the state,
and
Example 2.
Following is the Chen–Lee system [33] with the unbounded external disturbance
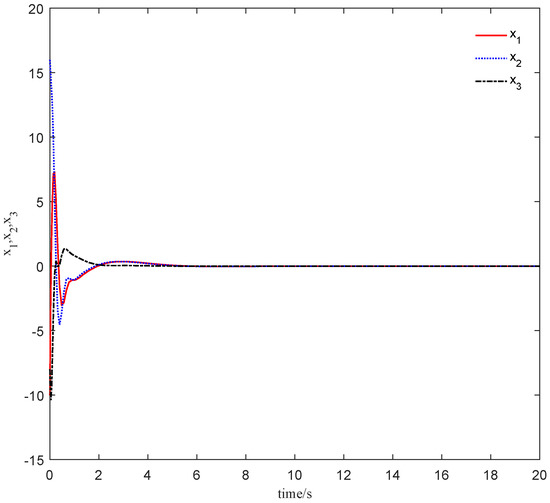
Figure 4.
The Lorenz system (27) is asymptotically stable.
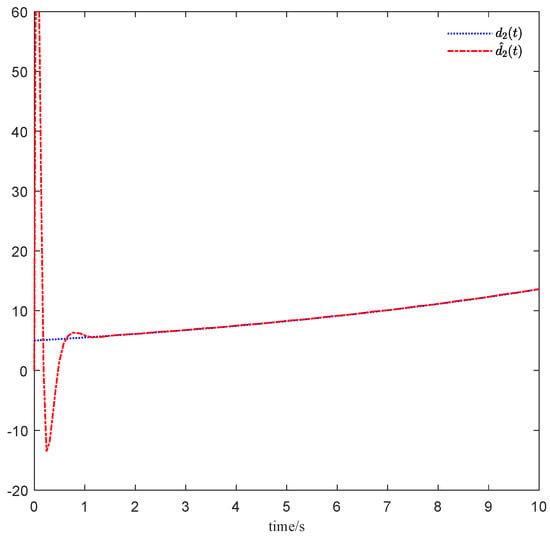
Figure 5.
Disturbance estimator converges to the disturbance .
Using similar procedures to Example 1, the DE-based controller is presented as follows
where
and is given in Equation (19).
Numerical simulations were made with the initial condition of the Chen–Lee system (40): , and . The controller , where is given in Equation (43), and is given in Equation (44).
It can be observed from Figure 6 that the controlled system is asymptotically stable under the DE-based controller u, and Figure 7 demonstrates that tends to the disturbance as , which shows the disturbance can be estimated asymptotically and thus it can be eliminated exactly.
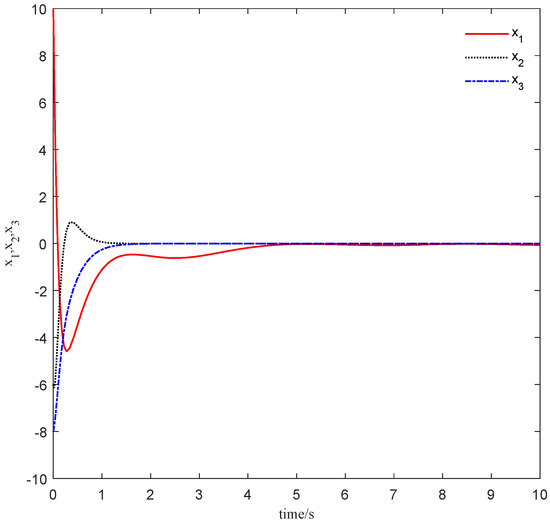
Figure 6.
The Chen−Lee system (40) is asymptotically stable.
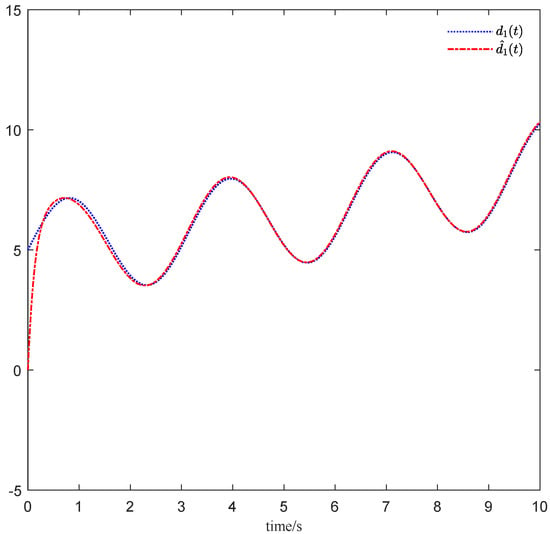
Figure 7.
Disturbance estimator tends to the disturbance .
6. Conclusions and Future Prospects
The stabilization of the nonlinear system with external disturbance (both bounded and unbounded) was investigated. Firstly, the stabilization of the nominal system was achieved by the dynamic feedback control method and linear feedback control method, and the corresponding stabilization controllers were proposed. Then, three suitable filters were designed and used to asymptotically estimate the corresponding bounded or unbounded disturbances; then, disturbance estimators were presented. Thus, the DE-based controllers were proposed and applied to realize the stabilization of the nonlinear systems. The stabilization problem of nonlinear systems was realized by estimating the disturbance asymptotically and eliminating it exactly, so it has some advantages over the existing ones. Finally, the effectiveness and validity of the proposed results was verified by the numerical simulations.
The limitations and shortcomings of the proposed method include the need for carefully considering the model uncertainty. In future work, we will consider the control problems of nonlinear systems including uncertainties and disturbances, and we wish to improve the performance of the existing UDE-based control method.
Author Contributions
K.S. wrote the original draft, X.W. conducted the numerical simulations, and R.G. reviewed and edited the entire paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Natural Science Foundation of Shandong Province under Grant (ZR2021MF012) and the Colleges and Universities Twenty Terms Foundation of Jinan City (2021GXRC100).
Data Availability Statement
No data is used in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Botmart, T.; Sabir, Z.; Raja, M.A.Z. A hybrid swarming computing approach to solve the biological nonlinear Leptospirosis system. Biomed. Signal Process. Control 2022, 77, 103789. [Google Scholar] [CrossRef]
- Ayub, A.; Sabir, Z.; Altamirano, G.C. Characteristics of melting heat transport of blood with time-dependent cross-nanofluid model using Keller-Box and BVP4C method. Eng. Comput. 2022, 38, 3705–3719. [Google Scholar] [CrossRef]
- Serrani, A.; Isidori, A. Global robust output regulation for a class of nonlinear systems. Syst. Control. Lett. 2000, 39, 133–139. [Google Scholar] [CrossRef]
- Liu, W.; Huang, J. Cooperative global robust output regulation for a class of nonlinear multi-agent systems with switching network. IEEE Trans. Autom. Control 2015, 60, 1963–1968. [Google Scholar] [CrossRef]
- Ge, S.; Wang, J. Robust adaptive tracking for time varying uncertain nonlinear systems with unknown control coefficients. IEEE Trans. Autom. Control 2003, 48, 1463–1469. [Google Scholar]
- Farza, M.; Ragoubi, A.; Hadj Said, S. Improved high gain observer design for a class of disturbed nonlinear systems. Nonlinear Dyn. 2021, 106, 631–655. [Google Scholar] [CrossRef]
- Krstic, M.; Kanellakopoulos, I.; Kokotovic, P. Adaptive neural control for stochastic pure-feedback non-linear time-delay systems with output constraint and asymmetric input saturation. IET Control Theory Appl. 2017, 11, 2288–2298. [Google Scholar]
- Zhang, Z.; Chen, W. Adaptive tracking control for actuator failure compensation based on MT-filters. J. Syst. Sci. Complex. 2010, 23, 759–768. [Google Scholar] [CrossRef]
- Wu, J.; Su, B.Y.; Li, J.; Zhang, X.; Li, X.B.; Chen, W.S. Adaptive fuzzy control for full states constrained systems with nonstrict-feedback form and unknown nonlinear dead zone. Inf. Sci. 2017, 376, 233–247. [Google Scholar] [CrossRef]
- Rui, W.; Zhang, H. Separation variable method combined with integral bifurcation method for solving time-fractional reaction-diffusion models. Comput. Appl. Math. 2020, 39, 1–26. [Google Scholar] [CrossRef]
- Kong, L.Q.; Dai, C. Some discussions about variable separation of nonlinear models using Riccati equation expansion method. Nonlinear Dyn. 2015, 81, 1553–1561. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, Y. Practical finite-time almost disturbance decoupling strategy for uncertain nonlinear systems. Nonlinear Dyn. 2019, 95, 117–128. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Leela, S.; Sambandham, M. Lyapunov theory for fractional differential equations. Commun. Appl. Anal. 2008, 12, 365. [Google Scholar]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Yu, C.; Xu, C. Backstepping Control and Synchronization for 4-D Lorenz-Stenflo Chaotic System with Single Input. Int. J. Fuzzy Log. Intell. Syst. 2011, 11, 143–148. [Google Scholar] [CrossRef]
- Yu, C.; Xu, C. Control and Synchronization of New Hyperchaotic System using Active Backstepping Design. Int. J. Fuzzy Log. Intell. Syst. 2011, 11, 77–83. [Google Scholar] [CrossRef]
- Liu, W.; Xie, F. Backstepping-based adaptive control for nonlinear systems with actuator failures and uncertain parameters. Circuits Syst. Signal Process. 2020, 39, 138–153. [Google Scholar] [CrossRef]
- Jia, F.; Wang, X.H.; Zhou, X.Y. Robust adaptive prescribed performance control for a class of nonlinear pure-feedback systems. Int. J. Robust Nonlinear Control 2019, 29, 3971–3987. [Google Scholar] [CrossRef]
- Wang, W.; Wen, C.; Huang, J. Distributed adaptive asymptotically consensus tracking control of nonlinear multi-agent systems with unknown parameters and uncertain disturbances. Automatica 2017, 77, 133–142. [Google Scholar] [CrossRef]
- Sui, S.; Tong, S.; Li, Y. Observer-based fuzzy adaptive prescribed performance tracking control for nonlinear stochastic systems with input saturation. Neurocomputing 2015, 158, 100–108. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, X.; Zong, G.; Li, H. Fuzzy-approximation-based adaptive output-feedback control for uncertain nonsmooth nonlinear systems. IEEE Trans. Fuzzy Syst. 2018, 26, 3847–3859. [Google Scholar] [CrossRef]
- Oh, M.; Han, C.; Sinitsyn, I. Recursive filtering in discrete nonlinear systems with unknown parameters. Autom. Remote Control 1998, 59, 36–43. [Google Scholar]
- Anan’evskii, I.M. Control of a nonlinear vibratory system of the fourth order with unknown parameters. Autom. Remote Control 2001, 64, 343–355. [Google Scholar] [CrossRef]
- Yi, X.; Guo, R.; Qi, Y. Stabilization of chaotic systems with both uncertainty and disturbance by the UDE-Based Control Method. IEEE Access 2020, 8, 62471–62477. [Google Scholar] [CrossRef]
- Song, J.; Niu, Y.; Zou, Y. Finite-time stabilization via sliding mode control. IEEE Trans. Autom. Control 2016, 62, 1478–1483. [Google Scholar] [CrossRef]
- Mobayen, S.; Baleanu, D. Stability analysis and controller design for the performance improvement of disturbed nonlinear systems using adaptive global sliding mode control approach. Nonlinear Dyn. 2016, 83, 1557–1565. [Google Scholar] [CrossRef]
- Bai, W.; Zhou, Q.; Li, T.; Li, H. Adaptive reinforcement learning neural network control for uncertain nonlinear system with input saturation. IEEE Trans. Cybern. 2019, 50, 3433–3443. [Google Scholar] [CrossRef]
- Yang, H.; Liu, J. An adaptive RBF neural network control method for a class of nonlinear systems. IEEE/CAA J. Autom. Sin. 2018, 5, 457–462. [Google Scholar] [CrossRef]
- Ren, B.; Zhong, Q.; Dai, J. Asymptotic reference tracking and disturbance rejection of UDE-based robust control. IEEE Trans. Ind. Electron. 2016, 64, 3166–3176. [Google Scholar] [CrossRef]
- Guo, R. Projective synchronization of a class of chaotic systems by dynamic feedback control method. Nonlinear Dyn. 2017, 90, 5593–5597. [Google Scholar] [CrossRef]
- Cao, L.; Guo, R. Partial anti-Synchronization problem of the 4D financial hyper-chaotic system with periodically external disturbance. Mathematics 2022, 10, 3373. [Google Scholar] [CrossRef]
- Curry, J.H. A generalized Lorenz system. Commun. Math. Phys. 1978, 60, 193–204. [Google Scholar] [CrossRef]
- Tam, L.M.; Si Tou, W.M. Parametric study of the fractional order Chen-Lee system. Chaos Solitons Fractals 2008, 37, 817–826. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).