The Existence of Odd Symmetric Periodic Solutions in the Generalized Elliptic Sitnikov $(N+1)$-Body Problem

Abstract

In this paper, we study the existence of the families of odd symmetric periodic solutions in the generalized elliptic Sitnikov $(N+1)$-body problem for all values of the eccentricity $e\in [0,1)$ using the global continuation method. First, we obtain the properties of the period of the solution of the corresponding autonomous equation (eccentricity $e=0$) using elliptic functions. Then, according to these properties and the global continuation method of the zeros of a function depending on one parameter, we derive the existence of odd periodic solutions for all $e\in [0,1)$. It is shown that the temporal frequencies of period solutions depend on the total mass $\lambda$ (or the number N) of the primaries in a delicate way.

1. Introduction

It is well known that the Sitnikov problem is the simplest model that cannot give an analytic solution in the restricted N-body problem, where two bodies (called primaries) of equal mass are moving in a circular or an elliptic orbit of the two-body problem, and the infinitesimal mass is moving on the straight line orthogonal to the plane of motion of the primaries which passes through their center of mass. The Sitnikov problem became important when Sitnikov, for the first time, showed the existence of oscillatory motions [1]. Since then, many other authors have studied this problem. We refer the reader to [2,3,4,5,6,7,8,9,10,11,12,13] and the references therein for a more detailed introduction.

In particular, there are many interesting results on periodic solutions of the Sitnikov problem [13,14,15,16,17,18,19,20,21]. For example, Abouelmagd et al. found periodic solutions of the circular Sitnikov problem using the multiple scales method [14]. Belbruno et al., obtained the analytical expressions for the solutions of the circular Sitnikov problem and the period function of its family of periodic orbits. In addition, they also numerically studied the linear stability of the family of periodic orbits of the Sitnikov problem [13]. Corbera and Llibre have studied the family of symmetric periodic orbits using the continuity of periodic solutions from the circular Sitnikov problem to the elliptic Sitnikov problem [16,17]. Galán et al. numerically studied the stability and bifurcation of even periodic solutions of the Sitnikov problem [18]. Based on the global continuation method, Libre and Ortega constructed the even symmetric periodic solutions of the Sitnikov problem [19]. Using a shooting method and Sturm oscillation theory, Ortega explored the existence of odd symmetric periodic solutions of the Sitnikov problem [20]. Owing to the theory for Hill’s equations, Zhang and his co-authors studied the stability of nonconstant symmetric periodic solutions of the Sitnikov problem, which emanate from the corresponding solutions of the circular Sitnikov problem [15,21,22].

In recent years, periodic solutions of the generalized Sitnikov $(N+1)$-body problem (i.e., there are multiple primaries in the Sitnikov problem) have attracted the attention of some researchers. In 2009, Bountis and Papadakis studied the stability of vertical motion and bifurcation in a three-dimensional periodic orbit family [23]. In 2013, Rivera studied some properties of two groups of families of periodic solutions, where one group is families that are globally continued from the generalized circular Sitnikov $(N+1)$-body problem to the generalized elliptic Sitnikov $(N+1)$-body problem ($e\ne 0$), and the other is families that arise as bifurcation from equilibrium solution at certain special values of the eccentricity [24]. In 2018, Misquero pointed out the existence of both types of symmetric periodic solutions and proved the existence of even symmetric periodic solutions using a shooting method and Sturm oscillation theory (see Lemma 6 of [25]).

Periodic solutions of the n-body problem have always been an important research field, whether in celestial mechanics or mathematics. Motivated by work in the literature [19,24], we will study the odd families of periodic solutions of the generalized elliptic Sitnikov $(N+1)$-body problem. Firstly, based on elliptic functions, we will deduce the properties of the period of the solution of the generalized circular Sitnikov $(N+1)$-body problem. Then, based on these properties, and for all values of the eccentricity $e\in [0,1)$, we will study the existence of odd periodic solutions of the generalized elliptic Sitnikov $(N+1)$-body problem by the global continuation of the zeros of a function depending on one parameter provided by Leray and Schauder (see [26] or Section 4 of [19]). The challenge we face is to prove the existence of the solutions of the Dirichlet problem. Although the global continuation method we use is the same as that in [19], there is a great difference. Specifically, we note that the study of [19] was conducted in the classical elliptical Sitnikov problem, but our study is conducted in the generalized elliptical Sitnikov $(N+1)$-body problem, which is the more general case. It shows that temporal frequencies of periodic solutions depend on the total mass $\lambda$ (or the number N) of the primaries in a delicate way. In addition, Refs. [19,24] have proved the existence of even periodic solutions using the global continuation method. To our knowledge, this is the first time that the existence of odd periodic solutions has been analytically studied using the global continuation method.

The rest of the paper is organized as follows: in Section 2, we introduce the generalized elliptic Sitnikov $(N+1)$-body problem and deduce the properties of the period of the solution in the generalized circular Sitnikov $(N+1)$-body problem; then, we explore the existence of odd periodic solutions of the generalized elliptic Sitnikov $(N+1)$-body problem for all $e\in [0,1)$ in Section 3; we finally conclude the paper in Section 4.

2. The Generalized Elliptic Sitnikov $(\mathit{N}+\mathbf{1})$-Body Problem

In this section, we first introduce the generalized elliptic Sitnikov $(N+1)$-body problem [24]. Then, we study the properties of the period of the solution in the generalized circular ($e=0$) Sitnikov $(N+1)$-body problem using elliptic functions.

Consider N (≥2) point masses $P_1,P_2,\cdots ,P_N$, called primaries, which have equal masses

$$m_N=\frac{1}{2{\mathrm{\Sigma }}_{k=1}^{N-1}csc\left(\frac{k\pi }{N}\right)}.$$

(1)

Suppose that $P_1$ moves along an elliptic orbit with eccentricity $e\in [0,1)$, whose semimajor axis is equal to $\frac{1}{2}$ and minimal period is $2\pi$. Then, $P_1,P_2,\cdots ,P_N(N\ge 2)$ satisfy the N-body problem where each body moves around the center of mass over an elliptic orbit with alike eccentricity, semimajor axis and minimal period. Meanwhile, the N primaries exactly form a stable positive N-sided structure, and its position just satisfies the Lagrange solution of the N-body problem. These orbits are located in the $OXY$ plane of the inertial frame of reference, and the mass center of the primaries is in the origin. The particle P, of infinitesimal mass, moves along the Z-axis in the gravitational field generated by the primaries $P_1,P_2,\cdots ,P_N$. Notice that the mass of P is so small that its effects on the primaries can be ignored. Let $z=z\left(t\right)$ be the position of P at the time t. Then, the equation of motion for P is given by

$$\ddot{z}+\frac{\lambda z}{{(z^2+r^2(t,e))}^{\frac{3}{2}}}=0,$$

(2)

where $r(t,e)=\frac{1}{2}(1-ecosu(t,e))$ is the distance from each primary $P_j(j=1,...,N)$ to the mass center, and $u=u(t,e)$ is the solution of the Kepler’s equation $u-esinu=t$. We call Equation (2) the generalized elliptic Sitnikov $(N+1)$-body problem (GESP).

In addition, $\lambda$ is the total mass of the system, i.e.,

$$\lambda =\lambda \left(N\right)=m_{N}N$$

(3)

and $\lambda \in (0,1]$. Notice that Equation (2) is only the classical Sitnikov problem when $\lambda =1$ (i.e., $N=2$). Figure 1 shows the GESP when $N=3$.

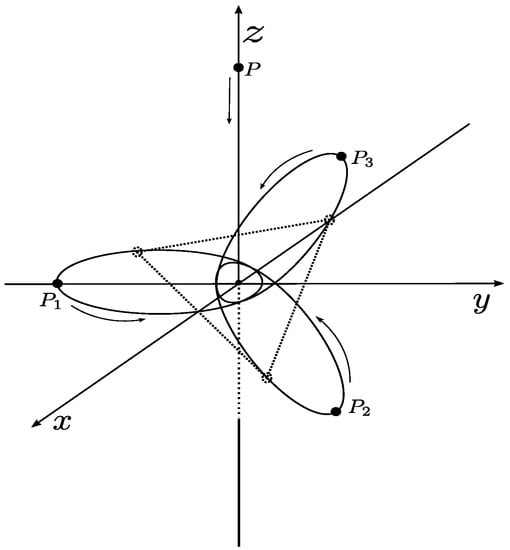
Figure 1. The generalized elliptic Sitnikov $(3+1)$-body problem.

In particular, when $e=0$, the primaries move along a circular orbit of radius $r_0$ and constant angular velocity. Then, Equation (2) becomes

$$\ddot{z}+\frac{\lambda z}{{(z^2+\frac{1}{4})}^{\frac{3}{2}}}=0.$$

(4)

We call Equation (4) the generalized circular Sitnikov $(N+1)$-body problem (GCSP). Moreover, the energy levels of solutions $z\left(t\right)$ are

$${\mathrm{\Gamma }}_h^{\lambda }:H^{\lambda }(z,\dot{z}):=\frac{1}{2}{\dot{z}}^2-\frac{\lambda }{\sqrt{z^2+\frac{1}{4}}}=h^{\lambda },$$

(5)

where $h^{\lambda }\in [-2\lambda ,+\infty ),$ while $h^{\lambda }=-2\lambda$, ${\mathrm{\Gamma }}_h^{\lambda }$ is just the equilibrium $O(0,0)$ of Equation (4), and for $h^{\lambda }\in (-2\lambda ,0)$, ${\mathrm{\Gamma }}_h^{\lambda }$ corresponds to periodic orbits of (4) whose minimal period is denoted by $T\left(h^{\lambda }\right)$. Motivated by work in the literature [13], we have the following theorem about the properties of $T\left(h^{\lambda }\right)$.

Theorem 1.

The period $T\left(h^{\lambda }\right)$ has the following three properties:

(i) 

${lim}_{h^{\lambda }\to -2\lambda +}T\left(h^{\lambda }\right)=\pi /\sqrt{2\lambda }$;

(ii) 

${lim}_{h^{\lambda }\to 0-}T\left(h^{\lambda }\right)=+\infty$;

(iii) 

$T^{\prime }\left(h^{\lambda }\right)=\frac{\mathrm{d}T\left(h^{\lambda }\right)}{\mathrm{d}{h}^{\lambda }}>0\forall h^{\lambda }\in (-2\lambda ,0).$

Theorem 1 is an extension of Theorem C in [13], because [13] dealt with the classical Sitnikov problem ($N=2$). Our proof is entirely analogous to that of [13]. Next, we need to introduce the following proposition.

Proposition 1.

By introducing the following transformation

$$\left\{\begin{array}{c}z=\frac{1}{2}{({\omega }^2-1)}^{\frac{1}{2}}\hfill \\ \dot{z}=2{(\frac{\lambda +\frac{h^{\lambda }}{2}\omega }{\omega })}^{\frac{1}{2}}\hfill \\ t=\frac{1}{4}\int {\omega }^2\mathrm{d}s,\hfill \end{array}\right.$$

(6)

the generalized circular Sitnikov $(N+1)$ problem defined by (5) on $H^{\lambda }(z,\dot{z})=h^{\lambda }$ is reformulated

$$\frac{\mathrm{d}\omega }{\mathrm{d}s}={[({\omega }^2-1)\omega (\lambda +\frac{h^{\lambda }}{2}\omega )]}^{\frac{1}{2}},$$

(7)

or equivalently,

$$s={\int }_1^{2\iota }{[({\omega }^2-1)\omega (\lambda +\frac{h^{\lambda }}{2}\omega )]}^{-\frac{1}{2}}\mathrm{d}\omega .$$

(8)

Proof. 

Letting $\omega =cosh\varpi$, the former two expressions of (6) are reformulated as follows:

$$\left\{\begin{array}{c}z=\frac{1}{2}sinh\varpi \hfill \\ \dot{z}=2\vartheta {(cosh\varpi )}^{-1},\hfill \end{array}\right.$$

(9)

where $\vartheta ={[cosh\varpi (\lambda +\frac{h^{\lambda }}{2}cosh\varpi )]}^{\frac{1}{2}}$. Substituting (9) into (5), the Hamiltonian of the generalized circular Sitnikov $(N+1)$-body problem is reformulated as follows:

$${\mathrm{\Gamma }}^{\lambda }(\varpi ,\vartheta )=2{(cosh\varpi )}^{-1}[{\vartheta }^2{(cosh\varpi )}^{-1}-\lambda ].$$

(10)

Here the transformation (9) is canonical because $\dot{z}dz=\vartheta d\varpi$ implies $d\dot{z}\wedge dz=d\vartheta \wedge d\varpi$. Furthermore, defining

$${\iota }^2=z^2+\frac{1}{4}=\frac{1}{4}{\omega }^2,$$

(11)

the third transformation of (6) is reformulated as follows:

$$t=\int {\iota }^2\mathrm{d}s.$$

(12)

Again, let ${\overline{\mathrm{\Gamma }}}^{\lambda }={\mathrm{\Gamma }}^{\lambda }-h^{\lambda }$. Then, the Hamiltonian (10) is reformulated as follows:

$${\tilde{\mathrm{\Gamma }}}^{\lambda }={\iota }^2{\overline{\mathrm{\Gamma }}}^{\lambda }=\frac{1}{2}{\vartheta }^2-\frac{1}{2}cosh\varpi (\lambda +\frac{1}{2}{h}^{\lambda }cosh\varpi ).$$

(13)

Because the transformation (12) is also canonical, the equation of motion on $\overline{\mathrm{\Gamma }}=0$ is given by

$$\left\{\begin{array}{c}\frac{\mathrm{d}\vartheta }{\mathrm{d}s}=-\partial {\tilde{\mathrm{\Gamma }}}^{\lambda }/\partial \varpi \hfill \\ \frac{\mathrm{d}\varpi }{\mathrm{d}s}=\partial {\tilde{\mathrm{\Gamma }}}^{\lambda }/\partial \vartheta .\hfill \end{array}\right.$$

(14)

Owing to the second equation of (14), we have

$$\frac{\mathrm{d}\varpi }{\mathrm{d}s}=\vartheta ={[cosh\varpi (\lambda +\frac{1}{2}{h}^{\lambda }cosh\varpi )]}^{\frac{1}{2}}.$$

(15)

Moreover, (15) is transformed into

$$\begin{array}{c}\hfill \frac{\mathrm{d}\omega }{\mathrm{d}s}={[({\omega }^2-1)\omega (\lambda +\frac{h^{\lambda }}{2}\omega )]}^{\frac{1}{2}}.\end{array}$$

By taking $s=0$ when $\omega =1$, it is just now that the infinitesimal body is at the origin. Noticing that $\omega =2\iota$, from (11), we have

$$s={\int }_1^{2\iota }{[({\omega }^2-1)\omega (\lambda +\frac{h^{\lambda }}{2}\omega )]}^{-\frac{1}{2}}\mathrm{d}\omega ,$$

which is an elliptic integral of the first kind. Thus, Proposition 1 is proved. □

Proof of Theorem 1.

From Formula (8), we have

$$\begin{array}{ccc}\hfill s& =& {\int }_1^{2\iota }{[({\omega }^2-1)\omega (\lambda +\frac{h^{\lambda }}{2}\omega )]}^{-\frac{1}{2}}\mathrm{d}\omega \hfill \\ \hfill & =& {\int }_1^{2\iota }{[(\omega -1)(\omega +1)\omega (\lambda +\frac{h^{\lambda }}{2}\omega )]}^{-\frac{1}{2}}\mathrm{d}\omega \hfill \\ \hfill & =& \sqrt{-\frac{2}{h^{\lambda }}}{\int }_1^{2\iota }{[(-\frac{2\lambda }{h^{\lambda }}-\omega )(\omega -1)\omega (\omega +1)]}^{-\frac{1}{2}}\mathrm{d}\omega .\hfill \end{array}$$

(16)

Recall Formula 256.00 in [27] as follows:

$${\int }_b^y{\left[(a-x)(x-b)(x-c)(x-d)\right]}^{-\frac{1}{2}}\mathrm{d}x=gF(\phi ,k).$$

(17)

Here, $a\ge y>b>c>d$ and

$$g=2{\left[(a-c)(b-d)\right]}^{-\frac{1}{2}},$$

$$k^2=\frac{(a-b)(c-d)}{(a-c)(b-d)},$$

$$\begin{array}{c}\hfill \phi ={sin}^{-1}{\left[\frac{(a-c)(y-b)}{(a-b)(y-c)}\right]}^{\frac{1}{2}},\end{array}$$

(18)

$$\begin{array}{c}\hfill F(\phi ,k)={\int }_0^{\phi }{(1-k^2{sin}^2\theta )}^{-\frac{1}{2}}\mathrm{d}\theta .\end{array}$$

(19)

$F(\phi ,k)$ is called the normal elliptic integral of the first kind. Moreover, by introducing the change of variable $sin\theta =\mu$ in (19), $F(\phi ,k)$ is reformulated as follows:

$$\nu :=F(\phi ,k)={\int }_0^{\gamma }{\left[(1-{\mu }^2)(1-k^2{\mu }^2)\right]}^{-\frac{1}{2}}\mathrm{d}\mu ,$$

(20)

where $\gamma =sin\phi$. The inverse function $\gamma =sn(\nu ,k)$ to (20) is called the sinus amplitude Jacobi elliptic function, and $sn(\nu ,k)$ is a doubly periodic function in $\nu$ of period $(4K,2i{K}^{\prime })$. Here $K=F(\frac{\pi }{2},k)$, $K^{\prime }=K\left(k^{\prime }\right)$, and $k^{\prime }=\sqrt{1-k^2}$ (see [27]).

Let $a=-\frac{2\lambda }{h^{\lambda }}$, $b=1$, $c=0$, $d=-1$ and $y=2\iota$ in Formula (17). Then, we have $g={(-\frac{\lambda }{h^{\lambda }})}^{-\frac{1}{2}}$, $\phi ={sin}^{-1}\sqrt{\frac{\lambda (2\iota -1)}{\iota (2\lambda +h^{\lambda })}}$ and $k=\sqrt{\frac{2\lambda +h^{\lambda }}{4\lambda }}(0<k<1).$ From Formula (17), s can be reformulated as follows:

$$s=\sqrt{-\frac{2}{h^{\lambda }}}gF(\phi ,k).$$

(21)

Clearly, we notice that $\nu =F(\phi ,k)=\frac{s}{\sqrt{2/\lambda }}$ from (21). Owing to (18), (20), (16) and the inverse function $\gamma =sin\phi =sn(\nu ,k)$, we have

$$sin\phi =sin\left[{sin}^{-1}\sqrt{\frac{\lambda (2\iota -1)}{\iota (2\lambda +h^{\lambda })}}\right]=sn\left(\frac{s}{\sqrt{2/\lambda }},\sqrt{\frac{2\lambda +h^{\lambda }}{4\lambda }}\right)$$

and further obtain that

$$\iota =\frac{1/2}{1-\left(\frac{2\lambda +h^{\lambda }}{2\lambda }\right)s{n}^2\left(\frac{s}{\sqrt{2/\lambda }},\sqrt{\frac{2\lambda +h^{\lambda }}{4\lambda }}\right)}.$$

(22)

Based on (11) and (22), we can obtain the solution of the generalized circular Sitnikov $(N+1)$-body problem for $-2\lambda <h^{\lambda }<0$, and the period $T\left(h^{\lambda }\right)$ in the variable s is also given by $4\sqrt{2/\lambda }K\left(k\right)$. Hence, based on Formula (12), the period $T\left(h^{\lambda }\right)$ in the variable t is reformulated as follows:

$$\begin{array}{ccc}\hfill T\left(h^{\lambda }\right)& =& {\int }_0^{T\left(h^{\lambda }\right)}\mathrm{d}t={\int }_0^{4\sqrt{2/\lambda }K}{\iota }^2\left(s\right)\mathrm{d}s=4{\int }_0^{\sqrt{2/\lambda }K}{\iota }^2\left(s\right)\mathrm{d}s\hfill \\ \hfill & =& {\int }_0^{\sqrt{2/\lambda }K}{\left[1-(\frac{2\lambda +h^{\lambda }}{2\lambda })s{n}^2(\frac{s}{\sqrt{2/\lambda }},\sqrt{\frac{2\lambda +h^{\lambda }}{4\lambda }})\right]}^{-2}\mathrm{d}s\hfill \\ \hfill & =& \sqrt{\frac{2}{\lambda }}{\int }_0^K{[1-{\rho }^{2}s{n}^2(\nu ,k)]}^{-2}\mathrm{d}\nu ,\hfill \end{array}$$

(23)

where ${\rho }^2=2k^2=\frac{2\lambda +h^{\lambda }}{2\lambda }$. Because $-2\lambda <h^{\lambda }<0$, we have $0<k<\frac{1}{\sqrt{2}}<1$. It is clear that $k^2<{\rho }^2<1$. So, we apply Formula 412.07 in [27] to (23) and obtain that

$$T\left(h^{\lambda }\right)=\frac{\sqrt{2/\lambda }}{1-2k^2}[E\left(k\right)+\frac{\pi }{2\sqrt{2(1-2k^2)}}(1-{\mathrm{\Lambda }}_0({sin}^{-1}\sqrt{\frac{-2h^{\lambda }}{2\lambda -h^{\lambda }}},\sqrt{\frac{2\lambda +h^{\lambda }}{4\lambda }}))].$$

(24)

Here,

$$E\left(k\right)={\int }_0^{\frac{\pi }{2}}{(1-k^2{sin}^2\theta )}^{\frac{1}{2}}\mathrm{d}\theta$$

(25)

is the complete elliptic integral of the second kind. Moreover, letting $\beta ={sin}^{-1}\sqrt{\frac{-2h^{\lambda }}{2\lambda -h^{\lambda }}}$, we have

$${\mathrm{\Lambda }}_0(\beta ,k)=\frac{2(1-k^2)sin\beta cos\beta }{\pi {(1-(1-k^2){sin}^2\beta )}^{\frac{1}{2}}}{\int }_0^K{[1-\frac{k^2}{1-(1-k^2){sin}^2\beta }s{n}^2\nu ]}^{-1}\mathrm{d}\nu ,$$

(26)

which is the Heuman Lambda Function (see Formula 150.01 in [27]).

From (25) and (26), we see that $E\left(0\right)=\frac{\pi }{2}$ and ${\mathrm{\Lambda }}_0(\beta ,0)=sin\beta$ (Formula 151.01 in [27]), respectively. Thus, when $h^{\lambda }\to -2\lambda +$, we have

$$\underset{h^{\lambda }\to -2\lambda +}{lim}T\left(h^{\lambda }\right)=\underset{k\to 0}{lim}T\left(h^{\lambda }\right)=\sqrt{\frac{2}{\lambda }}[E\left(0\right)+\frac{\pi }{2}[1-{\mathrm{\Lambda }}_0({sin}^{-1}1,0)]=\frac{\pi }{\sqrt{2\lambda }}.$$

(27)

In addition, from ${\mathrm{\Lambda }}_0(0,k)=0$, one has

$$\underset{h^{\lambda }\to 0-}{lim}T\left(h^{\lambda }\right)=\underset{k\to \frac{1}{\sqrt{2}}}{lim}T\left(h^{\lambda }\right)=\infty .$$

(28)

Hence, (i) and (ii) in Theorem 1 hold.

Next, we will prove (iii) in Theorem 1. We notice that $\frac{\mathrm{d}T\left(h^{\lambda }\right)}{\mathrm{d}{h}^{\lambda }}=\frac{\mathrm{d}T\left(h^{\lambda }\right)}{\mathrm{d}k}\times \frac{\mathrm{d}k}{\mathrm{d}{h}^{\lambda }}$, and $\frac{\mathrm{d}k}{\mathrm{d}{h}^{\lambda }}=\frac{1}{8\lambda }{\left(\frac{2\lambda +h^{\lambda }}{4\lambda }\right)}^{-\frac{1}{2}}>0$. Thus, it is sufficient to only consider $\frac{\mathrm{d}T\left(h^{\lambda }\right)}{\mathrm{d}k}>0$. Then, we first compute $\frac{\mathrm{d}T\left(h^{\lambda }\right)}{\mathrm{d}k}$, which needs these derivatives: $\frac{\mathrm{d}E}{\mathrm{d}k}$, $\frac{\partial {\mathrm{\Lambda }}_0}{\partial \beta }$ and $\frac{\partial {\mathrm{\Lambda }}_0}{\partial k}$. Based on Formula 710.02 in [27], we know

$$\frac{\mathrm{d}E}{\mathrm{d}k}=\frac{E-K}{k}.$$

(29)

Because $\beta ={sin}^{-1}\sqrt{\frac{-2h^{\lambda }}{2\lambda -h^{\lambda }}}={sin}^{-1}{\left(\frac{1-2k^2}{1-k^2}\right)}^{\frac{1}{2}}$, we have

$$\frac{\mathrm{d}\beta }{\mathrm{d}k}=-\frac{1}{(1-k^2)\sqrt{1-2k^2}}.$$

Owing to Formula 730.04 and 710.11 in [27], we further obtain

$$\frac{\partial {\mathrm{\Lambda }}_0(\beta ,k)}{\partial \beta }=\frac{\sqrt{2}(E-(1-2k^2)K)}{\pi k}$$

(30)

and

$$\frac{\partial {\mathrm{\Lambda }}_0(\beta ,k)}{\partial k}=\frac{\sqrt{2}(E-K)\sqrt{1-2k^2}}{\pi k(1-k^2)}.$$

(31)

Based on (29) and (31), we have

$$\begin{array}{ccc}\hfill \frac{\mathrm{d}T\left(h^{\lambda }\right)}{\mathrm{d}k}& =& \frac{3\pi k\sqrt{1/\lambda }(1-{\mathrm{\Lambda }}_0(\beta ,k))}{{(1-2k^2)}^{\frac{5}{2}}}+\frac{\sqrt{2/\lambda }(1+2k^2-2k^4)E}{k(1-k^2){(1-2k^2)}^2}-\frac{\sqrt{2/\lambda }(1-3k^2+2k^4)K}{k(1-k^2){(1-2k^2)}^2}\hfill \\ \hfill & =& \frac{3\pi k\sqrt{1/\lambda }(1-{\mathrm{\Lambda }}_0(\beta ,k))}{{(1-2k^2)}^{\frac{5}{2}}}+\frac{\sqrt{2/\lambda }[(1+2k^2-2k^4)E-(1-3k^2+2k^4)K]}{k(1-k^2){(1-2k^2)}^2}\hfill \\ \hfill & =& \frac{3\pi k\sqrt{1/\lambda }(1-{\mathrm{\Lambda }}_0(\beta ,k))}{{(1-2k^2)}^{\frac{5}{2}}}+\frac{\sqrt{2/\lambda }}{k(1-k^2){(1-2k^2)}^2}{\int }_0^{\frac{\pi }{2}}\frac{\varsigma \left(k\right)}{{(1-k^{2}sin\theta )}^{\frac{1}{2}}}\mathrm{d}\theta ,\hfill \end{array}$$

where $\varsigma \left(k\right)=5k^2-4k^4-k^2(1+2k^2-2k^4){sin}^2\theta$. By the fact that $k\in (0,1/\sqrt{2})$, we have $1-{\mathrm{\Lambda }}_0(\beta ,k)>0$ from [27]. Clearly, we only need to prove $\varsigma \left(k\right)>0$. Let ${\varsigma }_1\left(k\right)=5k^2-4k^4-k^2(1+2k^2-2k^4)=2k^2(2-3k^2+k^4)$. Because $2-3k^2+k^4>0$, we have ${\varsigma }_1\left(k\right)>0$ for $k\in (0,1/\sqrt{2})$. It implies that $\varsigma \left(k\right)>0$, i.e., $\frac{\mathrm{d}T\left(h^{\lambda }\right)}{\mathrm{d}k}>0$. Therefore, for an arbitrary $h^{\lambda }\in (-2\lambda ,0)$, we have $T^{\prime }\left(h^{\lambda }\right)=\frac{\mathrm{d}T\left(h^{\lambda }\right)}{\mathrm{d}{h}^{\lambda }}>0$.

Based on all the above analyses, Theorem 1 is proved.      □

Remark 1.

(i) From Theorem 1, we see that the former three conclusions, (a), (b) and (c) of Theorem C in the literature [13] can be extended to the GCSP. (ii) Notice that the origin is surrounded by a family of periodic orbits, whose minimal periods take values from $(\pi /\sqrt{2\lambda },+\infty )$.

3. The Existence of Odd Periodic Solutions

In this section, we intend to analyze the existence of odd periodic solutions of the GESP for all $e\in [0,1)$ by using the global continuation method of the zeros of a function depending on one parameter based in the Brouwer degree. For this, we introduce the following lemma.

Lemma 1

([19], Theorems 4.3 and 4.4). Let F: $\mathbb{R}\times [a,b]\mapsto \mathbb{R}$ be real and analytic, and $\mathrm{\Sigma }=\left\{\right(x,\mu ):F(x,\mu )=0\}$ be the set of zeros of F. Assume that

(H1) Σ is bounded;

(H2) The set ${\mathrm{\Sigma }}_a=\{(x,a):F(x,a)=0\}$ is finite, and there is a isolated point $(x_0,a)\in {\mathrm{\Sigma }}_a$ such that $ind(F(x,a),x_0)\ne 0$, where ind$(F(x,a),x_0)$ is the index of Brouwer at $(x_0,a)$.

Then, there is a continuum arc $\gamma :[0,1]\mapsto \mathrm{\Sigma }$, $\gamma \left(s\right)=\left(x\right(s),\mu (s\left)\right)$ with $\gamma \left(0\right)=(x_0,a)$ such that one of the following alternatives holds:

($D1$) $\gamma \left(1\right)=\left(x\right(1),b);$

($D2$) $\gamma \left(1\right)=\left(x\right(1),a)$ with $x\left(1\right)\ne x_0$.

For $\lambda \in (0,1]$ and given an integer $M\ge 1$, we are going to explore the existence of odd $2M\pi$-periodic solutions of the system (2). Based on the symmetry of Equation (2), it is equivalent to study the existence of nontrivial solutions of the following Dirichlet problem:

$$\ddot{z}+\frac{\lambda z}{{(z^2+r^2(t,e))}^{3/2}}=0,z\left(0\right)=z\left(M\pi \right)=0.$$

(32)

Let $z^{\lambda }(t;v,e)$ be the solution of (2) satisfying

$$z^{\lambda }\left(0\right)=0,{\dot{z}}^{\lambda }\left(0\right)=v.$$

This is a real analytic function in the arguments $(t;v,e)\in \mathbb{R}\times \mathbb{R}\times [0,1)$. Because the nonlinearity in (2) is bounded, these solutions are globally defined in $(-\infty ,+\infty )$. Define

$$F_M^{\lambda }:\mathbb{R}\times [0,1)\mapsto \mathbb{R},F_M^{\lambda }(v,e)=z^{\lambda }(M\pi ;v,e).$$

Then, studying the existence of nontrivial solutions of Equation (32) for all $e\in (0,1)$ is equivalent to studying the existence of zeros of the equation

$$F_M^{\lambda }(v,e)=0,\forall e\in (0,1).$$

3.1. Satisfiability of Hypotheses (H1) and (H2)

In this subsection, we will verify that $F_M^{\lambda }(v,e)$ satisfies the assumptions (H1) and (H2) of Lemma 1. For this, we have the following propositions.

Proposition 2.

Let $z^{\lambda }\left(t\right)=z^{\lambda }(t,v,e)$ satisfy the Dirichlet problem (32) and the set

$${\mathrm{\Sigma }}^{\lambda ,M}=\{(v,e):F_M^{\lambda }(v,e)=z^{\lambda }(M\pi ,v,e)=0\}.$$

Then, ${\mathrm{\Sigma }}^{\lambda ,M}$ is bounded.

Proof. 

Observe that

$${\int }_0^{M\pi }{\dot{z}}^{\lambda }(t,v,e)\mathrm{d}t=z^{\lambda }(M\pi ,v,e)-z^{\lambda }(0,v,e)=0.$$

(33)

So, ${\dot{z}}^{\lambda }(t,v,e)$ is a sign reversal function in (0, $M\pi$). Again assuming that $\tau \in (0,M\pi )$ is a zero of ${\dot{z}}^{\lambda }(t,v,e)$, we have

$${\dot{z}}^{\lambda }\left(t\right)={\int }_{\tau }^t{\ddot{z}}^{\lambda }\left(s\right)\mathrm{d}s,t\in [0,M\pi ].$$

Given a constant E and $0<E<1$, for $\forall e\in (0,E]$ we have

$$r(t,e)=\frac{1}{2}(1-ecosu(t,e))\ge \frac{1-e}{2}\ge \frac{1-E}{2}\circeq R\left(E\right).$$

So, for all $\xi \in \mathbb{R}$, we calculate and obtain

$$\frac{\lambda \left|\xi \right|}{{[{\xi }^2+r^2(t,e)]}^{3/2}}\le \frac{\lambda \left|\xi \right|}{{[{\xi }^2+R^2\left(E\right)]}^{3/2}}\le C,$$

where $C=C\left(E\right)$ is a constant associated with E.

Moreover, from the mean value theorem of integration, we have

$${\int }_{\tau }^t{\ddot{z}}^{\lambda }\left(s\right)\mathrm{d}s={\ddot{z}}^{\lambda }\left(\eta \right)·(t-\tau ),\eta \in (\tau ,t)andt\in [0,M\pi ].$$

(34)

Consequently, for all $t\in [0,M\pi ]$, we obtain

$$\left|{\dot{z}}^{\lambda }\left(t\right)\right|=\left|{\ddot{z}}^{\lambda }\left(\eta \right)\right|\left|t-\tau \right|\le \frac{\lambda \left|z^{\lambda }\left(\eta \right)\right|}{{\left[(z^{\lambda }\left(\eta \right)\right)}^2+r^2{(t,e)]}^{3/2}}M\pi \le CM\pi .$$

Thus, we have $\left|{\dot{z}}^{\lambda }\left(0\right)\right|=\left|v\right|\le CM\pi$ for $t=0$, which shows that ${\mathrm{\Sigma }}^{\lambda ,M}$ is bounded. □

Proposition 3.

Let ${\mathrm{\Sigma }}_0^{\lambda ,M}=\{(v,0):F_M^{\lambda }(v,0)=0\}$. Then, ${\mathrm{\Sigma }}_0^{\lambda ,M}$ is finite and there is $(v_0,0)\in {\mathrm{\Sigma }}_0^{\lambda ,M}$ satisfying $ind(F_M^{\lambda }(·,0),v_0)\ne 0$.

Proof. 

Considering the zeros of $F_M^{\lambda }(·,0)$, we only need to study the solutions of the following Dirichlet problem:

$$\ddot{z}+\frac{\lambda z}{{(z^2+1/4)}^{3/2}}=0,z\left(0\right)=z\left(M\pi \right)=0.$$

(35)

From Equation (5), we know that $0<v<2\sqrt{\lambda }$. Let $z^{\lambda }(t,v,0)$ be a periodic solution with the minimal period $T^{\lambda }\left(v\right)$ of Equation (4). Based on (5) and the third item (iii) of Theorem 1, we have

$$\frac{\mathrm{d}{T}^{\lambda }}{\mathrm{d}v}=\frac{\mathrm{d}{T}^{\lambda }}{\mathrm{d}{h}^{\lambda }}·\frac{\mathrm{d}{h}^{\lambda }}{\mathrm{d}v}>0,$$

(36)

where $h^{\lambda }=\frac{1}{2}{v}^2-2\lambda$. So, $T^{\lambda }\left(v\right)$ is an increasing function in v.

By the symmetry, $z^{\lambda }(t;v,0)$ is also a solution of the boundary problem (35) if and only if there is an integer $p\ge 1$ such that $T^{\lambda }\left(v\right)/2=M\pi /p$. From (ii) of Theorem 1 and Formula (36), we have inf $T^{\lambda }\left(v\right)=\pi /\sqrt{2\lambda }$. Therefore, $2M\pi /p>\pi /\sqrt{2\lambda }$ holds. Moreover, we obtain $p<2\sqrt{2\lambda }M$. Let $\nu ={\nu }_{M,\lambda }=\left[2\sqrt{2\lambda }M\right]$ and $v_{1,M}^{\lambda }>...>v_{\nu ,M}^{\lambda }>0$ be the solutions of $T^{\lambda }\left(v\right)/2=M\pi /p$ with $p=1,...,{\nu }_{M,\lambda }$. It is clear that M must satisfy $M\ge \left[\frac{1}{2\sqrt{2\lambda }}\right]$.

Based on the symmetry of Equation (2), denote

$${\mathrm{\Sigma }}_0^{\lambda ,M}=\{-v_{1,M}^{\lambda },...,-v_{{\nu }_{M,\lambda },M}^{\lambda },0,v_{{\nu }_{M,\lambda },M}^{\lambda },...,v_{1,M}^{\lambda }\}.$$

Because $T^{\lambda }\left(v\right)$ is an increasing function in v, we have

$$z^{\lambda }(M\pi ,v,0)>0\mathrm{if}v>v_{1,M}^{\lambda }\mathrm{close}\mathrm{to}{v}_{1,M}^{\lambda },$$

$$z^{\lambda }(M\pi ,v,0)<0\mathrm{if}v<v_{1,M}^{\lambda }\mathrm{close}\mathrm{to}{v}_{1,M}^{\lambda }.$$

From here, we obtain ind$(F_M^{\lambda }(·,0),v_{1,M}^{\lambda })=1$. Furthermore,

$$\mathrm{ind}(F_M^{\lambda }(·,0),v_{p,M}^{\lambda })={(-1)}^{p+1}.$$

(37)

Similarly, we can also compute the indices for $-v_{p,M}^{\lambda }$ because of the symmetry.

Next, we compute the index at 0. Let $y\left(t\right)$ be a solution of the following variational equation:

$$\ddot{y}+8\lambda y=0,y\left(0\right)=0and\dot{y}\left(0\right)=1.$$

Noting that $\frac{\partial F_M^{\lambda }}{\partial v}(0;0)=y\left(M\pi \right)$, we have

$$\mathrm{ind}(F_M^{\lambda }(·,0),0)=\mathrm{sign}\left(\sin \left(2\sqrt{2\lambda }M\pi \right)\right)={(-1)}^{{\nu }_{M,\lambda }}.$$

To sum up, when $e=0$, there exist ${\nu }_{M,\lambda }$ nontrivial, odd, and 2$M\pi$-periodic solutions of (35) with ${\dot{z}}^{\lambda }\left(0\right)>0$, where $M\ge \left[\frac{1}{2\sqrt{2\lambda }}\right]$. Then, they can be labeled by the number of zeros of $z^{\lambda }\left(t\right)$ in $(0,M\pi )$ for $p=1,\dots ,{\nu }_{M,\lambda }$. Moreover, the index of each of these solutions, ind$(F_M^{\lambda }(·,0),v_{p,M}^{\lambda })$, is ± 1. □

Remark 2.

From Propositions 2 and 3, we can see that $F_M^{\lambda }$ satisfies the hypotheses (H1) and (H2) of Lemma 1.

3.2. Main Results

In this subsection, we will apply Lemma 1 to prove the existence of odd periodic solutions of the GESP for all $e\in [0,1)$. For this, we need to introduce the following definition.

Definition 1

([28], Definition 2). Let ${\mathcal{G}}^{*}$ be a connected component of ${\mathrm{\Sigma }}^{\lambda ,M}$ (which is actually arcwise connected because $F_M^{\lambda }$ is analytic). Then,

$$\mathcal{G}:=\{z^{\lambda }(t,v,e):(v,e)\in {\mathcal{G}}^{*}\}$$

is a global family of solutions of (2), and ${\mathcal{G}}^{*}$ is the connected component associated with $\mathcal{G}$.

Proposition 4.

For each fixed $\lambda \in (0,1]$ and $M\ge \left[\frac{1}{2\sqrt{2\lambda }}\right]$, let $(z_n^{\lambda }\left(t\right),e_n)$ be a sequence of solutions of (2) satisfying $z_n^{\lambda }\left(0\right)=z_n^{\lambda }\left(M\pi \right)=0$, ${\dot{z}}_n^{\lambda }\left(0\right)\to 0$, ${\dot{z}}_n^{\lambda }\left(0\right)\ne 0$, $e_n\to e_0<1$. Then, for large n, the number of zeros of $z_n^{\lambda }\left(t\right)$ in $(0,M\pi )$ is equal to the number of zeros of in the same interval of the nontrivial solutions of

$$\ddot{y}+\frac{\lambda }{r^3(t,e_0)}y=0.$$

Proof. 

By the continuous dependence of the solution on the initial value, one has $z_n^{\lambda }\left(t\right)\to 0$ uniformly in $[0,M\pi ]$. Then, let $v_n^{\lambda }\left(t\right)=z_n^{\lambda }\left(t\right)/{\dot{z}}_n^{\lambda }\left(0\right)$ and $v_n^{\lambda }\left(t\right)$ satisfy the following equations:

$${\ddot{v}}_n+\frac{\lambda }{{(z_n^2+r^2(t,e_n))}^{3/2}}{v}_n=0,v_n\left(0\right)=0and{\dot{v}}_n\left(0\right)=1.$$

Moreover, from the continuous dependence of the solution on the parameters, we obtain that $v_n^{\lambda }\left(t\right)$ converges in $C^1[0,M\pi ]$ to the solution $y^{\lambda }\left(t\right)$ of the following equation

$$\ddot{y}+\frac{\lambda }{r^3(t,e_0)}y=0,y\left(0\right)=0and\dot{y}\left(0\right)=1.$$

It is clear that $v_n^{\lambda }\left(0\right)=v_n^{\lambda }\left(M\pi \right)=0$. So, it holds that $y^{\lambda }\left(0\right)=y^{\lambda }\left(M\pi \right)=0$. Because $v_n^{\lambda }\left(t\right)$ and $y^{\lambda }\left(t\right)$ are analytic, the zeros of $v_n^{\lambda }\left(t\right)$ and $y^{\lambda }\left(t\right)$ are isolated, and their number of zeros must be finite in any bounded closed interval. Then, there exists a small enough positive $\delta$ such that $v_n^{\lambda }\left(\delta \right)$, $y^{\lambda }\left(\delta \right)$, $v_n^{\lambda }(M\pi -\delta$) and $y^{\lambda }(M\pi -\delta )$ are not equal to zero. Furthermore, the number of zeros of $y^{\lambda }\left(t\right)$ (resp. $v_n^{\lambda }\left(t\right)$) in [$\delta$, $M\pi -\delta$] is the same as in (0, $M\pi$). Because $v_n^{\lambda }\to y$, ${\dot{v}}_n^{\lambda }\to \dot{y}$ uniformly, and all the zeros of $y^{\lambda }\left(t\right)$ are nondegenerate, we deduce that $v_n^{\lambda }\left(t\right)$ and $y^{\lambda }\left(t\right)$ have the same number of zeros in $[\delta ,M\pi -\delta ]$ for large n. That is, $z_n^{\lambda }\left(t\right)$ and $y^{\lambda }\left(t\right)$ have the same number of zeros in $(0,M\pi$). □

Proposition 5.

For each fixed $\lambda \in (0,1]$ and $M\ge \left[\frac{1}{2\sqrt{2\lambda }}\right]$, we assume that for both the following Dirichlet problem:

$$\ddot{y}+\frac{\lambda }{r^3(t,e)}y=0,y\left(0\right)=y\left(M\pi \right)=0$$

(38)

and (32) nontrivial solutions exist. Then, the number of zeros of any nontrivial solution of (32) in $(0,M\pi )$ is less than that of (38).

Proof. 

Let $y^{\lambda }\left(t\right)$ be a solution of (38) with ${\dot{y}}^{\lambda }\left(0\right)>0$, and assume that $y^{\lambda }\left(t\right)$ has $k_1$ zeros in $(0,M\pi )$. Then, we introduce polar coordinates $y^{\lambda }\left(t\right)+i{\dot{y}}^{\lambda }\left(t\right)={\rho }_{\lambda }{e}^{i{\theta }_{\lambda }}$ in (38) and find that the argument ${\theta }_{\lambda }$ satisfies

$${\dot{\theta }}_{\lambda }=-\frac{\lambda }{r^3(t,e)}{cos}^2{\theta }_{\lambda }-{sin}^2{\theta }_{\lambda },{\theta }_{\lambda }\left(0\right)=\frac{\pi }{2}.$$

(39)

Because ${\dot{\theta }}_{\lambda }$ is always negative, one has ${\theta }_{\lambda }\left(M\pi \right)=-\frac{\pi }{2}-k_1\pi$.

Again, let $z^{\lambda }\left(t\right)$ be a nontrivial solution of (32) for each fixed e and have $k_2$ zeros in $(0,M\pi )$. Obviously, $z^{\lambda }\left(t\right)$ is also a solution of the following linear equation:

$$\ddot{y}+\lambda a_{\lambda }\left(t\right)y=0,a_{\lambda }\left(t\right):={\left[(z^{\lambda }\right)}^2\left(t\right)+r^2(t,e^{\lambda }){]}^{-3/2}.$$

(40)

Moreover, the corresponding argument ${\psi }_{\lambda }\left(t\right)$ with $z^{\lambda }+i{\dot{z}}^{\lambda }=R_{\lambda }{e}^{i{\psi }_{\lambda }}$ satisfies

$${\dot{\psi }}_{\lambda }=-\lambda a_{\lambda }\left(t\right){cos}^2{\psi }_{\lambda }-{sin}^2{\psi }_{\lambda },{\psi }_{\lambda }\left(0\right)=\frac{\pi }{2}.$$

(41)

From the definition of $a_{\lambda }\left(t\right)$, we can obtain

$$\lambda a_{\lambda }\left(t\right)\le \frac{\lambda }{r^3(t,e^{\lambda })},t\in [0,M\pi ],$$

and this inequality is strict except for the zero of $z^{\lambda }\left(t\right)$. Thus, ${\psi }_{\lambda }$(t) is an upper solution of (39) and

$${\theta }_{\lambda }\left(t\right)<{\psi }_{\lambda }\left(t\right),\forall t\in (0,M\pi ].$$

From ${\psi }_{\lambda }\left(M\pi \right)=-\frac{\pi }{2}-k_2\pi$, we have $k_2<k_1$, which implies that Proposition 5 is proved. □

From Propositions 2 and 3, we see that ${\mathrm{\Sigma }}^{\lambda ,M}$ is bounded and ind$(F_M^{\lambda }(·,0),v_{p,M}^{\lambda })\ne 0$. Moreover, there is a unique $v_{p,M}^{\lambda }\in {\mathrm{\Sigma }}_0^{\lambda ,M}\cap (0,+\infty$) with $T^{\lambda }\left(v_{p,M}^{\lambda }\right)/2=M\pi /p$, where $p\le {\nu }_{M,\lambda }$. Thus, the solution of (4) with the initial value $z\left(0\right)=0$ and $\dot{z}\left(0\right)=v_{p,M}^{\lambda }$ is odd $2M\pi$-periodic and has exactly $p-1$ zeros in $(0,M\pi )$.

Afterward, we will further infer that there exists a continuous family ${\left\{(v^{\lambda }\left(s\right),e_s)\right\}}_{s\in [0,1]}$ in $\mathbb{R}\times [0,1-\epsilon ]$ such that

$$F_M^{\lambda }(v^{\lambda }\left(s\right),e_s)=0,v^{\lambda }\left(0\right)=v_{p,M}^{\lambda }and{e}_0=0,$$

and either

$$e_1=1-\epsilon$$

(42)

or

$$e_1=0,v^{\lambda }\left(1\right)\ne v_{p,M}^{\lambda }.$$

(43)

For $e=e_s$, let $z_s^{\lambda }\left(t\right)$ be the solution of (2) that satisfies $z_s^{\lambda }\left(0\right)=0$ and ${\dot{z}}_s^{\lambda }\left(0\right)=v^{\lambda }\left(s\right)$. In addition, for $\forall s\in [0,1]$, we see that $z_s^{\lambda }\left(t\right)=-z_s^{\lambda }(-t)$ and $z_s^{\lambda }(t+2M\pi )=z_s^{\lambda }\left(t\right)$. Then, we consider the following two cases.

Case 1. $\forall s\in [0,1]$, ${\dot{z}}_s^{\lambda }\left(0\right)\ne 0.$

Assuming ${\dot{z}}_s^{\lambda }\left(0\right)>0$, we notice that $z_0^{\lambda }\left(t\right)$ has $p-1$ zeros in $(0,M\pi )$. Furthermore, for any sufficiently small positive $ϵ$, $z_s^{\lambda }\left(t\right)\in C^1[ϵ,M\pi -ϵ]$ and satisfies

(i)

$\forall s\in [0,1]$, $z_s^{\lambda }\left(ϵ\right)\ne 0$, $z_s^{\lambda }(M\pi -ϵ)\ne 0$.

(ii)

$\forall s\in [0,1]$, $z_s^{\lambda }\left(t\right)$ is nontrivial, and the zeros of $z_s^{\lambda }\left(t\right)$ are nondegenerate.

(iii)

$(t,s)\in [ϵ,M\pi -ϵ]\times [0,1]\mapsto (z_s^{\lambda }\left(t\right),{\dot{z}}_s^{\lambda }\left(t\right))$ is continuous.

Thus, from Lemma 7.2 in the literature [19], we obtain that the number of zeros of $z_s^{\lambda }\left(t\right)$ in $[ϵ,M\pi -ϵ]$ is independent of s, implying that the number of zeros of $z_s^{\lambda }\left(t\right)$ in (0, $M\pi$) is also independent of s. Then, for arbitrary $s\in [0,1]$, $z_s^{\lambda }\left(t\right)$ has $p-1$ zeros in $(0,M\pi )$.

If the first alternative (42) holds, then we have $e_s\to 1-\epsilon$ and ${\dot{z}}_s^{\lambda }\left(0\right)\to v>0$. In this condition, the second alternative (43) cannot occur. Otherwise, $e_1=0$ and $v^{\lambda }\left(1\right)\ne v_{p,M}^{\lambda }$. Based on $v^{\lambda }\left(1\right)\in {\mathrm{\Sigma }}_0^{\lambda ,M}\cap (0,+\infty )$, we obtain $v^{\lambda }\left(1\right)=v_{q,M}^{\lambda }$ for some $q\ne p$, implying that $z_1^{\lambda }\left(t\right)$ has $q-1$ zeros in (0, $M\pi$). So, there is a contradiction.

Let the set $\mathcal{A}=\{(v^{\lambda }\left(s\right),e_s):s\in [0,1]$, $e_s\in [0,1)\}$ be a connected subset of ${\mathrm{\Sigma }}^{\lambda ,M}$ and ${\mathcal{A}}_{p,M,\lambda }^{*}$ be the connected component of ${\mathrm{\Sigma }}^{\lambda ,M}$ containing $\mathcal{A}$. Based on the above analysis, we obtain that each solution in ${\mathcal{A}}_{p,M,\lambda }=\{z^{\lambda }(t,v,e):(v,e)\in {\mathcal{A}}_{p,M,\lambda }^{*}\}$ is odd $2M\pi$-periodic and has $p-1$ zeros in $(0,M\pi )$. Letting $Pro{y}_2(v,e)=e$, we have $Pro{y}_2\left({\mathcal{A}}_{p,M,\lambda }^{*}\right)=[0,1)$.

Case 2. ${\dot{z}}_s^{\lambda }\left(0\right)$ vanishes for some $s\in [0,1]$.

Let $\sigma$ be the first zero of ${\dot{z}}_s^{\lambda }\left(0\right)$. Then, we have

$${\dot{z}}_s^{\lambda }\left(0\right)>0,\mathrm{if}s\in [0,\sigma )and{\dot{z}}_{\sigma }^{\lambda }\left(0\right)=0.$$

Now we consider the family ${\{{\widehat{z}}_s^{\lambda },{\widehat{e}}_s\}}_{s\in [0,1)}$ with ${\widehat{z}}_s^{\lambda }=z_{s\sigma }^{\lambda }$ and ${\widehat{e}}_s=e_{s\sigma }$. For $\forall s\in [0,1]$, we have ${\dot{\widehat{z}}}_s^{\lambda }\left(0\right)>0$. From Case 1, we further know that ${\widehat{z}}_s^{\lambda }\left(t\right)$ has $p-1$ zeros in $(0,M\pi )$. The definition of $\sigma$ implies that $\underset{s\to 1^{-}}{lim}{\widehat{e}}_s=e_{\sigma }\in [0,1-\epsilon ]$ and $\underset{s\to 1^{-}}{lim}{\widehat{z}}_s^{\lambda }\left(t\right)=0$. Owing to Proposition 4, we conclude that the equation

$$\ddot{y}+\frac{\lambda }{r^3(t,e_{\sigma })}y=0$$

has a nontrivial odd $2M\pi$-periodic solution with $p-1$ zeros in $(0,M\pi )$.

Similar to Case 1, let the set $\mathcal{B}=\{(v_{s\sigma }^{\lambda },e_{s\sigma }):s\in [0,1),e_{s\sigma }\in [0,e_{\sigma })\}$ be a connected subset of ${\mathrm{\Sigma }}^{\lambda ,M}$ and ${\mathcal{B}}_{p,M,\lambda }^{*}$ be the connected component of ${\mathrm{\Sigma }}^{\lambda ,M}$ containing $\mathcal{B}$. Hence, all of the solutions in ${\mathcal{B}}_{p,M,\lambda }=\{z^{\lambda }(t,v,e):(v,e)\in {\mathcal{B}}_{p,M,\lambda }^{*}\}$ are odd $2M\pi$-periodic and have $p-1$ zeros in $(0,M\pi )$. Because $[0,e_{\sigma })\subset Pro{y}_2\left({\mathcal{B}}_{p,M,\lambda }^{*}\right)$ and $e_{\sigma }\notin Pro{y}_2\left({\mathcal{B}}_{p,M,\lambda }^{*}\right)$, from Proposition 5, we have $Pro{y}_2\left({\mathcal{B}}_{p,M,\lambda }^{*}\right)=[0,e_{\sigma })$ with $e_{\sigma }<1$.

Above all, we have the following main theorem of our paper.

Theorem 2.

Let ${\mathcal{G}}_{p,M,\lambda }^{*}$ be the connected component of ${\mathrm{\Sigma }}^{\lambda ,M}$. For each fixed $\lambda \in (0,1]$, $M\ge \left[\frac{1}{2\sqrt{2\lambda }}\right]$ and $p=1,...,\nu$, there exists a global family ${\mathcal{G}}_{p,M,\lambda }:=\{z^{\lambda }(t,v,e):(v,e)\in {\mathcal{G}}_{p,M,\lambda }^{*}\}$ of nontrivial solutions of (2), and ${\mathcal{G}}_{p,M,\lambda }^{*}$ is the connected component associated with ${\mathcal{G}}_{p,M,\lambda }$. Moreover,

(1) 

all solutions of ${\mathcal{G}}_{p,M,\lambda }$ are odd $2M\pi$-periodic and have $p-1$ zeros in $(0,M\pi )$.

(2) 

${\mathcal{G}}_{p,M,\lambda }^{*}\cap \{e=0\}=\left\{(v_{p,M}^{\lambda },0)\right\}$ and one of the following alternatives holds:

(2.a) 

$Pro{y}_2\left({\mathcal{G}}_{p,M,\lambda }^{*}\right)=[0,1)$;

(2.b) 

$Pro{y}_2\left({\mathcal{G}}_{p,M,\lambda }^{*}\right)=[0,E^{\lambda })$ with $E^{\lambda }<1$.

Remark 3.

(i) If ${\mathcal{G}}_{p,M,\lambda }$ satisfies (2.a), then the family continues for all values of $e\in [0,1)$. (ii) If ${\mathcal{G}}_{p,M,\lambda }$ satisfies (2.b), then it ends in the equilibrium $z=0$ at a value of eccentricity $E^{\lambda }$. Additionally, the linear differential equation

$$\ddot{y}+\frac{\lambda }{r^3(t,E^{\lambda })}y=0$$

(44)

has a nontrivial odd $2M\pi$-periodic solution with exactly $p-1$ zeros in the interval $(0,M\pi )$.

Next, we consider the options of (2.a) and (2.b) of Theorem 2 and have the following theorem.

Theorem 3.

For any $k\in \mathbb{N}$ and $\lambda \in (0,1]$, we assume that k, M and λ satisfy $k<M$, and $\frac{{(M-k)}^2}{M^2}\le \lambda <\frac{{(M-k+1)}^2}{M^2}$. So, one has

(1) 

if $1\le p<M-k+1$, then statement (2.a) of Theorem 2 holds;

(2) 

if $p\ge M-k+1$, then ${\rho }_M<1-\epsilon$ and (2.b) of Theorem 2 holds, $E^{\lambda }>{\rho }_M$, where

$${\rho }_M=min\{2{\left(\frac{M}{\nu }\right)}^{2/3}-1,1-2{\left(\frac{M}{\nu +1}\right)}^{2/3}\}.$$

In order to prove Theorem 3, we introduce the following lemma.

Lemma 2

([19,29]). Assume that $a\left(t\right)$ is continuous, $2M\pi$-periodic and for some $n\ge 0$ satisfies

$${\left(\frac{n}{M}\right)}^2\le a\left(t\right)\le {\left(\frac{n+1}{M}\right)}^2,forallt\in \mathbb{R},$$

where both inequalities are strict somewhere. Then, $\ddot{y}+a\left(t\right)y=0$ has no $2M\pi$-periodic solution (excepting $y\equiv 0$).

Proof of Theorem 3.

Notice that $\zeta \left(t\right)=sin\sqrt{\lambda }t$ is a nontrivial odd-periodic solution of the equation

$$\ddot{\zeta }+\lambda \zeta =0.$$

(45)

For $k\in \mathbb{N}$, $k<M$ and $k,M$ satisfying $\frac{(M-k)\pi }{\sqrt{\lambda }}\le M\pi <\frac{(M-k+1)\pi }{\sqrt{\lambda }}$, i.e., $\frac{{(M-k)}^2}{M^2}\le \lambda <\frac{{(M-k+1)}^2}{M^2}$ and $\lambda \in (0,1]$, we obtain that $\zeta \left(t\right)$ has $M-k+1$ zeros in [0, $M\pi$]. Moreover, because $\frac{\lambda }{r^3(t,E^{\lambda })}>\lambda$, we apply the Sturm comparison theory and derive that the nontrivial odd-periodic solutions of (44) have at least $M-k$ zeros in (0, $M\pi$). However, if $p-1<M-k$, then there is no $2M\pi$-periodic solution of (44). Thus, if $1\le p<M-k+1$, we can conclude that statement (2.a) of Theorem 2 holds from Remark 3.

In addition, if $p-1>M-k$ and (2.b) of Theorem 2 holds, then we have $E^{\lambda }>{\rho }_M$, where ${\rho }_M=min\{2{\left(\frac{M}{\nu }\right)}^{2/3}-1,1-2{\left(\frac{M}{\nu +1}\right)}^{2/3}\}$ and ${\rho }_M<1-\epsilon$. Otherwise, $E^{\lambda }\le {\rho }_M$. Because $\frac{(1-E^{\lambda })}{2}\le r(t,E^{\lambda })\le \frac{(1+E^{\lambda })}{2}$, we have

$${\left(\frac{\nu \sqrt{\lambda }}{M}\right)}^2\le \frac{8\lambda }{{(1+E^{\lambda })}^3}\le \frac{\lambda }{r{(t,E^{\lambda })}^3}\le \frac{8\lambda }{{(1-E^{\lambda })}^3}\le {\left(\frac{\nu +1}{M}\right)}^2\lambda \le \frac{{(\nu \sqrt{\lambda }+1)}^2}{M^2}.$$

Letting $n=\nu \sqrt{\lambda }$ in Lemma 2, we obtain that Equation (44) has no $2M\pi$-periodic solution. However, we note that there is a contradiction from the item (ii) of Remark 3. So, if $p\ge M-k+1$, ${\rho }_M<1-\epsilon$ and (2.b) of Theorem 2 holds, then $E^{\lambda }>{\rho }_M$. □

Remark 4.

When $k=0$, we have the only choice $\lambda =1$, i.e, the generalized elliptic Sitnikov $(N+1)$-body problem is just the Sitnikov problem. At this time, there exist the odd $2M\pi$-periodic solutions with no zeros in $(0,M\pi )$ for all $e\in [0,1)$, which is in accordance with the conclusion in the literature [20].

4. Conclusions

In this paper, we studied the existence of the families of odd symmetric periodic solutions in the generalized elliptic Sitnikov $(N+1)$-body problem for all values of the eccentricity $e\in [0,1)$ using the global continuation method. We first studied the properties of the period of the solution of the generalized circular Sitnikov $(N+1)$-body problem $(e=0)$ using elliptic functions. Then, based on these properties of the period and applying the global continuation method of the zeros of a function depending on one parameter, the existence of odd periodic solutions was obtained for all $e\in [0,1)$. Specifically, according to the symmetry of the equation, the existence of an odd family of symmetric periodic solutions was transformed into the existence of solutions of the corresponding Dirichlet problem. Moreover, we defined an analytical function $F_M^{\lambda }$ such that the existence of the solutions of the Dirichlet problem is equivalent to the existence of the zero point of $F_M^{\lambda }$. It was finally verified that $F_M^{\lambda }$ satisfied the basic assumptions of the global continuation theorem, implying the existence of the odd family of symmetry periodic solutions. Meanwhile, the theoretical result showed that the temporal frequencies of periodic solutions depend on the total mass $\lambda$ (or the number N) of the primaries in a delicate way. Moreover, it is believed that these results have important significance and practical value for the design and control of satellite orbital motion in the field of aviation.

One of our plans for future work is to investigate the stability of these symmetric periodic solutions in the generalized elliptic Sitnikov $(N+1)$-body problem.