Killing Vector Fields of Static Cylindrically Symmetric Spacetime—A Rif Tree Approach

Abstract

In this paper, we use an algebraic approach to classify cylindrically symmetric static spacetimes according to their killing vector fields. This approach is based on using a maple algorithm to re-cast the Killing’s equations into a reduced involutive form and integrating the Killing’s equations subject to the constraints given by the algorithm. It is shown that this approach provides some additional spacetime metrics, which were not provided previously by solving the Killing’s equations using a direct integration technique. To discuss some physical implications of the obtained spacetime metrics, we use them in the Einstein equations and discuss their significance.

1. Introduction

Since the pioneering work of Newton in 1687, the study of gravity and its impact has been the focus of discussions by mathematicians and physicists. According to Newton, his theory of gravity is based mainly on two important elements involving the discussion of equations for a gravitational field and a corresponding response of matter to the gravitational field [1]. In 1916, Einstein came up with his theory of general relativity (GR), in which he revolutionized the Newtonian concept of force into a purely geometric concept. According to GR, the concept of gravitational force is interpreted in terms of curvature, in that the presence of matter in spacetime geometry produces curvature, and, in turn, curvature dictates how motions of test particles take place in that geometry. In addition, the GR nicely explains several phenomena, such as the perihelion advance of the planet Mercury—which was not explained precisely by Newtonian gravity—the gravitational deflection of light, and the existence of gravitationally compact objects such as black holes [1,2]. As for GR, it defines spacetime dynamics and related concepts in terms of a highly non-linear coupled system of Einstein’s field equations (EFEs) [3],

$$G_{ab}=R_{ab}-\frac{1}{2}{g}_{ab}R=\kappa T_{ab},$$

(1)

where $R_{ab}$, $g_{ab}$, and $T_{ab}$ respectively denote Ricci, metric, and stress energy tensor components, while R represents trace of the Ricci tensor and $\kappa$ a coupling constant. Physically, the EFEs describe how the distribution of matter is related to the presence of matter and energy in the spacetime. From their construction, the EFEs constitute a complex system of 10 highly non-linear coupled systems of partial differential equations. Due to this non-linear nature, these equations pose a serious challenge in finding their exact solutions [3,4]. It is because of this non-linear nature that very few physically interesting exact solutions of these equations are available in the literature [2]. Nevertheless, if we choose EFEs (1) to define the arbitrary stress energy momentum tensor, then any metric will represent some solution of these equations. However, not all such solutions are meaningful because the corresponding energy–momentum tensor may be highly non-physical. Therefore, in order to obtain physically interesting solutions, one would expect certain restrictions to be satisfied by the spacetime metric $g_{ab}$ representing those solutions. These restrictions are defined in terms of Killing’s vector fields (KVFs) [3]. In GR, a variety of symmetries are discussed which are of great interest in the subject [3]. Of these symmetries, the most fundamental one is given by a KVF. A KVF plays a pivotal role in spacetime physics by preserving the spacetime metric and providing certain conservation laws [3]. Apart from KVFs, some other well-known and physically interesting symmetries in GR are given by Ricci collineations (RCs), which preserve the Ricci tensor; matter collineations (MCs), which preserve the energy–momentum tensor; and curvature collineations (CCs), which preserve the curvature tensor. All these symmetries are defined by requiring that the Lie derivative of metric, Ricci, energy–momentum, and Riemann tensors is zero along a certain vector field [3]. Since our interest in this paper is to study symmetries given by Killing’s vector fields, we focus our attention to KVFs only. As stated above, a KVF is vector along which the Lie derivative of a metric tensor $g_{ab}$ is zero. In other words, a KVF defines a smooth vector field which preserves a spacetime metric. In mathematical terms, $\xi$ is called a KVF if,

$${\mathcal{L}}_{\xi }{g}_{ab}=0.$$

(2)

In addition, a Lie derivative may also preserve a spacetime metric up to a conformal factor times the metric itself. Such a symmetry is defined by a conformal Killing vector field (CKVF). In mathematical terms, a vector $\xi$ defines a CKVF if it satisfies the conformal Killing’s equation,

$${\mathcal{L}}_{\xi }{g}_{ab}=2\alpha \left(\underline{x}\right)g_{ab},$$

(3)

where $\alpha$ is some real valued function. The vector field $\xi$ becomes a KVF if $\alpha =0$ in (3). Moreover, if $\alpha$ is a constant in (3), then the vector field $\xi$ defines a homothetic vector field. In (3), if $g_{ab}$ is replaced by $R_{ab}$, it defines a conformal $RC$, which reduces an $RC$ if $\alpha =0$ in (3). In case $g_{ab}=R_{ab}$ and $\alpha$ is an arbitrary constant in (3), then $\xi$ becomes a homothetic $RC$ [3]. Similarly, we can define a conformal $MC$ if $g_{ab}$ is replaced by $T_{ab}$ in (3). The main purpose of this paper is to discuss the KVFs; therefore, we will focus our discussion on KVFs only. The KVFs are solutions of the Killing’s Equation (2), which comprises a system of 10 coupled first-order partial differential equations defined in terms of four unknown functions of four variables. In a coordinate system, the Killing’s equations (in a convenient form) become [5],

$${\mathcal{L}}_{\xi }{g}_{ab}=g_{ac}{\xi }_{,b}^c+g_{cb}{\xi }_{,a}^c+g_{ab,c}{\xi }^c=0$$

(4)

In a 4-spacetime geometry, the maximum number of KVFs is 10 when the spacetime time metric is flat or of constant curvature. However, when the spacetime geometry is non-flat, one expects less than maximal KVFs. For example, in a cylindrically symmetric spacetime geometry, there exists a minimal symmetry group of 3 KVFs while the maximal symmetry group is given by 10 KVFs [6].

To signify the importance of KVFs and their relationships with other well-known symmetries, we briefly overview some recent literature. Bokhari et al. classified spherically symmetric static spacetimes according to their KVFs [7,8]. In their work, they showed that a general static spherically symmetric spacetime metric can provide a Killing symmetry group of dimensions 10, 7, 6, or 4 only. Given that the method developed gave an interesting classification, the same authors extended their investigations to the study of the symmetry classification problem for both RC and CC symmetries for a spherically symmetric spacetime and obtained interesting relationships between KVFs, RCs, and CCs [9,10]. In 2008, Moopanar and Maharaj discussed CKVFs and published their investigations in [11]. Continuing their work, the same authors published an interesting result in 2010 [12]. In this work, they obtained a general conformal Killing symmetry without specifying the form of the matter distribution, thus showing that their previous result was a special case of the current one. In addition, they showed that there exists a hypersurface orthogonal conformal KVF in an exact solution of Einstein’s equations for a relativistic fluid which is expanding, accelerating, and shearing.

Although the investigations discussed above are quite significant, they are restricted to static spacetime geometries. In GR, non-static spacetimes are also of great interest from the cosmological point of view. In this context, various non-static spacetime geometries are discussed according to their KVFs. Of significant interest is an extensive work by Hussain et al. on non-static spherically symmetric spacetimes and their conformal Ricci collineations in 2019 [13].

The spacetime geometry endowed with a cylindrically symmetric metric has also been discussed and studied by many researchers. In 1998, Bokhari et. al. extended the idea of KVFs to present a complete classification of curvature collineations of cylindrically symmetric spacetimes [14,15]. In 2002, they extended their investigations of KVFs to discuss matter collineations of a specific metric admitting static cylindrical symmetry by showing that the considered metric admits proper matter collineations [16]. In 2004, Sharif provided symmetries of the energy momentum tensor of cylindrically symmetric static spacetimes [17]. They found that, in the non-degenerate case, the energy–momentum tensor would admit 3, 4, 5, 6, 7, and 10 matter collineations, in which three will represent isometries [17]. In 2007, Shabbir et al. presented a classification of cylindrically symmetric static spacetimes by their homothetic vector fields, concluding that the homothetic vector fields admitted by the metrics of this spacetime were 4, 5, 7, and 11 only. In the same year, Ziad et al. published an interesting work on the classification of cylindrically symmetric static spacetimes by their isometries and provided a complete set of metrics obtained in their classification and their corresponding Lie algebras [6]. Extending their work on KVFs [18], Farhad studied the conservation laws of cylindrically symmetric vacuum solutions of Einstein field equations in the presence of the Noether theorem [19]. Feroze extended their work to obtain a complete classification of cylindrically symmetric static spacetimes according to Conservation Laws [20].

Given that the cylindrically symmetric static spacetimes are of interest [21], we re-address the classification of cylindrically symmetric spacetimes by their KVFs using a new approach, known as the Rif tree approach. This approach is based on an algorithm (set of commands), called the Rif algorithm, that is developed using the Exterior package in Maple plate form. First of all, one needs to load the Exterior package, that is, “With(Exterior)”. The next step is to insert the system of differential equations which we want to convert to the simplified form using the command “sys{DEs}”. In our case, these differential equations are the Killing’s equations. In the third step, the command “symmetry, eq: = findsymmetry” is used to analyze the system of Killing’s equations and to find all the required conditions on metric functions under which the spacetime under consideration may admit Killing symmetries other than the minimum ones. As a result, the algorithm displays all such conditions on the metric functions. It is very useful to view these conditions graphically, and the command “caseplot(eq, pivots)” is used for this purpose. This graphical view is given in terms of a tree (called a Rif tree), whose branches signify the conditions on the metric functions under which the spacetime may admit KVFs other than the minimum ones. After that, one needs to solve the set of Killing’s equations under the conditions given by the branches of the Rif tree, giving the explicit form of KVFs.

While using the Rif algorithm, ordering of the dependent and independent variables is of great significance, as the complexity of the resulting Rif tree depends on this ordering. As such, there is no general rule that can be helpful in ordering variables to obtain a simplified Rif tree. In our problem, after trial and error, it is observed that the ordering $X^0>X^1>X^2>X^3$ for dependent and $t>\rho >\theta >z$ for independent variables produces the most simplified Rif tree. More recently, the Rif tree approach has also been used in another study relating to a classification problem of KVFs, showing that additional spacetime metrics were obtained there, which were not found previously [22]. Based on this, we re-address the classification of KVFs of cylindrically symmetric static spacetimes using the Rif tree approach. We show that, although these spacetimes admit 3, 4, 5, 6, 7, and 10 KVFs only, some additional spacetime metrics are obtained, which were not given previously by using a direct integration technique.

2. Killing’s Equations

Spherical and cylindrical symmetries are the simplest symmetries among the well-known spacetime symmetries studied in the literature. Both these symmetries are used to make it possible to find many exact solutions of Einstein’s field equations. Between these two symmetries, cylindrical symmetry is more important in the sense that it gives rise to the existence of linearly extended structures such as cosmic strings and the observed cosmic jets. Since the development of general relativity, many cylindrically symmetric static solutions have been obtained, for example vacuum, electrovacuum, and perfect fluid solutions. The general cylindrically symmetric static metric is given by the expression [6]:

$$d{s}^2=-A{\left(\rho \right)}^{2}d{t}^2+d{\rho }^2+B{\left(\rho \right)}^{2}d{\theta }^2+C{\left(\rho \right)}^{2}d{z}^2,$$

(5)

where $A,$ B, and C are non-zero functions of the variable $\rho$. The minimum KVFs admitted by this metric are ${\partial }_t,$${\partial }_{\theta },$ and ${\partial }_z$. If $A=B=C=1,$ the metric admits maximal symmetry given by ten KVFs. Moreover, for $B=C$, the above metric becomes a plane symmetric static metric which has been completely classified according to KVFs using the Rif tree approach. Using the above metric in the Killing’s equations, (4), we obtain the following system of ten differential equations:

$$\begin{array}{cc}\hfill A^{\prime }\left(\rho \right){\xi }^1+A\left(\rho \right){\xi }_{,0}^0& =0\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill A{\left(\rho \right)}^2{\xi }_{,1}^0-{\xi }_{,0}^1& =0\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill A{\left(\rho \right)}^2{\xi }_{,2}^0-B{\left(\rho \right)}^2{\xi }_{,0}^2& =0\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill A{\left(\rho \right)}^2{\xi }_{,3}^0-C{\left(\rho \right)}^2{\xi }_{,0}^3& =0\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\xi }_{,1}^1& =0\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\xi }_{,2}^1+B{\left(\rho \right)}^2{\xi }_{,1}^2& =0\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\xi }_{,3}^1+C{\left(\rho \right)}^2{\xi }_{,1}^3& =0\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill B^{\prime }\left(\rho \right){\xi }^1+B\left(\rho \right){\xi }_{,2}^2& =0\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill B{\left(\rho \right)}^2{\xi }_{,3}^2+C{\left(\rho \right)}^2{\xi }_{,2}^3& =0\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill C^{\prime }\left(\rho \right){\xi }^1+C\left(\rho \right){\xi }_{,3}^3& =0\hfill \end{array}$$

(15)

The above system of Killing’s equations has been completely classified previously by using a direct integration technique [6], showing that the spacetime admitted only 3, 4, 5, 7, and 10 KVF algebra. In the present study, we re-address this problem by using a different approach, known as the Rif tree approach. As stated in the introduction, this approach is based on using the ten Killing’s equations in an algorithm developed in Maple, which produces all possible metrics for which the above Killing’s Equations (6)–(15) are to be solved. We show that this approach provides additional spacetime metrics, which were not given previously by using a direct integration technique [6].

3. Classification of KVFs

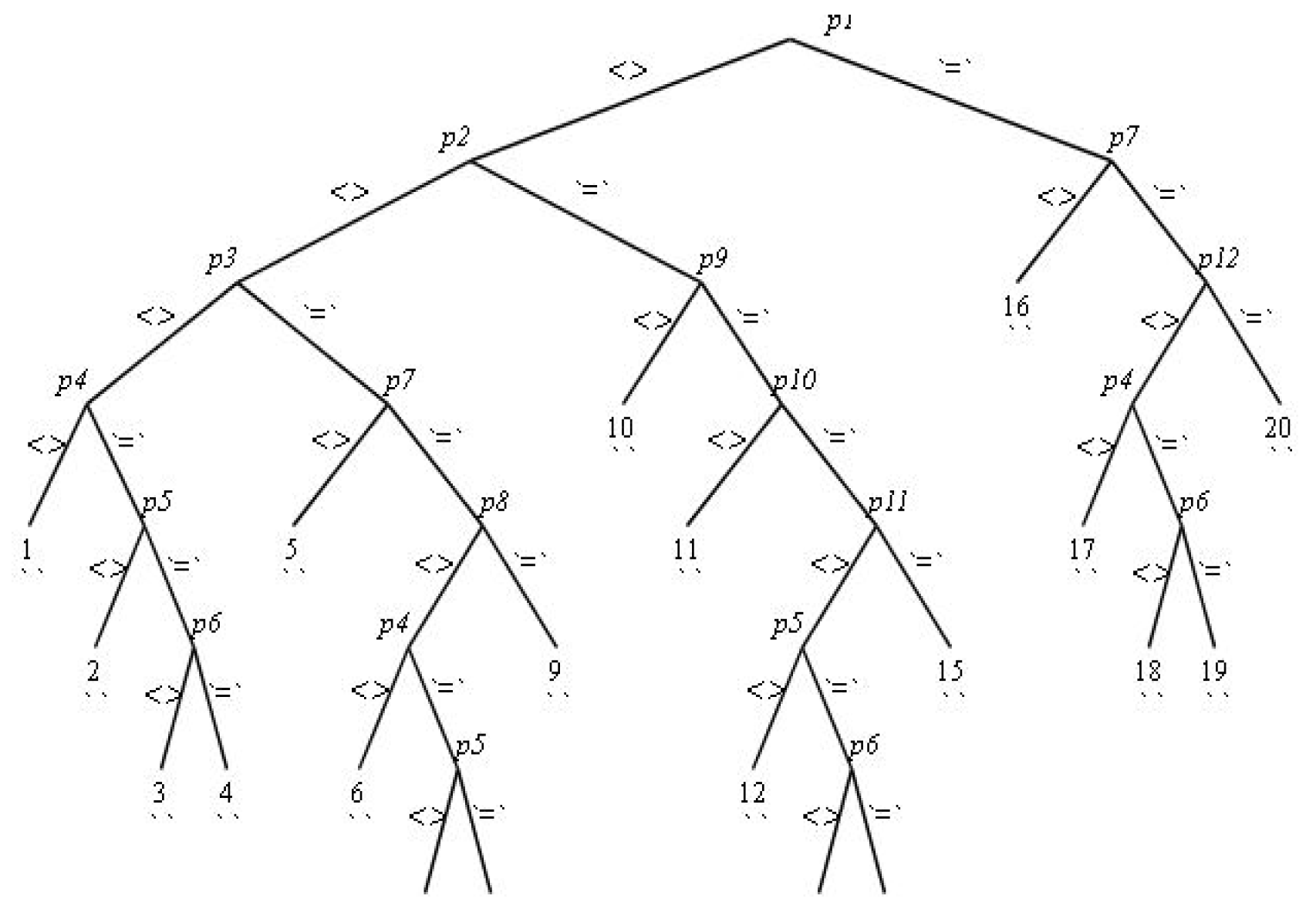
In this section, we use a computer algorithm to transform the system of Equations (6)–(15) into the reduced involutive form. As a result, we obtain the Rif tree given in Figure 1.

The nodes of the Rif tree are called pivots, which are given by:

$$\begin{array}{cc}\hfill P_1& =B^{\prime }\left(\rho \right)\hfill \\ \hfill P_2& =A^{\prime }\left(\rho \right)\hfill \\ \hfill P_3& =C^{\prime }\left(\rho \right)\hfill \\ \hfill P_4& =A^{\prime }{\left(\rho \right)}^2-A\left(\rho \right)A^{″}\left(\rho \right)\hfill \\ \hfill P_5& =B^{\prime }{\left(\rho \right)}^2-B\left(\rho \right)B^{″}\left(\rho \right)\hfill \\ \hfill P_6& =C^{\prime }{\left(\rho \right)}^2-C\left(\rho \right)C^{″}\left(\rho \right)\hfill \\ \hfill P_7& =A^{\prime }\left(\rho \right)A^{″}\left(\rho \right)-A\left(\rho \right)A^{‴}\left(\rho \right)\hfill \\ \hfill P_8& =A^{\prime }\left(\rho \right)B^{\prime }\left(\rho \right)-A^{″}\left(\rho \right)B\left(\rho \right)\hfill \\ \hfill P_9& =C^{\prime }\left(\rho \right)C^{″}\left(\rho \right)-C\left(\rho \right)C^{‴}\left(\rho \right)\hfill \\ \hfill P_{10}& =B^{\prime }\left(\rho \right)B^{″}\left(\rho \right)-B\left(\rho \right)B^{‴}\left(\rho \right)\hfill \\ \hfill P_{11}& =B^{\prime }\left(\rho \right)C^{\prime }\left(\rho \right)-C^{″}\left(\rho \right)B\left(\rho \right)\hfill \\ \hfill P_{12}& =A^{\prime }\left(\rho \right)C^{\prime }\left(\rho \right)-A^{″}\left(\rho \right)C\left(\rho \right)\hfill \end{array}$$

(16)

The branches of the Rif tree along with these pivots provide a complete set of constraints satisfied by the metric functions appearing in (5). The symbols = and $<>$ appearing in the Rif tree denote whether the corresponding pivot is zero or non-zero. For example in branch 1, $p_1, p_2, p_3$, and $p_4$ are non-zero, that is, $B^{\prime }\left(\rho \right)\ne 0,$ $A^{\prime }\left(\rho \right)\ne 0,$ $C^{\prime }\left(\rho \right)\ne 0$ and $A^{\prime }{\left(\rho \right)}^2-A\left(\rho \right)A^{″}\left(\rho \right)\ne 0$. Similarly, the constraints of branch 2 are $p_1\ne 0, p_2\ne 0, p_3\ne 0, p_4=0$, and $p_5\ne 0$. In the light of these conditions, we solve the ten Killing’s Equations (6)–(15) for each branch of the Rif tree to find the explicit form of KVFs. Since the procedure is quite lengthy but straightforward, we therefore restrict ourselves to mainly giving the results only. However, to show some procedural steps, we discuss one case arising from branch 1 of the Rif tree with brief detail. Integrating (10) with respect to $\rho$ gives:

$${\xi }^1=g^1(t,\theta ,z).$$

(17)

Integrating Equations (7), (11), and (12) over $\rho$ and using the above value of $x{i}^1$ gives:

$$\begin{array}{cc}\hfill {\xi }^0=& g_t^1\int \frac{1}{A{\left(\rho \right)}^2}d\rho +g^0(t,\theta ,z)\hfill \\ \hfill {\xi }^2=& -g_{\theta }^1\int \frac{1}{B{\left(\rho \right)}^2}d\rho +g^2(t,\theta ,z)\hfill \\ \hfill {\xi }^3=& -g_z^1\int \frac{1}{C{\left(\rho \right)}^2}d\rho +g^3(t,\theta ,z)\hfill \end{array}$$

(18)

It can be noted from branch 1 that $P_1=B^{\prime }\ne 0$, $P_2=A^{\prime }\ne 0,$$P_3=C^{\prime }\ne 0$, and $P_4=A^{\prime 2}-A{A}^{″}\ne 0$. Substituting (17) and (18) in Equation (6) and differentiating it twice with respect to $\rho ,$ we have $(A{A}^{‴}-A^{\prime }{A}^{″})g^1=0$. This provides two possibilities, namely, (i) $A{A}^{‴}-A^{\prime }{A}^{″}=0;g^1\ne 0;$ and (ii) $A{A}^{‴}-A^{\prime }{A}^{″}\ne 0;g^1=0$. We first consider case (i). Integrating (i) gives $A=m_1{e}^{k_1\rho }+m_2{e}^{-k_1\rho }$. However, this case leads to a contradiction, namely, $g^1=0$. Therefore, we do not discuss this case any further.

Now we consider case (ii), which reduces Equations (17) and (18) to:

$$\begin{array}{cc}\hfill {\xi }^0=& G^1(\theta ,z)\hfill \\ \hfill {\xi }^1=& 0\hfill \\ \hfill {\xi }^2=& g^2(t,\theta ,z)\hfill \\ \hfill {\xi }^3=& g^3(t,\theta ,z)\hfill \end{array}$$

(19)

Now, using above results in Equations (13) and (15), we obtain:

$$\begin{array}{cc}\hfill {\xi }^0=& G^1(\theta ,z)\hfill \\ \hfill {\xi }^1=& 0\hfill \\ \hfill {\xi }^2=& F(t,z)\hfill \\ \hfill {\xi }^3=& M(t,\theta )\hfill \end{array}$$

(20)

Substituting the above in Equation (8) gives rise to two sub cases (a) $A=B$ and (b) $A\ne B$. In case (a), two more sub cases arise: $A=B=C$ and $A=B\ne C$. In the first case, we obtain six KVFs, while the second case leads to a contradiction. Lastly, considering case (b), we again obtain two sub cases, namely, $C=A\ne B$ and $C\ne A\ne B$. In the former case, we obtain four KVFs, while the latter one provides the minimal symmetry given by three KVFs.

In next sections, we mainly provide results without giving detailed calculations. For case (a), the obtained six KVFs were: $X_1={\partial }_t$, $X^2={\partial }_{\theta }$ and $X^3={\partial }_z$, which are the minimum KVFs with $X_4=\theta {\partial }_t+t{\partial }_{\theta }$, $X_5=z{\partial }_t+t{\partial }_z$, $X_6=z{\partial }_{\theta }-\theta {\partial }_z$ being additional. However, in Case (b), when $C=A\ne B$, there are four KVFs: the minimum three KFVs and $X_4=\theta {\partial }_t+t{\partial }_{\theta }$. Note that, in the last case, we had only three minimum KVFs.

3.1. Three KVFs

In this section, we provide the list of all metrics admitting three KVFs: $X_1={\partial }_t$, $X_2={\partial }_{\theta }$, and $X_3={\partial }_z$. The minimum KVFs are obtained in 15 branches of the Rif tree, namely, 1–7, 10–13, and 15–18. The corresponding branches, along with their metric functions satisfying certain conditions, are presented in

Table 1. Metrics Admitting Three KVFs.

Branch	Metric Functions	Energy Density
1	$A=A\left(\rho \right),B=B\left(\rho \right),$$C=C\left(\rho \right),$$A{A}^{‴}-A^{\prime }{A}^{″}\ne 0$.	$\rho =\frac{-A^2(C^{\prime }{B}^{\prime }+B{C}^{″}+C{B}^{″})}{BC}$
2	$A=m_1{e}^{k_1\rho },$$C\ne A,$$C\ne B,$$B{B}^{‴}-B^{\prime }{B}^{″}\ne 0$	$\rho =\frac{-m_1^2{e}^{2k_1\rho }(C^{\prime }{B}^{\prime }+C{B}^{″}+B{C}^{″})}{BC}$
3	$A=m_1{e}^{k_1\rho },$$B=m_2{e}^{k_2\rho },$$k_1\ne k_2,$$C{C}^{‴}-C^{\prime }{C}^{″}\ne 0$	$\rho =\frac{-m_1^2{e}^{2k_1\rho }{C}^{″}}{C}$
4	$A=m_1{e}^{k_1\rho },$$B=m_2{e}^{k_2\rho },$$C=m_3{e}^{k_3\rho },$$k_1\ne k_2\ne k_3$	$\rho =0$
5	$A=A\left(\rho \right),B=B\left(\rho \right),$$C=const.,$$A^{\prime }\ne 0,$$B^{\prime }\ne 0,$$A{A}^{‴}-A^{\prime }{A}^{″}\ne 0,$$B\ne \gamma A$	$\rho =\frac{-A^2{B}^{″}}{B}$
6	(i) $A=m_1{e}^{k_1\rho }+m_2{e}^{-k_1\rho },$ $m_1\ne 0$,$m_2\ne 0,$ $B^{″}\ne ,0$ $B{B}^{‴}-B^{\prime }{B}^{″}\ne 0,$ $C=const.$	$\rho =\frac{-{(m_1{e}^{k_1\rho }+m_2{e}^{-k_1\rho })}^2{B}^{″}}{B}$
	(ii) $A=m_3\rho +m_4,$ $m_3\ne 0$, $B^{″}\ne 0,$ $B{B}^{‴}-B^{\prime }{B}^{″}\ne 0,$ $C=const.$	$\rho =\frac{-{(m_3\rho +m_4)}^2{B}^{″}}{B}$
7	$A=m_1{e}^{k_1\rho },$$B{B}^{‴}-B^{\prime }{B}^{″}\ne 0,$$C=const.$	$\rho =0$
10	$A=const.,$$B\ne C,$$B^{″}\ne 0,$$B{B}^{‴}-B^{\prime }{B}^{″}\ne 0$	$\rho =\frac{-(C^{\prime }{B}^{\prime }+B{C}^{″}+C{B}^{″})}{BC}$
11	(i) $A=const.$, $B=B\left(\rho \right)$, $C=m_1{e}^{k_1\rho }+m_2{e}^{-k_1\rho },$ where $m_1$ and $m_2$ are not simultaneously zero. (ii) $A=const.$, $B=B\left(\rho \right)$, $C=m_3\rho +m_4$ where $m_3,m_4$ are non-zero constants.	$\rho =\frac{-B^{″}}{B}$
12	(i) $A=const.$, $B=m_3{e}^{k_2\rho }+m_4{e}^{-k_2\rho }$, $C=m_1{e}^{k_1\rho }+m_2{e}^{-k_1\rho }$ where $m_1,m_2,m_3,m_4$ are non-zero constants.	$\rho =0$
	(ii) $A=const.$, $B=m_3{e}^{k_2\rho }+m_4{e}^{-k_2\rho }$, $C=m_5\rho +m_6,$ where $m_1,m_2,m_3,m_4\ne 0$
	(iii) $A=const.$, $B=m_7\rho +m_8$, $C=m_5\rho +m_6$, where $m_5,m_6,m_7,m_8$ are non-zero constants.
	(iv) $A=const.$, $B=m_7\rho +m_8,$ $C=m_1{e}^{k_1\rho }+m_2{e}^{-k_1\rho }$, where $m_1,m_2,m_7,m_8$ are non-zero constants.
13	(i) $A=const.$, $B=m_3{e}^{k_2\rho }$, $C=m_1{e}^{k_1\rho }+m_2{e}^{-k_1\rho }$ where $m_1,m_2,m_3$ are non-zero constants.	$\rho =0$
	(ii) $A=const.$, $B=m_3{e}^{k_2\rho }$, $C=m_4\rho +m_5,$ where $m_3,m_4,m_5$ are non-zero constants.
15	$A=const.$, $B=m_1{e}^{k_1\rho }-m_2{e}^{-k_1\rho }$, $C=m_1{e}^{k_1\rho }+m_2{e}^{-k_1\rho },$ where $m_1\ne 0$ and $m_2\ne 0.$	$\rho =0$
16	$A=A\left(\rho \right)$, $B=const.$, $C=C\left(\rho \right)$, $C^{\prime }\ne 0$	$\rho =\frac{-A^2{C}^{″}}{C}$
17	(i) $A=m_1{e}^{k_1\rho }+m_2{e}^{-k_1\rho },$ $B=const.$, $C^{\prime }\ne 0$, where $m_1\ne 0$ and $m_2\ne 0.$	If $C{C}^{‴}-C^{\prime }{C}^{″}=0,$ $\rho =0$ If $C{C}^{‴}-C^{\prime }{C}^{″}\ne 0,$ $\rho =\frac{-{(m_1{e}^{k_1\rho }+m_2{e}^{-k_1\rho })}^2{C}^{″}}{C}.$
	(ii) $A=m_3\rho +m_4$, $B=const.$, $C^{″}\ne 0$ where $m_3\ne 0.$	If $C{C}^{‴}-C^{\prime }{C}^{″}=0,$ $\rho =0$ If $C{C}^{‴}-C^{\prime }{C}^{″}\ne 0,$ $\rho =\frac{-{(m_3\rho +m_4)}^2{C}^{″}}{C}.$
18	$A=m_1{e}^{k_1\rho }$, $B=const.$ ,${C^{\prime }}^2-C{C}^{″}\ne 0$	$\rho =\frac{-{\left(m_1{e}^{k_1\rho }\right)}^2{C}^{″}}{C}$

. For the three KVFs case, earlier authors [23] missed some of the metrics, given in branches 13, 15, and 16, in their classification scheme. For completeness, we also provide expressions for the energy density for all the spacetime metrics in Table 1.

3.2. Four KVFs

The four KVFs are obtained in 13 branches of the Rif tree, namely, 1, 2, 4, 5, 8, 10, 11, 12, 14, 16, 17, and 19–20. The results of these branches are summarized in

Table 2. Metrics Admitting Four KVFs.

Branch	Metric Functions	Additional KVF	Lie Algebra	Energy Density
1	$A=A\left(\rho \right)$, $B=B\left(\rho \right)$, $C=C\left(\rho \right)$ (i) $A=B\ne C$	$X_4=\theta {\partial }_t+t{\partial }_{\theta }$	$[X_1,X_4]=X_2$ $[X_2,X_4]=X_1$	$\rho =\frac{-A(A^{\prime }{C}^{\prime }+A{C}^{″}+C{A}^{″})}{C}$
	(ii) $C=A\ne B$	$X_4=-z{\partial }_t+t{\partial }_z$	$[X_1,X_4]=X_3$ $[X_3,X_4]=-X_1$	$\rho =\frac{-A(A^{\prime }{B}^{\prime }+A{B}^{″}+B{A}^{″})}{C}$
2	$A=m_1{e}^{k_1\rho }$, $B=B\left(\rho \right)$, $C=C\left(\rho \right),$$B{B}^{‴}-B^{\prime }{B}^{″}\ne 0$ (i) $A=C\ne B$	$X_4=-z{\partial }_t+t{\partial }_z$	$[X_1,X_4]=X_3$ $[X_3,X_4]=X_1$	$\rho =\frac{-m_1^2{e}^{2k_1\rho }{B}^{″}}{B}$
	(ii) $A\ne B=C$	$X_4=z{\partial }_{\theta }-\theta {\partial }_z$	$[X_2,X_4]=-X_3$ $[X_3,X_4]=X_2$	$\rho =\frac{-m_1^2{e}^{2k_1\rho }(B^{\prime 2}+2B{B}^{″})}{B^2}$
3	$A=m_1{e}^{k_1\rho }$ , $B=m_2{e}^{k_2\rho }$ , $C=C\left(\rho \right)$ $C{C}^{‴}-C^{\prime }{C}^{″}\ne 0$ $k_1=k_2$	$X_4=\theta {\partial }_t+t{\partial }_{\theta }$	$[X_1,X_4]=X_2$ $[X_2,X_4]=X_1$	$\rho =\frac{-m_1^2{e}^{2k_1\rho }\left(C^{″}\right)}{C}$
4	$A=m_1{e}^{k_1\rho }$ , $B=m_2{e}^{k_2\rho }$ , $C=m_3{e}^{k_3\rho }$ $k_1\ne k_2\ne k_3$	$X_4=-k_{1}t{\partial }_t+{\partial }_{\rho }-k_2\theta {\partial }_{\theta }-k_{3}z{\partial }_z$	$[X_1,X_4]=-k_1{X}_1$ $[X_2,X_4]=-k_2{X}_2$ $[X_3,X_4]=-k_3{X}_3$	$\rho =0$
5	$A=A\left(\rho \right)$ , $B=\gamma A,$ $C=const.,$ where $\gamma$ is a constant	$X_4=\gamma \theta {\partial }_t+t{\partial }_{\theta }$	$[X_1,X_4]=X_2$ $[X_2,X_4]=\gamma X_1$	$\rho =-A{A}^{″}$
8	$A=m_1{e}^{k_1\rho }$ , $B=m_2{e}^{k_2\rho }$ , $C=const.$	$X_4=-k_{1}t{\partial }_t+{\partial }_{\rho }-k_2\theta {\partial }_{\theta }$	$[X_1,X_4]=-k_1{X}_1$ $[X_2,X_4]=-k_2{X}_2$	$\rho =0$
10	$A=const.$ , $B=\gamma C$ , $C=C\left(\rho \right)$ $B{B}^{‴}-B^{\prime }{B}^{″}\ne 0$	$X_4=z{\partial }_{\theta }-\gamma \theta {\partial }_z$	$[X_2,X_4]=-\gamma X_3$ $[X_3,X_4]=X_2$	$\rho =\frac{-(C^{\prime 2}+2C{C}^{″})}{C^2}$
11	$A=const.$ , $B=B\left(\rho \right)$ , $C=const.$	$X_4=z{\partial }_t+t{\partial }_z$	$[X_1,X_4]=X_3$ $[X_3,X_4]=X_1$	$\rho =\frac{-B^{″}}{B}$
14	$A=const.$ , $B=m_1{e}^{k_1\rho }$ , $C=m_2{e}^{k_2\rho }$ $k_1\ne k2$	$X_4={\partial }_{\rho }-k_2\theta {\partial }_{\theta }-k_{1}z{\partial }_z$	$[X_2,X_4]=-k_1{X}_2$ $[X_3,X_4]=-k_2{X}_3$	$\rho =0$
16	$A=A\left(\rho \right)$ , $B=const.$ , $C=C\left(\rho \right)$ (i) $C^{\prime }\ne 0$ $A^{\prime }=0$ $A=\gamma C$	$X_4=z{\partial }_t+\gamma t{\partial }_z$	$[X_1,X_4]=-\gamma X_3$ $[X_3,X_4]=X_1$	$\rho =-A{A}^{″}$
	(ii) $C=const.$	$X_4=z{\partial }_{\theta }-\theta {\partial }_z$	$[X_2,X_4]=-X_3$ $[X_3,X_4]=X_2$	$\rho =0$
17	$A=m_1\rho +m_2$ , $B=const.$ $C=m_1\rho +m_2$ ; $m_1,m_2\ne 0$	$X_4=z{\partial }_t+t{\partial }_z$	$[X_1,X_4]=X_3$ $[X_3,X_4]=X_1$	$\rho =0$
19	$A=m_1{e}^{k_1\rho }$ , $B=const.,$ $C=m_2{e}^{k_2\rho };$ $k_1\ne k2$	$X_4=-k_{1}t{\partial }_t+{\partial }_1-k_{2}z{\partial }_z$	$[X_1,X_4]=-k_1{X}_1$ $[X_3,X_4]=-k_2{X}_3$	$\rho =0$
20	$A=const.$ , $B=const.$ , $C=C\left(\rho \right),$ $C^{″}\ne 0,$ $C{C}^{‴}-C^{\prime }{C}^{\prime }\ne 0$	$X_4=\theta {\partial }_t+t{\partial }_{\theta }$	$[X_1,X_4]=X_2$ $[X_2,X_4]=X_1$	$\rho =0$

. For each branch, we list all the metric functions admitting four KVFs, their corresponding Lie algebras, and expressions for the energy density. As before, the earlier authors obtained only two metrics (branches 1 and 20) admitting four KVFs [23]. The four KVFs include the three minimum KVFs, given by ${\partial }_t,{\partial }_{\theta }$, and ${\partial }_z$, along with an additional one, denoted by $X_4$ in Table 2.

3.3. Five KVFs

Five KVFs are admitted in two sub cases of branch 4 of the Rif tree (refer to

Table 3. Metrics Admitting Five KVFs.

Branch	Metric Functions	KVFs	Lie Algebra
4	$A=m_1{e}^{k_1\rho },$$B=m_2{e}^{k_2\rho },$$C=m_3{e}^{k_3\rho }$
	(i)$k_1=k_2\ne k_3$	$X_4=-k_{1}t{\partial }_t+{\partial }_{\rho }-k_1\theta {\partial }_{\theta }-k_{3}z{\partial }_z$$X_5={\left(\frac{m_2}{m_1}\right)}^2\theta {\partial }_t+t{\partial }_{\theta }$	$[X_1,X_4]=-k_1{X}_1,$$[X_1,X_5]=X_2,$ $[X_2,X_4]=-k_1{X}_2,$$[X_2,X_5]={\left(\frac{m_2}{m_1}\right)}^2{X}_1$ $[X_3,X_4]=-k_3{X}_3$
	(ii) $k_3=k_1\ne k_2$	$X_4=-k_{1}t{\partial }_t+{\partial }_{\rho }-k_2\theta {\partial }_{\theta }-k_{1}z{\partial }_z$$X_5=z{\partial }_t+{\left(\frac{m_2}{m_1}\right)}^{2}t{\partial }_z$	$[X_1,X_4]=-k_1{X}_1,$$[X_1,X_5]={\left(\frac{m_2}{m_1}\right)}^2{X}_3$ $[X_2,X_4]=-k_2{X}_2,$$[X_3,X_4]=-k_1{X}_3$ $[X_3,X_5]=X_1$

). The energy density is zero in this case. The five-dimensional KVFs algebra consists of the minimum three KVFs, along with two additional KVFs denoted by $X_4$ and $X_5$ in Table 3. These metrics were also not listed in the previously published work [23].

3.4. Six KVFs

Six KVFs are admitted in five branches, namely, branch 1, 15, 17, 19, and 20 (

Table 4. Metrics Admitting Six KVFs.

Branch	Metric Functions	KVFs	Lie Algebra
1	$A=A\left(\rho \right),$$B=B\left(\rho \right),$$C=C\left(\rho \right),$$A=B=C$	$X_4=\theta {\partial }_t+t{\partial }_{\theta }$$X_5=z{\partial }_t+t{\partial }_z$$X_6=z{\partial }_{\theta }-\theta {\partial }_z$	$[X_1,X_4]=X_2$ $[X_1,X_5]=X_3$ , $[X_2,X_4]=X_1$ $[X_2,X_6]=-X_3$ , $[X_3,X_5]=X_1$ $[X_3,X_6]=X_2$ , $[X_4,X_5]=X_6$ $[X_4,X_6]=X_5$ , $[X_5,X_6]=X_4$
15	$A=const.,$$B=m_4{e}^{k\rho }+m_5{e}^{-k\rho }$$C=const.$$m_4$ and $m_5$ are not simultaneously zero.	$X_4=cosh\left(\beta \theta \right){\partial }_{\rho }-\left(\frac{k(m_4{e}^{k\rho }-m_5{e}^{-k\rho })}{\beta (m_4{e}^{k\rho }+m_5{e}^{-k\rho })}\right)sinh\left(\beta \theta \right){\partial }_{\theta }$$X_5=sin\left(\beta \theta \right){\partial }_{\rho }-\left(\frac{k(m_4{e}^{k\rho }-m_5{e}^{-k\rho })}{\beta (m_4{e}^{k\rho }+m_5{e}^{-k\rho })}\right)cosh\left(\beta \theta \right){\partial }_{\theta }$$X_6=z{\partial }_t+t{\partial }_z$	$[X_1,X_6]=X_3$ , $[X_2,X_4]=\beta X_5$ $[X_2,X_5]=\beta X_4$ , $[X_3,X_6]=X_1$ $[X_4,X_5]=\frac{k^2}{\beta }{X}^2$ , where $\beta =2k\sqrt{m_4{m}_5}$
17	$A=m_1{e}^{k\rho }+m_2{e}^{-k\rho }$$B=const.$$C=const.$$m_1,m_2\ne 0$	$X_4=\left(\frac{-k{m}_1(m_1{e}^{k\rho }-m_2{e}^{-k\rho })}{\beta (m_1{e}^{k\rho }+m_2{e}^{-k\rho })}\right)sin\left(\beta t\right){\partial }_t+cos\left(\beta t\right){\partial }_{\rho }$$X_5=\left(\frac{k{m}_1(m_1{e}^{k\rho }-m_2{e}^{-k\rho })}{\beta (m_1{e}^{k\rho }+m_2{e}^{-k\rho })}\right)cos\left(\beta t\right){\partial }_t+sin\left(\beta t\right){\partial }_{\rho }$$X_6=z{\partial }_{\theta }-\frac{1}{m^2}\theta {\partial }_z$	$[X_1,X_4]=-\beta X_5$ , $[X_1,X_5]=\beta X_4$ $[X_2,X_6]=-\frac{1}{m^2}{X}_1$ , $[X_3,X_6]=X_2$ $[X_4,X_5]=-\frac{k^2}{\beta }{X}_1$ , where $\beta =2k\sqrt{m_1{m}_2}$
19	$A=m{e}^{k\rho }$$B=const.$$C=const.$	$X_4=-\left(\frac{e^{-2k\rho }+{\left(mkt\right)}^2}{2mk}\right){\partial }_t+t{\partial }_{\rho }$$X_5=-kt{\partial }_t+{\partial }_{\rho }$$X_6=z{\partial }_{\theta }-\theta {\partial }_z$	$[X_1,X_4]=X_2$ , $[X_1,X_5]=-k{X}_1$ $[X_2,X_6]=-X_3$ , $[X_3,X_6]=X_2$ $[X_4,X_5]=k{X}_1$
20	$A=const.$$B=const.$$C=m_1{e}^{k\rho }+m_2{e}^{{}_k\rho }$$m_1$ and $m_2$ are not simultaneously zero.	$X_4=cosh\left(\beta z\right){\partial }_{\rho }+\left(\frac{-k(m_4{e}^{k\rho }-m_1{e}^{-k\rho })}{\beta (m_2{e}^{k\rho }+m_5{e}^{-k\rho })}\right)sinh\left(\beta z\right){\partial }_z$$X_5=sinh\left(\beta z\right){\partial }_{\rho }+\left(\frac{-k(m_4{e}^{k\rho }-m_1{e}^{-k\rho })}{\beta (m_2{e}^{k\rho }+m_5{e}^{-k\rho })}\right)cosh\left(\beta z\right){\partial }_z$$X_6=\theta {\partial }_t+t{\partial }_{\theta }$	$[X_1,X_6]=X_2$ , $[X_2,X_6]=X_1$ $[X_3,X_4]=\beta X_5$ , $[X_3,X_5]=\beta X_4$ $[X_4,X_5]=\frac{k^2}{\beta }{X}_3$ , where $\beta =2k\sqrt{m_4{m}_5}$

). They have three minimal KVFs along with three other KVFs represented by $X_4$, $X_5$, and $X_6$ in Table 4. The energy density for branches 1 and 20 are $\rho =-(A^{\prime }+2A{A}^{″})$ and $\rho =\frac{-C^{″}}{C}$, respectively, where other branches have zero energy density. Whereas the metrics arising in branches 1, 19, and 20 were discussed in Ref. [23], the metrics in branches 15 and 17 were not.

3.5. Seven KVFs

The seven KVFs were obtained in some sub cases of branches 9 and 20 with zero energy density for both branches. Here, the seven KVFs include three minimal KVFs along with four additional KVFs given in

Table 5. Metrics Admitting Seven KVFs.

Branch	Metric Functions	KVFs	Lie Algebra
9	(i) $A=m_1{e}^{k\rho }+m_2{e}^{-k\rho }$ $B=m_1{e}^{k\rho }-m_2{e}^{-k\rho }$ $C=const.$ $m_1,m_2\ne 0$	$X_4=-\frac{kB\left(\rho \right)}{\beta A\left(\rho \right)}sin\left(\beta t\right)cos\left(\beta \theta \right){\partial }_t+cos\left(\beta t\right)cos\left(\beta \theta \right){\partial }_{\rho }-\frac{kA\left(\rho \right)}{\beta B\left(\rho \right)}cos\left(\beta t\right)sin\left(\beta \theta \right){\partial }_{\theta }$$X_5=\frac{kB\left(\rho \right)}{\beta A\left(\rho \right)}cos\left(\beta t\right)cos\left(\beta \theta \right){\partial }_t+sin\left(\beta t\right)cos\left(\beta \theta \right){\partial }_{\rho }-\frac{kA\left(\rho \right)}{\beta B\left(\rho \right)}sin\left(\beta t\right)sin\left(\beta \theta \right){\partial }_{\theta }$$X_6=-\frac{kB\left(\rho \right)}{\beta A\left(\rho \right)}sin\left(\beta t\right)sin\left(\beta \theta \right){\partial }_t+cos\left(\beta t\right)sin\left(\beta \theta \right){\partial }_{\rho }+\frac{kA\left(\rho \right)}{\beta B\left(\rho \right)}cos\left(\beta t\right)cos\left(\beta \theta \right){\partial }_{\theta }$$X_7=-\frac{kB\left(\rho \right)}{\beta A\left(\rho \right)}cos\left(\beta t\right)sin\left(\beta \theta \right){\partial }_t+sin\left(\beta t\right)sin\left(\beta \theta \right){\partial }_{\rho }+\frac{kA\left(\rho \right)}{\beta B\left(\rho \right)}sin\left(\beta t\right)cos\left(\beta \theta \right){\partial }_{\theta }$	$[X_1,X_4]=-\beta X_5$ , $[X_1,X_5]=\beta X_4$ $[X_1,X_6]=-\beta X_7$ , $[X_1,X_7]=\beta X_6$ $[X_2,X_3]=\beta X_6$ , $[X_2,X_5]=\beta X_7$ $[X_2,X_6]=\beta X_4$ , $[X_2,X_7]=\beta X_5$ $[X_4,X_5]=\frac{k_2}{\beta }{X}_1$ , $[X_4,X_6]=-\frac{k_2}{\beta }{X}_2$ $[X_5,X_7]=\frac{k_2}{\beta }{X}_2$ , $[X_6,X_7]=\frac{k^2}{\beta }{X}_1$ where $\beta =2k\sqrt{m_1{m}_2}$
	(ii) $A=m_1{e}^{k\rho }$ $B=m_1{e}^{k\rho }$ $C=const.$	$X_4=-(\frac{e^{-2k\rho }}{2k{m}_1^2}+\frac{k{t}^2}{2}+\frac{k{\theta }^2}{2}){\partial }_t+t{\partial }_{\rho }-k\theta t{\partial }_{\theta }$$X_5=-k\theta t{\partial }_t+\theta {\partial }_{\rho }+(\frac{e^{-2k\rho }}{2k{m}_1^2}-\frac{k{t}^2}{2}-\frac{k{\theta }^2}{2}){\partial }_{\theta }$$X_6=-kt{\partial }_t+{\partial }_{\rho }-k\theta {\partial }_{\theta }$$X_7=\theta {\partial }_t+t{\partial }_{\theta }$	$[X_1,X_4]=k{X}_6$ , $[X_1,X_5]=k{X}_7$ $[X_1,X_6]=-X_1$ , $[X_1,X_7]=X_2$ $[X_2,X_4]=k{X}_7$ , $[X_2,X_5]=X_6$ $[X_2,X_6]=X_2$ , $[X_2,X_7]=X_1$ $[X_4,X_6]=k{X}_4$ , $[X_4,X_7]=X_5$ $[X_5,X_6]=-k{X}_5$ , $[X_5,X_7]=-k{X}_4$
20	$A=m_1{e}^{k\rho }+m_2{e}^{-k\rho }$$B=const.$$C=m_1{e}^{k\rho }-m_2{e}^{-k\rho }$$m_1,m_2\ne 0$	$X_4=-\frac{kC\left(\rho \right)}{\beta A\left(\rho \right)}sin\left(\beta t\right)cos\left(\beta z\right){\partial }_t+cos\left(\beta t\right)cos\left(\beta z\right){\partial }_{\rho }-\frac{kA\left(\rho \right)}{\beta C\left(\rho \right)}cos\left(\beta t\right)sin\left(\beta z\right){\partial }_z$$X_5=\frac{kC\left(\rho \right)}{\beta A\left(\rho \right)}cos\left(\beta t\right)cos\left(\beta z\right){\partial }_t+sin\left(\beta t\right)cos\left(\beta z\right){\partial }_{\rho }-\frac{kA\left(\rho \right)}{\beta C\left(\rho \right)}sin\left(\beta t\right)sin\left(\beta z\right){\partial }_z$$X_6=-\frac{kC\left(\rho \right)}{\beta A\left(\rho \right)}sin\left(\beta t\right)sin\left(\beta z\right){\partial }_t+cos\left(\beta t\right)sin\left(\beta z\right){\partial }_{\rho }+\frac{kA\left(\rho \right)}{\beta C\left(\rho \right)}cos\left(\beta t\right)cos\left(\beta z\right){\partial }_z$$X_7=-\frac{kC\left(\rho \right)}{\beta A\left(\rho \right)}cos\left(\beta t\right)sin\left(\beta z\right){\partial }_t+sin\left(\beta t\right)sin\left(\beta z\right){\partial }_{\rho }+\frac{kA\left(\rho \right)}{\beta C\left(\rho \right)}sin\left(\beta t\right)cos\left(\beta z\right){\partial }_z$	$[X_1,X_4]=-\beta X_5$ , $[X_1,X_5]=\beta X_4$ $[X_1,X_6]=\beta X_7$ , $[X_1,X_7]=\beta X_6$ $[X_3,X_4]=\beta X_6$ , $[X_3,X_5]=-\beta X_7$ $[X_3,X_6]=-\beta X_4$ , $[X_3,X_7]=\beta X_5$ $[X_4,X_5]=\frac{k^2}{\beta }{X}_1$ , $[X_4,X_6]=\frac{k^2}{\beta }{X}_3$ $[X_5,X^7]=\frac{k^2}{\beta }{X}^3$ , $[X_6,X_7]=\frac{k^2}{\beta }{X}_1$ where $\beta =2k\sqrt{m_1{m}_2}$

. It is worth noting that case 1 of branch 9 was discussed in [23] while case 2 was not.

3.6. Ten KVFs

This case provides a maximal symmetry group admitted by ten KVFs. These ten KVFs appeared in some sub cases of branches 4, 15, and 20. All these branches have zero energy density. These ten KVFs include three minimal and seven additional KVFs as given in

Table 6. Metrics Admitting Ten KVFs.

Branch	Metric Functions	KVFs	Lie Algebra
4	$A=m_1{e}^{k_1\rho }$$B=m_2{e}^{k_2\rho }$$C=m_3{e}^{k_3\rho }$ where $k_1=k_2=k_3=k$	$X_4=-(\frac{e^{-2k\rho }}{2k{m}_1^2}+\frac{k{t}^2}{2}+k{\left(\frac{m_2}{m_1}\right)}^2\frac{{\theta }^2}{2}+k{\left(\frac{m_3}{m_1}\right)}^2\frac{z^2}{2}){\partial }_t+t{\partial }_{\rho }-kt\theta {\partial }_{\theta }-ktz{\partial }_z$$X_5=-k\theta t{\partial }_t+\theta {\partial }_{\rho }+(\frac{e^{-2k\rho }}{2k{m}_2^2}-\frac{k{\theta }^2}{2}-k{\left(\frac{m_1}{m_2}\right)}^2\frac{t^2}{2}+k{\left(\frac{m_3}{m_2}\right)}^2\frac{z^2}{2}){\partial }_{\theta }-k\theta z{\partial }_z$$X_6=-kzt{\partial }_t+z{\partial }_{\rho }-kz\theta {\partial }_{\theta }+(\frac{e^{-2k\rho }}{2k{m}_3^2}-\frac{k{z}^2}{2}+k{\left(\frac{m_1}{m_3}\right)}^2\frac{t^2}{2}+k{\left(\frac{m_2}{m_3}\right)}^2\frac{{\theta }^2}{2}){\partial }_z$$X_7=-kt{\partial }_t+{\partial }_{\rho }-k\theta {\partial }_{\theta }-kz{\partial }_z$$X_8={\left(\frac{m_2}{m_1}\right)}^2\theta {\partial }_t+t{\partial }_{\theta }$$X_9={\left(\frac{m_3}{m_1}\right)}^{2}z{\partial }_t+t{\partial }_z$$X_{10}=z{\partial }_{\theta }-{\left(\frac{m_2}{m_3}\right)}^2\theta {\partial }_z$	$[X_1,X_4]=X_7$ , $[X_1,X_5]=-k{\left(\frac{m_1}{m_2}\right)}^2{X}_8$ $[X_1,X_6]=-k{\left(\frac{m_3}{m_1}\right)}^2{X}_9$ , $[X_1,X_7]=-k{X}_1$ $[X_1,X_8]=-k{X}_2$ , $[X_1,X_9]=X_3$ $[X_2,X_4]=-k{X}_8$ , $[X_2,X_5]=X_7$ $[X_2,X_6]=-k{X}_{10}$ , $[X_3,X_4]=-k{X}_9$ $[X_3,X_5]=k{\left(\frac{m_2}{m_3}\right)}^2{X}_{10}$ , $[X_3,X_6]=X_7$ $[X_3,X_7]=-k{X}_3$ , $[X_3,X_9]={\left(\frac{m_3}{m_2}\right)}^2{X}_1$ $[X_3,X_{10}]=X_2$ , $[X_4,X_7]=k{X}_4$ $[X_4,X_8]=-{\left(\frac{m_2}{m_1}\right)}^2{X}_5$ , $[X_4,X_9]={\left(\frac{m_3}{m_1}\right)}^2{X}_6$ $[X_4,X_{10}]=-k{X}_{10}$ , $[X_5,X_7]=-k{X}_5$ $[X_5,X_8]=X_4$ , $[X_5,X_{10}]=X_6$ $[X_6,X_7]=k{X}_6$ , $[X_6,X_9]=X_4$ $[X_6,X_{10}]={\left(\frac{m_2}{m_3}\right)}^2{X}_5$ , $[X_7,X_{10}]=k{X}_2$ $[X_8,X_9]=-{\left(\frac{m_3}{m_1}\right)}^2{X}_{10}$ , $[X_8,X_{10}]=-{\left(\frac{m_2}{m_3}\right)}^2{X}_9$ , $[X_9,X_{10}]=X_8$
15	$A=const.$$B=m_6\rho +m_7$$C=const.$$m_6,m_7\ne 0$	$X_4=(\rho +\frac{m_7}{m_6})cos\left(m_6\theta \right){\partial }_t+tcos\left(m_6\theta \right){\partial }_{\rho }-\left(\frac{t}{m_6\rho +m_7}\right)sin\left(m_6\theta \right){\partial }_{\theta }$$X_5=(\rho +\frac{m_7}{m_6})sin\left(m_6\theta \right){\partial }_t+tsin\left(m_6\theta \right){\partial }_{\rho }+\left(\frac{t}{m_6\rho +m_7}\right)cos\left(m_6\theta \right){\partial }_{\theta }$$X_6=zcos\left(m_6\theta \right){\partial }_{\rho }-\left(\frac{z}{m_6\rho +m_7}\right)sin\left(m_6\theta \right){\partial }_{\theta }-(\rho +\frac{m_7}{m_6})cos\left(m_6\theta \right){\partial }_z$$X_7=zsin\left(m_6\theta \right){\partial }_{\rho }+\left(\frac{z}{m_6\rho +m_7}\right)cos\left(m_6\theta \right){\partial }_{\theta }-(\rho +\frac{m_7}{m_6})sin\left(m_6\theta \right){\partial }_z$$X_8=cos\left(m_6\theta \right){\partial }_{\rho }-\left(\frac{1}{m_6\rho +m_7}\right)sin\left(m_6\theta \right){\partial }_{\theta }$$X_9=sin\left(m_6\theta \right){\partial }_{\rho }+\left(\frac{1}{m_6\rho +m_7}\right)cos\left(m_6\theta \right){\partial }_{\theta }$ ,$X_{10}=z{\partial }_t+t{\partial }_z$	$[X_1,X_4]=X_8$ , $[X_1,X_5]=X_9$ $[X_1,X_{10}]=X_3$ , $[X_2,X_4]=-m_6{X}_5$ $[X_2,X_5]=m_6{X}_4$ , $[X_2,X_6]=-m_6{X}_7$ $[X_2,X_7]=m_6{X}_6$ , $[X_2,X_8]=m_6{X}_9$ $[X_2,X_9]=m_6{X}_8$ , $[X_3,X_6]=X_8$ $[X_3,X_7]=X_9$ , $[X_3,X_{10}]=X_1$ $[X_4,X_5]=\frac{1}{m_6}{X}_2$ , $[X_4,X_6]=X_{10}$ $[X_4,X_8]=-X_1$ , $[X_4,X_{10}]=X_6$ $[X_5,X_7]=-X_{10}$ , $[X_5,X_9]=-X_1$ $[X_5,X_{10}]=-X_7$ , $[X_6,X_7]=-\frac{1}{m_6}{X}_2$ $[X^6,X^8]=-X^3$ , $[X_6,X_{10}]=-X_4$ $[X_7,X^9]=X_3$ , $[X_7,X_{10}]=-X_5$
20	$A=const.$$B=const.$$C=m_1\rho +m_2$$m_1,m_2\ne 0$	$X_4=(\rho +\frac{m_4}{m_3})cos\left(m_{3}z\right){\partial }_t+tcos\left(m_{3}z\right){\partial }_{\rho }-\left(\frac{t}{m_3\rho +m_4}\right)sin\left(m_{3}z\right){\partial }_z$$X_5=(\rho +\frac{m_4}{m_3})sin\left(m_{3}z\right){\partial }_t+tsin\left(m_{3}z\right){\partial }_{\rho }+\left(\frac{t}{m_3\rho +m_4}\right)cos\left(m_{3}z\right){\partial }_z$$X_6=\theta cos\left(m_{3}z\right){\partial }_{\rho }-(\rho +\frac{m_4}{m_3})cos\left(m_{3}z\right){\partial }_{\theta }-\left(\frac{\theta }{m_3\rho +m_4}\right)sin\left(m_{3}z\right){\partial }_z$$X_7=\theta sin\left(m_{3}z\right){\partial }_{\rho }-(\rho +\frac{m_4}{m_3})sin\left(m_{3}z\right){\partial }_{\theta }-\left(\frac{\theta }{m_3\rho +m_4}\right)cos\left(m_{3}z\right){\partial }_z$$X_8=cos\left(m_{3}z\right){\partial }_{\rho }-\left(\frac{1}{m_3\rho +m_4}\right)sin\left(m_3\theta \right){\partial }_{\theta }$$X_9=sin\left(m_{3}z\right){\partial }_{\rho }+\left(\frac{1}{m_3\rho +m_4}\right)cos\left(m_{3}z\right){\partial }_{\theta }$$X_{10}=\theta {\partial }_t+t{\partial }_{\theta }$	$[X_1,X_4]=X_8$ , $[X_1,X_5]=X_9$ $[X_1,X_{10}]=X_2$ , $[X_2,X_6]=X_8$ $[X_2,X_7]=X_9$ , $[X_2,X_{10}]=X_1$ $[X_3,X_4]=m_1{X}_5$ , $[X_3,X_5]=m_1{X}_4$ $[X_3,X_6]=-m_1{X}_7$ , $[X_3,X_7]=m_1{X}_6$ $[X_3,X_8]=-m_1{X}_9$ , $[X_3,X_9]=X_8$ $[X_4,X_5]=-\frac{1}{m_1}{X}_3$ , $[X_4,X_6]=X_{10}$ $[X_4,X_8]=-X_1$ , $[X_4,X_{10}]=X_6$ $[X_5,X_7]=-X_{10}$ , $[X_5,X_9]=X_1$ $[X_5,X_{10}]=-X_9$ , $[X_6,X_8]=-X_2$ $[X_6,X_{10}]=X_4$ , $[X_7,X_9]=X_2$ $[X_7,X_{10}]=X_5$
20	$A=m_5\rho +m_6$$B=const.$$C=const.$$m_5,m_6\ne 0$	$X_4=-\left(\frac{\theta cosh\left(m_{5}t\right)}{m_5\rho +m_6}\right){\partial }_t+\theta sinh\left(m_{5}t\right){\partial }_{\rho }-(\rho +\frac{m_6}{m_5})sinh\left(m_{5}t\right){\partial }_{\theta }$$X_5=-\left(\frac{\theta sinh\left(m_{5}t\right)}{m_5\rho +m_6}\right){\partial }_t+\theta cosnh\left(m_{5}t\right){\partial }_{\rho }-(\rho +\frac{m_6}{m_5})cosh\left(m_{5}t\right){\partial }_{\theta }$$X_6=-\left(\frac{zcosh\left(m_{5}t\right)}{m_5\rho +m_6}\right){\partial }_t+zsinh\left(m_{5}t\right){\partial }_{\rho }-(\rho +\frac{m_6}{m_5})sinh\left(m_{5}t\right){\partial }_z$$X_7=-\left(\frac{zsinh\left(m_{5}t\right)}{m_5\rho +m_6}\right){\partial }_t+zcosh\left(m_{5}t\right){\partial }_{\rho }-(\rho +\frac{m_6}{m_5})cosh\left(m_{5}t\right){\partial }_z$$X_8=-\left(\frac{cosh\left(m_{5}t\right)}{m_5\rho +m_6}\right){\partial }_t+sinh\left(m_{5}t\right){\partial }_{\rho }$$X_9=-\left(\frac{sinh\left(m_{5}t\right)}{m_5\rho +m_6}\right){\partial }_t+cosh\left(m_{5}t\right){\partial }_{\rho }$$X_{10}=z{\partial }_{\theta }-\theta {\partial }_z$	$[X_1,X_4]=m_5{X}_5$ , $[X_1,X_5]=m_5{X}_4$ $[X_1,X_6]=m_5{X}_7$ , $[X_1,X_7]=m_5{X}_6$ $[X_1,X_8]=m_5{X}_9$ , $[X_1,X_9]=m_5{X}_8$ $[X_2,X_4]=X_8$ , $[X_2,X_5]=-X_9$ $[X_2,X_{10}]=-X_3$ , $[X_3,X_6]=X_8$ $[X_3,X_7]=X_9$ , $[X_3,X_{10}]=X_2$ $[X_4,X_5]=\frac{1}{m_5}{X}_1$ , $[X_4,X_6]=X_{10}$ $[X_4,X_8]=X_1$ , $[X_4,X_{10}]=X_6$ $[X_5,X_7]=X_{10}$ , $[X_5,X_9]=-X_2$ $[X_5,X_{10}]=X_7$ , $[X_6,X_7]=\frac{1}{m_5}{X}_1$ $[X_6,X_8]=X_3$ , $[X_7,X_9]=X_3$ $[X_7,X_{10}]=X_5$

. It is worth mentioning that, whereas the metrics arising in branches 15 and 20 were obtained in Ref. [23], branch 4 was left out.

4. Summary and Discussion

In this paper, we have re-addressed the problem of classification of cylindrically symmetric static spacetimes according to the KVFs using an algebraic algorithm in Maple. This algorithm converts the Killing’s equations into a reduced involutive form providing all possible spacetime metrics in terms of a Rif tree. In our case, the resulting Rif tree for a cylindrically symmetric static spacetime produced a total of 20 branches. It was found that the considered cylindrically symmetric static spacetime metric admits 3, 4, 5, 6, 7, and 10 KVFs only. Lastly, it was observed that the Rif tree approach provides a complete classification of the KVFs by providing additional metrics which were not given previously by using a direct integration technique.

As mentioned in the introduction, each KVF admitted by a spacetime metric corresponds to a conservation law. Out of the obtained KVFs, the symmetry ${\partial }_t,$ wherever it appears, shows that law of conservation of energy holds. Similarly, the symmetries ${\partial }_{\rho },$ ${\partial }_{\theta }$, and ${\partial }_z$ correspond to the laws of conservation of linear momenta in three spatial directions. In some cases, two of the metric functions are found to be equal. In such cases, the spacetime admits an additional rotational symmetry, which shows that the law of conservation of angular momentum holds in all these cases. Apart from these cases, each of the obtained KVFs is associated with a conservation law and this correspondence between KVFs and conservation laws is given by the well-known Noether’s theorem.

The physical significance of the obtained metrics can be checked by looking into the structure of the energy–momentum tensor. Particularly, the component $T_{00}=\rho$ of the energy–momentum tensor gives the energy density of the metric and tells us whether the metric is physically realistic or not. For this purpose, we have calculated $\rho$ for all the obtained metrics. For some metrics, $\rho$ vanishes and, hence, all these metrics are physically realistic. In the remaining cases, further conditions on metric functions are needed to be imposed so that $\rho$ is non-negative. For example, for the metrics of branches 5 and 11 given in Table 1, we must impose the condition $\frac{B^{″}}{B}<0,$ so that $\rho$ is non-negative.