Abstract
The differential privacy histogram publishing method based on grouping cannot balance the grouping reconstruction error and Laplace noise error, resulting in insufficient histogram publishing accuracy. To address this problem, we propose a symmetric histogram publishing method DPHR (differential privacy histogram released). Firstly, the algorithm uses the exponential mechanism to sort the counting of the original histogram bucket globally to improve the grouping accuracy; secondly, we propose an optimal dynamic symmetric programming grouping algorithm based on the global minimum error, which uses the global minimum error as the error evaluation function based on the ordered histogram. This way, we can achieve a global grouping of the optimal error balance while balancing the reconstruction and Laplace errors. Experiments show that this method effectively reduces the cumulative error between the published histogram and the original histogram under long-range counting queries based on satisfying -differential privacy and improves the usability of the published histogram data.
1. Introduction
In the era of big data, a large number of personal information data are generated every day, such as social information [1], physiological signals collected by intelligent wearable devices [2], and data auctions in the internet of things [3]. Information digitization technology enables various institutions to easily collect a large amount of information and data, publish statistical results in various forms, and conduct data analysis and research. Although the analysis and mining results of these data can help people to analyze and study things, there will also be the problem that the private information contained will be stolen in the actual process of publishing information. Histograms, as a common method to intuitively display the characteristics of data distribution, are often used to publish statistical data. In this method, the published data is divided into disjoint buckets according to some attributes, and then the bucket count is used to represent the data characteristics. However, if we directly publish the statistical histogram without privacy protection in the process of publishing the information, an attacker can infer the user data by combining the background knowledge and the real count of the histogram bucket, resulting in the problem of user privacy disclosure.
For example, Table 1 shows some sensitive data records of whether a group of patients are infected with HIV, and Figure 1 shows the statistical histogram of HIV+ distribution in Table 1 after taking the values according to their age attributes. If the attacker already knows that Ava is 29 years old, and if the attacker obtains the disease information of three people in the bucket [20, 30] except Ava by some means, it can be accurately inferred that AVA is infected with HIV.

Table 1.
Sample patient data.
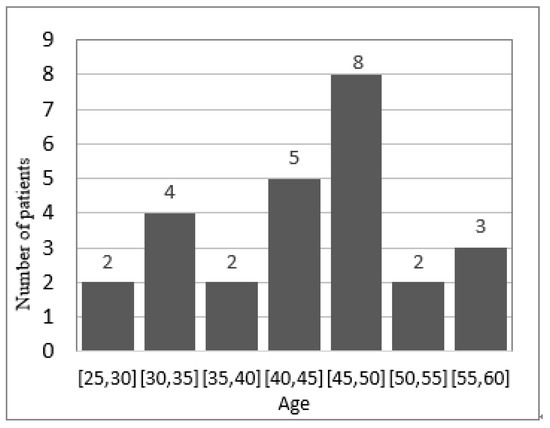
Figure 1.
Original histogram with age distribution.
In order to prevent the disclosure of users’ privacy, it is necessary to protect the privacy of data before publishing. The existing privacy protection models include k-anonymity [4,5] and a series of extended models [6,7,8], such as l-diversity, t-closeness, and so on. However, these typical privacy protection models limit the attacker’s background knowledge when they are defined, and are only effective for specific attack models. In practice, the attacker has much more background knowledge than this hypothesis. Dwork proposed a new privacy definition, differential privacy [9], in 2006 to solve the problem of database privacy disclosure. Compared with the traditional protection model, the differential privacy model has two significant advantages: (1) it does not depend on the background knowledge of the attacker; (2) it has a rigorous statistical model and can provide quantifiable privacy assurance. Therefore, differential privacy is widely used as the main technology of data privacy publishing. The main idea of differential privacy is to add enough noise to each histogram count, so that the attacker cannot use the information of the specific record owner to generate the histogram before processing. However, the increased noise for higher privacy requirements usually greatly reduces the accuracy of the published histogram. In order to solve this problem, this paper does not consider directly adding noise to the histogram count, but uses the reconstruction method to reduce the data sensitivity to reduce the noise amplitude. In this process, the reconstruction error and noise error are balanced at the same time, which greatly improves the availability of data when the histogram meets the privacy.
Although the current histogram publishing method based on grouping can ensure the privacy and security of the published histogram, it cannot improve the accuracy of the published histogram, resulting in low availability. The existing methods mainly have the following problems:
- The local grouping method only considers the similar bucket count of the nearest neighbor, but cannot measure the buckets with similar counts in the global range, so that there is a large reconstruction error in grouping.
- The global grouping method obtains the optimal error balance global grouping of the original histogram through fixed length grouping or greedy clustering grouping, which may fall into local optimization and cannot better balance the reconstruction error and Laplace error [10], resulting in the reduction in the availability of the published histogram.
In view of the above problems, this paper realizes the satisfaction -differential privacy histogram publishing method DPHR. Firstly, an approximate ranking algorithm based on an exponential mechanism is proposed, which considers the relationship between the difference between bucket counts and the outlier length , the exponential mechanism is used to sort the bucket count of the original histogram globally. Based on the sorting results, combined with the dynamic programming algorithm based on the global minimum error, the optimal grouping strategy is obtained. On the basis of meeting the requirements of differential privacy, this method balances the reconstruction error (RE) generated by the group mean and the Laplace error (LE) generated by adding Laplace noise in the grouping, and effectively reduces the reconstruction error (RE) in the sorting results, which not only ensures the privacy of the published histogram, but also improves the availability of the data.
The main contributions of this paper are as follows:
- Aiming at addressing the problem of low data availability of the existing grouping histogram publishing algorithm, an approximate sorting algorithm based on an exponential mechanism is adopted, which is based on the relationship between the difference between bucket counts and the length of outliers . The exponential mechanism is used to sort the bucket count of the original histogram globally, so as to improve the accuracy of the grouping.
- A dynamic programming algorithm based on the global minimum error is proposed, to realize the global grouping with the best error balance on the sorting histogram, balance the reconstruction error and Laplace error, and reduce the overall difference between the published histogram and the original histogram.
2. Related Work
Ref. [11] proposed the Laplacian mechanism (LPA), which publishes the differential privacy histogram by adding independent and identically distributed Laplacian noise to each bucket of the histogram, which lays a theoretical foundation for later research results. However, due to the addition of noise, the cumulative noise error of this method in the face of a long-range counting query is too large, which affects the accuracy of the data. In view of the above shortcomings, many scholars have put forward improved methods. The grouping method reconstructs the histogram grouping structure, uses the group mean to approximate the original histogram count, and then reduces the added Laplace noise error in the fixed privacy budget. Such methods use the group mean and Laplacian mechanism to protect privacy, which inevitably produces reconstruction errors caused by reconstruction and Laplacian errors caused by adding Laplacian noise. Ref. [12] proposed the Noisefirst and StructureFirst algorithms. The Noisefirst algorithm performs dynamic programming on the histogram after the addition of noise and divides the optimal grouping. Because too much noise is added first, the privacy cost is high. The StructureFirst algorithm uses an exponential mechanism to divide the optimal grouping of the histogram, and adds Laplace noise to the group mean. However, this method needs to specify the number of groups K, and does not take into account the balance between the reconstruction error and noise error caused by the groups. Ref. [13] proposed the P-HPartition algorithm, which uses an exponential mechanism combined with the greedy bisection strategy to continuously divide and group, so as to obtain the division scheme with the minimum error value. Both P-HPartition and StructureFirst are based on the idea of local grouping. They only consider the numerical nearest neighbor relationship of buckets in the local range, cannot measure the nearest neighbor relationship of global count, and cannot well balance the reconstruction error and Laplace error.
Aiming at the shortcomings of local grouping, here a histogram publishing method based on global grouping is developed. Ref. [14] proposed obtaining an ordered histogram by row sampling or column sampling, and divide the ordered histogram by equal width. However, a fixed length packet cannot effectively balance the reconstruction error and noise error, which affects the availability of data. The APH [15] method uses the threshold mechanism to count the buckets within the threshold without adding noise, and then obtains the grouping through greedy clustering. Although this method reduces the Laplace error, it leads to an imbalance between the reconstruction error and Laplace error when the privacy budget is small. Ref. [16] and others proposed using sampling technology to obtain an approximate correct ranking, and then greedy clustering to obtain global grouping. The IHP [17] method uses an exponential mechanism to continuously divide and group, so as to obtain the balance of the Laplace error and reconstruction error. Ref. [18] introduced a quantitative mechanism of associated privacy disclosure evaluation in the literature to evaluate the loss in privacy disclosure in the process of histogram publishing. Ref. [19] proposed an algorithm to publish a node strength histogram based on node differential privacy. Firstly, the “sequence edge” is used to reduce the query sensitivity and make the distribution of the node strength more dense. Then, the histogram is divided into groups by a clustering method, and finally, the node strength histogram is published. However, the algorithm also has the problem that it cannot balance the publishing errors of the two histograms.
3. Preliminaries
3.1. The Theoretical Basis of Differential Privacy
Differential privacy is a new privacy definition, proposed by [11] in 2006, for the privacy disclosure of databases. Differential privacy requires that the existence of any record in the dataset will not significantly affect the calculation and processing results of the dataset. Attackers cannot obtain accurate individual information by observing the calculation results. Its relevant definitions and concepts are as follows:
Definition 1
(Adjacent datasets [20]). If there is only one record difference between datasets D and , i.e., , then D and are called adjacent datasets.
Definition 2
(Differential privacy [11]). If the output result O ( and is the output range of M ) of a random algorithm M in any two adjacent datasets D and satisfies Equation (1), then algorithm M satisfies ε-differential privacy.
With the for privacy budgets, the smaller is, the higher the degree of privacy protection of algorithm M. -differential privacy controls the influence of any record on the output of algorithm M.
The basic idea of the differential privacy model is that the addition or deletion of one record in a statistical query has no effect on the result of the data query. That is, when a statistical query is performed on two datasets that differ by only one record, the probability ratio of the query to output the same result on the two datasets is close to 1. Therefore, the attacker cannot restore any record of the original dataset from the query output, to achieve the purpose of privacy protection.
In the process of realizing differential privacy protection, a noise mechanism is required to randomize the query results. Two common noise mechanisms are the Laplace mechanism and exponential mechanism. The amount of noise added depends on the concept of the global sensitivity of the query function f.
Definition 3
(Global sensitivity [9]). Set the query function , and the global sensitivity of f is
where is the 1-order norm distance between and .
Theorem 1
(Laplace mechanism [11]). For query function , the sensitivity is , random algorithm satisfies -differential. is the random noise obeying the Laplace distribution [21] with the parameter , and and jointly control the noise level. The Laplacian mechanism applies only to numeric query results, while some query results are non-numeric, hence the exponential mechanism.
Theorem 2
(Exponential mechanism [22]). If random algorithm M selects and outputs r from with a probability proportional to , algorithm M provides ε-differential privacy protection. Where D is the input dataset of M, is the utility function of output r, and is the global sensitivity of function .
3.2. Error in Histogram Grouping Publishing
Definition 4
(Reconstruction error, RE). The reconstruction error is generated in the grouping process. The original histogram bucket count sequence is divided into k groups, and the average bucket count of each group is used to replace each bucket count in the group, then the grouping result is expressed as: , . is the mean of group , . The reconstruction error in the i-th group is
Definition 5
(Laplace error, LE). The Laplace error is caused by the noise added to the histogram bucket count. is the variance measure using the Laplace distribution.
Therefore, the total error expected to publish the histogram is
4. Method
4.1. Symmetry Differential Privacy Histogram Released Algorithm
Aiming at the problems existing in the existing methods, this paper realizes the satisfaction symmetry -differential privacy histogram publishing method DPHR. The specific implementation details are shown in Algorithm 1.
| Algorithm 1 DPHR |
|
Correct sorting and grouping are the key to this algorithm. Given the privacy budget, the is divided into two parts: and , which are used for sorting and denoising. Given the original histogram H and privacy budget , the approximate ranking (line 2) is obtained by using the exponential mechanism. After sorting, the histogram is optimized for grouping (row 3) in order to reduce the global error of each group. Finally, the privacy budget is used to add Laplace noise to the mean of each group (lines 4–9).
4.2. Approximate_Sort algorithm
When reconstructing the original histogram, if only the bucket counts of the nearest neighbors are combined, it will bring huge errors in the grouping. Therefore, we consider the relationship between the difference between bucket counts and the discrete length , using the exponential mechanism to approximate sort the bucket count of the original histogram, and the correct sorting of histogram H is approximately obtained. Here, we give the following definitions.
Definition 6
(Discrete length). If the vertex set in an undirected graph is , for point , the discrete length δ is .
This method uses the exponential mechanism to approximate the correct ranking under the condition of differential privacy. If the histogram method is sorted directly, it will make its output different from the count sorting of adjacent histograms, which does not meet the definition requirements of differential privacy. Therefore, we use the exponential mechanism to select the nearest neighbor buckets and select the buckets with similar counts, and the result has a certain randomness. The definition of a nearest neighbor bucket is as follows.
We use the outlier length as the distance threshold, and define the nearest neighbor bucket set of base bucket
Taking bucket as the base bucket, each bucket of the nearest neighbor bucket set can be scored according to the bucket count difference and bucket order: , where is the absolute value of the count difference between and , and is the absolute value of the sequence difference between and . According to Definition 5, the exponential mechanism allocates the probability of output results according to the level of the scoring function. The larger the scoring function value, the greater the possibility of output. Therefore, the exponential mechanism can be used to continuously select the bucket whose count is most similar to that of the previous base bucket from the nearest neighbor bucket set to form an ordered histogram .
The detailed implementation process of the Approximate_Sort algorithm is as follows (Algorithm 2):
| Algorithm 2 Approximate_Sort algorithm |
 |
The histogram is shown in Figure 1, first, select as the base bucket for sorting, and the outlier length of bucket , obtain the nearest neighbor bucket set of bucket , then, , , , , select bucket according to the exponential mechanism and put it into the sorting queue. If the next benchmark bucket is , , , , put bucket into the sorting queue. The next benchmark bucket is . Continuously calculate the set of adjacent buckets, and use the exponential mechanism to select buckets with similar counts and put them into the sorting queue. The final sorting result is .
4.3. Optimized_Cluster algorithm
After using the exponential mechanism to obtain the ordered histogram, in order to adaptively obtain the ideal grouping scheme, we use dynamic programming technology to solve the grouping problem. The problem is described as follows: given the histogram bucket count sequence H, find several segmentation points, and find the best histogram group that minimizes the error evaluation function among all possible histograms with exactly K groups. The error evaluation function used in traditional methods such as the StructureFirst method is , which is the sum of the squares of errors between the group mean and the original value of the combined partial histogram sequence . The corresponding dynamic programming recurrence formula is as follows:
However, only taking the reconstruction error as the error evaluation function for dynamic programming, the grouping obtained may not be the grouping scheme with the smallest total error, and cannot effectively balance the reconstruction error and noise error. Therefore, we propose the calculation formula of the global error, and take the global error as the error evaluation function to obtain the global grouping scheme with the smallest total error.
Theorem 3.
For any group , it has a global error , where is the mean of group , is the reconstruction error RE, and is the Laplace error, LE.
Proof.
According to the reconstruction error and noise error released by the histogram grouping, we can know that the average value of the group count is , and the size of the Laplace noise added to is , then the expectation of can be expressed as
Therefore, the new dynamic programming recurrence formula is as follows:
represents the minimum global error in covering histogram and dividing it into k groups, and represents the global error in merging subsequences of partial histograms as a group. □
The Optimized_Cluster algorithm is presented in Algorithm 3:
| Algorithm 3 Optimized_Cluster algorithm |
 |
Using the data in Figure 1 for an example analysis. The specific analysis process is as follows. The privacy budget is taken as = 1, the number of groups :
Steps 1–3 in Figure 2 describe the results of each cycle of the optimized grouping algorithm. In each step, the algorithm can obtain the optimal grouping structure under the current number of groups. The two-dimensional table on the left-hand side of Figure 2 stores the intermediate result of the dynamic programming, which represents the minimum global error of each grouping structure recorded by dividing the grouping of n buckets in into one group, two groups, …, to k groups. The j-th row and i-th column in the two-dimensional table are used to store the minimum error caused by dividing the first i buckets into j packets. The outer layer circularly uses the grouping structure from to , and the inner layer circularly uses the bucket from to . T is calculated successively through the recursive Formula (7), and the backtracking method is used to traverse the two-dimensional table to determine its grouping structure. Finally, the grouping structure with the lowest and the optimal number of packets k are selected. Shaded cells represent the optimal histogram grouping division under the current number of groups. The list on the right-hand side of Figure 2 is , which represents the current optimal grouping structure stored under different groups, which is determined according to the minimum global error in the two-dimensional table.
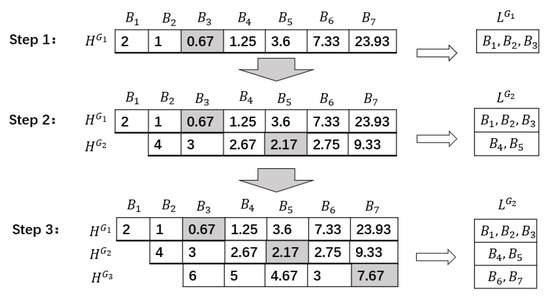
Figure 2.
Optimal grouping structure.
5. Analysis of Algorithm Privacy and Availability
5.1. Privacy of Algorithm
Theorem 4.
DPHR satisfies ε-differential privacy.
Proof.
In the DPHR method, (line 2, Approximate_Sort algorithm) uses the exponential mechanism to extract the most similar bucket from the original histogram H, which is equivalent to n queries, which are denoted as . According to Definition 3, it can be known that adding or deleting a record of H affects the count of one bucket in H at most, so . According to Theorem 2, (line 2) meets the -difference privacy.
For line 8, it adds Laplace noise, obeying distribution to the group mean. According to Theorem 1, it meets the following requirements -differential privacy. An algorithm satisfying differential privacy can provide a quantifiable privacy guarantee. According to Theorem 4, it can be seen that the DPHR algorithm meets -differential privacy. □
Theorem 5.
There are a series of algorithms , which respectively meet the differential privacy with the privacy protection budget of . If k algorithms act on the same dataset D, the combined algorithm meets -differential privacy.
5.2. The Analysis of Data Availability
The usability and convenience of the algorithm are measured and analyzed by histogram publishing error and algorithm time complexity. Table 2 shows the comparative analysis of histograms published by StructureFirst [12], AHP [18], IHP [17], and DPHR. In the StructureFirst algorithm, k is the number of its groups, and its total error and time complexity are the largest of the following four algorithms. For the remaining three algorithms, their release error is the same, which is composed of the reconstruction error and Laplace error. Their first item represents the reconstruction error in the publishing process, which is related to the reconstruction method of the specific algorithm. The time complexity of the DPHR algorithm and the IHP algorithm is relatively small, but the IHP algorithm directly uses the hierarchical partition algorithm to partition the original data when reconstructing, and the partition accuracy of datasets with discrete distributions of similar data is not high. The DPHR algorithm divides the sorted data, which greatly reduces the reconstruction error introduced by grouping, and can still divide the grouping better in the face of distributed discrete data.

Table 2.
Sample patient data.
Suppose that the data , corresponding to the original histogram in Figure 1, is released to the public by the DPHR algorithm. The DPHR algorithm uses the exponential mechanism to globally approximate sort the count of the bucket of the original histogram. After sorting, the sequence is . Then, the optimal grouping algorithm based on the global minimum error is used to group the data globally. The statistical sequence after grouping takes the mean is , order = 1, and random variables are extracted from the Laplace distribution with the compliance parameter of (0, 1/2) to obtain the Laplace noise sequence and add noise to each overall bucket. The added noise sequence is {−0.23803, 0.00466, −0.19543, −0.87709, 0.3216, −0.17054, 0.07014}. The statistical sequence after adding noise interference to is {1.76197, 3.50466, 1.80457, 5.62291, 6.8216, 1.82946, 3.57014}. The error between the published data after grouping and adding noise and the original data is shown in Table 3. Comparing the total error in the data released by the four algorithms with the original data, it can be seen from Table 3 that the total error in the DPHR algorithm has been reduced compared with the other algorithms.

Table 3.
Comparison of published data errors between DPHR algorithm and other algorithms.
6. Experiment and Analysis
6.1. Experimental Data and Environment
The hardware environment used in the experiment is an Intel (R) core (TM) i7CPU, 2.60 GHz, with 16 GB memory, and the operating system platform is the Windows 10 operating system. The StructureFirst algorithm [12], AHP algorithm [18], IHP algorithm [17], and DPHR algorithm in this paper are implemented on the experimental dataset using the Java programming language and C++ language, respectively, and the visual comparison is realized by the Python tool. The experiment uses two public datasets, Waitakere and Social_Network, commonly used in histogram publishing research. The Waitakere dataset is population block census data. A total of 7725 data records are taken to form a statistical histogram. The Social_Network dataset is social networking site data, including the social data of 11,342 users, and each user record contains the number of the user’s friends. The statistics of these two datasets are summarized in Table 4.

Table 4.
Experimental dataset information.
6.2. Error Evaluation Criteria
The experiment uses mean square error (MSE) as the evaluation standard to measure the accuracy and availability of the histograms issued by the StructureFirst algorithm [12], AHP algorithm [18], IHP algorithm [17], and DPHR algorithm in this paper.
The mean square error evaluates the degree to which the statistical value of the published histogram bucket deviates from the statistical value of the original histogram. Given a set of statistical queries , the MSE calculation formula of the original histogram H and published histogram is given as follows:
6.3. Experimental Results and Analysis
By setting different range query lengths and different privacy budgets, the experiment compares the mean square error (MSE) of different algorithms under a range query, so as to compare the accuracy and availability of the histograms published by different algorithms. The following figure compares the mean square error (MSE) of the four algorithms when the privacy budget is = 1, , 0.1, 0.01, and the range query length is 50–500.
As can be seen from Figure 3, the horizontal axis represents the query length of the range, and the query interval is 50. The vertical axis represents the mean square error MSE, which is the mean square error between the dataset published by the differential privacy histogram publishing method and the original dataset. When calculating MSE, the query length is set to 50–500. With the increase in query time, the obtained MSE value gradually tends to be stable. As can be seen from Figure 3, with the increase in the horizontal axis query range, the value of MSE also gradually increases, because with the increase in the length of the query range, there is an accumulation of noise error, and the MSE also increases. From Figure 3 we can know when increases from 0.01 to 1, the Laplace noise error added to the data will gradually decrease; when = 1, the global error is only composed of the reconstruction error, and the MSE is relatively small. It can also be found from Figure 3 that the query range of the Social_Network dataset is larger than that of the Waitakere dataset, and its MSE value is also larger.
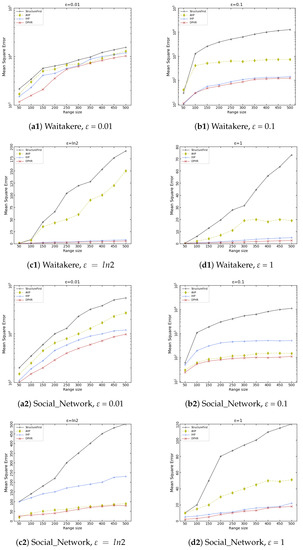
Figure 3.
Change of MSE under different query lengths.
It can be seen from Figure 3, that under the comparison of different datasets and privacy budget conditions, the MSE of the DPHR algorithm is relatively small, and its accuracy is better than other methods. Firstly, for the StructureFirst algorithm, it uses the combination of v-optimization and the exponential mechanism to directly divide the original histogram. The division accuracy is low, resulting in a large reconstruction error. Secondly, for the AHP algorithm, adding noise to the data outside the threshold, and sorting and grouping the noisy data, will reduce the availability of published data. With the IHP method, for data with an uneven bucket count distribution in the histogram, the Laplace noise will increase. The DPHR algorithm uses the exponential mechanism to globally approximate sort the count of the original histogram bucket, and then uses the dynamic programming algorithm based on the global minimum error to globally optimize the grouping of the data. Finally, it is released after adding Laplace noise, which improves the accuracy of the division, and makes the finally released data have a high availability while taking into account the privacy.
Experimental results of different privacy budgets under the Waitakere and Social_Network datasets.
7. Conclusions
Aiming at the differential privacy histogram publishing method, this paper proposes a histogram publishing DPHR method based on sorting and grouping. Aiming at addressing the problem that the existing methods cannot balance the reconstruction error caused by grouping and the noise error caused by noise, this method puts forward a solution. The DPHR algorithm includes two important algorithms: Approximate_Sort algorithm and Optimized_Cluster algorithm. Among them, the Approximate_Sort algorithm is mainly based on the idea of smooth grouping, which uses approximate sorting on the original histogram to prepare for reducing the error in the grouping reconstruction. The Optimized_Cluster algorithm mainly carries out adaptive grouping according to the optimized dynamic programming recursive formula, to obtain the grouping scheme with the minimum global error, and balance the reconstruction error and Laplace noise error, so as to improve the accuracy of the final published histogram. The privacy analysis of DPHR shows that this method can better protect the privacy of published histogram data, and the experimental tests show that the usability of this method is better than other methods.
The Optimized_Cluster algorithm mainly carries out adaptive grouping according to the optimized dynamic programming recursive formula to obtain the grouping scheme with the minimum global error, and balance the reconstruction error and Laplace noise error, so as to improve the accuracy of the final published histogram. The privacy analysis of DPHR shows that this method can better protect the privacy of published histogram data, and the experimental test shows that the usability of this method is better than other methods.
The research perspective of the differential privacy histogram publishing method in this paper is not comprehensive enough. The data published by the differential privacy publishing algorithm studied in this paper is a static dataset. Future research work can also study the privacy protection of continuous data in real time.
Author Contributions
T.T. designed the framework and realized and verified the proposed scheme. S.L., J.H., and S.H. were responsible for the organizational structure and edited the manuscript. H.G. reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Key Program of the Natural Science Foundation of the Educational Commission of Anhui Province of China (Grant No. 2022AH050319, 2022AH052740), and the Natural Science Foundation Project of Anhui Province of China (Grant No. 2008085QF305, 1908085MF212).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declared no potential conflict of interest with respect to the research, authorship, or publication of this article.
References
- Zhou, N.; Long, S.; Liu, H.; Liu, H. Structure–Attribute Social Network Graph Data Publishing Satisfying Differential Privacy. Symmetry 2022, 14, 2531. [Google Scholar] [CrossRef]
- Guo, J.; Yang, M.; Wan, B. A Practical Privacy-Preserving Publishing Mechanism Based on Personalized k-Anonymity and Temporal Differential Privacy for Wearable IoT Applications. Symmetry 2021, 13, 1043. [Google Scholar] [CrossRef]
- Jia, X.; Song, X.; Sohail, M. Effective Consensus-Based Distributed Auction Scheme for Secure Data Sharing in Internet of Things. Symmetry 2022, 14, 1664. [Google Scholar] [CrossRef]
- Sweeney, L. k-anonymity: A model for protecting privacy. Int. J. Uncertain. Fuzziness-Knowl.-Based Syst. 2002, 10, 557–570. [Google Scholar] [CrossRef]
- Sweeney, L. Achieving k-anonymity privacy protection using generalization and suppression. Int. J. Uncertain. Fuzziness-Knowl.-Based Syst. 2002, 10, 571–588. [Google Scholar] [CrossRef]
- Li, N.; Li, T.; Venkatasubramanian, S. t-closeness: Privacy beyond k-anonymity and l-diversity. In Proceedings of the 2007 IEEE 23rd International Conference on Data Engineering, Istanbul, Turkey, 15–20 April 2006; pp. 106–115. [Google Scholar]
- Machanavajjhala, A.; Kifer, D.; Gehrke, J.; Venkitasubramaniam, M. l-diversity: Privacy beyond k-anonymity. ACM Trans. Knowl. Discov. Data (TKDD) 2007, 1, 3-es. [Google Scholar] [CrossRef]
- Wong, R.C.W.; Li, J.; Fu, A.W.C.; Wang, K. (α, k)-anonymity: An enhanced k-anonymity model for privacy preserving data publishing. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 754–759. [Google Scholar] [CrossRef]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating noise to sensitivity in private data analysis. In Theory of Cryptography: Proceedings of the Third Theory of Cryptography Conference, TCC 2006 (Proceedings 3), New York, NY, USA, 4–7 March 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 265–284. [Google Scholar]
- Jantschi, L. Distribution fitting 1. Parameters estimation under assumption of agreement between observation and model. arXiv Prepr. 2009, arXiv:0907.2829. [Google Scholar] [CrossRef]
- Dwork, C. Differential privacy. In Automata, Languages and Programming: Proceedings of the 33rd International Colloquium, ICALP 2006, Venice, Italy, 10–14 July 2006; Proceedings, Part II 33; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–12. [Google Scholar]
- Xu, J.; Zhang, Z.; Xiao, X.; Yang, Y.; Yu, G.; Winslett, M. Differentially private histogram publication. Vldb J. 2013, 22, 797–822. [Google Scholar] [CrossRef]
- Acs, G.; Castelluccia, C.; Chen, R. Differentially private histogram publishing through lossy compression. In Proceedings of the IEEE 12th International Conference on Data Mining, Brussels, Belgium, 10–13 December 2012; pp. 1–10. [Google Scholar] [CrossRef]
- Kellaris, G.; Papadopoulos, S. Practical differential privacy via grouping and smoothing. Proc. VLDB Endow. 2013, 6, 301–312. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, R.; Xu, J.; Meng, X.; Xie, Y. Towards accurate histogram publication under differential privacy. In Proceedings of the 2014 SIAM International Conference on Data Mining, Philadelphia, PA, USA, 24–26 April 2014; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014; pp. 587–595. [Google Scholar] [CrossRef]
- Zhang, X.J.; Shao, C.; Meng, X.F. Accurate histogram release under differential privacy. J. Comput. Res. Develop. 2016, 53, 1106–1117. [Google Scholar]
- Li, H.; Cui, J.; Meng, X.; Ma, J. IHP: Improving the utility in differential private histogram publication. Distrib. Parallel Databases 2019, 37, 721–750. [Google Scholar] [CrossRef]
- Yang, X.; Gao, L.; Wang, H.; Guo, H.; Zheng, J. Balanced Correlation Differential Privacy Protection Method for Histogram Publishing. Jisuanji Xuebao/Chin. J. Comput. 2020, 43, 1414–1432. [Google Scholar]
- Liu, W.; Liu, B.; Xu, Q.; Lei, H. Graph Node Strength Histogram Publication Method with Node Differential Privacy. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 1757, p. 012186. [Google Scholar]
- Xiong, P.; Zhu, T.Q.; Wang, X.F. A survey on differential privacy and applications. Chin. J. Comput. 2014, 37, 101–122. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bálint, D.; Bálint, S.D. Multiple linear regressions by maximizing the likelihood under assumption of generalized Gauss-Laplace distribution of the error. Comput. Math. Methods Med. 2016, 8578156. [Google Scholar] [CrossRef] [PubMed]
- McSherry, F.; Talwar, K. Mechanism design via differential privacy. In Proceedings of the 48th Annual IEEE Symposium on Foundations of Computer Science (FOCS’07), Providence, RI, USA, 21–23 October 2007; pp. 94–103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).