Concepts of Picture Fuzzy Line Graphs and Their Applications in Data Analysis
Abstract
1. Introduction
2. Preliminaries
- , ;
- , .
- ;
- ;
- ;
- ;
3. Picture Fuzzy Intersection Graphs and Picture Fuzzy Line Graphs
3.1. Picture Fuzzy Intersection Graphs (PFIGs)
- ;
- .
- is a picture fuzzy subgraph of ;
- .
- (2) Let be the map defined by , . Obviously, function is a one-to-one function of onto . Now, iff and so
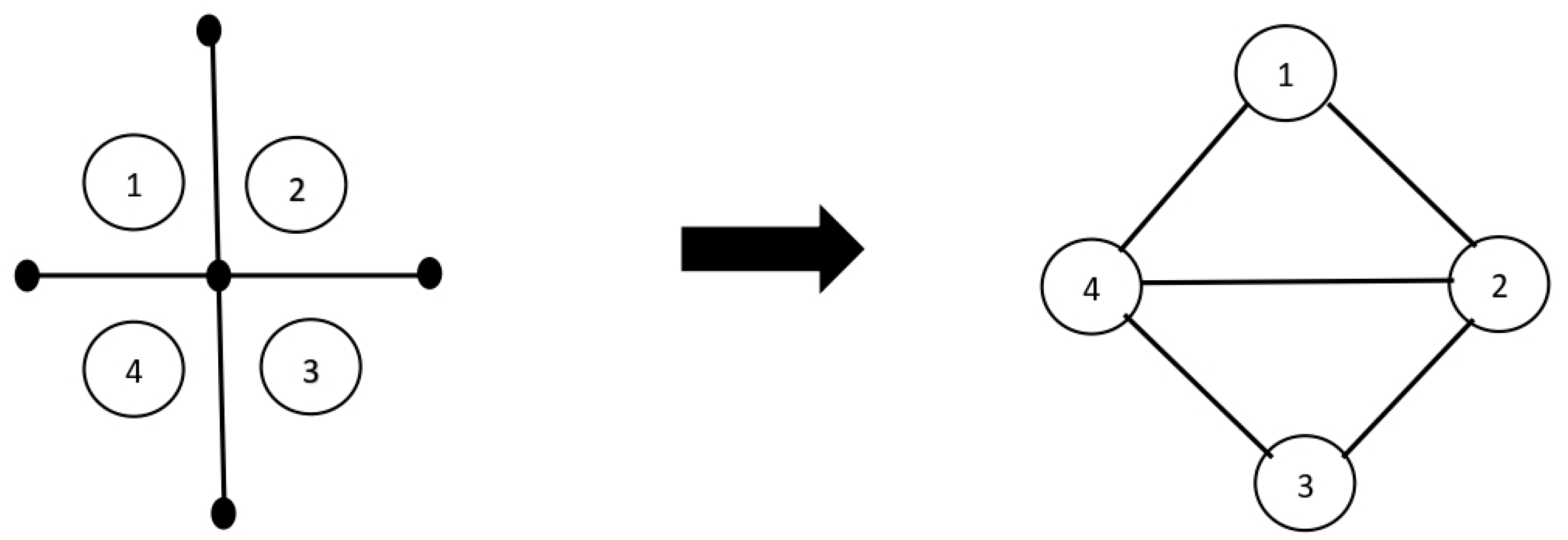
3.2. Picture Fuzzy Line Graphs (PFLGs)
- ;
- ;
- ;
- ;
- ;
- ;
- There exists a weak isomorphism of onto if and only if is cyclic and for an , , , , ; i.e., and are the constant functions on and , respectively, taking on the same value.
- is an isomorphism if it is a weak isomorphism of onto .
4. Applications of PFLGs towards Edge Clustering and c-means Algorithm
4.1. Layout of Application of PFLG as Cluster-Based Picture Fuzzy Edge Bundling (CBPFEB)
- i.
- The PFG can be the best for fuzzy partition visually. The (α, β, ϒ)-cut graph also corresponds to the (α, β, ϒ)-cut partition.
- ii.
- After obtaining the picture fuzzy cut-off values, we divide the data into three categories: membership, neutral membership, and non-membership values.
- iii.
- Now, the edges can be easily bundled based on their respective values.
- iv.
- We fixed the strength of the class (say A) based on the highest membership values for a specific cluster. This means that it will not be included in any other class.
- v.
- By eliminating the class A, we can continue bundling the other vertices termed neutral and non-membership classes. In this way, we make the clustering procedure easy for the other classes.
- vi.
- Finally, this technique decreases the data overall and easily bundles the edges, hence resulting in clustering.
4.2. Proposed Picture Fuzzy c-mean Algorithm Based on PFLGs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Infor. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Khan, M.B.; Othman, H.A.; Santos-García, G.; Saeed, T.; Soliman, M.S. On fuzzy fractional integral operators having exponential kernels and related certain inequalities for exponential trigonometric convex fuzzy-number valued mappings. Chaos Solitons Fractals 2023, 169, 113274. [Google Scholar] [CrossRef]
- Guo, X.; Shirkhani, M.; Ahmed, E.M. Machine-Learning-Based improved smith predictive control for MIMO processes. Mathematics 2022, 10, 3696. [Google Scholar] [CrossRef]
- Tavoosi, J.; Shirkhani, M.; Abdali, A.; Mohammadzadeh, A.; Nazari, M.; Mobayen, S.; Asad, J.H.; Bartoszewicz, A. A new general type-2 fuzzy predictive scheme for PID tuning. Appl. Sci. 2021, 11, 10392. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning. Infor. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Systs. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets: Theory and applications; Physica Heidelberg: Heidelberg, Germany, 1999. [Google Scholar] [CrossRef]
- Cuong, B.C.; Kreinovich, V. Picture fuzzy sets. J. Comp. Sci. Cybern. 2014, 30, 409–420. [Google Scholar]
- Khan, W.A.; Faiz, K.; Taouti, A. Bipolar picture fuzzy sets and relations with applications. Songklanakarin J. Sci. Technol. 2022, 44, 987–999. [Google Scholar]
- Rosenfeld, A. Fuzzy graphs. In Fuzzy Sets and Their Applications to Cognitive and Decision Processes; Acdemic Press: Cambridge, MA, USA, 1975; pp. 77–95. [Google Scholar]
- Shannon, A.; Atanassov, K.T. A first step to a theory of the intuitionistic fuzzy graphs. In Proceedings of the 1st Workshop on Fuzzy Based Expert Systems, Sofia, Bulgaria, 28–30 September 1994; pp. 59–61. [Google Scholar]
- Shao, Z.; Kosari, S.; Rashmanlou, H.; Shoaib, M. New concepts in intuitionistic fuzzy graph with application in water supplier systems. Mathematics 2020, 8, 1241. [Google Scholar] [CrossRef]
- Akram, M.; Davvaz, B. Strong intuitionistic fuzzy graphs. Filomat 2012, 26, 177–196. [Google Scholar] [CrossRef]
- Zuo, C.; Pal, A.; Dey, A. New concepts of picture fuzzy graphs with application. Mathematics 2019, 7, 470. [Google Scholar] [CrossRef]
- Das, S.; Ghorai, G. Analysis of road map design based on multigraph with picture fuzzy information. Int. J. Appl. Comput. Math. 2020, 6, 1–17. [Google Scholar] [CrossRef]
- Shoaib, M.; Mahmood, W.; Xin, Q.; Tchier, F. Certain operations on picture fuzzy graph with application. Symmetry 2021, 13, 2400. [Google Scholar] [CrossRef]
- Anjum, R.; Gumaei, A.; Ghaffar, A. Certain notions of picture fuzzy information with applications. J. Math. 2021, 2021, 9931792. [Google Scholar] [CrossRef]
- Amanathulla, S.; Bera, B.; Pal, M. Balanced picture fuzzy graph with application. Art. Intell. Rev. 2021, 54, 5255–5281. [Google Scholar] [CrossRef]
- Khan, W.A.; Ali, B.; Taouti, A. Bipolar picture fuzzy graphs with application. Symmetry 2021, 13, 1427. [Google Scholar] [CrossRef]
- Khan, W.A.; Faiz, K.; Taouti, A. Cayley picture fuzzy graphs and interconnected networks. Intell. Autom. Soft Comput. 2022, 35, 3317–3330. [Google Scholar] [CrossRef]
- Khan, W.A.; Faiz, K.; Taouti, A. Interval-valued picture fuzzy graphs. Demonstr. Math. First Revision submitted in 2023; Unpublished work.
- Kosari, S.; Shao, Z.; Rao, Y.; Liu, X.; Cai, R.; Rashmanlou, H. Some types of domination in vague graphs with application in medicine. J. Mult. Valued Log. Soft Comput. 2023, 40, 203–219. [Google Scholar]
- Kosari, S.; Rao, Y.; Jiang, H.; Liu, X.; Wu, P.; Shao, Z. Vague graph structure with application in medical diagnosis. Symmetry 2020, 12, 1582. [Google Scholar] [CrossRef]
- Kou, Z.; Kosari, S.; Akhoundi, M. A novel description on vague graph with application in transportation systems. J. Math. 2021, 4800499, 11. [Google Scholar] [CrossRef]
- Rao, Y.; Kosari, S.; Gheisari, M. New results in vague incidence graphs with application. J. Funct. Spaces 2022, 2022, 3475536. [Google Scholar] [CrossRef]
- Rao, Y.; Kosari, S.; Shao, Z.; Cai, R.; Xinyue, L. A study on domination in vague incidence graph and its application in medical sciences. Symmetry 2020, 12, 1885. [Google Scholar] [CrossRef]
- Rashmanlou, H.; Borzooei, R.A. Vague graphs with application. J. Intell. Fuzzy Syst. 2016, 30, 3291–3299. [Google Scholar] [CrossRef]
- Shi, X.; Kosari, S. Certain properties of domination in product vague graphs with an application in medicine. Front. Phys. 2021, 9, 680634. [Google Scholar] [CrossRef]
- Yamashita, T.; Saga, R. Cluster-based edge bundling based on a line graph. In VISIGRAPP (3: IVAPP); Osaka Prefecture University: Osaka, Japan, 2017; pp. 311–316. [Google Scholar]
- Miller, D.J.; Nelson, C.A.; Cannon, M.B.; Cannon, K.P. Comparison of fuzzy clustering methods and their applications to geophysics data. Appl. Comput. Intell. Soft Comput. 2009, 2009, 876361. [Google Scholar] [CrossRef]
- Mordeson, J.N. Fuzzy line graphs. Pattern Recognit. Lett. 1993, 14, 381–384. [Google Scholar] [CrossRef]
- Akram, M.; Parvathi, R. Properties of intuitionistic fuzzy line graphs. Notes Intuit. Fuzzy Sets 2012, 18, 52–60. [Google Scholar]
- Nusantara, T.; Rahmadani, D.; Trisanti, Y.; Gani, A.B. Anti-fuzzy line graphs. J. Phys. Conf. Ser. 2021, 1783, 012097. [Google Scholar] [CrossRef]
- McKee, T.A.; McMorris, F.R. Topics in Intersection Graph Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999; Volume 2. [Google Scholar]
- Harary, F. Graph Theory; Addison-Wesley Publishing Company: Boston, MA, USA, 1972. [Google Scholar]
- Mordeson, J.N.; Nair, P.S. Fuzzy Graphs and Fuzzy Hypergraphs; Physica-Verlag: Heidelberg, Germany, 2012; Volume 46. [Google Scholar]
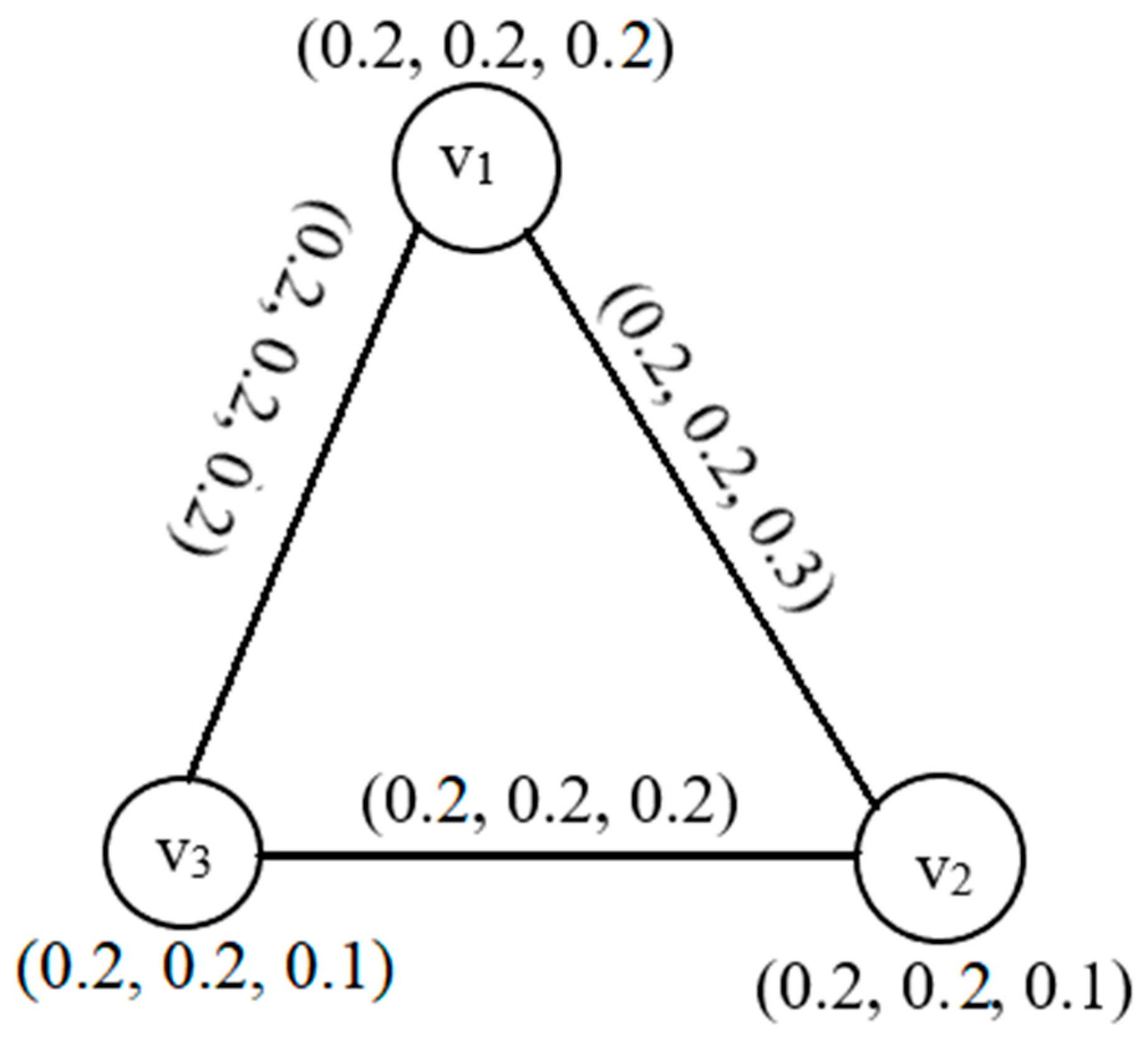
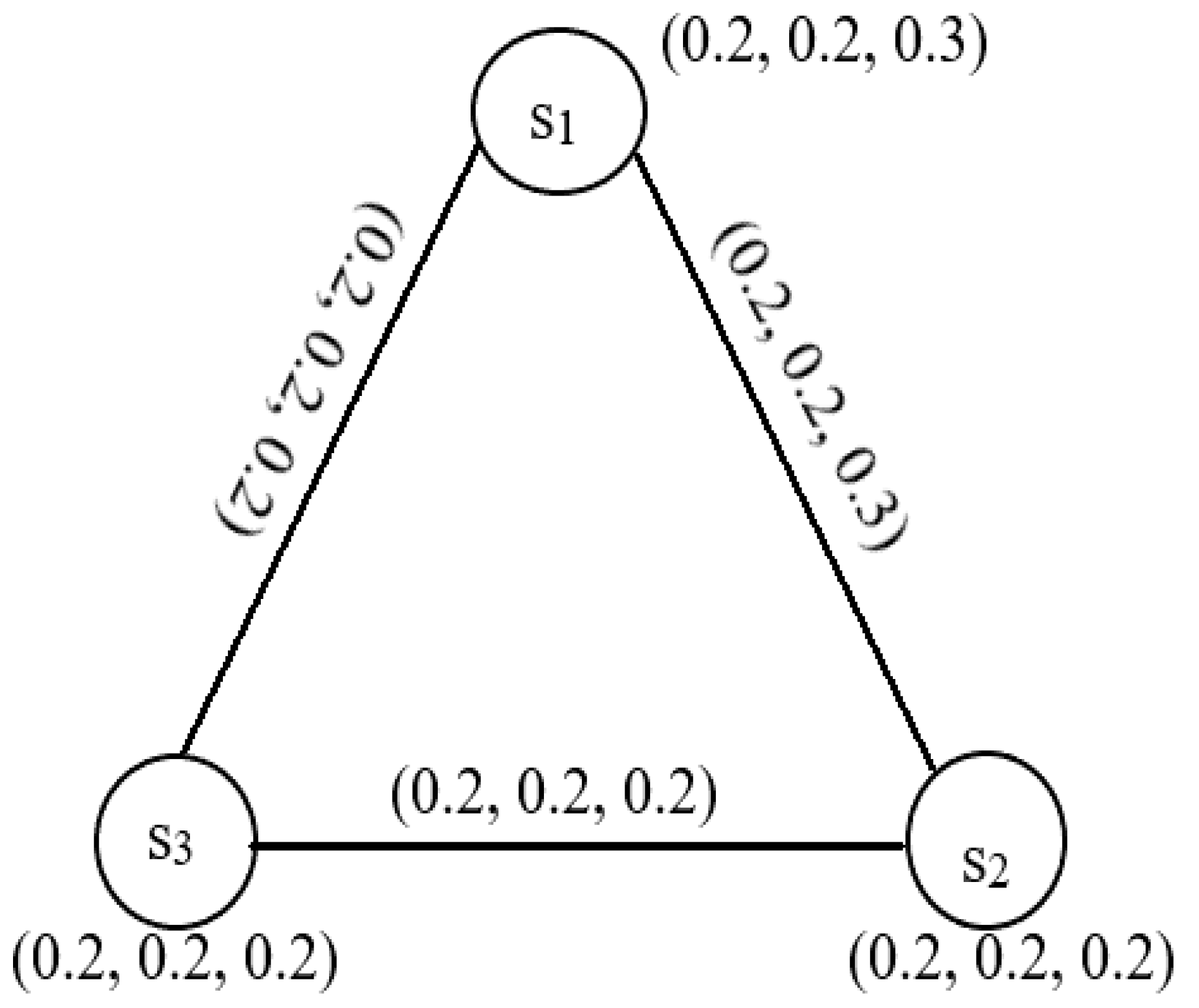
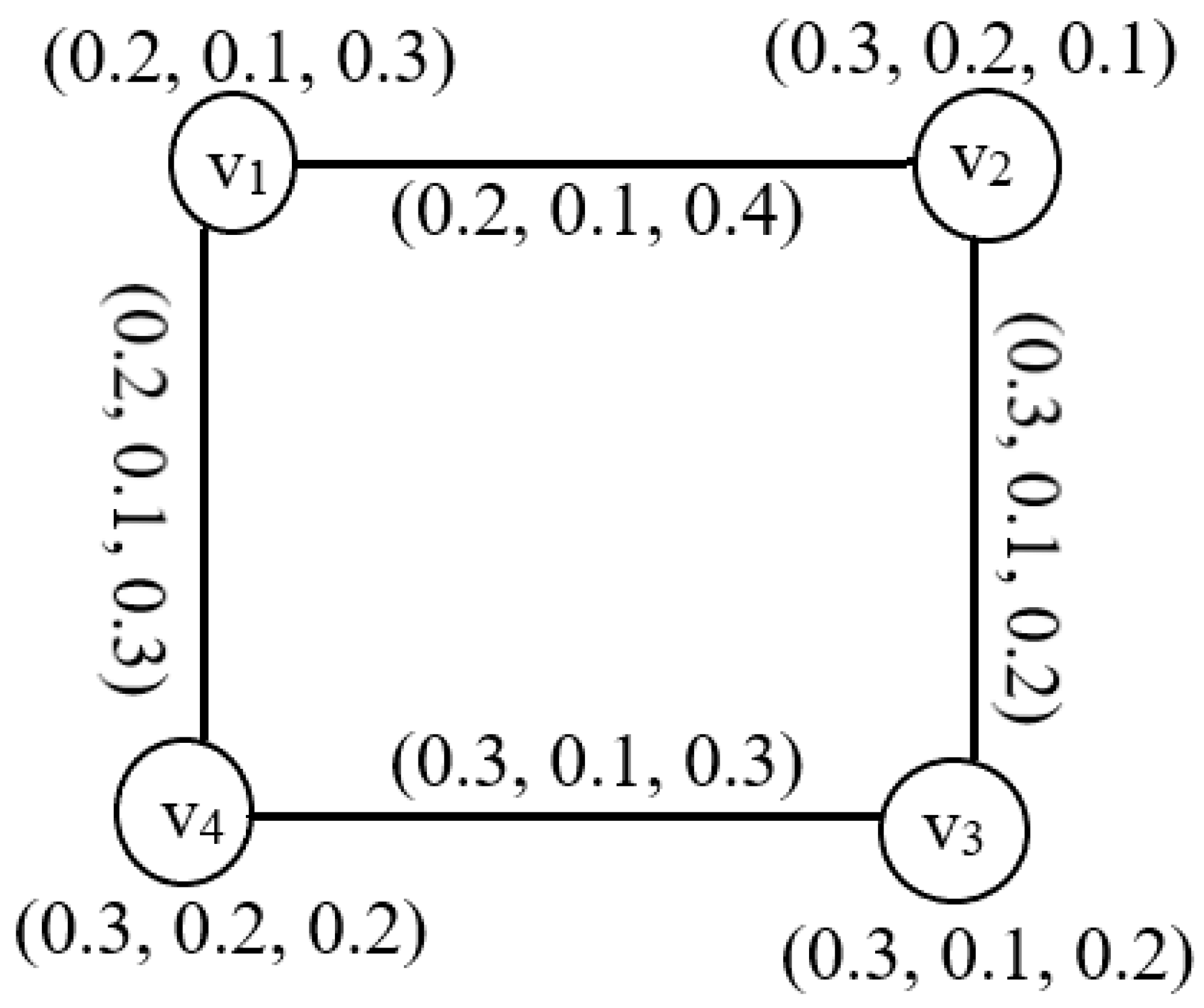
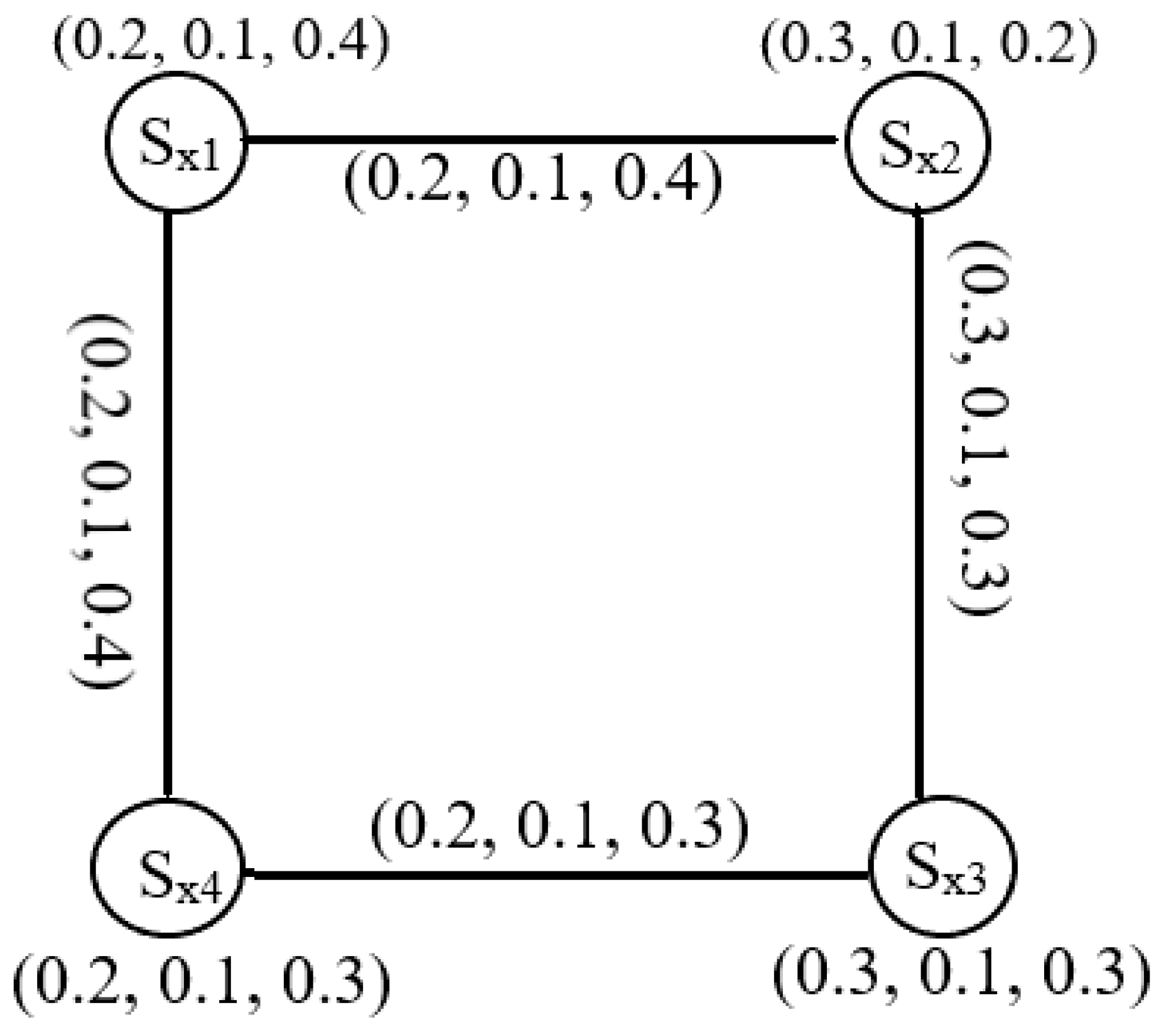

| 0.2 | 0.2 | 0.1 | |
| 0.2 | 0.3 | 0.3 | |
| 0.3 | 0.1 | 0.2 | |
| 0.2 | 0.1 | 0.1 | |
| 0.2 | 0.2 | 0.2 | |
| 0.3 | 0.2 | 0.3 |
| 0.2 | 0.3 | 0.3 | 0.3 | |
| 0.1 | 0.2 | 0.1 | 0.2 | |
| 0.3 | 0.1 | 0.2 | 0.2 | |
| 0.2 | 0.3 | 0.3 | 0.2 | |
| 0.1 | 0.1 | 0.1 | 0.1 | |
| 0.4 | 0.2 | 0.3 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Khan, W.A.; Khan, A. Concepts of Picture Fuzzy Line Graphs and Their Applications in Data Analysis. Symmetry 2023, 15, 1018. https://doi.org/10.3390/sym15051018
Chen Z, Khan WA, Khan A. Concepts of Picture Fuzzy Line Graphs and Their Applications in Data Analysis. Symmetry. 2023; 15(5):1018. https://doi.org/10.3390/sym15051018
Chicago/Turabian StyleChen, Zhihua, Waheed Ahmad Khan, and Aysha Khan. 2023. "Concepts of Picture Fuzzy Line Graphs and Their Applications in Data Analysis" Symmetry 15, no. 5: 1018. https://doi.org/10.3390/sym15051018
APA StyleChen, Z., Khan, W. A., & Khan, A. (2023). Concepts of Picture Fuzzy Line Graphs and Their Applications in Data Analysis. Symmetry, 15(5), 1018. https://doi.org/10.3390/sym15051018






