Abstract
Industries are increasingly shifting towards unmanned and intelligent systems that require efficient processing and monitoring of structures across various applications, ranging from machine manufacturing to waste disposal. In order to achieve the goal of intelligent processing, it is crucial to accurately classify and differentiate various components and parts. However, existing studies have not focused on simultaneously classifying electro-mechanical machinery components. This poses a challenge as these components, including capacitors, transistors, ICs, inductors, springs, locating pins, washers, nuts, and bolts, exhibit high intra- and inter-class similarity, making their accurate classification a tedious task. Furthermore, many of these components have symmetrical shapes but are asymmetrical among different classes. To address these challenges, this article introduces a new double-single (D-S) pooling method that focuses on the higher resemblance of seventeen electro-mechanical component classifications with minimum trainable parameters and achieves maximum accuracy. The industrial machine component classification model (IMCCM) consists of two convolutional neural network (CNN) blocks designed with a D-S pooling method that facilitates the model to effectively highlight the differences for the higher similar classes, and one block of grey-level co-occurrence matrix (GLCM) to strengthen the classification outcome. The extracted fused features from these three blocks are then forwarded to the random forest classifier to distinguish components. The accuracy achieved by this proposed model is 98.15%—outperforming the existing state of the arts (SOTAs) models, and has 141,346 trainable parameters– hence, highly effective for industrial implementation.
1. Introduction
In the twenty-first century, industrial production, massive in scale and diverse in scope, is difficult to organize and recognize the industrial parts for efficient use and meet the demands of the fourth revolution. The solution to this problem is the implementation of automatic systems that can efficiently classify industrial components to enhance industrial processing performance. Machines, regardless of size, from the Michigan Micro Mote to the Large Hadron Collider, are composed of numerous components that work in tandem to perform specific functions. For optimal performance, machines require automatic classification of their manufacturing, design, sorting, and handling functions. Industrial machinery components can be broadly categorized into four categories, namely mechanical, electrical, hydraulic, and optical, but mechanical and electrical components are predominantly utilized in industrial machinery.
The human brain can easily differentiate between objects, but machines require specific algorithms to learn and classify. Artificial intelligence has made this task easier. Industrial machine components, such as bolts, locating pins, diodes, capacitors, transistors, and potentiometers, have similar appearances across their various categories, generating similar features when viewed from different angles. Although these components have a symmetric shape, their depth varies within and between classes, making accurate and efficient classification a real challenge for an automated and robust industrial setup.
Industrial image classification is complex due to the plain background, which lacks information compared to colorful natural images [1,2]. This makes classification challenging, along with the minimal differences between inter and intra-class components. However, image-based processing is fast, efficient, and objective compared to manual processing, allowing for non-contact evaluation, optimization of solutions, and instant automatic processing of large amounts of data.
The existing literature focuses on component classification following three main methods: fine-tuning, transfer learning, and generic feature extraction [3,4,5]. The literature has focused on classifying individual mechanical or electrical components, but most machines comprise both components concurrently. The components from both categories show a higher resemblance and variation among inter and intra-classes; a few are shown in Figure 1. The problem of image classification is exacerbated by the fact that many electronic components, such as springs and inductors, appear similar when viewed from different angles, while others, such as transistors, capacitors, and LEDs, resemble each other only when viewed in a specific direction. Moreover, most components have a limited range of colors, consisting mainly of black and grey, against a plain background. As a result, existing technologies often struggle to achieve high precision and recall when dealing with these components. To overcome this problem, CNNs are used as they are powerful tools that utilize a hidden black box calculation to recognize images from given datasets, enabling accurate and efficient image classification even in the presence of challenging features such as similar classes, different color schemes, and plain backgrounds.

Figure 1.
Industrial components with higher resemblance.
The current literature on component classification predominantly relies on machine learning algorithms, but these methods lack the required level of precision and accuracy. Moreover, the research has been restricted to a limited number of components. Most CNN models used either max pooling or average pooling, both focusing on different features. While mixed pooling addresses this issue using both layers, it can use a single pooling method alternatively [6]. It lacks in collecting important features collection. As a result, they fail to accurately differentiate between highly similar inter and intra-classes. To address these limitations, we propose the solution with the D-S pooling method that focuses on the classification of highly similar components with its variable three pooling layers and GLCM that help us to differentiate diverse materials components. The model is designed with a combinational pooling layer that eliminates unwanted data and emphasizes specific key features. Considering the dataset characteristics and component types, a pooling layer focuses on the maximum and average values in a given region, highlighting the brighter and darker side of the images, respectively. A double average pooling layer will emphasize the darker section in a lighter area, while the max pool will collect the information from a brighter section in a darker part. The third pool layer will take full advantage of the findings and helps the model to distinguish these components more precisely, eradicating the unnecessary information that may lead to misclassification. So, this strategy classifies electro-mechanical components regardless of similarity, color, and background. It also offers the minimum number of trainable parameters that are highly effective for automatic industrial processing. This paper proposes IMCCM—a convolutional neural network-based model with the D-S pooling and GLCM feature extractor following the classifier. With its powerful strategy, CNN will facilitate forwarding the features while passing them through D-S pooling layers focusing on brighter and dull areas in both CNN blocks. GLCM-based features are added that signify the correlation, contrast, and dissimilarity among adjacent feature vectors highlighting the similarity and differences and enhancing the classification performance of colorful images. Pre-trained models focus on a specific classification problem. It shows higher performance for some cases and lowers for others. The IMCCM model has been designed considering all constraints, and its implementation offers better results.
Industrial machine components have a vast range. This study precisely considers seventeen electrical and mechanical components due to their extensive industrial usage. They have variations from large to small and have higher inter-class and intra-class similarity. The IMCCM model produces feature vectors extracted from dense layers of CNN blocks and GLCM, fused by direct fusion to pass on to a random forest classifier for categorization. The classifier distinguishes the seventeen classes with an accuracy of 98.15%, outperforming the existing SOTA. This article contributes the following:
- A framework for industrial machine components based on CNN and GLCM to effectively distinguish electrical and mechanical components simultaneously.
- It offers a unique pooling design that facilitates the model to efficiently differentiate highly similar components with a minimum number of trainable parameters.
- The proposed model experimented extensively with different numbers of components, and it outperforms the existing state-of-the-art with higher attained accuracy and precision.
The work has the potential to be extended in the coming days. Considering electrical and mechanical datasets, the proposed model has strong potential to be employed in hydraulic and optical components in the future.
2. Related Work
2.1. Mechanical Components Classification
The progression of industrial infrastructure, incorporating a transition towards unmanned development structures, has underscored the significance of intelligent and automated categorization of machine components. Mechanical components constitute a fundamental element of machining, spanning from the chipboard to the locomotive. Conventionally, human personnel are engaged in multiple tasks throughout the production cycle. Beyond manual sorting, other approaches have also relied upon rudimentary information for the purpose of component classification. In this case, considering literature [7,8,9,10] approaches: extract the geometric characteristics of the components and compare them to the parts data in the dataset collection. The authors in [11] employed particle swarm optimization and BP neural network for parts classification, utilizing invariant moment, circularity, and rectangularity features of multiple parts. Other researcher such as Dong et al. [12], Yildiz et al. [13], and Taheritanjani et al. [14] proposed classification models based on CNN. Dong et al. [12] proposed a model based on AlexNet with three convolutional layers amid to differentiate between multiple components. However, classification performance was limited by accuracy as well as time constraint, and it also did not count angle variation in similar classes images. Yildiz et al. [13] and Taheritanjani et al. [14] used a pre-trained model with fine-tuning. Yildiz et al. [13] classified the components covering multiple effects of the brightness, variation of angle, and rotation with various state-of-the-art models, e.g., EfficentB2A, DenseNet121, Densenet201, Resenet50v2. Parts detection for a large number of components was also carried out, and the dataset size used for training was reasonable. However, while EfficentB2A achieved an accuracy of 97%, its average precision did not exceed 0.75, indicating a limitation in its performance.
Siamese networks and the One-Shot learning algorithm have been employed to address the issue of similarity among various classes. Hossain et al. [15] proposed a model for banknotes that achieved similarity detection with minimal data availability, improving problem formulation with a small sample size while maintaining comparable results. Similarly, Tastimur et al. [16] presented a fastener classification approach based on Siamese Convolutional Neural Networks using one-shot learning for multiple-component classification. However, while the one-shot learning algorithm performed well for smaller datasets and similar classes, its performance was compromised for multi-inter-class problems.
2.2. Electrical Components Classification
In the digital age, electronic components carry information for communication and transmission. These components are embedded into micro to macro devices. Their common usage necessitates their identifiable classification in the era of unmanned assembling, disassembling, automatic handling, designing, etc. Limited literature is available on the classification of electrical components. However, the changing patterns of globalization and the soaring demand for automation have amplified the fastest implementation of Industry 4.0. The existing techniques-cum-approaches follow four essential solutions: the traditional method, machine and deep learning models, transfer learning, and the Siamese network.
Traditional methods focused on feature extraction with various representations, calculations, and diverse geometric elements, as observed in [17,18]. These methods present better classification performance, but their working performance was limited for large images. Multiple component classification could not be achieved at once as the calculation increased, ultimately aggregating the higher complexity level [19].
Salvador et al. [20] presented six types of electrical components classification based on transfer learning. The authors experimented on Matlab with three pre-trained models (GoogleNet, Inception V3, and Resnet101). The dataset used for research is small, holding 632 images. Incpetion-V3 shows a bit smoother training and validation results, while others showed higher disturbances after 200 epochs. Wang et al. [21] designed components classification and feature selection focusing on 2D patterns of electronic components with artificial neural networks (ANNs) and achieved an accuracy of 95.8%.
Atik [22] proposed a model that showed an accuracy of 98.9% for the three most fundamental components (resistor, capacitor, and inductor). It experimented on Matlab to classify the components with pre-trained models (AlexNet, GoogleNet, ShuffleNet, SqueezNet) and attained higher accuracy with the suggested model. Although the attained accuracy of the proposed model was very high, it just focused on three types of components. On the other hand, it did not show the time constraint for training, and the number of trainable parameters was also high. V. kaya et al. [23] explored machine learning-based classification performance for the same components using SVM, Random forest, and Naïve Bayes and attained an accuracy of 95.24%.
S. Hu et al. [24] experimented with electrical components that focused on three different brands of laptops. The author used Machine Learning and deep learning techniques to classify Apple, HP, and ThinkPad laptops. The dataset size was limited, containing 210 images. Machine learning techniques (Naïve Bayes (NB), Support vector machine (SVM), edge histogram descriptor(EHD) and Scale-invariant features(SIFT)) and deep learning techniques (Vgg-16, GoogleNet, Inception-V3, ResNet-50, and Inception-V4) were conducted. The experiment was performed with different scopes and attained the best performance with SVM-Poly(SIFT) with 90% training Accuracy and 69% testing accuracy. While GoogleNet performed best with a testing accuracy of 92% having minimum trainable parameters (5 million). Although this study gained quite good training and testing accuracy, it showed the performance with limited dataset size and types of classes.
Lefkaditis et al. [25] gained 92.3% accuracy by combining support vector machines (SVMs) and multilayer perceptions (MLPs) using an algorithm for six electronic components. However, the size of the dataset was minimal. X. Hu et al. [26] presented a hierarchical convolutional neural network to overcome the complexity and computational cost with other existing models and achieved an accuracy of 94.26%. Cheng et al. [27] introduced the Siamese network-based classification model using Vgg-16 as a feature extractor that attained very commendable results of 95%. However, the model performance was lacking as similar components appeared, and the number of components decreased. The tabular presentation of available works from the literature is shown in Table 1.

Table 1.
Existing literature representation of machine components.
The above-discussed literature on different electrical and mechanical component models shows better accuracy but with limited datasets and classes. Additionally, neither of them is simultaneously applicable to electrical and mechanical, and they have a higher number of trainable parameters. It has also been observed that they perform inadequately when applied to components of similar appearance, reflecting a gap that demands a model with higher accuracy, a minimum number of trainable parameters, and dual applicability (electrical and mechanical).
2.3. Feature Fusion
Feature Fusion is a technique that accumulates valuable and meaningful features vector from multiple sources. It is often used to improve the accuracy and robustness of computer vision algorithms. The fusion process of various sources can be weighted, direct, multi-level, multi-scale, etc. Numerous methods have been proposed for feature fusion to enhance the model performance for various imaging applications. Farman et al. [28] presented the fusion for sensors, documented daily record data, and witnessed improved performance with the fusion technique. The source for the feature vector can either be a model or layers. Fusion was implemented by extracting feature information from multiple pre-trained models, as Yang et al. [29], Cai et al. [30], and Kang et al. [31] presented. The literature showed feature fusion by extracting features from the last fully connected or middle layer or combination with pooling layers and producing highly accurate results for maritime and texture analysis [32,33]. Pan et al. [34] presented feature fusion by gathering the multiple classifier model features vector, ultimately enhancing classification accuracy.
3. Materials and Methods
3.1. IMCCM Design
The industrial machine components classification model (IMCCM) has been designed to classify machinery components robustly and correctly. The developed model comprises two convolutional neural network blocks (1 and 2) and GLCM-based feature extractor blocks, as presented in Figure 2. Blocks 1 and 2 have two convolutional layers following D-S pooling layers with the alternative combination. It also contains two dense layers; the final output layer contains the softmax functions output. The convolutional layers have 64 neurons with a 3 × 3 convolutional kernel and RELU [35] as an activation function. Both blocks follow the symmetric pattern for multiple layers. The number of neurons for all convolutional and dense layers is the same. The extracted features from blocks and GLCM vectors are fused and then forwarded to a random forest classifier.
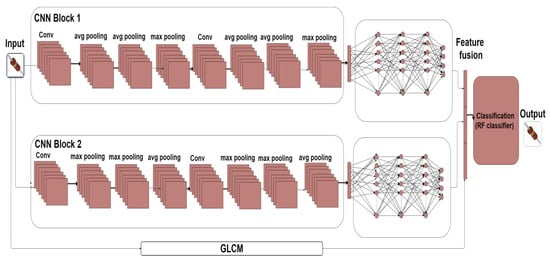
Figure 2.
Proposed framework of IMCCM.
3.2. D-S Pooling Layer
The pooling layer is a significant layer in a convolutional neural network, as it acts like a cleaner. The convolutional layers calculate too many features and excessive data, leading the model to overfit and misclassification. So, the compact pooling layers’ design eliminates undesirable data, focuses on significant features, and makes the model learning impeccable and efficient. Two conventional pooling types, max, and average pooling are widely used in neural network model designing [6]. Both categories have pros and cons and specific performance with specific images.
Primarily, Max pooling follows the phenomenon of finding the maximum value from a given region and eliminating the other values. The following formula defines the max pooling function:
The situation in a sample image can be challenging, following all high values in a feature vector or all lower values specifically for similar images. The performance of max pooling may have comprised the essential features as it highlights the brighter parts of the image.
On the other side, the average pooling function considers all values from feature vectors and passes the mean value toward the next layer. It believed all the features of the given vector to be significant. The average pooling function can be defined in the following formula:
All features’ mean values may prone the model towards unnecessary calculation and may subside the effect of the lower values features. Average pooling performance may affect the image by having smaller bright and larger dark areas. Both pooling functions have different outcomes and importance. The dataset used in this study comprised images with multiple brighter and darker regions. They also have higher similar representations at different angles producing similar situations. Here, we designed a unique and novel approach to pooling following both properties in such a way that it will help us emphasize the image’s essential features.
The D-S pooling stands for “Double-Single” combinational pooling. Considering the importance of both conventional pooling, the D-S pooling method has been designed in such a combination that it focuses on all the images with different characteristics, effectively eliminates unnecessary features, and distinguishes similar items by highlighting the notable features.
The D-S pooling works with max pooling following the max pooling that focuses on the brightest edges and corners, whereas activated lower values will be eliminated. While implementing the double max pooling layer will boost the brighter features in a darker region. The average pooling layer will spread the edges and corners of peak values achieved in y1 to help distinguish the more similar features.
Similarly, the second block will follow the double average pooling layer, as shown in Figure 3. Which will enhance the darker edges, specifically from the brighter areas, and result in the feature map focusing on the maximum value y2. It ultimately improves the quality of the image with less prominent features for classification. It also potentially offers a lower number of trainable parameters 141,346.
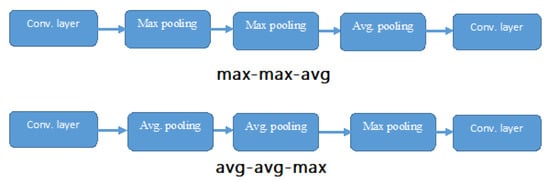
Figure 3.
Proposed D-S pooling.
The layer-wise implementation and their corresponding results are shown in the experiment section in Figure 4. First three maps (a, b, c) show the double max pooling layer following the average layer. At the same time, the last three (d, e, f) show the result of the convolutional layer following twice the average pooling impact and then the max pooling layer. After collecting features, the max pooling layer will focus on the highest features, improving the classification quality. From the figures, it can be seen that it eliminates unwanted features while focusing on the essential features and highlighting the shape of the corresponding element.

Figure 4.
D-S pooling implementation features maps, (a–c) pooling layers output max-max-avg, (d–f) pooling layers output avg-avg-max.
3.3. Hyperparameter Tuning, Loss Function, and Optimization
There are several parameters required to process the model for multiclass classification efficiently and optimally. The softmax function f(s) is most suitable for classifying multiclass problems. It evaluates the probability of each class at the final layer output. The softmax f(s) is presented as:
After evaluation conducted by the softmax function at the final layer output, the cross-entropy(CE) loss function is calculated to find the actual distance from accurate labels.
So, the cross entropy function is a loss function comprised of the log value of softmax function f(s). It helps the model evaluate the given problem’s more precise weight.
Adaptive moment estimation (Adam) is used as an optimizer because of its excellent convergence [36]. It adjusts the adaptive gradient and root means square propagation algorithm by adopting the mean and variance. The simulation has been configured with a batch size of 32 and a learning rate of 0.001.
3.4. Grey-Level-Co-Variance-Matrix (GLCM)
GLCM is a great tool that helps to estimate the different co-occurrence matrices in a given image [37]. It calculates the intensity variation of the image pixels, which helps distinguish the region of diverse classes with multiple colored areas and structures having higher likeness. Several features can be extracted using GLCM that help classify the original type. The dataset used for the given study consists of classes with higher similarity. The three most essential features, correlation, contrast, and dissimilarity are considered to assist our model in evaluating performance more effectively and correctly.
3.4.1. Correlation
Correlation is a statistical tool that calculates the linear relationship dependencies between two pixels. It calculates the dependencies based on the mean and the standard deviation.
where µk represents the mean of the ith and jth vectors of the images, and θ represents the standard deviation.
3.4.2. Contrast
Contrast focuses on the spatial frequency and moment of the image. It finds the variation of the neighboring pixel in an image, computing the object and background differences. It is also called inertia. The smaller value Gcon means lower variation in object and background, while the more significant value shows higher differences. The mathematical representation of the contrast is given below:
3.4.3. Dissimilarity
Dissimilarity presents the liner difference of the local variation in the pixels, and the mathematical representation is given below:
3.5. Feature Fusion
Features Fusion is a technique to combine and rearrange multiple features to enhance information collectively. Valuable features extracted from numerous sources can be combined differently for value-added results. Feature fusion has several methods for its implementation: direct fusion, weighted fusion, additive fusion, maximum fusion, etc. The fusion method used in this study follows the direct fusion method. Features extracted from CNN blocks 1 and 2 and GLCM-based elements are fused by concatenating them. The extracted features have been designed considering the features vector Fi with train images features Vj:
These feature vectors Fi is fused with direct (concatenate) fusion data as shown here:
where i = 1,2,3,.…n.
3.6. Random Forest Classifier
Random forest is an ensemble decision-based technique that uses multiple trees to decide the best outcome. Every tree makes a specific decision, and the final output is selected based on a maximum vote [38]. It works with the phenomenon of the same task performed by multiple groups without information sharing and finalizing the task having a higher similar outcome, as shown in Figure 5. The model has minimum association among different trees produced ensemble most suitable assessments, that is, the beauty of the model. This model does not generate overfitting problems where particular feature sets are forwarded to everyone, allowing every tree to sort out its specific error problems individually.
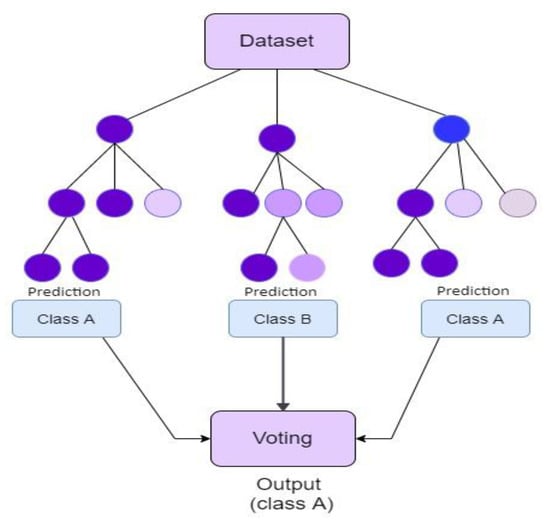
Figure 5.
Random forest classifier representation.
4. Experiment Results and Analysis
4.1. Dataset
Industrial machinery components have various sizes, types, and functions. The industrial and logistics distribution cell may not afford extensive processing and data storage. The virtual dataset decreases data collection costs and enables fast model retraining during rapid production cycles. The dataset chosen for the study of the mechanical components is mainly CAD model 2D images comprised of seven main classes (nuts, bolt, washers, locating pin, spring, bearing, and plug) and include 13,700 images. The electrical components’ dataset has been collected from images from various web sources. It included ten components: a diode, resistor, capacitor, inductor, transformer, LED, IC, pushbutton, transistor, and potentiometer. The electrical components dataset has 30,545 images for these ten types. Every category has unequal distribution, as can be seen in Table 2. The total dataset size is 44,245. The dataset has been divided into 80% for training and 20% for testing data and resized to 100 * 100. All class images are stored in the training and testing directory folder. These images are read from the folder with the folder’s name used as a class label. The corresponding images from each folder are stored with pre-processing. This accumulates the dataset into seventeen classes and is stored in arrays of testing and training.

Table 2.
Industrial machinery component dataset.
4.2. Data pre-Processing and Augmentation
The collected images need to be pre-processed before the implementation of classification techniques. All images are resized to 100 × 100 and filtered out unnecessary and vague photos. The images are converted into “.jpg” image format so that handling and implementation of the neural network can efficiently process. Depending upon the application, various data augmentation techniques can be implemented on a dataset. Some applications favor data augmentation; on the other hand, real-time industrial application has a time constraint. In this design, a few augmentation techniques are applied, e.g., rotation, height shift, fill mode, and zoom.
4.3. Performance Evaluation
The model’s performance is evaluated based on the confusion matrix and four parameters accuracy, precision, recall, and f1-score. The number of correct predictions to overall predictions defines accuracy. The formula for calculating accuracy can be expressed as the sum of true positive (TP) and true negative (TN), divided by the sum of true and false values.
where
TP: True Positive, the number of correctly predicted positive cases.
TN: True Negative, the number of correctly predicted negative cases.
FP: False Positive, the number of incorrectly predicted positive cases.
FN: False Negative, the number of incorrectly predicted negative cases.
4.4. Experiment Results
The experiment has been performed on the designed IMCCM model, as shown in Figure 2. Both blocks have two convolutional layers consisting of 64 neurons following D-S pooling layers and two fully connected layers following the softmax output layer. The total trainable parameter for blocks 1 and 2 is 80,913 and 60,433, respectively. To train the neural network model, Adam is used as an optimizer. The batch size for both blocks’ simulation is 32. Both blocks are trained with 50 epochs from scratch, and their valuable features are extracted from a fully connected layer after training. The features are also extracted from GLCM by considering the three characteristics discussed in the methodology section. These three types of extracted features are stacked and fused with direct fusion and forwarded to the random forest for its classification. With its powerful ensemble attributes, the random forest classified the machinery components following the 80 estimators and 42 as the random state. The classification performance of CNN with the standard pooling method has been presented in Figure 6. The confusion matrix of seventeen machinery components is shown in Figure 7. The use of D-pooling has significantly improved the performance, as evidenced by the confusion matrix. The layer-level significance of D-S pooling has been demonstrated in Figure 4. Compared to the standard method where many components were misclassified, the D-S pooling approach correctly identified the components with higher similarity. It is evident from the matrix that the locating pin, bolt and washer have a higher degree of similarity and are associated with the maximum misclassified components. Similarly, the transformer, inductor, and capacitor exhibit a higher degree of misclassification.
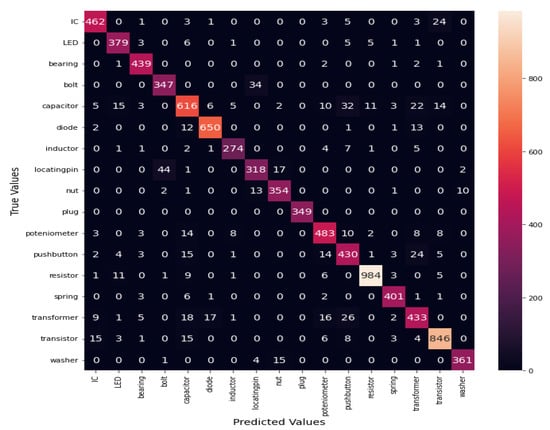
Figure 6.
Confusion matrix of CNN model with standard pooling.
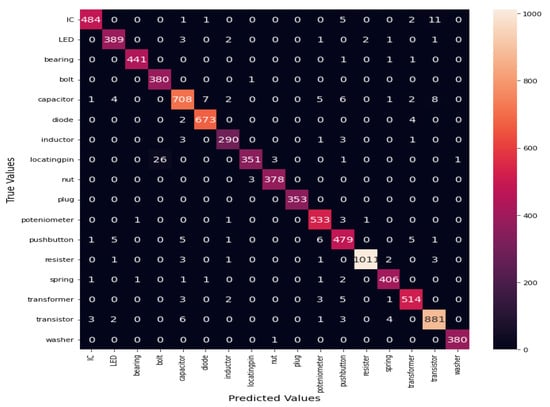
Figure 7.
IMCCM based confusion matrix of seventeen components.
The simulation of different machinery components has also been performed with our novel model for compact analysis of the existing state of the art.
The three electrical components show higher accuracy than others, around 99.34%. The experiment has also been executed considering electrical and mechanical components separately. Ten electrical components achieved an accuracy of about 97.5%, slightly lower than the final seventeen components’ performance presented in Figure 8 due to higher resemblance and imbalance in the datasets. Seven mechanical components attained an accuracy of 98.72%, higher than the seventeen components’ classification performance. Their corresponding confusion matrix is illustrated in Figure 7. The experiment has also been conducted, wherein the model was randomly tested using five images of each component, resulting in an accuracy of 98%. The experiment has also been performed for multiple existing deep learning models to check their performance for our dataset, as seen in Table 3.
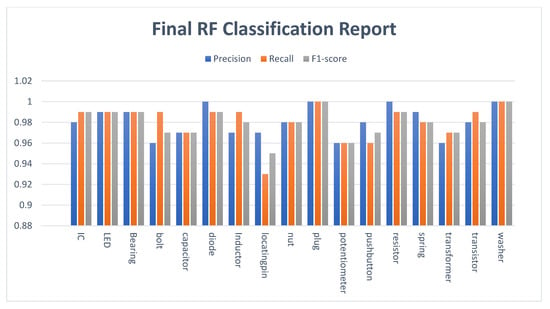
Figure 8.
IMCCM-based performance of seventeen components.

Table 3.
Deep learning models results.
The IMCCM has achieved higher accuracy with the minimum number of trainable parameters using the D-S pooling method. The D-S pooling-based IMCCM CNN BLOCK 1 and CNN Block2 has been tested for two well-known data sets: MNIST and CIFAR10. The resultant Top-1 and Top-5 accuracy for these three datasets can be seen in Table 4. The maximum Top-5 accuracy achieved by the MNIST dataset is 99.98. Although image size is different for all these datasets but still achievable Top-1 accuracy by all these is above 67%, and the Top-5 accuracy is above 97%. The number of trainable parameters is also limited, which shows that our D-S pooling strategy has shown excellent results.

Table 4.
Implementation for multiple datasets.
4.5. Discussion
As the world is swiftly moving for deeper integration and interconnectedness under the globalization paradigm, industrial components have gained currency for the Industry 4.0 vision and many to come. These components have a diverse range and are essential for all electrical and mechanical machines. Their automatic classification with advanced methods is the demand of the information revolution in the digital era. The proposed IMCCM will help the efficient automatic classification of electrical and mechanical components categories.
The IMCCM has been applied to classify industrial machinery’s most fundamental seventeen components. The accuracy attained by seventeen components is 98.15%, which is higher than the existing ones. Various components have shown even more than 99% classification performance (see Figure 8 wherein the graph represents that locating pin has recall as 93% and F1-score 95% smaller than all other components). The confusion matrix (see Figure 7) illustrated that the locating pin has a higher number of misclassification. Furthermore, the plug category achieved a perfect accuracy of 100% with no misclassification. On the other hand, ICs exhibited a higher degree of appearance similarity with transistors and pushbuttons from different angles, leading to some misclassified elements despite yielding satisfactory results. The potentiometer, bolt, and transformer displayed a lower precision rate of 96% due to their similar appearances. However, these components still demonstrated satisfactory outcomes. Conversely, the plug, washer, diode, and resistor achieved a perfect precision rate of 100%.
The designed model has also been tested individually for both electrical and mechanical categories (see Figure 9 and Figure 10). The accuracy achieved by both groups is 97.5% and 98.72%, respectively. The accuracy achieved by mechanical components is higher than seventeen components. On the other hand, the three electrical components’ accuracy has been recorded at 99.34%—higher than the result of the seventeen categories. In both cases (electrical and mechanical, as shown in Figure 9 and Figure 10), the different number of components leads to variation in the performance—for minimum number, IMCCM shows maximum accuracy of 100% for mechanical and 99.34% for electrical. However, the performance goes down slightly as the number of components increases. Nonetheless, the performance bar rises when the number of components increases—more than ten. The precision, recall, and F1-Score show symmetric behavior for different numbers of components. However, the performance curve for these evaluating parameters is more symmetric for electrical components than for mechanical components.
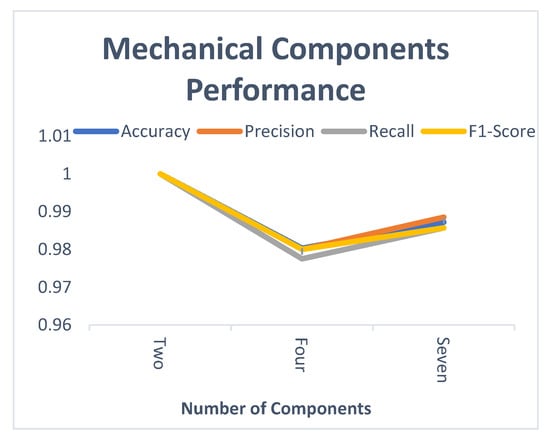
Figure 9.
Multiple Mechanical Component Performance.
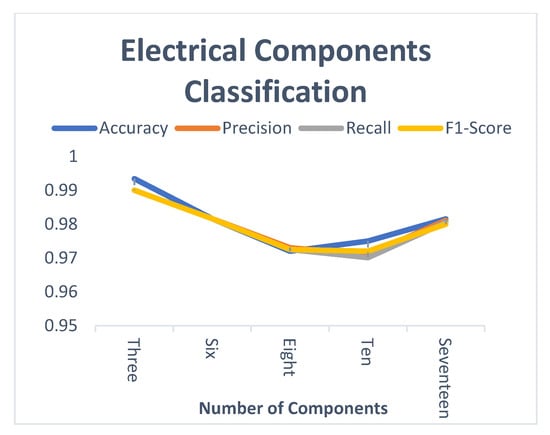
Figure 10.
Multiple Electrical Components performances.
In the existing techniques of component classification, the IMCCM model outperforms other existing models. Specifically, after being trained with seventeen components, the IMCCM achieved an accuracy of 98.15%, whereas Cheng’s (2022) model, which also utilized seventeen components, only achieved an accuracy of 94.6%. The IMCCM improved the accuracy by 4.41%. The model has been evaluated with a different number of components and the performance of the model. Similarly, IMCCM has shown (see Table 5) improved performance with multiple components and fewer trainee parameters.

Table 5.
Performance Improvement from existing SOTA.
Other models, for instance, DenseNet201 [39], VGG16 [40], and Resnet50 [41] have been trained on the industrial machinery components dataset, and their corresponding results have been shown in Table 3. It can be seen that the Xception [42] model achieved higher testing accuracy of 97.5% that too with 21 million trainable parameters. At the same time, Resnet50 presents the lowest results—69%. The IMCCM model results are the best among existing models—98.15%, with the highest accuracy and fewest number of trainable parameters—141,346. The lesser number of parameters, and highest accuracy, make the IMCCM model most suitable and robust for the automatic industrial classification system.
5. Conclusions
The industrial revolution has gradually pushed industries towards fully automatic handling of each process. To achieve the entire processing of the industrial task independently and systematically, it is necessary to monitor and control each component and part efficiently and intelligently. Machine components, in many cases, differ in size and functions but have higher inter-class and intra-class similarities. Machines generally have electrical and mechanical components that work in unison. They have a resemblance, for instance, capacitor and transistor, locating pin and transistor, push button, and potentiometer, to name a few. Despite these similarities and interrelationships in machines, they need to classify separately. For the said purpose, CNN classification models are required to be efficient in accuracy, precision, and recall while dealing with a large number of components. However, contemporary existing models lack desired sophistry and said parameters. The proposed IMCCM model has shown significant results while simultaneously considering the classification of electrical and mechanical components. IMCCM consists of two convolutional neural network (CNN) blocks, one grey-level co-occurrence matrix (GLCM) block, and a random forest as the classifier. CNN blocks utilized the D-S pooling method to differentiate machine components by extracting distinct features. The extracted features from these three blocks, fused with direct fusion, pass to the random forest to distinguish machine components. The model achieved 98.15% accuracy, outweighing other existing models and heralding great potential for effective industrial implementation. In a nutshell, this study proposes a convolutional neural network-based model with maximum accuracy and robustness to multiple components. It also offers a unique pooling design that controls the model in a range of a minimum number of trainable parameters and improves classification performance. Finally, this research proposes a new dual-used model: automatic classification of electrical and mechanical machine components simultaneously. The work has the potential to be extended in the upcoming days. The proposed IMCCM model, taking electrical and mechanical datasets into account, has strong potential to be employed in hydraulic and optical components.
Author Contributions
Conceptualization, A.B. and Y.D.; methodology, A.B., S.Y. and Y.D.; investigation, A.B., H.M. and Y.D.; writing—original draft preparation, A.B.; writing—review and editing, A.B., Y.D. and S.Y.; supervision, Y.D., H.M. and S.Y.; funding acquisition, H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially funded by the National Key Research and Development Plan of China (No. 2018AAA0101000) and the National Natural Science Foundation of China under grant 62076028.
Data Availability Statement
The dataset used in this study is available from the corresponding author via mathmhb@bit.edu.cn.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Canziani, A.; Culurciello, E.; Paszke, A. Evaluation of neural network architectures for embedded systems. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Liu, Z.; Zhao, B.; Zhu, H. Research of Sorting Technology Based on Industrial Robot of Machine Vision. In Proceedings of the 2012 Fifth International Symposium on Computational Intelligence and Design, Hangzhou, China, 28–29 October 2012; pp. 57–61. [Google Scholar] [CrossRef]
- Fechteler, M.; Schlüter, M.; Krüger, J. Prototype for enhanced product data acquisition based on inherent features in logistics. In Proceedings of the 2016 IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA), Berlin, Germany, 6–9 September 2016; pp. 1–4. [Google Scholar]
- Rawat, W.; Wang, Z. Deep Convolutional Neural Networks for Image Classification: A Comprehensive Review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.; Wang, H.; Chen, P.; Wei, Z. Mixed pooling for convolutional neural networks. In Rough Sets and Knowledge Technology: 9th International Conference, RSKT 2014, Shanghai, China, 24–26 October 2014; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 364–375. [Google Scholar]
- Schlüter, M.; Niebuhr, C.; Lehr, J.; Krüger, J. Vision-based identification service for remanufacturing sorting. Procedia Manuf. 2018, 21, 384–391. [Google Scholar] [CrossRef]
- You, F.C.; Zhang, Y.B. A Mechanical Part Sorting System Based on Computer Vision. In Proceedings of the 2008 International Conference on Computer Science and Software Engineering, Washington, DC, USA, 12–14 December 2008. [Google Scholar]
- Wang, Y.F.; Chen, H.D.; Zhao, K.; Zhao, P. A Mechanical Part Sorting Method Based on Fast Template Matching. In Proceedings of the 2018 IEEE International Conference on Mechatronics, Robotics, and Automation (ICMRA), Hefei, China, 18–21 May 2018; pp. 135–140. [Google Scholar] [CrossRef]
- Cicirello, V.; Regli, W. An approach to a feature-based comparison of solid models of machined parts. AI EDAM 2002, 16, 385–399. [Google Scholar] [CrossRef]
- Wei, B.; Hu, L.; Zhang, Y.; Zhang, Y. Parts Classification based on PSO-BP. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (IT-NEC), Chongqing, China, 12–14 June 2020; pp. 1113–1117. [Google Scholar] [CrossRef]
- Dong, Q.; Wu, A.; Dong, N.; Feng, W.; Wu, S. A convolution neural network for parts recognition using data augmentation. In Proceedings of the 2018 13th World Congress on Intelligent Control and Automation (WCICA), Changsha, China, 4–8 July 2018; pp. 773–777. [Google Scholar]
- Yildiz, E.; Wörgötter, F. DCNN-based screw classification in automated disassembly processes. In Proceedings of the International Conference on Robotics, Computer Vision and Intelligent Systems (ROBOVIS 2020), Budapest, Hungary, 4–6 November 2020; pp. 61–68. [Google Scholar]
- Taheritanjani, S.; Haladjian, J.; Bruegge, B. Fine-grained visual categorization of fasteners in overhaul processes. In Proceedings of the 2019 5th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 19–22 April 2019; pp. 241–248. [Google Scholar]
- Hossain, M.E.; Islam, A.; Islam, M.S. A proficient model to classify Bangladeshi bank notes for automatic vending machine Using a tıny dataset with One-Shot Learning & Siamese Networks. In Proceedings of the 2020 11th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kharagpur, India, 1–3 July 2020; pp. 1–4. [Google Scholar]
- Tastimu, C.; Akin, E. Fastener Classification Using One-shot learning with siamese convolution networks. JUCS—J. Univers. Comput. Sci. 2022, 28, 80–97. [Google Scholar] [CrossRef]
- Wang, B. Base and current situation of data standardization for electronic components & devices. Electron. Compon. Device Appl. 2010, 11, 30–32. [Google Scholar]
- Du, S.S.; Shan, Z.D.; Huang, Z.C.; Liu, H.Q.; Liu, S.L. The algorithmic of components auto-classification and system development of electronic components. Dev. Innov. Mach. Electr. Prod. 2008, 6, 133–135. [Google Scholar]
- Moetesum, M.; Younus, S.W.; Warsi, M.A.; Siddiqi, I. Segmentation and recognition of electronic components in hand-drawn circuit diagrams. ICST Trans. Scalable Inf. Syst. 2018, 5, 154478. [Google Scholar] [CrossRef]
- Salvador, R.; Bandala, A.; Javel, I.; Bedruz, R.A.; Dadios, E.; Vicerra, R. DeepTronic: An electronic device classification model using deep convolutional neural networks. In Proceedings of the 2018 IEEE 10th International Conference on Humanoid, Nanotechnology, Information Technology, Communication, and Control, Environment, and Management (HNICEM), Baguio City, Philippines, 29 November–2 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, Y.J.; Chen, Y.T.; Jiang, Y.S.F.; Horng, M.F.; Shieh, C.S.; Wang, H.Y.; Ho, J.H.; Cheng, Y.M. An artificial neural network to support package classification for SMT components. In Proceedings of the 2018 3rd International Conference on Computer and Communication Systems (ICCCS), Nagoya, Japan, 27–30 April 2018; pp. 130–134. [Google Scholar] [CrossRef]
- Atik, I. Classification of electronic components based on convolutional neural network Architecture. Energies 2022, 15, 2347. [Google Scholar] [CrossRef]
- Kaya, V.; Akgül, I. Classification of electronic circuit elements by machine learning based methods. In Proceedings of the 6th International Conference On Advances In Proceedings of the Natural & Applied Science Engineering, Online, 11–13 October 2022. [Google Scholar]
- Hu, S.; Zhang, X.; Liao, H.Y.; Liang, X.; Zheng, M.; Behdad, S. Deep learning and machine learning techniques to classify electrical and electronic equipment. In Proceedings of the ASME International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, IDETC/CIE 2021, Online, 17–20 August 2021. [Google Scholar]
- Lefkaditis, D.; Tsirigotis, G. Morphological feature selection, and neural classification. J. Eng. Sci. Technol. Rev. 2009, 2, 151–156. [Google Scholar] [CrossRef]
- Hu, X.; Xu, J.; Wu, J. A novel electronic component classification algorithm based on hierarchical convolution neural network. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Changchun, China, 21–23 August 2020; Volume 474, p. 052081. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, A.; Wu, L. A Classification Method for electronic components based on Siamese network. Sensors 2022, 22, 6478. [Google Scholar] [CrossRef] [PubMed]
- Ali, F.; Sappagh, S.A.; Islam, S.M.R.; Kwak, D.; Ali, A.; Imran, M.; Kwak, K.S. A smart healthcare monitoring system for heart disease prediction based on ensemble deep learning and feature fusio. Inf. Fusion 2020, 63, 208–222, ISSN 1566-2535. [Google Scholar] [CrossRef]
- Yang, L.; Xie, X.; Li, P.; Zhang, D.; Zhang, L. Part-based convolutional neural network for visual recognition. In Proceedings of the 2017 IEEE International Conference on Image Processing, Beijing, China, 17–20 September 2017; pp. 1772–1776. [Google Scholar]
- Cai, H.; Qu, Z.; Li, Z.; Zhang, Z.; Hu, X.; Hu, B. Feature-level fusion approaches based on multimodal EEG data for depression recognition. Inf. Fusion 2020, 59, 127–138. [Google Scholar] [CrossRef]
- Kang, Z.; Yang, J.; Li, G.; Zhang, Z. An automatic garbage classification system based on deep learning. IEEE Access 2020, 8, 140019–140029. [Google Scholar] [CrossRef]
- Fradi, H.; Fradi, A.; Dugelay, J. Multi-layer Feature Fusion and selection from convolutional neural networks for texture classification. In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Vienna, Austria, 8–10 February 2021; Volume 4, pp. 574–581, ISSN 2184-4321. [Google Scholar]
- Caglayan, A.; Buak, C.A. Exploiting multilayer features using a CNN-RNN approach for RGB-D object recognition. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Pan, Y.; Zhang, L.; Wu, X.; Skibniewski, M.J. Multi-classifier information fusion in risk analysis. Inf. Fusion 2020, 60, 121–136. [Google Scholar] [CrossRef]
- Agarap, A.F. Deep Learning Using Rectified Linear Units (Relu). arXiv 2008, arXiv:1803.08375. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980,. [Google Scholar]
- Bo, H.; Ma, F.L.; Jiao, L.C. Research on computation of GLCM of image texture. Acelectronicaica Sin. 2006, 34, 155. [Google Scholar]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Maaten, V.D.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).