An Efficient Analytical Approach to Investigate Fractional Caudrey–Dodd–Gibbon Equations with Non-Singular Kernel Derivatives
Abstract
1. Introduction
2. Preliminaries
3. Methodology
3.1. Case I
3.2. Case II
4. Convergence Analysis
5. Applications
- Solution in Terms of
- Solution in Terms of
- Solution in Terms of
- Solution in Terms of
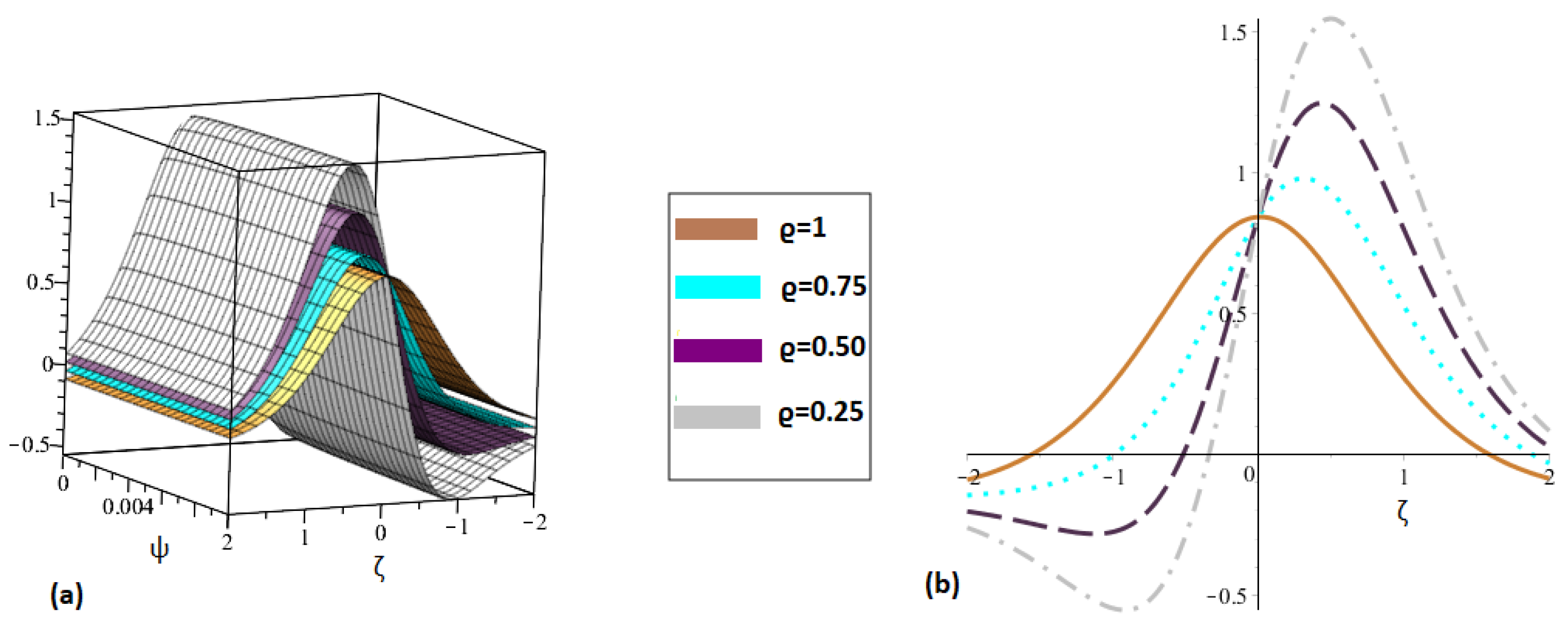
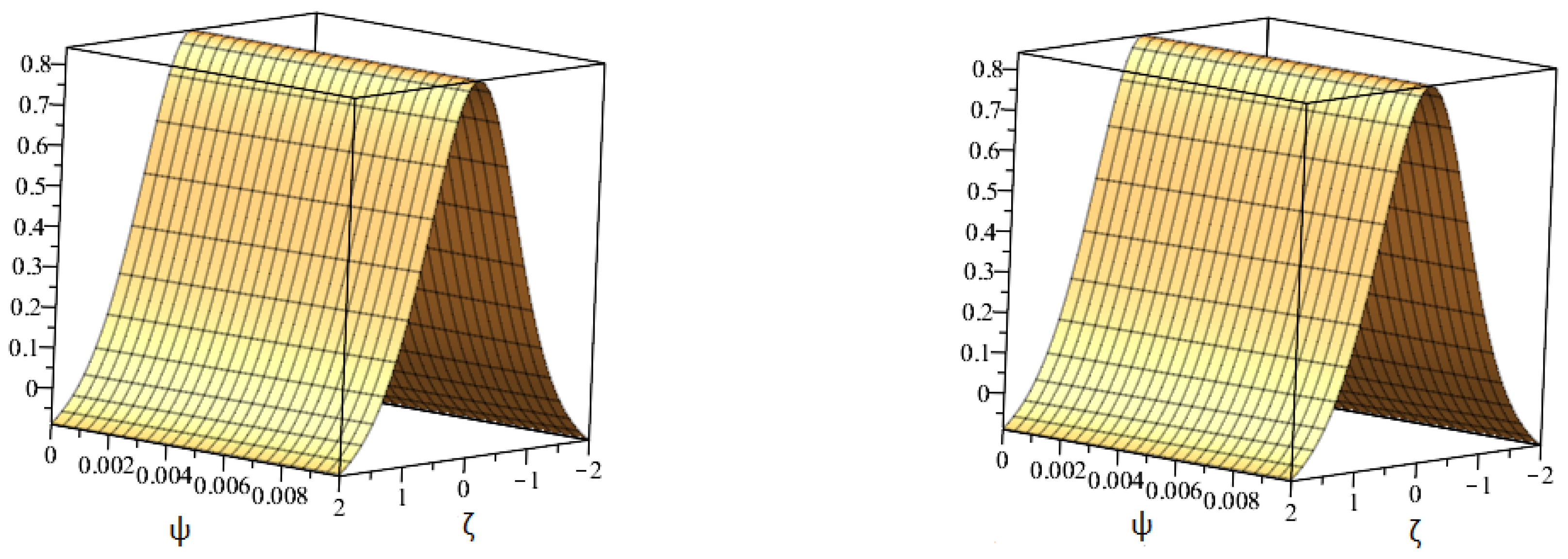
6. Numerical Simulation Studies
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ganie, A.H. New Bounds for Variables of Fractional Order. Pak. J. Statist 2022, 38, 211–218. [Google Scholar]
- AlBaidani, M.M.; Ganie, A.H.; Almuteb, A.F.M. Generalized notion of integral inequalities of variables. Open Phys. 2022, 20, 822–828. [Google Scholar] [CrossRef]
- Ganie, A.H. New approach for structural behaviour of variables. J. Nonlinear Sci. Appl. 2021, 14, 351–358. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763. [Google Scholar] [CrossRef]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.D.; Shah, R.; Khan, A. A comparative analysis of fractional-order kaup-kupershmidt equation within different operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Kbiri Alaoui, M.; Nonlaopon, K.; Zidan, A.M.; Khan, A.; Shah, R. Analytical investigation of fractional-order Cahn-Hilliard and gardner equations using two novel techniques. Mathematics 2022, 10, 1643. [Google Scholar] [CrossRef]
- Botmart, T.; Agarwal, R.P.; Naeem, M.; Khan, A.; Shah, R. On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators. AIMS Math. 2022, 7, 12483–12513. [Google Scholar] [CrossRef]
- Saad Alshehry, A.; Imran, M.; Khan, A.; Shah, R.; Weera, W. Fractional View Analysis of Kuramoto-Sivashinsky Equations with Non-Singular Kernel Operators. Symmetry 2022, 14, 1463. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasil’shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math. 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Alyobi, S.; Shah, R.; Khan, A.; Shah, N.A.; Nonlaopon, K. Fractional Analysis of Nonlinear Boussinesq Equation under Atangana-Baleanu-Caputo Operator. Symmetry 2022, 14, 2417. [Google Scholar] [CrossRef]
- Mishra, N.K.; AlBaidani, M.M.; Khan, A.; Ganie, A.H. Numerical Investigation of Time-Fractional Phi-Four Equation via Novel Transform. Symmetry 2022, 15, 687. [Google Scholar] [CrossRef]
- Kiliç, S.Ş.-S.; Çelik, E. Complex solutions to the higher-order nonlinear boussinesq type wave equation transform. Ric. Mat. 2022, 2022, 1–8. [Google Scholar] [CrossRef]
- Yazgan, T.; Ilhan, E.; Çelik, E.; Bulut, H. On the new hyperbolic wave solutions to Wu-Zhang system models. Opt. Quantum Electron. 2022, 54, 298. [Google Scholar] [CrossRef]
- Tazgan, T.; Celik, E.; GÜLnur, Y.E.L.; Bulut, H. On Survey of the Some Wave Solutions of the Non-Linear Schrödinger Equation (NLSE) in Infinite Water Depth. Gazi Univ. J. Sci. 2023, 2023, 1. [Google Scholar] [CrossRef]
- Kiliç, S.Ş.Ş. Multi and breather wave soliton solutions and the linear superposition principle for generalized Hietarinta equation. Int. J. Mod. Phys. 2022, 36, 2250019. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical investigation of Noyes-Field model for time-fractional Belousov-Zhabotinsky reaction. Complexity 2021, 2021, 1–21. [Google Scholar] [CrossRef]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. Aims Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift-Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Ali, A.; Khan, M.A.; Islam, S.; Ullah, S. Dynamics of fractional order COVID-19 model with a case study of Saudi Arabia. Results Phys. 2021, 21, 103787. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving fractional-order diffusion equations in a plasma and fluids via a novel transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. Aims Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Khan, A.; Kafle, J. Analysis of fractional-order regularized long-wave models via a novel transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Ali, A.; Islam, S.; Khan, M.R.; Rasheed, S.; Allehiany, F.M.; Baili, J.; Khan, M.A.; Ahmad, H. Dynamics of a fractionalorder Zika virus model with mutant. Alex. Eng. J. 2021, 61, 4821–4836. [Google Scholar] [CrossRef]
- Ma, W.; Jin, M.; Liu, Y.; Xu, X. Empirical analysis of fractional differential equations model for relationship between enterprise management and fnancial performance. Chaos Solitons Fractals 2019, 125, 17–23. [Google Scholar] [CrossRef]
- Tien, D.N. Fractional stochastic di?erential equations with applications to finance. J. Math. Anal. Appl. 2013, 397, 334–348. [Google Scholar] [CrossRef]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing. World Sci. 2016, 2016, 4. [Google Scholar]
- Chen, H.; Liu, M.; Chen, Y.; Li, S.; Miao, Y. Nonlinear lamb wave for structural incipient defect detection with sequential probabilistic ratio test. Secur. Commun. Netw. 2022, 2022, 9851533. [Google Scholar] [CrossRef]
- Li, X.; Dong, Z.Q.; Wang, L.P.; Niu, X.D.; Yamaguchi, H.; Li, D.C.; Yu, P. A magnetic field coupling fractional step lattice Boltzmann model for the complex interfacial behavior in magnetic multiphase flows. Appl. Math. Model. 2023, 117, 219–250. [Google Scholar] [CrossRef]
- Liu, Q.; Peng, H.; Wang, Z.A. Convergence to nonlinear diffusion waves for a hyperbolic-parabolic chemotaxis system modelling vasculogenesis. J. Differ. Equations 2022, 314, 251–286. [Google Scholar] [CrossRef]
- Xie, X.; Wang, T.; Zhang, W. Existence of solutions for the (p, q)-Laplacian equation with nonlocal Choquard reaction. Appl. Math. Lett. 2023, 135, 108418. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Yang, J. Analysis of stochastic process to model safety risk in construction industry. J. Civ. Eng. Manag. 2021, 27, 87–99. [Google Scholar] [CrossRef]
- Zhang, H.; Yue, D.; Dou, C.; Zhao, W.; Xie, X. Data-driven distributed optimal consensus control for unknown multiagent systems with input-delay. IEEE Trans. Cybern. 2018, 49, 2095–2105. [Google Scholar] [CrossRef] [PubMed]
- Dang, W.; Guo, J.; Liu, M.; Liu, S.; Yang, B.; Yin, L.; Zheng, W. A semi-supervised extreme learning machine algorithm based on the new weighted kernel for machine smell. Appl. Sci. 2022, 12, 9213. [Google Scholar] [CrossRef]
- Duan, J.S.; Rach, R.; Baleanu, D.; Wazwaz, A.M. A review of the Adomian decomposition method and its applications to fractional differential equations. Commun. Fract. Calc. 2012, 3, 73–99. [Google Scholar]
- Kumar, A.; Kumar, S.; Yan, S.-P. Residual power series method for fractional di?usion equations. Fundam. Informaticae 2017, 151, 213–230. [Google Scholar] [CrossRef]
- Wang, K.L.; Wang, K.J. A modification of the reduced differential transform method for fractional calculus. Therm. Sci. 2018, 22, 1871–1875. [Google Scholar] [CrossRef]
- Biazar, J.; Ghazvini, H. Convergence of the homotopy perturbation method for partial differential equations. Nonlinear Anal. Real World Appl. 2019, 10, 2633–2640. [Google Scholar] [CrossRef]
- He, J.H.; Latifizadeh, H. A general numerical algorithm for nonlinear differential equations by the variational iteration method. Int. J. Numer. Methods Heat Fluid Flow, 2020; in press. [Google Scholar] [CrossRef]
- Das, S.; Gupta, P.K. Homotopy analysis method for solving fractional hyperbolic partial differential equations. Int. J. Comput. Math. 2011, 88, 578–588. [Google Scholar] [CrossRef]
- Jin, H.Y.; Wang, Z.A.; Wu, L. Global dynamics of a three-species spatial food chain model. J. Differ. Equ. 2022, 333, 144–183. [Google Scholar] [CrossRef]
- Lu, S.; Ban, Y.; Zhang, X.; Yang, B.; Yin, L.; Liu, S.; Zheng, W. Adaptive control of time delay teleoperation system with uncertain dynamics. Front. Neurorobotics 2022, 152, 928863. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Guo, J.; Liu, S.; Yang, B.; Liu, M.; Yin, L.; Zheng, W. An improved algorithm of drift compensation for olfactory sensors. Appl. Sci. 2022, 12, 9529. [Google Scholar] [CrossRef]
- Khater, M.M. Novel computational simulation of the propagation of pulses in optical fibers regarding the dispersion effect. Int. Mod. Phys. 2022, 2022, 2350083. [Google Scholar] [CrossRef]
- Khater, M. Analytical and numerical-simulation studies on a combined mKdV-KdV system in the plasma and solid physics. Eur. Phys. Plus 2022, 137, 1–9. [Google Scholar]
- Khater, M.M. Nonlinear biological population model; computational and numerical investigations. Chaos Solitons Fractals 2022, 162, 112388. [Google Scholar] [CrossRef]
- Zada, L.; Nawaz, R.; Alqudah, M.A.; Nisar, K.S. A new technique for approximate solution of fractional-order partial differential equations. Fractals 2022, 30, 2240015. [Google Scholar] [CrossRef]
- Jhangeer, A.; Almusawa, H.; Rahman, R.U. Fractional derivative-based performance analysis to Caudrey-Dodd-Gibbon-Sawada-Kotera equation. Results Phys. 2022, 36, 105356. [Google Scholar] [CrossRef]
- Majeed, A.; Rafiq, M.N.; Kamran, M.; Abbas, M.; Inc, M. Analytical solutions of the fifth-order time fractional nonlinear evolution equations by the unified method. Mod. Phys. Lett. 2022, 36, 2150546. [Google Scholar] [CrossRef]
- Ciancio, A.; Yel, G.; Kumar, A.; Baskonus, H.M.; Ilhan, E. On the complex mixed dark-bright wave distributions to some conformable nonlinear integrable models. Fractals 2022, 30, 2240018. [Google Scholar] [CrossRef]
- Liu, F.-Y.; Gao, Y.-T.; Yu, X.; Hu, L.; Wu, X.-H. Hybrid solutions for the (2+1)-dimensional variable-coefficient Caudrey-Dodd-Gibbon-Kotera-Sawada equation in fluid mechanics. Chaos Solitons Fractals 2021, 152, 111355. [Google Scholar] [CrossRef]
- Ghanbari, B. Employing Hirota’s bilinear form to find novel lump waves solutions to an important nonlinear model in fluid mechanics. Results Phys. 2022, 29, 104689. [Google Scholar] [CrossRef]
- Singh, J.; Gupta, A.; Baleanu, D. On the analysis of an analytical approach for fractional Caudrey-Dodd-Gibbon equations. Alex. Eng. J. 2022, 61, 5073–5082. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G. A reliable analytical technique for fractional Caudrey-Dodd-Gibbon equation with Mittag-Leffler kernel. Nonlinear Eng. 2020, 9, 319–328. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Analytic study of the fifth order integrable nonlinear evolution equations by using the tanh method. Appl. Math. Comput. 2006, 174, 289–299. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple-soliton solutions for the fifth order Caudrey-Dodd-Gibbon (CDG) equation. Appl. Math. Comput. 2008, 197, 719–724. [Google Scholar] [CrossRef]
- Zhou, M.X.; Kanth, A.S.V.; Aruna, K.; Raghavendar, K.; Rezazadeh, H.; Inc, M.; Aly, A.A. Numerical Solutions of Time Fractional Zakharov-Kuznetsov Equation via Natural Transform Decomposition Method with Nonsingular Kernel Derivatives. J. Funct. Spaces 2021, 2021, 9884027. [Google Scholar] [CrossRef]
- Adomian, G. A new approach to nonlinear partial differential equations. J. Math. Anal. Appl. 1984, 102, 420–434. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Springer Dordrecht: Dordrecht, The Netherlands, 1994. [Google Scholar] [CrossRef]


| 0.2 | 0.81468 | 0.80893 | 0.80375 | 0.80317 | 0.80317 | |
| 0.4 | 0.71790 | 0.70803 | 0.69916 | 0.69818 | 0.69818 | |
| 0.01 | 0.6 | 0.57747 | 0.56588 | 0.55545 | 0.55429 | 0.55429 |
| 0.8 | 0.42425 | 0.41299 | 0.40286 | 0.40173 | 0.40173 | |
| 1 | 0.28190 | 0.27220 | 0.26347 | 0.26250 | 0.26250 | |
| 0.2 | 0.81531 | 0.80953 | 0.80432 | 0.80374 | 0.80374 | |
| 0.4 | 0.71898 | 0.70906 | 0.70015 | 0.69915 | 0.69915 | |
| 0.02 | 0.6 | 0.57874 | 0.56708 | 0.55660 | 0.55544 | 0.55544 |
| 0.8 | 0.42548 | 0.41416 | 0.40398 | 0.40285 | 0.40285 | |
| 1 | 0.28296 | 0.27321 | 0.26444 | 0.26346 | 0.26346 | |
| 0.2 | 0.81593 | 0.81012 | 0.80490 | 0.80430 | 0.80430 | |
| 0.4 | 0.72004 | 0.71009 | 0.70113 | 0.70013 | 0.70013 | |
| 0.03 | 0.6 | 0.57999 | 0.56829 | 0.55776 | 0.55659 | 0.55659 |
| 0.8 | 0.42670 | 0.41533 | 0.40511 | 0.40397 | 0.40397 | |
| 1 | 0.28401 | 0.27421 | 0.26540 | 0.26443 | 0.26443 | |
| 0.2 | 0.81655 | 0.81072 | 0.80547 | 0.80486 | 0.80486 | |
| 0.4 | 0.72111 | 0.71111 | 0.70211 | 0.70110 | 0.70110 | |
| 0.04 | 0.6 | 0.58124 | 0.56949 | 0.55892 | 0.55774 | 0.55774 |
| 0.8 | 0.42792 | 0.41650 | 0.40623 | 0.40509 | 0.40509 | |
| 1 | 0.28506 | 0.27522 | 0.26637 | 0.26540 | 0.26540 | |
| 0.2 | 0.81717 | 0.81131 | 0.80604 | 0.80541 | 0.80541 | |
| 0.4 | 0.72216 | 0.71212 | 0.70310 | 0.70207 | 0.70207 | |
| 0.05 | 0.6 | 0.58248 | 0.57068 | 0.56007 | 0.55889 | 0.55889 |
| 0.8 | 0.42912 | 0.41766 | 0.40735 | 0.40622 | 0.40622 | |
| 1 | 0.28610 | 0.27622 | 0.26734 | 0.26637 | 0.26637 |
| 0.00 | 0.0000000000 | 0.0000000000 | |
| 0.01 | 0.0000351211 | 6.6361100000 | |
| 0.5 | 0.02 | 0.0002810211 | 7.7452360000 |
| 0.03 | 0.0009486029 | 1.3820520000 | |
| 0.04 | 0.0022488807 | 1.1712320000 | |
| 0.05 | 0.0043929376 | 1.8875059000 | |
| 0.00 | 0.0000000000 | 0.0000000000 | |
| 0.01 | 0.0000141429 | 7.0112118000 | |
| 1.0 | 0.02 | 0.0001130449 | 2.7878834000 |
| 0.03 | 0.0003811928 | 1.2331435000 | |
| 0.04 | 0.0009027666 | 1.1006695700 | |
| 0.05 | 0.0017616292 | 1.0116290000 |
| 0.2 | 0.01 | 1.08932 | 1.02820 | 0.96711 |
| 0.4 | 1.07550 | 0.97075 | 0.86604 | |
| 0.6 | 0.97003 | 0.84689 | 0.72380 | |
| 0.8 | 0.81012 | 0.69050 | 0.57093 | |
| 1 | 0.63629 | 0.53322 | 0.43020 | |
| 0.2 | 0.02 | 1.09602 | 1.03458 | 0.97318 |
| 0.4 | 1.08698 | 0.98168 | 0.87644 | |
| 0.6 | 0.98352 | 0.85974 | 0.73603 | |
| 0.8 | 0.82323 | 0.70298 | 0.58281 | |
| 1 | 0.64758 | 0.54398 | 0.44044 | |
| 0.2 | 0.03 | 1.10265 | 1.04092 | 0.97925 |
| 0.4 | 1.09834 | 0.99255 | 0.88684 | |
| 0.6 | 0.99687 | 0.87252 | 0.74826 | |
| 0.8 | 0.83620 | 0.71539 | 0.59469 | |
| 1 | 0.65875 | 0.55467 | 0.45067 | |
| 0.2 | 0.04 | 1.10923 | 1.04725 | 0.98532 |
| 0.4 | 1.10962 | 1.00338 | 0.89725 | |
| 0.6 | 1.01013 | 0.88525 | 0.76049 | |
| 0.8 | 0.84908 | 0.72777 | 0.60657 | |
| 1 | 0.66985 | 0.56533 | 0.46091 | |
| 0.2 | 0.05 | 1.11578 | 1.05355 | 0.99139 |
| 0.4 | 1.12084 | 1.01419 | 0.90765 | |
| 0.6 | 1.02333 | 0.89796 | 0.77272 | |
| 0.8 | 0.86190 | 0.74011 | 0.61845 | |
| 1 | 0.68090 | 0.57597 | 0.47115 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathima, D.; Alahmadi, R.A.; Khan, A.; Akhter, A.; Ganie, A.H. An Efficient Analytical Approach to Investigate Fractional Caudrey–Dodd–Gibbon Equations with Non-Singular Kernel Derivatives. Symmetry 2023, 15, 850. https://doi.org/10.3390/sym15040850
Fathima D, Alahmadi RA, Khan A, Akhter A, Ganie AH. An Efficient Analytical Approach to Investigate Fractional Caudrey–Dodd–Gibbon Equations with Non-Singular Kernel Derivatives. Symmetry. 2023; 15(4):850. https://doi.org/10.3390/sym15040850
Chicago/Turabian StyleFathima, Dowlath, Reham A. Alahmadi, Adnan Khan, Afroza Akhter, and Abdul Hamid Ganie. 2023. "An Efficient Analytical Approach to Investigate Fractional Caudrey–Dodd–Gibbon Equations with Non-Singular Kernel Derivatives" Symmetry 15, no. 4: 850. https://doi.org/10.3390/sym15040850
APA StyleFathima, D., Alahmadi, R. A., Khan, A., Akhter, A., & Ganie, A. H. (2023). An Efficient Analytical Approach to Investigate Fractional Caudrey–Dodd–Gibbon Equations with Non-Singular Kernel Derivatives. Symmetry, 15(4), 850. https://doi.org/10.3390/sym15040850






