D-Wave Superconducting Gap Symmetry as a Model for Nb1−xMoxB2 (x = 0.25; 1.0) and WB2 Diborides
Abstract
1. Introduction
2. Utilized Models
3. Results
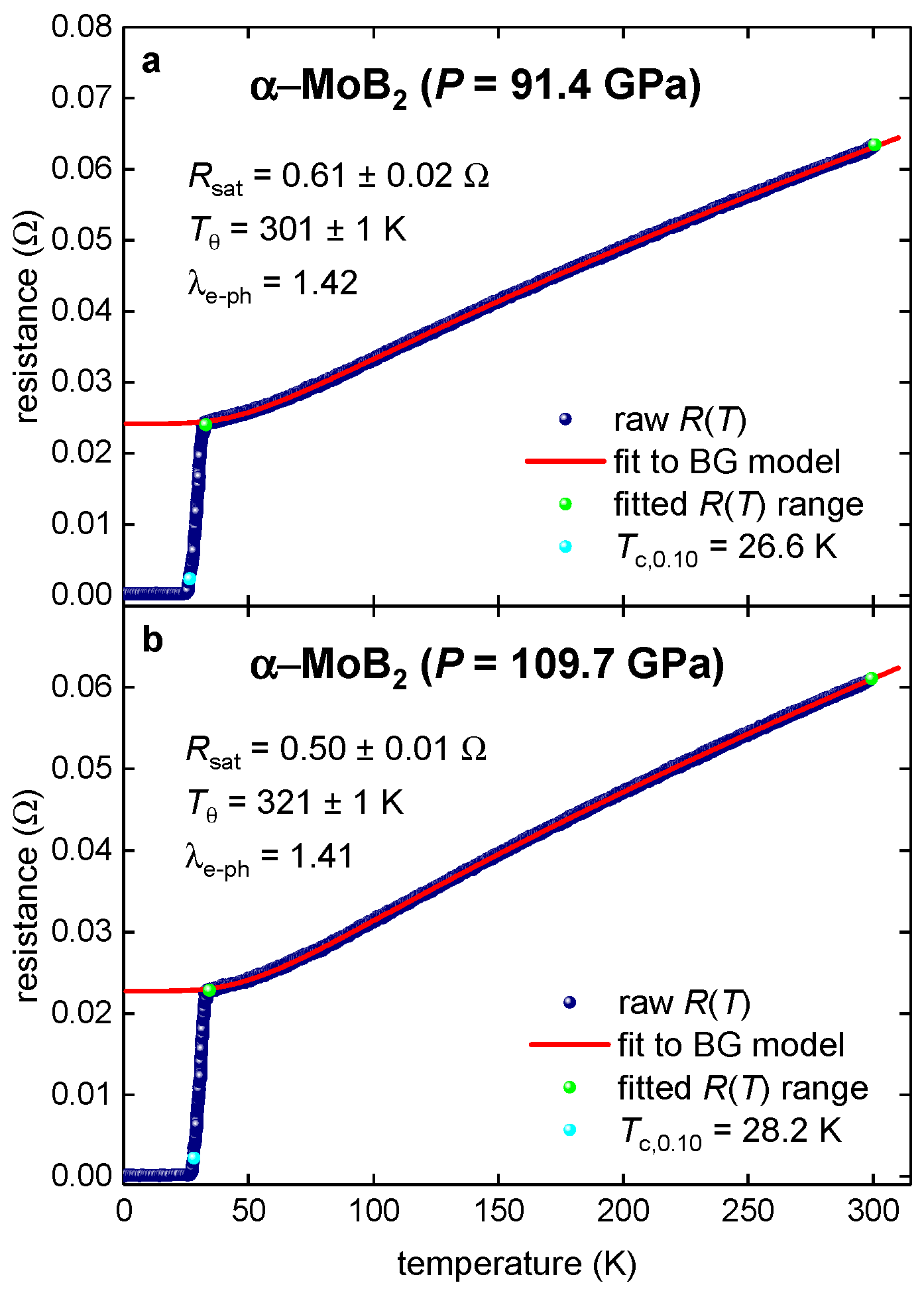
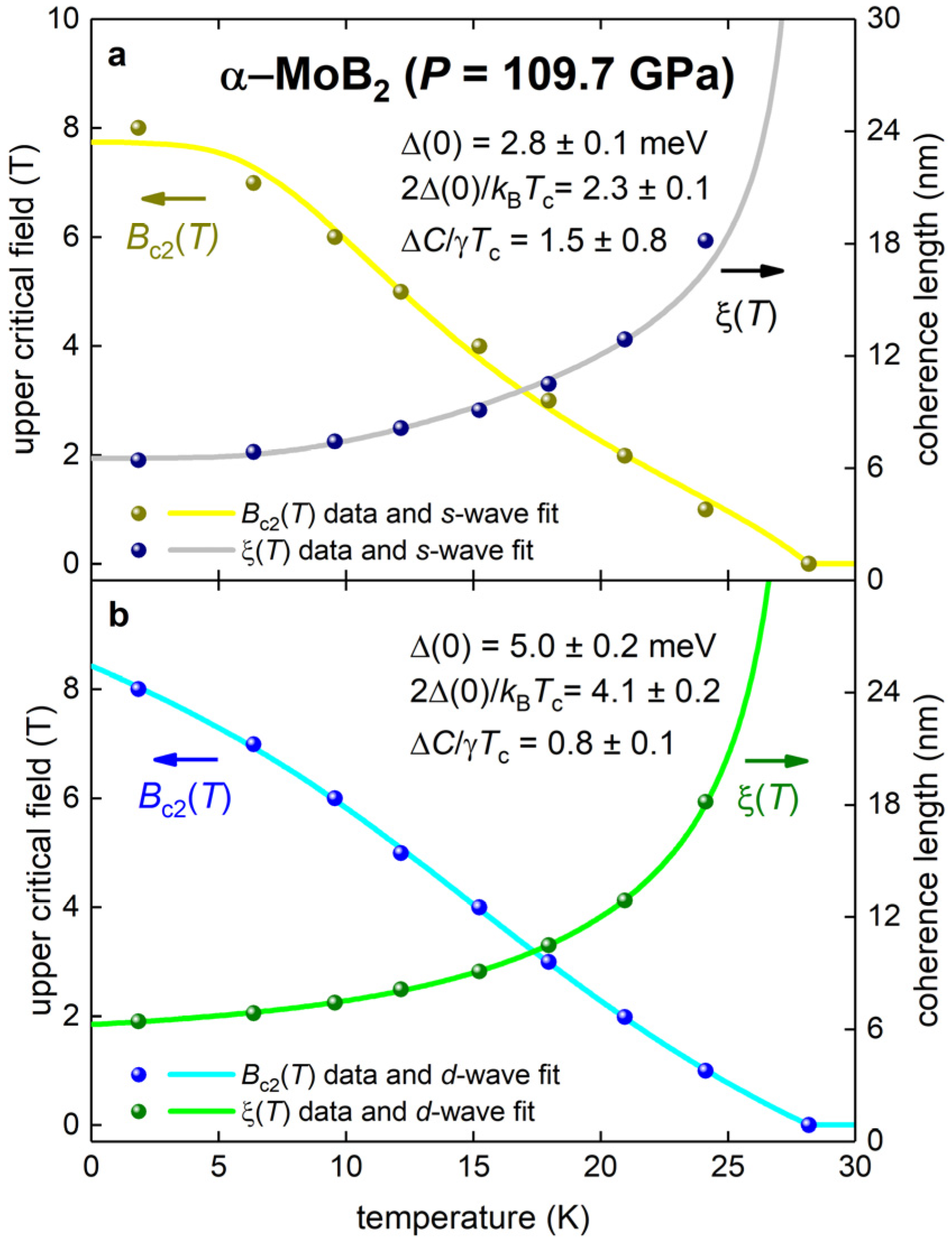
3.1. P6/mmm -MoB2 ()
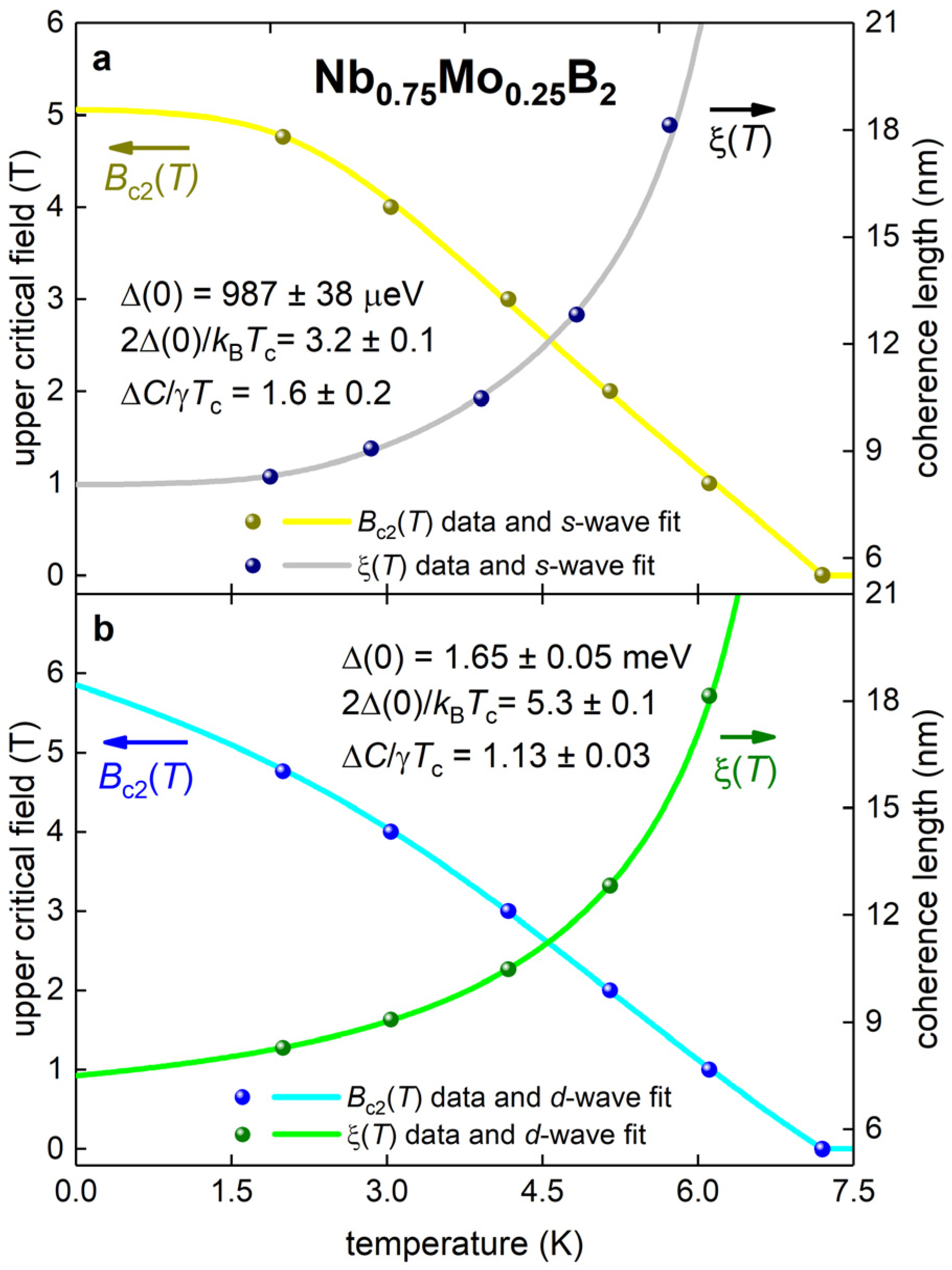
3.2. Ambient Pressure P6/mmm Nd0.75Mo0.25B2
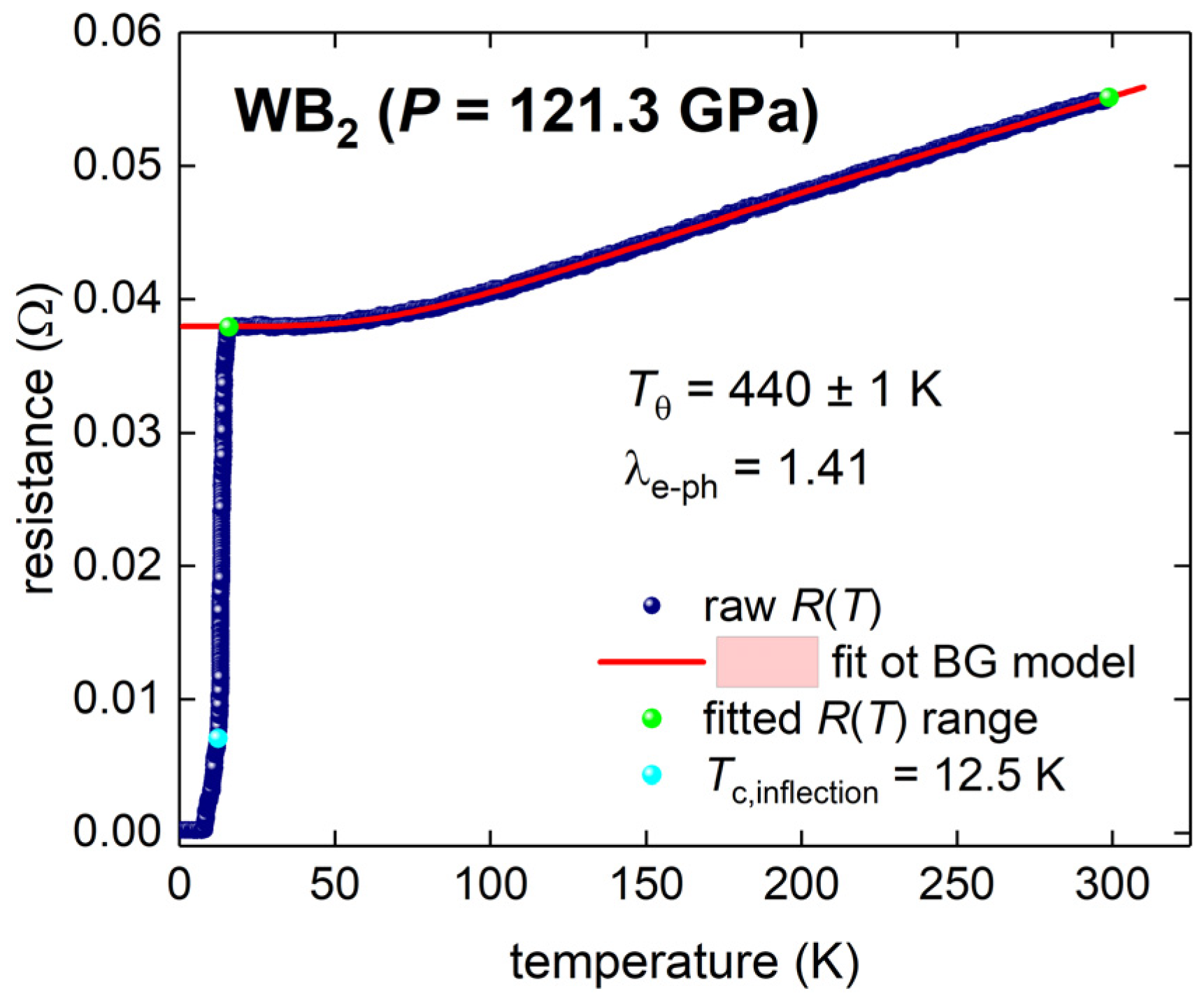
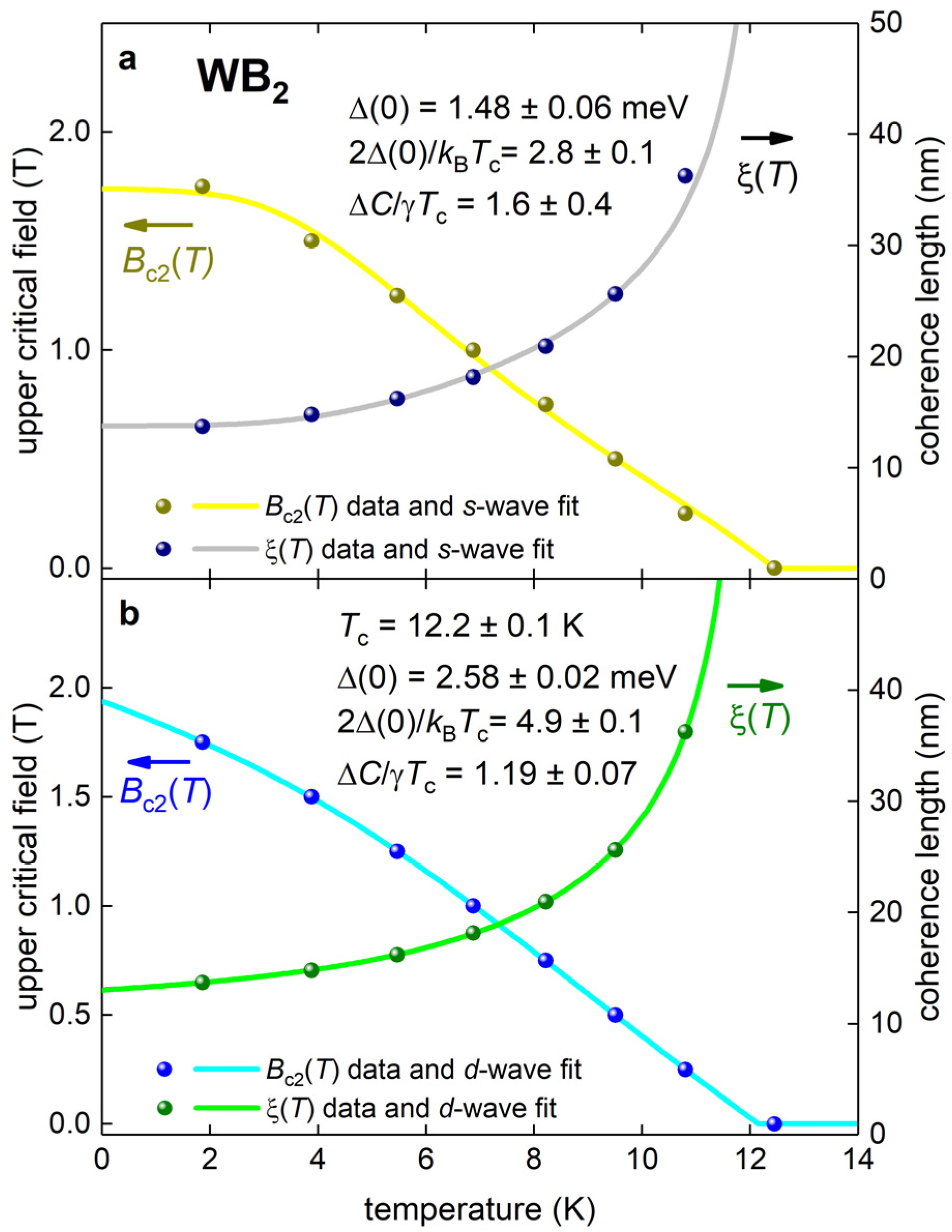
3.3. P63/mmc WB2 (P = 121.3 GPa)
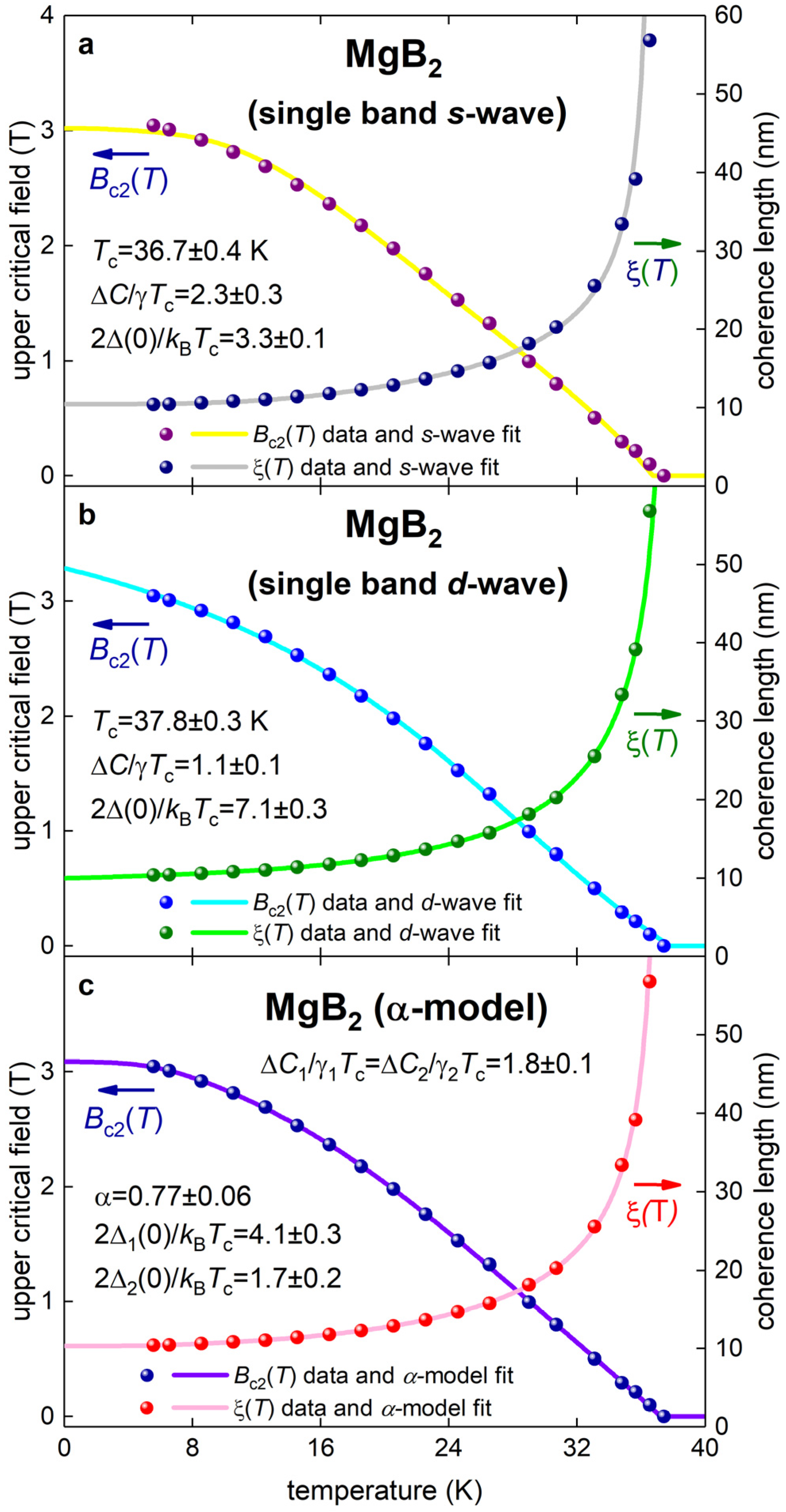
3.4. P6/mmm MgB2
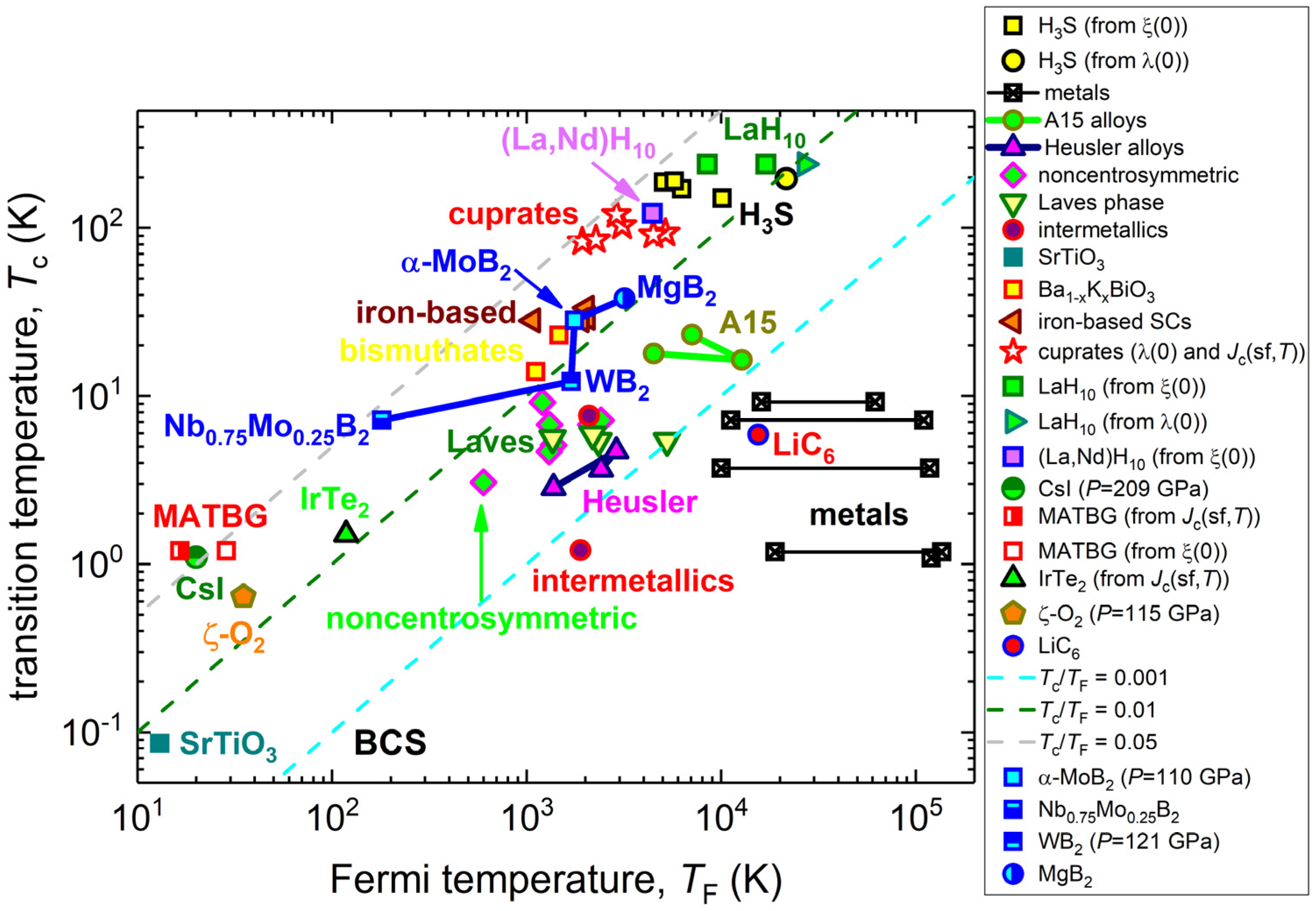
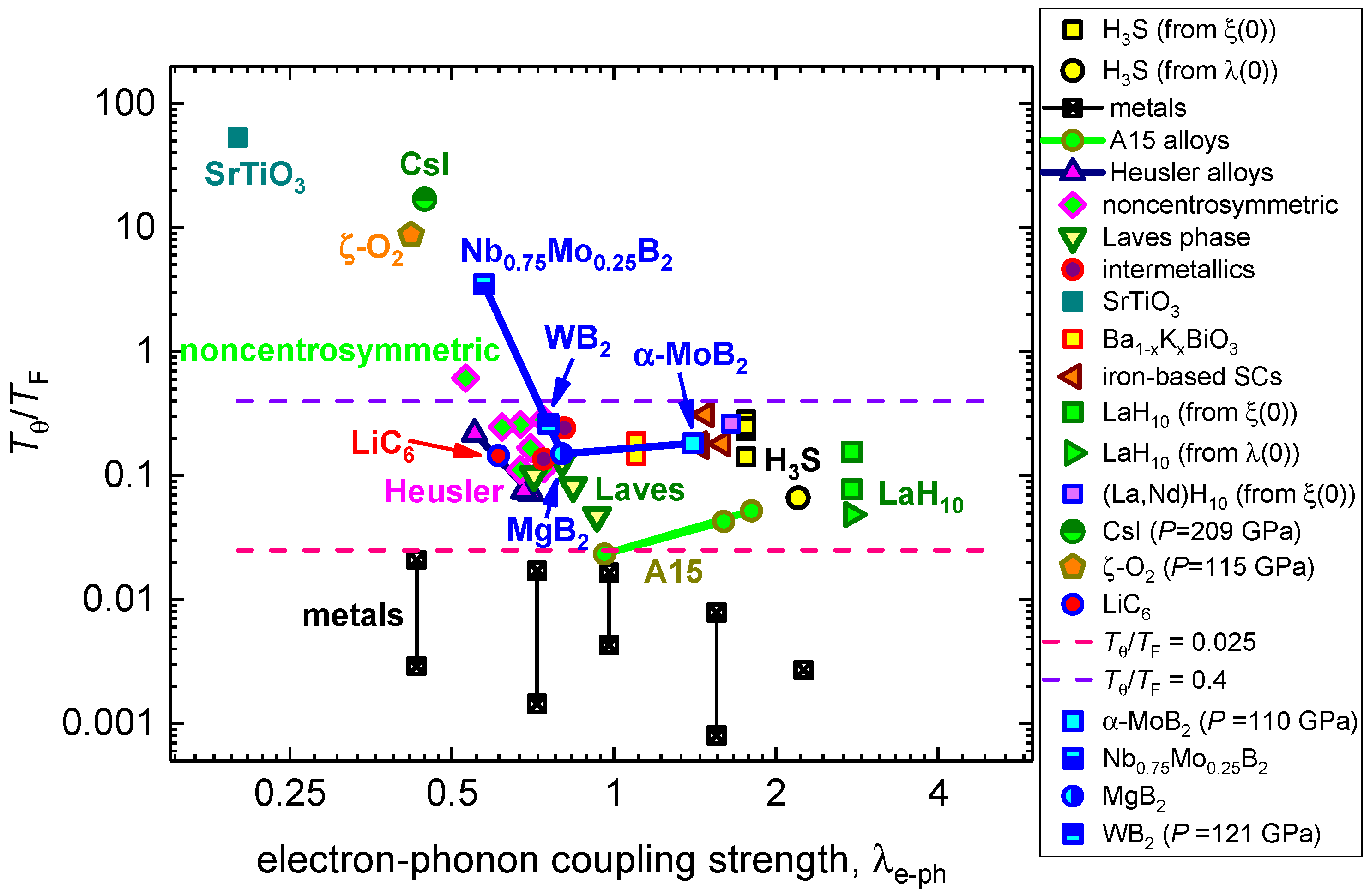
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Satterthwaite, C.B.; Toepke, I.L. Superconductivity of hydrides and deuterides of thorium. Phys. Rev. Lett. 1970, 25, 741–743. [Google Scholar] [CrossRef]
- Cooper, A.S.; Corenzwit, E.; Longinotti, L.D.; Matthias, B.T.; Zachariasen, W.H. Superconductivity: The transition temperature peak below four electrons per atom. Proc. Natl. Acad. Sci. USA 1970, 67, 313–319. [Google Scholar] [CrossRef]
- Fisk, Z. Superconducting borides. AIP Conf. Proc. 1991, 231, 155–164. [Google Scholar]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Kong, P.P.; Minkov, V.S.; Besedin, S.P.; Kuzovnikov, M.A.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Graf, D.E.; Prakapenka, V.B.; et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 2019, 569, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef] [PubMed]
- Semenok, D.V.; Kvashnin, A.G.; Ivanova, A.G.; Svitlyk, V.; Fominski, V.Y.; Sadakov, A.V.; Sobolevskiy, O.A.; Pudalov, V.M.; Troyan, I.A.; Oganov, A.R. Superconductivity at 161 K in thorium hydride ThH10: Synthesis and properties. Mater. Today 2020, 33, 36–44. [Google Scholar] [CrossRef]
- Troyan, I.A.; Semenok, D.V.; Kvashnin, A.G.; Sadakov, A.V.; Sobolevskiy, O.A.; Pudalov, V.M.; Ivanova, A.G.; Prakapenka, V.B.; Greenberg, E.; Gavriliuk, A.G.; et al. Anomalous high-temperature superconductivity in YH6. Adv. Mater. 2021, 33, 2006832. [Google Scholar] [CrossRef]
- Kong, P.; Minkov, V.S.; Kuzovnikov, M.A.; Drozdov, A.P.; Besedin, S.P.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Prakapenka, V.B.; Chariton, S.; et al. Superconductivity up to 243 K in yttrium hydrides under high pressure. Nat. Commun. 2021, 12, 5075. [Google Scholar] [CrossRef] [PubMed]
- Semenok, D.V.; Troyan, I.A.; Ivanova, A.G.; Kvashnin, A.G.; Kruglov, I.A.; Hanfland, M.; Sadakov, A.V.; Sobolevskiy, O.A.; Pervakov, K.S.; Lyubutin, I.S.; et al. Superconductivity at 253 K in lanthanum–yttrium ternary hydrides. Mater. Today 2021, 48, 18–28. [Google Scholar] [CrossRef]
- Mozaffari, S.; Sun, D.; Minkov, V.S.; Drozdov, A.P.; Knyazev, D.; Betts, J.B.; Einaga, M.; Shimizu, K.; Eremets, M.I.; Balicas, L. Superconducting phase-diagram of H3S under high magnetic fields. Nat. Commun. 2019, 10, 2522. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.; Minkov, V.S.; Mozaffari, S.; Sun, Y.; Ma, Y.; Chariton, S.; Prakapenka, V.B.; Eremets, M.I.; Balicas, L.; Balakirev, F.F. High-temperature superconductivity on the verge of a structural instability in lanthanum superhydride. Nat. Commun. 2021, 12, 6863. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Semenok, D.V.; Kvashnin, A.G.; Huang, X.; Kruglov, I.A.; Galasso, M.; Song, H.; Duan, D.; Goncharov, A.F.; Prakapenka, V.B.; et al. Synthesis of molecular metallic barium superhydride: Pseudocubic BaH12. Nat. Commun. 2021, 12, 273. [Google Scholar] [CrossRef]
- Bi, J.; Nakamoto, Y.; Zhang, P.; Shimizu, K.; Zou, B.; Liu, H.; Zhou, M.; Liu, G.; Wang, H.; Ma, Y. Giant enhancement of superconducting critical temperature in substitutional alloy (La,Ce)H9. Nat. Commun. 2022, 13, 5952. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, K.; Sun, Y.; Ma, L.; Wang, Y.; Zou, B.; Liu, G.; Zhou, M.; Wang, H. Synthesis and superconductivity in yttrium superhydrides under high pressure. Chinese Physics B 2022, 31, 106201. [Google Scholar] [CrossRef]
- Ma, L.; Wang, K.; Xie, Y.; Yang, X.; Wang, Y.; Zhou, M.; Liu, H.; Yu, X.; Zhao, Y.; Wang, H.; et al. High-temperature superconducting phase in clathrate calcium hydride CaH6 up to 215 K at a pressure of 172 GPa. Phys. Rev. Lett. 2022, 128, 167001. [Google Scholar] [CrossRef]
- Zhou, D.; Semenok, D.V.; Duan, D.; Xie, H.; Chen, W.; Huang, X.; Li, X.; Liu, B.; Oganov, A.R.; Cui, T. Superconducting praseodymium superhydrides. Sci. Adv. 2020, 6, eaax6849. [Google Scholar] [CrossRef]
- Hong, F.; Shan, P.F.; Yang, L.X.; Yue, B.B.; Yang, P.T.; Liua, Z.Y.; Sun, J.P.; Dai, J.H.; Yu, H.; Yin, Y.Y.; et al. Possible superconductivity at ∼70 K in tin hydride SnHx under high pressure. Mater. Today Phys. 2022, 22, 100596. [Google Scholar] [CrossRef]
- Chen, W.; Semenok, D.V.; Huang, X.; Shu, H.; Li, X.; Duan, D.; Cui, T.; Oganov, A.R. High-temperature superconducting phases in cerium superhydride with a Tc up to 115 K below a pressure of 1 Megabar. Phys. Rev. Lett. 2021, 127, 117001. [Google Scholar] [CrossRef]
- Osmond, I.; Moulding, O.; Cross, S.; Muramatsu, T.; Brooks, A.; Lord, O.; Fedotenko, T.; Buhot, J.; Friedemann, S. Clean-limit superconductivity in Im3m H3S synthesized from sulfur and hydrogen donor ammonia borane. Phys. Rev. B 2022, 105, L220502. [Google Scholar] [CrossRef]
- Semenok, D.V.; Troyan, I.A.; Sadakov, A.V.; Zhou, D.; Galasso, M.; Kvashnin, A.G.; Ivanova, A.G.; Kruglov, I.A.; Bykov, A.A.; Terent’ev, K.Y.; et al. Effect of magnetic impurities on superconductivity in LaH10. Adv. Mater. 2022, 34, 2204038. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; He, X.; Zhang, C.; Wang, X.; Zhang, S.; Jia, Y.; Feng, S.; Lu, K.; Zhao, J.; Zhang, J.; et al. Superconductivity above 200 K discovered in superhydrides of calcium. Nat. Commun. 2022, 13, 2863. [Google Scholar] [CrossRef] [PubMed]
- Minkov, V.S.; Bud’ko, S.L.; Balakirev, F.F.; Prakapenka, V.B.; Chariton, S.; Husband, R.J.; Liermann, H.P.; Eremets, M.I. Magnetic field screening in hydrogen-rich high-temperature superconductors. Nat. Commun. 2022, 13, 3194. [Google Scholar] [CrossRef]
- Minkov, V.S.; Prakapenka, V.B.; Greenberg, E.; Eremets, M.I. A boosted critical temperature of 166 K in superconducting D3S synthesized from elemental sulfur and hydrogen. Angew. Chem. Int. Ed. 2020, 59, 18970–18974. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Dong, Q.X.; Yang, P.T.; Shan, P.F.; Wang, B.S.; Sun, J.P.; Dun, Z.L.; Uwatoko, Y.; Chen, G.F.; Dong, X.L.; et al. Pressure-induced superconductivity up to 9 K in the quasi-one-dimensional KMn6Bi5. Phys. Rev. Lett. 2022, 128, 187001. [Google Scholar] [CrossRef]
- Minkov, V.S.; Ksenofontov, V.; Budko, S.L.; Talantsev, E.F.; Eremets, M.I. Trapped magnetic flux in hydrogen-rich high-temperature superconductors. arXiv 2022, arXiv:2206.14108. [Google Scholar] [CrossRef]
- He, X.; Zhang, C.L.; Li, Z.W.; Zhang, S.J.; Min, B.S.; Zhang, J.; Lu, K.; Zhao, J.F.; Shi, L.C.; Peng, Y.; et al. Superconductivity observed in tantalum polyhydride at high pressure. arXiv 2022, arXiv:2212.13739. [Google Scholar] [CrossRef]
- Wang, H.; Tse, J.S.; Tanaka, K.; Iitaka, T.; Ma, Y. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Natl. Acad. Sci. USA 2012, 109, 6463–6466. [Google Scholar] [CrossRef]
- Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 184, 1172–1182. [Google Scholar] [CrossRef]
- Li, Y.; Hao, J.; Liu, H.; Li, Y.; Ma, Y. The metallization and superconductivity of dense hydrogen sulphide. J. Chem. Phys. 2014, 140, 174712. [Google Scholar] [CrossRef]
- Duan, D.; Liu, Y.; Tian, F.; Li, D.; Huang, X.; Zhao, Z.; Yu, H.; Liu, B.; Tian, W.; Cui, T. Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity. Sci. Rep. 2014, 4, 6968. [Google Scholar] [CrossRef] [PubMed]
- Heil, C.; di Cataldo, S.; Bachelet, G.B.; Boeri, L. Superconductivity in sodalite-like yttrium hydride clathrates. Phys. Rev. B 2019, 99, 220502. [Google Scholar] [CrossRef]
- Flores-Livas, J.A.; Boeri, L.; Sanna, A.; Profeta, G.; Arita, R.; Eremets, M. A perspective on conventional high-temperature superconductors at high pressure: Methods and materials. Phys. Rep. 2020, 856, 1–78. [Google Scholar] [CrossRef]
- Struzhkin, V.; Li, B.; Ji, C.; Chen, X.-J.; Prakapenka, V.; Greenberg, E.; Troyan, I.; Gavriliuk, A.; Mao, H.-k. Superconductivity in La and Y hydrides: Remaining questions to experiment and theory. Matter Radiat. Extrem. 2020, 5, 028201. [Google Scholar] [CrossRef]
- Errea, I.; Belli, F.; Monacelli, L.; Sanna, A.; Koretsune, T.; Tadano, T.; Bianco, R.; Calandra, M.; Arita, R.; Mauri, F.; et al. Quantum crystal structure in the 250-kelvin superconducting lanthanum hydride. Nature 2020, 578, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Gregoryanz, E.; Ji, C.; Dalladay-Simpson, P.; Li, B.; Howie, R.T.; Mao, H.-K. Everything you always wanted to know about metallic hydrogen but were afraid to ask. Matter Radiat. Extrem. 2020, 5, 038101. [Google Scholar] [CrossRef]
- Boeri, L.; Hennig, R.; Hirschfeld, P.; Profeta, G.; Sanna, A.; Zurek, E.; Pickett, W.E.; Amsler, M.; Dias, R.; Eremets, M.I.; et al. The 2021 room-temperature superconductivity roadmap. J. Phys. Condens. Matter 2021, 34, 183002. [Google Scholar]
- Shao, M.; Chen, W.; Zhang, K.; Huang, X.; Cui, T. High-pressure synthesis of superconducting clathratelike YH4. Phys. Rev. B 2021, 104, 174509. [Google Scholar] [CrossRef]
- Amiel, Y.; Kafle, G.P.; Komleva, E.V.; Greenberg, E.; Ponosov, Y.S.; Chariton, S.; Lavina, B.; Zhang, D.; Palevski, A.; Ushakov, A.V.; et al. Silvanite AuAgTe4: A rare case of gold superconducting material. arXiv 2023, arXiv:2301.08033. [Google Scholar] [CrossRef]
- Mao, H.-K. Hydrogen and related matter in the pressure dimension. Matter Radiat. Extrem. 2022, 7, 063001. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, T.; Hutcheon, M.J.; Shipley, A.M.; Song, H.; Du, M.; Kresin, V.Z.; Duan, D.; Pickard, C.J.; Yao, Y. Design principles for high-temperature superconductors with a hydrogen-based alloy backbone at moderate pressure. Phys. Rev. Lett. 2022, 128, 047001. [Google Scholar] [CrossRef] [PubMed]
- Du, M.; Song, H.; Zhang, Z.; Duan, D.; Cui, T. Room-temperature superconductivity in Yb/Lu substituted clathrate hexahydrides under moderate pressure. Research 2022, 2022, 9784309. [Google Scholar] [CrossRef] [PubMed]
- Pei, C.; Zhang, J.; Wang, Q.; Zhao, Y.; Gao, L.; Gong, C.; Tian, S.; Luo, R.; Li, M.; Yang, W.; et al. Pressure-induced superconductivity at 32 K in MoB2. Natl. Sci. Rev. 2023, 10, nwad034, in press. [Google Scholar] [CrossRef]
- Zhuang, C.G.; Meng, S.; Zhang, C.Y.; Feng, Q.R.; Gan, Z.Z.; Yang, H.; Jia, Y.; Wen, H.H.; Xi, X.X. Ultrahigh current-carrying capability in clean MgB2 films. J. Appl. Phys. 2008, 104, 013924. [Google Scholar] [CrossRef]
- Quan, Y.; Lee, K.-W.; Pickett, W.E. MoB2 under pressure: Superconducting Mo enhanced by boron. Phys. Rev. B 2021, 104, 224504. [Google Scholar] [CrossRef]
- Hire, A.C.; Sinha, S.; Lim, J.; Kim, J.S.; Dee, P.M.; Fanfarillo, L.; Hamlin, J.J.; Hennig, R.G.; Hirschfeld, P.J.; Stewart, G.R. High critical field superconductivity at ambient pressure in MoB2 stabilized in the P6/mmm structure via Nb substitution. Phys. Rev. B 2022, 106, 174515. [Google Scholar] [CrossRef]
- Pei, C.; Zhang, J.; Gong, C.; Wang, Q.; Gao, L.; Zhao, Y.; Tian, S.; Cao, W.; Li, C.; Lu, Z.-Y.; et al. Distinct superconducting behaviours of pressurized WB2 and ReB2 with different local B layers. Sci. China-Phys. Mech. Astron. 2022, 65, 287412. [Google Scholar] [CrossRef]
- Lim, J.; Hire, A.C.; Quan, Y.; Kim, J.S.; Xie, S.R.; Sinha, S.; Kumar, R.S.; Popov, D.; Park, C.; Hemley, R.J.; et al. Creating superconductivity in WB2 through pressure-induced metastable planar defects. Nat. Commun. 2022, 13, 7901. [Google Scholar] [CrossRef]
- Zandbergen, H.W.; Gronsky, R.; Wang, K.; Thomas, G. Structure of (CuO)2 double layers in superconducting YBa2Cu3O7. Nature 1988, 331, 596–599. [Google Scholar] [CrossRef]
- Specht, E.D.; Goyal, A.; Li, J.; Martin, P.M.; Li, X.; Rupich, M.W. Stacking faults in YBa2Cu3O7−x: Measurement using X-ray diffraction and effects on critical current. Appl. Phys. Lett. 2006, 89, 162510. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Strickland, N.M.; Wimbush, S.C.; Storey, J.G.; Tallon, J.L.; Long, N.J. Hole doping dependence of critical current density in YBa2Cu3O7−δ conductors. Appl. Phys. Lett. 2014, 104, 242601. [Google Scholar] [CrossRef]
- Bloch, F. Zum elektrischen Widerstandsgesetz bei tiefen Temperaturen. Z. Phys. 1930, 59, 208–214. [Google Scholar] [CrossRef]
- Grüneisen, E. Die abhängigkeit des elektrischen widerstandes reiner metalle von der temperatur. Ann. Phys. 1933, 408, 530–540. [Google Scholar] [CrossRef]
- Fisk, Z.; Webb, G.W. Saturation of the high-temperature normal-state electrical resistivity of superconductors. Phys. Rev. Lett. 1976, 36, 1084–1086. [Google Scholar] [CrossRef]
- Wiesmann, H.; Gurvitch, M.; Lutz, H.; Ghosh, A.; Schwarz, B.; Strongin, M.; Allen, P.B.; Halley, J.W. Simple model for characterizing the electrical resistivity in A-15 superconductors. Phys. Rev. Lett. 1977, 38, 782–785. [Google Scholar] [CrossRef]
- Matsumoto, R.; Song, P.; Adachi, S.; Saito, Y.; Hara, H.; Yamashita, A.; Nakamura, K.; Yamamoto, S.; Tanaka, H.; Irifune, T.; et al. Pressure-induced superconductivity in tin sulfide. Phys. Rev. B 2019, 99, 184502. [Google Scholar] [CrossRef]
- Kudo, K.; Hiiragi, H.; Honda, T.; Fujimura, K.; Idei, H.; Nohara, M. Superconductivity in Mg2Ir3Si: A fully ordered Laves phase. J. Phys. Soc. Jpn. 2020, 89, 013701. [Google Scholar] [CrossRef]
- Talantsev, E.F. Advanced McMillan’s equation and its application for the analysis of highly-compressed superconductors. Supercond. Sci. Technol. 2020, 33, 094009. [Google Scholar] [CrossRef]
- Talantsev, E.F. The electron–phonon coupling constant and the Debye temperature in polyhydrides of thorium, hexadeuteride of yttrium, and metallic hydrogen phase III. J. Appl. Phys. 2021, 130, 195901. [Google Scholar] [CrossRef]
- Talantsev, E.F. Classifying superconductivity in compressed H3S. Mod. Phys. Lett. B 2019, 33, 1950195. [Google Scholar] [CrossRef]
- Talantsev, E.F. In-plane p-wave coherence length in iron-based superconductors. Results Phys. 2020, 18, 103339. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Mataira, R.C.; Crump, W.P. Classifying superconductivity in Moiré graphene superlattices. Sci. Rep. 2020, 10, 212. [Google Scholar] [CrossRef]
- Gross, F.; Chandrasekhar, B.S.; Einzel, D.; Andres, K.; Hirschfeld, P.J.; Ott, H.R.; Beuers, J.; Fisk, Z.; Smith, J.L. Anomalous temperature dependence of the magnetic field penetration depth in superconducting UBe13. Z. Phys. B 1986, 64, 175–188. [Google Scholar] [CrossRef]
- Gross-Alltag, F.; Chandrasekhar, B.S.; Einzel, D.; Hirschfeld, P.J.; Andres, K. London field penetration in heavy fermion superconductors. Z. Phys. B 1991, 82, 243–255. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Carbotte, J.P. Properties of boson-exchange superconductors. Rev. Mod. Phys. 1990, 62, 1027–1157. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Crump, W.P.; Tallon, J.L. Thermodynamic parameters of single- or multi-band superconductors derived from self-field critical currents. Ann. Phys. 2017, 529, 1700197. [Google Scholar] [CrossRef]
- Pietronero, L.; Boeri, L.; Cappelluti, E.; Ortenzi, L. Conventional/unconventional superconductivity in high-pressure hydrides and beyond: Insights from theory and perspectives. Quantum Stud. Math. Found. 2018, 5, 5–21. [Google Scholar] [CrossRef]
- Talantsev, E.F. Quantifying nonadiabaticity in major families of superconductors. Nanomaterials 2023, 13, 71. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Tallon, J.L. Universal self-field critical current for thin-film superconductors. Nat. Commun. 2015, 6, 7820. [Google Scholar] [CrossRef] [PubMed]
- Cappelluti, E.; Ciuchi, S.; Grimaldi, C.; Pietronero, L.; Strässler, S. High Tc superconductivity in MgB2 by nonadiabatic pairing. Phys. Rev. Lett. 2002, 88, 117003. [Google Scholar] [CrossRef] [PubMed]
- Papagelis, K.; Arvanitidis, J.; Margiolaki, I.; Brigatti, K.; Prassides, K.; Schenck, A.; Lappas, A.; Amato, A.; Iwasa, Y.; Takenobu, T. μSR studies of superconducting MgB1.96C0.04. Phys. B 2003, 326, 346–349. [Google Scholar] [CrossRef]
- Talantsev, E.F. Electron–phonon coupling constant and BCS ratios in LaH10−y doped with magnetic rare-earth element. Supercond. Sci. Technol. 2022, 35, 095008. [Google Scholar] [CrossRef]
- Patra, C.; Agarwal, T.; Chaudhari, R.R.; Singh, R.P. Two-dimensional multigap superconductivity in bulk 2H-TaSeS. Phys. Rev. B 2022, 106, 134515. [Google Scholar] [CrossRef]
- Park, S.; Kim, S.Y.; Kim, H.K.; Kim, M.J.; Kim, T.; Kim, H.; Choi, G.S.; Won, C.J.; Kim, S.; Kim, K.; et al. Superconductivity emerging from a stripe charge order in IrTe2 nanoflakes. Nat. Commun. 2021, 12, 3157. [Google Scholar] [CrossRef]
- Szczesniak, D.; Kaczmarek, A.Z.; Drzazga-Szczesniak, E.A.; Szczesniak, R. Phonon-mediated superconductivity in bismuthates by nonadiabatic pairing. Phys. Rev. B 2021, 104, 094501. [Google Scholar] [CrossRef]
- Szczesniak, D.; Szczesniak, R. Signatures of nonadiabatic superconductivity in lithium-decorated graphene. Phys. Rev. B 2019, 99, 224512. [Google Scholar] [CrossRef]
- Helfand, E.; Werthamer, N.R. Temperature and purity dependence of the superconducting critical field, Hc2. II. Phys. Rev. 1966, 147, 288–294. [Google Scholar] [CrossRef]
- Werthamer, N.R.; Helfand, E.; Hohenberg, P.C. Temperature and purity dependence of the superconducting critical field, Hc2. III. Electron spin and spin-orbit effects. Phys. Rev. 1966, 147, 295–302. [Google Scholar] [CrossRef]
- Zehetmayer, M.; Eisterer, M.; Jun, J.; Kazakov, S.M.; Karpinski, J.; Wisniewski, A.; Weber, H.W. Mixed-state properties of superconducting MgB2 single crystals. Phys. Rev. B 2002, 66, 052505. [Google Scholar] [CrossRef]
- Bouquet, F.; Wang, Y.; Fisher, R.A.; Hinks, D.G.; Jorgensen, J.D.; Junod, A.; Phillips, N.E. Phenomenological two-gap model for the specific heat of MgB2. Europhys. Lett. 2001, 56, 856. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Crump, W.P.; Island, J.O.; Xing, Y.; Sun, Y.; Wang, J.; Tallon, J.L. On the origin of critical temperature enhancement in atomically thin superconductors. 2D Mater. 2017, 4, 025072. [Google Scholar] [CrossRef]
- Szabó, P.; Samuely, P.; Kačmarčík, J.; Klein, T.; Marcus, J.; Fruchart, D.; Miraglia, S.; Marcenat, C.; Jansen, A.G.M. Evidence for two superconducting energy gaps in MgB2 by point-contact spectroscopy. Phys. Rev. Lett. 2001, 87, 137005. [Google Scholar] [CrossRef]
- Santi, G.; Jarlborg, T.; Peter, M.; Weger, M. Existence of both s and d-wave solutions of Eliashberg equations. J. Supercond. 1995, 8, 405–408. [Google Scholar] [CrossRef]
- Gor’kov, L.P. Superconductivity: Conventional and Unconventional Superconductors; Bennemann, K.H., Ketterson, J.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 201–224. [Google Scholar]
- Anderson, P.W. Theory of dirty superconductors. J. Phys. Chem. Solids 1959, 11, 26–30. [Google Scholar] [CrossRef]
- Openov, L.A. Critical temperature of an anisotropic superconductor containing both nonmagnetic and magnetic impurities. Phys. Rev. B 1998, 58, 9468–9478. [Google Scholar] [CrossRef]
- Openov, L.A. Effect of nonmagnetic and magnetic impurities on the specific heat jump in anisotropic superconductors. Phys. Rev. B 2004, 69, 224516. [Google Scholar] [CrossRef]
- Gu, Q.; Li, Y.; Wan, S.; Li, H.; Guo, W.; Yang, H.; Li, Q.; Zhu, X.; Pan, X.; Nie, Y.; et al. Single particle tunnelling spectrum of superconducting Nd1-xSrxNiO2 thin films. Nat. Commun. 2020, 11, 6027. [Google Scholar] [CrossRef]
- Chow, L.E.; Sudheesh, S.K.; Nandi, P.; Zeng, S.W.; Zhang, Z.T.; Du, X.M.; Lim, Z.S.; Chia, E.E.M.; Ariando, A. Pairing symmetry in infinite-layer nickelate superconductor. arXiv 2022, arXiv:2201.10038. [Google Scholar] [CrossRef]
- Harvey, S.P.; Wang, B.Y.; Fowlie, J.; Osada, M.; Lee, K.; Lee, Y.; Li, D.; Hwang, H.Y. Evidence for nodal superconductivity in infinite-layer nickelates. arXiv 2022, arXiv:2201.12971. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, G.-M.; Yang, Y.-f.; Zhang, F.-C. Distinct pairing symmetries of superconductivity in infinite-layer nickelates. Phys. Rev. B 2020, 102, 220501. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Luke, G.M.; Sternlieb, B.J.; Brewer, J.H.; Carolan, J.F.; Hardy, W.N.; Kadono, R.; Kempton, J.R.; Kiefl, R.F.; Kreitzman, S.R. Universal correlations between Tc and (carrier density over effective mass) in high-Tc cuprate. Phys. Rev. Lett. 1989, 62, 2317–2320. [Google Scholar] [CrossRef]
- Uemura, Y.J.; Keren, A.; Le, L.P.; Luke, G.M.; Wu, W.D.; Kubo, Y.; Manako, T.; Shimakawa, Y.; Subramanian, M.; Cobb, J.L.; et al. Magnetic-field penetration depth in Tl2Ba2CuO6+δ in the overdoped regime. Nature 1993, 364, 605–607. [Google Scholar] [CrossRef]
- Guguchia, Z.; Amato, A.; Kang, J.; Luetkens, H.; Biswas, P.K.; Prando, G.; von Rohr, F.; Bukowski, Z.; Shengelaya, A.; Keller, H.; et al. Direct evidence for a pressure-induced nodal superconducting gap in the Ba0.65Rb0.35Fe2As2 superconductor. Nat. Commun. 2015, 6, 8863. [Google Scholar] [CrossRef] [PubMed]
- in ’t Veld, Y.; Katsnelson, M.I.; Millis, A.J.; Rösner, M. Screening induced crossover between phonon- and plasmon-mediated pairing in layered superconductors. arXiv 2023, arXiv:2303.06220. [Google Scholar] [CrossRef]
- Talantsev, E.F. Classifying hydrogen-rich superconductors. Mater. Res. Express 2019, 6, 106002. [Google Scholar] [CrossRef]
- Jorba, P.; Regnat, A.; Tong, A.; Seifert, M.; Bauer, A.; Schulz, M.; Franz, C.; Schneidewind, A.; Kunkemöller, S.; Jenni, K.; et al. High-pressure studies of correlated electron systems. Phys. Status Solidi B 2022, 259, 2100623. [Google Scholar] [CrossRef]
- Ruangrungrote, S.; Chanpoom, T.; Thaninworapak, R.; Udomsamuthirun, P. Investigation of the gap-to-Tc ratio of LaH10 and LaD10 superconductors. Int. J. Mod. Phys. B 2023, 37, in press. [Google Scholar] [CrossRef]
- Chanilkul, G.; Changjan, A.; Nilkamjon, T.; Udomsamuthirun, P. External pressure effects on superfluid density of isotropic s-wave superconductors. J. Phys. Conf. Ser. 2023, 2431, 012043. [Google Scholar] [CrossRef]
- Talantsev, E.F. Universal Fermi velocity in highly compressed hydride superconductors. Matter Radiat. Extrem. 2022, 7, 058403. [Google Scholar] [CrossRef]
- Malik, G.P.; Varma, V.S. On the generalized BCS equations incorporating chemical potential for the Tc and the calculation of the coherence length of some elements and compressed H3S. J. Low Temp. Phys. 2023, in press. [Google Scholar] [CrossRef]
- van de Bund, S.; Ackland, G.J. Competition between superconductivity and molecularization in quantum nuclear behavior of Lanthanum Hydride. arXiv 2023, arXiv:2303.01441. [Google Scholar] [CrossRef]
- Feng, X.Y.; Zhao, Z.; Luo, J.; Yang, J.; Fang, A.F.; Yang, H.T.; Gao, H.J.; Zhou, R.; Zheng, G.-Q. Commensurate-to-incommensurate transition of charge-density-wave order and a possible quantum critical point in pressurized kagome metal CsV3Sb5. arXiv 2023, arXiv:2303.01225. [Google Scholar] [CrossRef]
- He, X.; Zhang, C.; Li, Z.; Liua, C.; Feng, S.; Zhao, J.; Lu, K.; Bin, B.; Zhang, S.; Peng, Y.; et al. Superconductivity above 30 K achieved in dense scandium. arXiv 2023, arXiv:2303.01062. [Google Scholar] [CrossRef]
- Yang, W.; Xiao, G.; Zhu, Q.; Song, S.; Cao, G.-H.; Ren, Z. Effect of carbon doping on the structure and superconductivity in AlB2-type (Mo0.96Ti0.04)0.8B2. arXiv 2023, arXiv:2302.14272. [Google Scholar] [CrossRef]
- Lim, J.; Sinha, S.; Hire, A.C.; Kim, J.S.; Dee, P.M.; Kumar, R.S.; Popov, D.; Hemley, R.J.; Hennig, R.G.; Hirschfeld, P.J.; et al. Suppression of superconductivity in Nb-substituted MoB2 at high pressure. arXiv 2023, arXiv:2302.13936. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, X.; Wang, L.; Tsang, C.W.; Wang, Z.; Lam, S.T.; Wang, W.; Xie, J.; Zhou, X.; Zhao, Y.; et al. Nodeless superconductivity in Kagome metal CsV3Sb5 with and without time reversal symmetry breaking. Nano Lett. 2023, 23, 872–879. [Google Scholar] [CrossRef] [PubMed]
- Troyan, I.A.; Semenok, D.V.; Ivanova, A.G.; Sadakov, A.V.; Zhou, D.; Kvashnin, A.G.; Kruglov, I.A.; Sobolevskiy, O.A.; Lyubutina, M.V.; Helm, T.; et al. Non-Fermi-liquid behavior of superconducting SnH4. arXiv 2023, arXiv:2303.06339. [Google Scholar] [CrossRef]
- Jung, S.G.; Seo, S.; Lee, S.; Bauer, E.D.; Lee, H.-O.; Park, T. A peak in the critical current for quantum critical superconductors. Nat. Commun. 2018, 9, 434. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.H.; Park, S.; Kwon, C.I.; Kim, S.Y.; Watanabe, K.; Taniguchi, T.; Kim, J.S. Two-dimensional multiband superconductivity of the optimally and uniformly Li-intercalated FeSe nanoflakes. Curr. Appl. Phys. 2023, 46, 27–33. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, W.; Lai, K.T.; Moriyama, K.; Tallon, J.L.; Yoshimura, K.; Goh, S.K. Peak in the critical current density in (CaxSr1−x)3Rh4Sn13 tuned towards the structural quantum critical point. Phys. Rev. B 2022, 105, 214524. [Google Scholar] [CrossRef]
- Nobukane, H.; Yanagihara, K.; Kunisada, Y.; Ogasawara, Y.; Isono, K.; Nomura, K.; Tanahashi, K.; Nomura, T.; Akiyama, T.; Tanda, S. Co-appearance of superconductivity and ferromagnetism in a Ca2RuO4 nanofilm crystal. Sci. Rep. 2020, 10, 3462. [Google Scholar] [CrossRef]
- Jung, S.-G.; Han, Y.; Kim, J.H.; Hidayati, R.; Rhyee, J.-S.; Lee, J.M.; Kang, W.N.; Choi, W.S.; Jeon, H.-R.; Suk, J.; et al. High critical current density and high-tolerance superconductivity in high-entropy alloy thin films. Nat. Commun. 2022, 13, 3373. [Google Scholar] [CrossRef]
- Li, C.; Zhao , Y.-F.; Vera, A.; Lesser, O.; Yi, H.; Kumari, S.; Yan, Z.; Dong, C.; Bowen, T.; Wang, K.; et al. Proximity-induced superconductivity in epitaxial topological insulator/graphene/gallium heterostructures. Nat. Mater. 2023, 22. in press. [Google Scholar] [CrossRef] [PubMed]

| Compound | Tθ (K) | Tc (K) | Assumed μ* | λe−ph |
|---|---|---|---|---|
| α-MoB2 | 321 | 28.2 | 0.00 | 0.935 |
| (109.7 GPa) | 0.05 | 1.10 | ||
| 0.10 | 1.29 | |||
| 0.13 | 1.41 | |||
| Nb1−xMoxB2 | 625 | 7.2 | 0.00 | 0.337 |
| (x = 0.25) | 0.05 | 0.422 | ||
| 0.10 | 0.514 | |||
| 0.13 | 0.573 | |||
| WB2 | 440 | 12.5 | 0.00 | 0.475 |
| (121.3 GPa) | 0.05 | 0.575 | ||
| 0.10 | 0.685 | |||
| 0.13 | 0.755 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talantsev, E.F. D-Wave Superconducting Gap Symmetry as a Model for Nb1−xMoxB2 (x = 0.25; 1.0) and WB2 Diborides. Symmetry 2023, 15, 812. https://doi.org/10.3390/sym15040812
Talantsev EF. D-Wave Superconducting Gap Symmetry as a Model for Nb1−xMoxB2 (x = 0.25; 1.0) and WB2 Diborides. Symmetry. 2023; 15(4):812. https://doi.org/10.3390/sym15040812
Chicago/Turabian StyleTalantsev, Evgeny F. 2023. "D-Wave Superconducting Gap Symmetry as a Model for Nb1−xMoxB2 (x = 0.25; 1.0) and WB2 Diborides" Symmetry 15, no. 4: 812. https://doi.org/10.3390/sym15040812
APA StyleTalantsev, E. F. (2023). D-Wave Superconducting Gap Symmetry as a Model for Nb1−xMoxB2 (x = 0.25; 1.0) and WB2 Diborides. Symmetry, 15(4), 812. https://doi.org/10.3390/sym15040812






