Passive Grouping Enhances Proto-Arithmetic Calculation for Leftward Correct Responses
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects and Rearing Conditions
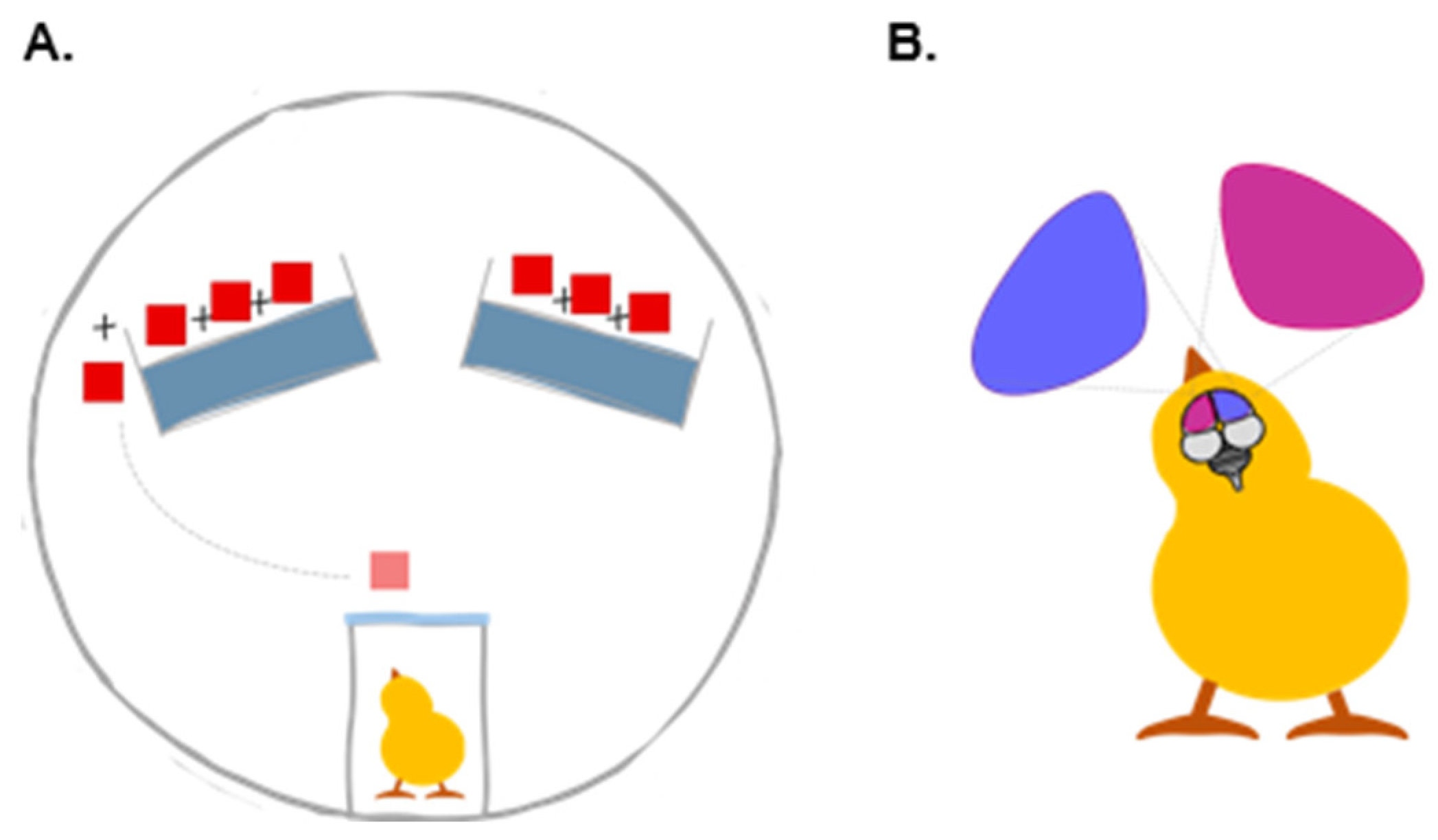
2.2. Training and Test
2.3. Data Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wynn, K. Addition and subtraction by human infants. Nature 1992, 358, 749–750. [Google Scholar] [CrossRef] [PubMed]
- Wynn, K. Psychological foundations of number: Numerical competence in human infants. Trends Cogn. Sci. 1998, 2, 296–303. [Google Scholar] [CrossRef]
- Kobayashi, T.; Hiraki, K.; Mugitani, R.; Hasegawa, T. Baby arithmetic: One object plus one tone. Cognition 2004, 91, B23–B34. [Google Scholar] [CrossRef] [PubMed]
- Beran, M.J. Summation and numerousness judgments of sequentially presented sets of items by chimpanzees (Pan troglodytes). J. Comp. Psychol. 2001, 115, 181–191. [Google Scholar] [CrossRef] [PubMed]
- Beran, M.J.; Beran, M.M. Chimpanzees Remember the Results of One-by-One Addition of Food Items to Sets Over Extended Time Periods. Psychol. Sci. 2004, 15, 94–99. [Google Scholar] [CrossRef]
- Cantlon, J.F.; Brannon, E.M. Basic Math in Monkeys and College Students. PLoS Biol. 2007, 5, e328. [Google Scholar] [CrossRef] [PubMed]
- Cantlon, J.F.; Merritt, D.J.; Brannon, E.M. Monkeys display classic signatures of human symbolic arithmetic. Anim. Cogn. 2016, 19, 405–415. [Google Scholar] [CrossRef] [PubMed]
- Perdue, B.M.; Talbot, C.F.; Stone, A.M.; Beran, M.J. Putting the elephant back in the herd: Elephant relative quantity judgments match those of other species. Anim. Cogn. 2012, 15, 955–961. [Google Scholar] [CrossRef]
- Miletto Petrazzini, M.E.; Wynne, C.D.L. What counts for dogs (Canis lupus familiaris) in a quantity discrimination task? Behav. Process. 2016, 122, 90–97. [Google Scholar] [CrossRef]
- Cox, L.; Montrose, V.T. Quantity Discrimination in Domestic Rats, Rattus norvegicus. Animals 2016, 6, 46. [Google Scholar] [CrossRef]
- Panteleeva, S.; Reznikova, Z.; Vygonyailova, O. Quantity judgments in the context of risk/reward decision making in striped field mice: First “count,” then hunt. Front. Psychol. 2013, 4, 53. [Google Scholar] [CrossRef] [PubMed]
- Pepperberg, I.M. Grey parrot (Psittacus erithacus) numerical abilities: Addition and further experiments on a zero-like concept. J. Comp. Psychol. 2006, 120, 1–11. [Google Scholar] [CrossRef]
- Ujfalussy, D.J.; Miklósi, Á.; Bugnyar, T.; Kotrschal, K. Role of mental representations in quantity judgments by jackdaws (Corvus monedula). J. Comp. Psychol. 2014, 128, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Agrillo, C.; Dadda, M.; Serena, G.; Bisazza, A. Do fish count? Spontaneous discrimination of quantity in female mosquitofish. Anim. Cogn. 2008, 11, 495–503. [Google Scholar] [CrossRef]
- Potrich, D.; Zanon, M.; Vallortigara, G. Archerfish number discrimination. eLife 2022, 11, e74057. [Google Scholar] [CrossRef]
- Gazzola, A.; Vallortigara, G.; Pellitteri-Rosa, D. Continuous and discrete quantity discrimination in tortoises. Biol. Lett. 2018, 14, 20180649. [Google Scholar] [CrossRef]
- Szabo, B.; Noble, D.W.A.; McCloghry, K.J.; Monteiro, M.E.S.; Whiting, M.J. Spontaneous quantity discrimination in a family-living lizard. Behav. Ecol. 2021, 32, 686–694. [Google Scholar] [CrossRef]
- Howard, S.R.; Schramme, J.; Garcia, J.E.; Ng, L.; Avarguès-Weber, A.; Greentree, A.D.; Dyer, A.G. Spontaneous quantity discrimination of artificial flowers by foraging honeybees. J. Exp. Biol. 2020, 223, jeb223610. [Google Scholar] [CrossRef]
- Gatto, E.; Carlesso, D. Spontaneous quantity discrimination in crickets. Ethology 2019, 9, 613–619. [Google Scholar] [CrossRef]
- Cross, F.R.; Jackson, R.R. Representation of different exact numbers of prey by a spider-eating predator. Interface Focus 2017, 7, 20160035. [Google Scholar] [CrossRef] [PubMed]
- Mc Comb, K.; Packer, C.; Pusey, A. Roaring and numerical assessment in contests between groups of female lions, Panthera leo. Anim. Behav. 1994, 47, 379–387. [Google Scholar] [CrossRef]
- Hunt, S.; Low, J.; Burns, K.C. Adaptive numerical competency in a food-hoarding songbird. Proc. R. Soc. B 2008, 275, 2373–2379. [Google Scholar] [CrossRef] [PubMed]
- Hager, M.C.; Helfman, G.S. Safety in numbers: Shoal size choice by minnows under predatory threat. Behav. Ecol. Sociobiol. 1991, 29, 271–276. [Google Scholar] [CrossRef]
- Rugani, R. Towards numerical cognition’s origin: Insights from day-old domestic chicks. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 20160509. [Google Scholar] [CrossRef] [PubMed]
- Rugani, R.; Loconsole, M.; Koslowski, M.; Regolin, L. Processing Individually Distinctive Schematic-Faces Supports Proto-Arithmetical Counting in the Young Domestic Chicken. Animals 2022, 12, 2322. [Google Scholar] [CrossRef] [PubMed]
- Jackson, P.S.; Bateson, P.P.G. Imprinting and exploration of slight novelty in chicks. Nature 1974, 251, 609–610. [Google Scholar] [CrossRef]
- Sluckin, W.; Salzen, E.A. Imprinting and Perceptual Learning. Q. J. Exp. Psychol. 1961, 13, 65–77. [Google Scholar] [CrossRef]
- Rugani, R.; Fontanari, L.; Simoni, E.; Regolin, L.; Vallortigara, G. Arithmetic in newborn chicks. Proc. R. Soc. B 2009, 276, 2451–2460. [Google Scholar] [CrossRef]
- Vallortigara, G. Comparative Neuropsychology of the Dual Brain: A Stroll through Animals’ Left and Right Perceptual Worlds. Brain Lang. 2000, 73, 189–219. [Google Scholar] [CrossRef]
- Daisley, J.N.; Mascalzoni, E.; Rosa-Salva, O.; Rugani, R.; Regolin, L. Lateralization of social cognition in the domestic chicken (Gallus gallus). Philos. Trans. R. Soc. B Biol. Sci. 2008, 364, 965–981. [Google Scholar] [CrossRef]
- Rugani, R.; Rosa Salva, O.; Regolin, L. Lateralized mechanisms for encoding of object. Behavioral evidence from an animal model: The domestic chick (Gallus gallus). Front. Psychol. 2014, 5, 150. [Google Scholar] [CrossRef] [PubMed]
- Rugani, R.; Vallortigara, G.; Priftis, K.; Regolin, L. Number-space mapping in the newborn chick resembles humans’ mental number line. Science 2015, 347, 534–536. [Google Scholar] [CrossRef] [PubMed]
- De Hevia, M.D.; Girelli, L.; Addabbo, M.; Cassia, V.M. Human Infants’ Preference for Left-to-Right Oriented Increasing Numerical Sequences. PLoS ONE 2014, 9, e96412. [Google Scholar] [CrossRef] [PubMed]
- Loconsole, M.; Regolin, L.; Rugani, R. Asymmetric number-space association leads to more efficient processing of congruent information in domestic chicks. Front. Behav. Neurosci. 2023, 17, 10. [Google Scholar] [CrossRef]
- Rugani, R.; Loconsole, M.; Simion, F.; Regolin, L. Individually distinctive features facilitate numerical discrimination of sets of objects in domestic chicks. Sci. Rep. 2020, 10, 16408. [Google Scholar] [CrossRef]
- Rosa-Salva, O.; Regolin, L.; Vallortigara, G. Faces are special for newly hatched chicks: Evidence for inborn domain-specific mechanisms underlying spontaneous preferences for face-like stimuli. Dev. Sci. 2010, 13, 565–577. [Google Scholar] [CrossRef]
- Rosa-Salva, O.; Farroni, T.; Regolin, L.; Vallortigara, G.; Johnson, M.H. The Evolution of Social Orienting: Evidence from Chicks (Gallus gallus) and Human Newborns. PLoS ONE 2011, 6, e18802. [Google Scholar] [CrossRef]
- Davidson, R.J. Well-being and affective style: Neural substrates and biobehavioural correlates. Phil. Trans. R. Soc. Lond. B 2004, 359, 1395–1411. [Google Scholar] [CrossRef]
- Vallortigara, G. Comparative cognition of number and space: The case of geometry and of the mental number line. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 20170120. [Google Scholar] [CrossRef]
- McKenzie, R.; Andrew, R.J.; Jones, R.B. Lateralization in chicks and hens: New evidence for control of response by the right eye system. Neuropsychologia 1998, 36, 51–58. [Google Scholar] [CrossRef]
- Rugani, R.; Loconsole, M.; Regolin, L. A strategy to improve arithmetical performance in four day-old domestic chicks (Gallus gallus). Sci. Rep. 2017, 7, 13900. [Google Scholar] [CrossRef] [PubMed]
- R v. A Language and Environment for Statistical Computing; R Core Team: v. 4.2.1. Available online: https://cran.r-project.org/bin/windows/base/ (accessed on 26 February 2023).
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Lenth, R. Emmeans: Estimated Marginal Means, aka Least-Squares Means. 2022. Available online: https://CRAN.R-project.org/package=emmeans (accessed on 26 February 2023).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis, 1st ed.; Springer: New York, NY, USA, 2009; ISBN 978-0-387-98140-6. [Google Scholar]
- Hyde, D.C.; Spelke, E.S. Neural signatures of number processing in human infants: Evidence for two core systems underlying numerical cognition. Dev. Sci. 2011, 14, 360–371. [Google Scholar] [CrossRef]
- Vallortigara, G. The evolutionary psychology of left and right: Costs and benefits of lateralization. Dev. Psychobiol. 2006, 48, 418–427. [Google Scholar] [CrossRef] [PubMed]
- Rogers, L.J.; Anson, J.M. Lateralisation of function in the chicken fore-brain. Pharmacol. Biochem. Behav. 1979, 10, 679–686. [Google Scholar] [CrossRef]
- Tommasi, L.; Vallortigara, G. Encoding of geometric and landmark information in the left and right hemispheres of the Avian Brain. Behav. Neurosci. 2001, 115, 602–613. [Google Scholar] [CrossRef]
- Morandi-Raikova, A.; Mayer, U. Selective activation of the right hippocampus during navigation by spatial cues in domestic chicks (Gallus gallus). Neurobiol. Learn. Mem. 2021, 177, 107344. [Google Scholar] [CrossRef] [PubMed]
- Mapstone, M.; Weintraub, S.; Nowinski, C.; Kaptanoglu, G.; Gitelman, D.R.; Mesulam, M.-M. Cerebral hemispheric specialization for spatial attention: Spatial distribution of search-related eye fixations in the absence of neglect. Neuropsychologia 2003, 41, 1396–1409. [Google Scholar] [CrossRef]
- Corballis, M.C. Mental Rotation and the Right Hemisphere. Brain Lang. 1997, 57, 100–121. [Google Scholar] [CrossRef]
- Loconsole, M.; Perovic, S.; Regolin, L. A leftward bias negatively correlated with performance is selectively displayed by domestic chicks during rule reversal (not acquisition). Laterality 2021, 26, 1–18. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loconsole, M.; Regolin, L.; Rugani, R. Passive Grouping Enhances Proto-Arithmetic Calculation for Leftward Correct Responses. Symmetry 2023, 15, 719. https://doi.org/10.3390/sym15030719
Loconsole M, Regolin L, Rugani R. Passive Grouping Enhances Proto-Arithmetic Calculation for Leftward Correct Responses. Symmetry. 2023; 15(3):719. https://doi.org/10.3390/sym15030719
Chicago/Turabian StyleLoconsole, Maria, Lucia Regolin, and Rosa Rugani. 2023. "Passive Grouping Enhances Proto-Arithmetic Calculation for Leftward Correct Responses" Symmetry 15, no. 3: 719. https://doi.org/10.3390/sym15030719
APA StyleLoconsole, M., Regolin, L., & Rugani, R. (2023). Passive Grouping Enhances Proto-Arithmetic Calculation for Leftward Correct Responses. Symmetry, 15(3), 719. https://doi.org/10.3390/sym15030719







