Cancellation of the Sigma Mode in the Thermal Pion Gas by Quark Pauli Blocking
Abstract
1. Introduction
2. The Interacting Pion Gas
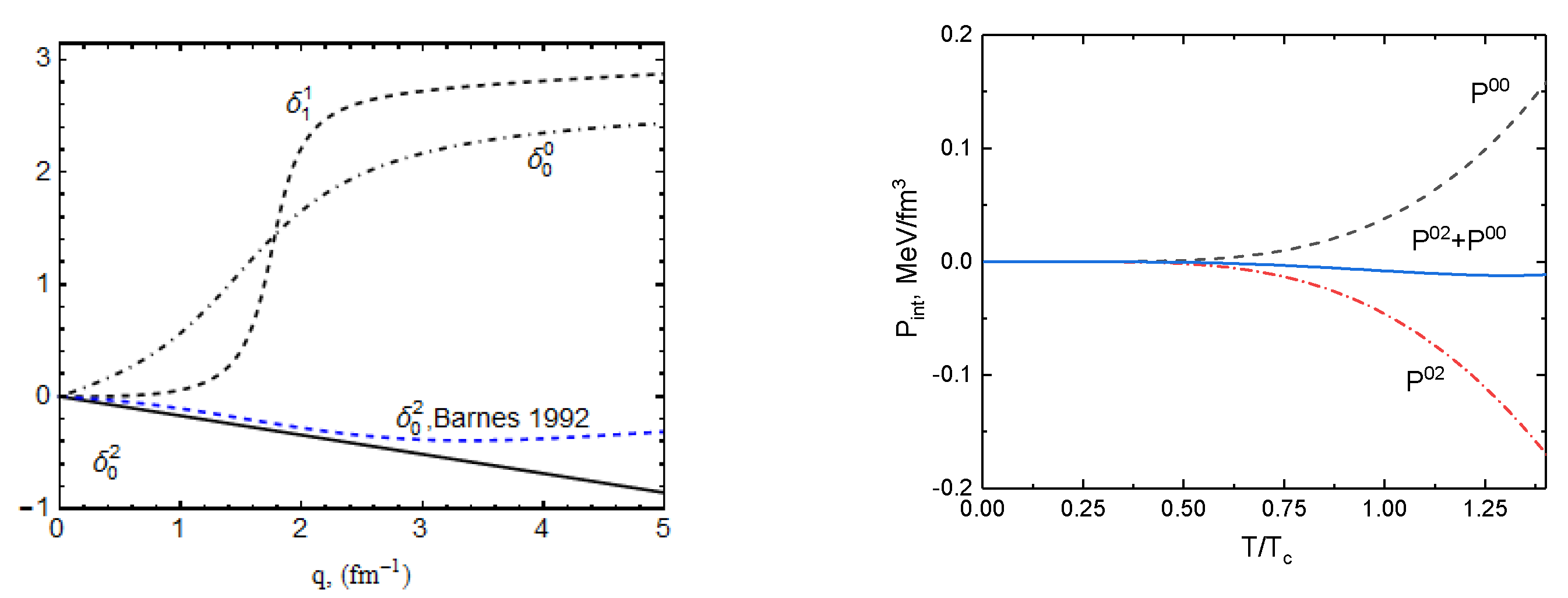
2.1. Beth–Uhlenbeck Equation and Cancellation of the σ Meson
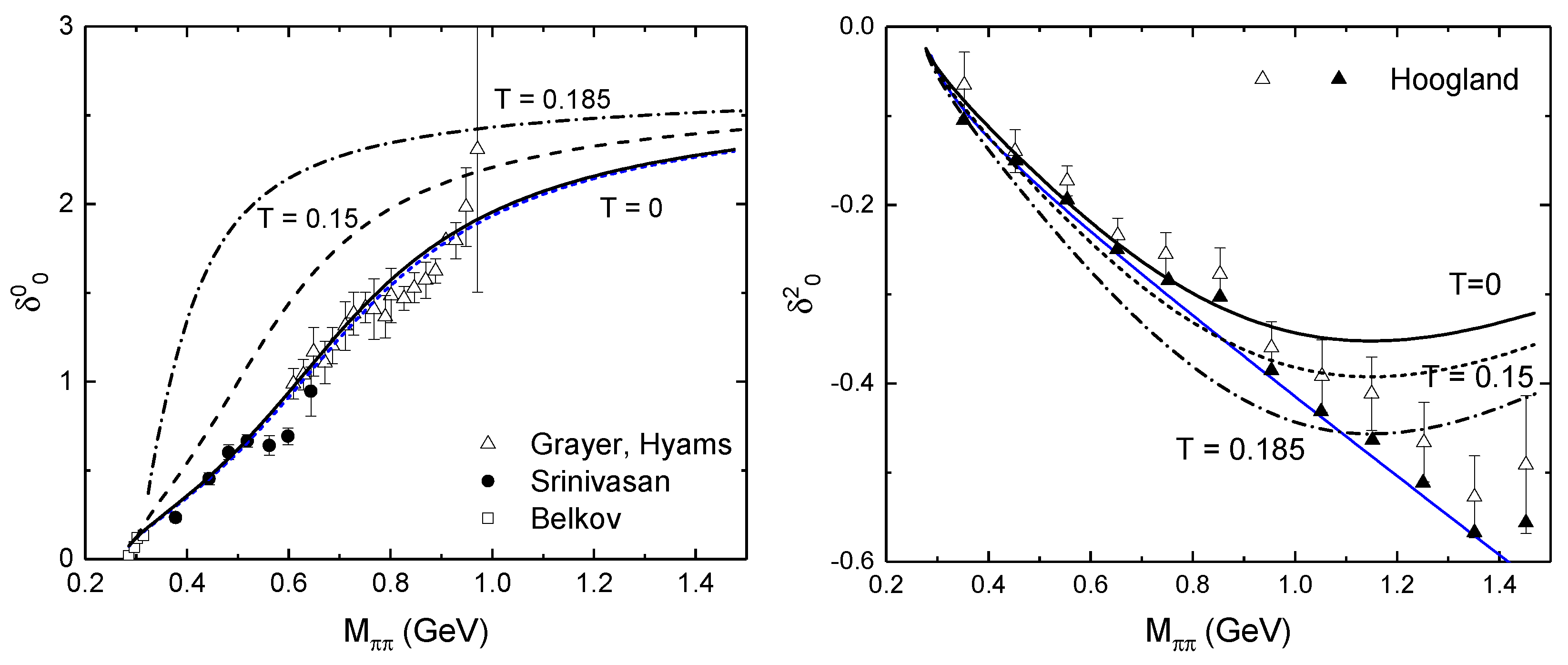
2.2. Analytic Justification for the Cancellation
3. Mesons at a Finite Temperature in the Nambu–Jona-Lasinio Model
4. Results and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Venugopalan, R.; Prakash, M. Thermal properties of interacting hadrons. Nucl. Phys. A 1992, 546, 718–760. [Google Scholar] [CrossRef]
- Welke, G.M.; Venugopalan, R.; Prakash, M. The Speed of sound in an interacting pion gas. Phys. Lett. B 1990, 245, 137–141. [Google Scholar] [CrossRef]
- Quack, E.; Zhuang, P.; Kalinovsky, Y.; Klevansky, S.P.; Hufner, J. π-π scattering lengths at finite temperature. Phys. Lett. B 1995, 348, 1–6. [Google Scholar] [CrossRef]
- Barnes, T.; Swanson, E.S. A Diagrammatic approach to meson meson scattering in the nonrelativistic quark potential model. Phys. Rev. D 1992, 46, 131–159. [Google Scholar] [CrossRef]
- Broniowski, W.; Giacosa, F.; Begun, V. Cancellation of the σ meson in thermal models. Phys. Rev. C 2015, 92, 034905. [Google Scholar] [CrossRef]
- Giacosa, F.; Begun, V.; Broniowski, W. Irrelevance of f0(500) in bulk thermal properties. Acta Phys. Pol. Suppl. 2016, 9, 213. [Google Scholar] [CrossRef]
- Friman, B.; Lo, P.M.; Marczenko, M.; Redlich, K.; Sasaki, C. Strangeness fluctuations from K − π interactions. Phys. Rev. D 2015, 92, 074003. [Google Scholar] [CrossRef]
- Dash, A.; Samanta, S.; Mohanty, B. Thermodynamics of a gas of hadrons with attractive and repulsive interactions within an S -matrix formalism. Phys. Rev. C 2019, 99, 044919. [Google Scholar] [CrossRef]
- Dashen, R.; Ma, S.K.; Bernstein, H.J. S Matrix formulation of statistical mechanics. Phys. Rev. 1969, 187, 345–370. [Google Scholar] [CrossRef]
- Lo, P.M. Thermal study of a coupled-channel system: A brief review. Eur. Phys. J. A 2021, 57, 60. [Google Scholar] [CrossRef]
- Steinert, T.; Cassing, W. Covariant interacting Hadron-Resonance Gas model. Phys. Rev. C 2018, 98, 014908. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Thermal hadron production in relativistic nuclear collisions: The Hadron mass spectrum, the horn, and the QCD phase transition. Phys. Lett. B 2009, 673, 142–145, Erratum in Phys. Lett. B 2009, 678, 516. [Google Scholar] [CrossRef]
- Volkov, M.K.; Kuraev, E.A.; Blaschke, D.; Ropke, G.; Schmidt, S.M. Excess low-energy photon pairs from pion annihilation at the chiral phase transition. Phys. Lett. B 1998, 424, 235–243. [Google Scholar] [CrossRef]
- Blaschke, D.; Röpke, G. Quark exchange contribution to the effective meson meson interaction potential. Phys. Lett. B 1993, 299, 332–337. [Google Scholar] [CrossRef]
- Hüfner, J.; Klevansky, S.P.; Rehberg, P. Soft deconfinement-critical phenomena at the Mott transition in a field theory for quarks and mesons. Nucl. Phys. A 1996, 606, 260–282. [Google Scholar] [CrossRef]
- Weinberg, S. Pion scattering lengths. Phys. Rev. Lett. 1966, 17, 616–621. [Google Scholar] [CrossRef]
- Klevansky, S.P. The Nambu—Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649–708. [Google Scholar] [CrossRef]
- Volkov, M.K.; Ebert, D.; Nagy, M. Excited pions, rho and omega mesons and their decays in a chiral SU(2) x SU(2) Lagrangian. Int. J. Mod. Phys. A 1998, 13, 5443–5458. [Google Scholar] [CrossRef]
- Volkov, M.K.; Radzhabov, A.E. The Nambu-Jona-Lasinio model and its development. Phys. Usp. 2006, 49, 551–561. [Google Scholar] [CrossRef]
- Ebert, D.; Kalinovsky, Y.L.; Munchow, L.; Volkov, M.K. Mesons and diquarks in a NJL model at finite temperature and chemical potential. Int. J. Mod. Phys. A 1993, 8, 1295–1312. [Google Scholar] [CrossRef]
- Zhuang, P.; Yang, Z. Sigma decay at finite temperature and density. Chin. Phys. Lett. 2001, 18, 344–346. [Google Scholar] [CrossRef]
- Friesen, A.V.; Kalinovsky, Y.L.; Toneev, V.D. Decay of a scalar σ-meson near the critical end-point in the PNJL model. Phys. Part. Nucl. Lett. 2012, 9, 1. [Google Scholar] [CrossRef]
- Grigorian, H. Parametrization of a nonlocal, chiral quark model in the instantaneous three-flavor case: Basic formulas and tables. Phys. Part. Nucl. Lett. 2007, 4, 223–231. [Google Scholar] [CrossRef]
- Zablocki, D.; Blaschke, D.; Röpke, G. BEC-BCS Crossover in Strongly Interacting Matter. In Metal-to-Nonmetal Transitions; Springer Series in Materials Science; Redmer, R., Hensel, F., Holst, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 132, pp. 161–182. [Google Scholar] [CrossRef]
- Belkov, A.A.; Bunyatov, S.A.; Mukhin, K.N.; Patarakin, O.O.; Sidorov, V.M.; Sulkovskaya, M.M.; Sustavov, A.F.; Yarba, V.A. PI PI SCATTERING PHASES FROM ANALYSIS OF REACTION π−p→π−π+ N NEAR THRESHOLD. JETP Lett. 1979, 29, 597. (In Russian) [Google Scholar]
- Grayer, G.; Hyams, B.; Jones, C.; Schlein, P.; Weilhammer, P.; Blum, W.; Dietl, H.; Koch, W.; Lorenz, E.; Lütjens, G.; et al. High Statistics Study of the Reaction π−p→π−π+ n: Apparatus, Method of Analysis, and General Features of Results at 17-GeV/c. Nucl. Phys. B 1974, 75, 189–245. [Google Scholar] [CrossRef]
- Hyams, B.; Jones, C.; Weilhammer, P.; Blum, W.; Dietl, H.; Grayer, G.; Koch, W.; Lorenz, E.; Lütjens, G.; Männer, W.; et al. ππ Phase Shift Analysis from 600-MeV to 1900-MeV. Nucl. Phys. B 1973, 64, 134–162. [Google Scholar] [CrossRef]
- Srinivasan, V.; Helland, J.A.; Lennox, A.J.; Poirier, J.A.; Prukop, J.P.; Rey, C.A.; Sander, O.R.; Biswas, N.N.; Cason, N.M.; Kenney, V.P.; et al. π−π+→π−π+ Interactions Below 0.7-GeV from π−p−→ π−π+ n Data at 5-GeV/c. Phys. Rev. D 1975, 12, 681. [Google Scholar] [CrossRef]
- Hoogland, W.; Peters, S.; Grayer, G.; Hyams, B.; Weilhammer, P.; Blum, W.; Dietl, H.; Hentschel, G.; Koch, W.; Lorenz, E.; et al. Measurement and Analysis of the π+π+ System Produced at Small Momentum Transfer in the Reaction π+p→π+π+ n at 12.5-GeV. Nucl. Phys. B 1977, 126, 109–123. [Google Scholar] [CrossRef]


| T = 0 | T = 0.14 | T = 0.16 | T = 0.19 | T = 0.2 | |
|---|---|---|---|---|---|
| 0.148 | 0.155 | 0.164 | 0.202 | 0.237 | |
| −0.036 | −0.037 | −0.037 | −0.041 | −0.043 | |
| −0.826 | −0.85 | −0.88 | −0.996 | −1.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blaschke, D.; Friesen, A.; Kalinovsky, Y. Cancellation of the Sigma Mode in the Thermal Pion Gas by Quark Pauli Blocking. Symmetry 2023, 15, 711. https://doi.org/10.3390/sym15030711
Blaschke D, Friesen A, Kalinovsky Y. Cancellation of the Sigma Mode in the Thermal Pion Gas by Quark Pauli Blocking. Symmetry. 2023; 15(3):711. https://doi.org/10.3390/sym15030711
Chicago/Turabian StyleBlaschke, David, Alexandra Friesen, and Yuri Kalinovsky. 2023. "Cancellation of the Sigma Mode in the Thermal Pion Gas by Quark Pauli Blocking" Symmetry 15, no. 3: 711. https://doi.org/10.3390/sym15030711
APA StyleBlaschke, D., Friesen, A., & Kalinovsky, Y. (2023). Cancellation of the Sigma Mode in the Thermal Pion Gas by Quark Pauli Blocking. Symmetry, 15(3), 711. https://doi.org/10.3390/sym15030711








