Primordial Gravitational Wave Circuit Complexity
Abstract
1. Introduction
- In Section 2, we provide a brief review of quantum circuit complexity and how it can be related to quantum chaos.
- In Section 3, we provide the squeezed state formalism of the cosmological perturbation of PGW. We give a list of various scale factors that we are interested in. As our initial state, we choose different vacua such as the Motta-Allen vacua, vacua and Bunch–Davies vacua. Finally, we show how the squeezed state formalism in PGW dominated primordial cosmology.
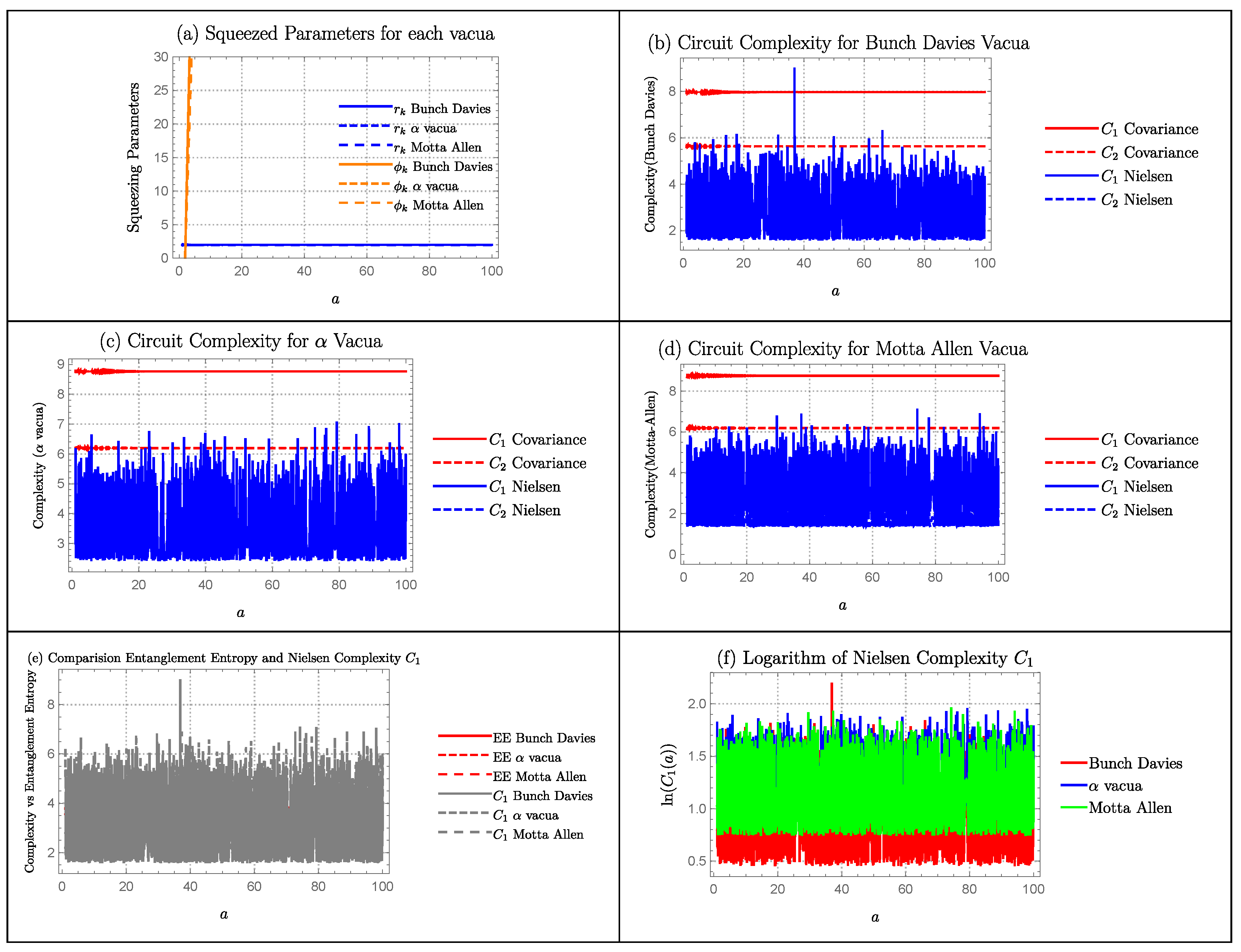
- In Section 4, we compute the quantum circuit complexity of PGW from squeezed states using both Covariance and Nielsen’s wave function approach for all three vacua.
- In Section 5, we compute the entanglement entropy of PGW from squeezed states for each vacua: Motta-Allen vacua, vacua and Bunch–Davies vacua.
- In Section 6, we perform numerical analyses for various cosmological models. In particular, we compute quantum complexity, entanglement entropy and quantum chaos.
- Finally, in Section 7, we present the concluding remarks and future prospects.
2. Chaos and Complexity: Old Wine in a New Glass
2.1. Framework of Quantum Circuit Complexity
- Continuity: Here, we have , which implies that we need to consider a continuous cost function. This is expected because of the physical reason.
- Positivity: The continuous cost function should satisfy the constraint . Here, is obtained from . This also means that when this equality condition is satisfied, the reference and target should be same.
- Positive homogeneity: For any positive real number and any vector v, we obtain .
- Triangle Inequality: The continuous cost function should strictly satisfy the triangle inequality, which is given by for all tangent vectors v and . Now, if both of these vectors belong to the same ray, the equality holds perfectly.
2.2. Quantum Chaos and Complexity
3. Squeezed State Formalism of Cosmological Perturbation Theory of PGW
3.1. Classical Perturbation Due to PGW
- 1.
- De Sitter:
- 2.
- Inflation/Quasi De Sitter:
- 3.
- Reheating ():During reheating, the equation of the state parameter lies within the window , which was discussed in detail in refs. [55,70]. However, there is always an ambiguity when having the equation of the state parameter within this prescribed window, as the micro-physics of the epoch of reheating are not known yet and, to date, it was studied from the phenomenological perspective only. Regarding the ambiguity, let us mention ref. [71], where the authors pointed out that during such an epoch the equation of state parameter is . We have restricted the equation of state parameter within because it is believed that the classically reheating epoch should lie between matter domination () and radiation (). The exact form of the equation of state during this epoch is unknown to date.
- 4.
- Radiation ():
- 5.
- Matter ():
- 6.
- Contraction (Pre-Bounce):
- 7.
- Matter Bounce:
- 8.
- Sechyperbolic Bounce:
- 9.
- Coshyperbolic Bounce:
- 10.
- Sinhyperbolic Bounce:In this case, the mass parameter can be evaluated as
- 11.
- Cosechyperbolic Bounce:
- 12.
- Exponential Bounce:
- 13.
- Power-Law Bounce ():
- 14.
- Polynomial Bounce:
- 15.
- Matter Cyclic:
- 16.
- Radiation Cyclic:
- 17.
- Black Hole Gas:
3.2. Classical Mode Function for PGW
- 1.
- Motta-Allen () vacua:This is a specific choice where the arbitrary coefficients appearing in the classical solution of the PGW are parametrized by two real parameters, and , followingThis is considered as an excited isometric vacuum state having an oscillating feature. One can explicitly show that this type of quantum-excited vacua is CPT symmetry breaking in nature and is characterised by the real parameter . Apart from having this issue to describe various physical situations, the explicit role of this quantum vacuum state is extremely important. In this paper, we will investigate the role of these two real parameters and in the parametrization of Motta-Allen vacua to determine the quantum complexity and to study the underlying phenomena of quantum chaos from the various cosmological primordial models of our universe using PGW perturbation. We are excited about this finding because such possibilities have not been explored. In this context, the solution for the PGW field variable for the Motta-Allen vacua can be written asFor the case of heavy field, we have the following simplified expression:The limiting results for the super-Hubble, sub-Hubble and horizon exit scale are given as follows:
- 2.
- vacua:This is a specific choice where the arbitrary coefficients that are appearing in the classical solution of the PGW are parametrized by one real parameter family , by:This is identified as a excited isommetric vacuum state which is CPT symmetry preserving in nature. The real parameter of vacua determine the quantum complexity and to study the underlying phenomena of quantum chaos from the various cosmological primordial models of our universe using PGW perturbation. Like the previous case this issue was not have been studied before and for this reason we are very hopeful to explore some interesting underlying physical facts from our analysis. It is important to note that by fixing in the vacua or Motta-Allen vacua one can obtain the results for the vacua, which in tern implies that by fixing this choice of the parameter one can able to transform a CPT violating vacua to a CPT preserving vacua. In this context, we get:For the case of heavy field case the PGW field can be expressed as:The limiting results for super-Hubble, the sub-Hubble and horizon exit scale are given by:
- 3.
- Bunch-Davies vacuum:This is a specific choice where the arbitrary coefficients that are appearing in the classical solution of the PGW are parametrized by the following expression:which is a isommetric ground state of the initial vacuum used in primordial cosmology. In literature Bunch-Davies vacuum state is identified as Cherenkov vacuum or Hartle-Hawking vacuum state, which is actually an Euclidean state. The general solution for PGW field variable for the Bunch-Davies vacuum is given by:For the case of heavy field case the solution for the PGW field for the Bunch-Davies vacuum can be written as:The limiting results for super-Hubble, the sub-Hubble and horizon exit scale are given by:
3.3. Quantization of Hamiltonian for PGW
- 1.
- Motta-Allen () vacua:In presence of Motta-Allen vacua the PGW tensor mode velocity can be written as:Now for the case of heavy Hubble effective mass the PGW tensor perturbed field velocity can be expressed as:In the super-Hubble, horizon crossing and sub-Hubble limit we have the following results:
- 2.
- vacua:In presence of vacua the expression for the PGW tensor mode velocity can be simplified as:Now for the case of heavy field case the PGW tensor mode velocity can be simplified as:In the super-Hubble, horizon crossing and sub-Hubble limit we have the following results:
- 3.
- Bunch-Davies vacuum:For vacua the expression for the PGW tensor mode velocity can be written as:Now for the case of heavy field case the PGW tensor mode velocity can be simplified as:In the super-Hubble, horizon crossing and sub-Hubble limit we have the following results:
3.4. Time Evolution of Quantized PGW
3.4.1. Fixing the Initial Condition at Horizon Crossing
3.4.2. Squeezed State Formalism in PGW Dominated Primordial Cosmology
3.4.3. Role of Unitary Time Evolution of PGW Fluctuations in Squeezed State Formalism
4. Complexity of PGW from Squeezed States
4.1. Circuit Complexity of Two Mode Squeezed States
Covariance Matrix Method:
- 1.
- .
- 2.
- .
Complexity via Nielsen’s Wave-Function Method:
4.2. Complexity in PGW
Motta Allen Squeezed Quantum Vacua State:
Covariance Matrix Approach:
Nielsen’s Wave Function Approach:
Squeezed Quantum Vacua State:
Covariance Matrix Approach:
Nielsen’s Wave Function Approach:
Bunch Davies Squeezed Quantum Vacua State:
Covariance Matrix Approach:
Nielsen’s Wave Function Approach:
5. Entanglement Entropy of PGW from Squeezed States
Motta Allen Squeezed Quantum Vacua State:
Squeezed Quantum Vacua State:
Bunch Davies Squeezed Quantum Vacua State:
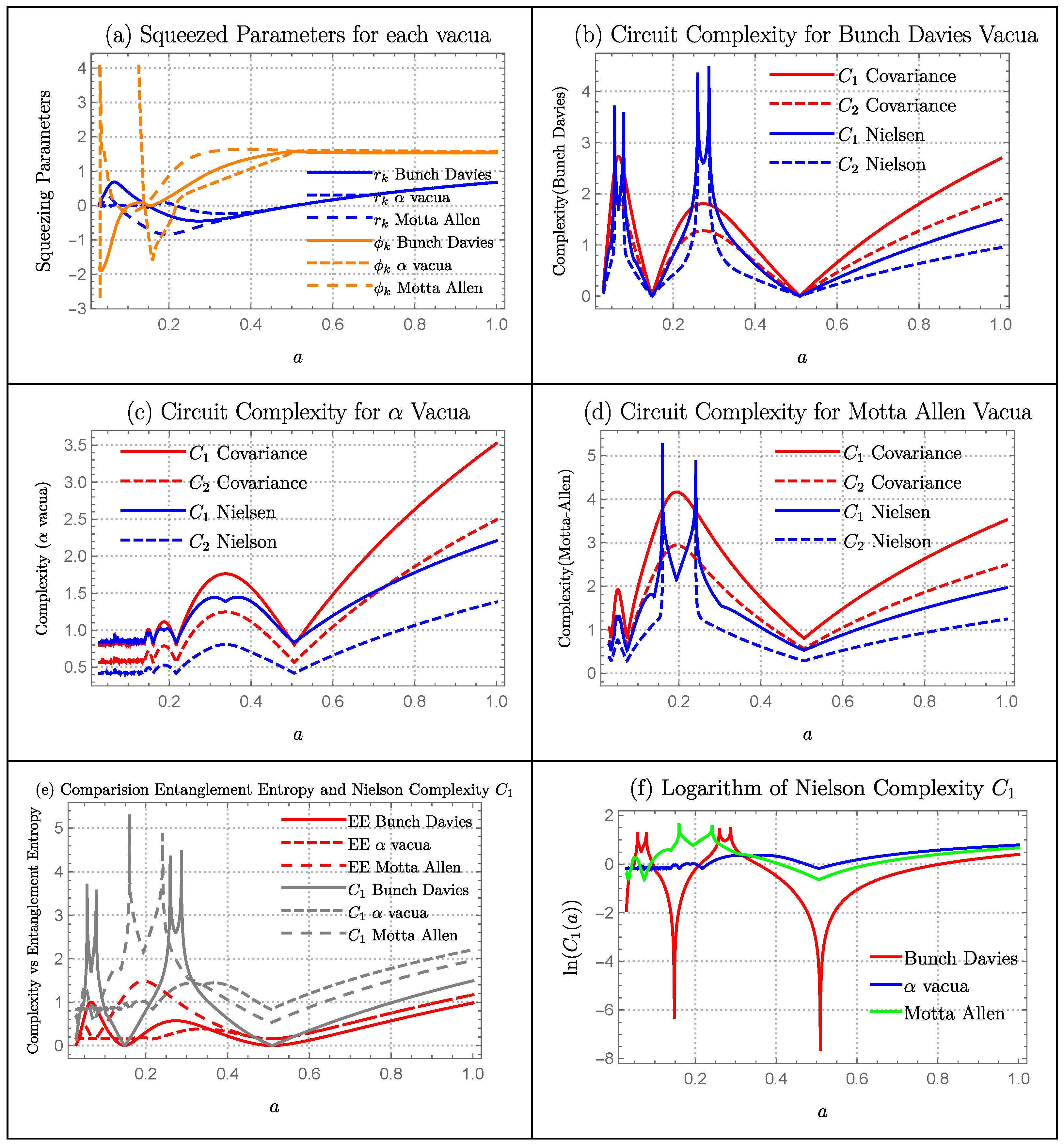
6. Numerical Results and Interpretation
- Covariance measure of circuit complexity is not sensitive to the squeezing angle while circuit complexity obtained via Nielsen’s approach is. Since, entanglement entropy is also independent of the the squeezing angle it is easier to make comparison of entropy with Covariance measure rather than Nielsen’s ones.
- The circuit complexity via covariance approach is always linearly dependent on the squeezing parameter while this is not true for Nielsen’s measure. Furthermore on different limiting conditions, structure of the Nielsen’s measure of complexity can be very different. In contrast, we always have one limiting condition in Covariance measure: .
- Nielsen’s measure of circuit complexity is sensitive to the details of evolution of the wave function while covariance measure is not. This is because Nielsen’s measure is dependent on both parameters: squeezing angle and squeezing parameter .
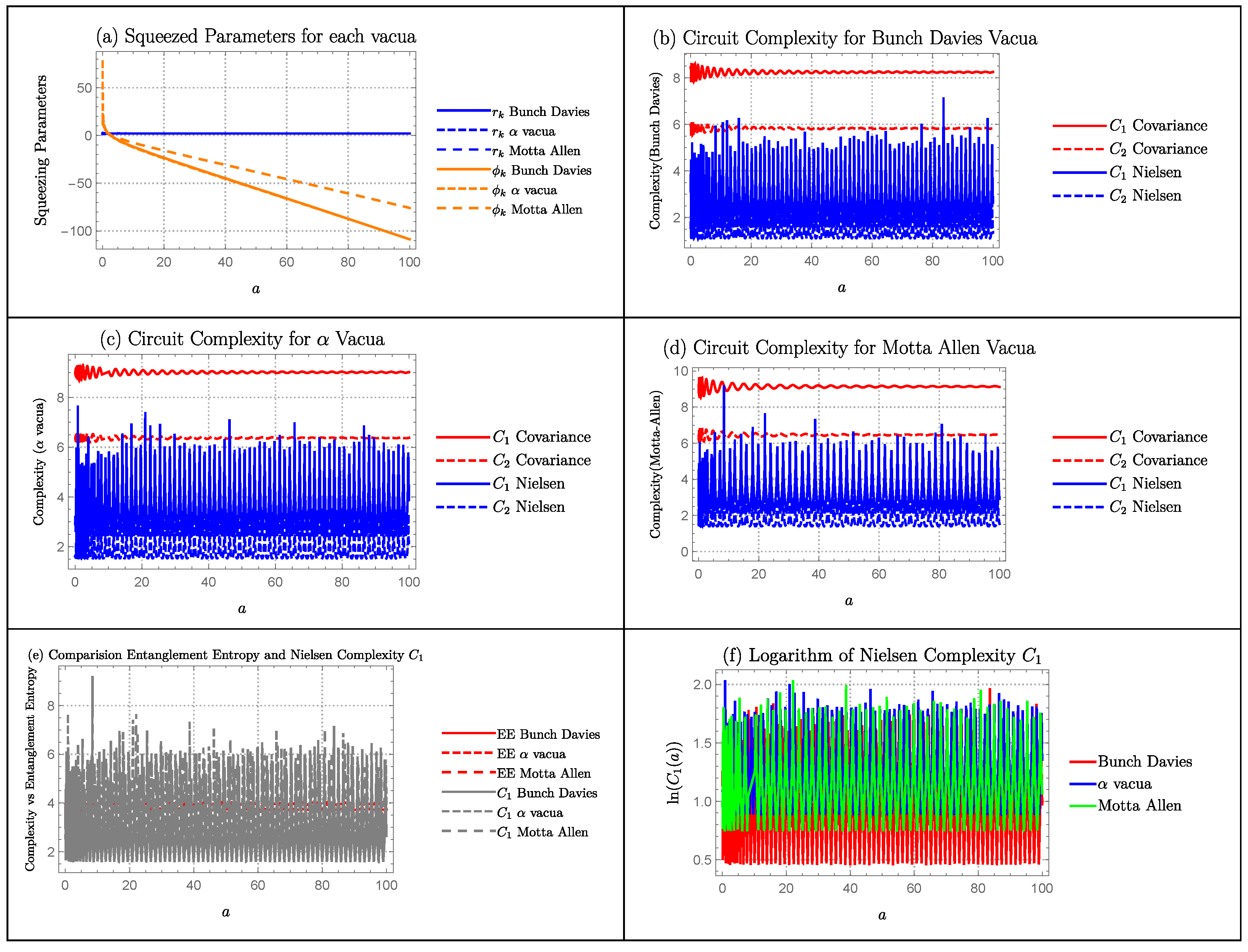
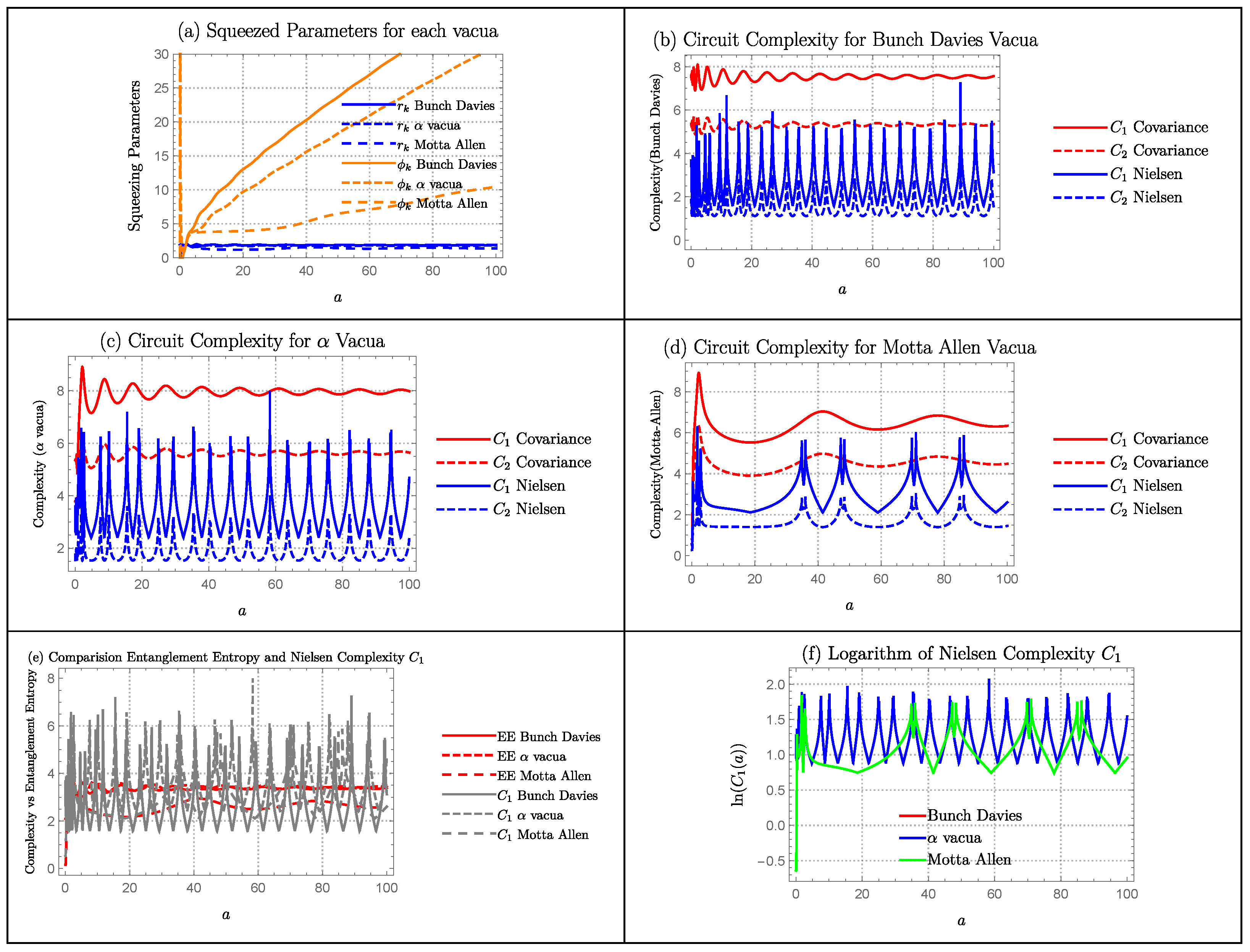
6.1. De Sitter
Squeezing Parameters
Complexity Measure
Comparison of Entanglement Entropy with Complexity
Quantum Lyapunov Exponent
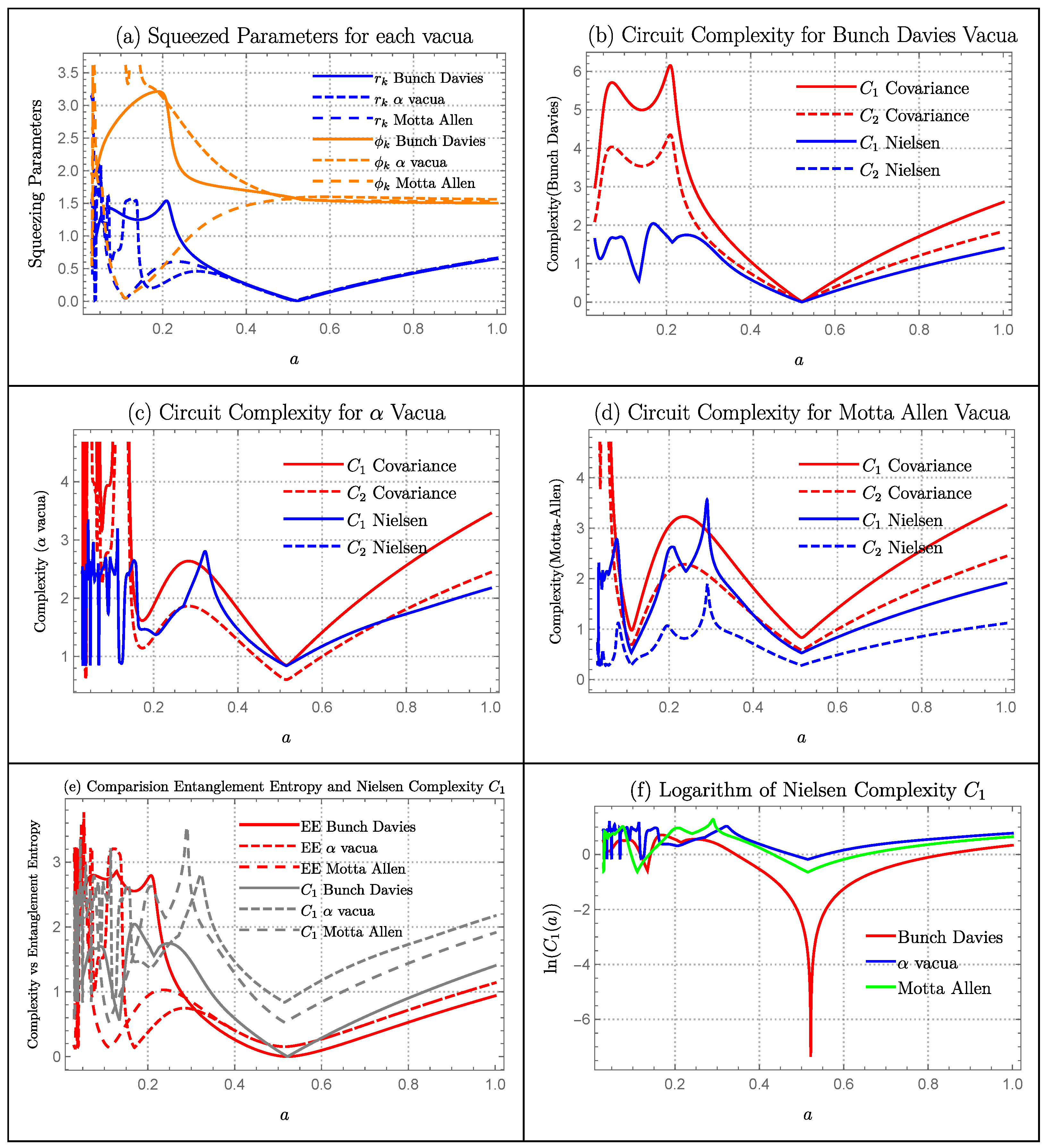
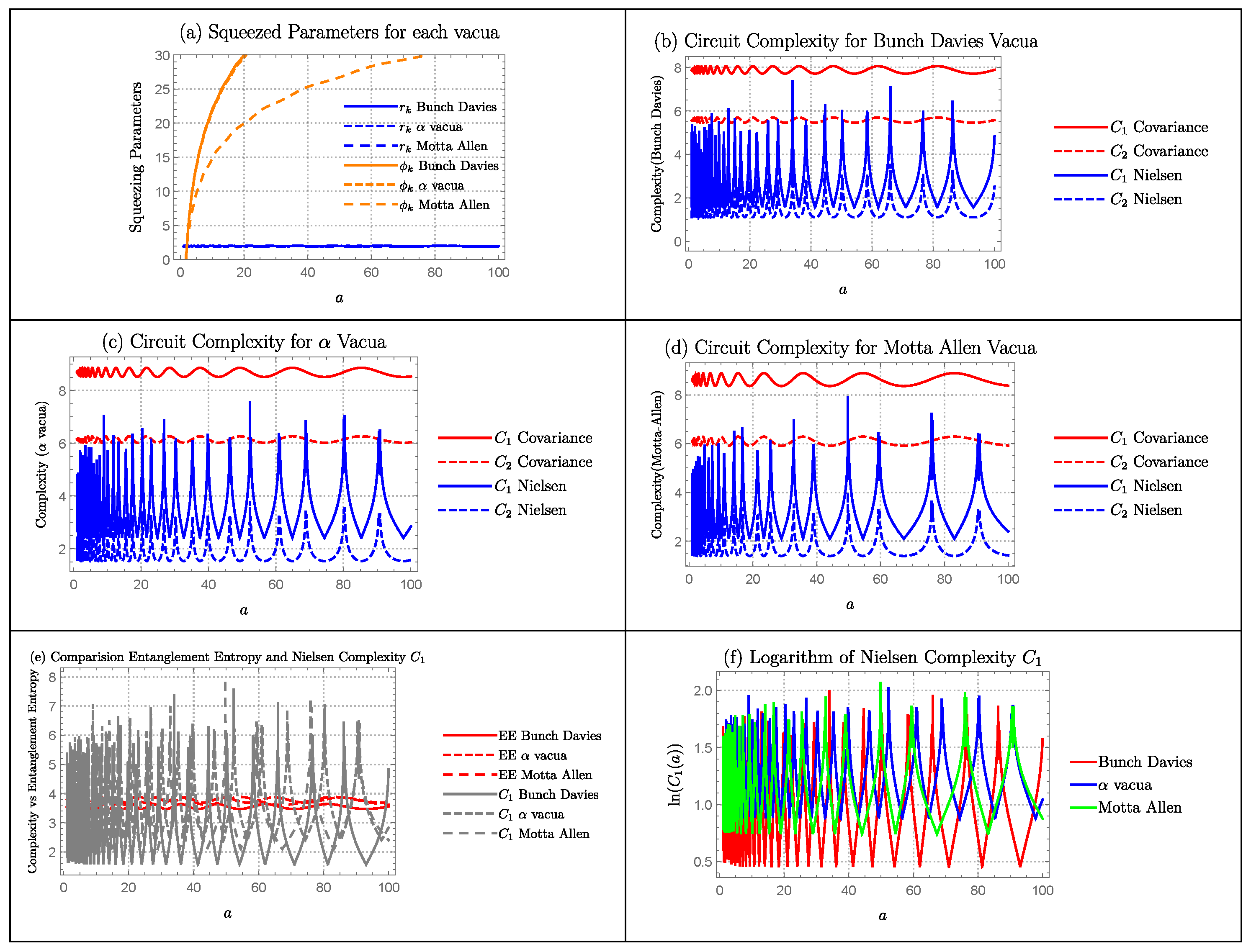
6.2. Inflation/Quasi De Sitter
Squeezing Parameters
Complexity Measure
Comparison of Entanglement Entropy with Complexity
Quantum Lyapunov Exponent
6.3. Reheating
Squeezing Parameters
Complexity Measure
Comparison of Entanglement Entropy with Complexity
Quantum Lyapunov Exponent
6.4. Radiation
Squeezing Parameters
Complexity Measure
Comparison of Entanglement Entropy with Complexity
Quantum Lyapunov Exponent
6.5. Matter
Squeezing Parameters
Complexity Measure
Comparison of Entanglement Entropy with Complexity
Quantum Lyapunov Exponent
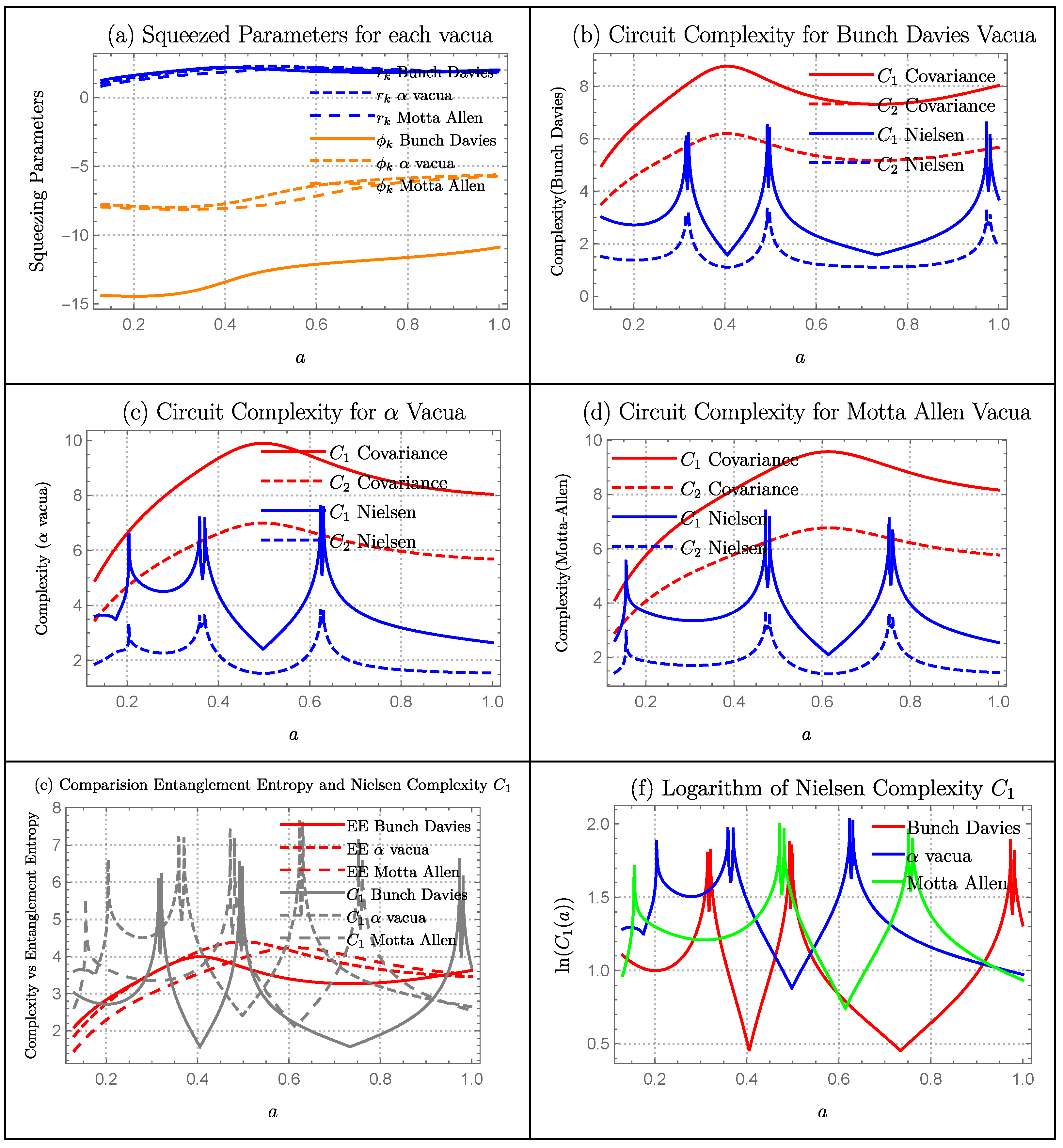
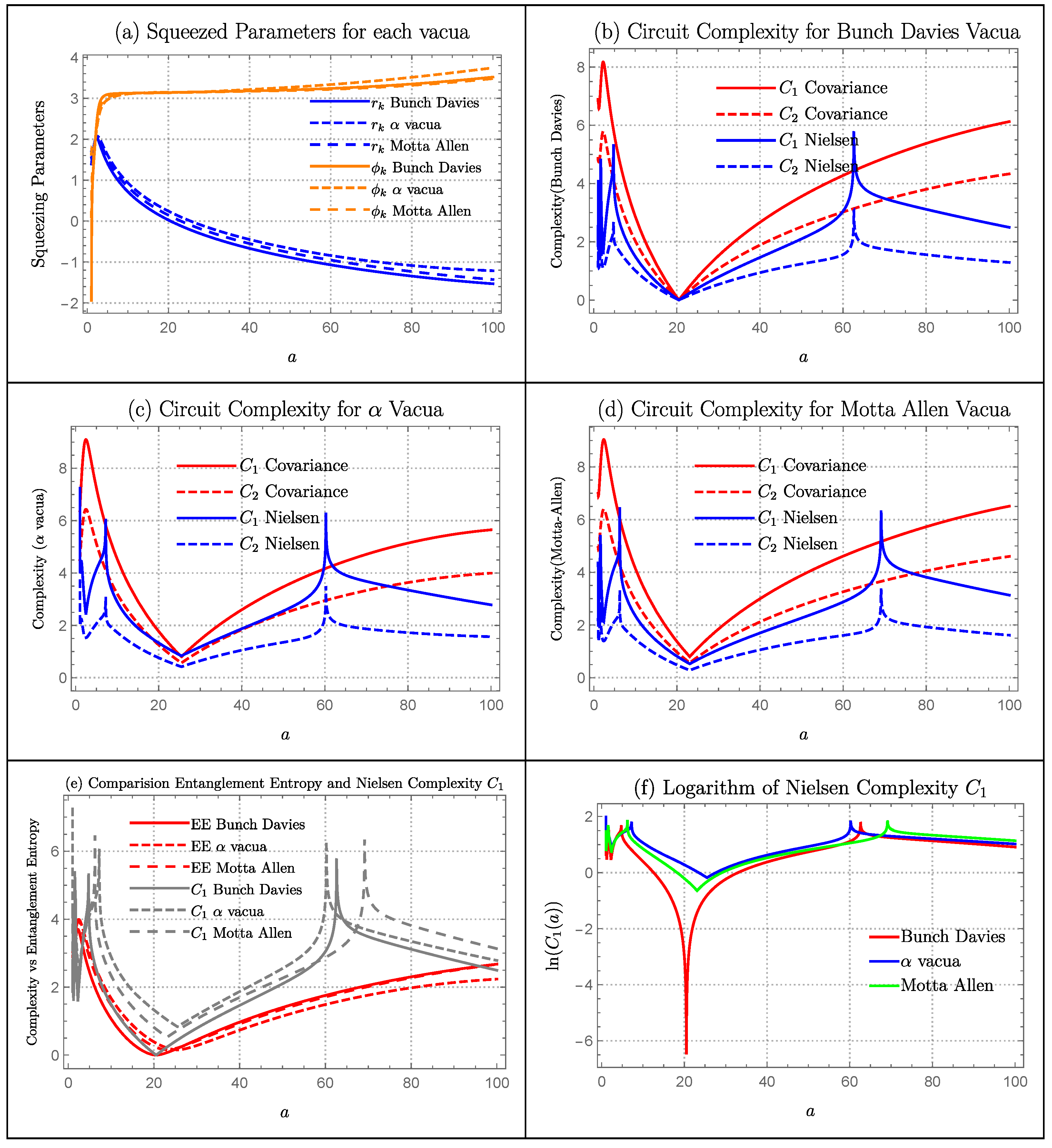
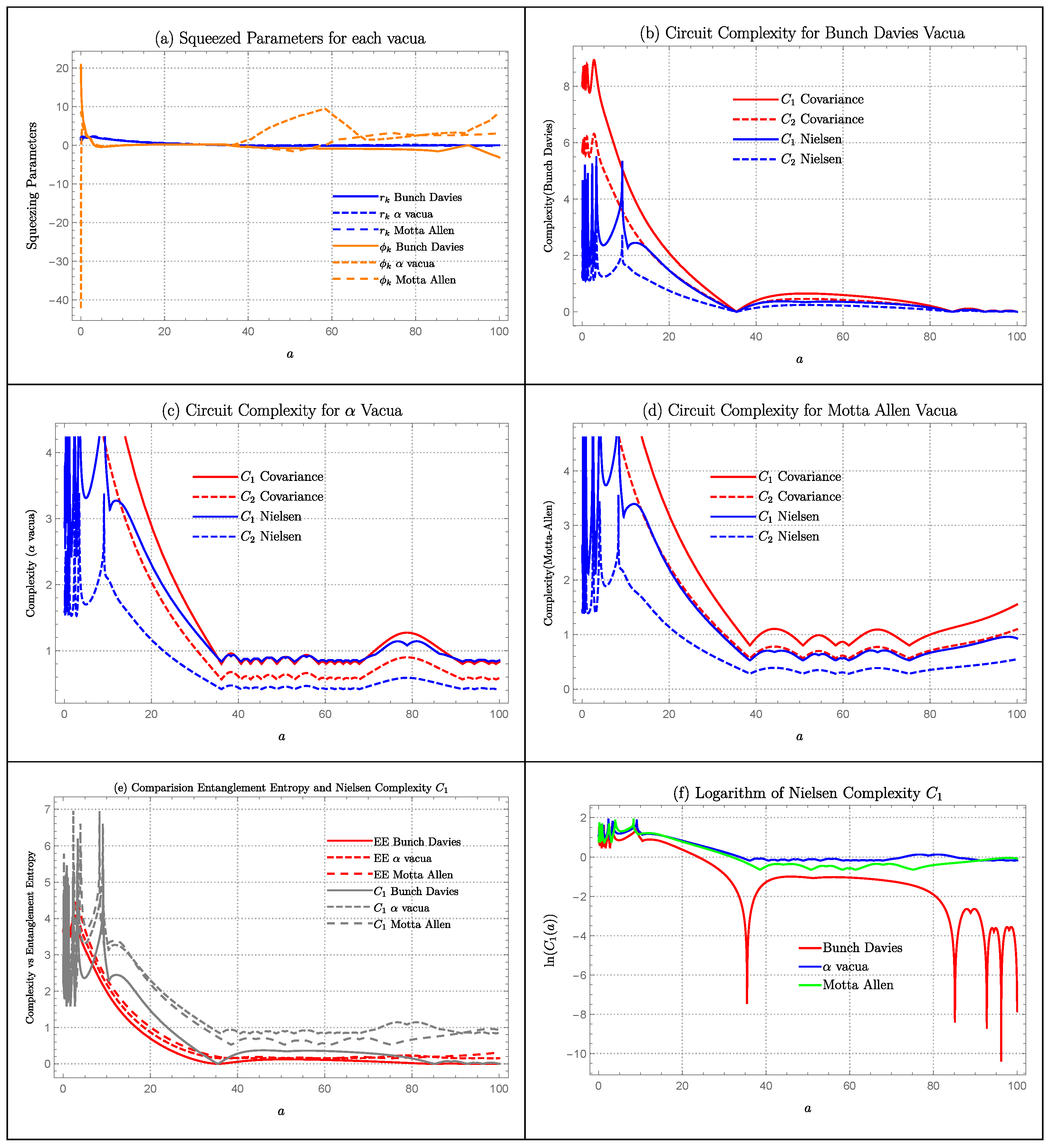
6.6. Bouncing Model
Squeezing Parameters
- 1.
- Contraction Bounce Model: In Figure 6a, we have plotted squeezing parameters and for each vacua using the parameters and . The growth of is very small for all vacua and they merge at each other. The evolution of is different to Motta-Allen vacua than and Bunch-Davies Vacua.
- 2.
- Matter Bounce Model: In Figure 7a, we have plotted squeezing parameters and for each vacua using the parameters and . For all three vacua, grows at the early values of scale factor a, and then keeps dropping. While for all three vacua, grows and then saturates.
- 3.
- Sechyperbolic Bounce Model: In Figure 8a, we have plotted squeezing parameters and for each vacua using the parameters and . For all three vacua, keeps growing with respect to the scale factor a. While the behavior of is different for each vacua at early a. Then, they starts to merge after some time.
- 4.
- Cosinehyperbolic Bounce Model: In Figure 9a, we have plotted squeezing parameters and for each vacua using the parameters and . The growth of is very small for all vacua and they merge at each other. At early time, starts to grow together with the evolution of being different to Motta-Allen vacua than and Bunch-Davies Vacua at later a.
- 5.
- Sinehyperbolic Bounce Model: In Figure 10a, we have plotted squeezing parameters and for each vacua using the parameters and . The growth of is very small for all vacua and they merge at each other. At early time, starts to grow together with the evolution of being different to Motta-Allen vacua than and Bunch-Davies Vacua at later a.
- 6.
- Cosechyperbolic Bounce Model: In Figure 11a, we have plotted squeezing parameters and for each vacua using the parameters and . The growth of takes a dip around and then keeps a linear growth. This holds for all vacua. While value of are different for each vacua until , and then they merge. After that, they keep on dropping until it merge with .
- 7.
- Exponential Bounce Model: In Figure 12a, we have plotted squeezing parameters and for each vacua using the parameters and . The value of is constant up to , and then they starts to grow linearly. The value of keeps dropping until it merges with . This holds for all vacua.
- 8.
- Power Law Bounce Model: In Figure 13a, we have plotted squeezing parameters and for each vacua using the parameters and . The value of takes a sharp growth and starts to drop. While grows and then saturates.
- 9.
- Polynomial Bounce Model: In Figure 14a, we have plotted squeezing parameters and for each vacua using the parameters and . The growth of is constant and almost same for each vacua. Bunch-Davies vauca has the largest growth of followed by Alpha and then Motta-Allen vacua.
- 10.
- Expansion (Post-Bounce) Model: In Figure 15a, we have plotted squeezing parameters and for each vacua using the parameters and . The growth of is constant and almost same for each vacua. The growth of is similar in the beginning for each vacua but they starts to diverge around .
Complexity Measure
- 1.
- Contraction Bounce Model: Circuit complexity plots for each vacua is identical in overall pattern except for the magnitude. Overall, Motta-Allen Vacua has the largest magnitude with Bunch-Davies being lowest which is due to Motta-Allen Vacua having largest number of external parameters. Covariance measure of complexity is similar to the growth of the squeezing parameter with increase in magnitude. However, Nielsen’s measure is telling a different story. Nielsen’s measure of complexity is highly oscillatory for each vacua and for both cost function and .
- 2.
- Matter Bounce Model: Circuit complexity plots for each vacua is identical in overall pattern except for the magnitude. The plot for the covariance measure of complexity is smooth with a growth at early times and then taking a dip around . After the dip, both and growing linearly. Nielsen measure of complexity has similar pattern but with more details on it. Around , we can observe a pick in both and . Even in early values of a, we can observe some oscillatory behaviour.
- 3.
- Sechyperbolic Bounce Model: Interestingly, we can observe different behaviour in evolution of complexity for each vacua. For Bunch-Davies case, both and Covariance’s complexity is oscillatory before , and then they keep growing with being bounded by . While this pattern is visible for Nielsen’s approach too, there is a oscillatory around . For vacua, more such peaks are visible in Nielsen’s measure of complexity. In Motta-Allen Vacua, both covariance and Nielsen’s measure of complexity is oscillatory before after which they starts to take a smooth rise.
- 4.
- Cosinehyperbolic Bounce Model: Circuit complexity plots for each vacua is identical in overall pattern except for the magnitude. Overall, Motta-Allen Vacua has the largest magnitude with Bunch davies being lowest which is due to Motta-Allen Vacua having largest number of external parameters. Covariance measure of complexity is similar to the growth of the squeezing parameter with increase in magnitude. However, Nielsen’s measure is telling a different story. Nielsen’s measure of complexity is highly oscillatory for each vacua and for both cost function and . In all cases, is being bounded by .
- 5.
- Sinehyperbolic Bounce Model: Circuit complexity plots for each vacua is identical in overall pattern except for the magnitude. Overall, Motta-Allen Vacua has the largest magnitude with Bunch davies being lowest which is due to Motta-Allen Vacua having largest number of external parameters. Covariance measure of complexity is similar to the growth of the squeezing parameter with increase in magnitude. However, Nielsen’s measure is telling a different story. Nielsen’s measure of complexity is highly oscillatory for each vacua and for both cost function and . In all cases, is being bounded by .
- 6.
- Cosechyperbolic Bounce Model: Interestingly, we can observe different behavior in evolution of complexity for each vacua. For Bunch-Davies case, both and Covariance’s complexity is oscillatory before , and then they keep growing with being bounded by . While this pattern is visible for Nielsen’s approach too, there is a oscillatory peak around . Before , the complexity measure is oscillatory just like for Bunch- Davies case but with more sharp peaks visible. In all cases, is being bounded by .
- 7.
- Exponential Bounce Model: The overall pattern of complexity measure is identical for each vacua expect for the change in magnitude. Covariance measure of complexity is similar to the growth of with being bounded by . Nielsen’s measure of complexity is very oscillatory before after which it takes a growth and saturates.
- 8.
- Power Law Bounce Model: The overall pattern of complexity measure is identical for each vacua expect for the change in magnitude. Covariance measure of complexity takes a sharp growth and takes a dip until and then keep a linear growth with being bounded by . While this is also true for Nielsen’s measure, there are some peaks visible around .
- 9.
- Polynomial Bounce Model: Circuit complexity plots patter for Bunch-Davies and vacua is identical in overall pattern except for the magnitude. For both vacua, covariance measure has the growth pattern similar to the squeezing parameter . However, Nielsen’s measure of complexity is very oscillatory. For the case of Motta-Allen vacua, there are more gaps in the oscillatory peaks.
- 10.
- Expansion (Post-Bounce) Model: For each vacua, circuit complexity drops until and then saturates around that point. In all vacua, Nielsen’s measure of complexity is quite chaotic and oscillatory before . For and Motta-Allen vacua, there are also more oscillatory bumps visible after the point .
Comparison of Entanglement Entropy with Complexity
- 1.
- Contraction Bounce Model: Complexity is highly oscillatory compared to the entanglement entropy.
- 2.
- Matter Bounce Model: Both entanglement entropy and complexity measure has similar growth pattern. However, complexity measure has more peaks visible around .
- 3.
- Sechyperbolic Bounce Model: Again complexity measure has more oscillatory peaks compared to the entanglement entropy. This allows us to understand the system in more detail.
- 4.
- Cosinehyperbolic Bounce Model: Complexity is highly oscillatory compared to the entanglement entropy.
- 5.
- Sinehyperbolic Bounce Model: Complexity is highly oscillatory compared to the entanglement entropy.
- 6.
- Cosechyperbolic Bounce Model: Both entanglement entropy and complexity has similar growth pattern but entanglement entropy has a very huge peak at early values of a.
- 7.
- Exponential Bounce Model: Nielsen’s measure of complexity is very oscillatory before after which it takes a growth and saturates while entanglement entropy is not. But, entanglement entropy also takes a growth and saturates just like complexity measure.
- 8.
- Power Law Bounce Model: Both complexity and entanglement entropy has a similar growth pattern, but there are some peaks visible around for the case of complexity measure.
- 9.
- Polynomial Bounce Model: Complexity is highly oscillatory compared to the entanglement entropy.
- 10.
- Expansion (Post-Bounce) Model: Nielsen’s measure of complexity is quite chaotic and oscillatory before but the overall pattern is similar to of entanglement entropy.
Quantum Lyapunov Exponent
- 1.
- Contraction Bounce Model: The log. complexity plot is too oscillatory to get the chaotic measure.
- 2.
- Matter Bounce Model:All three vacua has similar lyapunov exponent, so they have similar chaotic properties.
- 3.
- Sechyperbolic Bounce Model:Motta-Allen Vacua has the largest lyapunov exponent, so it is the most chaotic cosmological model followed by Bunch-Davies and vacua.
- 4.
- Cosinehyperbolic Bounce Model: The log. complexity plot is too oscillatory to get the chaotic measure.
- 5.
- Sinehyperbolic Bounce Model: The log. complexity plot is too oscillatory to get the chaotic measure.
- 6.
- Cosechyperbolic Bounce Model:Bunch-Davies Vacua has the largest Lyapunov exponent, so it is the most chaotic cosmological model followed by Motta-Allen and vacua.
- 7.
- Exponential Bounce Model:All three vacua has similar Lyapunov exponent, so they have similar chaotic properties.
- 8.
- Power Law Bounce Model:All three vacua has similar Lyapunov exponent, so they have similar chaotic properties.
- 9.
- Polynomial Bounce Model: The log. complexity plot is too oscillatory to get the chaotic measure.
- 10.
- Expansion (Post-Bounce) Model: There is no growth or saturation point of complexity, so we will not be able to get the chaotic measure.
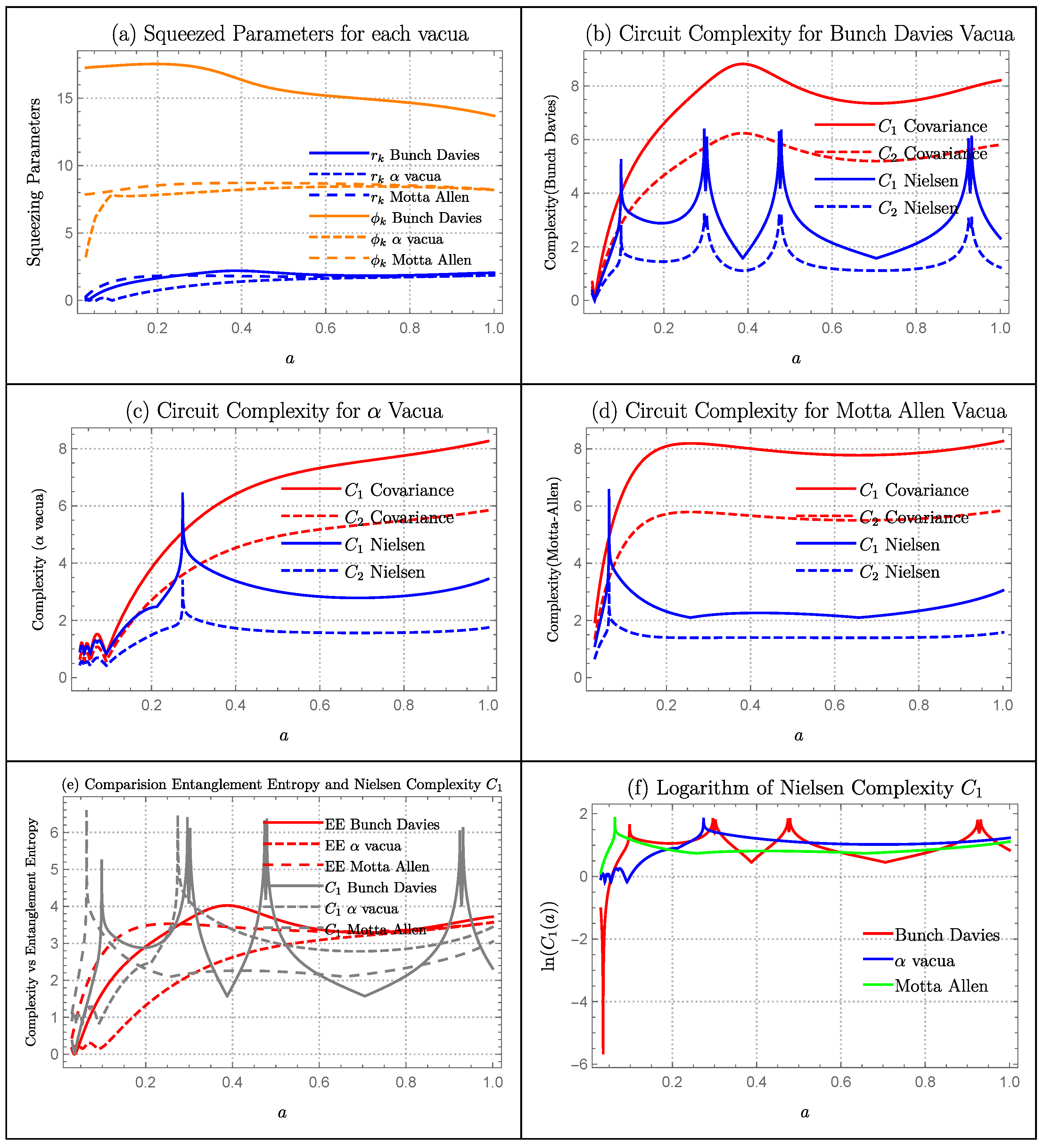
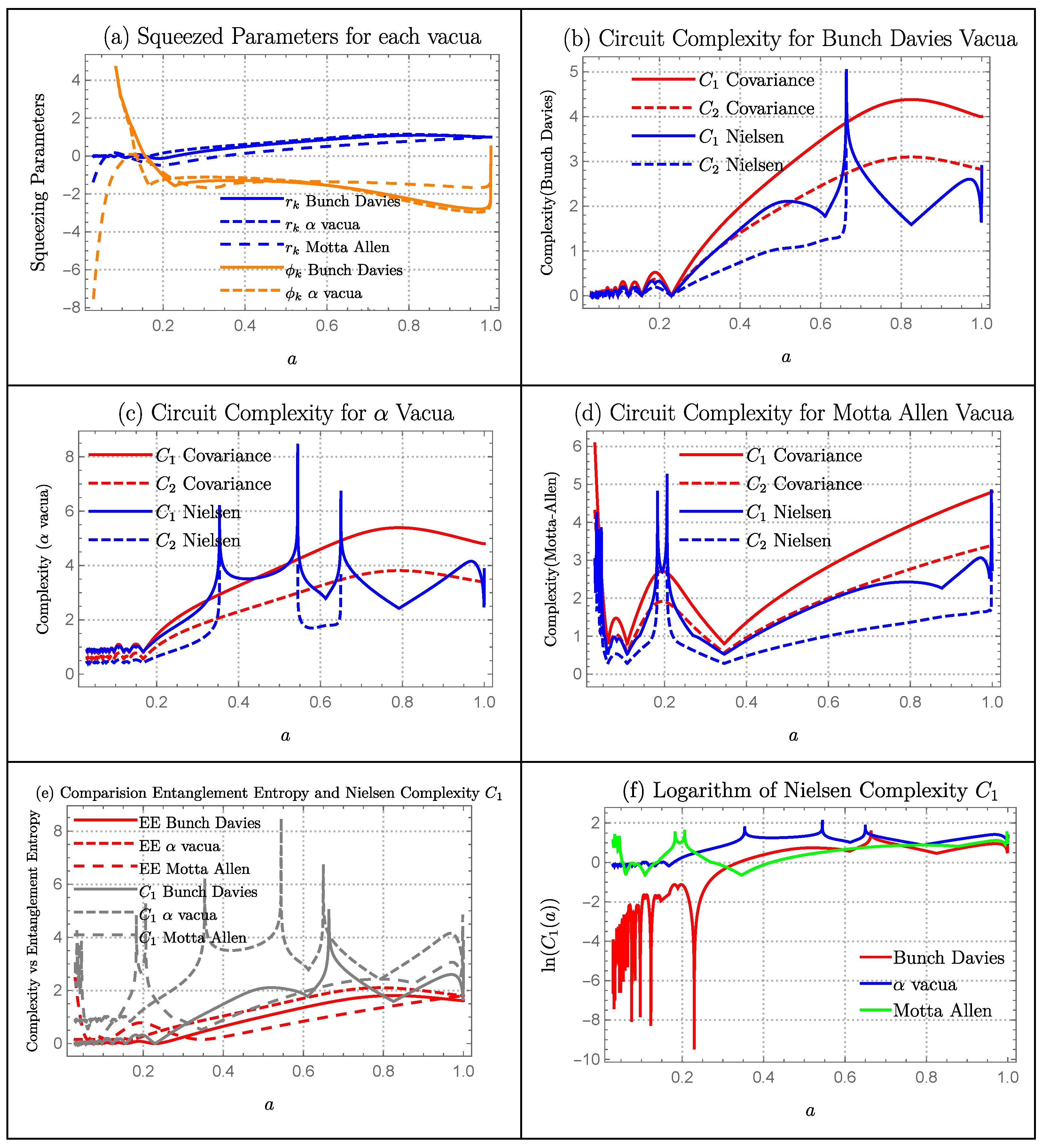
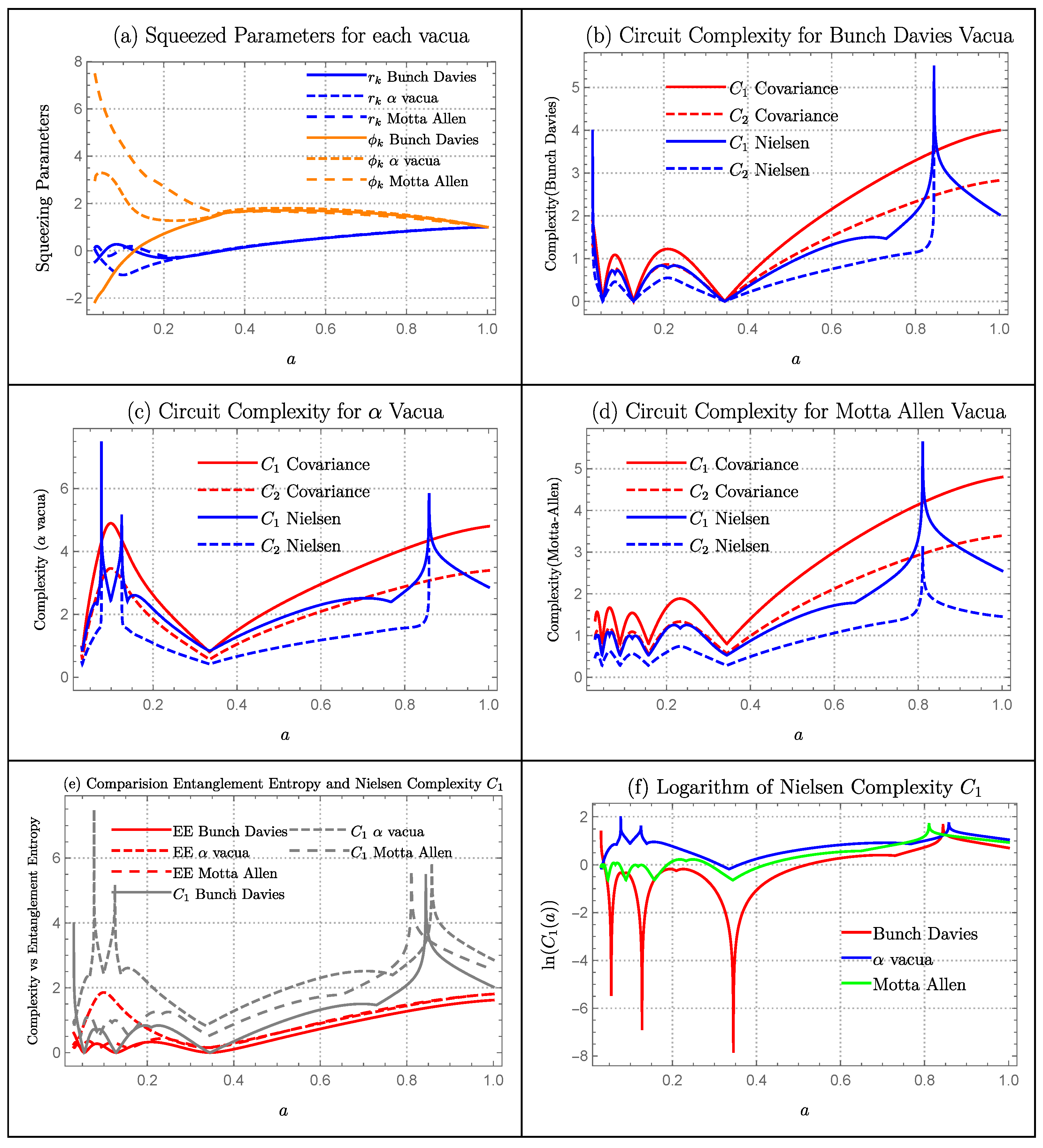
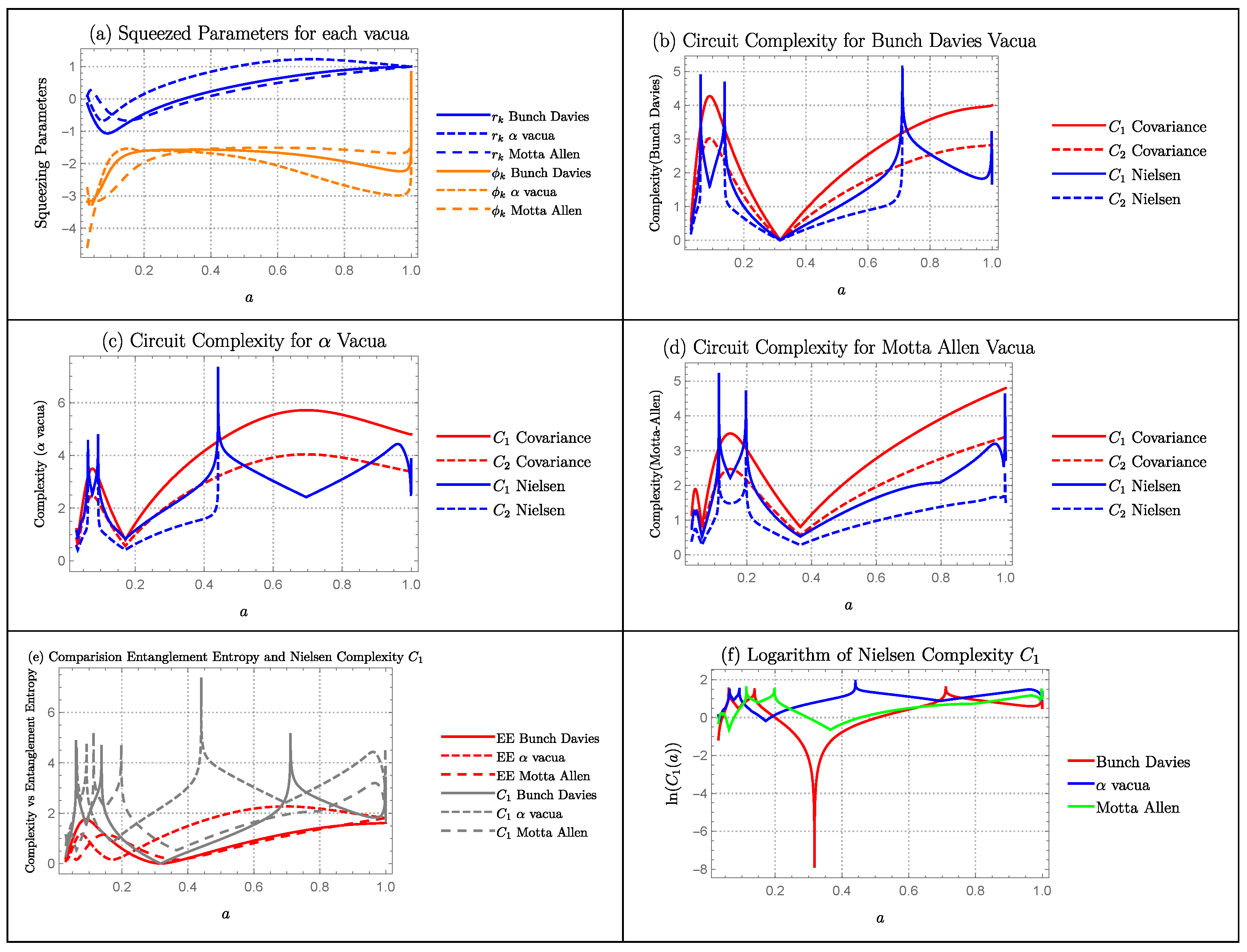
6.7. Cyclic Models
Squeezing Parameters
- 1.
- Matter cyclic model: In Figure 16a, we have plotted squeezing parameters and for each vacua using the parameters and . Before , is different for each vacua. However, after that point, they merge and starts to grow linearly. While before , is different for each vacua, after that point they merge and saturates.
- 2.
- Radiation cyclic model: In Figure 17a, we have plotted squeezing parameters and for each vacua using the parameters and . The value of grows for each vacua but with a different magnitude. vacua has the largest magnitude while Bunch-Davies and Motta-Allen have comparable values of . At early values of a, grows for each vacua and saturates. However at around , all three vacua merges and takes a sharp growth.
Complexity Measure
- 1.
- Matter cyclic model: For Bunch-Davies and Motta-Allen Vacua, covariance measure of complexity has a similar pattern but with different magnitude. Until , it is oscillatory in nature with small magnitude. After which, it takes a linear growth. For vacua, complexity grows at early values of a, then take a dip at , and then grows linearly. Nielsen’s measure of complexity also has a similar pattern as covariance but has a peak around .
- 2.
- Radiation cyclic model: Covariance measure of complexity has the similar pattern for all three vacua. It grows at early values of a, then take a dip and then grows linearly. The point of dip is different for each vacua. However, Nielsen’s measure of complexity has more details coming from peaks at different values of a.
Comparison of Entanglement Entropy with Complexity
- 1.
- Matter Cyclic Model: Both entanglement entropy and complexity measure has similar growth pattern. However, complexity measure has more peaks visible around .
- 2.
- Radiation Cyclic Model: Both entanglement entropy and complexity measure has similar growth pattern. However, complexity measure has more peaks. This shows that complexity measure is able to carry more details regarding the system compared to matter cyclic model.
Quantum Lyapunov Exponent
- 1.
- Matter Cyclic Model:Bunch-Davies Vacua has the largest lyapunov exponent, so it is the most chaotic cosmological model followed by Motta-Allen and vacua.
- 2.
- Radiation Cyclic Model:
6.8. Black Hole Gas
Squeezing Parameters
Complexity Measure
Comparison of Entanglement Entropy with Complexity
Quantum Lyapunov Exponent
7. Conclusions
- Compared to that calculated using the covariance matrix method, the circuit complexity computed using Nielsen’s wave function approach offers a much better understanding because it relies on the squeezing angle and the squeezing parameter and can therefore be linked to the entanglement entropy.
- We have computed the circuit complexity using both Nielsen’s wave function approach and Covariance matrix approach. From the study of both approaches to compute complexity in different cosmological models, it is clear that the overall pattern one obtain is similar in both cases. However, the circuit complexity computed from Nielsen’s wave function approach gives a much detailed understanding of the evolution of the system. The reason is that covariance measure of complexity is insensitive to the squeezing angle.
- The behaviour of the squeezing parameter is also different for each vacua: Bunch-Davies, vacua and Motta-Allen Vacua. The reason for this is that dispersion relation for each vacua is different. So, while solving the set of differential equations, we will get different solutions for the squeezing parameter.
- We have computed the circuit complexity for all three vacua: Bunch-Davies, vacua and Motta-Allen Vacua. Because the dispersion relation for each vacua is different, the solutions for the squeezing parameter is also different. This has the direct consequence in the properties of complexity measure. In addition, Motta-Allen and vacua have more parameters than the simple Bunch-Davies vacua. This is also reflected in the complexity measure. Most of the times, Motta-Allen vacua has the largest complexity magnitude followed by vacua and then Bunch-Davies vacua.
- The behavior of the entanglement entropy is also different for each vacua. Again, this is the result of having different set of solutions for the squeezing parameter. The values of entanglement entropy is bounded by the covariance measure of complexity and . Entanglement entropy has the similar pattern as the covariance measure of complexity because both are independent of the squeezing angle . However, entanglement entropy has the different behaviour than the Nielsen’s measure of complexity. We are able to see more details in the complexity that is not visible in entanglement entropy growth. This shows that, complexity could also be a probe to detect important properties of a quantum system just like entanglement entropy. Since entanglement entropy is sometimes ridiculously difficult to compute, complexity could be a better alternative at those cases.
- The behaviour of circuit complexity is very dependent on the model and scale factor involved. For example: Nielsen’s measure of complexity is extremely oscillatory for models like Polynomial bounce and Sinehyperbolic bounce while very smooth for models like de-Sitter.
- We have made qualitative comments on the relation between growth of complexity and quantum chaos. It would be interesting to see if it can be rigorously proven. One way could be to use the quantum speed limit properties to show the bound on complexity. Using Random Matrix theory, one can associate the bound on quantum speed limit to quantum chaos.
- For the framework of two-mode squeezed states, quantum complexity computed using Covariance matrix show similar feature that of entanglement entropy. It would be interesting to see if this holds true for other models.
- The relation between entanglement entropy and complexity can be studied in even more detail.
- In this paper, we have only studied the complexity measure for various cosmological models. It would be interesting to apply the lesson from these complexity plots to study the physical evolution of these models and observe to what extent it actually matches. Furthermore, concrete experimental prediction would be much desirable.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Role of Squeezing in the Dispersion Relation for PGW
Appendix A.1. Sub-Hubble Limiting Result
Appendix A.2. Super-Hubble Limiting Result
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Cavalieri, R. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Guzzetti, M.C.; Bartolo, N.; Liguori, M.; Matarrese, S. Gravitational waves from inflation. Riv. Nuovo Cim. 2016, 39, 399–495. [Google Scholar]
- Mather, J.C.; Cheng, E.S.; Eplee, R.E., Jr.; Isaacman, R.B.; Meyer, S.S.; Shafer, R.A.; Wilkinson, D.T. A Preliminary Measurement of the Cosmic Microwave Background Spectrum by the Cosmic Background Explorer (COBE) Satellite. Astrophys. J. 1990, 354, L37. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Savelainen, M. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Roudier, G. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum: Astron. Astrophys. 2021, 652, C4. [Google Scholar]
- Baumann, D. Tasi Lectures on Inflation. arXiv 2012, arXiv:0907.5424. [Google Scholar]
- Baumann, D. Tasi lectures on primordial cosmology. arXiv 2018, arXiv:1807.03098. [Google Scholar]
- Mukhanov, V.; Winitzki, S. Introduction to Quantum Effects in Gravity; Cambridge University Press: Cambridge, UK, 2007; p. 6. [Google Scholar]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Grishchuk, L.P.; Sazhin, M.V. Squeezed quantum states of a harmonic oscillator in the problem of gravitational wave detection. Sov. Phys. JETP 1983, 57, 1128–1135. [Google Scholar]
- Guth, A.H.; Pi, S.-Y. The Quantum Mechanics of the Scalar Field in the New Inflationary Universe. Phys. Rev. D 1985, 32, 1899–1920. [Google Scholar] [CrossRef]
- Grishchuk, L.P.; Sidorov, Y.V. On the Quantum State of Relic Gravitons. Class. Quant. Grav. 1989, 6, L161–L165. [Google Scholar] [CrossRef]
- Grishchuk, L.P.; Sidorov, Y.V. Squeezed quantum states of relic gravitons and primordial density fluctuations. Phys. Rev. D 1990, 42, 3413–3421. [Google Scholar] [CrossRef]
- Albrecht, A.; Ferreira, P.; Joyce, M.; Prokopec, T. Inflation and squeezed quantum states. Phys. Rev. D 1994, 50, 4807–4820. [Google Scholar] [CrossRef] [PubMed]
- Barnett, S.M.; Radmore, P.M. Methods in Theoretical Quantum Optics; Oxford Series in Optical and Imaging Sciences; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Allen, B.; Flanagan, E.E.; Papa, M.A. Is the squeezing of relic gravitational waves produced by inflation detectable? Phys. Rev. D 2000, 61, 024024. [Google Scholar] [CrossRef]
- Bose, S.; Grishchuk, L.P. On the observational determination of squeezing in relic gravitational waves and primordial density perturbations. Phys. Rev. D 2002, 66, 043529. [Google Scholar] [CrossRef]
- Baskaran, D.; Grishchuk, L.P.; Zhao, W. Primordial Gravitational Waves and Cosmic Microwave Background Radiation. In Proceedings of the 12th Marcel Grossmann Meeting on General Relativity, UNESCO Headquarters, Paris, France, 12–18 July 2009; Volume 4. [Google Scholar]
- Chapman, S.; Marrochio, H.; Myers, R.C. Complexity of Formation in Holography. JHEP 2017, 1, 62. [Google Scholar] [CrossRef]
- Chapman, S.; Marrochio, H.; Myers, R.C. Holographic complexity in Vaidya spacetimes. Part I. JHEP 2018, 6, 46. [Google Scholar] [CrossRef]
- Chapman, S.; Marrochio, H.; Myers, R.C. Holographic complexity in Vaidya spacetimes. Part II. JHEP 2018, 6, 114. [Google Scholar] [CrossRef]
- Caceres, E.; Chapman, S.; Couch, J.D.; Hernandez, J.P.; Myers, R.C.; Ruan, S.-M. Complexity of Mixed States in QFT and Holography. JHEP 2020, 3, 12. [Google Scholar] [CrossRef]
- Bernamonti, A.; Galli, F.; Hernandez, J.; Myers, R.C.; Ruan, S.-M.; Simón, J. Aspects of The First Law of Complexity. arXiv 2020, arXiv:2002.05779. [Google Scholar] [CrossRef]
- Bai, C.; Li, W.-H.; Ge, X.-H. Towards the non-equilibrium thermodynamics of the complexity and the Jarzynski identity. arXiv 2021, arXiv:2107.08608. [Google Scholar]
- Doroudiani, M.; Naseh, A.; Pirmoradian, R. Complexity for Charged Thermofield Double States. JHEP 2020, 1, 120. [Google Scholar] [CrossRef]
- Jefferson, R.; Myers, R.C. Circuit complexity in quantum field theory. JHEP 2017, 10, 107. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Nandy, P.; Sinha, A. Renormalized Circuit Complexity. Phys. Rev. Lett. 2020, 124, 101602. [Google Scholar] [CrossRef] [PubMed]
- Guo, M.; Hernandez, J.; Myers, R.C.; Ruan, S.-M. Circuit Complexity for Coherent States. JHEP 2018, 10, 11. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, X. Circuit Complexity for Fermionic Thermofield Double states. Phys. Rev. D 2019, 99, 026011. [Google Scholar] [CrossRef]
- Khan, R.; Krishnan, C.; Sharma, S. Circuit Complexity in Fermionic Field Theory. Phys. Rev. D 2018, 98, 126001. [Google Scholar] [CrossRef]
- Hackl, L.; Myers, R.C. Circuit complexity for free fermions. JHEP 2018, 7, 139. [Google Scholar] [CrossRef]
- Camargo, H.A.; Heller, M.P.; Jefferson, R.; Knaute, J. Path integral optimization as circuit complexity. Phys. Rev. Lett. 2019, 123, 011601. [Google Scholar] [CrossRef] [PubMed]
- Stanford, D.; Susskind, L. Complexity and Shock Wave Geometries. Phys. Rev. D 2014, 90, 126007. [Google Scholar] [CrossRef]
- Brown, A.R.; Roberts, D.A.; Susskind, L.; Swingle, B.; Zhao, Y. Holographic Complexity Equals Bulk Action? Phys. Rev. Lett. 2016, 116, 191301. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.R.; Roberts, D.A.; Susskind, L.; Swingle, B.; Zhao, Y. Complexity, action, and black holes. Phys. Rev. D 2016, 93, 086006. [Google Scholar] [CrossRef]
- Brown, A.R.; Susskind, L. Second law of quantum complexity. Phys. Rev. D 2018, 97, 086015. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Das, S.; Haque, S.S.; Underwood, B. Rise of cosmological complexity: Saturation of growth and chaos. Phys. Rev. Res. 2020, 2, 033273. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Das, S.; Haque, S.S.; Underwood, B. Cosmological Complexity. Phys. Rev. D 2020, 101, 106020. [Google Scholar] [CrossRef]
- Lehners, J.-L.; Quintin, J. Quantum Circuit Complexity of Primordial Perturbations. Phys. Rev. D 2021, 103, 063527. [Google Scholar] [CrossRef]
- Bhargava, P.; Choudhury, S.; Chowdhury, S.; Mishara, A.; Selvam, S.P.; Panda, S.; Pasquino, G.D. Quantum aspects of chaos and complexity from bouncing cosmology: A study with two-mode single field squeezed state formalism. SciPost Phys. Core 2021, 4, 26. [Google Scholar] [CrossRef]
- Choudhury, S.; Chowdhury, S.; Gupta, N.; Mishara, A.; Selvam, S.P.; Panda, S.; Pasquino, G.D.; Singha, C.; Swain, A. Circuit Complexity from Cosmological Islands. Symmetry 2021, 13, 1301. [Google Scholar] [CrossRef]
- Rangamani, M.; Takayanagi, T. Holographic Entanglement Entropy; Springer: Cham, Switzerland, 2017; Volume 931. [Google Scholar]
- Calabrese, P.; Cardy, J.L. Entanglement entropy and quantum field theory. J. Stat. Mech. 2004, 0406, P06002. [Google Scholar] [CrossRef]
- Maldacena, J.; Pimentel, G.L. Entanglement entropy in de Sitter space. JHEP 2013, 2, 038. [Google Scholar] [CrossRef]
- Arias, C.; Diaz, F.; Sundell, P. De Sitter Space and Entanglement. Class. Quant. Grav. 2020, 37, 015009. [Google Scholar] [CrossRef]
- Iizuka, N.; Noumi, T.; Ogawa, N. Entanglement entropy of de Sitter space α-vacua. Nucl. Phys. B 2016, 910, 23–29. [Google Scholar] [CrossRef]
- Matsumura, A.; Nambu, Y. Large scale quantum entanglement in de Sitter spacetime. Phys. Rev. D 2018, 98, 025004. [Google Scholar] [CrossRef]
- Adhikari, K.; Choudhury, S.; Chowdhury, S.; Shirish, K.; Swain, A. Circuit Complexity as a novel probe of Quantum Entanglement: A study with Black Hole Gas in arbitrary dimensions. arXiv 2021, arXiv:2104.13940. [Google Scholar] [CrossRef]
- Brahma, S.; Alaryani, O.; Brandenberger, R. Entanglement entropy of cosmological perturbations. Phys. Rev. D 2020, 102, 043529. [Google Scholar] [CrossRef]
- Eisert, J. Entangling Power and Quantum Circuit Complexity. Phys. Rev. Lett. 2021, 127, 020501. [Google Scholar] [CrossRef]
- Allen, B. Vacuum States in de Sitter Space. Phys. Rev. D 1985, 32, 3136. [Google Scholar] [CrossRef]
- Tagirov, E.A. Consequences of field quantization in de Sitter type cosmological models. Ann. Phys. 1973, 76, 561–579. [Google Scholar] [CrossRef]
- Chernikov, N.A.; Tagirov, E.A. Quantum theory of scalar fields in de Sitter space-time. Ann. Inst. Henri Poincare Phys. Theor. A 1968, 9, 109. [Google Scholar]
- Mottola, E. Particle Creation in de Sitter Space. Phys. Rev. D 1985, 31, 754. [Google Scholar] [CrossRef]
- Choudhury, S. The Cosmological OTOC: Formulating new cosmological micro-canonical correlation functions for random chaotic fluctuations in Out-of-Equilibrium Quantum Statistical Field Theory. Symmetry 2020, 9, 1527. [Google Scholar] [CrossRef]
- Choudhury, S. The Cosmological OTOC: A New Proposal for Quantifying Auto-correlated Random Non-chaotic Primordial Fluctuations. Symmetry 2021, 4, 599. [Google Scholar] [CrossRef]
- Orús, R. Tensor networks for complex quantum systems. APS Phys. 2019, 1, 538–550. [Google Scholar] [CrossRef]
- Choudhury, S.; Dutta, A.; Ray, D. Chaos and Complexity from Quantum Neural Network: A study with Diffusion Metric in Machine Learning. JHEP 2021, 4, 138. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Jafari, G.; Naseh, A. First law of holographic complexity. Phys. Rev. D 2020, 102, 106008. [Google Scholar] [CrossRef]
- Nielsen, M.A. A geometric approach to quantum circuit lower bounds. arXiv 2005, arXiv:quant-ph/0502070. [Google Scholar] [CrossRef]
- Nielsen, M.A. Quantum computation as geometry. Science 2006, 311, 1133–1135. [Google Scholar] [CrossRef]
- Dowling, M.R.; Nielsen, M.A. The geometry of quantum computation. Quantum Inf. Comput. 2008, 8, 861–899. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Dowling, M.R.; Gu, M.; Doherty, A.C. Optimal control, geometry, and quantum computing. Phys. Rev. A 2006, 73, 062323. [Google Scholar] [CrossRef]
- D’Alessio, L.; Kafri, Y.; Polkovnikov, A.; Rigol, M. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 2016, 65, 239–362. [Google Scholar] [CrossRef]
- Maldacena, J.; Shenker, S.H.; Stanford, D. A bound on chaos. JHEP 2016, 8, 106. [Google Scholar] [CrossRef]
- Maldacena, J.; Stanford, D. Remarks on the Sachdev-Ye-Kitaev model. Phys. Rev. D 2016, 94, 106002. [Google Scholar] [CrossRef]
- Sekino, Y.; Susskind, L. Fast Scramblers. JHEP 2008, 10, 065. [Google Scholar] [CrossRef]
- Shenker, S.H.; Stanford, D. Black holes and the butterfly effect. JHEP 2014, 3, 067. [Google Scholar] [CrossRef]
- Ali, T.; Bhattacharyya, A.; Haque, S.S.; Kim, E.H.; Moynihan, N.; Murugan, J. Chaos and Complexity in Quantum Mechanics. Phys. Rev. D 2020, 101, 026021. [Google Scholar] [CrossRef]
- Munoz, J.B.; Kamionkowski, M. Equation-of-State Parameter for Reheating. Phys. Rev. D 2015, 91, 043521. [Google Scholar] [CrossRef]
- Liu, X.-J.; Zhao, W.; Zhang, Y.; Zhu, Z.-H. Detecting Relic Gravitational Waves by Pulsar Timing Arrays: Effects of Cosmic Phase Transitions and Relativistic Free-Streaming Gases. Phys. Rev. D 2016, 93, 024031. [Google Scholar] [CrossRef]
- Brandenberger, R.H. Cosmology of the Very Early Universe. AIP Conf. Proc. 2010, 1268, 3–70. [Google Scholar]
- Brandenberger, R.H. The Matter Bounce Alternative to Inflationary Cosmology. arXiv 2012, arXiv:1206.4196. [Google Scholar]
- Bramberger, S.F.; Lehners, J.-L. Nonsingular bounces catalyzed by dark energy. Phys. Rev. D 2019, 99, 123523. [Google Scholar] [CrossRef]
- Gao, X.; Wang, Y.; Xue, W.; Brandenberger, R. Fluctuations in a Hořava-Lifshitz Bouncing Cosmology. JCAP 2010, 2010, 20. [Google Scholar] [CrossRef]
- Koehn, M.; Lehners, J.-L.; Ovrut, B.A. Cosmological super-bounce. Phys. Rev. D 2014, 90, 025005. [Google Scholar] [CrossRef]
- Koehn, M.; Lehners, J.-L.; Ovrut, B. Nonsingular bouncing cosmology: Consistency of the effective description. Phys. Rev. D 2016, 93, 103501. [Google Scholar] [CrossRef]
- Mathur, S.D. Three puzzles in cosmology. Int. J. Mod. Phys. D 2020, 29, 2030013. [Google Scholar] [CrossRef]
- Mathur, S.D. The Information paradox: A Pedagogical introduction. Class. Quant. Grav. 2009, 26, 224001. [Google Scholar] [CrossRef]
- Horowitz, G.T.; Polchinski, J. A Correspondence principle for black holes and strings. Phys. Rev. D 1997, 55, 6189–6197. [Google Scholar] [CrossRef]
- Veneziano, G. A Model for the big bounce. JCAP 2004, 2004, 4. [Google Scholar] [CrossRef]
- Fischler, W.; Susskind, L. Holography and cosmology. arXiv 1988, arXiv:hep-th/9806039. [Google Scholar]
- Ali, T.; Bhattacharyya, A.; Haque, S.S.; Kim, E.H.; Moynihan, N. Time Evolution of Complexity: A Critique of Three Methods. J. High Energy Phys. 2019, 4, 87. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adhikari, K.; Choudhury, S.; Pandya, H.N.; Srivastava, R. Primordial Gravitational Wave Circuit Complexity. Symmetry 2023, 15, 664. https://doi.org/10.3390/sym15030664
Adhikari K, Choudhury S, Pandya HN, Srivastava R. Primordial Gravitational Wave Circuit Complexity. Symmetry. 2023; 15(3):664. https://doi.org/10.3390/sym15030664
Chicago/Turabian StyleAdhikari, Kiran, Sayantan Choudhury, Hardey N. Pandya, and Rohan Srivastava. 2023. "Primordial Gravitational Wave Circuit Complexity" Symmetry 15, no. 3: 664. https://doi.org/10.3390/sym15030664
APA StyleAdhikari, K., Choudhury, S., Pandya, H. N., & Srivastava, R. (2023). Primordial Gravitational Wave Circuit Complexity. Symmetry, 15(3), 664. https://doi.org/10.3390/sym15030664





