Abstract
The study of the flows of curves is one of the most fascinating research areas in differential geometry. In this paper, we investigate the geometry of the flows of timelike curves according to the quasi-frame in Minkowski space (In this paper, we refer to these curves as “quasi-timelike curves”). We investigate the evolution of quasi-timelike curves using the velocity functions and obtain the necessary and sufficient conditions for inextensibility. Additionally, we obtain the explicit forms of the time evolution equations for the quasi-orthonormal frames (tangent, quasi-normal, and quasi-binormal vectors) of the quasi-timelike curve as well as the time evolution equations of their quasi-curvatures. We present a new application for motion with velocities equal to the quasi-curvatures of the quasi-timelike curve. In this application, the time evolution equations of the quasi-curvatures arise as a system of partial differential equations with the form of the heat equation, and by solving this system, we visualize the evolution of quasi-curvatures and the evolution of the quasi-timelike curve. In addition, the acceleration functions are used to investigate the flows of inextensible quasi-timelike curves, and an application for accelerations equal to the quasi-curvatures is given. Through this application, the position vector of the quasi-timelike curve satisfies the one-dimensional wave equation, and the time evolution equations of the quasi-curvatures arise as a system of transport equations. We obtain the solutions and graph them using Wolfram Mathematica 12.
MSC:
35C08; 51B20; 53A04; 53A17; 53A35; 53B20; 53C50; 53E10; 53Z0
1. Introduction
The theories of curves and surfaces are essential topics in differential geometry. They have diverse applications in many fields of science, such as physics, engineering, and image processing. Researchers have studied the motion and integrability of curves widely. Geometric characterizations of the integrable curves and the evolution of inelastic plane curves have been extensively studied in [,,,,].
The study of the flows of curves in Euclidean space has attracted the interest of many researchers. Hasimoto [] studied the motion of a vortex filament (smoke ring) and obtained the equations of the time evolution of the curves. In [], the inextensible flows of curves (IFC) that move according to the type Bishop frame in were studied. In [], a general formulation for IFC on an oriented surface in was derived. In [], the motion of curves in was studied, and the time evolution equations for the given orthonormal Frenet frame and for the higher curvatures were derived. In [], the surfaces were generated by the motion of IFC in according to the Frenet frame. The geometric properties of these surfaces were described and visualized.
In [], the dynamics of inextensible flows for adjoint curves in three-dimensional Euclidean space were investigated. A new method for the inextensible flows of adjoint curves using the Frenet frame was constructed, and the ferromagnetic and antiferromagnetic chain equations were given as an application. Gaber [] constructed new models of the normal motions of inextensible curves that are moving according to the type Bishop frame in . In [], an analysis was presented for the acceleration and jerk vectors of particles that are moving along a space curve in three-dimensional Euclidean space. Based on the quasi-frame, the alternative resolutions of the accelerations and jerks were derived by applying this resolution and Siacci’s theorem. An acceleration vector was resolved in the osculating plane by summing its tangential and radial components. In the rectifying and osculating planes, the jerk vector was also resolved along the tangential direction and two special radial directions. According to the jerk vector formula, the maximum permissible speed on a space curve was determined at all trajectory points.
The flows of curves in Minkowski space and De Sitter space have been investigated by many authors. In [], the soliton solutions to the KdV equation were studied, and a motion of spacelike curves in was described. In [], the IFC of nonnull curves was investigated in n-dimensional pseudo-Euclidean space according to the Frenet frame. Gaber [] studied and described the binormal motions of curves in De Sitter space and constructed Hasimoto surfaces. In [], a new type of Bishop frame called “Type Bishop Frame” was introduced by using the binormal vector field of a regular curve. A new spherical image called type Bishop spherical images was introduced by translating type Bishop frame vectors into the center of the unit sphere of three-dimensional Euclidean space.
In [], a new method was constructed for inextensible flows of timelike curves in a conformally flat, quasi-conformally flat, and conformally symmetric 4-dimensional LP-Sasakian manifold. The necessary and sufficient condition for the timelike curve to be inextensible was derived. Some characterizations were given for the curvatures of the timelike curve in a conformally flat, quasi-conformally flat, and conformally symmetric 4-dimensional LP-Sasakian manifold. Moreover, the flows of some associated curves of timelike curves were obtained. In [], some conditions for nonnull curve flows to be inextensible in the 6-dimensional Lorentzian space were studied. The family of inextensible nonnull curves was characterized by partial differential equations.
The flows of curves in Galilean space have been discussed by many researchers. In [], the flows of curves were investigated in the pseudo-Galilean three-dimensional space and its equiform geometry without any constraints, and the motions were described in terms of the inviscid and viscous Burgers’ equations. In [], the inextensible flows of curves in three-dimensional pseudo-Galilean space were studied. The necessary and sufficient conditions for the inextensible flows of curves were derived according to equiform geometry in pseudo-Galilean space. In [], the inextensible flows of curves in three-dimensional Galilean space were investigated by using the Sabban frame, and the necessary and sufficient conditions for inextensible flows were derived. In [], Fermi–Walker derivatives for inextensible curve flows were investigated in three-dimensional Galilean space . A novel approach to these flows was expressed using Frenet and Darboux frames with the help of Fermi–Walker derivatives. Sorour [] studied the inextensible flows of focal curves associated with tube-like surfaces in Galilean three-dimensional space and gave some characterizations for the curvatures of the focal curves associated with tube-like surfaces.
The main purpose of the current work is to investigate the geometric flows of timelike curves by using the quasi-frame in Minkowski space . Through this work, we derive the evolution of quasi-timelike curves by velocity and acceleration functions. In addition, we give some new applications with certain types of velocity and acceleration functions. In these applications, we choose the velocity and acceleration functions equal to the quasi-curvatures of the quasi-timelike curve. We obtain and visualize the evolution of the quasi-timelike curve and the evolution of the quasi-curvatures.
The present work is organized as follows: In Section 2, some geometric concepts of timelike curves in Minkowski space are given according to the Frenet frame and the quasi frame. In Section 3, the main results and discussions for the time evolution equations (TEEs) for quasi-timelike curves (QTIC) in are obtained. In Section 4, an application on the motion of QTIC by velocity fields is given. In Section 6, the inextensible flows of the QTIC via acceleration fields are presented, and an application of the motion of the QTIC by acceleration fields is provided. Finally, we give our conclusions.
2. Basic Geometric Concepts of Timelike Curves in Minkowski Space
Definition 1.
The three dimensional Minkowski space is the real vector space provided with the Lorentzian inner product given by with []. Consider the vectors , where , the inner product is defined by , and the vector product is defined by . The vector is spacelike if , timelike if , and null (lightlike) if . The signature of the vector u is 1 if u is spacelike, if u is timelike, and 0 if u is lightlike.
Definition 2.
Let , be a regular parameterized curve in . Then, α is []:
Definition 3.
The angle between any two nonnull vectors X and Y is defined in [] according to the classification of vectors in as follows:
- Let X and Y be spacelike vectors ; if X and Y span a timelike vector subspace, then , and there is a unique positive real number θ such thatwhere the real number θ is called the Lorentz timelike angle between X and Y.
- Let X and Y be spacelike vectors in that span a spacelike vector subspace; then, there is a unique real number , such thatwhere the real number θ is called the Lorentz spacelike angle between X and Y.
- Let X and Y be future pointing (past pointing) timelike vectors in ; then, there is a unique nonnegative real number θ, such thatwhere the real number θ is called the Lorentz timelike angle between X and Y.
- Let X be a spacelike vector and Y a future pointing timelike vector in ; then, there is a unique nonnegative real number , such thatwhere the real number θ is called the Lorentz timelike angle between X and Y.
2.1. Frenet Frame for Timelike Curves in
The Frenet frame is the most famous adapted frame for curves. It plays a significant role in investigating curves and tube surfaces in the classical differential geometry of curves.
Definition 4.
Let be the parameter of the timelike curve α and define as the arc length of the regular parameterized timelike curve α by []
For a regular timelike curve α, we define by If for all , then the timelike curve called an arc-length parameterized curve ( ).
Definition 5.
Let α be an arc-length parameterized timelike curve. Assume , where . Define the unit tangent vector T, the unit principal normal vector N, and the unit binormal vector B to the timelike curve α, and let be the Frenet–Serret frame for the timelike curve α. The Frenet–Serret frame in satisfies the following properties []:
- ,, , , and
- , and .
- where k and τ are the curvature and torsion for the timelike curve, respectively.
Lemma 1.
Let be the timelike curve in , then the Frenet–Serret equations are given by []:
where
2.2. Quasi-Frame for Timelike Curves in
The Frenet–Serret frame is inadequate to study space curves when the curvatures have discrete zero points. To solve this problem, we use a quasi-frame and a formula that corresponds to the Frenet–Serret equations. We study the timelike curves according to a quasi-frame (q-frame) and we call them the quasi-timelike curve (QTIC). The q-frame has some advantages, such as that it can be defined even along the tangent line equal to zero. Moreover, whether or not the space curve has unit speed does not affect the construction of the q-frame. In addition, the q-frame can be easily calculated.
Definition 6.
Let be the parameter of the timelike curve α. The q-frame consists of three orthonormal vectors , where T is the unit tangent vector, is the quasi-normal vector, and is the quasi-binormal vector. The q-frame is defined by []:
where u is the projection vector, and for simplicity, we can choose it as the unit vector .
Definition 7.
Let be the q-frame of the timelike curve on a point p, and let be the Frenet frame at the same point p on the same timelike curve. The relation between these frames is defined in [] by:
or
Definition 8.
The q-frame has the following properties []:
Definition 9.
The relation between the curvature k and torsion τ of the timelike curve specified by the Frenet frame and the curvatures and specified by the q-frame are defined in [] by:
In this paper, we call , and quasi-curvatures, and they are defined by:
3. Main Results and Discussion
Time Evolution Equations for the Quasi-Timelike Curves (QTIC) in
Theorem 1.
Let be the QTIC with a spacelike quasi-normal vector and a spacelike quasi-binormal vector ; then,
Proof.
The tangent vector T is the same tangent vector in both frames (the Frenet frame and the quasi-frame), where
Substituting (5) and (7) into (11),
From (4), we have
Taking the derivative of (13) and using (2), (4), and (7), we obtain:
From (4), we have
Taking the s-derivative of (15), and using (2), (4), and (7),
From (12), (14), and (16), the theorem holds. □
Definition 10.
Let be the initial QTIC in , where s is the arc length and it is defined by (1). Assume that the curve moves with the time parameter t. The family of curves represents the flows of the QTIC at different time values, and it can be defined as . The time evolution equation that describes the motion of the QTIC according to the q-frame in is expressed by the velocity functions , and as follows:
where , and are the velocity functions in the direction of the tangent vector T, the quasi-normal vector , and the quasi binormal vector . In this study, we call the q-tangential velocity, the q-normal velocity, and the q-binormal velocity.
Theorem 2.
The TEEs for the q-frame in are given by:
and the TEEs for the quasi-curvatures , and are:
where
Proof.
Since by differentiating this equation with respect to v we obtain:
Taking the derivative of (21) with respect to t, we have:
Differentiating (17) with respect to v, we have:
For simplicity, we choose:
Then,
Applying the compatibility condition () for Equations (22) and (25), we obtain:
and
Taking the derivative of (27) with respect to v and by a straightforward computation, we obtain:
From (10), we have ; by taking the derivative of this equation, we obtain:
Substituting (28) and (29) into the compatibility condition (), we obtain:
and
To determine and explicitly, we assume that:
By using the properties of the q-frame that are given in Definition 8, we obtain
Substituting (33) into (32), we have:
Substituting (34) into (31), we obtain:
Assuming that and ; then . Hence, we obtain
Since , we have:
By taking the t-derivative of (38) and then using (27) and (37), we obtain:
Taking the v-derivative of (36),
We apply the compatibility condition () for the Equations (39) and (40). By using the properties of the q-frame in Definition 8,
Hence,
Based on the above, the theorem holds. □
4. An Application for the Motion of the QTIC by Velocity Fields
Consider the inextensible flows of the QTIC, and assume that . Suppose that the QTIC evolves with q-tangential velocity ; then from (41), we have . Substituting in (42), we obtain the TEEs for the quasi-curvatures:
From (44), we have
Substituting (46) into (45),
Now, we study the case when and . Then, the TEEs (47) for the quasi-curvatures and take the form of heat equations:
One solution of the system (48) takes the following form:
Hence, the curve is defined by their quasi-curvatures , , and ; these curvatures are illustrated in Figure 1 and Figure 2.
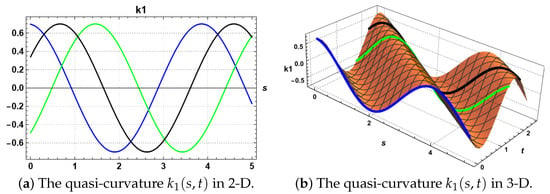
Figure 1.
The time evolution of the quasi-curvature of the QTIC and its evolution in 2-D and 3-D for , , , and . The blue, green, and black curves represent the flows of the quasi-curvatures of the QTIC at time , respectively.
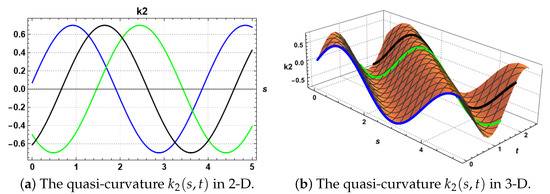
Figure 2.
The time evolution of the quasi-curvature of the QTIC and its evolution in 2-D and 3-D for , , , and . The blue, green, and black curves represent the flows of the quasi-curvatures of the QTIC at time , respectively.
Substituting (49) into (9), (10), (17), and (18) and solving the PDE systems numerically, we can determine and plot the surface that is generated by the flows of the QTIC. It is important to use the properties of the q-frame defined by Definition 8, which can be rewritten explicitly as:
The conditions (50) are necessary to validate the general solution. The surface generated by the motion of the QTIC is illustrated in Figure 3.
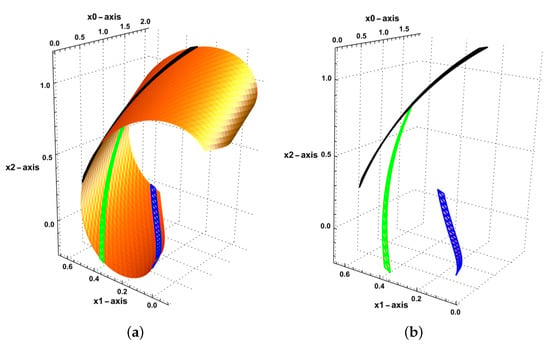
Figure 3.
The evolution of the QTIC via velocity functions () for , , , and . The blue, green, and black curves represent the flows of the QTIC at time , respectively. (a) The evolution of the QTIC for and time ; (b) the evolution of the QTIC for at time .
Figure 1a represents the evolution of the first quasi-curvature of the QTIC for different time values at in two dimensions. Figure 1b represents the three-dimensional graph of the first quasi-curvature of the QTIC for and , , and . The blue, green, and black curves represent the flows of the QTIC at time , respectively. It is obvious that the flows of the first quasi-curvature had a forward shift with increasing time, but the shape did not change.
Figure 2a represents the evolution of the second quasi-curvature of the QTIC for some different time values at in two dimensions. Figure 2b represents the three-dimensional graph of the second quasi-curvature of the QTIC for and , , and . The blue, green, and black curves represent the flows of the QTIC at time , respectively. We note that the flows of the second quasi-curvature had a forward shift with increasing time, but the shape did not change.
5. The Flows of the QTIC via the Acceleration Fields
Let be the initial inextensible QTIC in . Let be the family of curves, it represents the flows of the QTIC, where , and t represents the time parameter. Assume that the inextensible QTIC evolves by the acceleration fields and in the direction of the q-tangent vector T, q-normal vector , and q-principal binormal vector , where are functions in the quasi-curvatures and their derivatives. The QTIC evolves according to the acceleration fields in the q-frame by the following law:
Lemma 3.
Proof.
We differentiate (17) with respect to t; then, we have:
Substituting (18) and (20) into (54). Hence (52) holds.
Another relation between the velocity fields and acceleration fields can be given as follows: Taking the s-derivative of (51), we obtain
Since , then . Taking the second derivative of the first equation of (18) with respect to t and using (18), we have:
Since the QTIC is inextensible, the compatibility condition is satisfied, equating (55) and (56). Hence, (53) holds. □
An Application for the Motion of the QTIC by the Acceleration Fields
Assume that is the QTIC evolving by the accelerations functions:
Assume ; then, the TEE described by (51) takes the form:
Since , then the third equation of (42) gives:
Substituting (61) into (60), hence , and , and the PDE system (59) takes the form of transport equations:
This system of transport equations has the following general solution:
where and are arbitrary functions.
This represents the one-dimensional wave equation. If we consider the initial conditions and , we obtain the general solution of the form:
In this application, we take the following initial conditions:
Then, we obtain the general solution:
The evolution represents the family of quasi-timelike curves for different time values t. This family of QTIC is plotted for different time values in Figure 4.
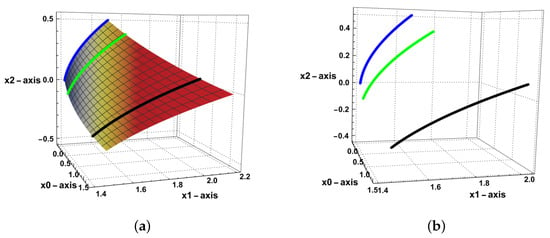
Figure 4.
The evolution of the QTIC via accelerations ( and ) for and . The blue, green, and black curves represent the quasi-curvatures of the QTIC at time , respectively. (a) The evolution of the QTIC for and time ; (b) The evolution of the QTIC for at time .
Figure 4a represents the evolution of the QTIC described by the acceleration functions ( and ) for and . The blue, green, and black curves in Figure 4b represent the evolution of the QTIC at time , respectively.
We consider the QTIC with the parametrization (68); the first and second quasi-curvatures and given by (63) can be computed using (3) and (8); hence:
We can verify the solutions by using the properties of the q-frame in Definition 8, where the QTIC (68) satisfies the following PDEs:
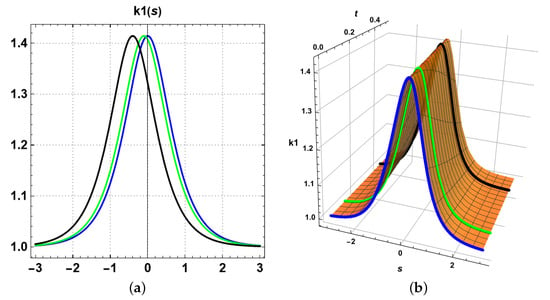
Figure 5.
The time evolution of the quasi-curvatures of the QTIC, in 2-D and 3-D for and . The blue, green, and black curves represent the quasi-curvature of the QTIC at time , respectively. (a) The 2-D graph for the evolution of at ; (b) the 3-D graph for the evolution of for and .
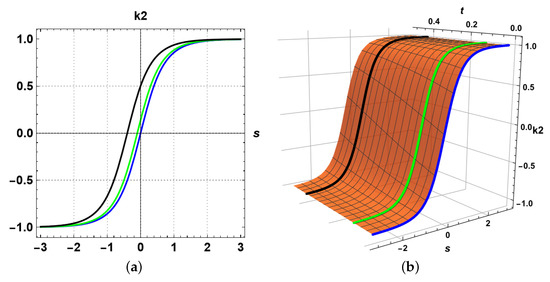
Figure 6.
The time evolution of the quasi-curvatures of the QTIC, in 2-D and 3-D for and . The blue, green, and black curves represent the quasi-curvature of the QTIC at time , respectively. (a) The 2-D graph for the evolution of at ; (b) the 3-D graph for the evolution of for and .
Figure 5a represents the evolution of the first quasi-curvature of the QTIC for different time values at in two dimensions. Figure 5b represents the three-dimensional graph of the flows of the first quasi-curvature for and . The blue, green, and black curves represent the evolution of the first quasi-curvature at time , respectively. It is obvious that the evolution of the first quasi-curvature had a right shift with an increase in time, and the shape did not change.
Figure 6a represents the evolution of the second quasi-curvature of the QTIC for some different time values at in two dimensions. Figure 6b represents the three-dimensional graph of the flows of the second quasi-curvature for and . The blue, green, and black curves represent the evolution of the second quasi-curvature at time , respectively. There was not any obvious shift for the evolution of the second quasi-curvature with the increase in time, and the shape did not change.
6. Discussion
The study of the evolution of curves is an attractive research topic in differential geometry. In this paper, we investigated the flows of timelike curves in Minkowski space according to a quasi-frame, which we called “quasi-timelike curves”. The quasi-frame is an important frame in the study of the evolution of curves; it is very effective at the points where the curvature of the curve vanishes. In this work, the motion of quasi-timelike curves was specified by velocity and acceleration. The equations of the evolution of the quasi-frame and the evolution of the curvatures (we called them quasi-curvatures) were derived, and some applications were given. In these applications, partial differential equations played an important role in describing the motion of the QTIC. They arose in the form of heat equations and transport equations. Moreover, the flows of the QTIC satisfied the one-dimensional wave equation. With the aid of Wolfram Mathematica 12, we obtained the solutions of these partial differential equations and graphed them.
7. Conclusions
The present paper investigated the motion of the quasi-timelike curve (QTIC) in Minkowski space . The results of this paper are summarized as follows:
- 1.
- We studied the motion of the QTIC by the velocity fields , and , with the equation of motion , where , and represented the velocity functions in the direction of the q- frame .
- 2.
- The time evolution equations (TEEs) for the q-frame of the QTIC in Minkowski space were derived, and the TEEs for the quasi-curvatures and were obtained as a system of PDEs (Theorem 2).
- 3.
- 4.
- We studied the motion of the QTIC described by the acceleration fields with the equation of motion .
- 5.
- 6.
- Through the given applications, we presented the description of the graphs, which indicated the flows of the quasi-timelike curves and their first and second quasi-curvatures.
Author Contributions
Software, S.G.; Investigation, S.G. and A.H.S.; Writing—original draft, S.G. and A.H.S.; Writing—review and editing, A.H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Ambitious Researcher Track (Grant No.2972).
Data Availability Statement
No data were used to support this study.
Acknowledgments
This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Ambitious Researcher Track. Project No. GRANT 2972), King Faisal University (KFU), AL-Ahsa, Saudi Arabia. The authors, therefore, acknowledge the technical and financial support of the DSR at KFU.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| (2-D) | Two dimensions. |
| (3-D) | Three dimensions. |
| IFC | Inextensible flows of curves. |
| PDE(s) | Partial Differential Equation(s) |
| q-frame | Quasi-frame. |
| QTIC | Quasi-timelike curve. |
| TEEs | Time evolution equations. |
References
- Nakayama, K.; Wadati, M. Motion of curves in the plane. J. Phys. Soc. JPN 1993, 62, 473–479. [Google Scholar] [CrossRef]
- Nakayama, K.; Segur, H.; Wadati, M. Integrability and the motion of curves. Phys. Rev. Lett. 1992, 69, 2603–2606. [Google Scholar] [CrossRef] [PubMed]
- Abdel-All, N.H.; Hussien, R.A.; Youssef, T. Evolution of curves via the velocities of the moving frame. J. Math. Comput. Sci. 2012, 2, 1170–1185. [Google Scholar]
- Doliwa, A.; Santini, P. An elementary geometric characterization of the integrable motions of a curve. Phys. Lett. A 1994, 185, 373–384. [Google Scholar] [CrossRef]
- Kwon, D.Y.; Park, F.C. Evolution of inelastic plane curves. Appl. Math. Lett. 1999, 12, 115–119. [Google Scholar] [CrossRef]
- Hasimoto, H. A soliton on a vortex filament. J. Fluid Mech. 1972, 52, 477–485. [Google Scholar] [CrossRef]
- Kızıltuğ, S. On characterization of inextensible flows of curves according to type-2 Bishop Frame in . Math. Comput. Appl. 2014, 19, 69–77. [Google Scholar]
- Yıldız, O.G.; Ersoy, S.; Masal, M. A Note on inextensible flows of curves on oriented Surface. CUBO A Math. J. 2014, 16, 11–19. [Google Scholar] [CrossRef]
- Abdel All, N.; Mohamed, S.; Al-Dossary, M. Evolution of generalized space curve as a function of its local geometry. Appl. Math. 2014, 5, 2381–2392. [Google Scholar] [CrossRef]
- Hussien, R.; Gaber, S. Generated surfaces via inextensible flows of curves in . J. Appl. Math. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Selçuk, B. A new method for inextensible flows of adjoint curves in space. AIP Con. Proc. 2019, 2116, 240003. [Google Scholar]
- Gaber, S. New models of normal motions of the inextensible curves according to type-1 Bishop frame in . Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150009. [Google Scholar]
- Elshenhab, A.M.; Moaaz, O.; Dassios, I.; Elsharkawy, A. Motion along a Space Curve with a Quasi-Frame in Euclidean 3-Space: Acceleration and Jerk. Symmetry 2022, 14, 1610. [Google Scholar] [CrossRef]
- Ding, Q.; Wang, W.; Wang, Y. A motion of spacelike curves in the Minkowski 3-space and the KdV equation. Phys. Lett. A 2010, 374, 3201–3205. [Google Scholar] [CrossRef]
- Yıldız Ö., G.; Tosun, M. A note on inextensible flows of curves in . Int. Electron. J. Geom. 2013, 6, 118–124. [Google Scholar]
- Gaber, S. Binormal motions of inextensible curves in de-sitter space . J. Egypt. Math. Soc. 2017, 25, 313–318. [Google Scholar]
- Yılmaz, S.; Turgut, M. A new version of Bishop frame and an application to spherical images. J.Math. Anal. Appl. 2010, 371, 764–776. [Google Scholar] [CrossRef]
- Korpinar, T.; Turgut, M. A new method for inextensible flows of timelike curves in 4-dimensional LP-Sasakian manifolds. Asian-Eur. J. Math. 2015, 8, 1550073. [Google Scholar] [CrossRef]
- Aslan, M.C.; Unluturk, Y. The evaluation of the conditions for the non-null curves to be Inextensible in Lorentzian 6-Space. Kyungpook Math. J. 2021, 61, 805–812. [Google Scholar] [CrossRef]
- Suleyman, C.; Ozturk, E.; Ozturk, U. Motions of curves in the Pseudo-Galilean Space . Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Oztekin, H.; Bozok, H.G. Inextensible flows of curves in the Equiform Geometry of the pseudo-Galilean space . WMS J. App. Eng. Math. 2016, 6, 175–184. [Google Scholar]
- Bozok, H.G. Inextensible flows of curves according to Sabban frame in Galilean space . J. Univers. Math. 2019, 2, 75–81. [Google Scholar] [CrossRef]
- Bozok, H.G.; Sertkol, I.N. A note on inextensible flows of curves with fermi-walker derivative in Galilean space . Honam Math. J. 2020, 42, 769–780. [Google Scholar] [CrossRef]
- Sorour, A.H. A study of the inextensible flows of tube-like surfaces associated with focal curves in Galilean 3-space . Stud. Univ. Babeş-Bolyai Math. 2017, 62, 341–352. [Google Scholar] [CrossRef]
- López, R.l. Differential geometry of curves and surfaces in Lorentz-Minkowski space. Int. Electron. J. Geom. 2014, 7, 44–107. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, X.S. Classification of timelike constant slope Surfaces in 3-Dimensional Minkowski spaces. Results Math. 2013, 63, 1095–1108. [Google Scholar] [CrossRef]
- Yavuz, A. A Dynamical approach to position vector of timelike Curve by Vectorial Momentum, Torque and Tangential Dual Curve. J. Nonlinear Math. Phys. 2022, 29, 818–842. [Google Scholar] [CrossRef]
- Ekici, C.; Göksel, M.; Mustafa, D. Smarandache curves according to q-Frame in Minkowski 3-Space. Conf. Proc. Sci. Technol. 2019, 2, 110–118. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).