Numerical Analysis of the Time-Fractional Boussinesq Equation in Gradient Unconfined Aquifers with the Mittag-Leffler Derivative

Abstract

In this study, two numerical methods—the variational iteration transform method (VITM) and the Adomian decomposition (ADM) method—were used to solve the second- and fourth-order fractional Boussinesq equations. Both methods are helpful in approximating non-linear problems effectively, easily, and accurately. The fractional Atangana–Baleanu operator and ZZ transform were utilized to derive solutions for the equation. Two examples are discussed to validate the methods and solutions. The results demonstrate that both the VITM and ADM methods are effective in obtaining accurate and reliable solutions for the time-fractional Boussinesq equation.

1. Introduction

Fractional differential equations are mathematical models that describe the behaviors of dynamic systems where the order of differentiation is not an integer. Unlike traditional differential equations, which use integer derivatives to describe changes in a system over time, fractional differential equations use fractional derivatives to account for the non-integer rate of the change in a system [1,2]. This approach is useful for describing complex systems that involve memory effects, long-term persistence, and anomalous diffusion, as well as modeling real-world phenomena, such as turbulence, viscoelasticity, and fractional diffusion [3,4].

Applications of fractional differential equations span a wide range of fields, including physics, engineering, finance, and biology. In physics, fractional differential equations have been used to describe the behaviors of viscoelastic materials, such as rubber and biological tissues, which exhibit non-Newtonian behavior and respond differently to changes in stress and strain compared to traditional materials [5,6,7]. In engineering, fractional differential equations have been used to model the behaviors of complex systems, such as electrical circuits and control systems, where the order of differentiation cannot be described by an integer derivative. In finance, fractional differential equations have been used to model the price dynamics of financial assets, such as stocks and bonds, which exhibit persistent behavior and long-term dependencies [8,9,10]. In biology, fractional differential equations have been used to describe the diffusion of molecules, cells, and pathogens, which exhibit anomalous behaviors and do not follow traditional Fickian diffusion laws.

Symmetry is a fundamental concept in mathematics and physics, and it can be used to simplify the solution of partial differential equations (PDEs). In particular, the use of symmetry in the solutions of fractional PDEs can greatly simplify the mathematical analyses and lead to exact or approximate solutions [11,12,13]. Symmetry can be used to reduce the number of independent variables in a fractional PDE, which can simplify the solution process. Additionally, symmetry can be used to obtain solutions that are invariant under certain transformations, such as translations, rotations, and scaling. This can lead to solutions that are more physically meaningful and easier to interpret. Overall, symmetry is a powerful tool for solving fractional PDEs and can greatly aid in understanding the underlying physical phenomena [14,15,16]. There are several important references that provide an overview of fractional differential equations and their applications. A comprehensive overview of fractional calculus, fractional differential equations, and their applications in various fields are thoroughly discussed in [17,18]. The theory of fractional differential equations and their applications in the field of viscoelasticity has been analyzed [19,20].

The Boussinesq equation is a mathematical model used to describe the behaviors of fluid systems. It is a partial differential equation that relates fluid flow velocity and pressure. The equation was first introduced by Joseph Valentin Boussinesq in 1872 and has been widely used in many engineering and scientific fields, including hydrology, oceanography, and geology [21,22,23]. The traditional Boussinesq equation is a second-order equation and has been widely used for many years to study the behaviors of fluid systems. However, the study of fluid systems became more complex, leading to more sophisticated mathematical models. This has led to the development of time-fractional Boussinesq equations [24,25,26].

The second and fourth-order time-fractional Boussinesq equations are extensions of the traditional Boussinesq equation; they take into account the fractional order derivative of time in their formulations. The fractional derivative of time represents the non-local and non-Markovian behaviors of the fluid system and provides a better description of the behavior of the fluid system compared to the traditional Boussinesq equation. The second-order time-fractional Boussinesq equation is linear, while the fourth-order time-fractional Boussinesq equation is nonlinear [27]. These equations have been used to study the behaviors of complex fluid systems, such as turbulent flows, waves, and heat transfer, and they have proven to be more accurate and reliable than the traditional Boussinesq equation [28].

The variational iteration transform method (VITM) is a numerical technique used to solve nonlinear partial differential equations. It is a relatively new method that has gained popularity in recent years due to its simplicity and effectiveness in solving a wide range of problems [29,30]. The VITM is based on the concept of variational iteration, which is a powerful tool for solving nonlinear problems. The method involves transforming the original equation into a new form that is easier to solve, and then using an iterative process to find the solution. The VITM has been applied successfully to a variety of problems, including nonlinear boundary value problems, nonlinear differential equations, and fractional differential equations [31,32].

The fractional partial differential equation is a type of mathematical equation that describes the behavior of complex systems with memory and nonlocal effects. It is a generalization of the classical partial differential equation and can be used to model a wide range of physical, biological, and engineering processes [33,34]. The fractional derivative is a nonlocal operator that captures the long-range memory effects of the system and is defined using the Riemann–Liouville or the Caputo fractional derivative. The VITM starts with a guess function and then iteratively improves it using the variational principle. The first step is to convert the fractional partial differential equation into a nonlinear integral equation by using the fractional derivative operator. Then, the guess function is used to approximate the solution of the integral equation and the residual is calculated. The residual is then used to update the guess function in the next iteration. The iteration continues until the residual is small enough to satisfy a desired level of accuracy [35,36]. The VITM has several advantages over other numerical methods for solving FPDEs. It is simple to implement, does not require the solution of linear systems, and has a fast convergence rate. It is also flexible and can be applied to a wide range of FPDEs with different boundary conditions. Furthermore, it can be easily extended to solve systems of FPDEs and to incorporate additional constraints. In conclusion, the VITM is a powerful and efficient numerical technique for solving fractional partial differential equations. It has been widely used in various scientific and engineering fields and has proven to be a valuable tool for modeling complex systems with memory and nonlocal effects [37].

The Adomian decomposition transform method is a numerical technique used to solve fractional partial differential equations (FPDEs). FPDEs are mathematical models that describe physical phenomena with non-integer order derivatives, and they are widely used in fields such as physics, engineering, and finance. The Adomian decomposition transform method is an innovative approach to solving FPDEs, as it combines the advantages of both the Adomian decomposition and the Laplace Transform methods [38,39]. The Adomian decomposition transform method involves dividing the solution domain into sub-domains and transforming the FPDEs into a set of algebraic equations. These equations are then solved using numerical methods, such as finite difference and finite element methods. The solution is then transformed back to the original domain, and the solution is obtained by combining the solutions from each sub-domain [40].

The Adomian decomposition transform method has been applied to various types of FPDEs, including time-fractional diffusion equations, space-fractional diffusion equations, and coupled fractional partial differential equations. The method is efficient and accurate, and it has been used to study various physical and engineering problems, such as heat transfer, fluid flow, and financial modeling [41].

The manuscript is organized as follows: Basic definitions, theorems, and their proofs are mentioned in Section 2. The proposed methods are thoroughly discussed in Section 3 and Section 4. In Section 5, two examples are presented for validation of the proposed methods. The conclusion is discussed in Section 6.

2. Preliminaries

Definition 1. 

The Aboodh transformation of functions is achieved by

$$B=\left\{\mathit{U}\left(\varrho \right):\exists M,n_1,n_2>0,\left|\mathit{U}\left(\varrho \right)\right|<M{e}^{-\epsilon \varrho }\right\}$$

and is expressed as [42,43]

$$A\left\{\mathit{U}\left(\varrho \right)\right\}=\frac{1}{\epsilon }{\int }_0^{\infty }\mathit{U}\left(\varrho \right)e^{-\epsilon \varrho }d\varrho ,\varrho >0\mathrm{and}{n}_1\le \epsilon \le n_2.$$

Theorem 1. 

Let us examine G and F as the Laplace and Aboodh transformations of $\mathit{U}\left(\varrho \right)$ in the set B [44,45]

$$G\left(\epsilon \right)=\frac{F\left(\epsilon \right)}{\epsilon }.$$

(1)

The ZZ transformation, introduced by Zain Ul Abadin Zafar [46], is a generalization of the Laplace and Aboodh integral transformations. The definition of the ZZ transform is as follows:

Definition 2. 

(ZZ Transformation) The Z-transform $Z(\kappa ,\epsilon )$ of the function $\mathit{U}\left(\varrho \right)$ for all values of $\varrho \ge 0$ can be represented as follows [46]

$$ZZ\left(\mathit{U}\left(\varrho \right)\right)=Z(\kappa ,\epsilon )=\epsilon {\int }_0^{\infty }\mathit{U}\left(\kappa \varrho \right)e^{-\epsilon \varrho }d\varrho .$$

Similar to the Laplace and Aboodh transforms, the Z-transform is also linear in nature. The Mittag-Leffler function (MLF), on the other hand, is an expansion of the exponential function.

$$E_{\delta }\left(z\right)=\sum _{m=0}^{\infty }\frac{z^m}{\mathrm{\Gamma }(1+m\delta )},Re\left(\delta \right)>0.$$

Definition 3. 

The Atangana–Baleanu Caputo derivative of a function $\mathit{U}(\phi ,\varrho )$ belonging to the space $H^1(a,b)$ is defined as follows for $\mathrm{ß}\in$$(0,1)$ [47]

$${ABC}_a{D}_{\varrho }^{\mathrm{ß}}\mathit{U}(\phi ,\varrho )=\frac{B(\mathrm{ß})}{1-\mathrm{ß}}{\int }_a^{\varrho }{\mathit{U}}^{\prime }(\phi ,\varrho )E_{\mathrm{ß}}\left(\frac{-\mathrm{ß}{(\varrho -\eta )}^{\mathrm{ß}}}{1-\mathrm{ß}}\right)d\eta .$$

Definition 4. 

The Atangana–Baleanu Riemann–Liouville derivative, denoted as $\mathit{U}(\phi ,\varrho )$, is a member of the space $H^1(a,b)$. For any value of ß within the interval $(0,1)$, the derivative can be expressed as [47]

$${}_a^{ABR}{D}_{\varrho }^{\mathrm{ß}}\mathit{U}(\phi ,\eta )=\frac{B(\mathrm{ß})}{1-\mathrm{ß}}\frac{d}{d\varrho }{\int }_a^{\varrho }\mathit{U}(\phi ,\eta )E_{\mathrm{ß}}\left(\frac{-\mathrm{ß}{(\varrho -\eta )}^{\mathrm{ß}}}{1-\mathrm{ß}}\right)d\eta .$$

The function $B(\mathrm{ß})$ has the property that it evaluates to 1 for both 0 and 1. Furthermore, the value of $B(\mathrm{ß})$ is always greater than a when ß is greater than 0.

Theorem 2. 

We attain the ZZ and Aboodh transformations of $\mathit{U}\left(\varrho \right)\in B$, represented as $G\left(\epsilon \right)$ and $Z(\kappa ,\epsilon )$, respectively [45]

$$Z(\kappa ,\epsilon )=\frac{{\epsilon }^2}{{\kappa }^2}G\left(\frac{\epsilon }{\kappa }\right)$$

Proof. 

According to the Z-transform definition,

$$Z(\kappa ,\epsilon )=\epsilon {\int }_0^{\infty }\mathit{U}\left(\kappa \varrho \right)e^{-\epsilon \varrho }d\varrho$$

(2)

By substituting $\kappa \varrho =\varrho$ into Equation (2), we obtain

$$Z(\kappa ,\epsilon )=\frac{\epsilon }{\kappa }{\int }_0^{\infty }\mathit{U}\left(\varrho \right)e^{-\frac{\pi z}{\kappa }}d\varrho$$

(3)

The expression on the right side of Equation (3) can be rephrased as

$$Z(\kappa ,\epsilon )=\frac{\epsilon }{\kappa }F\left(\frac{\epsilon }{\kappa }\right).$$

(4)

By utilizing Theorem 2.1, Equation (4) can be reinterpreted as the Laplace transformation of $\mathit{U}\left(\varrho \right)$, represented as $F(.)$.

$$Z(\kappa ,\epsilon )=\frac{\epsilon }{\kappa }\frac{F\left(\frac{\epsilon }{\kappa }\right)}{\left(\frac{\epsilon }{\kappa }\right)}\times \left(\frac{\epsilon }{\kappa }\right)={\left(\frac{\epsilon }{\kappa }\right)}^{2}G\left(\frac{\epsilon }{\kappa }\right).$$

(5)

The Aboodh transformation, represented by $G(.)$, transforms the function $\mathit{U}\left(\varrho \right)$. □

Theorem 3. 

The $\mathrm{ZZ}$ transformation of $\mathit{U}\left(\varrho \right)={\varrho }^{\mathrm{ß}-1}$ is define as

$$Z(\kappa ,\epsilon )=\mathrm{\Gamma }(\mathrm{ß}){\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}-1}$$

(6)

Proof. 

The Aboodh transformation of $\mathit{U}\left(\varrho \right)={\varrho }^{\mathrm{ß}},\mathrm{ß}\ge 0$ is

$$G\left(\epsilon \right)=\frac{\mathrm{\Gamma }(\mathrm{ß})}{{\epsilon }^{\mathrm{ß}+1}}$$

$$\mathrm{Now},G\left(\frac{\epsilon }{\kappa }\right)=\frac{\mathrm{\Gamma }(\mathrm{ß}){\kappa }^{\mathrm{ß}+1}}{{\epsilon }^{\mathrm{ß}+1}}.$$

Applying Equation (6), we achieve:

$$Z(\kappa ,\epsilon )=\frac{{\epsilon }^2}{{\kappa }^2}G\left(\frac{\epsilon }{\kappa }\right)=\frac{{\epsilon }^2}{{\kappa }^2}\frac{\mathrm{\Gamma }(\mathrm{ß}){\kappa }^{\mathrm{ß}+1}}{{\epsilon }^{\mathrm{ß}+1}}=\mathrm{\Gamma }(\mathrm{ß}){\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}-1}$$

□

Theorem 4. 

Let ß and ω be complex numbers and assume that the real part of ß is greater than 0. The $\mathrm{ZZ}$ transformation of $E_{\mathrm{ß}}\left(\omega {\varrho }^{\mathrm{ß}}\right)$ can be defined as [45]

$$ZZ\left\{\left(E_{\mathrm{ß}}\left(\omega {\varrho }^{\mathrm{ß}}\right)\right)\right\}=Z(\kappa ,\epsilon )={\left(1-\omega {\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}\right)}^{-1}$$

(7)

Proof. 

The Aboodh transformation of $E_{\mathrm{ß}}\left(\omega {\varrho }^{\mathrm{ß}}\right)$ is defined as follows:

$$G\left(\epsilon \right)=\frac{F\left(\epsilon \right)}{\epsilon }=\frac{{\epsilon }^{\mathrm{ß}-1}}{\epsilon \left({\epsilon }^{\mathrm{ß}}-\omega \right)}$$

(8)

So,

$$G\left(\frac{\epsilon }{\kappa }\right)=\frac{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}-1}}{\left(\frac{\epsilon }{\kappa }\right)\left({\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}-\omega \right)},$$

(9)

$$\begin{array}{c}Z(\kappa ,\epsilon )={\left(\frac{\epsilon }{\kappa }\right)}^{2}G\left(\frac{\epsilon }{\kappa }\right)={\left(\frac{\epsilon }{\kappa }\right)}^2\frac{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}-1}}{\left(\frac{\epsilon }{\kappa }\right)\left({\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}-\omega \right)}\\ =\frac{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}}{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}-\omega }={\left(1-\omega {\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}\right)}^{-1}.\end{array}$$

□

Theorem 5. 

The ZZ transform of the Atangana–Baleanu Caputo derivative can be defined as follows: If $G\left(\epsilon \right)$ and $Z(\kappa ,\epsilon )$ are the ZZ and Aboodh transformations of $\mathit{U}\left(\varrho \right)$, respectively [45]

$$ZZ\left\{\begin{array}{c}ABC\hfill \\ 0\hfill \end{array}{D}_{\varrho }^{\mathrm{ß}}\mathit{U}\left(\varrho \right)\right\}=\left[\frac{B(\mathrm{ß})}{1-\mathrm{ß}}\frac{\frac{{\epsilon }^{a+2}}{{\kappa }^{\mathrm{ß}+2}}G\left(\frac{\epsilon }{\kappa }\right)-\frac{{\epsilon }^{\mathrm{ß}}}{{\kappa }^{\mathrm{ß}}}f\left(0\right)}{\frac{{\epsilon }^{\mathrm{ß}}}{{\kappa }^{\mathrm{ß}}}+\frac{\mathrm{ß}}{1-\mathrm{ß}}}\right]$$

(10)

Proof. 

Applying Equation (1), we obtain:

$$G\left(\frac{\epsilon }{\kappa }\right)=\frac{\kappa }{\epsilon }\left[\frac{B(\mathrm{ß})}{1-\mathrm{ß}}\frac{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}+1}G\left(\frac{\epsilon }{\kappa }\right)-{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}-1}f\left(0\right)}{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}+\frac{\mathrm{ß}}{1-\mathrm{ß}}}\right]$$

(11)

The Atangana–Baleanu Caputo Z transformation is represented as follows:

$$\begin{array}{cc}\hfill Z(\kappa ,\epsilon )=& {\left(\frac{\epsilon }{\kappa }\right)}^{2}G\left(\frac{\epsilon }{\kappa }\right)={\left(\frac{\epsilon }{\kappa }\right)}^2\frac{\kappa }{\epsilon }\left[\frac{B(\mathrm{ß})}{1-\mathrm{ß}}\frac{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}+1}G\left(\frac{\epsilon }{\kappa }\right)-{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}-1}f\left(0\right)}{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}+\frac{\mathrm{ß}}{1-\mathrm{ß}}}\right]\hfill \\ & =\left[\frac{B(\mathrm{ß})}{1-\mathrm{ß}}\frac{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}+2}G\left(\frac{\epsilon }{\kappa }\right)-{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}f\left(0\right)}{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}+\frac{\mathrm{ß}}{1-\mathrm{ß}}}\right]\hfill \end{array}$$

□

Theorem 6. 

Let us assume that the ZZ transformation of $\mathit{U}\left(\varrho \right)$ is represented by $G\left(\epsilon \right)$ and the Aboodh transformation of $\mathit{U}\left(\varrho \right)$ is represented by $Z(\kappa ,\epsilon )$. Then, the ZZ transformation of the Atangana–Baleanu Riemann–Liouville derivative is defined as [45]

$$ZZ\left\{\begin{array}{c}ABR\hfill \\ 0\hfill \end{array}{D}_{\varrho }^{\mathrm{ß}}f\left(\varrho \right)\right\}=\left[\frac{B(\mathrm{ß})}{1-\mathrm{ß}}\frac{\frac{{\epsilon }^{\mathrm{ß}+2}}{{\kappa }^{\mathrm{ß}+2}}G\left(\frac{\epsilon }{\kappa }\right)}{\frac{{\epsilon }^{\mu }}{{\kappa }^{\mu }}+\frac{\mathrm{ß}}{1-\mathrm{ß}}}\right]$$

(12)

Proof. 

Applying Equation (1), we obtain:

$$G\left(\frac{\epsilon }{\kappa }\right)=\frac{\kappa }{\epsilon }\left[\frac{B(\mathrm{ß})}{1-\mathrm{ß}}\frac{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}+1}G\left(\frac{\epsilon }{\kappa }\right)}{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}+\frac{\mathrm{ß}}{1-\mathrm{ß}}}\right]$$

(13)

The ZZ transform of the Atangana–Baleanu Riemann–Liouville is expressed in Equation (5).

$$\begin{array}{cc}\hfill Z(\kappa ,\epsilon )={\left(\frac{\epsilon }{\kappa }\right)}^{2}G\left(\frac{\epsilon }{\kappa }\right)={\left(\frac{\epsilon }{\kappa }\right)}^2\left(\frac{\kappa }{\epsilon }\right)& \left[\frac{B(\mathrm{ß})}{1-\mathrm{ß}}\frac{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}+1}G\left(\frac{\epsilon }{\kappa }\right)}{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}+\frac{\mathrm{ß}}{1-\mathrm{ß}}}\right]\hfill \\ & =\left[\frac{B(\mathrm{ß})}{1-\mathrm{ß}}\frac{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}+2}G\left(\frac{\epsilon }{\kappa }\right)}{{\left(\frac{\epsilon }{\kappa }\right)}^{\mathrm{ß}}+\frac{\mathrm{ß}}{1-\mathrm{ß}}}\right]\hfill \end{array}$$

□

3. Methodology of ADTM

Consider the general application of ADTM to analyze the fractional partial differential equations.

$$D_{\wp }^{\mathrm{ß}}\mathit{U}(\phi ,\wp )+{\overline{\mathcal{G}}}_1(\phi ,\wp )+{\mathcal{N}}_1(\phi ,\wp )=\mathcal{F}(\phi ,\wp ),0<\mathrm{ß}\le 1,$$

(14)

with the initial conditions

$$\mathit{U}(\phi ,0)=\zeta \left(\phi \right),\frac{\partial }{\partial \wp }\mathit{U}(\phi ,0)=\zeta \left(\phi \right).$$

The fractional AB operator, represented by $D_{\wp }^{\mathrm{ß}}$, is a derivative of order ß with respect to ℘. It acts on linear operator ${\overline{\mathcal{G}}}_1$ and non-linear operator ${\mathcal{N}}_1$ and is applied to the source term $\mathcal{F}(\phi ,\wp )$.

By using the Z-transform method, we successfully

$$\mathit{Z}[D_{\wp }^{\mathrm{ß}}\mathit{U}(\phi ,\wp )+{\overline{\mathcal{G}}}_1(\phi ,\wp )+{\mathcal{N}}_1(\phi ,\wp )]=\mathit{Z}\left[\mathcal{F}(\phi ,\wp )\right].$$

(15)

By utilizing the differentiation property of ZZ, we obtain:

$$\mathit{Z}\left[\mathit{U}(\phi ,\wp )\right]=\mathit{U}(\phi ,\wp )-\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}[{\overline{\mathcal{G}}}_1(\phi ,\wp )+{\mathcal{N}}_1(\phi ,\wp )].$$

(16)

By applying the inverse Z-transform to (16), we obtain:

$$\mathit{U}(\phi ,\wp )=\mathit{U}(\phi ,\wp )-{\mathit{Z}}^{-1}\left\{\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}[{\overline{\mathcal{G}}}_1(\phi ,\wp )+{\mathcal{N}}_1(\phi ,\wp )]\right\}.$$

(17)

The solution to $\mathit{U}(\phi ,\wp )$ using the ADTM, can be expressed as an infinite sequence with the term $\mathrm{\Theta }(\phi ,\wp )$.

$$\mathit{U}(\phi ,\wp )=\sum _{m=0}^{\infty }{\mathit{U}}_m(\phi ,\wp ).$$

(18)

Decomposing the nonlinear operator ${\mathcal{N}}_1$

$${\mathcal{N}}_1(\phi ,\wp )=\sum _{m=0}^{\infty }{\mathcal{A}}_m.$$

(19)

Adomian polynomials, represented by ${\mathcal{A}}_m$, are determined by a specific method.

$${\mathcal{A}}_m=\frac{1}{m!}{\left[\frac{{\partial }^m}{\partial {\ell }^m}\left\{{\mathcal{N}}_1\left(\sum _{k=0}^{\infty }{\ell }^k{\phi }_k,\sum _{k=0}^{\infty }{\ell }^k{\wp }_k\right)\right\}\right]}_{\ell =0}.$$

(20)

By combining Equations (18) and (20) into Equation (17), the result is obtained

$$\sum _{m=0}^{\infty }{\mathit{U}}_m(\phi ,\wp )=\mathit{U}(\phi ,\wp )-{\mathit{Z}}^{-1}\left\{\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}[{\overline{\mathcal{G}}}_1(\sum _{m=0}^{\infty }{\phi }_m,\sum _{m=0}^{\infty }{\wp }_m)+\sum _{m=0}^{\infty }{\mathcal{A}}_m]\right\},$$

(21)

The given terms are derived.

$${\mathit{U}}_0(\phi ,\wp )=\mathit{U}(\phi ,\wp ),$$

(22)

$${\mathit{U}}_1(\phi ,\wp )={\mathit{Z}}^{-1}\left\{\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}[{\overline{\mathcal{G}}}_1({\phi }_0,{\wp }_0)+{\mathcal{A}}_0]\right\}.$$

For $m\ge 1$, the terms can be determined as follows:

$${\mathit{U}}_{m+1}(\phi ,\wp )={\mathit{Z}}^{-1}\left\{\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}[{\overline{\mathcal{G}}}_1({\phi }_m,{\wp }_m)+{\mathcal{A}}_m]\right\}.$$

4. Methodology of VITM

VITM is a method used to tackle fractional-order partial differential equations.

$$\begin{array}{cc}\hfill & D_{\wp }^{\delta }\mathit{U}(\phi ,\wp )+\mathcal{M}\mathit{U}(\phi ,\wp )+\mathcal{N}\mathit{U}(\phi ,\wp )-\mathcal{P}(\phi ,\wp )=0,m-1<\delta \le m,\hfill \end{array}$$

(23)

with the initial condition

$$\mathit{U}(\phi ,0)=g_1\left(\phi \right).$$

(24)

By using the Z-transform, we obtain:

$$\begin{array}{cc}\hfill & \mathit{Z}\left[D_{\wp }^{\delta }\mathit{U}(\phi ,\wp )\right]+\mathit{Z}[\mathcal{M}\mathit{U}(\phi ,\wp )+\mathcal{N}\mathit{U}(\phi ,\wp )-\mathcal{P}(\phi ,\wp )]=0.\hfill \end{array}$$

(25)

$D_{\wp }^{\delta }=\frac{{\partial }^{\delta }}{\partial {\wp }^{\delta }}$ represent the fractional AB operator of order $\delta$, $\mathcal{M}$ linear and $\mathcal{N}$ non-linear terms, respectively, and sources of function $\mathcal{P}$. By applying the principle of differentiation in ZZ, we obtain:

$$\begin{array}{cc}\hfill & \mathit{Z}\left[\mathit{U}(\phi ,\wp )\right]=\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\left[\mathcal{M}\mathit{U}(\phi ,\wp )+\mathcal{N}\mathit{U}(\phi ,\wp )-\mathcal{P}(\phi ,\wp )\right].\hfill \end{array}$$

(26)

The iteration technique for Equation (26)

$$\begin{array}{cc}\hfill & {\mathit{U}}_{m+1}(\phi ,\wp )={\mathit{U}}_m(\phi ,\wp )+\left[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\left[\mathcal{M}\mathit{U}(\phi ,\wp )+\mathcal{N}\mathit{U}(\phi ,\wp )-\mathcal{P}(\phi ,\wp )\right]\right].\hfill \end{array}$$

(27)

The solution using the inverse Z-transform and Equation (27) is presented in series form.

$${\mathit{U}}_0(\phi ,\wp )=\mathit{U}\left(0\right)+{\mathit{Z}}^{-1}\left[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}[-\mathcal{P}(\phi ,\wp )]\right],$$

$$\begin{array}{cc}\hfill & {\mathit{U}}_1(\phi ,\wp )={\mathit{Z}}^{-1}\left[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}[\mathcal{M}\mathit{U}(\phi ,\wp )+\mathcal{N}\mathit{U}(\phi ,\wp )]\right],\hfill \\ \hfill & ⋮\hfill \end{array}$$

$$\begin{array}{c}\hfill {\mathit{U}}_{n+1}(\phi ,\wp )={\mathit{Z}}^{-1}\left[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\left[\mathcal{M}\left[{\mathit{U}}_0(\phi ,\wp )+{\mathit{U}}_1(\phi ,\wp )+\dots ,{\mathit{U}}_n(\phi ,\wp )\right]\right]\right.\\ \hfill \left.+\mathcal{N}\left[{\mathit{U}}_0(\phi ,\wp )+{\mathit{U}}_1(\phi ,\wp ),\dots ,{\mathit{U}}_n(\phi ,\wp )\right]\right].\end{array}$$

5. Applications

5.1. Example

Consider the fractional fourth-order Boussinesq equation, given as [48]

$$D_{\wp }^{\mathrm{ß}}\mathit{U}(\phi ,\wp )=\delta D_{\phi }^4\mathit{U}(\phi ,\wp )+\gamma D_{\phi }^2\mathit{U}(\phi ,\wp )+\theta D_{\phi }^2{\mathit{U}}^2(\phi ,\wp )-4\theta {\mathit{U}}^2(\phi ,\wp )1<\mathrm{ß}\le 2,\wp >0,$$

(28)

with the initial condition

$$\mathit{U}(\phi ,0)=exp\left(\phi \right),{\mathit{U}}_{\wp }(\phi ,0)=0.$$

By the inverse ZZ transformation, we have

$$\mathit{U}(\phi ,\wp )=exp\left(\phi \right)+{\mathit{Z}}^{-1}\left[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\left[\delta D_{\phi }^4\mathit{U}(\phi ,\wp )+\gamma D_{\phi }^2\mathit{U}(\phi ,\wp )+\theta D_{\phi }^2{\mathit{U}}^2(\phi ,\wp )-4\theta {\mathit{U}}^2(\phi ,\wp )\right]\right].$$

(29)

The resolution of $\mathit{U}(\phi ,\wp )$ through ADTM can be described as an infinite sequence.

$$\mathit{U}(\phi ,\wp )=\sum _{m=0}^{\infty }{\mathit{U}}_m(\phi ,\wp ).$$

(30)

The Adomian polynomials $\mathit{U}\left(\mathit{U}\right)\phi \phi$ and ${\mathit{U}}^2$ represent the non-linear function and can be defined as the sum of an infinite number of terms, $\sum {m=0}^{\infty }\mathcal{A}m$ and $\sum {m=0}^{\infty }{\mathcal{B}}_m$, respectively.

$$\sum _{m=0}^{\infty }{\mathit{U}}_m(\phi ,\wp )=exp\left(\phi \right)+{\mathit{Z}}^{-1}\left[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\left[\delta D_{\phi }^4\mathit{U}(\phi ,\wp )+\gamma D_{\phi }^2\mathit{U}(\phi ,\wp )+\theta \sum _{m=0}^{\infty }{\mathcal{A}}_m-4\theta \sum _{m=0}^{\infty }{\mathcal{B}}_m\right]\right].$$

(31)

The calculation of nonlinear terms through the use of Adomian polynomials involves the decomposition process,

$$\begin{array}{cc}\hfill & {\mathcal{A}}_0={\left({\mathit{U}}_0^2\right)}_{\phi \phi },{\mathcal{A}}_1=2{\left({\mathit{U}}_0\right)}_{\phi \phi }{\left({\mathit{U}}_1\right)}_{\phi \phi },{\mathcal{A}}_2=2{\left({\mathit{U}}_0\right)}_{\phi \phi }{\left({\mathit{U}}_2\right)}_{\phi \phi }+{\left({\mathit{U}}_1^2\right)}_{\phi \phi },\hfill \\ \hfill & {\mathcal{B}}_0={\mathit{U}}_0^2,{\mathcal{B}}_1=2{\mathit{U}}_0{\mathit{U}}_1,{\mathcal{B}}_2=2{\mathit{U}}_0{\mathit{U}}_2+{\left({\mathit{U}}_1\right)}^2.\hfill \end{array}$$

(32)

Therefore, by comparing both sides of Equation (31).

$${\mathit{U}}_0(\phi ,\wp )=exp\left(\phi \right),$$

For $m=0$

$${\mathit{U}}_1(\phi ,\wp )=(\delta +\gamma )exp\left(\phi \right)\left[\frac{\mathrm{ß}{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+(1-\mathrm{ß})\right].$$

For $m=1$

$${\mathit{U}}_2(\phi ,\wp )={(\delta +\gamma )}^{2}exp\left(\phi \right)\left[\frac{{\mathrm{ß}}^2{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+2\mathrm{ß}(1-\mathrm{ß})\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^2\right].$$

For $m=2$

$${\mathit{U}}_3(\phi ,\wp )={(\delta +\gamma )}^{3}exp\left(\phi \right)\left[\frac{{\mathrm{ß}}^3{\wp }^{3\mathrm{ß}}}{\mathrm{\Gamma }(3\mathrm{ß}+1)}+3{\mathrm{ß}}^2(1-\mathrm{ß})\frac{{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+3\mathrm{ß}{(1-\mathrm{ß})}^2\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^3\right].$$

Therefore, the solution in series form is established:

$$\mathit{U}(\phi ,\wp )=\sum _{m=0}^{\infty }{\mathit{U}}_m(\phi ,\wp )={\mathit{U}}_0(\phi ,\wp )+{\mathit{U}}_1(\phi ,\wp )+{\mathit{U}}_2(\phi ,\wp )+{\mathit{U}}_3(\phi ,\wp )+\dots .$$

$$\begin{array}{cc}\hfill & \mathit{U}(\phi ,\wp )=exp\left(\phi \right)+(\delta +\gamma )exp\left(\phi \right)\left[\frac{\mathrm{ß}{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+(1-\mathrm{ß})\right]+{(\delta +\gamma )}^{2}exp\left(\phi \right)[\frac{{\mathrm{ß}}^2{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+2\mathrm{ß}(1-\mathrm{ß})\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+\hfill \\ \hfill & {(1-\mathrm{ß})}^2]+{(\delta +\gamma )}^{3}exp\left(\phi \right)\left[\frac{{\mathrm{ß}}^3{\wp }^{3\mathrm{ß}}}{\mathrm{\Gamma }(3\mathrm{ß}+1)}+3{\mathrm{ß}}^2(1-\mathrm{ß})\frac{{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+3\mathrm{ß}{(1-\mathrm{ß})}^2\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^3\right]+\dots .\hfill \end{array}$$

The solution to the problem with integer-order $\mathrm{ß}=1$ can be expressed as $\mathit{U}(\phi ,\wp )=exp\left(\phi +(\delta +\gamma )\wp \right)$.

By applying the VITM method, we can use the iteration formula in Equation (17) to further simplify the expression.

$$\begin{array}{cc}\hfill & {\mathit{U}}_{m+1}(\phi ,\wp )={\mathit{U}}_m(\phi ,\wp )-{\mathit{Z}}^{-1}[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\{\frac{B(\mathrm{ß})}{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}\delta D_{\phi }^4{\mathit{U}}_m(\phi ,\wp )+\gamma D_{\phi }^2{\mathit{U}}_m(\phi ,\wp )+\hfill \\ \hfill & \theta D_{\phi }^2{\mathit{U}}_m^2(\phi ,\wp )-4\theta {\mathit{U}}_m^2(\phi ,\wp )\left\}\right],\hfill \end{array}$$

(33)

where

$${\mathit{U}}_0(\phi ,\wp )=exp\left(\phi \right).$$

For $m=0,1,2,\dots$

$$\begin{array}{cc}\hfill & {\mathit{U}}_1(\phi ,\wp )={\mathit{U}}_0(\phi ,\wp )-{\mathit{Z}}^{-1}[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\{\frac{B(\mathrm{ß})}{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}\delta D_{\phi }^4{\mathit{U}}_0(\phi ,\wp )+\gamma D_{\phi }^2{\mathit{U}}_0(\phi ,\wp )+\hfill \\ \hfill & \theta D_{\phi }^2{\mathit{U}}_0^2(\phi ,\wp )-4\theta {\mathit{U}}_0^2(\phi ,\wp )\left\}\right],\hfill \\ \hfill & {\mathit{U}}_1(\phi ,\wp )=(\delta +\gamma )exp\left(\phi \right)\left[\frac{\mathrm{ß}{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+(1-\mathrm{ß})\right],\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & {\mathit{U}}_2(\phi ,\wp )={\mathit{U}}_1(\phi ,\wp )-{\mathit{Z}}^{-1}[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\{\frac{B(\mathrm{ß})}{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}\delta D_{\phi }^4{\mathit{U}}_1(\phi ,\wp )+\gamma D_{\phi }^2{\mathit{U}}_1(\phi ,\wp )+\hfill \\ \hfill & \theta D_{\phi }^2{\mathit{U}}_1^2(\phi ,\wp )-4\theta {\mathit{U}}_1^2(\phi ,\wp )\left\}\right],\hfill \\ \hfill & {\mathit{U}}_2(\phi ,\wp )={(\delta +\gamma )}^{2}exp\left(\phi \right)\left[\frac{{\mathrm{ß}}^2{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+2\mathrm{ß}(1-\mathrm{ß})\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^2\right],\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & {\mathit{U}}_3(\phi ,\wp )={\mathit{U}}_2(\phi ,\wp )-{\mathit{Z}}^{-1}[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\{\frac{B(\mathrm{ß})}{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}\delta D_{\phi }^4{\mathit{U}}_2(\phi ,\wp )+\gamma D_{\phi }^2{\mathit{U}}_2(\phi ,\wp )+\hfill \\ \hfill & \theta D_{\phi }^2{\mathit{U}}_2^2(\phi ,\wp )-4\theta {\mathit{U}}_2^2(\phi ,\wp )\left\}\right],\hfill \\ \hfill & {\mathit{U}}_3(\phi ,\wp )={(\delta +\gamma )}^{3}exp\left(\phi \right)\left[\frac{{\mathrm{ß}}^3{\wp }^{3\mathrm{ß}}}{\mathrm{\Gamma }(3\mathrm{ß}+1)}+3{\mathrm{ß}}^2(1-\mathrm{ß})\frac{{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+3\mathrm{ß}{(1-\mathrm{ß})}^2\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^3\right].\hfill \end{array}$$

(36)

The series form solution of the given example is

$$\begin{array}{cc}\hfill & \mathit{U}(\phi ,\wp )=\sum _{m=0}^{\infty }{\mathit{U}}_m(\phi ,\wp )={exp}^{\phi }+(\delta +\gamma )exp\left(\phi \right)\left[\frac{\mathrm{ß}{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+(1-\mathrm{ß})\right]+{(\delta +\gamma )}^{2}exp\left(\phi \right)[\frac{{\mathrm{ß}}^2{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}\hfill \\ \hfill & +2\mathrm{ß}(1-\mathrm{ß})\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^2]+{(\delta +\gamma )}^{3}exp\left(\phi \right)[\frac{{\mathrm{ß}}^3{\wp }^{3\mathrm{ß}}}{\mathrm{\Gamma }(3\mathrm{ß}+1)}+3{\mathrm{ß}}^2(1-\mathrm{ß})\frac{{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+\hfill \\ \hfill & 3\mathrm{ß}{(1-\mathrm{ß})}^2\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^3]+\dots .\hfill \end{array}$$

(37)

The solution to the problem with an integer order of 1 is represented as $U(\phi ,\wp )=exp(\phi +(\delta +\gamma )\wp )$.

Figure 1 presents the results of the evolution of $\mathit{U}(\phi ,\wp )$ for both exact and approximate solutions, respectively, when $\mathrm{ß}=1$ of example 1. The three-dimensional and two-dimensional plots in Figure 1 show the behaviors of the solutions for various fractional-order values of 1, $0.9$, $0.8$, and $0.7$. It was observed that the solutions converge rapidly, and the absolute error is derived from a limited number of terms, indicating a high level of approximation. The functional model is expected to provide new insight into the relationship between the gradient unconfined aquifer and saturated hydraulic conductivity.

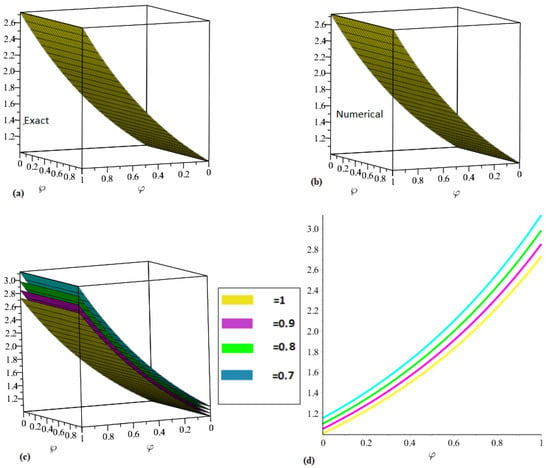
Figure 1. (a) Graph of the exact solution. (b) Graph of the numerical solution. (c,d) Graphs represent various fractional orders of example 1.

5.2. Example

The fractional order Boussinesq equation is given as [48]

$$\begin{array}{cc}\hfill & D_{\wp }^{\mathrm{ß}}\mathit{U}(\phi ,\wp )=D_{\phi }^{\left(2n\right)}\mathit{U}(\phi ,\wp )+D_{\phi }^{(2n-1)}\mathit{U}(\phi ,\wp )+\dots +D_{\phi }^2\mathit{U}(\phi ,\wp )+\theta D_{\phi }^2{\mathit{U}}^2(\phi ,\wp )-4\theta {\mathit{U}}^2(\phi ,\wp )\hfill \\ \hfill & 1<\mathrm{ß}\le 2,\wp >0,\hfill \end{array}$$

(38)

with the initial condition

$$\mathit{U}(\phi ,0)=exp\left(\phi \right),{\mathit{U}}_{\wp }(\phi ,0)=0.$$

equivalently, we have

$$\begin{array}{cc}\hfill & \mathit{Z}\left[\mathit{U}(\phi ,\wp )\right]=exp\left(\phi \right)+{\mathit{Z}}^{-1}[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}[D_{\phi }^{\left(2n\right)}\mathit{U}(\phi ,\wp )+D_{\phi }^{(2n-1)}\mathit{U}(\phi ,\wp )+\dots +D_{\phi }^2\mathit{U}(\phi ,\wp )\hfill \\ \hfill & +\theta D_{\phi }^2{\mathit{U}}^2(\phi ,\wp )-4\theta {\mathit{U}}^2(\phi ,\wp )\left]\right].\hfill \end{array}$$

(39)

The resolution of $\mathit{U}(\phi ,\wp )$ through ADTM utilizes an infinite sequence.

$$\mathit{U}(\phi ,\wp )=\sum _{m=0}^{\infty }{\mathit{U}}_m(\phi ,\wp ).$$

(40)

Equation (30) can be expressed using the Adomian polynomials $\mathit{U}\left(\mathit{U}\right)\phi \phi$ and ${\mathit{U}}^2$, which represent the nonlinear terms. The polynomials can be represented as the sum of their components, with $\mathit{U}\left(\mathit{U}\right)\phi \phi ={\sum }_{m=0}^{\infty }\mathcal{A}m$ and ${\mathit{U}}^2=\sum {m=0}^{\infty }{\mathcal{B}}_m$.

$$\begin{array}{cc}\hfill & \sum _{m=0}^{\infty }{\mathit{U}}_m(\phi ,\wp )=exp\left(\phi \right)+{\mathit{Z}}^{-1}[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}[D_{\phi }^{\left(2n\right)}\mathit{U}(\phi ,\wp )+D_{\phi }^{(2n-1)}\mathit{U}(\phi ,\wp )+\dots +D_{\phi }^2\mathit{U}(\phi ,\wp )\hfill \\ \hfill & +\theta \sum _{m=0}^{\infty }{\mathcal{A}}_m-4\theta \sum _{m=0}^{\infty }{\mathcal{B}}_m\left]\right].\hfill \end{array}$$

(41)

By using the Adomian polynomials, we can calculate the nonlinear terms

$${\mathit{U}}_0(\phi ,\wp )=exp\left(\phi \right),$$

For $m=0$

$${\mathit{U}}_1(\phi ,\wp )=nexp\left(\phi \right)\left[\frac{\mathrm{ß}{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+(1-\mathrm{ß})\right].$$

For $m=1$

$${\mathit{U}}_2(\phi ,\wp )={\left(n\right)}^{2}exp\left(\phi \right)\left[\frac{{\mathrm{ß}}^2{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+2\mathrm{ß}(1-\mathrm{ß})\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^2\right].$$

For $m=2$

$${\mathit{U}}_3(\phi ,\wp )={\left(n\right)}^{3}exp\left(\phi \right)\left[\frac{{\mathrm{ß}}^3{\wp }^{3\mathrm{ß}}}{\mathrm{\Gamma }(3\mathrm{ß}+1)}+3{\mathrm{ß}}^2(1-\mathrm{ß})\frac{{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+3\mathrm{ß}{(1-\mathrm{ß})}^2\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^3\right].$$

Therefore, the solution of the series is established as

$$\mathit{U}(\phi ,\wp )=\sum _{m=0}^{\infty }{\mathit{U}}_m(\phi ,\wp )={\mathit{U}}_0(\phi ,\wp )+{\mathit{U}}_1(\phi ,\wp )+{\mathit{U}}_2(\phi ,\wp )+{\mathit{U}}_3(\phi ,\wp )+\dots .$$

$$\begin{array}{cc}\hfill & \mathit{U}(\phi ,\wp )=exp\left(\phi \right)+nexp\left(\phi \right)\left[\frac{\mathrm{ß}{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+(1-\mathrm{ß})\right]+{\left(n\right)}^{2}exp\left(\phi \right)[\frac{{\mathrm{ß}}^2{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+2\mathrm{ß}(1-\mathrm{ß})\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+\hfill \\ \hfill & {(1-\mathrm{ß})}^2]+{\left(n\right)}^{3}exp\left(\phi \right)\left[\frac{{\mathrm{ß}}^3{\wp }^{3\mathrm{ß}}}{\mathrm{\Gamma }(3\mathrm{ß}+1)}+3{\mathrm{ß}}^2(1-\mathrm{ß})\frac{{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+3\mathrm{ß}{(1-\mathrm{ß})}^2\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^3\right]+\dots .\hfill \end{array}$$

The problem’s integer-order $\mathrm{ß}=1$ solution $\mathit{U}(\phi ,\wp )=exp\left(\phi +n\wp \right).$

With the utilization of the VITM approach, Equation (38) can be re-expressed using the iterative formula.

$$\begin{array}{cc}\hfill & {\mathit{U}}_{m+1}(\phi ,\wp )={\mathit{U}}_m(\phi ,\wp )-{\mathit{Z}}^{-1}[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\{\frac{B(\mathrm{ß})}{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{D}_{\phi }^{\left(2n\right)}{\mathit{U}}_m(\phi ,\wp )+D_{\phi }^{(2n-1)}{\mathit{U}}_m(\phi ,\wp )\hfill \\ \hfill & +\dots +D_{\phi }^2\mathit{U}(\phi ,\wp )+\theta D_{\phi }^2{\mathit{U}}_m^2(\phi ,\wp )-4\theta {\mathit{U}}_m^2(\phi ,\wp )\left\}\right],\hfill \end{array}$$

(42)

where

$${\mathit{U}}_0(\phi ,\wp )=exp\left(\phi \right).$$

For $m=0,1,2,\dots$

$$\begin{array}{cc}\hfill & {\mathit{U}}_1(\phi ,\wp )={\mathit{U}}_0(\phi ,\wp )-{\mathit{Z}}^{-1}[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\{\frac{B(\mathrm{ß})}{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{D}_{\phi }^{\left(2n\right)}{\mathit{U}}_0(\phi ,\wp )+D_{\phi }^{(2n-1)}{\mathit{U}}_0(\phi ,\wp )\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & +\dots +D_{\phi }^2{\mathit{U}}_0(\phi ,\wp )+\theta D_{\phi }^2{\mathit{U}}_0^2(\phi ,\wp )-4\theta {\mathit{U}}_0^2(\phi ,\wp )\left\}\right],\hfill \\ \hfill & {\mathit{U}}_1(\phi ,\wp )=nexp\left(\phi \right)\left[\frac{\mathrm{ß}{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+(1-\mathrm{ß})\right],\hfill \\ \hfill & {\mathit{U}}_2(\phi ,\wp )={\mathit{U}}_1(\phi ,\wp )-{\mathit{Z}}^{-1}[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\{\frac{B(\mathrm{ß})}{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{D}_{\phi }^{\left(2n\right)}{\mathit{U}}_1(\phi ,\wp )+D_{\phi }^{(2n-1)}{\mathit{U}}_1(\phi ,\wp )\hfill \\ \hfill & +\dots +D_{\phi }^2{\mathit{U}}_1(\phi ,\wp )+\theta D_{\phi }^2{\mathit{U}}_1^2(\phi ,\wp )-4\theta {\mathit{U}}_1^2(\phi ,\wp )\left\}\right],\hfill \\ \hfill & {\mathit{U}}_2(\phi ,\wp )={\left(n\right)}^{2}exp\left(\phi \right)\left[\frac{{\mathrm{ß}}^2{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+2\mathrm{ß}(1-\mathrm{ß})\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^2\right],\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill & {\mathit{U}}_3(\phi ,\wp )={\mathit{U}}_2(\phi ,\wp )-{\mathit{Z}}^{-1}[\frac{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{B(\mathrm{ß})}\mathit{Z}\{\frac{B(\mathrm{ß})}{1-\mathrm{ß}+\mathrm{ß}{\left(\frac{\kappa }{\epsilon }\right)}^{\mathrm{ß}}}{D}_{\phi }^{\left(2n\right)}{\mathit{U}}_2(\phi ,\wp )+D_{\phi }^{(2n-1)}{\mathit{U}}_2(\phi ,\wp )\hfill \\ \hfill & +\dots +D_{\phi }^2{\mathit{U}}_2(\phi ,\wp )+\theta D_{\phi }^2{\mathit{U}}_2^2(\phi ,\wp )-4\theta {\mathit{U}}_2^2(\phi ,\wp )\left\}\right],\hfill \\ \hfill & {\mathit{U}}_3(\phi ,\wp )={\left(n\right)}^{3}exp\left(\phi \right)\left[\frac{{\mathrm{ß}}^3{\wp }^{3\mathrm{ß}}}{\mathrm{\Gamma }(3\mathrm{ß}+1)}+3{\mathrm{ß}}^2(1-\mathrm{ß})\frac{{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+3\mathrm{ß}{(1-\mathrm{ß})}^2\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^3\right],\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill & \mathit{U}(\phi ,\wp )=\sum _{m=0}^{\infty }{\mathit{U}}_m(\phi ,\wp )=exp\left(\phi \right)+nexp\left(\phi \right)\left[\frac{\mathrm{ß}{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+(1-\mathrm{ß})\right]+{\left(n\right)}^{2}exp\left(\phi \right)[\frac{{\mathrm{ß}}^2{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+\hfill \\ \hfill & 2\mathrm{ß}(1-\mathrm{ß})\frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^2]+{\left(n\right)}^{3}exp\left(\phi \right)[\frac{{\mathrm{ß}}^3{\wp }^{3\mathrm{ß}}}{\mathrm{\Gamma }(3\mathrm{ß}+1)}+3{\mathrm{ß}}^2(1-\mathrm{ß})\frac{{\wp }^{2\mathrm{ß}}}{\mathrm{\Gamma }(2\mathrm{ß}+1)}+3\mathrm{ß}{(1-\mathrm{ß})}^2\hfill \\ \hfill & \frac{{\wp }^{\mathrm{ß}}}{\mathrm{\Gamma }(\mathrm{ß}+1)}+{(1-\mathrm{ß})}^3]+\dots .\hfill \end{array}$$

(46)

The problem’s integer-order $\mathrm{ß}=1$ solution $\mathit{U}(\phi ,\wp )=exp\left(\phi +n\wp \right).$

Figure 2 presents the results of the evolution of $\mathit{U}(\phi ,\wp )$ for both the exact and approximate solutions, respectively, where $\mathrm{ß}=1$. The three-dimensional and two-dimensional plots in Figure 2 show the behaviors of the solutions for various fractional-order values of 1, $0.9$, $0.8$, and $0.7$. It was observed that the solutions converge rapidly, and the absolute error is derived from a limited number of terms, indicating a high level of approximation. The functional model is expected to provide new insight into the relationship between the gradient unconfined aquifer and saturated hydraulic conductivity.

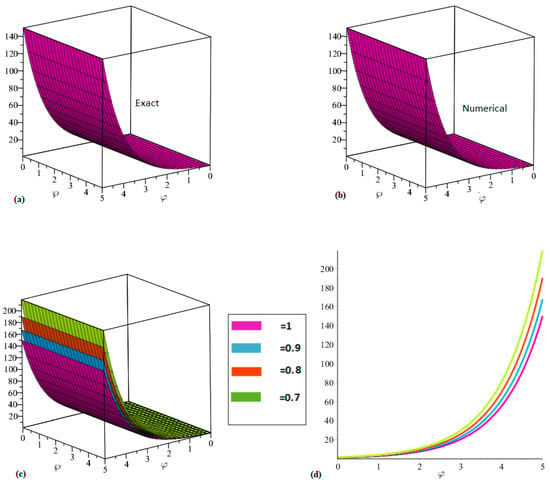
Figure 2. (a) Graph of the exact solution. (b) Graph of the numerical solution (c,d). Graphs represent various fractional orders of example 2.

6. Conclusions

In conclusion, the variational iteration transform method and Adomian decomposition method are effective in solving second- and fourth-order time-fractional Boussinesq equations. The ZZ transform and Atangana-Baleanu fractional derivative operator provide a theoretical framework for solving the equation. These methods offer a new approach to numerically solving fractional differential equations and can be applied to a wide range of real-world problems. The results of this study demonstrate that the variational iteration transform method and Adomian decomposition method are promising for solving fractional differential equations and warrant further exploration and investigation.