Fractional Order Operator for Symmetric Analysis of Cancer Model on Stem Cells with Chemotherapy
Abstract
1. Introduction
2. Basic Concepts
3. Materials and Method
Positivity of Solutions with ABC Operator
4. Numerical Scheme with Atangana–Toufik
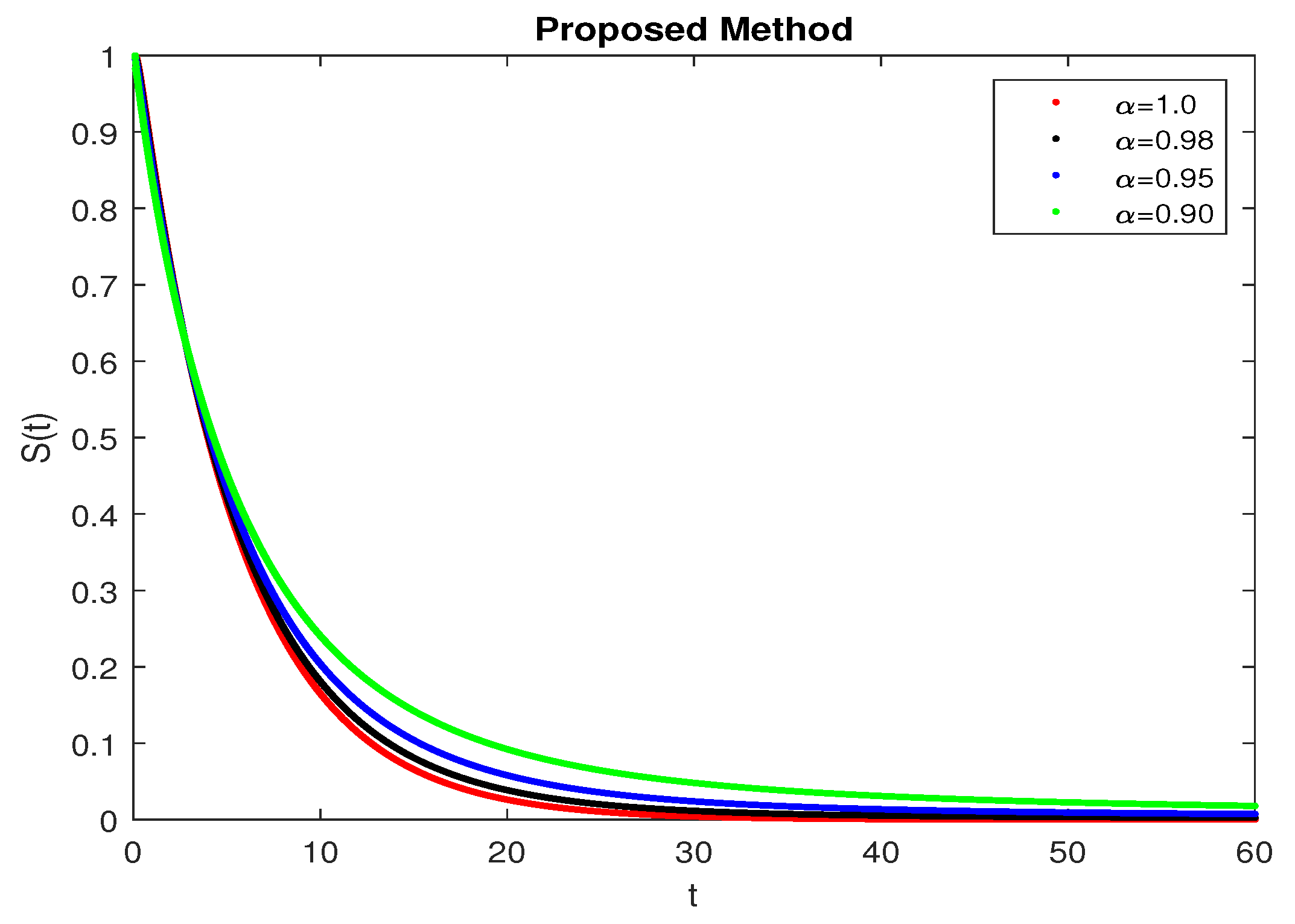
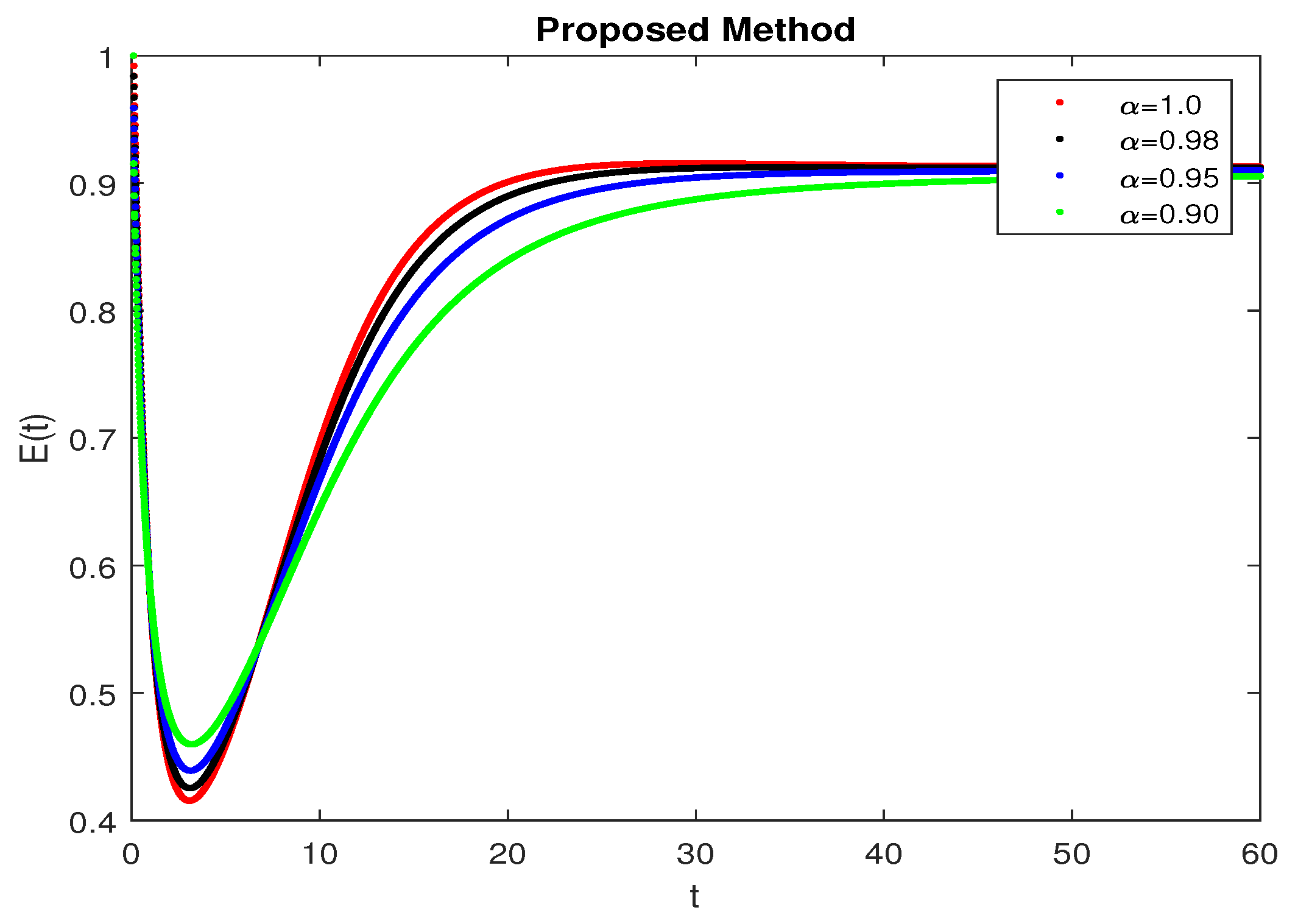
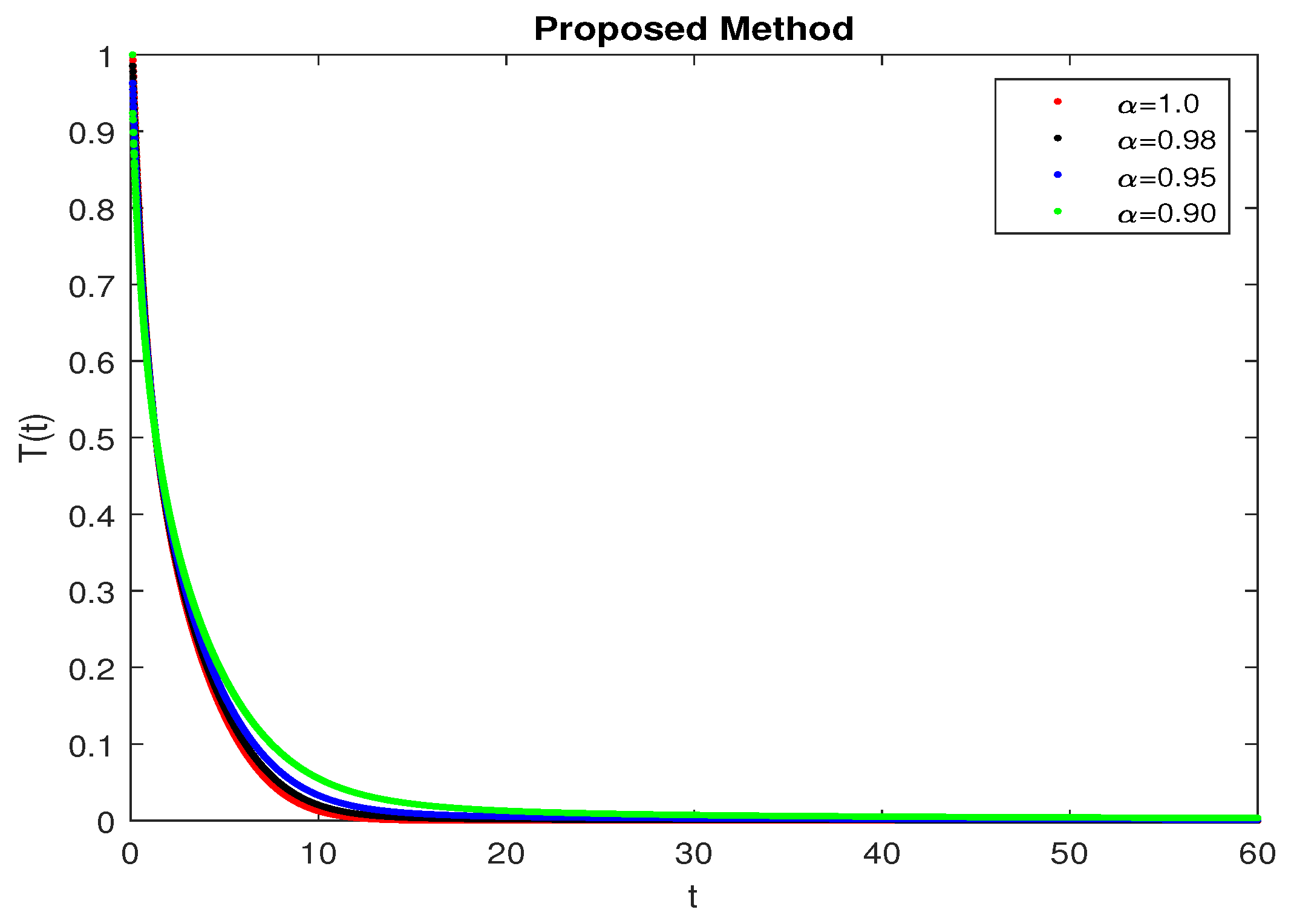
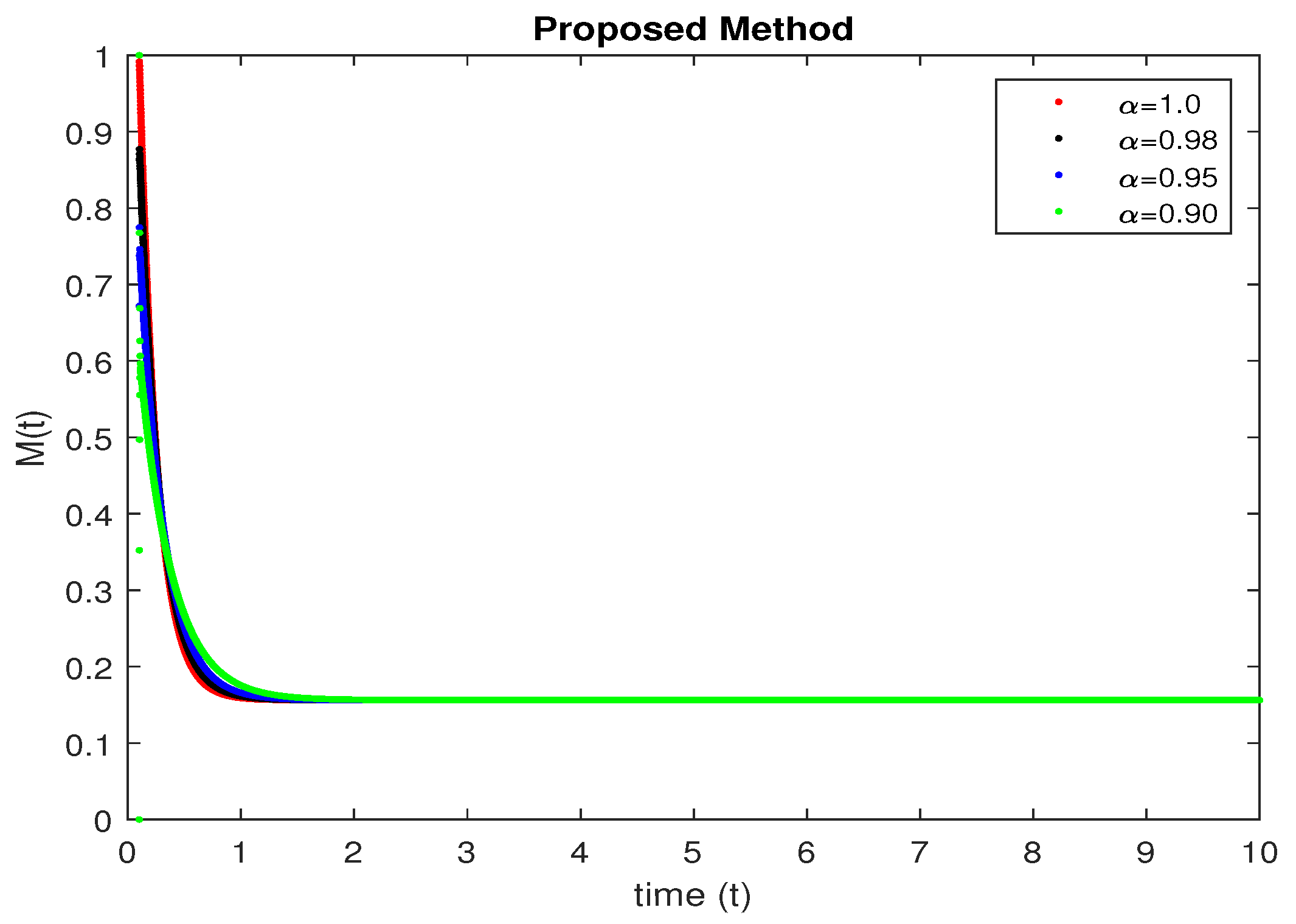
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Medina, M.A. Mathematical modeling of cancer metabolism. Crit. Rev. Oncol./Hematol. 2018, 124, 37–40. [Google Scholar] [CrossRef] [PubMed]
- Bellomo, N.; Bellouquid, A.; Delitala, M. Mathematical topics on the modeling of multicellular systems in competition between tumor and immune cells. Math. Models Methods Appl. Sci. 2004, 14, 1683–1733. [Google Scholar] [CrossRef]
- Aggarwal, S.K.; Carter, G.T.; Sullivan, M.D.; ZumBrunnen, C.; Morrill, R.; Mayer, J.D. Medicinal use of cannabis in the United States: Historical perspectives, current trends, and future directions. J. Opioid. Manag. 2009, 5, 153–168. [Google Scholar] [CrossRef] [PubMed]
- Baleanu, D.; Mustafa, O.G. On the global existence of solutions to a class of fractional differential equations. Comp. Math. Appl. 2010, 59, 1835–1841. [Google Scholar] [CrossRef]
- Odibat, Z. Approximations of fractional integrals and Caputo fractional derivatives. Appl. Math. Comput. 2006, 178, 527–533. [Google Scholar] [CrossRef]
- Baleanu, D.; Guvenc, Z.B.; Machado, J. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Dordrecht, The Netherland, 2010. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherland, 2006. [Google Scholar]
- Bulut, H.; Baskonus, H.M.; Belgacem, F.B. The analytical solutions of some fractional ordinary differential equations by Sumudu transform method. Abstr. Appl. Anal. 2013, 2013, 203875. [Google Scholar] [CrossRef]
- Ahmad, A.; Farman, M.; Yasin, F.; Ahmad, M.O. Dynamical transmission and effect of smoking in society. Int. J. Adv. Appl. Sci. 2018, 5, 71–75. [Google Scholar] [CrossRef]
- Ahmad, A.; Farman, M.; Ahmad, M.O.; Raza, N.; Abdullah, M. Dynamical behavior of SIR epidemic model with non-integer time fractional derivatives: A mathematical analysis. Int. J. Adv. Appl. Sci. 2018, 5, 123–129. [Google Scholar] [CrossRef]
- Thompson, R.N.; Hollingsworth, T.D.; Isham, V.; Arribas-Bel, D.; Ashby, B.; Britton, T.; Challenor, P.; Chappell, L.H.; Clapham, H.; Cunniffe, N.J.; et al. Key questions for modelling COVID-19 exit strategies. Proc. R. Soc. 2020, 287, 20201405. [Google Scholar] [CrossRef]
- Erturk, V.S.; Zaman, G.; Momani, S. A numeric analytic method for approximating a giving up smoking model containing fractional derivatives. Comput. Math. Appl. 2012, 64, 3068–3074. [Google Scholar] [CrossRef]
- Haq, F.; Shah, K.; Khan, A.; Shahzad, M.; Rahman, G.U. Numerical Solution of Fractional Order Epidemic Model of a Vector Born Disease by Laplace Adomian Decomposition Method. Punjab Univ. J. Math. 2017, 49, 13–22. [Google Scholar]
- Bushnaq, S.; Khan, S.A.; Shah, K.; Zaman, G. Mathematical analysis of HIV/AIDS infection model with Caputo-Fabrizio fractional derivative. Cogent Math. Stat. 2018, 5, 1432521. [Google Scholar] [CrossRef]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 8792. [Google Scholar]
- Farman, M.; Saleem, M.U.; Ahmad, A.; Imtiaz, S.; Tabassum, M.F.; Akram, S.; Ahmad, M.O. A control of glucose level in insulin therapies for the development of artificial pancreas byAtangana Baleanu fractional derivative. Alex. Eng. J. 2020, 59, 2639–2648. [Google Scholar] [CrossRef]
- Farman, M.; Akgül, A.; Ahmad, A.; Baleanu, D.; Saleem, M.U. Dynamical Transmission of Coronavirus model with Analysis and Simulation. Comput. Model. Eng. Sci. 2021, 127, 753–769. [Google Scholar] [CrossRef]
- Amin, M.; Farman, M.; Akgul, A.; Alqahtani, R.T. Effect of Vaccination to Control COVID-19 with Fractal-Fractional Operator. Alex. Eng. J. 2022, 61, 3551–3557. [Google Scholar] [CrossRef]
- Farman, M.; Akgül, A.; Abdeljawad, T.; Naik, P.A.; Bukhari, N.; Ahmad, A. Modeling and Analysis of Fractional Order Ebola Virus Model with Mittag-Lefler Kernel. Alex. Eng. J. 2022, 61, 2062–2073. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A. Analysis of fractal-fractional model of tumor-immune interaction. Results Phys. 2021, 25, 104178. [Google Scholar] [CrossRef]
- Farman, M.; Aslam, M.; Akgül, A.; Ahmad, A. Modeling of Fractional Order COVID-19 Epidemic Model with Quarantine and Social Distancing. Math. Method Appl. Sci. 2021, 44, 9334–9350. [Google Scholar] [CrossRef]
- Aqeel, A.; Naik, P.A.; Zafar, N.; Akgül, A.; Saleem, M.U. Modeling and numerical investigation of fractional-order bovine babesiosis disease. Numer Methods Partial Differ Equ. 2022, 37, 1946–1964. [Google Scholar]
- Naeem, M.; Zidan, A.M.; Nonlaopon, K.; Syam, M.I.; Al-Zhour, Z.; Shah, R. A New Analysis of Fractional-Order Equal-Width Equations via Novel Techniques. Symmetry 2021, 13, 886. [Google Scholar] [CrossRef]
- Theswan, S.; Ntouyas, S.K.; Ahmad, B.; Tariboon, J. Existence Results for Nonlinear Coupled Hilfer Fractional Differential Equations with Nonlocal Riemann Liouville and Hadamard-Type Iterated Integral Boundary Conditions. Symmetry 2022, 14, 1948. [Google Scholar] [CrossRef]
- Iqbal, Z.; Macías-Díaz, J.E.; Ahmed, N.; Javaid, A.; Rafiq, M.; Raza, A. Analytical and Numerical Boundedness of a Model with Memory Effects for the Spreading of Infectious Diseases. Symmetry 2022, 14, 2540. [Google Scholar] [CrossRef]
- Alyobi, S.; Shah, R.; Khan, A.; Shah, N.A.; Nonlaopon, K. Fractional Analysis of Nonlinear Boussinesq Equation under Atangana Baleanu Caputo Operator. Symmetry 2022, 14, 2417. [Google Scholar] [CrossRef]
- Atangana, A.; Bonyah, E.; Elsadany, A.A. A fractional order optimal 4D chaotic financial model with Mittag-Leffler law. Chin. J. Phys. 2020, 65, 38–53. [Google Scholar] [CrossRef]
- Alqudah, M.A. Cancer treatment by stem cells and chemotherapy as a mathematical model with numerical simulations. Alex. Eng. J. 2020, 59, 1953–1957. [Google Scholar] [CrossRef]
- Alqudah, M.A. Mathematical model of stem cells therapy for the treatment of cancer. In Proceedings of the International Conference on Computational Methods in Applied Sciences (IC2MAS19), Istanbul, Turkey, 12–16 July 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azeem, M.; Farman, M.; Akgül, A.; De la Sen, M. Fractional Order Operator for Symmetric Analysis of Cancer Model on Stem Cells with Chemotherapy. Symmetry 2023, 15, 533. https://doi.org/10.3390/sym15020533
Azeem M, Farman M, Akgül A, De la Sen M. Fractional Order Operator for Symmetric Analysis of Cancer Model on Stem Cells with Chemotherapy. Symmetry. 2023; 15(2):533. https://doi.org/10.3390/sym15020533
Chicago/Turabian StyleAzeem, Muhammad, Muhammad Farman, Ali Akgül, and Manuel De la Sen. 2023. "Fractional Order Operator for Symmetric Analysis of Cancer Model on Stem Cells with Chemotherapy" Symmetry 15, no. 2: 533. https://doi.org/10.3390/sym15020533
APA StyleAzeem, M., Farman, M., Akgül, A., & De la Sen, M. (2023). Fractional Order Operator for Symmetric Analysis of Cancer Model on Stem Cells with Chemotherapy. Symmetry, 15(2), 533. https://doi.org/10.3390/sym15020533








