Abstract
Mathematical difficulty remains in many classical financial problems, especially for a closed-form expression of asset value. The European option evaluation problem based on a regime-switching has been formally modeled since early 2000, for which a recursive algorithm was developed to solve it. The key mathematical difficulty of this problem relies on the expectation , where h is a payoff function and denotes a geometric Brownian motion with Markovian regime-switching. It is long since attempted to conclude this problem with closed form formulas. Towards the same target, this paper applies some novel techniques to draw explicit formulas for cases with more states for regime-switching (whereas the former deals the cases with two states) for any integrable function h (whereas the former only applies to the payoff of a European option). This paper combines the technique of occupation time of Markov chains and inverse Laplace transform to achieve the density function of geometric Brownian motion with Markovian regime-switching. Extension along this technique creates potential for probabilistic computations in addition to European option pricing. The reflection from the inverse Laplace transform to the expression of a moment-generating function is the core technique developed by this paper, and it is presented in symmetric forms.
1. Introduction
Regime-switching models were introduced by Hamilton in [1] for discrete-time and are among the most popular and effective risky asset models, where the switched regimes may well match the changeable states of the underlying environment. As developed for various demands, regime-switching is widely applied to equip those commonly used models (see [2,3] etc.). Particularly, geometric Brownian motion is convenient for this combination since two parameters of geometric Brownian motion can be randomized and governed by Markov chains, which denote the switched regimes.
As is well-known, to capture the price dynamics, the classical Black–Scholes model involves two parameters, the expected rate of return and the volatility, both assumed as deterministic constants. However, observations of market environment changes are not reflected by this pair of parameters, and it yields the needs for regime-switching. As pointed out by [4], another widely acknowledged shortfall of the classical model is its failure to capture the volatility smile. That is, the implied volatility of the underlying security (implied by the market price of the option on the underlying security via the Black–Scholes formula), rather than being a constant, should change with respect to the maturity and the exercise price of the option.
European options have been priced in continuous-time regime-switching models in [4] via a recursive algorithm and in [5] using the fast Fourier transform. Till now, regime-switching models are widely applied and theoretically investigated for option pricing, as shown in the recently published research [6,7] for European options and [8,9] for American style options.
This paper develops a new method to price the European options with explicit expressions. The general methodology we designed applies standard techniques of stochastic analysis and inverse Laplace transform. After some deduction and simplification, the main difficulty relies on the computation of the occupation time of a Markov chain. As for this problem, there already existed some useful results in [10,11,12]. It becomes possible for us to improve those results about the computation of Markovian occupation times for the expectation computation of the geometric Brownian motion with Markovian regime-switching. Besides techniques of stochastic analysis, such as infinitesimal generator and Markov semigroup, the inverse Laplace transform also plays a key role. However, it differs from [7], which applies the inverse Laplace transform to solve their PDEs.
The innovation of this paper is to combine the technique of the occupation time of Markov chains and inverse Laplace transform for probabilistic computation, and this technical contribution is absolutely original. Applying this, European option pricing based on a regime-switching model becomes computable by closed-form expressions, and it also contributes to the practice of mathematical finance.
We proceed as follows. Section 2 formulates the value function of European options. By investigating the problem of occupation time of Markov chains, Section 3 aims to provide the explicit expression of the European put premium. Hence, based on the formulas obtained in Section 3, Section 4 numerically implements the computation and verifies our formulas for both accuracy and efficiency when compared with other methods.
2. Formulation
Given a standard Brownian motion independent of the Markov chain , and the filtration generated by and , we consider an asset price modeled by a geometric Brownian motion
with regime-switching driven by a finite-state continuous-time Markov chain on , let denote the transition rate matrix of the Markov chain , and let denote the transition probability matrix of , namely for each entry of this matrix , . In the definition (1) of GBM above, and are deterministic functions. Based on this setting, we consider a European call option (put option can be similarly treated) with strike price and maturity . Hence, its payoff function is given by
According to [4], given the asset price at time is and the state of the Markov chain is , the call option premium is expressed as follows,
which equals
where the expectation is taken under the risk-neural measure that
and is given by
with a -measured standard Brownian motion . Hence, it become obvious to see that (2) equals
Finally, without loss of generality and indeed equivalently, we substitute with T and equivalently consider the expectation (denoting the call option premium) based on the following expression:
for some and , where is given by
with the Brownian motion defined initially. For the European put option, we can redefine the payoff function as for ; thereafter, the analysis and computation follow a very similar approach.
3. Calculation
In this section, we intend to give an explicit expression to the expression (3) of the option value. Three steps are designed to achieve that. First, in Section 3.1, the infinitesimal generator of is investigated. Secondly, Section 3.2 studies the moment-generating function of in (4) applying this infinitesimal generator. Finally, a technique of inverse Laplace transform is used to obtain the density function of , and also in Section 3.3, expression of the option price in (3) will be given in terms of a closed-form density function of .
3.1. Infinitesimal Generator
As stated above, we will consider the moment-generating function of in (4); hence, we define a random variable Z such that :
based on which, we define its moment-generating function that
Define the filtration generated by as . Substituting the expression (5) of Z into the above expression (6) yields that
Therefore, in this subsection, we figure out the infinitesimal generator of as a preparation to compute the expectation in (7). One may consider the infinitesimal generator of only, but it is impracticable because alone is not a Markov process. Indeed, follows the Markovian property by checking the fact that for . As we also note, ref. [4] provides the infinitesimal generator of that for any smooth function , we have
Indeed, we can apply our method in the next subsection accompanied by this generator to compute (6) directly; however, computation based on (7) and the infinitesimal generator of is easier. Formally, we define the infinitesimal generator as follows,
for any , , and arbitrary . Here, we recall the definition of matrix P and Q in the remark of expression (1) and for any . Split the expectation in (8) into a summation as follows:
and further substitute with
and then we see that
where we applied the fact that
After rewriting (9), we express the infinitesimal generator in the following proposition.
Proposition 1.
Denoted as in (8), the infinitesimal generator of is specified by the following expression with any partial differentiable function F on :
where denotes a diagonal matrix with its diagonal entries being orderly, denotes a vertical vector whose elements are orderly, and we use the notation to denote the i-th element of any vector η and is at least twice differentiable with respect to x.
3.2. Moment-Generating Function
As defined in (6), is the moment-generating function of Z in (5), and it is shown by (7) that for any and . In this section, we will apply the infinitesimal generator of to compute this .
To apply Proposition 1 for the computation of moment-generating function, we specify this function F in Proposition 1 as for any , and . It follows that and
Therefore, we define a matrix that
where denotes a diagonal matrix with its diagonal entries being orderly. Hence, we have
where denotes a vertical vector whose elements are orderly, and we use the notation to denote the i-th element of any vector . Applying the Formulas (7) and (11), we express the moment-generating function of Z as follows,
where the matrix is given by (10), and denotes a vertical vector of m elements all being 1, and we applied the properties of the Markov semigroup (see [13]).
3.3. Expression of Value Function
As designed at the beginning of this section, the value function (3) will be expressed with the density function. Applying the Formula (12) of the moment-generating function , it is now possible to obtain the density function of given . By (6), we see that
where the Laplace transform operator is defined by . Combining (12) and (13), we obtain that, for any and ,
where some notations are defined below (11) and (12). By (3)–(5) and (14), we have
In most cases, we can safely assume that m eigenvectors of defined in (10) are mutually independent (otherwise, the standard arguments are applicable by changing s with slight variation and approaching the final expression), listed as , and their correspondent eigenvalues are . Denote the diagonal matrix with its diagonal entries listed as as for , and denote the matrix as ; hence, we have
To summarize and conclude, we have the following proposition.
Proposition 2.
Defined by (3), the value function of the call option has the following expression:
for any and , where we use the notation to denote the i-th element of any vector η and to denote a vertical vector of m elements all being 1.
For the numerical implementation of (16), the remaining difficulty relies on the reverse Laplace transform. Indeed, applying many existing techniques such as in [14,15,16], most cases encountered in (16) are solvable with closed-form expression of the reverse Laplace transform. However, a uniform expression for different numbers of states is not available. Here, we take a two-state space as an example. Assume that , and hence, ; in addition, assume , and define the transition rate matrix by letting , for positive real number and .
4. Verification
In this section, we will verify the results stated in Section 3, especially Proposition 2. In particular, we take two approaches. First, a special case is considered for testing our proposed formulas in Section 3.2. Next, we apply the Formulas (17) and (18) to price the European call premium and compare the results with those by the recursive algorithm in [4] and by a Monte Carlo simulation, respectively.
4.1. A Special Case to Justify Our Formulas
In particular, we test the numerical results based on the parameters as follows:
In this case, the asset price may fluctuate extraordinarily above the strike price K, and hence, the final results of option pricing should be close to that with the payoff function . Therefore, it becomes possible to justify our formulas by comparison with a simple and closed form expression. That is, the call option premium is approximately given by
For any . On the other hand, we apply (17) and (18) to compute the call when . By (19), the theoretical value of the call should be 8.5184, but influenced by the difference between h and , , it should be a little higher than 8.5184. By increasing the value of volatility parameters and , the gap between h and is further magnified, as we observe in Figure 1 below. Furthermore, as illustrated by this figure, by (19) is a decent substitute for when K is relatively too small and the volatility is not high.
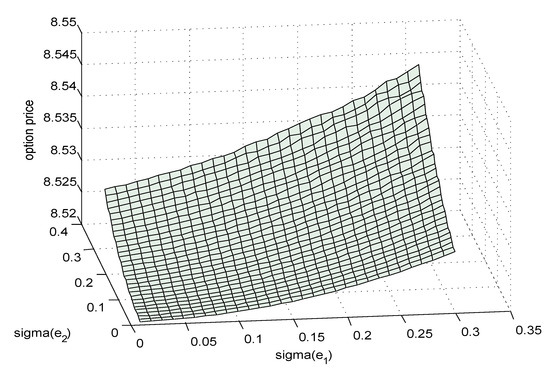
Figure 1.
Option prices with different values of and .
4.2. Comparison with Other Methods
This comparison is taken based on a normal case, the parameter settings of which are unlike that in Table 1, with a huge gap between the initial asset price and the strike. Instead, the parameters are given in Table 2 below.

Table 1.
Parameters of a special case.

Table 2.
Values of parameters.
We have three ways to compute the option prices:
- Ref. [4] provides a recursive algorithm, which designs the recursion based on the jump times of a Markov chain. An alternative to this might be a backward recursive algorithm designed in [17], which applies a discretization of the time interval, where its value function and reward function are defined as and , respectively. The backward recursive algorithm is briefly shown by the pseudo-code (Algorithm 1) below.
Algorithm 1 Algorithm to compute the option value function V Require: Maturity date T, strike price K, drift factor , volatility , risk-free capital return rate r. Ensure: and for each and . 1: for all do 2: for all do 3: calculate ; 4: end for 5: end for 6: for each backwardly do 7: for all do 8: for each sample given do 9: if then 10: obtain a sample ; 11: else [] 12: obtain a sample ; 13: end if 14: average the samples of to obtain ; 15: end for 16: end for 17: end for - The traditional method to compute this expectation uses Monte Carlo simulation to obtain the mean value of samples. We attach the codes of this algorithm in the Appendix A, and indeed, the way of simulating the regime-switching model based on geometric Brownian motion is optimized and very efficient.
Applying the above three methods, we show the term structure of this European put option premium by Figure 2 as follows. Obviously, curves yielded by different approaches highly coincide. Moreover, a closer check may find that the curve generated by Monte Carlo simulation is a little rougher, while the one obtained by our formula is of the best smoothness. Furthermore, the time consumed in the three methods is different; the Monte Carlo simulation spends 110 s, the recursive algorithm is more efficient, halving the time, while computation based on our formula takes only 6 s. From this perspective, our approach outperforms the former two.
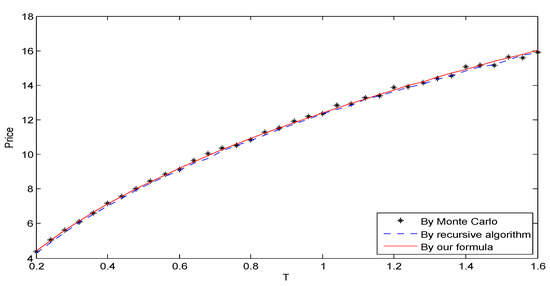
Figure 2.
Structure and comparison between three approaches.
Next, we investigate the implied volatility and show the volatility smile by graphs. Based on the parameter setting shown in Table 3 below, we apply Formulas (17) and (18) to compute the option price and transform them to the implied volatility using the standard Black–Scholes formula (refer to [18]).

Table 3.
Values of parameters.
As shown by Figure 3, we obtain the implied volatility surfaces for different values of strike and while is fixed. Applying Formulas (17) and (18) and the Monte Carlo simulation, respectively, we plot these two surfaces and find them to merge with only slight differences; however, the efficiencies are at the same level, as our approach only consumes about one and half minutes while Monte Carlo simulation spends one hour and more to obtain the same level of precision in terms of the smoothness of the surfaces.
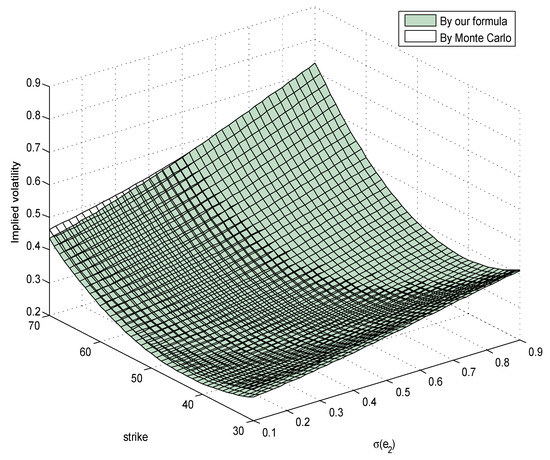
Figure 3.
Implied volatility and comparison with the Monte Carlo method.
Figure 4 (let ) and Figure 5 (let ) are cross sections from Figure 3. It is interesting to observe the curve of implied volatility in Figure 5; it will, of course, not form a smile shape since the horizon axis is not the strike price. However, we compare it with the average values of and to find that
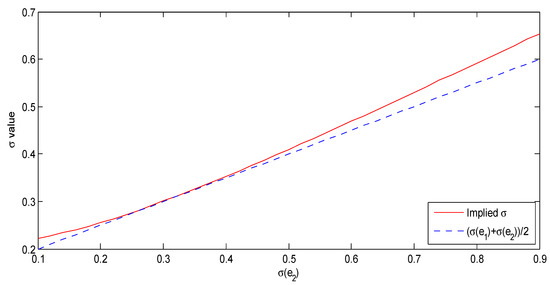
Figure 4.
Implied volatility compared with volatility parameters of the model.
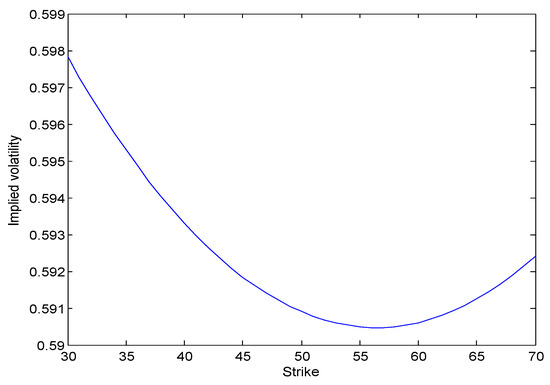
Figure 5.
Volatility smile.
- The curve of implied volatility is in all ranges higher than the average of the volatility parameters. The reason for accounting for this phenomenon is that switching regimes will bring in some variance, and it will enlarge the volatility of the whole system.
- By increasing the value of another volatility parameter (namely ), the gap between the curve of implied volatility and the average volatility is also amplifying. The reason behind it is that a larger difference between states will cause larger influences on the variance of the model once regime-switching happens.
- Two curves join when , indeed, that is, . Because when parameters of different regimes are the same, there will exist virtually no regime-switching. Hence, the extra variance caused by regime-switching perishes, and the implied volatility equals the average value of volatility parameters.
5. Conclusions
This paper provides explicit formulas to price the European option and largely improves the computational efficiency of option pricing. Applying new techniques to combine the computation of occupation time of Markov chains and inverse Laplace transform, the closed-form expression of asset value becomes possible. By comparison with the existed and widely applied method for this computation problem, we have shown great superiority of our proposed technique over the recursive backward computation algorithm with Monte Carlo simulation. In particular, for the same computational accuracy, our method consumes less time when programming.
In addition, the essential mathematical results of (11) and (12) are applicable to price options of other styles, and most significantly, the methodology we developed in this article has great potential to solve other problems with Markovian regime-switching, such as risk hedging and asset evaluation.
Author Contributions
Conceptualization, C.-Y.F. and Y.L.; methodology, C.-Y.F.; software, C.-Y.F.; validation, C.-Y.F. and Y.L.; formal analysis, Y.L.; investigation, C.-Y.F.; resources, Y.L.; data curation, Y.L.; writing—original draft preparation, C.-Y.F.; writing—review and editing, C.-Y.F.; visualization, C.-Y.F.; supervision, Z.-Y.S. and C.C.; project administration, Z.-Y.S.; funding acquisition, C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partly supported by a grant from the National Natural Science Foundation of China (72004082); Major programs of the National Social Science Foundation of China (22&ZD136); Special Science and Technology Innovation Program for Carbon Peak and Carbon Neutralization of Jiangsu Province (BE2022612, BE2022610); China Postdoctoral Science Foundation (2022M711662); and College Student Innovation Major Program in Jiangsu Province.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
As mentioned at the beginning of Section 4.2, the codes shown in Figure A1. below are run on Microsoft Visual Studio C++ to implement the Monte Carlo simulation of option pricing based on the regime-switching model.

Figure A1.
Codes of Monte Carlo simulation.
References
- Hamilton, J.D. A new approach to the economic analysis of non-stationary time series. Econometrica 1989, 57, 357–384. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, L.X.; Sun, H.P.; Zhang, X.L.; Kong, C.M. Option pricing of carbon asset and its application in digital decision-making of carbon asset. Appl. Energy 2022, 310, 118375. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, L.X.; Xie, Z.Y.; Zhen, Z.L.; Sun, H.P. Option to survive or surrender: Carbon asset management and optimization in thermal power enterprises from China. J. Clean. Prod. 2021, 314, 128006. [Google Scholar] [CrossRef]
- Yao, D.D.; Zhang, Q.; Zhou, X.Y. A regime-switching model for European options. Int. Ser. Oper. Res. Manag. Sci. 2006, 94, 281–300. [Google Scholar]
- Liu, R.H.; Zhang, Q.; Yin, G. Option pricing in a regime-switching model using the fast Fourier transform. Int. J. Stoch. Anal. 2006, 12–19. [Google Scholar]
- Biswas, A.; Goswami, A.; Overbeck, L. Option pricing in a regime switching stochastic volatility model. Stat. Probab. Lett. 2018, 138, 116–126. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, Z. Convergence Analysis of iterative Laplace transform methods for the coupled PDEs from regime-switching option pricing. J. Sci. Comput. 2018, 75, 1656–1674. [Google Scholar] [CrossRef]
- Tour, G.; Thakoor, N.; Khaliq, A.Q.M.; Tangman, D.Y. COS method for option pricing under a regime-switching model with time-changed Levy processes. Quant. Financ. 2018, 18, 673–692. [Google Scholar] [CrossRef]
- Yang, A.J.; Liu, Y.; Xiang, J.; Yang, H.Q. Optimal buying at the global minimum in a regime switching model. Math. Soc. Sci. 2016, 84, 50–55. [Google Scholar] [CrossRef]
- Darroch, J.N.; Morris, K.W. Passage-Time Generating Functions for Continuous-Time Finite Markov Chains. J. Appl. Prob. 1968, 5, 414–426. [Google Scholar] [CrossRef]
- Heidergott, B.; Leahu, H.; Löpker, A.; Pflug, G. Perturbation Analysis of Inhomogeneous Finite Markov Chains. Adv. Appl. Probab. 2016, 84, 255–273. [Google Scholar] [CrossRef]
- Pedler, P.J. Occupation times for two state markov chains. J. Appl. Prob. 1971, 8, 381–390. [Google Scholar] [CrossRef]
- Privault, N. Understanding Markov Chains—Examples and Applications; Springer Undergraduate Mathematics Series; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Jagerman, D.L. An inversion technique for the Laplace trasform. Bell Labs Tech. J. 1982, 61, 669–710. [Google Scholar]
- Puri, P.; Kythe, P.K. Some inverse Laplace transforms of exponential form. Z. Angew. Math. Und Phys. Zamp 1988, 39, 150–156. [Google Scholar] [CrossRef]
- Sheng, H.; Li, Y.; Chen, Y.Q. Application of numerical inverse Laplace transform algorithms in fractional calculus. J. Frankl. Inst. 2011, 348, 315–330. [Google Scholar] [CrossRef]
- Liu, Y.; Nicolas, P. A recursive algorithm for selling at the ultimate maximum in regime-switching models. Methodol. Comput. Appl. Probab. 2018, 20, 369–384. [Google Scholar] [CrossRef]
- Hull, J.C. Options, Futures, and Other Derivatives, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).