Fractional Order Operator for Symmetric Analysis of Cancer Model on Stem Cells with Chemotherapy

Abstract

Cancer is dangerous and one of the major diseases affecting normal human life. In this paper, a fractional-order cancer model with stem cells and chemotherapy is analyzed to check the effects of infection in individuals. The model is investigated by the Sumudu transform and a very effective numerical method. The positivity of solutions with the ABC operator of the proposed technique is verified. Fixed point theory is used to derive the existence and uniqueness of the solutions for the fractional order cancer system. Our derived solutions analyze the actual behavior and effect of cancer disease in the human body using different fractional values. Modern mathematical control with the fractional operator has many applications including the complex and crucial study of systems with symmetry. Symmetry analysis is a powerful tool that enables the user to construct numerical solutions of a given fractional differential equation in a fairly systematic way. Such an analysis will provide a better understanding to control the of cancer disease in the human body.

1. Introduction

Cancer is considered to cause different diseases with different characteristics for a complex system. To better understand the dynamics of cancer, many researchers are attempting to use a variety of methodologies to investigate the relationships between immune cells and tumor cells [1,2]. Diseases are categorized; cancer is one of them which represents out-of-control cell growth. When two things arise, malignant tumors or extra hazards appear in the human body. The first one is when cancer cells move through the blood or lymph system through the body and destroy flourishing tissues, which is known as invasion. The second issue is when cancerous cells try to split and proliferate to nourish themselves in a practice producing new blood vessels, which is known as angiogenesis. Hence a tumor destroys the other healthy tissues and can spread throughout the body in a process called metastasizing. This phase is more difficult to treat, and this process is called metastasis [3].

Because of its significance, fractional calculus is useful to depict dynamic processes in several fields together with physics, economics and finance [4,5], engineering, biology and medicine, and plenty of other current fields [6]. The inclusion of reminiscence and genetic markers, which give a extra rational approach to the cancer remedy epidemic version, highlights the requirement of managing fractional order outputs. This was in part assisted by Saeedian et al. who built the epidemic model and learning [7], which study the behavior and the effect of memory on the disease’s spread. Considering the ABC fractional operators, the power of the smoking model type and its community was given by Ucar et al. [8]. The famous German chemist Paul Ehelich began to develop therapeutic drugs for infectious diseases in the early $1900\mathrm{s}$. He began to use the term “chemotherapy”, which he described as the use of chemicals to treat cancer of its powerful anti-inflammatory chemicals. He was the first person to do so. Although Ehrlich was not optimistic about the future, he was particularly interested in cancer treatment, including aniline dyes and early alkylating agents. He wrote “Give up hope you who enter”. In the $1960\mathrm{s}$ surgery and radiotherapy dominated in the field of cancer treatment until the standard of treatment after all local therapies had stabilized when the 33A statistical fractional-order model protective test method for the body became clear by using the framework of fractional differential equations (FDEs) [9]. Mathematical models are used to analyze the interaction between different tumor cells and antibodies and dengue based on the system of fractional differential equations [10]. FDEs and a partial mathematical model have been used as an alternative operator to discuss the clinical effects of diabetes and the coexistence of tuberculosis [11].

The fractional derivative is initially divided into two major types. The fractionals with a singular kernel are Riemann–Liouville (RL) and Caputo [12]. The fractionals without singular kernels are ABC (Mittag–Leffler) and Caputo–Fabrizio (exponential) [13,14]. Fractional calculus is used in finance, chemical, biological, pharmaceutical, physical, and engineering fields as it has many application in our daily life [15,16]. Furthermore, several applications are given in [17,18,19,20,21,22] for fractional order versions. With the aid of Caputo–Fabrizio, fractional-order equal-width equations were solved using the homotopy perturbation transform approach in [23,24]. At both of the fractional-order epidemic model’s steady states, local and global stability are examined. After analytical treatment, the fractional-order epidemic model is numerically solved using a template that preserves the structure [25,26].

This paper aims to examine the fractional order cancer model with stem cells and chemotherapy. Furthermore, we verified the results using the advanced technique of Atangana–Toufik. Positivity of the proposed model was also derived. In terms of uniqueness of our study, one important point was the stability analysis of a scheme furnished with the aid of fixed point theorem.

2. Basic Concepts

Definition 1

(Ref. [27]). Atangana–Baleanu in the Liouville–Caputo sense (ABC) derivative is as follows

$${}_{\gamma }^{ABC}{D}_t^{\gamma }\{f(t)\}=\frac{AB(\gamma )}{1-\gamma }{\int }_{\gamma }^t\frac{d}{dw}f(w)E_{\gamma }[-\gamma \frac{{(t-w)}^{\gamma }}{1-\gamma }]dw,n-1<\gamma <n,$$

(1)

where $E_{\gamma }$ represents the function as Mittag–Leffler, and $AB(\gamma )$ represents the function as normalization and $AB(0)=AB(1)=1.$ The Laplace transform is given for above as

$$[{}_{\gamma }^{ABC}{D}_t^{\gamma }f(t)](s)=\frac{AB(\gamma )}{1-\gamma }\frac{s^{\gamma }L[f(t)](s)-s^{\gamma -1}f(0)}{s^{\gamma }+\frac{\gamma }{1-\gamma }}.$$

(2)

By applying the Sumudu transform (ST), we obtain the following result:

$$ST[{}_{\gamma }^{ABC}{D}_t^{\gamma }f(t)](s)=\frac{AB(\gamma )}{1-\gamma }(\gamma \Gamma (\gamma +1)E_{\gamma }(-\frac{1}{1-\gamma }{\nu }^{\gamma }))\times [ST(f(t))-f(0)].$$

(3)

3. Materials and Method

In order to treat the majority of cancers by using the handiest stem cellular therapy, we developed a fractional order mathematical model that considered three populations: $T(t)$ tumor cells, $E(t)$ effector cells, and $S(t)$ stem cells. Furthermore, we added an amplification A at the realization of the simplified ODEs that described the interaction among all three populations. $M(t)$ is a chemotherapeutic attention medication, and specifics of the parameters and their values are given in [28,29]. The subsequent equations deliver an ABC derivative-based fractional order version for cancer.

$${}_0^{ABC}{D}_t^{\gamma }\mathsf{S}(t)={\gamma }_1\mathsf{S}-k_{\mathsf{S}}\mathsf{MS},$$

$${}_0^{ABC}{D}_t^{\gamma }\mathsf{E}(t)=\alpha -\mu \mathsf{E}+\frac{p_1\mathsf{ES}}{(\mathsf{S}+1)}-p_2(\mathsf{T}+\mathsf{M})\mathsf{E},$$

$${}_0^{ABC}{D}_t^{\gamma }\mathsf{T}(t)=r(1-b\mathsf{T})\mathsf{T}-(p_3\mathsf{E}+k_{\mathsf{T}}\mathsf{M})\mathsf{T},$$

$${}_0^{ABC}{D}_t^{\gamma }M(t)=-{\gamma }_{2}M+V(t),$$

(4)

with beginning conditions as

$${\mathsf{S}}_0(t)=\mathsf{S}(0),{\mathsf{E}}_0(t)=\mathsf{E}(0),{\mathsf{T}}_0(t)=\mathsf{T}(0),{\mathsf{M}}_0(t)=\mathsf{M}(0).$$

(5)

By applying Sumudu transform operator on both sides, we obtain

$$O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })\left(\mathbb{ST}[\mathsf{S}(t))-\mathsf{S}(0)]\right)=\mathbb{ST}[{\gamma }_1\mathsf{S}-k_S\mathsf{MS}],$$

$$O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })\left(\mathbb{ST}[\mathsf{E}(t))-\mathsf{E}(0)]\right)=\mathbb{ST}[\alpha -\mu \mathsf{E}+\frac{p_1\mathsf{ES}}{(\mathsf{S}+1)}-p_2(\mathsf{T}+\mathsf{M})\mathsf{E}],$$

$$O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })\left(\mathbb{ST}[\mathsf{T}(t))-\mathsf{T}(0)]\right)=\mathbb{ST}[r(1-b\mathsf{T})\mathsf{T}-(p_3\mathsf{E}+k_T\mathsf{M})T],$$

$$O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })\left(\mathbb{ST}[\mathsf{M}(t))-\mathsf{M}(0)]\right)=\mathbb{ST}[-{\gamma }_2\mathsf{M}+\mathsf{V}(t)],$$

(6)

where $O_{\gamma }=\frac{B(\gamma )\gamma \Gamma (\gamma +1)}{1-\gamma }$ system (7) becomes

$$\mathbb{ST}[\mathsf{S}(t)]=\mathsf{S}(0)+\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[{\gamma }_1\mathsf{S}-k_S\mathsf{MS}],$$

$$\mathbb{ST}[\mathsf{E}(t)]=\mathsf{E}(0)+\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[\alpha -\mu \mathsf{E}+\frac{p_1\mathsf{ES}}{(\mathsf{S}+1)}-p_2(\mathsf{T}+\mathsf{M})\mathsf{E}],$$

$$\mathbb{ST}[\mathsf{T}(t)]=\mathsf{T}(0)+\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[r(1-b\mathsf{T})\mathsf{T}-(p_3\mathsf{E}+k_T\mathsf{M})\mathsf{T}],$$

$$\mathbb{ST}[\mathsf{M}(t)]=\mathsf{M}(0)+\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[-{\gamma }_2\mathsf{M}+\mathsf{V}(t)].$$

(7)

Using inverse Sumudu Transform, we have

$$\mathsf{S}(t)=\mathsf{S}(0)+{\mathbb{ST}}^{-1}\left\{\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[{\gamma }_1\mathsf{S}-k_{\mathsf{S}}\mathsf{MS}]\right\},$$

$$\mathsf{E}(t)=\mathsf{E}(0)+{\mathbb{ST}}^{-1}\left\{\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[r(1-b\mathsf{T})\mathsf{T}-(p_3\mathsf{E}+k_{\mathsf{T}}\mathsf{M})\mathsf{T}]\right\},$$

$$\mathsf{T}(t)=\mathsf{T}(0)+{\mathbb{ST}}^{-1}\left\{\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[r(1-b\mathsf{T})\mathsf{T}-(p_3\mathsf{E}+k_{\mathsf{T}}\mathsf{M})\mathsf{T}]\right\},$$

$$\mathsf{M}(t)=\mathsf{M}(0)+{\mathbb{ST}}^{-1}\left\{\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[-{\gamma }_2\mathsf{M}+\mathsf{V}(t)]\right\}.$$

(8)

Therefore, we obtain

$${\mathsf{S}}_{(j+1)}(t)={\mathsf{S}}_j(0)+{\mathbb{ST}}^{-1}\{\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[{\gamma }_1{\mathsf{S}}_j(t)-k_{{\mathsf{S}}_j(t)}{\mathsf{M}}_j(t){\mathsf{S}}_j(t)]\},$$

$${\mathsf{E}}_{(j+1)}(t)={\mathsf{E}}_j(0)+{\mathbb{ST}}^{-1}\{\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[\alpha -\mu {\mathsf{E}}_j(t)+\frac{p_1{\mathsf{E}}_m(t){\mathsf{S}}_j(t)}{({\mathsf{S}}_j(t)+1)}$$

$$-p_2({\mathsf{T}}_j(t)+{\mathsf{M}}_j(t)){\mathsf{E}}_j(t)]\},$$

$${\mathsf{T}}_{(j+1)}(t)={\mathsf{T}}_j(0)+{\mathbb{ST}}^{-1}\{\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[r(1-b{\mathsf{T}}_j(t)){\mathsf{T}}_j(t)$$

$$-(p_3{\mathsf{E}}_j(t)+k_{{\mathsf{T}}_j(t)}{\mathsf{M}}_j(t)){\mathsf{T}}_j(t)]\},$$

$${\mathsf{M}}_{(j+1)}(t)={\mathsf{M}}_j(0)+{\mathbb{ST}}^{-1}\{\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[-{\gamma }_2{\mathsf{M}}_j(t)+\mathsf{V}(t)]\}.$$

(9)

The solution of system (4) is represented as

$$\mathsf{S}=\underset{j\to \infty }{lim}{\mathsf{S}}_j;\mathsf{E}=\underset{j\to \infty }{lim}{\mathsf{E}}_j;\mathsf{T}=\underset{j\to \infty }{lim}{\mathsf{T}}_j(t);\mathsf{M}=\underset{j\to \infty }{lim}{\mathsf{M}}_j.$$

(10)

Positivity of Solutions with ABC Operator

All solutions are positive if all of the beginning conditions are true for nonlocal operators. We need to define the norm

$${\parallel \Pi \parallel }_{\infty }={Sup}_{t\in D_{\Pi }}|\Pi (t)|,$$

(11)

such that $D_{\Pi }$ is the domain of $\Pi$. By applying this norm, we obtain for the Atangana–Baleanu derivative

$$\begin{array}{ccc}\hfill \mathsf{S}(t)& \ge & {\mathsf{S}}_0{E}_{\gamma }\left(-\frac{\gamma k_{\mathsf{S}}{\parallel \mathsf{M}\parallel }_{\infty }-{\gamma }_1}{\mathsf{AB}(\gamma )-(1-\gamma )(k_{\mathsf{S}}\parallel \mathsf{M}{\parallel }_{\infty }-{\gamma }_1)}\right)t,\forall t>0\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill \mathsf{E}(t)& \ge & {\mathsf{E}}_0{E}_{\gamma }\left(-\frac{\gamma \mu -\frac{p_1{\parallel \mathsf{S}\parallel }_{\infty }}{{\parallel \mathsf{S}\parallel }_{\infty }+1}+p_2{(\parallel \mathsf{T}\parallel }_{\infty }+{\parallel \mathsf{M}\parallel }_{\infty }}{\mathsf{AB}(\gamma )-(1-\gamma )(\mu -\frac{p_1{\parallel \mathsf{S}\parallel }_{\infty }}{{\parallel \mathsf{S}\parallel }_{\infty }+1}+p_2{(\parallel \mathsf{T}\parallel }_{\infty }+{\parallel \mathsf{M}\parallel }_{\infty })}\right)t,\forall t>0\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill \mathsf{T}(t)& \ge & {\mathsf{T}}_0{E}_{\gamma }\left(-\frac{\gamma p_3{\parallel \mathsf{E}\parallel }_{\infty }+k_{\mathsf{T}}{\parallel \mathsf{M}\parallel }_{\infty }}{\mathsf{AB}(\gamma )-(1-\gamma )(p_3\parallel \mathsf{E}{\parallel }_{\infty }+k_{\mathsf{T}}\parallel \mathsf{M}{\parallel }_{\infty })}\right)t,\forall t>0\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill \mathsf{M}(t)& \ge & {\mathsf{M}}_0{E}_{\gamma }\left(-\frac{\gamma {\gamma }_2}{\mathsf{AB}(\gamma )-(1-\gamma )({\gamma }_2)}\right)t,\forall t>0\hfill \end{array}$$

(15)

Theorem 1.

Assume $(\mathbf{X},|·|)$ to be a Banach space and consider $\mathbf{H}$ to be a self-map of $\mathbf{X}$ satisfying

$$\parallel {\mathbf{H}}_{r_1}-{\mathbf{H}}_x\parallel \le \theta \parallel \mathbf{X}-{\mathbf{H}}_{r_1}\parallel +\theta \parallel r_1-x\parallel ,$$

(16)

for every $r_1,xϵ\mathbf{X}$, where $0\le \theta <1$.

Suppose that the system (4), and we obtain the following result as

$$\frac{1-\gamma }{\mathsf{B}(\gamma )\gamma \Gamma (\gamma +1)E_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}.$$

(17)

Proof. 

Defining $\mathbf{K}$ as a self-map, we may then write this as

$$\mathbf{K}[{\mathsf{S}}_{(j+1)}]={\mathsf{S}}_{(j+1)}={\mathsf{S}}_j(0)+S{T}^{-1}[\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[{\gamma }_1{\mathsf{S}}_j(t)-k_{{\mathsf{S}}_j(t)}{\mathsf{M}}_j(t){\mathsf{S}}_j(t)],$$

$$\mathbf{K}[{\mathsf{E}}_{(j+1)}]={\mathsf{E}}_{(j+1)}={\mathsf{E}}_j(0)+{\mathbb{ST}}^{-1}[\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}$$

$$\times ST[\alpha -\mu E_j(t)+\frac{p_1{E}_j(t){\mathsf{S}}_j(t)}{({\mathsf{S}}_j(t)+1)}-p_2({\mathsf{T}}_j(t)+{\mathsf{M}}_j(t)){\mathsf{E}}_j(t)],$$

$$\mathbf{K}[{\mathsf{T}}_{(j+1)}(t)]={\mathsf{T}}_{(j+1)}(t)={\mathsf{T}}_j(0)+{\mathbb{ST}}^{-1}[\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}$$

$$\times \mathbb{ST}[r(1-b{\mathsf{T}}_j(t)){\mathsf{T}}_j(t)-(p_3{\mathsf{E}}_j(t)+k_{{\mathsf{T}}_j(t)}{\mathsf{M}}_j(t)){\mathsf{T}}_j(t)],$$

$$\mathbf{K}[{\mathsf{M}}_{(j+1)}(t)]={\mathsf{M}}_{(j+1)}(t)={\mathsf{M}}_j(0)+{\mathbb{ST}}^{-1}[\frac{1}{O_{\gamma }{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}$$

$$\times \mathbb{ST}[-{\gamma }_2{\mathsf{M}}_j(t)+\mathsf{V}(t)].$$

(18)

Using the norm’s aspects along with triangular inequality,

$$\parallel \mathbf{K}[{\mathsf{S}}_j(t)]-\mathbf{K}[{\mathsf{S}}_i(t)]\parallel \le \parallel {\mathsf{S}}_j(t)-{\mathsf{S}}_i(t)\parallel +\parallel {\mathbb{ST}}^{-1}\{\frac{1-\gamma }{\mathbf{B}{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}$$

$$\times \mathbb{ST}[{\gamma }_1{\mathsf{S}}_j(t)-{\mathbf{K}}_{{\mathsf{S}}_j(t)}{\mathsf{M}}_j(t){\mathsf{S}}_j(t)]\}-{\mathbb{ST}}^{-1}\{\frac{1-\gamma }{\mathbf{B}{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}$$

$$\times \mathbb{ST}[{\gamma }_1{\mathsf{S}}_i(t)-{\mathbf{K}}_{{\mathsf{S}}_i(t)}{\mathsf{M}}_i(t){\mathsf{S}}_i(t)]\}\parallel ,$$

$$\parallel \mathbf{K}[{\mathsf{E}}_j(t)]-\mathbf{K}[{\mathsf{E}}_i(t)]\parallel \le \parallel {\mathsf{E}}_j(t)-{\mathsf{E}}_i(t)\parallel +\parallel {\mathbb{ST}}^{-1}[\frac{1-\gamma }{\mathbf{B}{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}$$

$$\times \mathbb{ST}[\alpha -\mu E_j(t)+\frac{p_1{\mathsf{E}}_j(t){\mathsf{S}}_j(t)}{({\mathsf{S}}_j(t)+1)}-p_2({\mathsf{T}}_j(t)+{\mathsf{M}}_j)(t)E_j(t)]$$

$$-{\mathbb{ST}}^{-1}[\frac{1-\gamma }{\mathbf{B}{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}\times \mathbb{ST}[\alpha -\mu {\mathsf{E}}_i(t)+\frac{p_1{\mathsf{E}}_i(t){\mathsf{S}}_i(t)}{({\mathsf{S}}_i(t)+1)}-p_2({\mathsf{T}}_i(t)+{\mathsf{M}}_i(t)){\mathsf{E}}_i(t)]\}\parallel ,$$

$$\parallel \mathbf{K}[{\mathsf{T}}_j(t)]-\mathbf{K}[{\mathsf{T}}_i(t)]\parallel \le \parallel {\mathsf{T}}_j(t)-{\mathsf{T}}_i(t)\parallel +\parallel {\mathbb{ST}}^{-1}[\frac{1-\gamma }{\mathbf{B}{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}$$

$$\times \mathbb{ST}[r(1-\mathbf{B}{\mathsf{T}}_j(t)){\mathsf{T}}_j(t)-(p_3{E}_j(t)+{\mathbf{K}}_{{\mathsf{T}}_j(t)}{\mathsf{M}}_j(t)){\mathsf{T}}_j(t)]\}-{\mathbb{ST}}^{-1}[\frac{1-\gamma }{\mathbf{B}{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}$$

$$\times \mathbb{ST}[r(1-\mathbf{B}{\mathsf{T}}_i(t)){\mathsf{T}}_i(t)-(p_3{\mathsf{E}}_i(t)+{\mathbf{K}}_{{\mathsf{T}}_i(t)}{\mathsf{M}}_i(t)){\mathsf{T}}_i(\mathsf{T})]\}\parallel ,$$

$$\parallel \mathbf{K}[{\mathsf{M}}_j(t)]-\mathbf{K}[{\mathsf{M}}_i(t)]\parallel \le \parallel {\mathsf{M}}_j(t)-{\mathsf{M}}_i(t)\parallel +\parallel {\mathbb{ST}}^{-1}[\frac{1-\gamma }{\mathbf{B}{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}$$

$$\times \mathbb{ST}[-{\gamma }_2{\mathsf{M}}_j(t)+\mathsf{V}(t)]\}-{\mathbb{ST}}^{-1}[\frac{1-\gamma }{\mathbf{B}{E}_{\gamma }(-\frac{1}{1-\gamma }{\omega }^{\gamma })}$$

$$\times \mathbb{ST}[-{\gamma }_2{\mathsf{M}}_i(t)+\mathsf{V}(t)]\}\parallel ,$$

(19)

where $B=B(\gamma )\gamma \Gamma (\gamma +1)$ K satisfied when

$$\theta =(0,0,0,0)=\left\{\begin{array}{c}\parallel {\mathsf{S}}_j(t)-{\mathsf{S}}_i(t)\parallel \times \parallel -{\mathsf{S}}_j(t)+{\mathsf{S}}_i(t)\parallel \hfill \\ +{\gamma }_1\parallel {\mathsf{S}}_j(t)-{\mathsf{S}}_i(t)\parallel -k\parallel {\mathsf{S}}_j(t)-{\mathsf{S}}_i(t)\parallel \parallel {\mathsf{M}}_j(t)-{\mathsf{M}}_i(t)\parallel \parallel {\mathsf{S}}_j(t)-{\mathsf{S}}_i(t)\parallel ,\hfill \\ \times \parallel {\mathsf{E}}_j(t)-{\mathsf{E}}_i(t)\parallel \times \parallel -{\mathsf{E}}_j(t)+{\mathsf{E}}_i(t)\parallel \hfill \\ +\alpha -\mu \parallel {\mathsf{E}}_j(t)-{\mathsf{E}}_i(t)\parallel +\frac{p_1\parallel {\mathsf{E}}_j(t)-{\mathsf{E}}_i(t)\parallel \parallel {\mathsf{S}}_j(t)-{\mathsf{S}}_i(t)\parallel }{(\parallel {\mathsf{S}}_j(t)-S_i(t)\parallel +1)},\hfill \\ -p_2(\parallel {\mathsf{T}}_j(t)-{\mathsf{T}}_i(t)\parallel +\parallel {\mathsf{M}}_j(t)-{\mathsf{M}}_i(t)\parallel )\parallel {\mathsf{E}}_j(t)-{\mathsf{E}}_i(t)\parallel \hfill \\ \times \parallel {\mathsf{T}}_j(t)-{\mathsf{T}}_i(t)\parallel \times \parallel -{\mathsf{T}}_j(t)+{\mathsf{T}}_i(t)\parallel \hfill \\ +r(1-b\parallel {\mathsf{T}}_j(t)-{\mathsf{T}}_i(t)\parallel )\parallel {\mathsf{T}}_j(t)-{\mathsf{T}}_i(t)\parallel -(p_3\parallel -{\mathsf{E}}_j(t)+{\mathsf{E}}_i(t)\parallel \hfill \\ +k_{\parallel {\mathsf{T}}_j(t)-{\mathsf{T}}_i(t)\parallel }\parallel {\mathsf{M}}_j(t)-{\mathsf{M}}_i(t)\parallel )\parallel {\mathsf{T}}_j(t)-{\mathsf{T}}_i(t)\parallel ,\hfill \\ \times \parallel {\mathsf{M}}_j(t)-{\mathsf{M}}_i(t)\parallel \times \parallel -{\mathsf{M}}_j(t)+{\mathsf{M}}_i(t)\parallel \hfill \\ -{\gamma }_2\parallel {\mathsf{M}}_j(t)-{\mathsf{M}}_i(t)\parallel +\mathsf{V}(t),\hfill \end{array}\right.$$

(20)

and we find that $\mathbf{K}$ is Picard $\mathbf{K}$-stable. □

Theorem 2.

System (9) is a unique and distinct solution found by utilizing the iteration method

Proof. 

Let us consider the Hilbert space,

$$H=L^2((q,p)\times (0,T))$$

$$h:(q,p)\times [0,T]\to R,\int \int ghdgdh<\infty .$$

(21)

For this purpose, the following operators are used

$$\theta =(0,0,0,0)=\left\{\begin{array}{c}{\gamma }_1\mathsf{S}-k_{\mathsf{S}}MS,\hfill \\ \alpha -\mu \mathsf{E}+\frac{p_{1}ES}{(\mathsf{S}+1)}-p_2(\mathsf{T}+\mathsf{M})\mathsf{E},\hfill \\ r(1-bT)\mathsf{T}-(p_3\mathsf{E}+k_{\mathsf{T}}\mathsf{M})\mathsf{T},\hfill \\ -{\gamma }_2\mathsf{M}+V(t).\hfill \end{array}\right.$$

(22)

We have

$$\mathsf{T}({\mathsf{S}}_{11}(t)-{\mathsf{S}}_{12}(t),{\mathsf{E}}_{21}(t)-{\mathsf{E}}_{22}(t),{\mathsf{T}}_{31}(t)-{\mathsf{T}}_{32}(t),{\mathsf{M}}_{41}(t)-{\mathsf{M}}_{42}(t),(v_1,v_2,v_3,v_4),$$

(23)

where $({\mathsf{S}}_{11}(t)-{\mathsf{S}}_{12}(t),{\mathsf{E}}_{21}(t)-{\mathsf{E}}_{22}(t),{\mathsf{T}}_{31}(t)-{\mathsf{T}}_{32}(t),{\mathsf{M}}_{41}(t)-{\mathsf{M}}_{42}(t)$, which displays the system’ $\mathsf{S}$ special solutions. We may obtain this by using the inner function and norm.

$$\{{\gamma }_{1}A-k_{A}DA,v_1\}\le {\gamma }_1\parallel A\parallel \parallel v_1\parallel -k_{\parallel A\parallel \parallel v_1\parallel }\parallel D\parallel \parallel v_1\parallel \parallel A\parallel \parallel v_1\parallel ,$$

$$\{\alpha -\mu B+\frac{p_{1}A}{(A+1)}-p_2(C+D)B,v_2\}\le \alpha -\mu \parallel B\parallel \parallel v_2\parallel$$

$$+\frac{p_1\parallel B\parallel \parallel A\parallel \parallel v_2\parallel }{(\parallel A\parallel \parallel v_2\parallel +1)}-p_2(\parallel C\parallel \parallel v_2\parallel +\parallel D\parallel \parallel v_2\parallel )\parallel B\parallel \parallel v_2\parallel ,$$

$$\{r(1-bC)C-(p_3(B+k_{C\parallel }D)C,v_3\}\le r(1-b\parallel C\parallel \parallel v_3\parallel )C\parallel v_2\parallel -(p_3\parallel B\parallel \parallel v_3\parallel$$

$$+k_{\parallel B\parallel \parallel v_3\parallel }\parallel D\parallel \parallel v_2\parallel )\parallel C\parallel \parallel v_3\parallel ,$$

$$\{-{\gamma }_{2}D+V(t),v_4\}\le -{\gamma }_2\parallel D\parallel \parallel v_4\parallel +V(t)\parallel v_4\parallel ,$$

where $A={\mathsf{S}}_{11}(t)-{\mathsf{S}}_{12}(t)$, $B={\mathsf{E}}_{21}(t)-{\mathsf{E}}_{22}(t)$, $C={\mathsf{T}}_{31}(t)-{\mathsf{T}}_{22}(t)$ and $D={\mathsf{M}}_{41}(t)-{\mathsf{M}}_{42}(t).$ In the case of a large number ${\mathsf{E}}_1,{\mathsf{E}}_2,{\mathsf{E}}_3,$ and ${\mathsf{E}}_4$, all of the results converge to an exact solution. By utilizing four positive and very small parameters and the topology concept, we have ${\chi }_{\mathsf{E}1},{\chi }_{\mathsf{E}2},{\chi }_{\mathsf{E}3},{\chi }_{\mathsf{E}4}.$

$$\parallel \mathsf{S}(t)-{\mathsf{S}}_{11}(t)\parallel ,\parallel \mathsf{S}(t)-{\mathsf{S}}_{12}(t)\parallel <\frac{{\chi }_{\mathsf{E}1}}{\omega },$$

$$\parallel \mathsf{E}(t)-{\mathsf{E}}_{21}(t)\parallel ,\parallel \mathsf{E}(t)-{\mathsf{E}}_{22}(t)\parallel <\frac{{\chi }_{\mathsf{E}2}}{\varsigma },$$

$$\parallel \mathsf{T}(t)-{\mathsf{T}}_{31}(t)\parallel ,\parallel \mathsf{T}(t)-{\mathsf{T}}_{32}(t)\parallel <\frac{{\chi }_{\mathsf{E}3}}{\vartheta },$$

and

$$\parallel \mathsf{M}(t)-{\mathsf{M}}_{41}(t)\parallel ,\parallel \mathsf{M}(t)-{\mathsf{M}}_{32}(t)\parallel <\frac{{\chi }_{\mathsf{E}4}}{\varrho },$$

where

$$\omega =4({\gamma }_1\parallel A\parallel -k_{\parallel A\parallel \parallel v_1\parallel }\parallel D\parallel \parallel A\parallel )\parallel v_1\parallel ,$$

$$\varsigma =4(\alpha -\mu \parallel B\parallel +\frac{p_1\parallel B\parallel \parallel A\parallel }{(\parallel A\parallel \parallel v_2\parallel +1)}-p_2(\parallel C\parallel +\parallel D\parallel )\parallel B\parallel )\parallel v_2\parallel ,$$

$$\vartheta =4(r(1-b\parallel C\parallel \parallel v_3\parallel )\parallel C\parallel -(p_3\parallel B\parallel +k_{\parallel B\parallel }\parallel D\parallel )\parallel C\parallel )\parallel v_3\parallel ,$$

$$\varrho =4(-{\gamma }_2\parallel D\parallel +V(t))\parallel v_4\parallel ,$$

where

$${\gamma }_1\parallel A\parallel -k_{\parallel A\parallel \parallel v_1\parallel }\parallel D\parallel \parallel A\parallel \ne 0,$$

$$\alpha -\mu \parallel B\parallel +\frac{p_1\parallel B\parallel \parallel A\parallel }{(\parallel A\parallel \parallel v_2\parallel +1)}-p_2(\parallel C\parallel +\parallel D\parallel )\parallel B\parallel \ne 0,$$

$$r(1-b\parallel C\parallel \parallel v_3\parallel )\parallel C\parallel -(p_3\parallel B\parallel +k_{\parallel B\parallel }\parallel C\parallel )\parallel D\parallel \ne 0,$$

$$-{\gamma }_2\parallel D\parallel \parallel +V(t))\ne 0,$$

where

$$\parallel v_1\parallel ,\parallel v_2\parallel ,\parallel v_3\parallel ,\parallel v_4\parallel \ne 0;\parallel {\mathsf{S}}_{11}(t)-{\mathsf{S}}_{12}(t)\parallel ,$$

$$\parallel {\mathsf{E}}_{21}(t)-{\mathsf{E}}_{22}(t)\parallel ,\parallel {\mathsf{T}}_{31}(t)-{\mathsf{T}}_{32}(t)\parallel ,\parallel {\mathsf{M}}_{41}(t)-{\mathsf{M}}_{42}(t)\parallel =0.$$

$${\mathsf{S}}_{11}(t)={\mathsf{S}}_{12}(t);{\mathsf{E}}_{21}(t)={\mathsf{E}}_{22}(t);{\mathsf{T}}_{31}(t)={\mathsf{T}}_{32}(t);{\mathsf{M}}_{41}(t)={\mathsf{M}}_{42}(t).$$

(24)

The uniqueness proof is now complete. □

4. Numerical Scheme with Atangana–Toufik

In this article, an advanced scheme was applied for nonlinear FD equations on account of FD with nonsingular kernel and non-nearby fractional derivative. For this purpose, recollect the nonlinear system given in (5) and apply the technique we have used.

$$\mathsf{S}(t)-\mathsf{S}(0)=\frac{(1-\gamma )}{ABC(\gamma )}\{{\gamma }_1\mathsf{S}(t)-k_{\mathsf{S}(t)}\mathsf{M}(t)\mathsf{S}(t)\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}{\int }_0^t\{{\gamma }_1\mathsf{S}({\tau }_1)-k_{\mathsf{S}({\tau }_1)}\mathsf{M}({\tau }_1)\mathsf{S}({\tau }_1)\}{(t-{\tau }_1)}^{\gamma -1}d{\tau }_1,$$

$$\mathsf{E}(t)-\mathsf{E}(0)=\frac{(1-\gamma )}{ABC(\gamma )}\{\alpha -\mu \mathsf{E}(t)+\frac{p_1\mathsf{E}(t)\mathsf{S}(t)}{(\mathsf{S}(t)+1)}-p_2(T(t)+\mathsf{M}(t))\mathsf{E}(t)\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}{\int }_0^t\{\alpha -\mu \mathsf{E}({\tau }_1)+\frac{p_1\mathsf{E}({\tau }_1)\mathsf{S}({\tau }_1)}{(\mathsf{S}({\tau }_1)+1)}-p_2(T({\tau }_1)+\mathsf{M}({\tau }_1))\mathsf{E}({\tau }_1)\}$$

$${(t-{\tau }_1)}^{\gamma -1}d{\tau }_1,$$

$$T(t)-T(0)=\frac{(1-\gamma )}{ABC(\gamma )}\{r(1-bT(t))T(t)-(p_3\mathsf{E}(t)+k_{T(t)}\mathsf{M}(t))T(t)\}$$

$$+\frac{{\alpha }_1}{\Gamma (\gamma )\times ABC(\gamma )}{\int }_0^t\{r(1-bT({\tau }_1))T({\tau }_1)-(p_3\mathsf{E}({\tau }_1)+k_{T({\tau }_1)}\mathsf{M}({\tau }_1))T({\tau }_1)\}$$

$${(t-{\tau }_1)}^{\gamma -1}d{\tau }_1,$$

$$\mathsf{M}(t)-\mathsf{M}(0)=\frac{(1-\gamma )}{ABC(\gamma )}\{-{\gamma }_2\mathsf{M}(t)+V(t)\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}{\int }_0^t\{-{\gamma }_2\mathsf{M}({\tau }_1)+V(t)\}{(t-{\tau }_1)}^{\gamma -1}d{\tau }_1.$$

As given $t_{\mathsf{M}+1},\mathsf{M}=0,1,2,3\dots$, then the above equation can be reformulated as

$$\mathsf{S}(t_{\mathsf{M}+1})-\mathsf{S}(0)=\frac{(1-\gamma )}{ABC(\gamma )}\{{\gamma }_1\mathsf{S}(t_{\mathsf{M}})-k_{\mathsf{S}(t_{\mathsf{M}})}\mathsf{M}(t_{\mathsf{M}})\mathsf{S}(t_{\mathsf{M}})\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}{\int }_{t_{k_1}}^{t_{k_1+1}}\{{\gamma }_1\mathsf{S}({\tau }_1)-k_{\mathsf{S}({\tau }_1)}\mathsf{M}({\tau }_1)\mathsf{S}({\tau }_1)\}$$

$${(t_{\mathsf{M}+1}-{\tau }_1)}^{\gamma -1}d{\tau }_1,$$

$$\mathsf{E}(t_{\mathsf{M}+1})-\mathsf{E}(0)=\frac{(1-\gamma )}{ABC(\gamma )}\{\alpha -\mu \mathsf{E}(t_{\mathsf{M}})+\frac{p_1\mathsf{E}(t_{\mathsf{M}})\mathsf{S}(t_{\mathsf{M}})}{(\mathsf{S}(t_{\mathsf{M}})+1)}-p_2(T(t_{\mathsf{M}})+\mathsf{M}(t_{\mathsf{M}}))\mathsf{E}(t_{\mathsf{M}})\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}{\int }_{t_{k_1}}^{t_{k_1+1}}\{\alpha -\mu \mathsf{E}({\tau }_1)+\frac{p_1\mathsf{E}({\tau }_1)\mathsf{S}({\tau }_1)}{(\mathsf{S}({\tau }_1)+1)}-p_2(T({\tau }_1)+\mathsf{M}({\tau }_1))\mathsf{E}({\tau }_1)\}$$

$${(t_{\mathsf{M}+1}-{\tau }_1)}^{\gamma -1}d{\tau }_1,$$

$$T(t_{\mathsf{M}+1})-T(0)=\frac{(1-\gamma )}{ABC(\gamma )}\{r(1-bT(t_{\mathsf{M}}))T(t_{\mathsf{M}})-(p_3\mathsf{E}(t_{\mathsf{M}})+k_{T(t_{\mathsf{M}})}\mathsf{M}(t_{\mathsf{M}}))T(t_{\mathsf{M}})\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}{\int }_{t_{k_1}}^{t_{k_1+1}}\{r(1-bT({\tau }_1))T({\tau }_1)-(p_3\mathsf{E}({\tau }_1)+k_{T({\tau }_1)}\mathsf{M}({\tau }_1))T({\tau }_1)\}$$

$${(t_{\mathsf{M}+1}-{\tau }_1)}^{\gamma -1}d{\tau }_1,$$

$$\mathsf{M}(t_{\mathsf{M}+1})-\mathsf{M}(0)=\frac{(1-\gamma )}{ABC(\gamma )}\{-{\gamma }_2\mathsf{M}(t_{\mathsf{M}})+V(t)\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}{\int }_{t_{k_1}}^{t_{k_1+1}}\{-{\gamma }_2\mathsf{M}({\tau }_1)+V(t)\}{(t_{\mathsf{M}+1}-{\tau }_1)}^{\gamma -1}d{\tau }_1.$$

By using the above equation, we have

$${\mathsf{S}}_{\mathsf{M}+1}={\mathsf{S}}_0+\frac{(1-\gamma )}{ABC(\gamma )}\{{\gamma }_1\mathsf{S}(t_{\mathsf{M}})-k_{\mathsf{S}(t_{\mathsf{M}})}\mathsf{M}(t_{\mathsf{M}})\mathsf{S}(t_{\mathsf{M}})\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}(\frac{{\gamma }_1{\mathsf{S}}_{k_1}-k_{{\mathsf{S}}_{k_1}}{\mathsf{M}}_{k_1}{\mathsf{S}}_{k_1}}{h}{B}_1$$

$$-\frac{{\gamma }_1{\mathsf{S}}_{k_1-1}-k_{{\mathsf{S}}_{k_1-1}}{\mathsf{M}}_{k_1-1}{\mathsf{S}}_{k_1-1}}{h}{A}_{\gamma ,k_1,2}),$$

$${\mathsf{E}}_{\mathsf{M}+1}={\mathsf{E}}_0+\frac{(1-\gamma )}{ABC(\gamma )}\{\alpha -\mu \mathsf{E}(t_{\mathsf{M}})+\frac{p_1\mathsf{E}(t_{\mathsf{M}})\mathsf{S}(t_{\mathsf{M}})}{(\mathsf{S}(t_{\mathsf{M}})+1)}-p_2(T(t_{\mathsf{M}})+\mathsf{M}(t_{\mathsf{M}}))\mathsf{E}(t_{\mathsf{M}})\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}(\frac{\alpha -\mu {\mathsf{E}}_{k_1}+\frac{p_1{\mathsf{E}}_{k_1}{\mathsf{S}}_{k_1}}{({\mathsf{S}}_{k_1}+1)}-p_2(T_{k_1}+{\mathsf{M}}_{k_1}){\mathsf{E}}_{k_1}}{h}{B}_1$$

$$-\frac{\alpha -\mu {\mathsf{E}}_{k_1-1}+\frac{p_1{\mathsf{E}}_{k_1-1}{\mathsf{S}}_{k_1-1}}{({\mathsf{S}}_{k_1-1}+1)}-p_2(T_{k_1-1}+{\mathsf{M}}_{k_1-1}){\mathsf{E}}_{k_1-1}}{h}{A}_{\gamma ,k_1,2}),$$

$$T_{\mathsf{M}+1}=T_0+\frac{(1-\gamma )}{ABC(\gamma )}\{r(1-bT(t_{\mathsf{M}}))T(t_{\mathsf{M}})-(p_3\mathsf{E}(t_{\mathsf{M}})+k_{T(t_{\mathsf{M}})}\mathsf{M}(t_{\mathsf{M}}))T(t_{\mathsf{M}})\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}(\frac{r(1-b{T}_{k_1})T_{k_1}-(p_3{\mathsf{E}}_{k_1}+k_{T_{k_1}}{\mathsf{M}}_{k_1})T_{k_1}}{h}{B}_1$$

$$-\frac{r(1-b{T}_{k_1-1})T_{k_1-1}-(p_3{\mathsf{E}}_{k_1-1}+k_{T_{k_1-1}}{\mathsf{M}}_{k_1-1})T_{k_1-1}}{h}{A}_{\gamma ,k_1,2}),$$

$${\mathsf{M}}_{\mathsf{M}+1}={\mathsf{M}}_0+\frac{(1-\gamma )}{ABC(\gamma )}\{-{\gamma }_2\mathsf{M}(t_{\mathsf{M}})+V(t)\}$$

$$+\frac{\gamma }{\Gamma (\gamma )\times ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}(\frac{-{\gamma }_2{\mathsf{M}}_{k_1}+V(t)}{h}{B}_1$$

$$-\frac{-{\gamma }_2{\mathsf{M}}_{k_1-1}+V(t)}{h}{A}_{\gamma ,k_1,2}),$$

where $A_{\gamma ,k_1,2}={\int }_{t_{k_1}}^{t_{k_1+1}}({\tau }_1-t_{k_1}){(t_{\mathsf{M}+1}-{\tau }_1)}^{\gamma -1}d{\tau }_1$ and $B_1={\int }_{t_{k_1}}^{t_{k_1+1}}({\tau }_1-t_{k_1-1}){(t_{\mathsf{M}+1}-{\tau }_1)}^{\gamma -1}d{\tau }_1.$ By integrating the above and putting in a system of equations, we have

$${\mathsf{S}}_{\mathsf{M}+1}={\mathsf{S}}_0+\frac{(1-\gamma )}{ABC(\gamma )}\{{\gamma }_1\mathsf{S}(t_{\mathsf{M}})-k_{\mathsf{S}(t_{\mathsf{M}})}\mathsf{M}(t_{\mathsf{M}})\mathsf{S}(t_{\mathsf{M}})\}$$

$$+\frac{\gamma }{ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}(\frac{h^{\gamma }\{{\gamma }_1{\mathsf{S}}_{k_1}-k_{{\mathsf{S}}_{k_1}}{\mathsf{M}}_{k_1}{\mathsf{S}}_{k_1}\}}{h}{B}_1$$

$$-\frac{h^{\gamma }\{{\gamma }_1{\mathsf{S}}_{k_1-1}-k_{{\mathsf{S}}_{k_1-1}}{\mathsf{M}}_{k_1-1}{\mathsf{S}}_{k_1-1}\}}{h}{A}_{\gamma ,k_1,2}),$$

$${\mathsf{E}}_{\mathsf{M}+1}={\mathsf{E}}_0+\frac{(1-\gamma )}{ABC(\gamma )}\{\alpha -\mu \mathsf{E}(t_{\mathsf{M}})+\frac{p_1\mathsf{E}(t_{\mathsf{M}})\mathsf{S}(t_{\mathsf{M}})}{(\mathsf{S}(t_{\mathsf{M}})+1)}-p_2(T(t_{\mathsf{M}})+\mathsf{M}(t_{\mathsf{M}}))\mathsf{E}(t_{\mathsf{M}})\}$$

$$+\frac{\gamma }{ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}(\frac{h^{\gamma }\{\alpha -\mu {\mathsf{E}}_{k_1}+\frac{p_1{\mathsf{E}}_{k_1}{\mathsf{S}}_{k_1}}{({\mathsf{S}}_{k_1}+1)}-p_2(T_{k_1}+{\mathsf{M}}_{k_1}){\mathsf{E}}_{k_1}\}}{h}{B}_1$$

$$-\frac{h^{\gamma }\{\alpha -\mu {\mathsf{E}}_{k_1-1}+\frac{p_1{\mathsf{E}}_{k_1-1}{\mathsf{S}}_{k_1-1}}{({\mathsf{S}}_{k_1-1}+1)}-p_2(T_{k_1-1}+{\mathsf{M}}_{k_1-1}){\mathsf{E}}_{k_1-1}\}}{h}{A}_{\gamma ,k_1,2}),$$

$$T_{\mathsf{M}+1}=T_0+\frac{(1-\gamma )}{ABC(\gamma )}\{r(1-bT(t_{\mathsf{M}}))T(t_{\mathsf{M}})-(p_3\mathsf{E}(t_{\mathsf{M}})+k_{T(t_{\mathsf{M}})}\mathsf{M}(t_{\mathsf{M}}))T(t_{\mathsf{M}})\}$$

$$+\frac{\gamma }{ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}(\frac{h^{\gamma }\{r(1-b{T}_{k_1})T_{k_1}-(p_3{\mathsf{E}}_{k_1}+k_{T_{k_1}}{\mathsf{M}}_{k_1})T_{k_1}\}}{h}{B}_1$$

$$-\frac{h^{\gamma }\{r(1-b{T}_{k_1-1})T_{k_1-1}-(p_3{\mathsf{E}}_{k_1-1}+k_{T_{k_1-1}}{\mathsf{M}}_{k_1-1})T_{k_1-1}\}}{h}{A}_{\gamma ,k_1,2}),$$

$${\mathsf{M}}_{\mathsf{M}+1}={\mathsf{M}}_0+\frac{(1-\gamma )}{ABC(\gamma )}\{-{\gamma }_2\mathsf{M}(t_{\mathsf{M}})+V(t)\}$$

$$+\frac{\gamma }{ABC(\gamma )}\sum _{k_1=0}^{\mathsf{M}}(\frac{h^{\gamma }\{-{\gamma }_2{\mathsf{M}}_{k_1}+V(t)\}}{h}{B}_1$$

$$-\frac{h^{\gamma }\{-{\gamma }_2{\mathsf{M}}_{k_1-1}+V(t)\}}{h}{A}_{\gamma ,k_1,2}),$$

where

$$A_1={\{\mathsf{M}+1-k_1)}^{\gamma +1}-{(\mathsf{M}-k_1)}^{\gamma }(\mathsf{M}-k_1+1+\gamma )\}$$

and

$$A_2={\{\mathsf{M}+1-k_1)}^{\gamma }(\mathsf{M}-k_1+2+\gamma )-{(\mathsf{M}-k_1)}^{\gamma }(\mathsf{M}-k_1+2+2\gamma )\}.$$

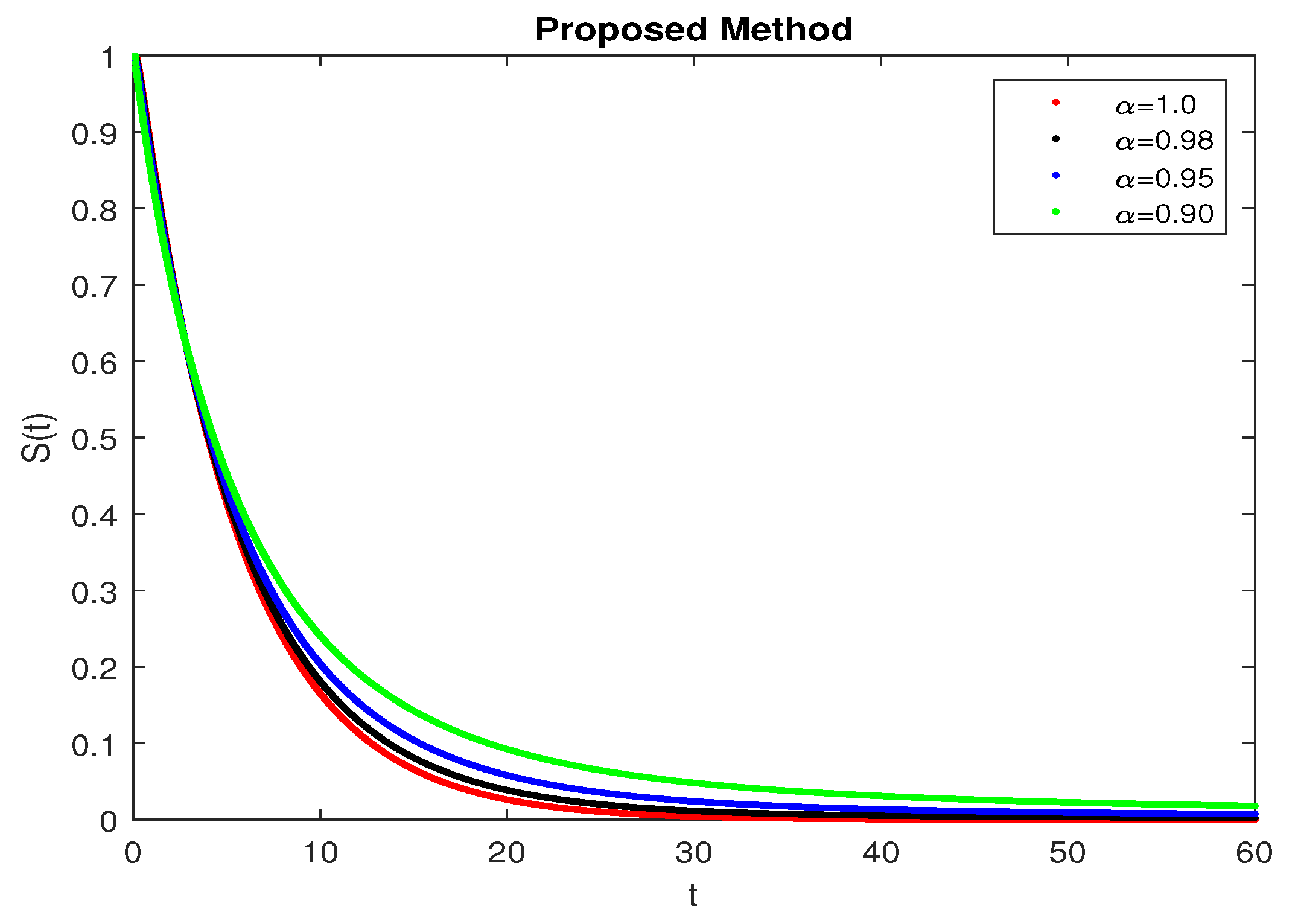
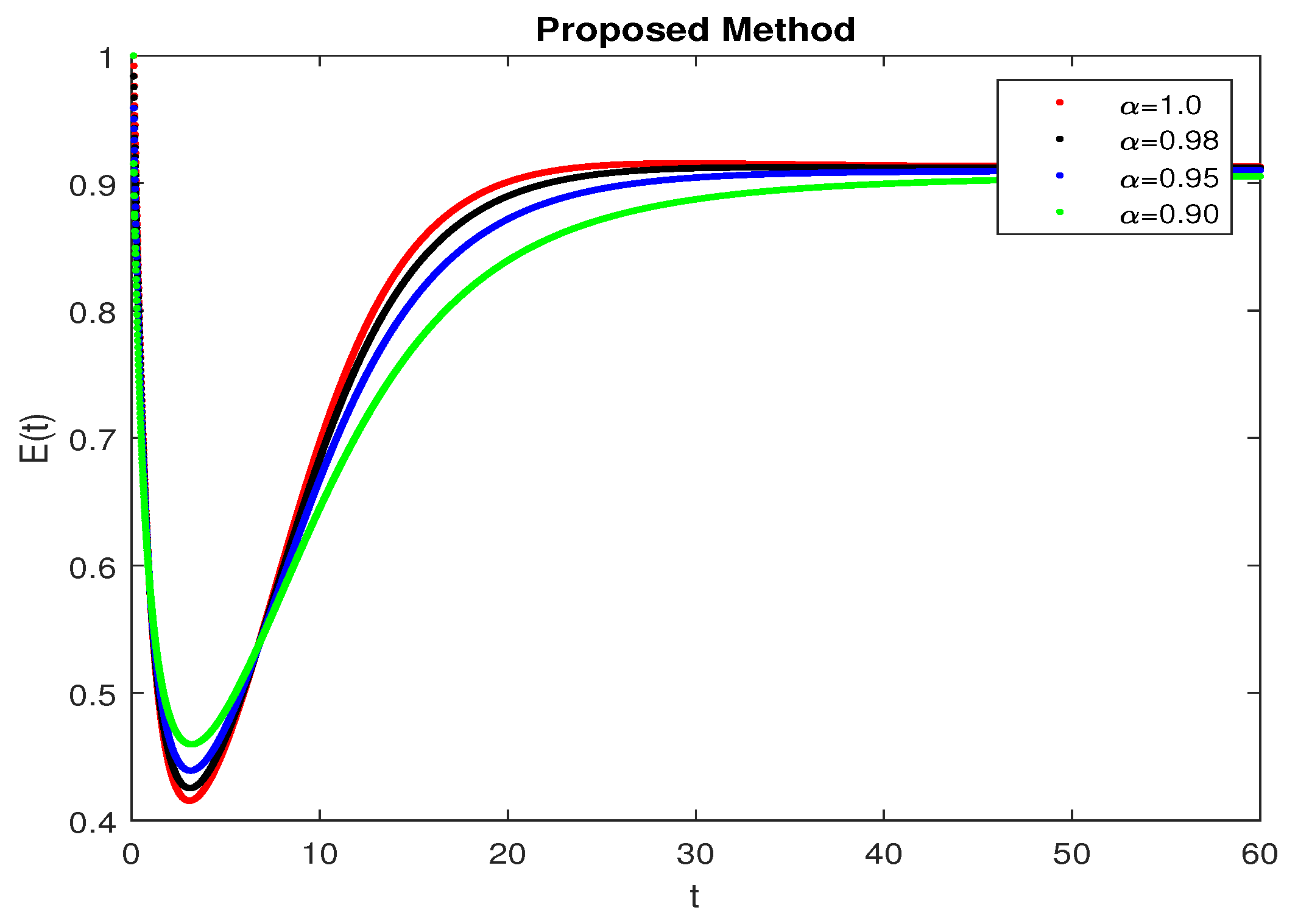
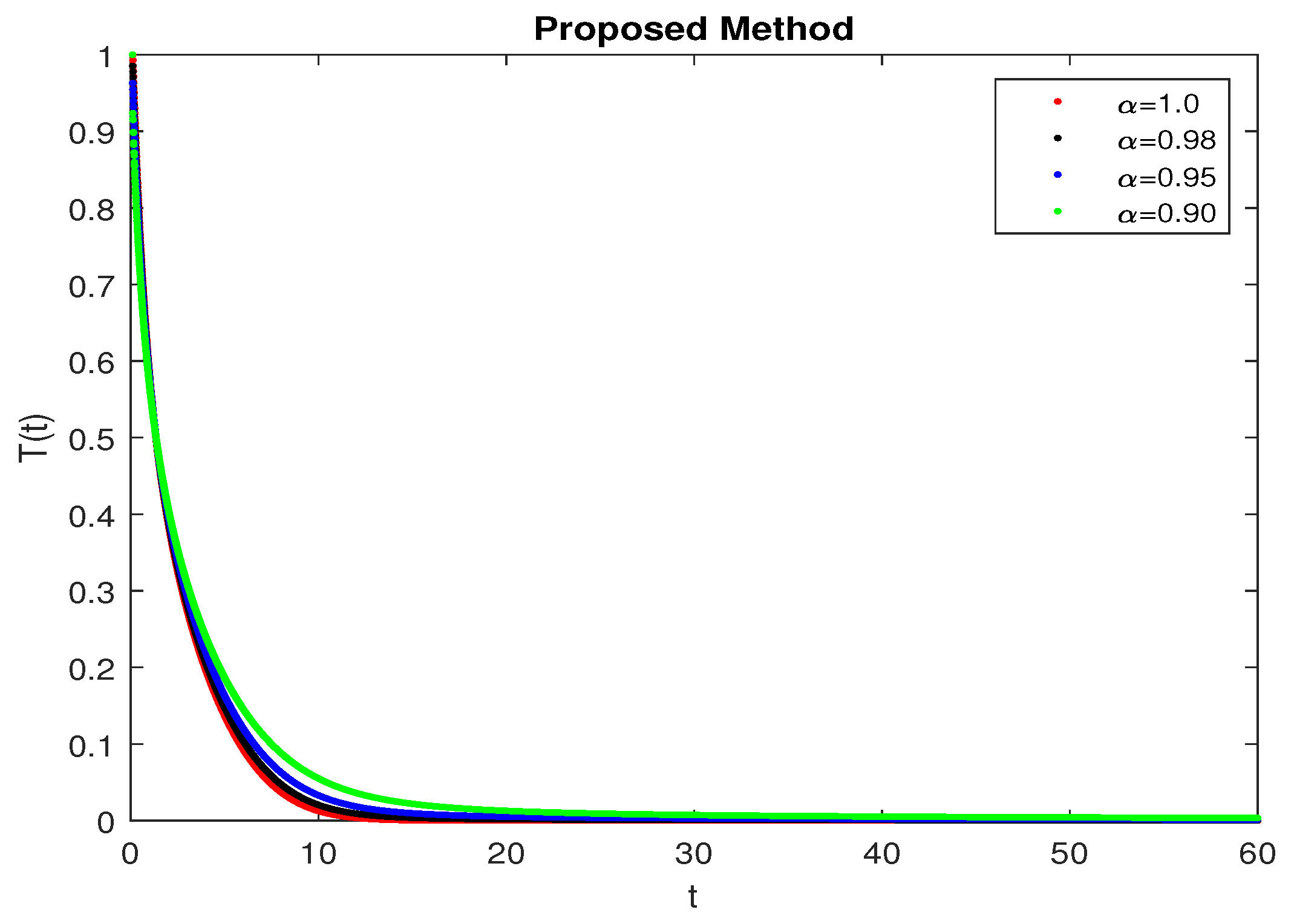
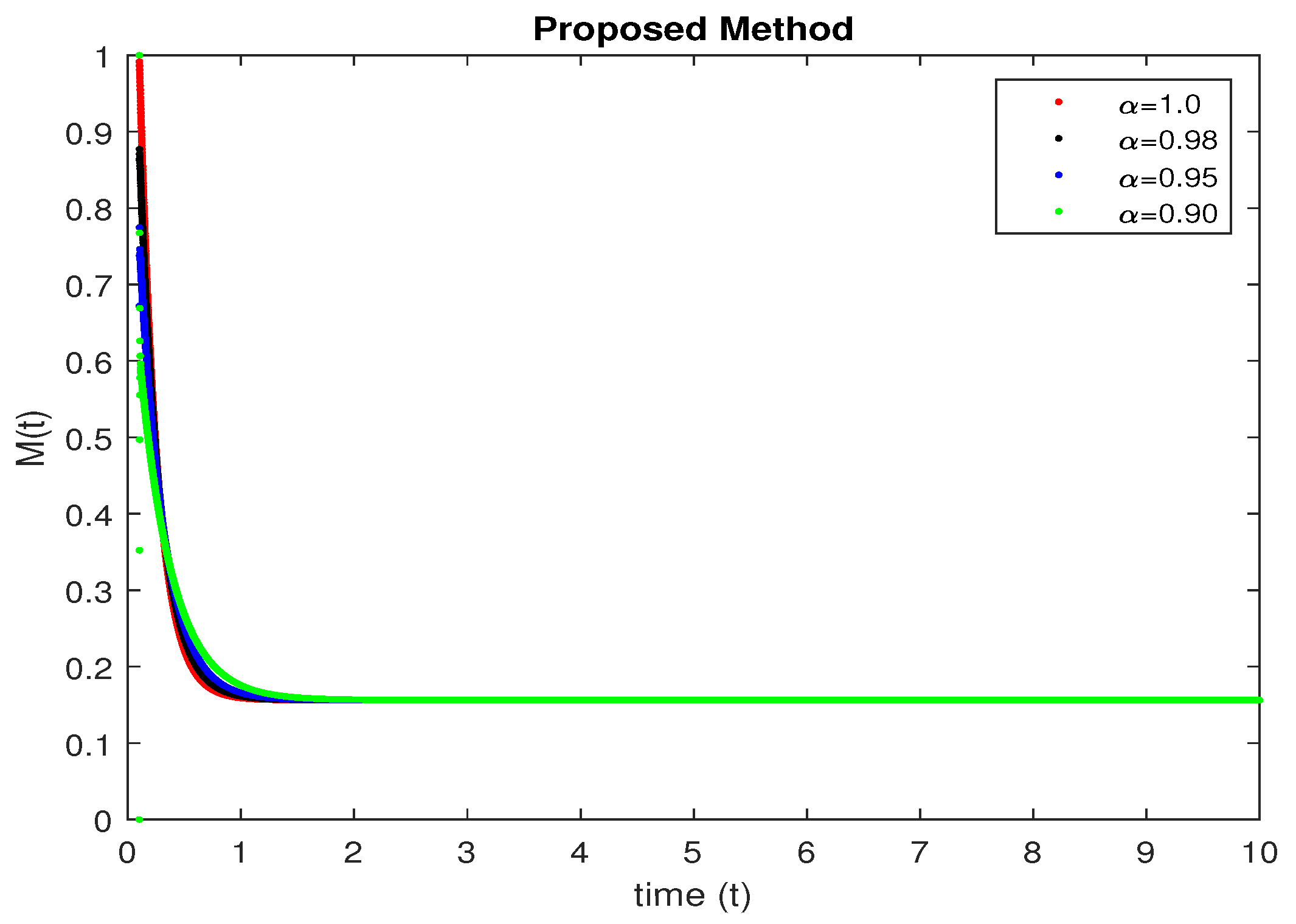
5. Numerical Results and Discussion

To evaluate the possible effectiveness of cancer transmission within the community, the cancer fractional-order version with stem cells and chemotherapy was furnished. This is why, for the fractional-order version of the cancer model, we employed Atangana–Baleanu in a Caputo sense derivative with the Samudu transform and a better Atangana–Toufik numerical scheme. The mechanical aspects of the fractional-order version were identified with time-fractional parameters by using the numerous numerical tactics. In order to acquire an analytical solution in the form of convergent series with easily calculable components, we first applied a relatively approach to the analysis method on the resulting time-fractional partial differential equations. With the aid of our numerical analysis, we were able to make some suggestions regarding the proper order (fractional) of derivatives in time to be applied while simulating a cancer tumor. The numerical study, which was performed in Matlab 2020R, uncovered some of the reasons why some cancer tumor models require fractional order of derivative in time. The findings demonstrated that the concentration of cancer cells decreased with time until it reached zero with this kind of killing rate and the specified initial condition. Here, the fractional order has no discernible impact. It is easily observed that the solution lies in the bounded domain and converged to a steady state for all Figure 1, Figure 2, Figure 3 and Figure 4 according to different fractional order values. Moreover, it can be seen from Figure 3 that stem and tumor cells reached zero after a few days, while effector cells and chemotherapy came to a stable position, as shown in Figure 4. The behavior of the system was analyzed through simulation by comparing the results at integer values ($\alpha =1$) and noninteger values ($\alpha \ne 1$) by using the proposed technique.

6. Conclusions

We tested the cancer version with stem cells and chemotherapy by using a fractional operator to look at the disorder’s dynamic behavior in the community. We employed the Sumudu transform and a numerical scheme to gain a sensible technique in order to develop knowledge of the epidemic’s real behavior. The fixed point concept was used to validate the existence and distinctiveness of the system’s answer. Within the framework of the fractional derivatives, nonlinear FDEs were suggested from derivatives of the usage of nonsingular as well as nonlocal kernels. Simulations were demonstrated to check the actual effects of cancer with stem cells and chemotherapy in a community. This kind of research will assist physicians with cancer disease treatment plans, decision making, and remedy.

Chemotherapeutic medications caused a symmetrical behavior with distinct fractional values in which the percentage of tumor cells started to decline and the percentage of immune cells and normal cells grew. These solutions have the same pattern of bounding to the steady state point. By proving the relationship between chemotherapy medications and increasing immunity against a particular malignancy, this represents a breakthrough in the treatment of cancer tumors. Furthermore, it is noted that the suggested methods are an effective method that may be used to resolve further nonlinear fractional-order differential equations that are appearing in the field of biological sciences.