Halo Orbits under Some Perturbations in cr3bp
Abstract
1. Introduction
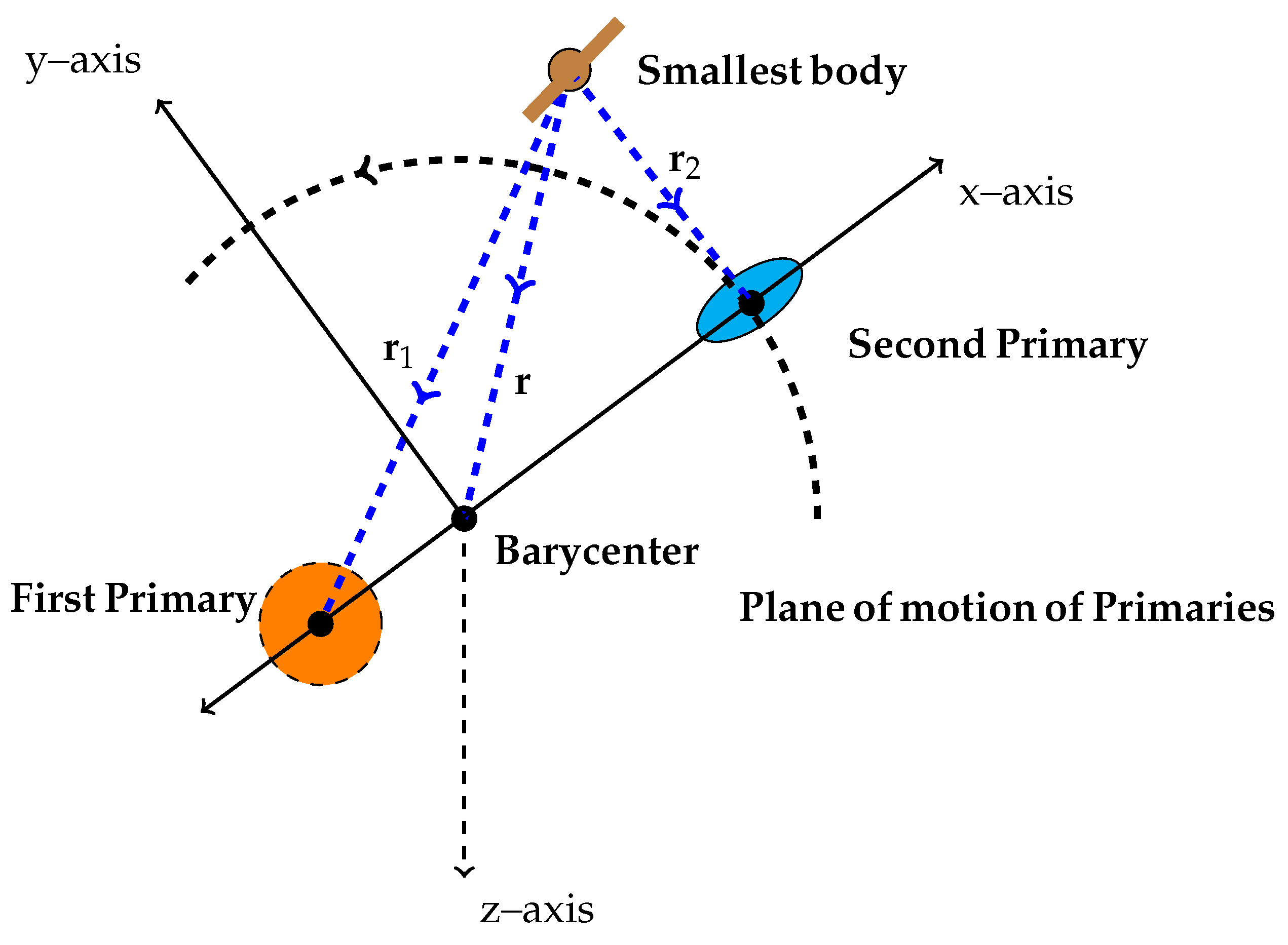
2. Equations of Motion
3. Numerical Studies
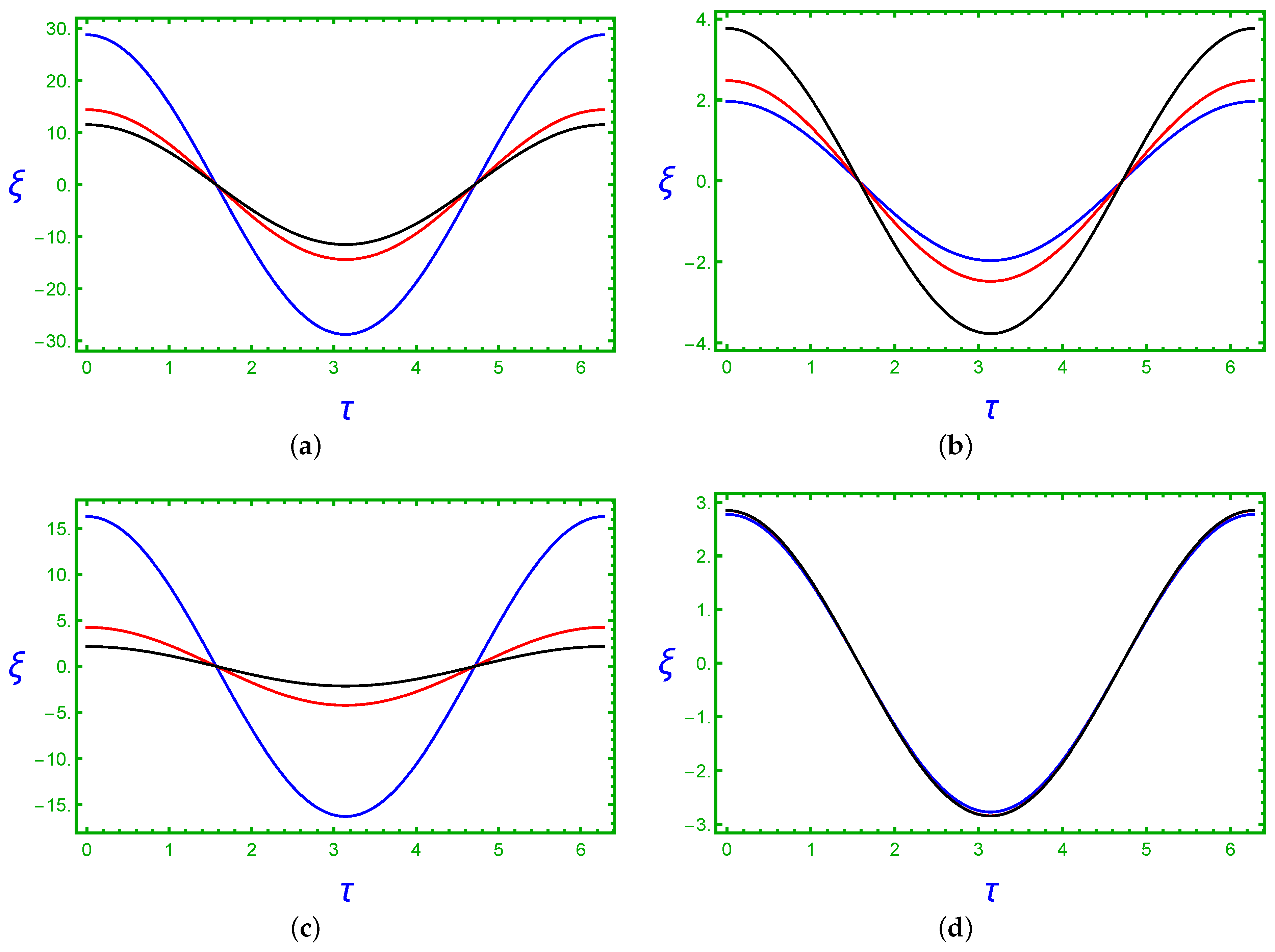
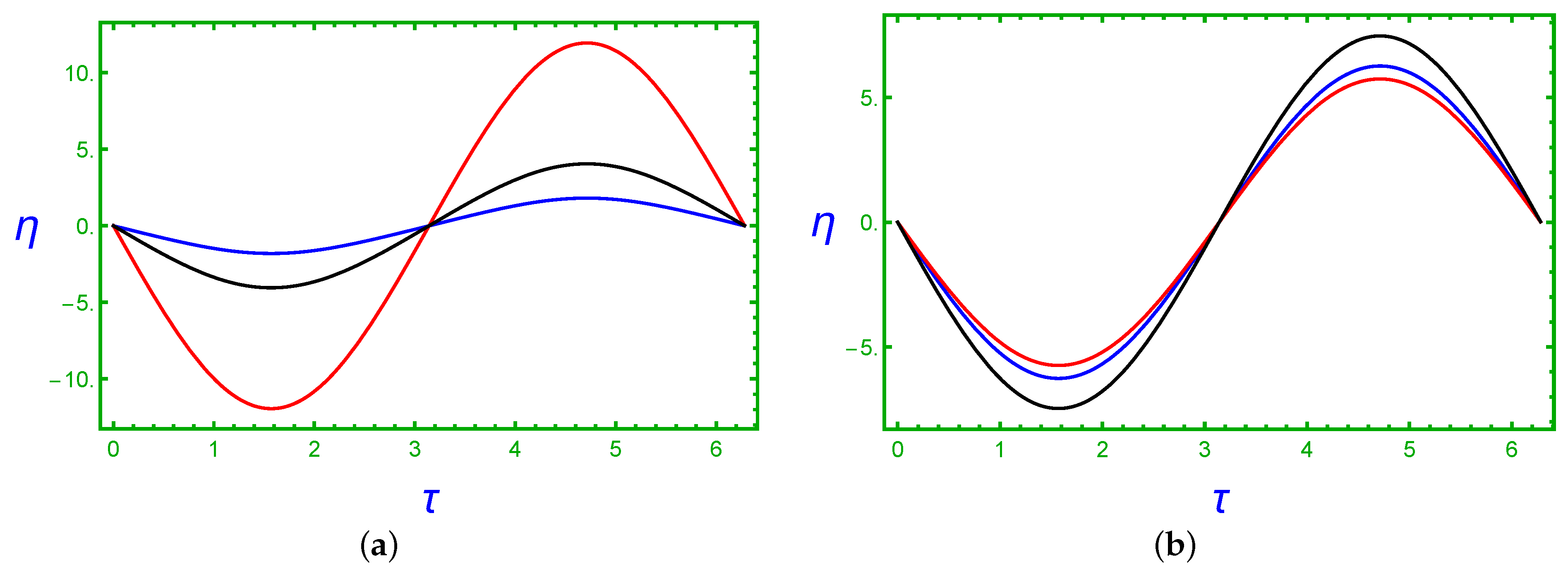
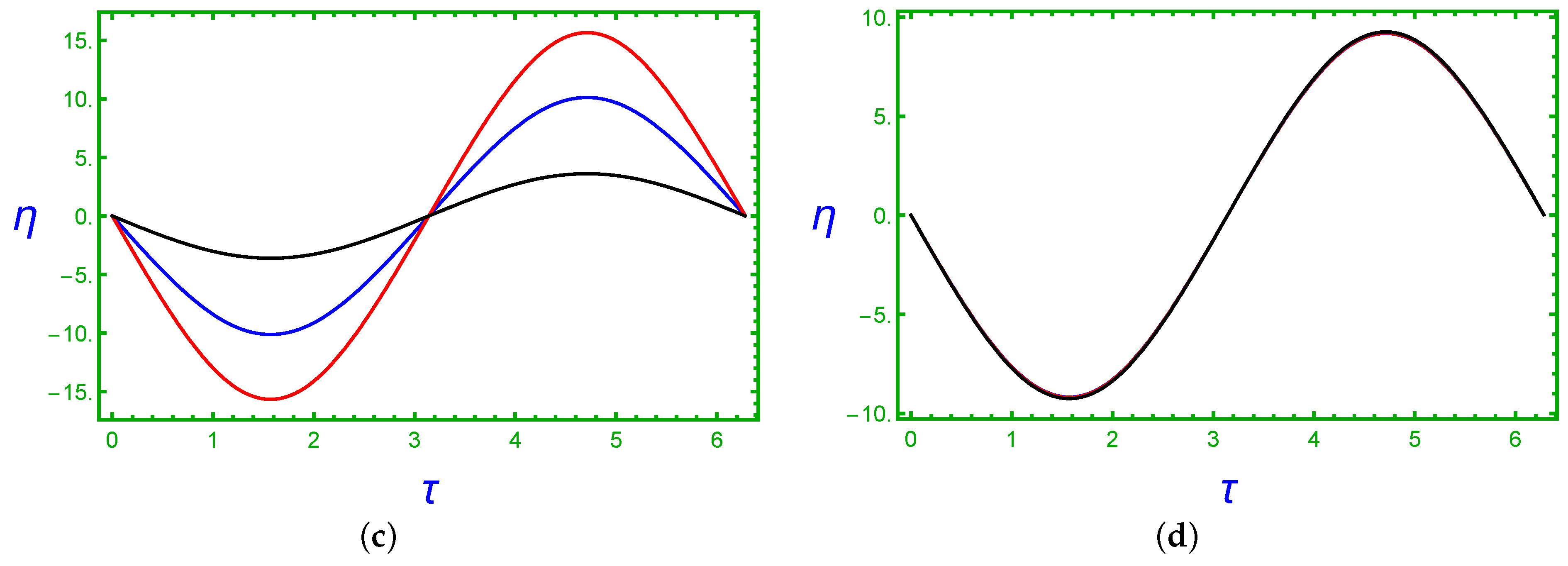
3.1. Time Series
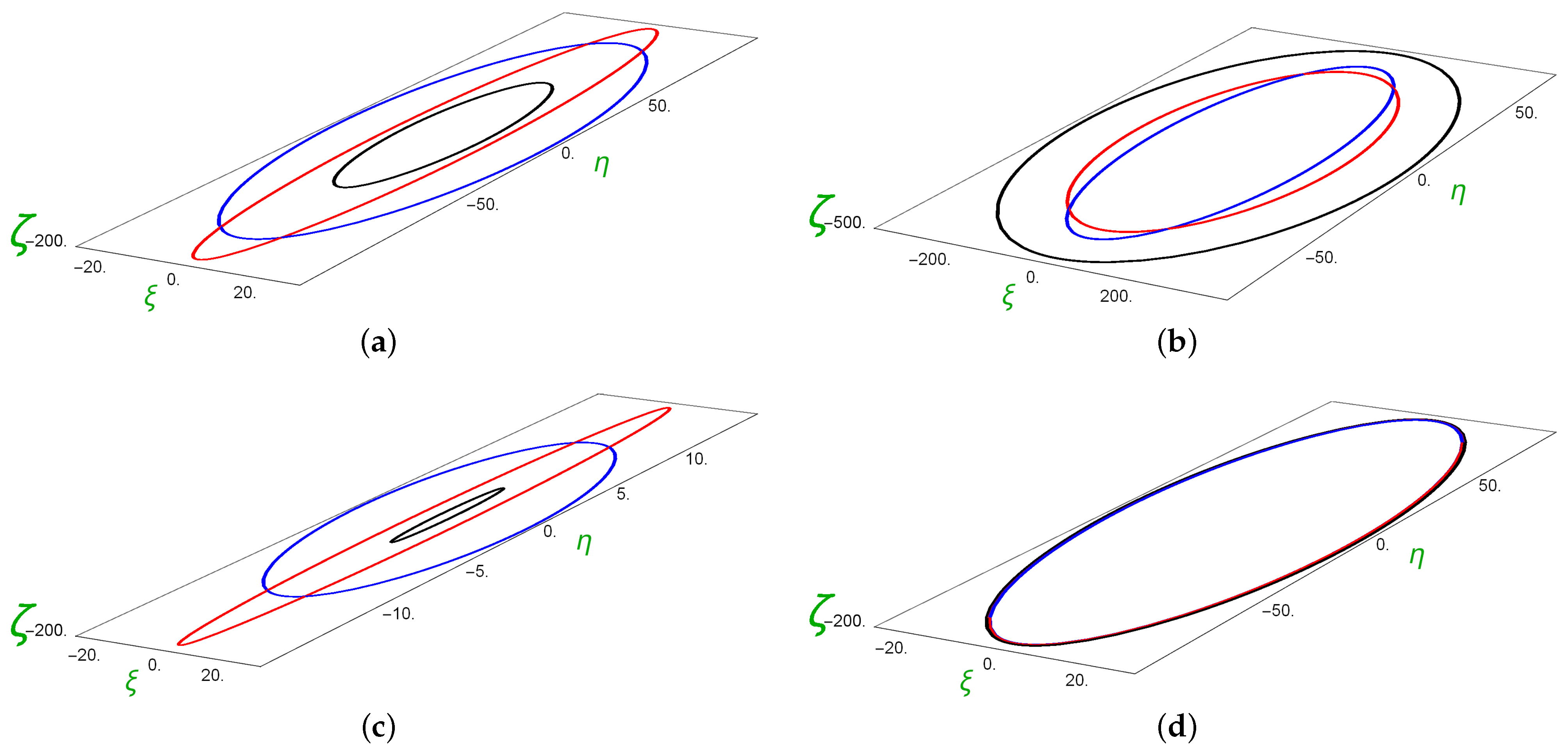
3.2. Halo Orbits
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| (x, y, z) | Coordinate of the test particle |
| n | Mean motion |
| Mass of the primary | |
| Mass of the secondary | |
| Mass of the test particle | |
| Initial mass of the test particle | |
| Radiation parameter | |
| Oblateness factor | |
| Distance of the test particle from the primary | |
| Distance of the test particle from the secondary | |
| Mass ratio | |
| Mass variation parameters | |
| Position vector of the test particle |
Appendix A
References
- Farquhar, R.W.; Muhonen, D.P.; Richardson, D.L. Mission design for halo orbiter of the Earth. J. Spacecr. Rocket. 1977, 14, 170–177. [Google Scholar] [CrossRef]
- Breakwell, J.; Brown, J.V. The ‘halo’ family of 3-dimensional periodic orbits in the Earth–Moon restricted three-body problem. Celest. Mech. 1979, 20, 389–404. [Google Scholar] [CrossRef]
- Richardson, D.L. Halo orbit formulation for the ISEE-3 mission. J. Guid. Control 1980, 3, 543–548. [Google Scholar] [CrossRef]
- Howell, K.C. Three-dimensional, periodic, ‘halo’ orbits. Celest. Mech. 1984, 32, 53–71. [Google Scholar] [CrossRef]
- Cielaszyk, D.; Wie, B. New approach to halo orbit determination and control. J. Guid. Control Dyn. 1996, 19, 266–273. [Google Scholar] [CrossRef]
- Gomez, G.; Jorba, A.; Masdemont, A.; Simo, C. Study of the transfer between halo orbits. Acta Astronaut. 1998, 43, 493–520. [Google Scholar] [CrossRef]
- Serban, R.; Koon, W.S.; Lo, M.W.; Marsden, J.E.; Petzold, L.R.; Ross, S.D.; Wilson, R.S. Halo orbit mission correction maneuvers using optimal control. Automatica 2002, 38, 571–583. [Google Scholar] [CrossRef]
- Rahmani, A.; Jalali, M.A.; Pourtakdoust, S. Optimal approach to halo orbit control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, TX, USA, 11–14 August 2003; p. 5748. [Google Scholar]
- Farres, A.; Jorba, A. A dynamical system approach for the station keeping of a solar sail. J. Astron. Sci. 2008, 56, 199–230. [Google Scholar] [CrossRef]
- Tiwary, R.D.; Kushvah, B.S. Computation of halo orbits in the photogravitational Sun–Earth system with oblateness. Astrophys. Space Sci. 2015, 357, 73. [Google Scholar] [CrossRef]
- Pal, A.K.; Kushvah, B.S. Geometry of halo and lissajous orbits in the circular restricted three-body problem with drag forces. Mon. Not. R. Astron. Soc. 2016, 446, 959–972. [Google Scholar] [CrossRef]
- Bucciarelli, S.; Ceccaroni, M.; Celletti, A.; Pucacco, G. Qualitative and analytical results of the bifurcation thresholds to halo orbits. Ann. Mat. Pura Appl. 2016, 195, 489–512. [Google Scholar] [CrossRef]
- Chidambararaj, P.; Sharma, R.K. Halo orbits around Sun–Earth L1 in photogravitational restricted three-body problem with oblateness of smaller primary. Int. J. Astron. Astrophys. 2016, 6, 293. [Google Scholar] [CrossRef]
- Srivastava, V.K.; Kumar, J.; Kushvah, B.S. The effects of oblateness and solar radiation pressure on halo orbits in the photogravitational Sun–Earth system. Acta Astronaut. 2016, 129, 389–399. [Google Scholar] [CrossRef]
- Nath, P.; Ramanan, R.T. Precise halo orbit design and optimal transfer to halo orbits from earth using differential evolution. Adv. Space Res. 2016, 57, 202–217. [Google Scholar] [CrossRef]
- Qian, Y.; Yang, X.; Jing, W.; Zhang, W. An improved numerical method for constructing Halo/Lissajous orbits in a full solar system model. Chin. J. Aeronaut. 2018, 31, 1362–1374. [Google Scholar] [CrossRef]
- Boudad, K.K.; Howell, K.C.; Davis, D.C. Dynamics of synodic resonant near rectilinear halo orbits in the bicircular four-body problem. Adv. Space Res. 2020, 66, 2194–2214. [Google Scholar] [CrossRef]
- Sharma, R.K.; SubbaRao, P.V. Stationary solutions and their characteristic exponents in the restricted three-body problem when the more massive primary is an oblate spheroid. Celest. Mech. 1976, 13, 137–149. [Google Scholar] [CrossRef]
- Abdulraheem, A.; Singh, J. Combined effects of perturbations, radiation and oblateness on the periodic orbits in the restricted three-body problem. Astrophys. Space Sci. 2008, 317, 9–13. [Google Scholar] [CrossRef]
- Ceccaroni, M.; Celletti, A.; Pucacco, G. Birth of periodic and artificial halo orbits in the restricted three-body problem. Int. J. Non-Linear Mech. 2016, 81, 65–74. [Google Scholar] [CrossRef]
- Farres, A.; Jorba, A. Station keeping of a solar sail around a Halo orbit. Acta Astronaut. 2014, 94, 527–539. [Google Scholar] [CrossRef]
- Kumari, R.; Pal, A.K.; Abouelmagd, E.I.; Alhowaity, S. Approximation solution of the nonlinear circular Sitnikov restricted four-body problem. Symmetry 2021, 13, 1966. [Google Scholar] [CrossRef]
- Pal, A.K.; Abouelmagd, E.I.; Guirao, J.L.G.; Brzeziński, D.W. Periodic solutions of nonlinear relative motion satellites. Symmetry 2021, 13, 595. [Google Scholar] [CrossRef]
- Ansari, A.A.; Alhowaity, S.; Abouelmagd, E.I.; Sahdev, S.K. Analysis of Equilibrium points in Quantized Hill system. Mathematics 2022, 10, 2186. [Google Scholar] [CrossRef]
- Zhang, M.J.; Zhao, C.Y.; Xiong, Y.Q. On the triangular libration points in photo-gravitational restricted three-body problem with variable mass. Astrophys. Space Sci. 2012, 337, 107–113. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Ansari, A.A.; Ullah, M.S.; Guirao, J.L.G. A Planar Five-body Problem in a Framework of Heterogeneous and mass-variation effects. Astron. J. 2020, 160, 216. [Google Scholar] [CrossRef]
- Ansari, A.A. The circular restricted four- body problem with triaxial primaries and variable infinitesimal mass. Appl. Appl. Math. Int. J. 2018, 13, 818–838. [Google Scholar]
- Ansari, A.A.; Meena, K.R.; Prasad, S.N. Perturbed six-body configuration with variable mass. Rom. Astron. J. 2020, 30, 135–152. [Google Scholar]
- Ansari, A.A.; Abouelmagd, E.I. Variable mass motion in the Hénon-Heiles system. Mod. Phys. Lett. A 2021, 36, 2150150. [Google Scholar] [CrossRef]
- Sahdev, S.K.; Ansari, A.A. Various perturbations considered on the generalized circular restricted three-body problem. Sci. Int. Lahore 2020, 32, 771–776. [Google Scholar]
- Ansari, A.A.; Sahdev, S.K. The Kerr-like primaries in the circular hill problem with variable mass. Sol. Syst. Res. 2022, 56, 433–444. [Google Scholar] [CrossRef]
- Ansari, A.A.; Kellil, R.; Sahdev, S.K. Impact of some perturbations on the generalized elliptic hill problem. Mech. Solids 2022, 57, 1104–1117. [Google Scholar] [CrossRef]
- Albidah, A.B.; Ansari, A.A.; Kellil, R. Interaction of bodies in the circular restricted three-body problem with variable mass. Astron. Comput. 2023, 42, 100688. [Google Scholar] [CrossRef]
- Deng, Z.L.; Gao, Z.F.; Li, X.D.; Shao, Y. On the formation of PSR J1640+2224: A Neutron Star Born Massive? Astrophys. J. 2020, 892, 4. [Google Scholar] [CrossRef]
- Deng, Z.L.; Gao, Z.F.; Li, X.D.; Shao, Y. Evolution of LMXBs under Different Magnetic Braking Prescriptions. Astrophys. J. 2021, 909, 174. [Google Scholar] [CrossRef]
- Gao, Z.F.; Li, X.D.; Wang, N.; Yuan, J.P.; Wang, P. Constraining the braking indices of magnetars. Mon. Not. R. Astron. Soc. 2016, 456, 55–65. [Google Scholar] [CrossRef]
- Gao, Z.F.; Wang, N.; Shan, H.; Li, X.D.; Wang, W. The dipole Magnetic Field and Spin-down Evolutions of the High Braking index pulsar PSR J1640-4631. Astrophys. J. 2017, 849, 19. [Google Scholar] [CrossRef]
- Gao, Z.F.; Song, D.L.; Li, X.D.; Shan, H.; Wang, N. The equilibrium equations of Boson–Fermi systems in the Newtonian approximation. Astron. Nachr. 2019, 340, 241. [Google Scholar] [CrossRef]
- Gao, Z.F.; Xing, C.C.; Wang, N. The scattering of Dirac spinors in rotating spheroids. Eur. Phys. J. C 2020, 80, 582. [Google Scholar]
- Abouelmagd, E.I.; Mostafa, A. Out of plane equilibrium points locations and the forbidden movement regions in the restricted three-body problem with variable mass. Astrophys. Space Sci. 2015, 357, 58. [Google Scholar] [CrossRef]
- Jeans, J.H. Astronomy and Cosmogony; Cambridge University Press: Cambridge, MA, USA, 1928. [Google Scholar]
- Meshcherskii, I.V. Works on the Mechanics of Bodies of Variable Mass. GITTL Mascow 1949, 10, 142–149. [Google Scholar]
- Thurman, R.; Worfolk, P.A. The Geometry of Halo Orbits in the Circular Restricted Three-Body Problem; Technical Report; University of Minnesota: Minneapolis, MN, USA, 1996. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albidah, A.B.; Abdullah. Halo Orbits under Some Perturbations in cr3bp. Symmetry 2023, 15, 481. https://doi.org/10.3390/sym15020481
Albidah AB, Abdullah. Halo Orbits under Some Perturbations in cr3bp. Symmetry. 2023; 15(2):481. https://doi.org/10.3390/sym15020481
Chicago/Turabian StyleAlbidah, Abdulrahman B., and Abdullah. 2023. "Halo Orbits under Some Perturbations in cr3bp" Symmetry 15, no. 2: 481. https://doi.org/10.3390/sym15020481
APA StyleAlbidah, A. B., & Abdullah. (2023). Halo Orbits under Some Perturbations in cr3bp. Symmetry, 15(2), 481. https://doi.org/10.3390/sym15020481






