Topological Structure of the Order Parameter of Unconventional Superconductors Based on d- and f- Elements

Abstract

The superconducting order parameter (SOP) of a triplet superconductor UTe${}_2$ was constructed using the topological space group approach, in which, in contrast to phenomenological and topological approaches, the single pair function and phase winding in condensate are different quantities. The connection between them is investigated for the $D_{2h}$ point group and the $m^{\prime }{m}^{\prime }m$ magnetic group. It is shown how a non-unitary pair function of UTe${}_2$ can be constructed using one-dimensional real irreducible representations and Ginzburg–Landau phase winding. It is also shown that the total phase winding is non-zero in magnetic symmetry only. Experimental data on the superconducting order parameter of topological superconductors UPt${}_3$, Sr${}_2$RuO${}_4$, LaPt${}_3$P, and UTe${}_2$ are considered and peculiarities of their nodal structures are connected with the theoretical results of the topological space group approach.

1. Introduction

Superconductivity provides an ‘energy superhighway’ that greatly improves efficiency and capacity. The economic and energy impacts of superconductors are predicted to be huge. Many challenges are being addressed in order for superconductivity to play this important role in the electric power system. The main advantages of devices made from superconductors are low power dissipation, high-speed operation, and high sensitivity. Topological superconductors have also attracted great interest due to potential applications in topological quantum computing [1]. Consideration of time-reversal symmetry, parity symmetry, crystallographic symmetries, and topological phases in recent years has induced a breakthrough in our understanding of unconventional superconductors, whose properties are defined by d- and f- elements [2,3,4]. The concept of topological order is now firmly established as a key characteristic of condensed matter systems, such as topological metals and unconventional superconductors. Although the concept of topology is fundamentally different from the concept of symmetry or group theory, there is much interest in whether a nontrivial relationship between the two exists. A superconducting gap is one of the key parameters in the research of superconductivity. In conventional superconductors described by Bardeen–Cooper–Schrieffer (BCS) theory [5], the superconducting gap has a fully gapped s- wave structure. Ginzburg and Landau [6] introduced an additional degree of freedom for a totally symmetric pairing state, i.e., a phase $exp\left(im\varphi \right)$ with (m = $0,1,2\dots$), which follows from the gauge invariance of SOP (superconducting order parameter), which was identified with the wavefunction of a Cooper pair (or pairs). Thus, the concept of topology was incorporated into the fundamental work on superconductivity. However, in classical or s- type superconductors, the phase does not result in any additional observable structure of SOP. Nevertheless, subsequent studies of unconventional or nodal superconductors have revealed their unusual properties, which require the use of topological and group theory approaches to understand them. In topological superconductors, a nontrivial structure arises from the phase winding of SOP in a momentum space. This can be regarded as a natural extension of a vortex of the superconducting order to momentum space [7].

The first experiments on heavy fermion superconductor UPt${}_3$ revealed a non-singlet pairing [8] with the nodal line of SOP on the FS (Fermi surface) [9]. The odd parity of SOP and the triplet pairing of topological superconductors and in particular UPt${}_3$ manifest themselves by no change in Knight shift across the superconducting transition temperature, $T_c$; thus, it was demonstrated that UPt${}_3$ is an odd-parity triplet superconductor [10]. Longitudinal and ultrasonic velocity measurements of UPt${}_3$ indicated the presence of several transitions; namely, one corresponding to high-temperature A-phase ($T_c$ = 0.550 K), a second to a low temperature B phase ($T_c$ = 0.480 K), and a third C- phase at high magnetic field ($B>$^~1.3 T) [11]. The anisotropy and temperature dependence of the magnetic field penetration in the B- phase of UPt${}_3$ measured by μSR (muon spin relaxation) was accounted for by a superconducting gap function with a line of nodes in the basal plane and axial point nodes [12]. Neutron scattering experiments showed that the superconducting gap has a lower rotational symmetry than crystal symmetry [13]. The results of Kerr effect [14] and that of Josephson interferometry [15,16] manifest a transition between real and complex SOP, corresponding to A and B phases, respectively, which are consistent with the spatial symmetries of the $E_{2u}$ order parameter written as:

$$f\left(k\right)=\widehat{z}\left[{\eta }_1{k}_z\left(k_x^2-k_y^2\right)\pm 2i{\eta }_2{k}_z{k}_x{k}_y\right].$$

(1)

In this formula vanishing of ${\eta }_2$ and ${\eta }_1$ phases correspond to A and B phases, respectively, and $\widehat{z}$ stands for the $M_S=0$ projection of triplet spin OSP (opposite spin pairing state). However, it is not clear how this formula represents non-unitary SOP. Indeed, at zero ${\eta }_1$ we get $f\left(k\right)=\widehat{z}\left[\pm 2i{\eta }_2{k}_z{k}_x{k}_y\right]$. However, in quantum mechanics, any single wavefunction can be multiplied by an arbitrary phase factor, say $exp(i\pi /2)$, and such a complex SOP can be converted into a real one. Field orientation-dependent thermal conductivity measurements of UPt${}_3$ identified two point nodes at the poles, two line nodes below and above the equator in both B and C phases, and a striking two-fold oscillation within the basal plane in C phase [17]. The structure SOP was proposed as [18]:

$$f\left(k\right)=\widehat{z}\left(k_x+i{k}_y\right)(5k_z^2-1).$$

(2)

The complex phase diagram may be understood from the competing effects of the superconducting order parameter, the symmetry breaking field, and the Fermi surface anisotropy [19].

The first experiments on Sr${}_2$RuO${}_4$ showed no changes in the Knight shift in the ${}^{17}$O NMR (nuclear magnetic resonance) spectrum on passing through $T_c$, indicating an oddness of the SOP [20]. The results of $\mathsf{\mu }$SR experiments on superconductor Sr${}_2$RuO${}_4$ indicated the presence of spontaneous internal magnetic fields, i.e., TRSB (time-reversal symmetry breaking) [21], and the structure, corresponding to the IR (irreducible representation) $E_u$ of the $D_{4h}$ group was proposed as [22]:

$$E_u:\mathbf{d}\left(\mathbf{k}\right)=\widehat{z}\left(k_x\pm i{k}_y\right).$$

(3)

This non-unitary structure corresponds to angular momentum projections $m=\pm 1$. The square modulus of this function is constant and nodeless in any plane normal to $k_z$- direction and does not represent experimentally observed lines of nodes [23], which were identified as gap minima or zeros along $\left(100\right)$ and $\left(110\right)$ directions [24] and also in horizontal plane [25]. Observed Kerr rotation below $T_c$ implies TRSB [26] and is consistent with a non-unitary SOP of the form (3). However, a reduction in the ${}^{17}$O Knight shift observed for all strain values and temperatures at T$<T_c$ [27,28,29] suggests even SOP and singlet pairs, which were described by an even chiral function:

$$E_g:\mathbf{d}\left(\mathbf{k}\right)=d_{zx}\pm i{d}_{zy}.$$

(4)

On the other hand, for the unstrained samples, the reduction in Knight shift of approximately 50% is not inconsistent with the helical states of $A_{1u,2u}$ or $B_{1u,2u}$ symmetry, which are written as [27]:

$$A_{1u}\left(B_{1u}\right):\mathbf{d}\left(\mathbf{k}\right)=\widehat{x}{k}_x\pm \widehat{y}{k}_y,$$

(5)

$$B_{2u}\left(A_{2u}\right):\mathbf{d}\left(\mathbf{k}\right)=\widehat{x}{k}_y\pm \widehat{y}{k}_x,$$

(6)

where $\widehat{x}$ and $\widehat{y}$ stand for the components of triplet spin in the case of ESP (equal spin pairing).

Nevertheless, there is no doubt about other unusual properties of this superconductor. Recent $\mathsf{\mu }$SR experiments established a splitting between $T_c$ and the temperature of TRSB, which rules out any mechanism based on interaction of magnetic fluctuations and conventional superconductivity [30].

Making use of resonant ultrasound spectroscopy, the symmetry-resolved elastic tensor of Sr${}_2$RuO${}_4$ was measured and a two-component order parameter in the two following forms was proposed [31]:

$$\left\{d_{zx}{d}_{zy}\right\},$$

(7)

$$\left\{d_{x^2-y^2,}{g}_{xy(x^2-y^2)}\right\}.$$

(8)

Formula (8) represents an exotic state which includes simultaneously two angular moments, $L_z=2$ and $L_z=4$, and it can also be plotted in a complex form [32]:

$$\left\{d+i{g}_{xy(x^2-y^2)}\right\}.$$

(9)

On the basis of theoretical calculations, it was argued that Hund’s coupling, which already dominates response functions in the normal state, remains key also for the superconducting pairing in Sr${}_2$RuO${}_4$ [33]. Therefore, the order parameter symmetry for Sr${}_2$RuO${}_4$ remains an open question. Using $\mathsf{\mu }$SR measurements and symmetry analysis it was shown that LaPt${}_3$P is a singlet chiral d- wave superconductor with a gap function (4) [34].

Recently discovered triplet superconductor UTe${}_2$ has a strongly anisotropic upper critical field, $H_{c2}$ = 35 T, which exceeds the Pauli limit for a singlet pair [35], and the Knight shift is constant through the superconducting transition [36,37], which corresponds to triplet pairing. The phase diagram under high magnetic fields depicts a regime in which superconductivity can be field stabilized [35]. The combination of thermal expansion and heat capacity under pressure shows clear evidence for two competing superconducting transitions in UTe${}_2$ [38]. However, recent experiments report a single superconducting transition [39] and bring into question whether UTe${}_2$ is a multicomponent superconductor at ambient pressure. A polar Kerr effect confirmed the TRSB in UTe${}_2$ and non-unitary complex SOP [40]. However, all IRs of symmetry group $D_{2h}$ are real and one-dimensional and the SOP is usually represented by a complex combination of two IRs of $D_{2h}$ [41].

$$B_{3u}+i{B}_{2u},$$

(10)

which represents the orbital momentum projection of a pair $m=1$. The results of specific heat measurements are most likely described by a vector order parameter with point node in the a- direction [42].

$$d\left(k\right)=(\widehat{y}+i\widehat{z})(k_y+i{k}_z).$$

(11)

This order parameter represents coupling of spin and orbital moments into orbital momentum projection $m=2$.

Models of superconductivity in UTe${}_2$ are connected with on-site or interatomic Coulomb (exchange) interactions. For example, a Hund’s–Kondo pairing mechanism has the ability to harness the coherence of Kondo hybridization to couple pre-formed Hund’s triplets into a superconducting condensate [43].

Triplet basis functions for the $D_{2h}$ point group written in terms of direct products of k- vector components and real triplet spin vectors are presented in

Table 1. Triplet basis function of Cooper pairs for the $D_{2h}$ point group [44].

IR	Basis Functions
$A_u$	$k_x\widehat{x}$, $k_y\widehat{y}$, $k_z\widehat{z}$
$B_{1u}$	$k_y\widehat{x}$, $k_x\widehat{y}$, $k_x{k}_y{k}_z\widehat{z}$
$B_{2u}$	$k_x\widehat{z}$, $k_z\widehat{x}$, $k_x{k}_y{k}_z\widehat{y}$
$B_{3u}$	$k_z\widehat{y}$, $k_y\widehat{z}$, $k_x{k}_y{k}_z\widehat{x}$

.

In the presence of a magnetic field along one of the axes, the SOP is expressed as a complex linear combination of basis functions of different IRs (see

Table 2. Triplet basis functions with angular momentum for UTe${}_2$ in a magnetic field [44].

H	IRs
$H_x$	$A_u+i{B}_{3u}$, $B_{1u}+i{B}_{2u}$
$H_y$	$A_u+i{B}_{2u}$, $B_{1u}+i{B}_{3u}$
$H_z$	$A_u+i{B}_{1u}$, $B_{2u}+i{B}_{3u}$

).

Thus, experimental results represented in terms of model functions show various topological structures, which are the topic for investigation by phenomenological, topological, and group theory methods which will be considered in this paper.

According to Anderson [45], the wavefunction of a Cooper pair is constructed taking into account the Pauli exclusion principle. Thus, for k, a general point in a BZ (Brillouin zone), the wavefunctions of singlet and triplet pairs may be written by the two following formulas, respectively:

$$\begin{array}{ccc}\hfill {\psi }_k^s& =& \hfill \left({\phi }_k\left(r_1\right){\phi }_{-k}\left(r_2\right)+{\phi }_k\left(r_2\right){\phi }_{-k}\left(r_1\right)\right)S^0.\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\psi }_k^t& =& \hfill \left({\phi }_k\left(r_1\right){\phi }_{-k}\left(r_2\right)-{\phi }_k\left(r_2\right){\phi }_{-k}(r_1\right)S_{m_s}^1,m_s=-1,0,1.\hfill \end{array}$$

(13)

Formula (12) corresponds to a single pair in k- space. In a spherically symmetric case, to represent the SOP, which includes all pairs, one can replace the Ginzburg–Landau two-dimensional phase factor $exp\left(im\varphi \right)$ by a spherical function, $Y_m^l(\theta ,\varphi )$. In point group symmetry, linear combinations which transform according to IRs of point groups are used to represent the nodal structure and angular momentum of pairs in heavy fermion materials [46,47], UPt${}_3$ [48], and Sr${}_2$RuO${}_4$ [22]. In a singlet case, symmetry of the SOP is described by spherical functions with even l- values, and in a triplet case, spherical functions with odd l- values are used.

It should be noted that in a general case, for each IR $D^{\left(l\right)}$, of a rotation group $SO\left(3\right)$, there are even $D^{(l+)}$ and odd $D^{(l-)}$ extensions in the rotation group extended by the space inversion $SO\left(3\right)+I\times SO\left(3\right)$ [49]. Hence, the direct relation between the parity of angular momentum value and the spatial parity of pair function is a consequence of the basis function choice, but not of the symmetry requirements. Furthermore, transformation of triplet spin $S^1$ function into real components is possible if time-reversal symmetry is not violated [50].

Some representations of the SOP in $D_{4h}$ symmetry are presented in

Table 3. Phenomenological pair functions for $D_{4h}$ symmetry [22,46].

	Singlet Pair		Triplet Pair
IR	Basis function	IR	Basis function
$A_{1g}$	$k_x^2+k_y^2$	$A_{1u}$	$\widehat{x}{k}_x+\widehat{y}{k}_y$
$A_{1g}$	$k_z^2$	$A_{1u}$	$\widehat{z}{k}_z$
$A_{2g}$	$k_x{k}_y\left(k_x^2-k_y^2\right)$	$A_{2u}$	$\widehat{x}{k}_y-\widehat{y}{k}_x$
$B_{1g}$	$k_x^2-k_y^2$	$B_{1u}$	$\widehat{x}{k}_x-\widehat{y}{k}_y$
$B_{2g}$	$k_x{k}_y$	$B_{2u}$	$\widehat{x}{k}_y+\widehat{y}{k}_x$
$E_g$	$k_z\left(k_x,k_y\right),$	$E_u$	$\widehat{z}\left(k_x,k_y\right),$$k_z\left(\widehat{x},\widehat{y}\right),$$\widehat{z}(k_x\pm i{k}_y)$

. Real combinations are similar to basis functions in crystal field theory. Functions of type $\widehat{x}{k}_x+\widehat{y}{k}_y$ represent coupling of spin and orbital pair moments and are called helical. Complex function $\widehat{z}(k_x\pm i{k}_y)=\widehat{z}\left|k\right|\exp (\pm i\varphi )$ represents chiral states with phase winding with $m=\pm 1$ in the plane normal to the $k_z$ direction. Furthermore, one can write the triplet SOP as $k_z\left(\widehat{x},\pm i\widehat{y}\right)$, the momentum of which is defined by the spin of the pair. Phenomenological nodal structures of a unitary SOP for the symmetry group $D_{4h}$ are unique for one-dimensional IRs, and for two-dimensional IRs only one vertical nodal plane, $\left(100\right)$ (or $\left(010\right)$), was obtained [51]. It should be noted that for two-dimensional IRs, the number of functions may be larger and the structure of the SOP may be classified on the basis of additional quantum numbers [52,53]. Since in the triplet case the spatial part of a pair is multiplied by the three-dimensional spin vector (12), the total number of possible IRs increases, and it was shown that a complete ban on triplet pairs of any certain symmetry is absent in planes of symmetry [54] (Blount theorem).

In the case of the $D_{2h}$ group (symmetry group of UTe${}_2$), all IRs are one-dimensional and real (see Table 1). Since the symmetry of the non-unitary SOP cannot be reproduced by basis functions of one IR, complex linear combinations of two IRs (see Formula (10) and Table 2) are used to represent experimental data. It was shown that in this case, the symmetry corresponds to magnetic group $m^{\prime }{m}^{\prime }m$ and a non-unitary SOP can be represented by a basis function of a single ICR (irreducible corepresentation) [55].

Topological approaches to the SOP are based on BdG (Bogoliubov–de Gennes) Hamiltonians for superconductors, and may be classified into ten symmetry classes (eight real classes and two complex classes) based on the presence and the absence of the fundamental discrete symmetries (particle-hole symmetry (PHS), time-reversal symmetry (TRS), and chiral symmetry (CS)), which are called the Altland–Zirnbauer (AZ) symmetry classes [56,57].

The symmetry classification of BdG systems in terms of the presence or absence of $SU\left(2\right)$ spin-rotation symmetry and TRS is presented in

Table 4. Symmetry classification of BdG systems. The symbols (+) and (−) denote the presence and the absence, respectively, of $SU\left(2\right)$ spin-rotation symmetry and TRS. In classes A and AIII, Hamiltonians are invariant under rotations about the z or any fixed axis in spin space, but not under full $SU\left(2\right)$ rotations, as denoted by R [58].

AZ Class	TRS	$\mathit{SU}\left(2\right)$	Examples in $2\mathit{d}$
D	−	−	Spinless chiral $(p\pm ip)$ wave
DIII	+	−	Superposition of $(p+ip)$ and $(p-ip)$ waves
A	−	R	Spinfull chiral $(p\pm ip)$ wave
AIII	+	R	Spinfull $p_x$ or $p_y$ wave
C	−	+	$(d\pm id)$ wave
CI	+	+	$d_{x^2-y^2}$ or $d_{xy}$ wave

.

The interplay between the symmetry group approach and topology is an active and perspective field of research which reveals the nature of order parameter and nodes in topological superconductors [59,60,61,62,63].

Weyl nodes are calculated through a topological Weyl charge [64,65]:

$$q_i=\frac{1}{2\pi }\underset{S}{\oint }dk\overrightarrow{F}\left(k\right),$$

where Berry flux is defined as:

$$F_i\left(k\right)=-i{\epsilon }^{ijk}\sum _{E_n\left(k\right)<0}{\partial }_{k_j}\langle u_n\left(k\right)|{\partial }_{k_k}{u}_n\left(k\right)\rangle .$$

Integration is provided on a closed surface surrounding an isolated point node.

Weyl nodes are described via defining the $k_z$-dependent Chern number on a plane $k_x-k_y$:

$$\nu \left(k_z\right)=\frac{1}{2\pi }\int d{k}_{\left|\right|}{F}_z\left(k\right).$$

Weyl charges for symmetry-related point nodes are defined by the following expression [66]:

$$\nu (k_z+0)-\nu (k_z-0)=\sum _i{q}_i.$$

(14)

The Chern number indicates the number of chiral surface modes. The number of chiral modes coincides with the $k_z$-dependent Chern number. The sign reversal of chirality is in accordance with the sign change of the Chern number [65].

A chiral superconductor is a superconductor in which the phase of the complex superconducting gap function, $\Delta (\overrightarrow{k})$, winds in a clockwise or counter-clockwise sense as $\overrightarrow{k}$ moves about some axis on the FS [67]. They indicate novel transport properties that depend on the topology of the order parameter, the topology of the FS, and the spectrum of the bulk [68].

Chiral superconductors are characterized by a Chern number equal to the winding number, $\nu$, of the phase of the Cooper pairs. Three-dimensional candidates for chiral superconductors are Sr${}_2$RuO${}_4$ and UPt${}_3$ [68].

Some experiments have suggested that UTe${}_2$ may be a chiral superconductor [35,37,69,70]. As a result of the orthorhombic structure of UTe${}_2$, there is no underlying symmetry argument for the existence of a two-component order parameter. Using a tight-binding model in [41], the authors showed that Weyl nodes generically exist for a two-component parameter order (10) with the charges $\pm 1$.

For superconductors with chiral symmetry, it is possible to define the topological winding number as [7]:

$$w_{1D}=\frac{i}{4\pi }\underset{C}{\oint }d{k}_{\mathsf{\mu }}tr\left[\mathsf{\Gamma }{H}^{-1}{\partial }_{k\mathsf{\mu }}H\right],$$

(15)

where $\mathsf{\Gamma }=iIC$ is the unitary operator and I and C are the time reversal symmetry and particle-hole symmetry, respectively.

Chiral pairing states in UPt${}_3$ are usually connected with $E_{1u}$ and $E_{2u}$. For the first order point nodes of the $E_{1u}$ and $E_{2u}$ states it was shown that ${\nu }_1=L_z=\pm 1$ and ${\nu }_2=L_z=\pm 2$, respectively [71]. These $L_z$- values were equal to those obtained by group theory for UPt${}_3$ [53]. The Chern number on the plane $k_x-k_y$ for a fixed $k_z$ is equal to $2\left(4\right)$ for the states $E_{1u}\left(E_{2u}\right)$ [7]. Non-zero Chern numbers lead to a Weyl arc along the surface projection of a path connecting the (anti) monopole node points.

In superconductor Sr${}_2$RuO${}_4$, the Chern number of chiral order parameter is equal to one ($\nu =1$) for a gap function of $E_u$ symmetry [72].

2. Preliminaries

As it follows from the introduction, most of the authors agree that superconductivity in UTe${}_2$, UPt${}_3$, Sr${}_2$RuO${}_4$, and LaPt${}_3$P is not associated with phonons, as it is postulated in BCS theory, but is eventually determined by the Coulomb interaction of d- or f- electrons at one center and/or the exchange interaction with neighbors or some spin fluctuations. These superconductors have many common features, i.e., their SOPs are chiral and nodal, but their types of spin coupling are different; namely, UTe${}_2$ is an ESP triplet, UPt${}_3$ is an OSP triplet, and Sr${}_2$RuO${}_4$ and LaPt${}_3$P are singlets.

Since the nature of the interactions responsible for superconductivity is still not known for certain, significant progress in understanding the nature of this phenomenon is provided by a symmetry analysis of experimental data. Phenomenological and topological approaches make it possible to describe the structure of the entire set of Cooper pairs (condensate) and do not include a quantum mechanical description of individual electron pairs.

The space group approach to the wavefunction of a Cooper pair [73,74] is based on the Anderson approach (12) [45], which describes a pair as a state of two equivalent electrons, constructed with allowance for the Pauli principle. In recent years, a general approach has been developed that takes into account the Pauli principle, the crystal structure, and the topological winding of the phase, and has been applied to UPt${}_3$[53] and Sr${}_2$RuO${}_4$ [50].

The present paper has two goals.

The first goal is to apply and further develop this method, which we will call the topological space group approach, to UTe${}_2$, and to obtain all possible structures of its triplet SOP.

The second goal is to reveal general trends of the influence of pair momentum and spin on the nodal structure by comparing the results for a number of superconductors based on d- and f- elements.

Paper Construction

In Section 3, the main formulas of the space group approach to the wavefunction of a Cooper pair are introduced.

In Section 4, the features of coupling of electrons with non-zero angular momentum are considered.

In Section 5, the topological space group approach is used to construct Cooper pairs’ wavefunctions for four odd IRs of group $D_{2h}$ and for four odd ICRs of magnetic group $m^{\prime }{m}^{\prime }m$.

In Section 6, general features of pair functions belonging to two-dimensional IRs, taking as examples the $D_{4h}$ and $D_{6h}$ groups, are considered.

In Section 7, the applications of theoretical results on experimental data of UPt${}_3$, Sr${}_2$RuO${}_4$, LaPt${}_3$P, and UTe${}_2$ are discussed.

3. Space Group Approach to the Wavefunction of a Cooper Pair

The space group approach to the wavefunction of a Cooper pair [73,74] is the generalization of the Anderson approach (12) for a Cooper pair on space group symmetries. This approach makes it possible to take into account point group symmetry, magnetic group symmetry, and non-symmorphic structures of the space groups. In recent years, some significant results have been obtained using the space group approach [75,76,77,78,79].

One-electron states in a crystal with symmetry group G are labeled by the wavevector k, its symmetry group H (little group), and the index $\kappa$ of small IR $D^{\kappa k}$ of H. In what follows, we will assume that one index $\kappa$ includes also k and therefore we will omit the index k. Consider a left coset decomposition of a space group with respect to H:

$$G=\sum _{\sigma }{s}_{\sigma }H.$$

(16)

The action of the left coset representatives $s_{\sigma }$ on k results in all prongs $k_{\sigma }$ of the wavevector star $\left\{k\right\}$:

$$k_{\sigma }=s_{\sigma }k+b_{\sigma },$$

(17)

where $b_{\sigma }$ is a reciprocal lattice vector. Thus, in crystal solids, one-electron states are defined by a wavevector star instead of two vectors k and $-k$ in the case of a spherically symmetric Fermi liquid. The IR of the space group is an induced representation $D^{\kappa }\uparrow G,$ defined as [80]:

$$D^{\kappa }{\uparrow G\left(g\right)}_{\sigma i,\tau j}=D_{i,j}^{\kappa }\left(s_{\sigma }^{-1}g{s}_{\tau }\right)\delta \left(s_{\sigma }^{-1}g{s}_{\tau },H\right),$$

(18)

where $\sigma$ and $\tau$ correspond to a left coset decomposition (16) of the space group with respect H and i and j correspond to the rows and columns of the matrix $D^{\kappa }$. In a general point of a BZ, the dimension of IR $D^{\kappa }\uparrow G$ is equal to the number n of point group elements of $\overline{G}$ (central extension of G). Two-electron space is a Kronecker square of this space and its dimension in a general $k-$ point is equal to $n^2$. This space can be easily decomposed into physically different parts by using the double coset decomposition of G with respect to H [80]:

$$G=\sum _{\delta }H{d}_{\delta }H.$$

(19)

The double coset representatives $d_{\delta }$ denote different terms in a Kronecker square $D^{\kappa }\uparrow G$ $\times D^{\kappa }\uparrow G$ decomposition. The notation × for a direct (Kronecker) product is used throughout. For each double coset $\delta$, a representation $P_{\delta }^{\kappa }$ is considered, which can be written as:

$$\chi \left(P_{\delta }^{\kappa }\left(m\right)\right)=\chi \left(D^{\kappa }\left(d_{\delta }^{-1}m{d}_{\delta }\right)\times D^{\kappa }\left(m\right)\right),$$

(20)

where $m\subset M_{\delta }=H\cap d_{\delta }^{-1}H{d}_{\delta }$. For self-inverse double cosets, i.e., if $H{d}_{\alpha }H=H{d}_{\alpha }^{-1}H$, there are two extensions of $P_{\alpha }^{\kappa }$ on group ${\tilde{M}}_{\alpha }=M_{\alpha }+a{M}_{\alpha }$:

$$\chi \left(P_{\alpha }^{\kappa +}\left(am\right)\right)=+\chi \left(D^{\kappa }\left(amam\right)\right),$$

(21)

$$\chi \left(P_{\alpha }^{\kappa -}\left(am\right)\right)=-\chi \left(D^{\kappa }\left(amam\right)\right),$$

(22)

where the coset representative a is chosen from the relation

$$ah=\overline{h}a,h,\overline{h}\subset H.$$

According to the Mackey–Bradley theorem [80], symmetrized (square brackets) and antisymmetrized (curly brackets) parts of the Kronecker square can be written as

$$\left[D^{\kappa }\uparrow G\times D^{\kappa }\uparrow G\right]=\left[D^{\kappa }\times D^{\kappa }\right]\uparrow G+\sum _{\alpha }{P}_{\alpha }^{{}_{{}^{\kappa +}}}\uparrow G+\sum _{\beta }{P}_{\beta }^{\kappa }\uparrow G,$$

(23)

$$\left\{D^{\kappa }\uparrow G\times D^{\kappa }\uparrow G\right\}=\left\{D^{\kappa }\times D^{\kappa }\right\}\uparrow G+\sum _{\alpha }{P}_{\alpha }^{\kappa -}\uparrow G+\sum _{\beta }{P}_{\beta }^{\kappa }\uparrow G.$$

(24)

The symmetrization (antisymmetrization) of the first item is performed by a standard point group technique on subgroup H, the sum in the second item runs over self-inverse double cosets, and the sum in the third item runs over non-self-inverse double cosets, i.e., if $H{d}_{\beta }H\ne H{d}_{\beta }^{-1}H$.

The total momentum of the resulting electron pair depends on a double coset representative and is written as:

$$K_{\alpha }=k+d_{\alpha }k+b_{\alpha },$$

(25)

where $b_{\alpha }$ is a reciprocal lattice vector. In the case of Cooper pairs, the double coset representative $d_{\alpha }$ is a space inversion, I, and in some symmetrical points on the surface of a BZ (Brillouin zone), $d_{\alpha }$ is an identity element E. In this case, zero total momentum of a pair is achieved by translation periodicity (25).

According to the Pauli exclusion principle, a symmetrized square $\left[D^{\kappa }\uparrow G\times D^{\kappa }\uparrow G\right]$ of the spatial part of the wavefunction corresponds to a singlet pair and antisymmetrized square $\left\{D^{\kappa }\uparrow G\times D^{\kappa }\uparrow G\right\}$ corresponding to a triplet pair. In the case of strong spin–orbit coupling, the total pair wavefunction belongs to an antisymmetrized square of a double valued IR. For $K=0$, the induced representation $P_{\alpha }^{{}_{{}^{\kappa \pm }}}\uparrow G$ is a reducible representation of a point group $\overline{G}$. The frequency, $f_{\kappa \alpha \pm }^q$, of appearance of any IR, ${\mathsf{\Gamma }}^q$, of $\overline{G}$ in the decomposition of induced representation $P_{\alpha }^{{}_{{}^{\kappa \pm }}}\uparrow \widehat{G}$ is given by Frobenius’ reciprocity theorem [80], i.e., by the formula:

$$f_{\kappa \alpha \pm }^q=\frac{1}{\left|{\tilde{M}}_{\alpha }\right|}\sum _{m\in {\tilde{M}}_{\alpha }}{\chi }^{*}\left({\mathsf{\Gamma }}^q\left(m\right)\right)\chi \left(P_{\alpha }^{{}_{{}^{\kappa \pm }}}\left(m\right)\right).$$

(26)

For k at a general point in the BZ, the group $M_{\alpha }$ consists only of the identity element and the group ${\tilde{M}}_{\alpha }=\{E,I\}$. The characters of the representations $P_{\alpha }^{\kappa +}$ and $P_{\alpha }^{\kappa -}$ for a spatial inversion I are equal to $+1$ and $-1$, respectively, and for the identity element E, both characters are $+1$. Using the reciprocity theorem, we find that at a general point of the BZ (one-electron) for singlet pairs, all even IRs are possible, and the spatial parts of triplet pairs are odd. Moreover, each IR of the point group enters the expansion as many times as its dimension. Thus, it follows from the Mackey–Bradley theorem that at a general point in the BZ, the dimensions of the spaces of singlet pairs and spatial part triplet pairs coincide and are equal to $\overline{G}/2$. In an $L-S$ coupling scheme, the spatial part of a triplet pair is multiplied by the three components of triplet spin, $\widehat{x}$, $\widehat{y}$, and $\widehat{z}$, and total dimension of the space of the total triplet pairs’ wavefunctions for k, a general point in a BZ, is $3\overline{G}/2$.

In a strong spin–orbit coupling case, the spin is included in the one-electron wavefunction and the pair wavefunction is calculated as the antisymmetrized square of the double-valued IRs of the space groups [80,81]. However, in k- points of low symmetry, an additional degeneracy due to time-reversal symmetry should be taken into account [74].

Inside the BZ, in the majority of cases (but not in all), the spatial part of a singlet pair is even and the spatial part of a triplet pair is odd. If IR $D^{\kappa }$ is two-dimensional (it takes place on the 3-fold, 4-fold, and 6-fold axes), one obtains from (20)–(22) that $\chi \left(P_I^{\kappa \pm }\left(E\right)\right)=4$, $\chi \left(P_I^{\kappa +}\left(I\right)\right)=2$, and $\chi \left(P_I^{\kappa -}\left(I\right)\right)=-2.$ Hence, it follows that in this case, even and odd IRs are mixed in the decomposition of symmetrized and antisymmetrized squares.

4. Coupling with Larger Total Angular Momentum

In the superconductors based on d- and f- elements, the on-site crystal field and term splitting is essential and should be taken into account in the theories of superconductivity. It has been pointed out that an unconventional gap structure can be realized with purely local (on-site) interactions and the Hund’s coupling. The electron–phonon interactions can enhance such anisotropic pairing states and a nontrivial momentum dependence of a superconducting gap function with ${\mathsf{\Gamma }}_9\times {\mathsf{\Gamma }}_9$ in the $D_6$ symmetry group was obtained [82].

In a strong spin–orbit coupling, electrons with angular moments $j=l+1/2$ and $j=l-1/2$ have different energies and are non-equivalent. For example, in YPtBi and in LuPtBi, the chemical potentials lie close to the four-fold degeneracy point of the ${\mathsf{\Gamma }}_8$ band, and the microscopic theory of the superconductivity must therefore describe the pairing between $j_{3/2}$ fermions [83]. When two electrons with the same j are coupled into total angular momentum J, the parity of the state with respect to the permutation of wavefunctions ${\psi }_{j{m}_1}$ and ${\psi }_{j{m}_2}$ in the product equals the parity of the number $j+j+J$. Thus, one can assemble

Table 5. Symmetry of two-electron states ${\left(j_{3/2}\right)}^2$.

J		IR of ${\mathit{O}}_{\mathit{h}}$
0	Odd	$A_{1g}$
2	Odd	$E_g+T_{2g}$
1	Even	$T_{1g}$
3	Even	$A_{2g}+T_{1g}+T_{2g}$

[84], where the parity and symmetry in rotational and cubic groups are presented.

In this approach, instead of a spin multiplicity of $S=0$ or $S=1$, the pair acquires quantum number J. According to the Pauli exclusion principle, a total pair’s function should be antisymmetric with respect to the permutation of electron coordinates. The values $J=0,2$ correspond to the odd parity and the values $J=1,3$ correspond to the even parity and should be excluded.

This approach can be generalized taking into account the dependence on the wavevector k position in a BZ.

Suppose that two equivalent electrons or holes $j=3/2$ on one center are coupled in total momentum J, forming a state with lower energy. Since the total wavefunction is antisymmetric with respect to the permutation of electrons, we conclude that only states $J=0,2$ are possible. The wavefunctions are presented in

Table 6. Two-electron wavefunctions constructed from function $j_{3/2}$. Normalization factors are omitted. Functions for $M=-1$ and $M=-2$ may be obtained from functions $M=1$ and $M=2$ by changing the signs of magnetic quantum numbers. Note that functions $J=1,3$ are forbidden by the Pauli exclusion principle.

J	M	Function
0	0	$\left\{\left(\frac{1}{2},-\frac{1}{2}\right)-\left(-\frac{1}{2},\frac{1}{2}\right)\right\}$$+\left\{\left(\frac{3}{2},-\frac{3}{2}\right)-\left(-\frac{3}{2},\frac{3}{2}\right)\right\}$
2	2	$\left\{\left(\frac{3}{2},\frac{1}{2}\right)-\left(\frac{1}{2},\frac{3}{2}\right)\right\}$
2	1	$\left\{\left(\frac{3}{2},\frac{-1}{2}\right)-\left(\frac{-1}{2},\frac{3}{2}\right)\right\}$
2	0	$\left\{\left(\frac{1}{2},-\frac{1}{2}\right)-\left(-\frac{1}{2},\frac{1}{2}\right)\right\}$$-\left\{\left(\frac{3}{2},-\frac{3}{2}\right)+\left(-\frac{3}{2},\frac{3}{2}\right)\right\}$

.

However, these states correspond to an isolated atom. In solid state atomic one-electron states form electron bands, the Wannier functions can be constructed as follows [85]. Starting from one localized function, let $m_j=3/2$, and acting by the element of little group H of wavevector k, one obtains the basis set for this vector. Then, acting by the elements of left coset representatives in the decomposition of G with respect to H, one obtains the basis sets for the prongs of the star $\left\{k\right\}$. For k, a general point of a BZ, and for any $m_j$ value, the Wannier basis consists of one element only and other $m_j$ appear at the other prongs of the star $\left\{k\right\}$. Following this technique, we obtain at $-k$ the same value of $m_j$ as in k and one more value $-m_j$ due to time reversal symmetry. Thus, for k, a general point of a BZ, the coupling of the states with $j=3/2$ does not result in any symmetry difference from the case of $s=1/2$. On the other hand, in high symmetry directions in a BZ, some symmetry difference appear. Consider the $k_z$ direction in a space group with point group $D_{6h}$. The representation $D^{(1/2)}$ corresponds to IR $E_1^{\prime }$ of the wavevector group $C_{6v}$, and $D^{(3/2)}$ decomposes into $E_1^{\prime }+E_3^{\prime }$. Total one-electron functions are induced representations $E_1^{\prime }\uparrow D_{6h}$ for $j=1/2$ and $E_1^{\prime }\uparrow D_{6h}+$ $E_3^{\prime }\uparrow D_{6h}$ for $j=3/2$. In the $j-j$ coupling scheme, the total wavefunction belongs to an antisymmetrized square [74,78]:

$$\left\{E_{1\left(2\right)}^{\prime }\uparrow D_{6h}\times E_{1\left(2\right)}^{\prime }\uparrow D_{6h}\right\}=A_{1g}+A_{1u}+E_{1u},$$

$$\left\{E_3^{\prime }\uparrow D_{6h}\times E_3^{\prime }\uparrow D_{6h}\right\}=A_{1g}+A_{1u}+B_{1u}+B_{2u}.$$

In a weak spin–orbit coupling, one also obtains in the $k_z$- directions the dependence of possible Cooper pair symmetry on the small IR of the wavevector group. In $D_{6h}$ symmetry, all four one-dimensional spatial symmetries of a Cooper pair are $A_{2u}$ and for all two two-dimensional small IRs one obtains the possible symmetries of triplet pairs as:

$$\left\{E\uparrow D_{6h}\times E\uparrow D_{6h}\right\}=A_{1u}+E_{2u}+A_{1g}.$$

(27)

In the case of UPt${}_3$, an OSP pairing is usually assumed. When multiplying IRs of the spatial part by $A_{2g}$, corresponding to the OSP case, we obtain possible symmetries $A_{1u}$ and $A_{2u}+E_{2u}+A_{2g}$ for one-dimensional and two-dimensional small IRs, respectively.

5. Phase Winding and Group Theory

Superconductivity is a manifestation of broken symmetry in nature. Spontaneously broken gauge symmetry $U\left(1\right)$ means that below the $T_c$ the wavefunction of the system spontaneously develops a definite phase, which can be treated as a thermodynamic variable [86]. Furthermore, time-reversal symmetry is broken in many topological supercoductors [87,88]. The quantum mechanical phase of one wavefunction itself is not a physically observable quantity; however, the phase difference between two or more wavefunctions results in interference effects, which are observable. Phenomenological approaches to chiral non-unitary superconductors usually use spherical functions (see Table 3) or complex combinations of basis functions of different IRs (see Table 2). However, complex spherical functions of $m=\pm 1$ (see Formula (3)) are nodeless in the vertical plane, but experimental results show vertical nodal planes [24]. Linear combinations of basis functions of different IRs may represent experimental data (see Table 2 and Formula (9)), but simultaneous use of two IRs for one physical quantity is not clear from the point of view of group theory. In recent works, group theory and phase winding are unified and magnetic symmetry groups have been used to uncover underlying symmetries and to construct a new class of superconducting order parameters [50,53,55].

According the to the space group theory, the wavevector runs over the basis domain of a BZ, the volume of which is $\left|\overline{G}\right|$ times less then the volume of the whole BZ [80]. The wavevectors and wavefunctions of other domains are obtained by the actions of point group elements $\overline{G}$ on k and ${\phi }_k$ in the basis domain. Since the space inversion is included in the definition of a Cooper pair, the dimension of the basis is reduced to $\left|\overline{G}\right|/2$. Each basis domain for the pair includes two basis domains for representation connected by inversion. To obtain possible winding numbers for representations of the $D_{nh}$ group, it is sufficient to consider the $C_{nh}$ subgroup. In the case of the one-dimensional IRs of the $C_{nh}$ subgroup, angular momentum can be easily determined from the values of the matrix elements for rotations [53]. With further induction, the correspondence between the angular momentum and the representation is preserved.

Table 7. Odd IRs of point group $D_{2h}$ and magnetic group $m^{\prime }{m}^{\prime }m$. Non-unitary element is $A=\theta {\sigma }_y$.

	E	${\mathit{C}}_{2\mathit{z}}$	I	${\mathit{\sigma }}_{\mathit{z}}$	$\mathit{\theta }{\mathit{\sigma }}_{\mathit{y}}$	$\mathit{\theta }{\mathit{\sigma }}_{\mathit{x}}$	$\mathit{\theta }{\mathit{C}}_{2\mathit{y}}$	$\mathit{\theta }{\mathit{C}}_{2\mathit{x}}$
$A_u^{\pm }$	1	1	$-1$	$-1$	$\pm 1$	$\pm 1$	$\mp 1$	$\mp 1$
$B_u^{\pm }$	1	$-1$	$-1$	1	$\pm 1$	$\mp 1$	$\mp 1$	$\pm 1$
$A_u$	1	1	$-1$	$-1$	$-1$	$-1$	1	1
$B_{1u}$	1	1	$-1$	$-1$	1	1	$-1$	$-1$
$B_{2u}$	1	$-1$	$-1$	1	$-1$	1	1	$-1$
$B_{3u}$	1	$-1$	$-1$	1	1	$-1$	$-1$	1

shows the odd representations of the $C_{2h}$ group, as well as the corepresentations of the magnetic group $m^{\prime }{m}^{\prime }m$ that come from them. It can be seen from Table 7 that $A_u\left(C_{2z}\right)=1,$ $B_{1u}\left(C_{2z}\right)=1$, $B_{2u}\left(C_{2z}\right)=-1$, and $B_{3u}\left(C_{2z}\right)=-1$. Hence, it follows that $A_u$ and $B_{1u}$ correspond to $\overline{m}=\pm 2$, and $B_{2u}$ and $B_{3u}$ correspond to $\overline{m}=\pm 1$ for discrete rotations.

In the case of the $D_{2h}$ group, there is only one magnetic group, $m^{\prime }{m}^{\prime }m$, compatible with a net angular momentum, corresponding to the ferromagnetic state (see [53] and Table 7.7 in [80]). Figure 1 shows the intersection of a BZ of the space group $Immm$ ($D_{2h}^{25}$) of UTe${}_2$ with the plane (001). Note that all k vectors of electrons have nonzero $k_z$ components and the sectors connected by inversion are included in the definition of a pair, with the pairs momentum equal to zero. The initial vector $k_1$ is close to the $k_y$ direction and its phase is close to zero; thus, the value of the pair function ${\psi }_1$ is positive. The other k- vectors are obtained by the action of group elements as follows:

$$k_2={\sigma }_x{k}_1,k_3=C_{2z}{k}_1,k_4={\sigma }_y{k}_1.$$

The pair basis functions are transformed according to the IRs of group $D_{2h}$, for example:

$${\psi }_3={\psi }_1\mathrm{for}{A}_u\mathrm{and}{B}_{1u}$$

$${\psi }_3=-{\psi }_1\mathrm{for}{B}_{2u}\mathrm{and}{B}_{3u}$$

When the initial $k_1$ vector runs over the first sector, we obtain all pairs in condensate. The wavefunction of a Cooper pair can have a phase winding in the sector 1 and we suppose that it corresponds to $m=1$ for $B_{2u}$ and $B_{3u}$, and to $m=2$ for $A_u$ and $B_{1u}$. Thus, in the sector 1, the phases of $B_{2u}$ and $B_{3u}$ change from 0 to $\pi /2$ and the phases of $A_u$ and $B_{1u}$ change from 0 to $\pi$. Consider IR $B_{3u}$ (see Figure 1d). When acting on function ${\psi }_1$ by the group element $C_{2z}$ and multiplying it by $B_{3u}\left(C_{2z}\right)=-1$, we obtain phase $\pi$ at the beginning of the sector 3 and phase $3\pi /2$ at its end. The function $k_2$ in the sector 2 is obtained by the reflection ${\sigma }_x$. Since $B_{3u}$(${\sigma }_x)=-1$, the sign of the pair function changes, which corresponds to the phase $\pi$. It can be easily shown that the reflections change the phase winding direction [53], and we obtain phase $3\pi /2$ in the sector 2 near the $k_y$ axis. 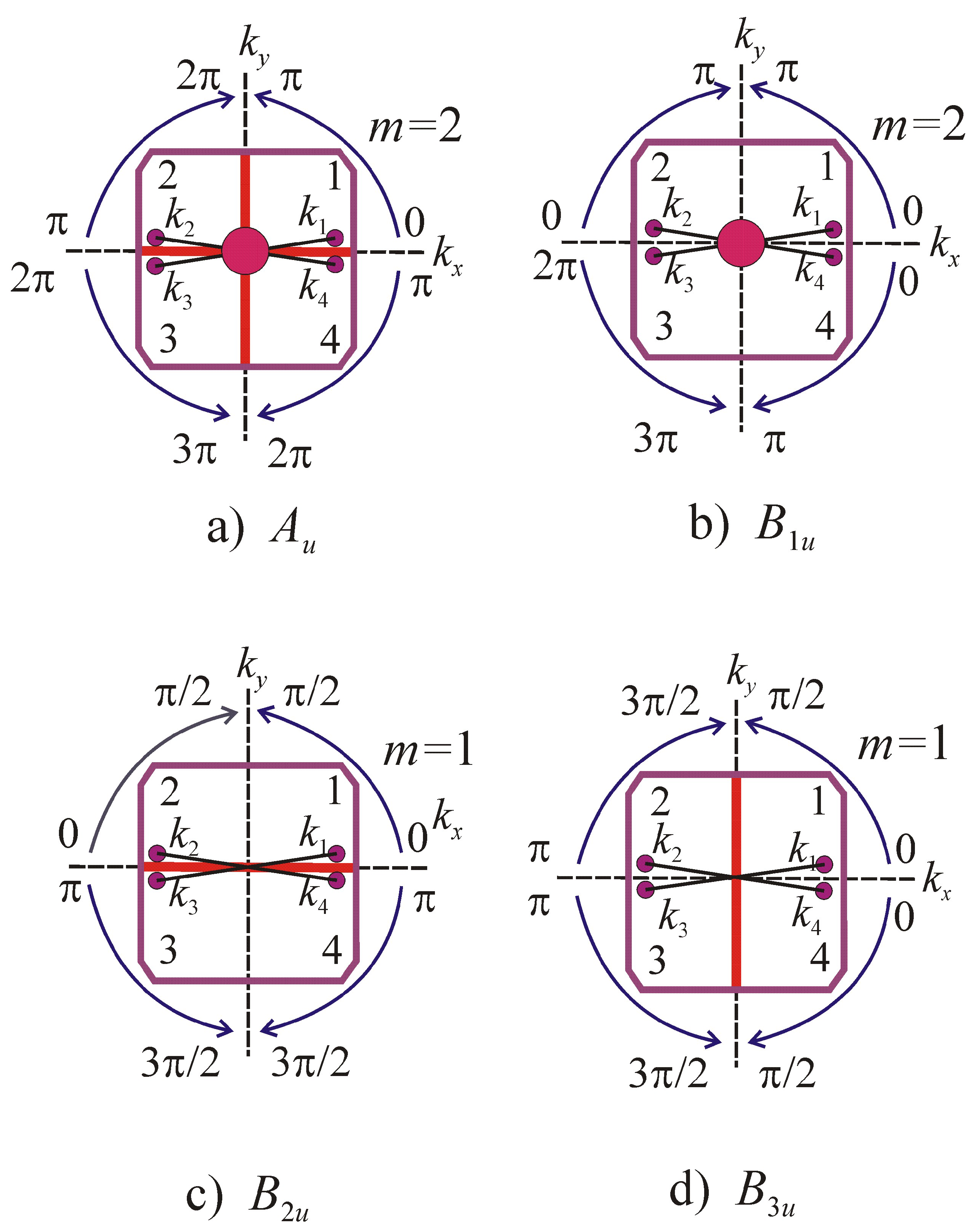Thus, we obtain the phase winding structure shown in Figure 1d. It can be seen in Figure 1d that the phases in sectors 1 and 2 (and in sectors 3 and 4) differ by $\pi ,$ which results in the nodes denoted by the bold red line. In the phase structure of $B_{2u}$, shown in Figure 1c, the pair functions meet at the $k_x$ axis with opposite phases, which results in their destructive interference and line nodes shown by the red lines. Both structures $B_{3u}$ and $B_{2u}$ are non-unitary, but the functions of the individual pairs are transformed by real IRs. The total phase winding is equal to zero. It can be shown similarly that the IR $A_u$, shown in Figure 1a, has nodes in both vertical planes and IR $B_{1u}$ in Figure 1b) is nodeless in both vertical planes. The nodes in the basal plane are defined by the sign of character for the element ${\sigma }_z$, and therefore $B_{2u}$ and $B_{3u}$ are nodeless and $A_u$ and $B_{1u}$ are nodal in the basal plane. The nodes in the basal plane are denoted by red circles.

Making use of the Herring criterion [80], we find that the corepresentations of magnetic group $m^{\prime }{m}^{\prime }m$ belong to type (a), i.e., for a unitary subgroup they are just its IRs and for a non-unitary left coset they are extended with signs + or −, which are denoted in Table 7 by superscripts. 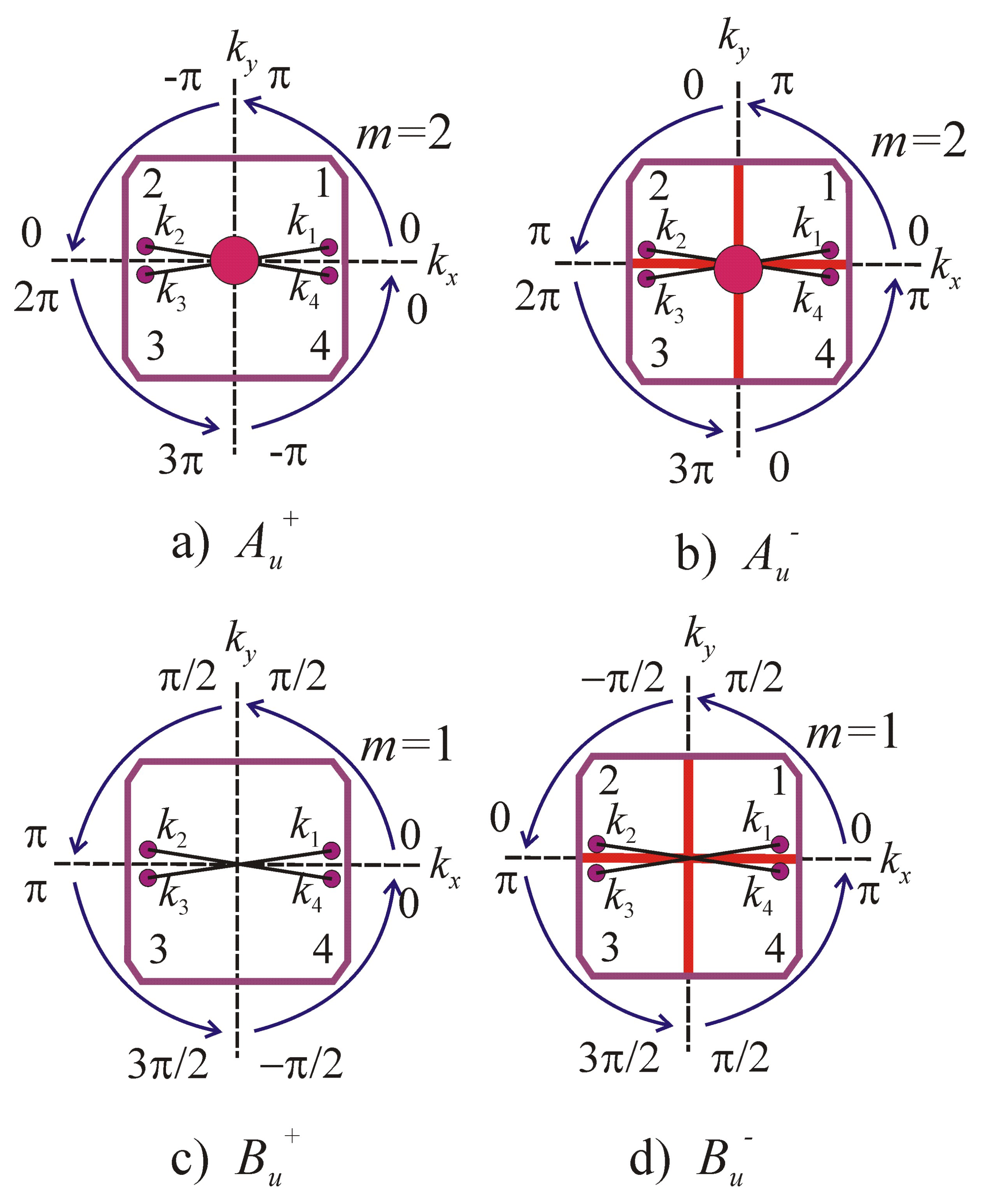It can be directly verified that reflection with time reversal (complex conjugation) does not change the phase winding direction [53], and one similarly obtains phase structures for ICRs $A_u^{\pm }$ and $B_u^{\pm }$, shown in Figure 2, where the notations for the nodes are the same as in Figure 1. The SOPs of $A_u^{\pm }$ symmetry correspond to magnetic quantum number $m=2$ and the total phase winding is equal to $4\pi$, and SOPs of $B_u^{\pm }$ symmetry correspond to magnetic quantum number $m=1$ and the total phase winding is equal to $2\pi .$ In the structures of $A_u^{+}$ and $B_u^{+}$ symmetry in Figure 2a,c, the phase is continuous when passing through the axes (vertical planes in the three-dimensional picture) and there are no nodes in these planes. In the structures $A_u^{-}$ and $B_u^{-}$ in Figure 2b,d, the phase changes by $\pi$ when passing through the axes, resulting in nodes, which are denoted by two bold red lines.

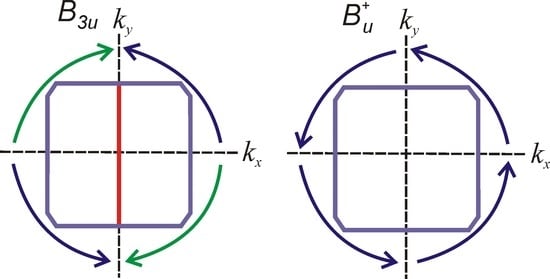
6. Order Parameters of Sr${}_2$RuO${}_4$ and UPt${}_3$

We now turn our attention to the group $D_{4h}$, which has two-dimensional IRs. In a space-group approach, the basis sets for singlet and triplet pairs consist of eight basis functions, obtained by the action of elements of group $C_{4v}$ on the basis function $k_1$ in the basis domain, i.e., if k runs in the interval $0<\theta <\pi /4$ in the $(k_x,k_y)$ plane and $0<k_z<k_{z0}$ [52]. The structures of the one-dimensional SOP are unique and coincide in all approaches [51,52]. However, since two-dimensional IRs can be transformed by unitary matrices, their nodal structures are not unique. There are two possibilities for the phase winding in the basis domain for two-dimensional IRs $E_u$ and $E_g$; namely, zero phase winding and real IRs or phase winding with $m=1$ and complex form IRs [81]. When the wavefunctions of pairs are constructed from the functions of the basis domain group theoretically, they can have different phases on opposite sides of the symmetry planes and the interference of real and imaginary parts takes place. This interference is represented numerically as follows. The wavefunctions of pairs in a finite number of points in the interval $0<\theta <2\pi$ are represented by a normalized sum of real and imaginary Gaussians, whose relative values and signs correspond to the theoretical phase. After that, the contributions from all pairs are summed at each point. Inside the sectors, the phase difference between adjacent pairs is small and constructive interference takes place. At the boundaries of the sectors, both constructive and destructive interference of the wavefunctions is possible, where the interference of the real and imaginary parts is taken into account independently. When squaring modulus of the complex function at every point, we obtain the structure of the SOP in the plane normal to the $k_z$- axis. Figure 3a shows the structures of real $E_u$ and $E_g$ with one vertical nodal plane. The structures of $E_g$ and $E_u$ at vertical planes are the same; however, these structures differ by nodes in the basal plane, which are defined by characters of $E_g$ and $E_u$ for the element ${\sigma }_h$, which is invariant under unitary transformations. Consider a pair function ${\psi }_{k1}$, expressed as a linear combination of basis function and a function, ${\sigma }_h{\psi }_{k1}$. When the vector $k_1$ approaches the basal plane, two functions may merge if ${\sigma }_h{\psi }_{k1}={\psi }_{k1}$ or cancel if ${\sigma }_h{\psi }_{k1}=-{\psi }_{k1}$, with the latter case corresponding to a nodal plane. The case that is realized is determined by the character of the IR. Since $\chi \left(E_g({\sigma }_h\right))=-2$ and $\chi \left(E_u({\sigma }_h\right))=2$, we conclude that $E_g$ is nodal and $E_u$ is nodeless in the basal plane. Multiplication of $E_g$ and $E_u$ by $A_{2g}$ does not change their characters, but changes the signs of the function connected by reflection in vertical planes and therefore changes the nodal structure. Figure 3b shows the nodal structures of real IRs $E_g\times A_{2g}$ and $E_u\times A_{2g}$ with three vertical nodal planes.

Furthermore, complex forms of $E_u$ and $E_g$ are possible in which diagonal matrix elements of the IR correspond to the angular momentum projection $m=\pm 1$ [50,81]. Possible structures calculated with phase winding $m=1$ in the basis domain are presented in Figure 4a,b. The first structure corresponds to complex matrices [81] and in the second, the matrices were multiplied by $A_{2g}$. These structures have nodes in vertical coordinate planes $\left(010\right)$ or $\left(100\right)$, respectively, and deeps in diagonal planes $\left(110\right)$ and $(-110)$. Nodes correspond to a phase difference of $\pi$ on two sides of a plane, and deeps correspond to a phase difference of $\pi /2$. Phase winding directions in sectors 1, 3, 5, and 7 correspond to $m=1$ and in sectors 2, 4, 6, and 8, they correspond to $m=-1$ and the pair function is non-unitary. Horizontal nodal planes are the same as in the case of real IRs. Thus, we see that in axial symmetry groups, e.g., $D_{4h}$, horizontal nodal planes of two-dimensional IRs are topologically stable, but vertical nodal planes of two-dimensional IRs are topologically unstable, as according to Kobayashi et al. [89], they can be added (removed) by unitary transformation (multiplication by $A_{2g}$), which can be considered as a small perturbation.

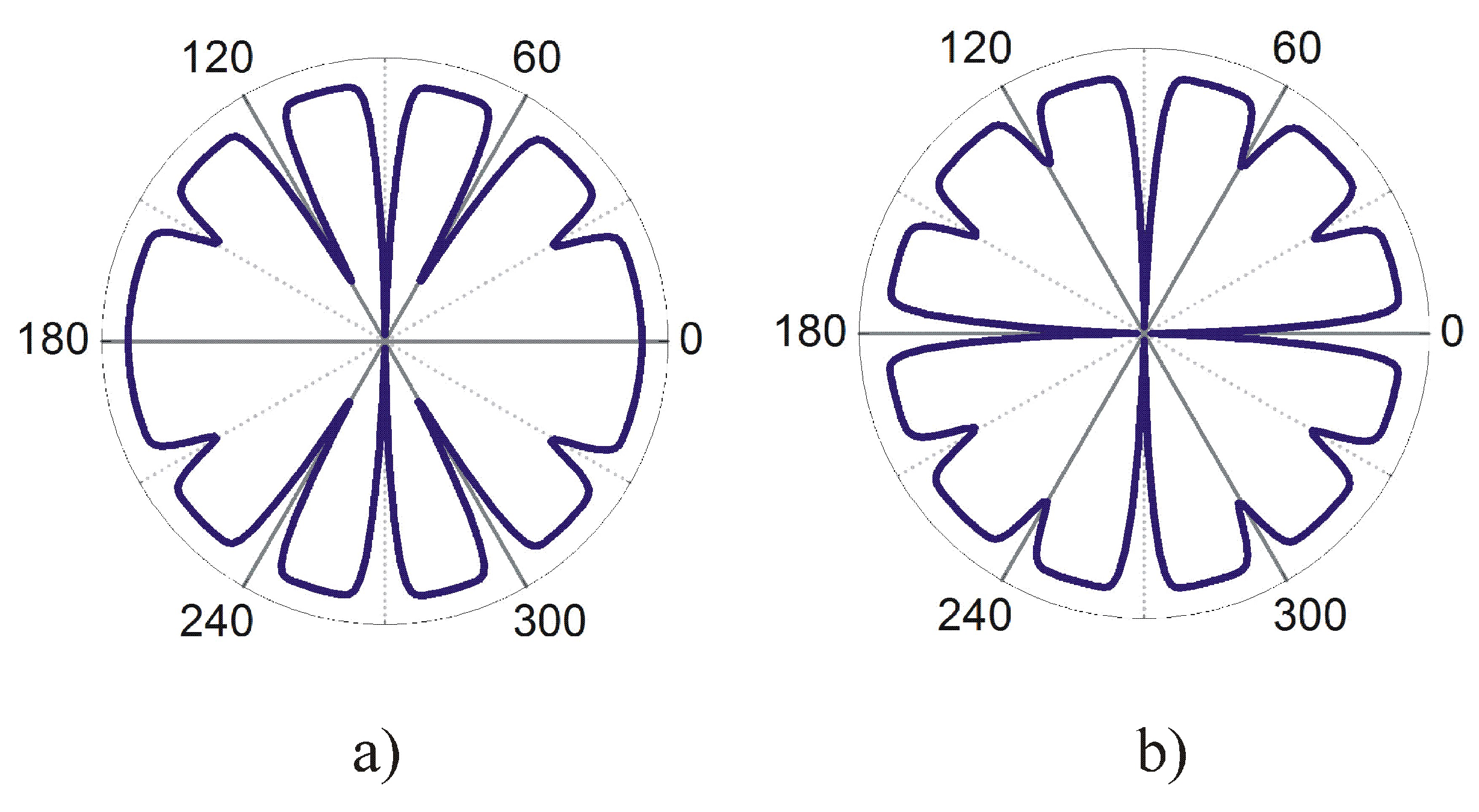
Figure 5a,b shows possible structures of complex SOPs $E_{1u}$ and $E_{2u}$ of the $D_{6h}$ symmetry group of UPt${}_3$ [53]. In both cases, pair function is non-unitary, $E_{1u}$ has $m=\pm 1$ in the nodal plane is (010), and $E_{2u}$ has $m=\pm 2$ in nodal planes $\left(100\right)$ and $\left(010\right)$. In addition, both structures have deeps in the other vertical planes. When multiplying by $A_{2g}$, one obtains $E_{1u}$ with nodal plane $\left(100\right)$ and $E_{2u}$ without nodes in the vertical planes (not shown in the figure). The phase winding in all sectors obtained by rotations of the $C_{6z}$ subgroup correspond to the positive m- value and in other sectors m is negative, resulting in zero phase winding.

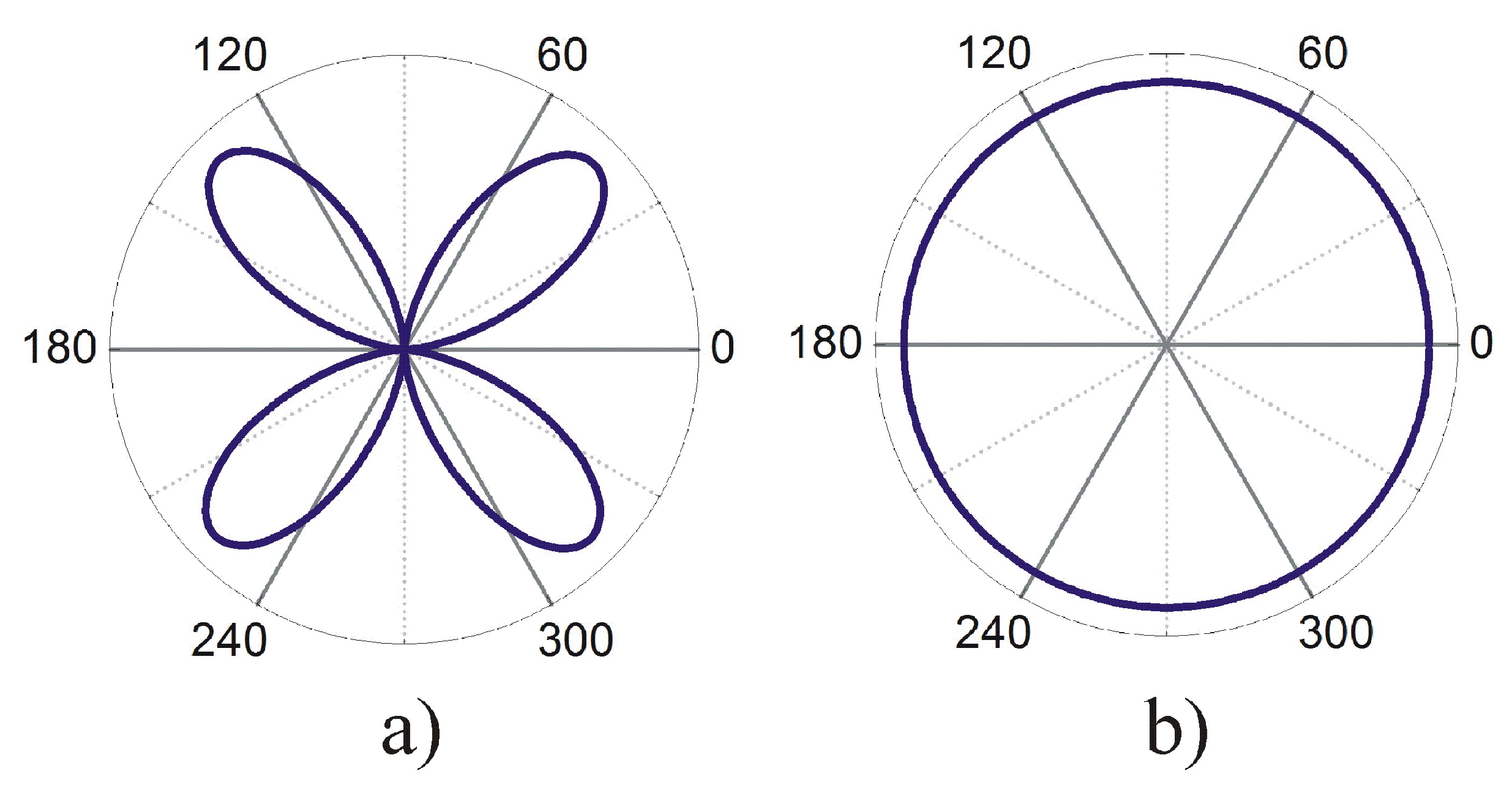
Figure 6a shows the differences in two complex conjugate chiral IRs $1/2(E_{2u}-E_{2u}^{*})$ with nodes in vertical coordinate planes. The values of the pair function are imaginary at all angles. This structure can be converted into a real structure by multiplication by a constant phase factor i. Furthermore, one can consider the sum of two complex conjugate functions $1/2(E_{2u}+E_{2u}^{*})$ in which nodal planes are rotated by $\pi /4$ (not shown in the figure).

Figure 6b shows the SOP for magnetic group $6/m^{\prime }{m}^{\prime }m$, in which reflections in the vertical planes are accompanied by time reversal. In this case, the structure is nodeless, which corresponds to phase B of UP${}_3$ [16]. The structure in Figure 6b corresponds to ICRs induced by one-dimensional IRs $E_{1u}^{\prime }$ and $E_{2u}^{\prime }$ of the $C_{6h}$ subgroup. In the case of the Shubnikov group $6/m^{\prime }{m}^{\prime }m$, the winding direction is the same at all angles and the total phase winding is $2\pi$ and $4\pi$ for these ICRs, respectively.

7. Discussion

In the present paper, a topological space group approach that combines Anderson treatment of a Cooper pair, space group theory, and Ginzburg–Landau phase winding is applied for the investigation of SOP structures of unconventional superconductors of $D_{2h}$, $D_{4h}$, and $D_{6h}$ symmetry. In this approach, the phase winding magnetic quantum number m in the basis domain of a BZ equals the group theoretical phase factor $\overline{m}$ for discrete rotations. Non-unitary order parameters are constructed by this method for all odd IRs of the $D_{2h}$ group and for all odd ICRs of the magnetic group $m^{\prime }{m}^{\prime }m$. It is shown that for axial symmetry groups $D_{2h}$, $D_{4h}$, and $D_{6h}$, the total phase winding is equal to zero. A total phase winding of $2\pi m$ corresponds to ferromagnetic groups obtained from these point groups (see Table 7.7 in [80]); namely, $m{m}^{\prime }{m}^{\prime }$, $4/m{m}^{\prime }{m}^{\prime }$, and $6/m{m}^{\prime }{m}^{\prime }$.

In UTe${}_2$, the ESP spin triplet state (10) [41] with a total phase winding of $2\pi$ corresponds to ICR $B_u^{+}$. If the same spin state is coupled with a spatial chiral part, the angular momentum projection m is equal to 2. Such a state corresponds to ICR $A_u^{+}$ and experimental structure (11) [42]. In addition, $A_u^{+}$ is nodal but $B_u^{+}$ is nodeless in the basal plane.

In $D_{4h}$ symmetry, the possible vertical nodal planes of $E_u$ and $E_g$ are similar, but these IRs differ by nodes in the basal plane; namely, $E_u$ is nodeless but $E_g$ is nodal. The latter assertion has been confirmed experimentally for Sr${}_2$RuO${}_4$ [25] and LaPt${}_3$P [34].

The structure of the C phase of UPt${}_3$ is $(5k_z^2-1)$ in the $k_z$ direction and with in-plane twofold oscillation in [17], it may be represented by projecting of the $L=3$ basis function $\widehat{z}(k_x+i{k}_y)(5k_z^2-1)$ on complex IR $E_{1u}$ (see Figure 5a) with one vertical nodal plane. The unitary structure $(k_x^2-k_y^2)k_z$ in Figure 6a corresponds to the SOP in the A phase of UPt${}_3$ and the non-unitary structure in Figure 6b corresponds to the B phase [16]. It should be noted that the nodes in the structures of the SOP of UPt${}_3$ $k_x^2-k_y^2$ and $(5k_z^2-1)$ in phases A and C, respectively, appear beyond symmetry planes and they are purely topological, i.e., they are not derived from point group symmetry.

Point nodes in the $k_z$- direction for chiral states with $m=1$ and $m=2$ are often called Weil nodes. Similar constraints may be obtained in a space group approach as follows. Consider two electrons in the $k_z$- direction forming a triplet Cooper pair. If one-electron states belong to a one-dimensional small IR, using the Formulas (20)–(22), one easily obtains possible symmetries of triplet pairs $B_{1u}$, $A_{2u}$, and $A_{2u}$ for groups $D_{2h}$, $D_{4h}$, and $D_{6h}$, respectively. Hence, it follows that pairs of $B_{2u}$ and $B_{3u}$ symmetry are forbidden in $D_{2h}$ symmetry and all two-dimensional IRs are forbidden in $D_{4h}$ and $D_{6h}$ symmetry in the $k_z$- direction. Note that $B_{2u}$, $B_{3u}$, $E_u$, and $E_{1u}$ correspond to $m=1$, and that $E_{2u}$ corresponds to $m=2$. For two-dimensional small IRs in the $k_z$- direction, spatial parts of the triplet pair belong to $A_{2u}+B_{1u}+B_{2u}+A_{2g}$ in $D_{4h}$ symmetry [50] and to $A_{1u}+E_{2u}+A_{1g}$ in $D_{6h}$ symmetry (27). Hence, it follows that in $D_{6h}$ symmetry for coupling of one-electron states with non-zero angular momentum, states with $m=2$ are possible in the $k_z$- direction.

8. Conclusions

The SOPs of triplet superconductor UTe${}_2$ were constructed using the topological space group approach. In this approach, the phase winding in the basis domain of a BZ zone is equated to the phase shift at discrete rotations determined by the IR. In this approach, in contrast to the phenomenological and topological approaches, the single pair function and phase winding in condensate are different quantities, and the single pair functions in a non-unitary case may belong to unitary IRs of the point group. The total phase winding is equal to zero for IRs of the point group $D_{2h}$ and equal to $2\pi$ for ICR $B_u^{\pm }$ and $4\pi$ for ICR $A_u^{\pm }$ of magnetic group $m^{\prime }{m}^{\prime }m$. States denoted as $B_u^{+}$ and $A_u^{+}$ correspond to phenomenological expressions $B_{2u}+i{B}_{3u}$ and $(\widehat{y}+i\widehat{z})(k_y+i{k}_z)$, respectively.

In the case of two-dimensional IRs of $D_{4h}$ and $D_{6h}$ groups, nodes in vertical planes are topologically unstable, i.e., for one IR different nodal structures are possible. Nodes in the basal plane are topologically stable, i.e., they are defined by the IR. Thus, nodes in the basal plane of chiral singlet superconductors LaPt${}_3$P and of Sr${}_2$RuO${}_4$ correspond to a singlet SOP.

The structure of the C phase in UPt${}_3$ may be represented by projecting of $L=3$ basis function $\widehat{z}(k_x+i{k}_y)(5k_z^2-1)$ on complex IR $E_{1u}$ with one vertical nodal plane, but nodal plane $k_z=1/\sqrt{5}$ is is purely topological, i.e., is not connected with symmetry planes.

Superconductivity is a macroscopic quantum phenomenon and therefore provides a unique opportunity to directly compare the results of group theory with experiment. In other areas of physics, such as the theory of the electronic structure of molecules and of condensed matter, group theory provides a method for constructing correct wavefunctions of the initial approximation for calculations from the first principles. Therefore, another application of the space group approach to the Cooper wavefunction can be the construction of the correct wavefunctions of a pair, necessary for an accurate quantum mechanical calculation of the superconductivity phenomenon.