Abstract
A general single-node second-order Dirichlet boundary condition for curved boundaries for the convection–diffusion equation based on the lattice Boltzmann method has been developed. The boundary condition simply utilizes the bounce back rule for the temperature distribution and linear interpolation. The developed boundary condition is quite general and stable. The asymptotic analysis indicates that the proposed boundary scheme is of second-order accuracy. The comparison in terms of -norm between the simulation results and the analytical solutions confirms that it is indeed second-order accurate for 2D and 3D symmetric flows comprising straight and curved boundaries. Moreover, the Nusselt numbers for a spherical particle in uniform flow obtained by current simulations agree very well with the predictions of empirical correlations and the data of previous direct numerical simulations with a maximal relative deviation within 8%.
1. Introduction
Particulate multiphase flows are ubiquitous in nature and industrial applications, e.g., volcanic eruption [1,2], biomass gasification [3,4] and nanotechnology [5,6]. To model these flows at the most detailed level with the so-called direct numerical simulations (DNSs), appropriate boundary conditions are required to account for the interactions between particles and a fluid, for example, Dirichlet boundary conditions for velocity and temperature. Thus, numerically stable and accurate boundary conditions are of great importance for the DNS methods.
Among all the DNS methods available, the lattice Boltzmann method (LBM) provides an alternative approach to solve the Navier–Stokes and convection–diffusion equations. The widely used second-order Dirichlet boundary schemes are interpolation-based boundary methods [7,8,9] and immersed boundary methods [10,11]. However, these boundary schemes are not purely local since they require at least two fluid nodes to achieve second-order accuracy. For dense suspensions, the number of fluid nodes between particles may not be sufficient for the interpolation-based boundary schemes when the gap between particles is small. In this case, the boundary schemes only have first-order accuracy. Therefore, a single-node Dirichlet boundary condition which still has second-order accuracy is essential for the application of the lattice Boltzmann method. To this end, Guo et al. [12] developed a non-equilibrium extrapolation method for the LBM. The comparison between the simulation results and the analytical solution for the porous plate problem with a temperature gradient indicates that the boundary condition is second-order accurate. Tang et al. [13] extended the boundary method of Guo et al. [12] for the internal-energy-based double population model. The simulation results for the thermal channel flow are in good agreement with the simulation results using the finite volume method. However, the sharp interface of the boundaries cannot be preserved since the boundary scheme developed by Guo et al. [12] is independent of the exact location of the boundaries. Huang and Yong [14] proposed a single-node second-order Dirichlet boundary condition for straight boundaries by employing an asymptotic analysis technique. However, the boundary method is only first-order accurate for curved boundaries. Zhang et al. [15] developed a single-node Dirichlet boundary condition for the convection–diffusion equation based on the lattice Boltzmann method. They modified the equilibrium temperature distribution by introducing a first-order spatial derivative of the fluid temperature. The boundary scheme is shown to be second-order accurate for straight and circular walls. Ginzburg and Silva [16], on the other hand, proposed a boundary approach called A-LSOB to enhance the locality and accuracy of single-node Dirichlet boundary condition. However, these two boundary conditions are very complicated due to the calculation of spatial derivative of the fluid temperature. Zhang et al. [17] developed a general single-node second-order Dirichlet boundary condition for curved boundaries for the MRT-LBM. A free parameter is introduced which is in the range [0, ], where is the scaled distance between the wall node and the nearest fluid node. However, the choice of the free parameter has to be more careful for inclined and curved boundaries since ranges from 0 to 1 in these cases. The free parameter may be valid for one boundary node but invalid for another.
In this work, we extend the range of validity of Zhang et al.’s [17] single-node second-order Dirichlet boundary condition to [0, ] for the regular lattice Boltzmann method. Therefore, the free parameter can be arbitrarily chosen within this range. The bounce back rule and linear interpolation are used to construct the second-order boundary scheme. The Dirichlet boundary condition is independent of the lattice model and collision operator. Moreover, the boundary condition proposed here is quite general, stable and suitable for inclined and curved boundaries.
2. Numerical Methods
2.1. The Convection–Diffusion Equation
The convection–diffusion equation is given as [18]:
where is a scalar variable which represents the temperature or mass concentration. and are the fluid velocity component in the direction and diffusion coefficient, respectively. The Dirichlet boundary condition is expressed as
where is the temperature or mass concentration at the boundary.
2.2. The Lattice Boltzmann Model
The lattice Boltzmann equation for the convection–diffusion equation with a Bhatnagar–Gross–Krook (BGK) [19] collision model is as follows:
where and are the temperature distribution function and equilibrium temperature distribution function, respectively. is the lattice speed, where (). is the single relaxation time. The D3Q7 lattice (Figure 1) is given by
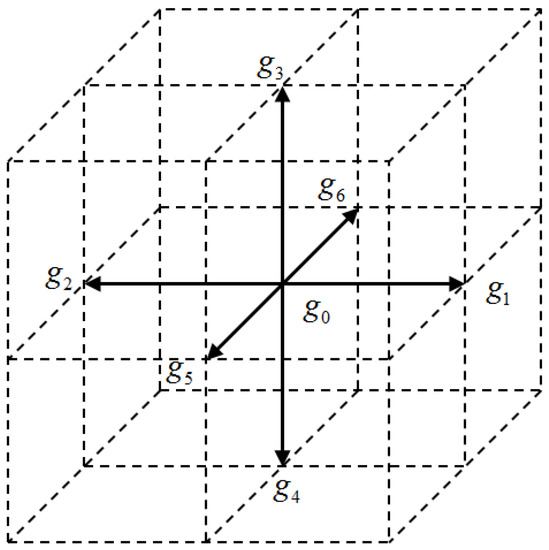
Figure 1.
Schematic description of lattice structure for D3Q7.
The equilibrium temperature distribution is defined as:
where is equal to . In the multiple-relaxation-time (MRT) model proposed by [18], the evolution equation for the temperature distribution becomes
where denotes the total number of discrete velocities. is the transformation matrix and given by
The relaxation time matrix is defined as
where , , are the components of the Cartesian coordinates. The non-zero value of the off-diagonal components in the relaxation matrix accounts for anisotropic diffusion. The relaxation coefficients can be calculated using the diffusion coefficient
where is the Kronecker’s delta. The macroscopic fluid temperature can be obtained via
The LBE can be split into two steps, namely, the collision and streaming operations.
3. Dirichlet Boundary Condition
Figure 2 illustrates a wall located between two lattice nodes. To describe the relative position of the wall node, a coefficient is defined as
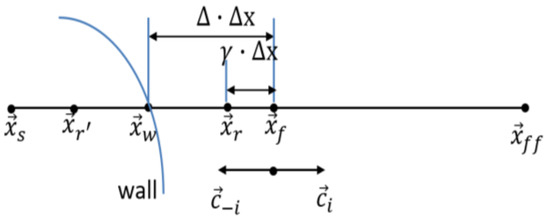
Figure 2.
Illustration of a wall located between a solid node () and a fluid node ().
In addition, the points and are defined, and can be calculated as
where . Therefore, the two points ( and ) are symmetric with respect to the boundary point. Based on Equations (14)–(16), we have
After the streaming step, the temperature distribution functions at the fluid node nearest to the wall are unknown. To calculate the unknown distributions, an interpolation scheme is used:
Using Equation (13), we have
To calculate , the bounce back rule is adopted:
The equilibrium temperature distributions at and are constructed using the wall temperature and velocity, where
Thus,
In Equation (24), is obtained by interpolation:
To calculate in Equation (25), the temporal approximation is applied, where
Recalling Equation (13) and inserting Equations (24)–(26) into Equation (19), we obtain
To ensure the numerical stability, and have to be non-negative. Therefore, the constraint for is [0, ]. Note that, if we set , Equation (27) becomes the boundary condition proposed by Zhang et al. [17] with , which implies that Equation (27) is equivalent to the boundary condition proposed by Zhang et al. [17]. To overcome the shortcoming of Equation (27), we set
Equation (28) ensures that the proposed boundary condition (Equation (27)) is always a convex combination of the temperature distributions for γ within the range [0, 2Δ]. Thus, the range of validity of the boundary condition proposed by Zhang et al. [17] is extended which is more suitable for the inclined and curved boundaries. Moreover, the proposed boundary condition is simple and purely local since it only involves one fluid node.
The implementation of the lattice Boltzmann method with the proposed Dirichlet boundary method involves the following steps:
- (1)
- Calculate the equilibrium temperature distribution function .
- (2)
- Perform the collision step to calculate .
- (3)
- Apply domain boundary conditions for the temperature distribution functions and Dirichlet boundary condition for immersed objects and external walls.
- (4)
- Perform the streaming step .
- (5)
- Calculate the fluid temperature .
- (6)
- Go to step (1) until the calculation is converged.
4. Asymptotic Analysis
With the diffusive scaling ( and ) [20], the evolution equation and equilibrium distribution become
Expanding the temperature distribution function and the fluid temperature in series of up to first order yields:
According to Equation (11), we have
Expanding Equation (29) as a series of yields:
Rearranging the terms having the same power of for Equation (34), we have
With Equations (35) and (36), we can derive the following relationships:
Assuming that the boundary is located between and , we have
Inserting Equation (39) into Equation (27) and applying the Taylor expansion up to first order, we obtain
Moreover, we have
Equation (27) expressed in zeroth order with regard to yields
Using Equation (35), we obtain
Therefore, the Dirichlet boundary condition is satisfied by the zeroth-order solution. Considering the terms in , we have
Using Equations (35) and (36) yields
Due to Equations (35) and (38), we obtain
Hence, at the boundary Equation (27) recovers the following boundary condition:
which demonstrates that the proposed Dirichlet boundary condition is second-order accurate.
5. Numerical Simulations
In the following, the newly proposed Dirichlet boundary condition is used to simulate 2D channel flow, 2D cylindrical Couette flow, 3D circular pipe flow and a fluid flowing over a sphere to assess the accuracy of the boundary scheme. In the present work, only isotropic diffusion is considered. In addition, and ( = 3, 4 in 2D and 4, 5, 6 in 3D) are used in all the simulations.
5.1. 2D Steady-State Symmetric Channel Flow
The first numerical case is the steady-state channel flow with heat transfer (Figure 3). The height of the channel is . The numbers of lattices in and directions are and , respectively. Therefore, the lattice size is . On the walls at and , the temperature is given as
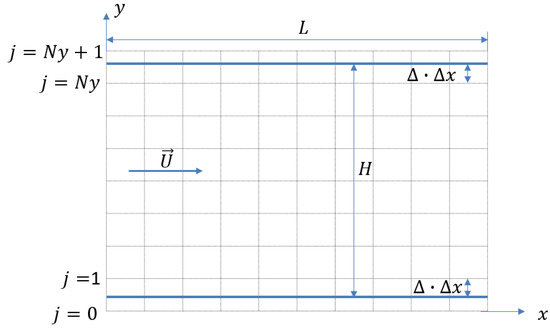
Figure 3.
Schematic description of computational set up for the channel flow.
The analytical solution expressed in complex form for the fluid temperature is as follows:
where , is the fluid velocity. The heat transfer for the channel flow is characterized by the Peclect number, where . In all the simulations, is fixed at 10. A periodic boundary condition for the fluid temperature is applied to the direction. The newly proposed thermal Dirichlet boundary condition is imposed at top and bottom walls. is set to 1, 0.75 and 0.51, respectively. Figure 4 shows the temperature contour for , and as an illustration. It is clear that the temperature distribution is symmetric. The accuracy of the thermal boundary condition is evaluated in terms of the -norm, :
where is the analytical solution for the fluid temperature (Equation (51)). If , is equal to 0, , and , whereas it is set to 0, , 1 and if . Figure 5 plots the convergence order of the thermal boundary condition for different and . At , the errors for different are almost the same as shown in Figure 5c,f,i. As increases, a noticeable difference between different is observed. For , the error decreases with increasing , whereas it increases with increasing for . The comparison between different boundary schemes is shown in Figure 6. It demonstrates that the two-point boundary schemes proposed by Li et al. [8] and Ginzburg [7] are all second-order accurate. Moreover, it also implies that the current boundary condition only requires one fluid node to achieve the same accuracy as the boundary schemes proposed by Li et al. [8] and Ginzburg [7]. Figure 5 indicates that the Dirichlet boundary condition is numerically stable and second-order accurate over a wide range of and .
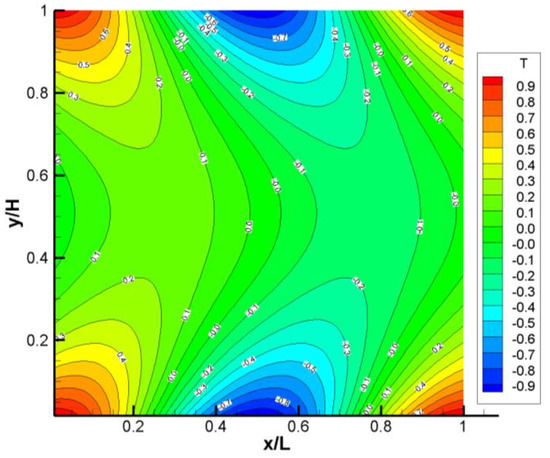
Figure 4.
Temperature contour for the channel flow at steady state for , and .
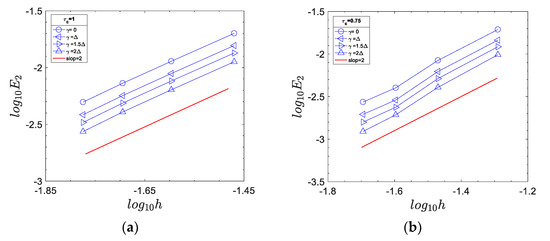
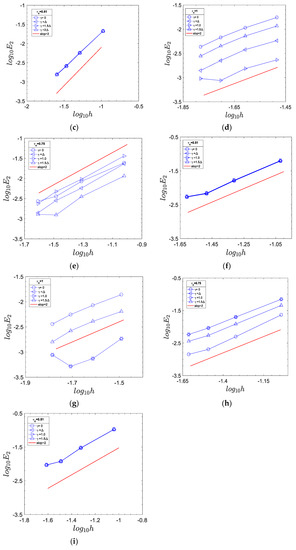
Figure 5.
Convergence order of the boundary condition for 2D steady-state channel flow. (a)–(c) ; (d)–(f) ; (g)−(i) .
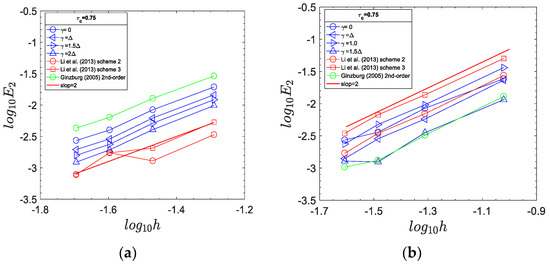
Figure 6.
Comparison of -norm for different boundary schemes: (a) ; (b) .
5.2. Couette Flow between Two Circular Cylinders
The analytical solution for the fluid temperature for the Couette flow between two circular cylinders (Figure 7) is given as
where and are the Prandtl number and the rotational velocity of the inner cylinder, where . and are the radii of inner and outer cylinders, respectively. is the ratio of to . The Reynolds number is defined as . The Reynolds number and Prandtl number are fixed at 10 and 1 for all the simulations. In these cases, , and . The temperatures of the inner cylinder () and outer cylinder () are set to 1 and 0, respectively. The non-slip hydrodynamic boundary condition proposed by Chen et al. [21] and the thermal Dirichlet boundary condition proposed in this work are applied to the inner and outer cylinders. The normalized temperature profiles for different are plotted in Figure 8 at , and . It is clear that the simulation results are in good agreement with the analytical solutions. The convergence order of the boundary condition described by Equation (52) is shown in Figure 9. Unlike 2D channel flow, a small difference between different is observed. In Figure 10, we can see that the errors for the boundary schemes developed by Li et al. [8] are slightly smaller compared to the boundary schemes proposed by Ginzburg [7] and in the current work. All schemes have second-order accuracy for and . Figure 9 demonstrates that the Dirichlet boundary condition is numerically stable and second-order accurate over a wide range of and within the range [0, ] for 2D curved boundaries.
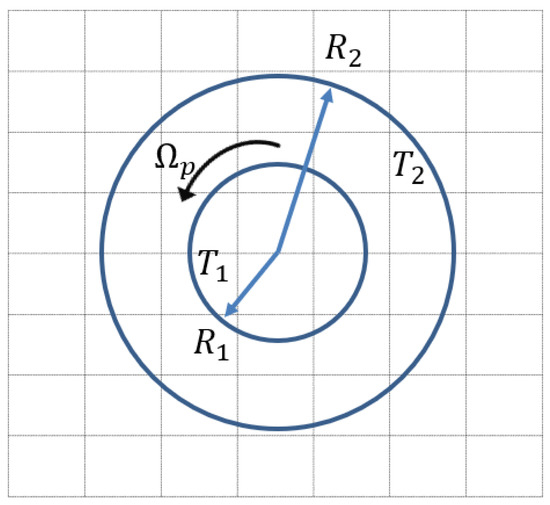
Figure 7.
Computational set up for the Couette flow.
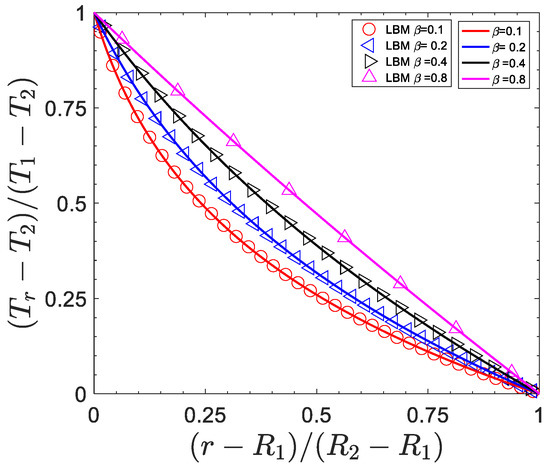
Figure 8.
Normalized temperature profiles of the Couette flow at and
for different . The lines plot the analytical solutions.
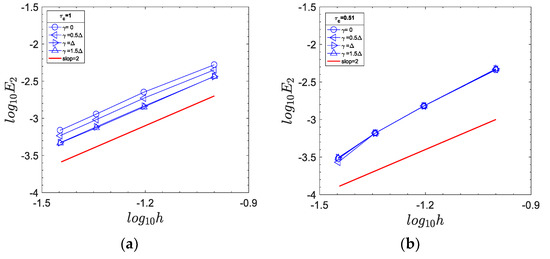
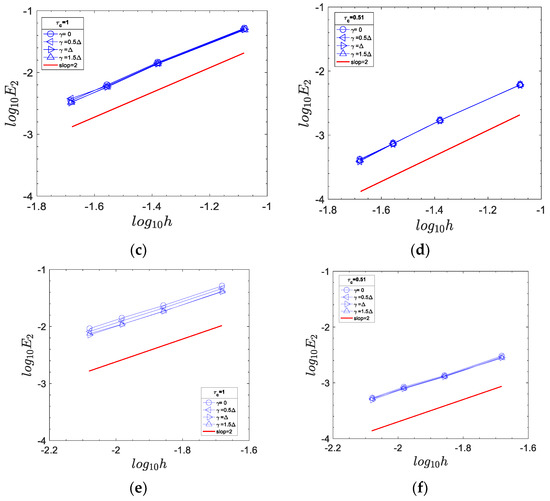
Figure 9.
The convergence order of the Dirichlet boundary condition for 2D Couette flow. (a,b) ; (c,d) ; (e,f) .
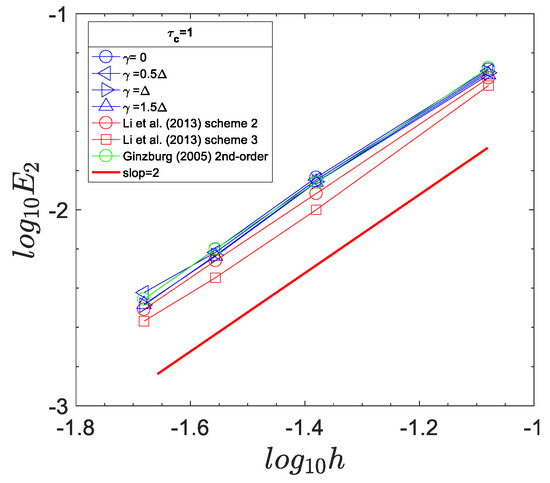
Figure 10.
Comparison of the error for different boundary schemes for .
5.3. 3D Steady-State Symmetric Circular Pipe Flow
The third validation case is the 3D steady-state circular pipe flow with heat conduction. The temperature boundary conditions for the wall, inlet and outlet are as follows, respectively:
The analytical solution for the fluid temperature at steady state in terms of complex form is solved to be
where is the modified Bessel’s function of the first kind of order 0.
is the pipe length. Equation (56) indicates that the temperature distribution in the radial direction is symmetric. Figure 11 shows the -norm for the fluid temperature with respect to the grid resolution. The difference between different is very small at as already observed for 2D channel flow. As increases, the error decreases with increasing . In general, Figure 11 indicates that the Dirichlet boundary condition converges quadratically with increasing grid refinement.
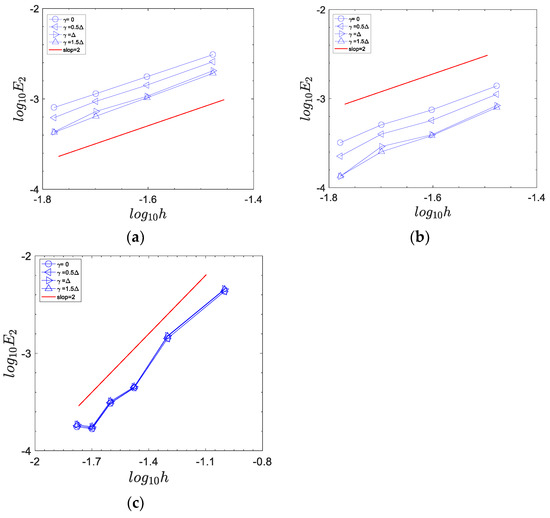
Figure 11.
The convergence order of the Dirichlet boundary condition for 3D circular pipe flow: (a) ; (b) ; (c) .
5.4. Forced Convection of a Hot Sphere in Uniform Flow
In the past several decades, various empirical [22,23] and numerically [24] derived Nusselt number correlations have been proposed. In the last validation case, the heat transfer between a sphere and surrounding fluid in unform flow has been studied for . The diameter of the sphere is 20 in lattice units. The sphere is placed in the middle of the computational domain with a domain size . The Dirichlet boundary condition for the fluid velocity and temperature were imposed onto the fluid at the inlet, whereas the Neumann boundary condition for the fluid velocity and temperature (the derivative in the flow direction is zero) were assigned at the outlet. The inlet fluid velocity was 0.05 for all the simulations. Symmetrical boundary conditions for the velocity and temperature were applied to the other boundaries. The fluid temperature around the hot sphere is symmetric and is shown in Figure 12 for as an illustration. The simulation results together with the predictions of [22,23,24,25,26] are plotted in Figure 13. The maximal relative deviation is within 8% between current simulation results and the predictions of [22,23,24,25,26]. Our simulation results are in good agreement with the predictions of [24,26] with a maximal relative deviation within 2%. The comparison indicates that the thermal Dirichlet boundary condition can accurately calculate the heat transfer for forced convection involving curved boundaries.
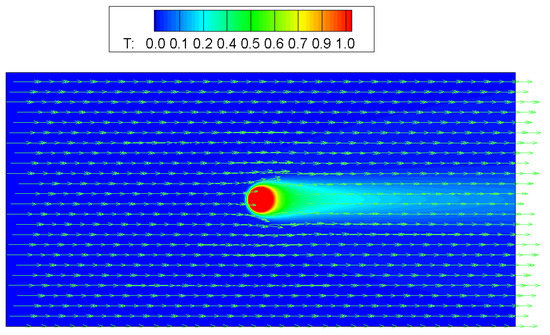
Figure 12.
Temperature distribution of the fluid around a hot sphere. The arrows represent the fluid velocity vector.
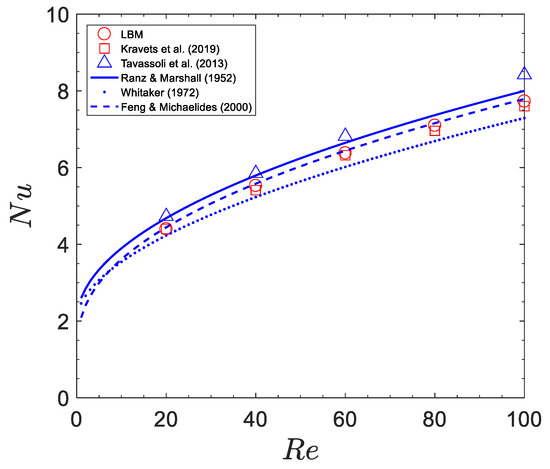
Figure 13.
Nusselt number of an isolated sphere in uniform flow for .
6. Conclusions
A general single-node second-order Dirichlet boundary condition for curved boundaries for the lattice Boltzmann method has been developed. The numerical simulations of 2D and 3D symmetric flows with heat transfer indicate that the boundary condition is numerically stable over a wide range of and γ within the range [0, 2∆]. In addition, we show that the newly proposed boundary condition only needs one fluid node to achieve the same convergence order as the two-point boundary schemes for straight and curved boundaries. Comparisons with the analytical solution for 2D channel flow, cylindrical Couette flow and 3D pipe flow indicate that the boundary condition has second-order accuracy for 2D and 3D straight and curved boundaries, which is consistent with the asymptotic analysis. Further comparison of the Nusselt number for a spherical particle between present simulation results and the predictions of previous studies demonstrates that the boundary condition can accurately capture the convective heat transfer for curved boundaries since the maximal relative deviation is within 8%. In the future, the lattice Boltzmann method with proposed Dirichlet boundary condition will be used to study a gas–solid fluidized bed with heat transfer comprising spherical and non-spherical particles.
Author Contributions
Conceptualization, Y.C.; methodology, Y.C.; validation, Y.C., X.W. and H.Z.; writing—original draft preparation, Y.C.; writing—review and editing, X.W. and H.Z.; supervision, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Sanya Science and Education Innovation Park of Wuhan University of Technology, grant number 2021KF0023.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mani, L.; Tzachor, A.; Cole, P. Global catastrophic risk from lower magnitude volcanic eruptions. Nat. Commun. 2021, 12, 4756. [Google Scholar] [CrossRef]
- German, J.; Redi, A.; Ong, A.; Prasetyo, Y.; Sumera, V. Predicting factors affecting preparedness of volcanic eruption for sustainable community: A case study in the Philippines. Sustainability 2022, 14, 11329. [Google Scholar] [CrossRef]
- Yang, S.; Liu, X.; Wang, S.; Zhang, K.; Wang, H. Eulerian-Lagrangian simulation study of the gas-solid reacting flow in a bubbling fluidized coal gasifier. Chem. Eng. J. 2021, 426, 130825. [Google Scholar] [CrossRef]
- Yang, S.; Wang, S.; Wang, H. Particle-scale evaluation of the pyrolysis process of biomass material in a reactive gas-solid spouted reactor. Chem. Eng. J. 2021, 421, 127787. [Google Scholar] [CrossRef]
- Ghadikolaei, S.; Yassari, M.; Sadeghi, H.; Hosseinzadeh, K.; Ganji, D. Investigation on thermophysical properties of Tio2-Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Powder Technol. 2017, 322, 428–438. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Asadi, A.; Mogharrebi, A.; Azari, M.; Ganji, D. Investigation of mixture fluid suspended by hybrid nanoparticles over vertical cylinder by considering shape factor effect. J. Therm. Anal. Calorim. 2021, 143, 1081–1095. [Google Scholar] [CrossRef]
- Ginzburg, I. Generic boundary conditions for lattice Boltzmann models and their application to advection and anisotropic dispersion equations. Adv. Water Resour. 2005, 28, 1196–1216. [Google Scholar] [CrossRef]
- Li, L.; Mei, R.; Klausner, J.F. Boundary conditions for thermal lattice Boltzmann equation method. J. Comput. Phys. 2013, 237, 366–395. [Google Scholar] [CrossRef]
- Huang, H.; Lee, T.S.; Shu, C. Thermal curved boundary treatment for the thermal lattice Boltzmann equation. Int. J. Mod. Phys. C 2006, 17, 631–643. [Google Scholar] [CrossRef]
- Jalali, A.; Amiri Delouei, A.; Khorashadizadeh, M.; Golmohamadi, A.; Karimnejad, S. Mesoscopic Simulation of Forced Convective Heat Transfer of Carreau-Yasuda Fluid Flow over an Inclined Square: Temperature-dependent Viscosity. J. Appl. Comput. Mech. 2020, 6, 307–319. [Google Scholar]
- Karimnejad, S.; Delouei, A.; AmiriBaşağaoğlu, H.; Nazari, M.; Shahmardan, M.; Falcucci, G.; Lauricella, M.; Succi, S. A Review on Contact and Collision Methods for Multi-Body Hydrodynamic Problems in Complex Flows. Commun. Comput. Phys. 2022, 32, 899–950. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, B.; Zheng, C. A coupled lattice BGK model for the Boussinesq equations. Int. J. Numer. Methods Fluids 2002, 39, 325–342. [Google Scholar] [CrossRef]
- Tang, G.H.; Tao, W.Q.; He, Y.L. Thermal boundary condition for the thermal lattice Boltzmann equation. Phys. Rev. E 2005, 72, 016703. [Google Scholar] [CrossRef]
- Huang, J.; Yong, W. Boundary conditions of the lattice Boltzmann method for convection-diffusion equations. J. Comput. Phys. 2015, 300, 70–79. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, S.; Zeng, Z.; Chew, J. Consistent second-order boundary implementations for convection-diffusion lattice Boltzmann method. Phys. Rev. E 2018, 97, 023302. [Google Scholar] [CrossRef]
- Ginzburg, I.; Silva, G. Mass-balance and locality versus accuracy with the new boundary and interface-conjugate approaches in advection-diffusion lattice Boltzmann method. Phys. Fluids 2022, 33, 057104. [Google Scholar] [CrossRef]
- Zhang, M.; Zhao, W.; Lin, P. Lattice Boltzmann method for general convection-diffusion equations: MRT model and boundary schemes. J. Comput. Phys. 2019, 389, 147–163. [Google Scholar] [CrossRef]
- Yoshida, H.; Nagaoka, M. Multiple-relaxation-time lattice Boltzmann model for the convection and anisotropic diffusion equation. J. Comput. Phys. 2010, 229, 7774–7795. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Junk, M.; Klar, A.; Luo, L.S. Asymptotic analysis of the lattice Boltzmann equation. J. Comput. Phys. 2005, 210, 676–704. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Zhu, H. A general single-node second-order boundary condition for the lattice Boltzmann method. Phys. Fluids 2021, 33, 041137. [Google Scholar] [CrossRef]
- Ranz, W.E.; Marshall, E.R. Evaporation from drops. Chem. Eng. Prog. 1952, 48, 146. [Google Scholar]
- Whitaker, S. Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles. AIChE J. 1972, 18, 361–371. [Google Scholar] [CrossRef]
- Feng, Z.G.; Michaelides, E.E. A numerical study on the transient heat transfer from a sphere at high Reynolds numbers and Peclet numbers. Int. J. Heat Mass Transf. 2000, 43, 219–229. [Google Scholar] [CrossRef]
- Tavassoli, H.; Kriebitzsch, S.H.L.; van der Hoef, M.A.; Peters, E.A.J.F.; Kuipers, J.A.M. Direct numerical simulation of particulate flow with heat transfer. Int. J. Multiph. Flow 2013, 57, 29–37. [Google Scholar] [CrossRef]
- Kravets, B.; Rosemann, T.; Reinecke, S.R.; Kruggel-Emden, H. A new drag force and heat transfer correlation derived from direct numerical LBM-simulations of flown through particle packings. Powder Technol. 2019, 345, 438–456. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).