2. The Quantum Potential Fluctuations Induced by the Background of Stochastic Gravitational Waves
With the emergence of evidence for dark energy in the form of a gravitational background, whether of relic origin or due to the dynamics of general relativity bodies, the quantum hydrodynamic representation offers the possibility of describing the dynamic fluctuations in a system without the need to introduce an external environment. This approach does not introduce divergent results that contradict established theories such as decoherence and the Copenhagen foundation of quantum mechanics; instead, it enhances and complements our understanding of these theories. The noise arising from spacetime curvature ripples can be incorporated into Madelung’s quantum hydrodynamic description by leveraging the foundational assumption of relativity, which allows us to consider the energy associated with a spacetime curvature as virtual mass.
The Madelung quantum hydrodynamic representation transforms the Schrodinger equation [
5,
6,
7]
for the complex wave function
into two equations of real variables: the conservation of the mass density
and the motion equation for the momentum
,
where
and
To introduce the fluctuating virtual mass due to the spacetime background, we assume the following:
The virtual mass density fluctuations own the wave function and density
The associated energy density (of the spacetime background fluctuations) is proportional to
The virtual mass is defined by the identity ;
The virtual mass does not interact with the mass of the physical system (since the gravity is sufficiently weak to be ignored).
Given that, the overall wave function
reads as
Moreover, since the virtual mass
is much smaller than
of the system (i.e.,
), it follows that (4) reads as
Furthermore, given the fluctuating mass density of wavelength
related to the wave function of the mass fluctuation
we have that the energy fluctuations due to the quantum potential read as
Following the procedure described in reference [
8], the energy fluctuation reads as
and, in 3D space, leads to
The outcome indicated by Equation (11) demonstrates that the energy arising from fluctuations in the mass density of the vacuum rises in inverse proportion to the square of its wave-length . Consequently, fluctuations in the quantum potential with extremely short wavelengths (i.e., ) may result in disproportionately large energy, even when the noise amplitudes approach zero (i.e., ). This observation raises concerns about the attainment of the deterministic zero noise limit (2)–(4) that represents quantum mechanics.
Conversely, the assurance of convergence to the deterministic limit (2)–(4) in quantum mechanics for stems from the improbability of uncorrelated fluctuations occurring in increasingly shorter distances. Consequently, the necessity for convergence to conventional quantum mechanics for imposes an additional condition on the spatial correlation function of the noise, specifically as .
The derivation of the shape of the space correlation of noise
is a heavy stochastic calculation [
9]. A simpler and more straightforward way to calculate
is obtained by considering the spectrum
of the noise that reads as [
8]
showing a not-white characteristic, with wavelength
smaller than
that goes fast to zero. From (12),
reads as
where
is the De Broglie length.
Equation (13) reveals that uncorrelated mass density fluctuations on increasingly shorter distances are gradually dampened by the quantum potential. This damping effect facilitates the achievement of conventional “deterministic” quantum mechanics for systems with physical lengths much smaller than the de Broglie wavelength .
In a sufficiently general case that holds practical significance, where the mass density noise correlation function can be reasonably assumed to be Gaussian, featuring a null correlation time, isotropy throughout space, and independence among different coordinates, it can be postulated in the following form:
where in systems of physical length
such as
,
read as
On this ansatz, Equation (3) assumes the stochastic form [
10] (see
Appendix B)
where [
8,
10]
where
is a pure not-zero number [
10].
It is worth noting that the probability mass density (PMD) function , defined by the Smolukowski conservation equation stemming from (17), obeys the condition , since by (13) and (14), convergence to quantum mechanics is warranted.
The gravitational dark energy introduces the concept of a self-fluctuating system where the noise is an intrinsic property that does not require the presence of an environment.
3. The Schrodinger-Langevin Equation from Stochastic Madelung Quantum Hydrodynamics
Langevin equations, commonly utilized for depicting underlying dynamics, can be obtained through various methods, including Poisson transformation [
11] and Fock space formalism [
12]. Exact definitions occasionally can be obtained for nonlinear chemical kinetics and a few other issues. Alternatively, one can approach a Langevin equation from a phenomenological standpoint, where the approximated dynamics are determined beforehand. In this context, achieving a rigorous Langevin description can prove to be quite challenging.
In our current study, we have the advantage of employing an exact microscopic quantum mechanical model.
Generally, assuming for the stochastic case, the complex field is
where
obeys the Smolukowski conservation equation [
8,
13] that, near the deterministic limit of quantum mechanics for
with
, reads as
where the diffusional dissipation
is detailed in ref. [
8]. Moreover, for
of quantum mechanics, it follows that the quantum hydrodynamic Equations (2)–(4) read as
leading to
that, with the help of (20) rearranged in the form
leads to the quantum irreversible Langevin-like equation that, for time-independent systems, reads as
Although, within the frame of the quantum hydrodynamic formalism, quantum mechanics serves as the deterministic limit of the theory with no dissipation, it is interesting to analyze a case when, approaching the zero-noise limit, dissipation is still important.
Close to the zero noise condition, it is possible to characterize the ability of the system to dissipate by the semiempirical parameter
defined by the relation [
10]
.
On this ansatz, (24) reads as
from which we can see that the realization of quantum mechanics is warranted (see Equation (17)) by the condition
. In this case, it can be readily seen that Equation (24) reduces to the Schrodinger equation.
When physical dissipation is significant at the quantum level, the parameter
remains quite high, close to the quantum limit, such as
In this case, it is straightforward to see that Equation (24) converges to quantum Brownian motion. In fact, under condition (26) and by utilizing dimensional considerations, the following identities apply:
Thus, by (28) and (29) being
, the term
can be disregarded in (24), and for
, it follows the conventional Langevin equation for quantum Brownian motion
The emergence of the Schrödinger-Langevin equation through the stochastic extension of the quantum hydrodynamic model is noteworthy, showcasing a precise alignment with traditional quantum mechanics.
4. The Quantum Path Integral Motion Equation in the Presence of Stochastic Noise
The Markov process (17) can be described by the Smolukowski equation for the Markov probability transition function (PTF) [
13]
where the PTF
is the probability that a quantity of probability mass density (PMD)
in time interval τ is transferred to point q [
13].
The conservation of the PMD shows that the PTF displaces the PMD according to the rule [
13]
Generally, for the quantum case, Equation (31) cannot be reduced to a Fokker–Planck equation (FPE). The functional dependence of
by
and by the PTF
produces non-Gaussian terms (see
Appendix C).
Nonetheless, if, at initial time,
is stationary (e.g., quantum eigenstate) and close to the long-time final stationary distribution
, it is possible to assume that the quantum potential is constant in time as a Hamilton potential following the approximation
The quantum potential being independent by the wave function, the PMD
quasi-stationary long-time solutions can be approximately described by the Fokker–Planck equation
where
leading to the final equilibrium of the stationary quantum configuration
In
Appendix D, the stationary states of a harmonic oscillator obeying (36) are shown. The results show that the quantum eigenstates are stable and maintain their shape (with a small change in their variance) when subject to fluctuations.
4.1. Evolution of Quantum Superposition of States Submitted to Stochastic Noise
The quantum evolution of not-stationary state superpositions (not considering fast kinetics and jumps) involves the integration of Equation (17) that, removing fast variables, reads as
By utilizing both the Smolukowski Equation (37) and the associated conservation Equation (32) for the PMD
, it is possible to integrate (37) by using its second-order discrete expansion
where
where
has a Gaussian zero mean and unitary variance which probability function
, for
, reads as
where the midpoint approximation has been introduced
and where
and
are the solutions of the deterministic problem
As shown in ref. [
8], the PTF
can be achieved after successive “
u” steps of approximation and reads as
and the PMD at the
-th instant reads as
leading to the velocity field
Moreover, the continuous limit of the PTF gives
where
.
The resolution of the recursive Expression (50) offers the advantage of being applicable to nonlinear systems that are challenging to handle using conventional approaches [
14,
15,
16,
17].
4.2. General Features of Relaxation of the Quantum Superposition of States
The classical Brownian process admits the stationary long-time solution
where
, leading to solution [
3]
As far as it concerns in (50), it cannot be expressed in a closed form, unlike (51), because it is contingent on the particular relaxation path the system follows toward the steady state. This path is significantly influenced by the initial conditions , and, consequently, the initial time at which the quantum superposition of states is subjected to fluctuations.
In addition, from (38), we can see that depends on the exact sequence of inputs of stochastic noise, since, in classically chaotic systems, very small differences can lead to relevant divergences of the trajectories in a short time. Therefore, in principle, different stationary configurations (i.e., eigenstates) can be reached whenever starting from identical superposition of states. Therefore, in classically chaotic systems, Born’s rule can also be applied to the measurement of a single quantum state.
Even if , it is worth noting that, to have finite quantum lengths and (necessary to have the quantum stochastic dynamics) and the quantum decoupled (classical) environment or measuring apparatus), the nonlinearity of the overall system (system–environment) is necessary: Quantum decoherence, leading to the decay of superposition states, is significantly promoted by the widespread classical chaotic behavior observed in real systems.
On the other hand, a perfect linear universal system would maintain quantum correlations on a global scale and would never allow quantum decoupling between the system and the experimental apparatus performing the measure (see
Section 5). It should be noted that even the quantum decoupling of the system from the environment would be impossible, as quantum systems function as a unified whole. Merely assuming the existence of separate systems and environments subtly introduces a classical condition into the nature of the overall supersystem.
Furthermore, given that the relationship (A31) and (A38) are valid only in the leading order of approximation of (i.e., during a slow relaxation process with small amplitude fluctuations), in instances of large fluctuations occurring on a timescale much longer than the relaxation period of , transitions may occur that are not captured by (50), potentially leading from a stationary eigenstate to a general superposition of states.
In this case, relaxation will follow again toward another stationary state. The PMD (48) describes the relaxation process occurring in the time interval between two large fluctuations rather than the system evolution toward a statistical mixture. Due to the extended timescales associated with these jumping processes, a system comprising a significant number of particles (or independent subsystems) undergoes a gradual relaxation towards a statistical mixture. The statistical distribution of this mixture is dictated by the temperature-dependent behavior of the diffusion coefficient.
5. Emerging Classical Mechanics on Large Size Systems
If the quantum potential is manually eliminated from the quantum hydrodynamic equations of Motion (1)–(3), the classical equation of the motion is revealed [
7]. Despite the apparent validity of this approach, it is not mathematically sound, as it alters the fundamental characteristics of the quantum hydrodynamic equations. Specifically, this operation eliminates the stationary configurations (i.e., eigenstates), since it nullifies the balancing force of the quantum potential against the Hamiltonian force [
18], crucial for establishing the stationary condition. Consequently, even a small quantum potential is important and cannot be disregarded in the deterministic quantum hydrodynamic model (2)–(4).
Conversely, in the stochastic generalization, it is permissible to accurately disregard the quantum potential in (17) and (37) when its force is significantly inferior to the force noise
, such as
, that, by using (17), leads to
and hence, in a coarse-grained description with an elemental cell side
, to
where
is the physical system length.
In addition, even if the noise
has a zero mean, the mean of the quantum potential fluctuations
is not null, resulting in the emergence of the dissipative force
in (17). Consequently, the stochastic sequence of noise inputs disrupts the coherent evolution of the quantum superposition of states. Additionally, upon closer examination of the stochastic noise,
we observe that is proportional to the size of the system; for
in macroscopic systems, (53) is satisfied if
To attain a comprehensive large-scale description that is entirely free from quantum correlations, we can impose more stringent requirements.
Therefore, by noting that, in the case of linear systems,
it follows that they cannot lead to the classical mechanics on a macroscopic scale.
In general, the greater the strength of the Hamiltonian potential, the more localized the wave function and the more pronounced the quantum potential behavior at infinity. This observation is easily substantiated by considering the MDD.
where
is a polynomial of order k.
In order to establish a finite range of interaction for the quantum potential, it is imperative that . Therefore, linear systems, with , have an infinite range of action of quantum potential.
A concrete illustration arises in the context of solids possessing a quantum lattice. When examining phenomena at intermolecular distances characterized by linear interactions, the quantum behavior becomes apparent (as seen in phenomena like X-ray diffraction). However, when investigating the macroscopic properties, a transition to classical behavior occurs. This shift is attributed to the Lennard-Jones potential, which goes to zero at infinity, resulting in a finite quantum range of interaction (see (60)–(62)). In such cases, classical behavior emerges, exemplified by low-frequency acoustic waves with wavelengths much larger than the linear range of interatomic distances. For instance, when particles interact through the Lennard-Jones potential, the long-distance wave function is given by [
19]
the quantum potential reads as
leading to the quantum force
So that, by (53) and (57), the macroscopic classical behavior may manifest [
20,
21] in a phase with adequate sparsity. It is noteworthy that, in Equation (61), the quantum potential underpins the hard sphere potential within the “pseudopotential Hamiltonian model” of the Gross–Pitaevskii equation [
22,
23], where
denotes the boson–boson s-wave scattering length.
By recognizing that, to meet Condition (57), we can appropriately demand that
we can determine the distance
at which the quantum potential is effective [
20,
21] by the formula
where
reads
5.1. Lindemann Constant for Quantum Lattice-to-Classical Fluid Transition
For a L-J gas and its condensed liquid phase, the distance of quantum potential interaction
reads as
where
is the distance up to which the L-J force is linear (
) and where
is the molecular equilibrium position.
An empirical validation of practical significance of the quantum potential interaction length is observed during the quantum-to-classical transition in a crystalline solid at melting point. During this transition, the system shifts from a quantum lattice state to a fluid, amorphous classical phase.
If we make the assumption that, within the quantum lattice, the atomic wave function (around the equilibrium distance) has a smaller extent than the quantum potential interaction distance, then it can be deduced that, at the melting point, its variance equals .
Therefore, the Lindemann constant
[
24] reads as
, and it can be theoretically calculated, since
that, being typically
and
, leads to
A more precise assessment, employing the potential well approximation for molecular interactions [
20,
21], results in
and yields a value for the Lindemann constant
that aligns closely with the measured values, falling within the range of 0.2 to 0.25 [
24].
5.2. Fluid–Superfluid Transition
Since the de Broglie distance
is a function of temperature, its influence on the fluid–superfluid transition in monomolecular liquids at very low temperatures, such as for
, can be detected. The treatment of this case is detailed in ref. [
20,
21], where, for the
–
interaction, the potential well is assumed to be
where
and where
is the mean
–
atomic distance.
By posing that, at the superfluid transition, the de Broglie length progressively reaches the
–
atomic distance, being in the length interval
we have, for
, that the ratio of superfluid/normal
density is approximately null, while, for
, we have almost 100% superfluid
. Therefore, at the condition
when the superfluid/normal
density ratio is 50%, it follows that the temperature
for the
mass of
reads as
which agrees well with the experimental data in ref. [
25] of approximately
.
On the other hand, since, by (72) for
, all the couples of
fall into the quantum state, the superfluid ratio of 100% is reached at the temperature
well agreeing with the experimental data in ref. [
25] of approximately
.
Moreover, by utilizing the superfluid ratio of 38% at the
-point of
, the transition temperature
reads as
in good agreement with the measured
superfluid transition temperature of
.
As a concluding observation, it is noteworthy to mention that there are two methods for establishing macroscopic quantum behavior. The first method entails reducing the temperature, thereby effectively augmenting the de Broglie length. The second method involves intensifying the strength of the Hamiltonian interaction among the particles within the system.
With regard to the latter, it is crucial to highlight that the restricted potency of the Hamiltonian interaction over extended distances serves as the pivotal factor enabling the manifestation of classical behavior. In the analysis of systems dictated by a quadratic or more potent Hamiltonian potential, the interaction range linked to the quantum potential becomes infinite, as depicted in Equation (96). Consequently, attaining a classical phase becomes unachievable, irrespective of the system’s size being .
In this specific scenario, we exclusively witness the full realization of classical behavior on a macroscopic scale in systems characterized by interactions that are sufficiently feeble, even weaker than linear interactions, which exhibit classical chaos. In such instances, the quantum potential is incapable of exerting its nonlocal influence over substantial distances.
Hence, classical mechanics arises as a decoherent result of quantum mechanics in the presence of fluctuating spacetime.
5.3. The Coarse-Grained Approach
The PMD current
reads as
The macroscopic behavior can be derived through the discrete coarse-grained spatial representation of Equation (77), utilizing local cells with a side length of
, where the mass density
for the j-th cell is expressed as
where
where
where
is the correlation length of the noise, where the matrices
,
and
, as well as
, correspond to the discrete derivatives
at the j-th point.
In general, the quantum potential interaction arising from the k-th cell is contingent upon the magnitude of the Hamiltonian potential .
In a system comprising a large number of particles, configuring the side length
to match the mean intermolecular distance
allows the attainment of a classic phase. This condition is met when
significantly surpasses the quantum potential length of interaction
, which, as per Equation (64), is also contingent upon the de Broglie length. Typically, the Lennard-Jones potential (62) yields
This results in the nullification of the interaction of the quantum potential originating from the k-th cell with the adjacent cells, rendering diagonal. Consequently, the quantum effects are restricted to each individual molecule cell domain.
In classical systems where
, the correlation length of the noise reads as
, resulting in spatially uncorrelated fluctuations in macroscopic systems. Conversely, in systems with interactions stronger than linear with
, where the quantum potential of each cell extends its influence to others, quantum characteristics manifest in the coarse-grained description. As detailed in
Section 5.2, employing the quantum stochastic hydrodynamic model (SQHM) allows the derivation of descriptions for dense phases where quantum effects become apparent on the macroscopic scale.
5.4. Measurement Process and the Finite Distance of Quantum Entanglement
Throughout the process of measurement, consisting of a “deterministic” conventional quantum interaction between the sensing component of the experimental setup and the system being measured, the interaction ceases when the experimental apparatus is moved far away from the system, well beyond the distances and .
The interpretation and handling of the “interaction output” are subsequently managed by the measuring apparatus, typically involving a classical, irreversible procedure characterized by a clear arrow of time. This procedure ultimately yields the macroscopic measurement result.
Nonetheless, the phenomenon of decoherence plays a pivotal role in the measurement process. It allows for the emergence of a large-scale classical framework that ensures genuine quantum isolation between the experimental setup and the system, both before and after the measurement event.
This quantum-isolated state, both initially and finally, is essential for determining the conclusion of the measurement and for gathering statistical data from a set of independent repeated measurements.
It is worth emphasizing that, within the framework of the SQHM, the standard condition of moving the measured system to an infinite distance before and after the measurement is not sufficient to guarantee the independence of the system and the measuring apparatus if either or .
5.5. Minimum Measurement Uncertainty of Quantum Systems in Fluctuating Spacetime Backgrounds
Any quantum theory striving to elucidate the evolution of a physical system across various orders of magnitude in size must inherently provide an explanation for the transition from quantum mechanical properties to the emergent classical behavior observed at larger scales. The fundamental distinctions between the two descriptions lie in the minimum uncertainty principle of quantum mechanics and the finite speed of propagation of interactions and information in local classical relativistic mechanics.
If, at a specific distance
, which is smaller than
, a system completely adheres to the conventional principles of quantum mechanics, where its subparts lack distinct identities, then, for an independent observer to gather information about the system, he must be positioned at a distance at least as far as
from the observed system, both before and after the process (refer to
Appendix E).
Hence, owing to the finite speed of propagation of interactions and information, the execution of the process cannot be completed within a time shorter than
Furthermore, considering the Gaussian noise (18) with the diffusion coefficient proportional to
, it follows that the mean value of the energy fluctuation is
for degree of freedom. Therefore, a nonrelativistic (
) scalar structureless particle of mass
m has an energy variance
from which it follows that
It is worth noting that the product remains constant, as the increase in energy variance precisely compensates for the corresponding decrease in the minimum acquisition time . This holds true due to the growth following the square root of . The same outcome is attained when establishing the uncertainty relations between the position and momentum of a particle with mass m.
Moreover, if, as the external (quantum disentangled) measuring system, we can acquire information about the spatial position of a particle with precision
the variance
of its momentum
due to the fluctuations in the low-velocity limit
/ reads as
leading to uncertainty relation
Moreover, by (90), the uncertainty condition
or
requires that
represents the physical length below which quantum entanglement is fully effective, and it denotes the minimum distance—both initial and final—between the system and the measuring apparatus. Regarding the theoretical minimum uncertainty of nonrelativistic quantum mechanics (i.e.,
), which is obtainable from the minimum uncertainty (91) and (92) in the limit of zero noise (
), it follows that
but the uncertainty relations
remain finite and constitute the minimum uncertainty of the quantum deterministic limit.
It is interesting to note that, in the relativistic limit, the minimum acquisition time of measure in the conventional quantum limit reads as
The output (99) shows that it is not possible to carry out any measurement in the deterministic fully quantum mechanical global system, since its duration is infinite.
Moreover, by increasing the temperature we can localize the system in a domain of smaller physical length satisfying the choice (88). Nevertheless, the minimum uncertainty (98) in the context of quantum mechanics remains unchanged in the limit.
Given that nonlocality is restricted to domains with a physical length on the order of and information about a quantum system cannot be transmitted faster than the speed of light (as violating the uncertainty principle), local realism is affirmed in the realm of coarse-grained macroscopic physics, where the domains of order reduce to a point. Meanwhile, the paradox of “spooky action at a distance” is confined to microscopic distances (smaller than ), where quantum mechanics in the low-velocity limit are fully assumed.
It is crucial to note that, in the low-velocity limit of quantum mechanics, the conditions and are implicitly incorporated into the theory, resulting in the (apparent) instantaneous transmission of an interaction at an infinite distance.
It is also noteworthy that, in the presence of noise, the measurement indeterminacy experiences a relativistic correction, given that
leads to the minimum uncertainty in a quantum system, subjected to gravitational background noise (
), which reads as
and
The relativistic correction can become significant for light particles (with ), but in the realm of conventional quantum mechanics for , the uncertainty relations remain unchanged.
5.6. The Noisy Quantum Hydrodynamic Theoryl and the Decoherence Approach
In the framework of the SQHM, ensuring statistically reproducible measurement processes and guaranteeing the complete independence of the measuring apparatus from the measured system (free from quantum potential coupling both before and after the measurement) necessitates a global system with a finite length of quantum potential interaction.
In this scenario, the SQHM suggests that, given the finite speed of light and information transmission, it becomes feasible to conduct the measurement within a finite time interval. As a result, having the finite length of a quantum potential interaction, the subsequent decoherence become essential prerequisites for the execution of the measurement process.
The decoherence theory [
26,
27,
28,
29,
30,
31] does not aim to address the measurement problem or the collapse of the wave function. Its focus lies in elucidating the transition of a system to the statistical mixture of states, brought about by the leakage of quantum entanglement with the environment. Additionally, while the decoherence process may be prolonged for a microscopic system, the decoherence time
for macroscopic systems composed of n microscopic quantum elements can be very short
. However, in the context of decoherence theory, the superposition of states within the global universal wave function persists, maintaining its global coherence.
This puzzle finds a logical resolution through the solution proposed by Poincaré, recently extended to quantum systems [
4]. The solution elucidates that irreversible phenomena can manifest in a globally reversible system due to an exceedingly long recurrence time (far surpassing the lifespan of the universe). The global quantum system locally emulates classical behavior, indistinguishable from that of a large-scale classical universe, as the recurrence time significantly exceeds the lifetime of the universe. For instance, Boltzmann’s calculated recurrence time for a single cubic centimeter of gas to revert to its initial state spans many trillions of digits, dwarfing the thirteen-digit timespan of the universe.
In the context of Madelung’s approach, the Wigner distribution and the quantum hydrodynamic theory are closely connected and do not contradict each other [
7]. However, the interpretation of the global system as classical or quantum in nature is ultimately a matter of interpretation. Essentially, we cannot determine whether the noise from the environment is truly random or pseudorandom. In computer simulations, it is widely accepted that any algorithm generating noise will actually produce pseudorandom outputs, but this distinction is not critical when describing irreversible phenomena.
The theory of decoherence can explain macroscopic behavior as a result of dissipative quantum dynamics, but it cannot determine the conditions that allow for a truly classical global system.
In contrast, the SQHM approach offers a criterion for the shift from quantum dynamics to classical dynamics at a suitable macroscopic scale, eliminating the requirement for an external environment. Furthermore, the SQHM demonstrates the potential for a classical global system within a self-fluctuating spacetime, characterized by background curvature fluctuations aligning with the quantum gravitational portrayal of the universe. In this context, gravity is viewed as a source of global decoherence [
32,
33].
From a conceptual standpoint, the SQHM theory addresses the problematic issue of spontaneous entropy reduction in the global quantum reversible system, which is necessary for the system to return to its initial state, as required by the recurrence theorem. Furthermore, since quantum pseudo-diffusion evolution [
34] shows that entropic and antientropic processes occur simultaneously in different regions of a quantum system, the question of why spontaneous antientropic processes are not observed anywhere and at any time in the universe remains unsolved in the context of decoherence theory.
In relation to this aspect, it is important to clarify that, when the environment size is considered infinite, the recurrence time is pushed beyond infinity. This can be easily demonstrated by examining what are known as free Gaussian coherent states. These states are obtained as the limit of eigenstates of harmonic oscillators when the quadratic coefficient of the potential approaches zero, which is equivalent to increasing the size of the system to infinity.
While we can observe the emergence of antientropic behavior in the harmonic Gaussian states after half of the oscillating period time has passed, this behavior is never observed in the coherent states, because their period of oscillation extends to infinity. Consequently, the expansion of the environment to infinity is a tricky mathematical procedure that eliminates the unavoidable antientropic behavior of conventional (deterministic) quantum mechanics, which contradicts physical evidence.
5.7. The SQHM and the Copenhagen Foundations of Quantum Mechanics
The path integral solution of the SQHM (50) is specific and applies to the small noise limit before the occurrence of a significant fluctuation. It characterizes the “microscopic stage” of the decoherence process at the de Broglie physical length scale.
Furthermore, the SQHM characterizes quantum-to-classical transition through the utilization of two physical lengths, and , treating quantum mechanics as the asymptotic behavior for . As a result, it provides additional insights into the measurement process.
While the measurement process can be asymptotically described as a quantum interaction between the system and the measurement apparatus, marginal decoherence effects persist during its realization, attributed to
- i.
need for real decoupling at the initial and final state of the measure between the system and the measuring apparatus and
- ii.
utilization of classical experimental equipment for the collection and treatment of data.
The marginal decoherence is ignored or disregarded, because the classical equipment is mistakenly assumed to be decoupled at infinity, while the assumption of a perfect global quantum interaction (which extends itself at infinity, such as and ) does not allow the realization of such conditions.
To describe the decoherence due to external apparatus
, the SQHM reads as
where
In principle, marginal decoherence, characterized by a time constant , could influence the measurement if is comparable to the measurement duration time . The absence of marginal effects is considered in the analysis as a specific instance, namely, when the measurement is sufficiently fast, such as .
From a broader perspective, the SQHM reveals that the steady state following relaxation is contingent upon the system’s initial configuration:
at moment
, enabling the system to potentially attain any eigenstate within the superposition.
Considering that the quantum superposition of energy eigenstates exhibits a cyclic evolution, characterized by a recurrence time
, the probability of relaxation to the i-th energy eigenstate in the SQHM model can be expressed as follows:
where
is the total number of time intervals
centered around the instants
(with
and
) in which the system is initially submitted to fluctuations, and
is the number of times the
i-th energy eigenstate is reached in the final steady state.
Moreover, since the eigenstates are stable and stationary, it also follows that the transition probability between the
k-th and the
i-th eigenstates reads as
Since the finite quantum lengths and , allowing quantum decoupling between the system and the measuring apparatus, necessarily implies “marginal decoherence”, it follows that the output of the measure is produced in a finite time lapse (larger than of (85)) due to the wave function decay time.
Regarding the Copenhagen interpretation of quantum mechanics, the measurement is a process that triggers the collapse of the wave function, and the result (e.g., the energy value
for the state (104)) is delineated by the transition probability given by
That, for the i-th eigenstate, reads as
To analyze the interconnection between the wavefunction decay and the wavefunction collapse, we assume, as a starting point, that they are different phenomena and have independent realizations.
In the first instance, we can assume that the wavefunction decay (with characteristic time
) occurs first and then the wavefunction collapses (with characteristic time
) during the measurement process. Without loss of generality, we can assume
, and therefore, in this case, we obtain
On the other hand, for the Copenhagen interpretation, the measure on a quantum state with
by (107)–(109), it follows that
The outputs (109) and (110) show that the wavefunction collapse beyond the duration of the wavefunction decay is ineffective for the output of the measure. Furthermore, we can infer that, since after the wavefunction decays, the system has already reached its final steady eigenstate, and the wavefunction collapse does not occur at all since it does not affect the eigenstates.
Therefore, we can shorten the measure duration
up to the wavefunction decay time
without changing the result (109) for the measure, leading to the relation
On the other hand, by considering in the second instance that the wavefunction collapse
is much shorter than the wavefunction decoherence, such as
(i.e.,
), the output reads as
showing that the wave function decay, due to the marginal decoherence, does not impact the measurement, even if it might proceed beyond the wave function collapse. More precisely, we can affirm that, since the wavefunction decay does not affect the eigenstates, it does not occur at all after the wavefunction collapse.
Therefore, both the wavefunction collapse and the wavefunction decoherence occur together only during the time of the measure
. In the case of (112), we might shorten the measure duration time
to
, as the wavefunction decay finishes at the end of the measure, Identities (105) and (112) also lead to
The proof of (113) can be validated by the numerical output of the motion Equation (37).
The SQHM through Identity (113) furnishes the linkage between the collapse and the decay of the wave function generated by the marginal decoherence, possibly showing that they are the same phenomenon.
5.8. Stochastic Quantum Hydrodynamics, EPR Paradox and Completeness of Quantum Mechanics
Several unresolved facets persist within quantum theories. The EPR paradox [
35] and the completeness of quantum mechanics represent fundamental aspects that do not find a clear placement within a comprehensive theoretical framework.
The Copenhagen interpretation assumes quantum theory as a closed system, requiring acceptance of its probabilistic foundations regardless of the validity of the principle of causality. A notable challenge to this perspective was presented by the Einstein–Podolsky–Rosen objection, articulated in a renowned paper [
35], which argued the EPR paradox analytically.
It is therefore noteworthy to consider the perspective of the SQHM concerning these irreconcilable aspects. Initially, the SQHM highlights that quantum theory, despite its mathematical precision, remains incomplete with respect to its foundational postulates. Specifically, the SQHM underscores that the measurement process is not explicated within the deterministic “Hamiltonian” framework of standard quantum mechanics. Instead, it manifests as a phenomenon comprehensively described within the framework of a quantum stochastic generalized approach.
The SQHM reveals that quantum mechanics represents the deterministic (zero noise) limit of a broader stochastic theory. From this standpoint, quantum mechanics defines the deterministic evolution of the “probabilistic wave”. Moreover, the SQHM suggests that the term “probabilistic” is inaccurately introduced, arising from the inherent probabilistic nature of the measurement process, as the standard quantum mechanics itself cannot fully describe its output. Given the capacity of the SQHM to describe both wavefunction decay and the measurement process, thereby achieving a comprehensive quantum theory, the term “state wave” is a more appropriate substitute for the expression “probabilistic wave”. The SQHM theory restores the principle of determinism into the quantum theory, leading to a deterministic evolution of a “state wave”, explaining the probabilistic output coming from the fluctuations of the gravitational background. This acknowledges a curved spacetime characterized by stochastic fluctuations in both curvature and geodesic distance.
Furthermore, it is noteworthy to observe that the SQHM addresses the lingering question of preexisting reality before measurement. In contrast, the Copenhagen interpretation posits that only the measurement process allows the system to decay into a stable state, establishing a persistent reality over time. Consequently, it remains indeterminate within this framework whether a persistent reality exists prior to measurement.
At this juncture, the SQHM introduces a subtle innovation: the world is capable of self-decay through macroscopic-scale decoherence, resulting in stable macroscopic eigenstates. These states, being stable with respect to fluctuations, establish a persistent reality that exists prior to measurement.
Regarding the EPR paradox, the SQHM demonstrates that, in a perfect quantum deterministic universe, achieving two completely decoupled parts of the system is not feasible. Instead, this condition can only be realized within a classical system—a self-fluctuating quantum system with finite distances, where the interaction of the quantum potential extends.
In summary, the SQHM reveals the following key points:
- i.
Classical reality emerges at the macroscopic level, persisting as a preexisting reality before measurement.
- ii.
The measurement process is feasible in a classical macroscopic world, because we can have independent systems, namely the system and the measuring apparatus.
- iii.
Determinism is acknowledged within standard quantum mechanics under the condition of zero noise.
- iv.
Locality and causality are achieved at the macroscopic scale, where quantum nonlocal domains condense to punctual domains.
- v.
The maximum light speed of the propagation of information aligns with quantum uncertainty.
Moreover, if we consider the SQHM as a complete theory, it should be capable of elucidating the “hidden variable” theory of Bohm that endeavors to restore the determinism of quantum mechanics by introducing the concept of a pilot wave. The fundamental concept posits that, in addition to the particles themselves, there exists a “guidance” or influence from the pilot wave function that dictates the behavior of the particles. Although this pilot wave function is not directly observable, it does impact the measurement probabilities of the particles.
On the other hand, the SQHM posits that quantum mechanics represents the deterministic limit of a broader quantum stochastic theory. In a perfect quantum universe, the measurement process cannot be executed. Furthermore, measurement becomes feasible in a macroscopically classical universe generated through quantum decoherence induced by the fluctuating gravitational background. While the Bohm theory attributes the indeterminacy of the measurement process to the undeterminable pilot wave, the SQHM attributes it to the fluctuating gravitational background (difficult to determine due to its predominantly early-generation nature during the Big Bang and the weak force of gravity). This indeterminacy is compounded by the inherently chaotic nature of the classical law of motion, further contributing to the uncertainty of measurement outcomes.
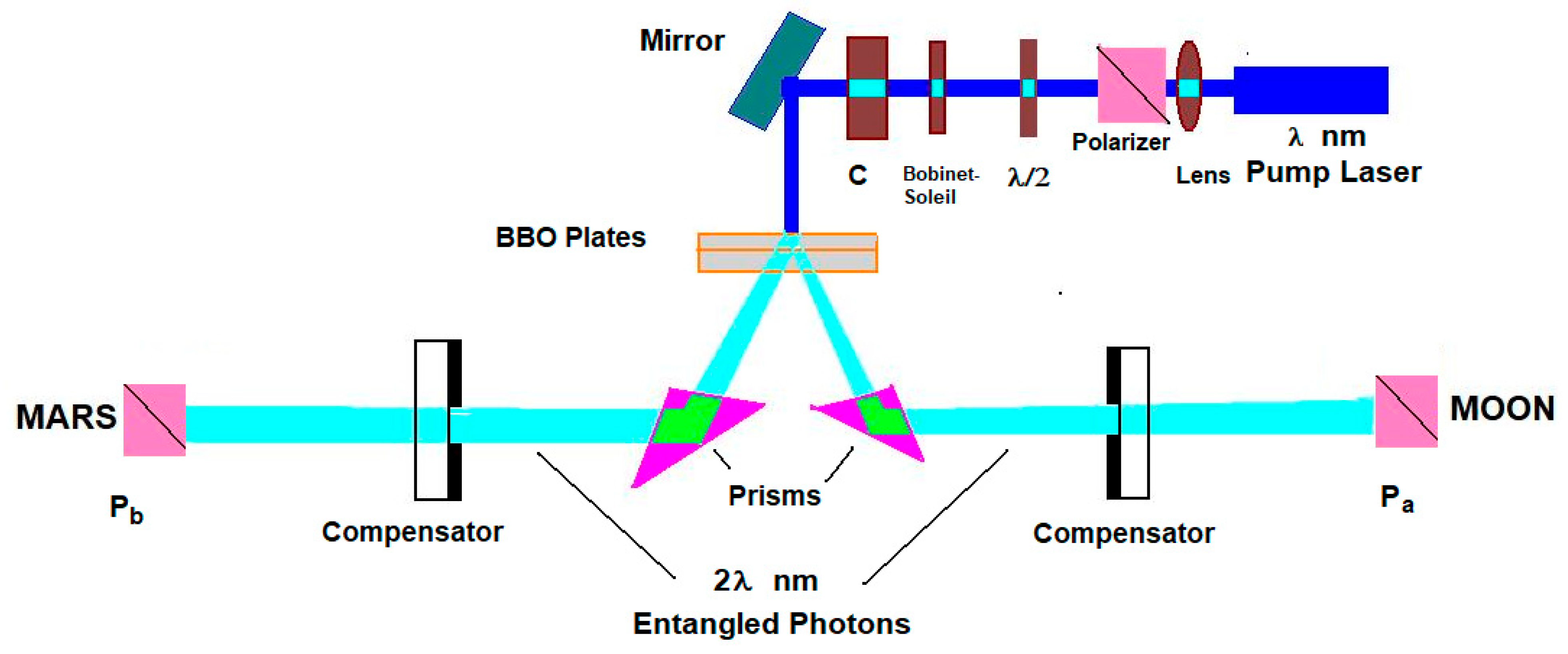
6. Measurement of Photon Entanglement on Large Distances
Once we establish a unified theory where quantum mechanics governs at the microscopic level, classical physics prevails at the macroscopic scale and fluctuations seamlessly coexist, we understand how the range of effectiveness of quantum entanglement is important in obtaining the classical independence of two distinct systems, as discussed in the EPR paradox. Therefore, it is of paramount importance to test the theoretical predictions in measures on entangled photons, since the length of effectiveness of their quantum potential extends itself at macroscopic distances (see
Section 6.1) typical of the macroscopic world.
As the time of wave function decay plays a crucial role in the measuring process, the output of quantum entanglement experiments is necessarily influenced by this. While it is challenging to precisely measure the time it takes for information to transfer itself via entangled photons in a laboratory, this parameter can be more accurately controlled in experiments conducted over planetary distances (see
Figure 1).
SQHM theory aligns with the idea that relativistic causality and quantum nonlocality are compatible, a concept that is already supported by relativistic quantum field theory. To check this, we analyze the output of two entangled photon experiments traveling in opposite directions in the state
where
and
are vertical and horizontal polarizations, respectively, and
is a constant phase coefficient. Photons “one” and “two” impact polarizers
(Alice) and
(Bob) with polarization axes positioned at angles
and
relative to the horizontal axis, respectively. For our purpose, we can assume
.
The probability that photon “two” also passes through Bob’s polarizer is .
As widely held by the majority of the scientific community in quantum mechanics physics, when photon “one” passes through polarizer with its axes at an angle of , the state of photon “two” instantaneously collapses to a linear polarized state at the same angle , resulting in the combined state . In the context of the SQHM, we posit that the collapse is not instantaneous, and following the Copenhagen quantum mechanics standpoint, we assert rigorously that the state of photon “two” is not defined before its measurement at the polarizer .
Therefore, after photon “one” passes through polarizer , from the standpoint of SQHM, we assume that the combined state is , where the state represents the state of photon “two” in the interaction with the residual quantum potential field generated by photon “one” at polarizer . When the residual part of the two entangled photons also passes through Bob’s polarizer, it makes the transition with probability .
Since, in the SQHM, the wave function collapse is not instantaneous but takes a finite time interval, we designate these time intervals as and for the two photons, respectively.
Furthermore, we posit that the measurement interval commences upon the detection of the first entangled photon by the polarizer photon counter system (at time ) and concludes when the second entangled photon is detected at the second polarizer photon counter system (at time ). Additionally, we presume that the detection of each photon promptly occurs upon the completion of its wavefunction collapse.
The optimal approach for conducting the experiment involves maximizing the separation distance, denoted as , between the two polarizer photon counter systems. To meet this condition, we can contemplate situating the photon source on Earth, positioning the first polarizer photon counter system on the moon and situating the second system on Mars.
For instance, let us consider a scenario where the moon, Earth and Mars are aligned. In this case, it follows that the distance between the two polarizer photon counter systems is determined by , from which we obtain that and , where the Earth–Mars and Earth–moon distances are denoted as and , respectively.
To determine the modality by which the quantum potential transfers the information of the first photon measure to the second photon, we assume that
- i.
The quantum potential interaction propagates at the speed of light;
- ii.
The quantum potential has a spatial extension equal to the physical length
At the time
, the first photon arrives and interacts at the moon polarizer; at time
, its wavefunction decays at the final measured state, the second photon arrives on Mars at
, and the quantum potential signal generated by the first photon interaction (at
) reaches the second polarizer on Mars at the time
The second photon on Mars decays to its final state and is measured.
Thus, assuming no superluminal transmission of information, it follows that
and therefore,
where
must be measured by utilizing parallel nonentangled photons.
Moreover, in order for the two photons to be quantum entangled, it must also hold that
The value
in (119) can be obtained by knowing the spectral composition of the photon (see
Appendix F). In this case, when photon “one” interacts with the polarizer on the moon, it is still entangled with photon “two” traveling toward Mars.
In this scenario, photons “one” and “two” form a single quantum system that interacts with the polarizer on the moon when photon “one” reaches it. After interacting with the polarizer on the moon, photon “two” travels to Mars, carrying in its quantum potential the information about the polarization of photon “one”. At this point, we essentially have an “entangled interaction” of the two photons with the first polarizer.
Equation (118) has been derived by assuming that the decay of photon “two” to the final measured state begins upon its arrival at the polarizer on Mars and that the quantum potential effect, resulting from photon “one”, starts to affect photon “two” after its arrival at the polarizer on Mars (but not during its travel), since it is assumed that the quantum potential interaction does not travel faster than light.
It is worth mentioning that the quantum entanglement in the low-velocity limit of quantum mechanics may be superluminal, since, in that limit, the velocity of light goes to infinity, but that is not so for the photon dynamics.
However, if
this implies that the photon wave function’s decay on Mars, leading to the polarizer photon counter interaction, takes place prior to the arrival of the quantum potential interaction (information) from the first photon detection on the moon. If the measurement output adheres to the quantum correlation law, this contravenes relativistic local causality.
Furthermore, to detect the entangled interaction of photons with the moon polarizer, a counter experiment can be conducted by enclosing the moon polarizer detector in a Faraday cage (approximately 300 m long), with a diaphragm that closes as soon as the photon enters the cage and before it reaches the moon polarizer. The closure of the diaphragm forces the two-photon system to interact with the macroscopic environment before interacting with the moon polarizer. As a result, the photons should decay into decoherent states before their detection and show stochastic polarization states.
6.1. The Quantum Potential Range of Photon Interactions
Given the photon wavefunction,
With Gaussian spectrum
, the quantum correlation length
reads as (see
Appendix F)
The same result is obtained if we use the superposition of the two photon fields in calculating the quantum coherence length .
This output allows the possibility that the two entangled photons undergo an “entangled interaction” when interacting with the first polarizer on the moon, generating the “synchronized decay” at the second polarizer on Mars.
6.2. Discussion
The SQHM theory is in line with the concept that relativistic causality and quantum nonlocality can coexist, a notion already substantiated by the relativistic quantum field theory. It elucidates the synchronization of photon polarization separated by a large distance without necessitating faster-than-light arguments. This is accomplished by leveraging the infinite length of the interaction provided by the quantum potential, which effectively binds the two photons into a unique quantum system.
The quantum potential, with its extensive range of interaction , establishes a connection between both photons, one situated on the moon and the other traveling towards Mars. At the first photon interaction with the polarizer, the quantum potential changes and will influence the evolution of the other photon and its interaction at the second polarizer. This connection allows for the synchronization of both final states. There is no concealed mechanism at play that involves the two entangled photons, even when they are separated by a distance greater than the de Broglie length .
For the SQHM, there exists a state wave before the measurement is conducted by the polarizers. This state wave comprises two entangled photons, giving rise to an aggregate quantum potential. Subsequently, when the measurement occurs, the polarizers alter this state wave, resulting in the production of the polarized state as an output.
If, for any reason, the polarizers at both ends become desynchronized for a duration longer than the wave function decay time of the photon upon which the initial polarizer is applied, the SQHM theory anticipates that the measurement of the first photon will influence the second photon, regardless of the temporary desynchronization of the polarizers. According to SQHM, this correlation will endure, as it is inherently embedded in the quantum potential, even if the polarizers remain unsynchronized for a period surpassing the collapse of the wave function of the initial photon.
The polarization detection of two quantum-entangled photons is a specific measurement process conducted at two separate moments in time. During the first measurement, only a portion of the quantum system is affected (and destroyed) and not the entire system. However, during this initial measurement, the “two-photon system” transitions into the measured state as it interacts with the polarizer. Subsequently, when the second photon is detected on Mars, its quantum state is found to be coherent with the one measured at the first photon.
The underlying challenge lies in understanding how the information, which may also be encoded within the quantum potential, can effectively transmit from the first photon to the second photon as the second photon travels towards Mars. If information does not propagate faster than the light speed, it becomes difficult to explain how the second photon’s wave function collapses before the quantum potential energy manages to reach the second polarizer. Therefore, in this case, the second photon’s wavefunction decay time will result in a detection delay time relative to the arrival of a nonentangled photon that was simultaneously launched from Earth. In this context, the time of application of the first polarizer is possibly defined by another nonentangled photon simultaneously launched from Earth to the moon.
8. Conclusions
The SQHM presents a framework for characterizing the behavior of quantum systems in a physical vacuum, incorporating a fluctuating metric. This model posits that the spatial noise spectrum is non-white, featuring a correlation function defined by the de Broglie characteristic length. Consequently, effective quantum entanglement emerges, persisting in systems where the physical length is significantly smaller than this characteristic length.
Nonlocal quantum interactions may extend beyond the de Broglie length, reaching a finite distance in nonlinear weakly bonded systems. The dynamics of such systems can be described by the Schrodinger-Langevin equation, deviating from the deterministic bounds of quantum mechanics.
As the physical length of the system increases, classical physics may predominate when the scale surpasses the range of interaction of the quantum potential. The long-distance characteristics of the quantum potential govern the existence of a coarse-grained classical large-scale description.
The SQHM further elucidates that the minimum uncertainty during the measurement process tends to approach the quantum uncertainty relations in the absence of noise. The principle of minimum uncertainty holds when interactions and information propagate no faster than the speed of light, aligning with the relativistic macroscopic locality and nonlocal quantum interactions at the microscale.
The SQHM posits that the interaction between a quantum system and the gravitational background induces a gradual loss of coherence, resulting in classical-like behavior and outcomes nearly identical to those predicted by the decoherence approach. A key distinction lies in the self-generation of fluctuations in the SQHM, intrinsic to the spacetime characteristics originating at the Big Bang, without the reliance on an external environment. Within the SQHM framework, weak quantum potentials fail to sustain coherence in the presence of fluctuations as a drag force emerges, leading to decoherence.
This phenomenon is observable in macroscopic systems, such as those comprised of molecules and atoms interacting through long-range weak potentials, as seen in the Lennard-Jones gas phase. In such scenarios, the impacts of decoherence become more pronounced, and the quantum characteristics of the system become increasingly challenging to discern as the system’s size and complexity grow. The SQHM offers a valuable framework for comprehending the intricate interplay between quantum mechanics and classical behavior in such systems.
The stochastic quantum hydrodynamic model proposes that classical mechanics can manifest in a quantum system when the physical length of the system far exceeds the range of interaction of the quantum potential .
When the eigenstates of a quantum system experience fluctuations, their stationary configurations undergo slight perturbations but persist as stationary and are closely aligned with those predicted by quantum mechanics. However, when the system evolves in a superposition of states, fluctuations induce the relaxation of the superposition to the stationary configuration of one of the eigenstates composing the superposition. This results in the emergence of classical mechanics on a large scale, influenced by the temperature dependence of the de Broglie length, as observed in phenomena like the fluid–superfluid transition. Additionally, this classical emergence is influenced by the extension of the quantum potential range of interactions, as seen in events such as the solid–fluid transition occurring at the melting point of the crystal lattice.
The model offers a comprehensive path integral solution that can be derived in a recursive manner. Additionally, it encompasses conventional quantum mechanics as the deterministic limit of the theory.
In accordance with the stochastic quantum hydrodynamic model, decoherence is deemed essential for a quantum measurement to transpire within finite time intervals, playing a role in the execution, data collection and management of the measuring apparatus. The model posits that the wavefunction collapse phenomenon in the Copenhagen interpretation of quantum mechanics may align with the concept of wavefunction decay. This decay process is characterized by unique kinetics and occurs within a finite timespan.
With the premise that wavefunction decay occurs within a finite timeframe during the measurement process, a thought experiment is conducted to scrutinize the measurement of the photon entanglement. The SQHM posits the existence of an underlying wave state prior to the polarizer measurements. This preexisting wave state consists of two entangled photons, which give rise to an aggregate quantum potential. When a measurement takes place, the polarizers modify this preexisting wave state, resulting in the emergence of polarized states as the outcome. According to the SQHM framework, the process of polarization detection for two quantum-entangled photons occurs over two distinct steps. During the first one, only a portion of the quantum system is affected. However, during the first part of the measurement, the “two-photon system” transitions into the measured state as it interacts with the polarizer. Consequently, when the second photon is detected on Mars, its quantum state is found to be coherent with the state measured for the first photon. The quantum hydrodynamic approach posits that the information encoded within the quantum potential can effectively transfer from the first photon to the second one, resulting in a delay of the second photon’s detection due to its prolonged wavefunction decay time.
The model reveals that canonical quantum mechanics is applicable only in a perfectly static universal spacetime. In real-world scenarios, due to fluctuations in the spacetime background caused by the Big Bang and other cosmological sources, the quantum evolution of mass densities encounters a resistance force while traveling through spacetime with oscillating metrics. This phenomenon shows some analogy to the effect observed with the Higgs Boson, where its field imparts inertia to elementary particles as they move through it.
The description offered by the stochastic quantum hydrodynamic theory envisions a situation where classical mechanics emerges on a macroscopic scale within a spacetime characterized by fluctuations in the curvature. This portrayal seamlessly aligns with the quantum gravitational representation of the cosmos, where gravity serves as the catalyst for universal decoherence.
The model shows that, if reversible quantum mechanics are realized in a static vacuum, the measurement process cannot take a finite time to occur.