Geometric Stochastic Resonance in an Asymmetric T-Shaped Chamber

Abstract

The investigation of a Brownian particle subjected to an AC force that diffuses within a T-shaped chamber was conducted. This T-shaped chamber is composed of a strip cavity and a trapezoidal cavity positioned below it. The interplay between the AC force and asymmetric geometry creates a spatially bistable potential perpendicular to the AC force. With the assistance of noise, the particles can transition between two stable states and oscillate along the AC force at corresponding amplitudes at every spatially stable state. The asymmetric geometry facilitates the trapezoid cavity’s ability to more easily trap the Brownian particle than the upper strip cavity in the weak noise limit. Our observations reveal that proper noise can ensure the particle’s efficient trapping within the upper strip cavity and synchronization with the AC force, indicating the occurrence of geometric stochastic resonance. The T-shaped chamber serves as a simplified model, aiding in the further understanding of geometric stochastic resonance induced by irregular geometries and enabling the manipulation of microscopic particles in various small-scale systems.

1. Introduction

Stochastic resonance (SR) refers to the phenomenon where the right amount of noise can significantly enhance the response of a system to external drives. This concept was initially proposed by Benzi et al., who used it to rationalize the recurring ice ages periodically [1,2]. Initially, the study on SR mainly focused on systems with two states, particularly bistable systems [3,4,5,6,7]. Currently, this research has been extended to monostable and multistable potentials [8,9]. Meanwhile, many properties about stochastic processes and stochastic resonance have been proposed and developed, such as the time evolution of stochastic processes, probability density of residence times, correlation function, signal-to-noise ratio, and theoretical methods, including linear response theory and critical analyses [10]. The notion of SR has been widely introduced to various systems in different fields with various mechanisms [10,11], including physics, biology, and chemistry [12,13,14,15].

Most previous research on SR has focused on the purely energetic barriers. However, in certain situations, the transportation and control of particles or biomacromolecules are crucial in small-scale biological and soft matter systems [16,17,18]. The defining feature of microdynamic systems is the imposed confinements, which restrict the available space of these systems and impact the movement of particles inside them. Smooth confining geometries can be modeled as entropic (i.e., noise-dependent or temperature-dependent) potentials [19,20]. When considering the SR of a Brownian particle in such a confined system, the confinement plays a significant role. In [21,22], Burada et al. proposed the concept of entropic stochastic resonance (ESR) for a Brownian particle moving in a double-cavity with a smooth structure. In contrast to ESR, Ghosh et al. proposed the geometric stochastic resonance (GSR) in [23,24], which is also related to a Brownian particle moving in a double-cavity with a sharp geometric structure rather than a smooth one, which cannot be considered entropic in nature. The original studies on ESR and GSR have guiding significance for investigating the motion of small particles in multiple cavities, which has motivated numerous investigations into manipulating small particles in various small-scale systems [25,26,27,28].

The reference ref. [24] discusses the occurrence of GSR in a two-cavity structure with a passable separation wall whose slope tends to infinity or in which the separation walls tilt into the cavities when a Brownian particle is subjected to an AC drive. The distinction between GSR and ESR lies in the fact that the geometry of the systems cannot be regarded as an entropic potential, and the diffusion dynamics of the particle cannot be reduced to a one-dimensional stochastic process. However, in some systems with complex geometry, the transversal forces play a crucial role in diffusion, mobility, and directed transport. For instance, a constant transversal force may lead to ESR, entropic trapping [29], entropic transport [30], longitudinal transportation enhancement [31], or other effects.

However, the research on ESR/GSR mentioned above has primarily focused on symmetrical geometric configurations, such as symmetrical double- and triple-cavity structures [23,24,28]. While some researchers have explored the impact of asymmetrical bi-/triple-stable potential barriers on SR, it is challenging to maintain a truly symmetrical physical system in practice. As a result, the ordinary SR or ESR of asymmetrical bistable or geometric systems has been proposed and investigated [26,32,33,34]. It is crucial to understand how the asymmetry of the geometry affects GSR.

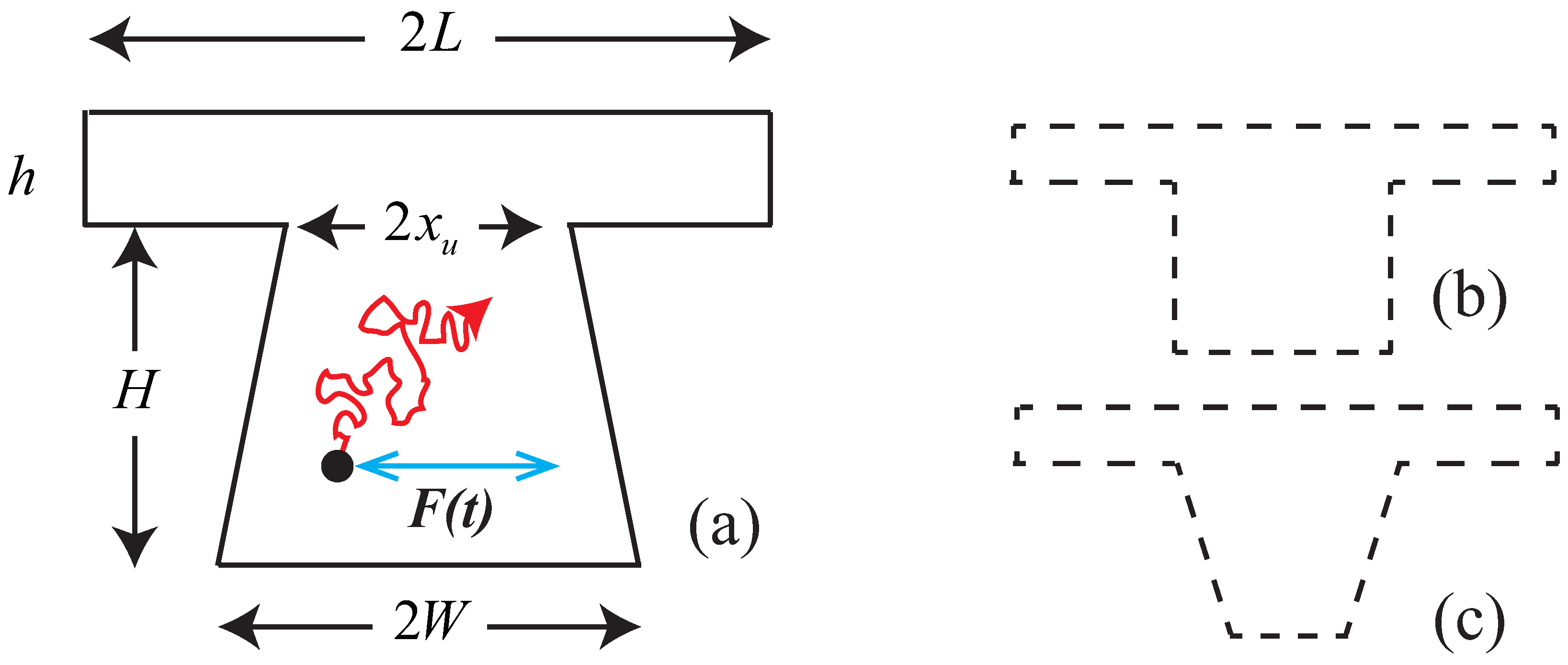
Motivated by the aforementioned discussion, we conducted a study on the dynamics of a Brownian particle subjected to an AC force and confined in an upper-down asymmetrical geometry, such as a T-shaped chamber. Our findings revealed that SR occurs in this scenario. In contrast to the symmetrical case, geometric stochastic resonance in an asymmetrical structure exhibits unique features, such as the different capacities of trapping the Brownian particle in the two cavities.

This paper is organized as follows: In Section 2, we introduce the geometric configuration of the model and the Langevin equations used to simulate the stochastic dynamics of the system. The simulated results and their physical implications are discussed in Section 3. Finally, our conclusions are presented in Section 4.

2. Model

In this study, we investigated the behavior of Brownian particles subjected to an AC force that drives them in a T-shaped 2D chamber with a strip cavity above and a trapezoidal cavity below, as depicted in Figure 1. This T-shaped chamber exhibits up-down asymmetry and is perpendicular to the AC force, unlike the conventional case where the symmetry axis of the geometry is parallel to the driving force [24]. The motion of a Brownian particle in such a confined two-dimensional (2D) structure under the influence of an AC force $F\left(t\right)$ along the x-axis can be described by the following dimensionless Langevin equation:

$$d\overrightarrow{r}/dt=-F\left(t\right){\overrightarrow{e}}_x+\sqrt{2D}\overrightarrow{\zeta }\left(t\right)$$

(1)

where $\overrightarrow{r}$ represents the position of the particle. ${\overrightarrow{e}}_x$ and ${\overrightarrow{e}}_y$ are the unit vectors along the x and y directions, respectively. The stochastic term $\overrightarrow{\zeta }\left(t\right)$ is zero mean white Gaussian noise with autocorrelation functions $〈{\overrightarrow{\zeta }}_i\left(t\right){\overrightarrow{\zeta }}_j\left(t^{\prime }\right)〉={\delta }_{ij}\left(t-t^{\prime }\right)$ with $i,j=x,y$, and D is the scaled noise intensity. The explicit form of the external oscillating force is expressed by $F\left(t\right)=F_{0}cos\left(\omega t\right)$, where F is the amplitude and $\omega$ is the frequency of the force.

The simulations with Equation (1) were performed using the following standard stochastic Euler algorithm [21]:

$$x_m(n+1)=x_m\left(n\right)-F_0\left(n\right)\Delta t+\sqrt{2D\Delta t}{\zeta }_{x,n}^m$$

(2)

$$y_m(n+1)=y_m\left(n\right)+\sqrt{2D\Delta t}{\zeta }_{y,n}^m$$

(3)

$$\langle x\left(n\right)\rangle =\frac{1}{M}\sum _{m=1}^M{x}_m\left(n\right)$$

(4)

where ($x_m\left(n\right)$, $y_m\left(n\right)$) indicates the position in the 2-D plane of mth particle at time $n\Delta t$. ${\zeta }_{x,n}^m$ and ${\zeta }_{y,n}^m$ are Gaussian random numbers with the mean and standard deviation of 0 and 1. In the simulations, a Brownian particle with initial random distribution should exceed ${10}^7$ steps with the time step $\Delta t={10}^{-3}$. Stochastic averages are the ensemble averages of the above process repeated more than ${10}^5$ times with random initial positions in the T-shaped chamber. The walls of the cavity to constrain the Brownian particles are defined as follows:

$$\left\{\begin{array}{cc}y=h,& x\in (-L,L)\\ 0<y<h,& \left|x\right|=L\\ y=0,& \left|x\right|\in (x_u,L)\\ y=k(x_u-\left|x\right|),& \left|x\right|\in (x_u,W)\end{array}\right.,$$

(5)

where $k=H/(W-x_u)$ is the slope of the wall of the trapezoidal cavity. At the wall of the cavity, we adopted the reflecting boundary condition [35].

Let us assume the response of the particles to the AC force $F\left(t\right)$, whose trajectories along the x axis can embed a persistent harmonic component $\overline{x}\left(D\right)cos(\omega t-\varphi \left(D\right))$. The amplitude $\overline{x}\left(D\right)$ and phase $\varphi \left(D\right)$ were obtained by evaluating [36]

$$\overline{x}\left(D\right)cos\left(\varphi \left(D\right)\right)=\frac{1}{T}{\int }_0^T\langle x\left(n\right)\rangle cos\left(\omega t\right)dt$$

(6)

$$\overline{x}\left(D\right)sin\left(\varphi \left(D\right)\right)=\frac{1}{T}{\int }_0^T\langle x\left(n\right)\rangle sin\left(\omega t\right)dt$$

(7)

where T is the simulation time of each time serial.

3. Results and Analysis

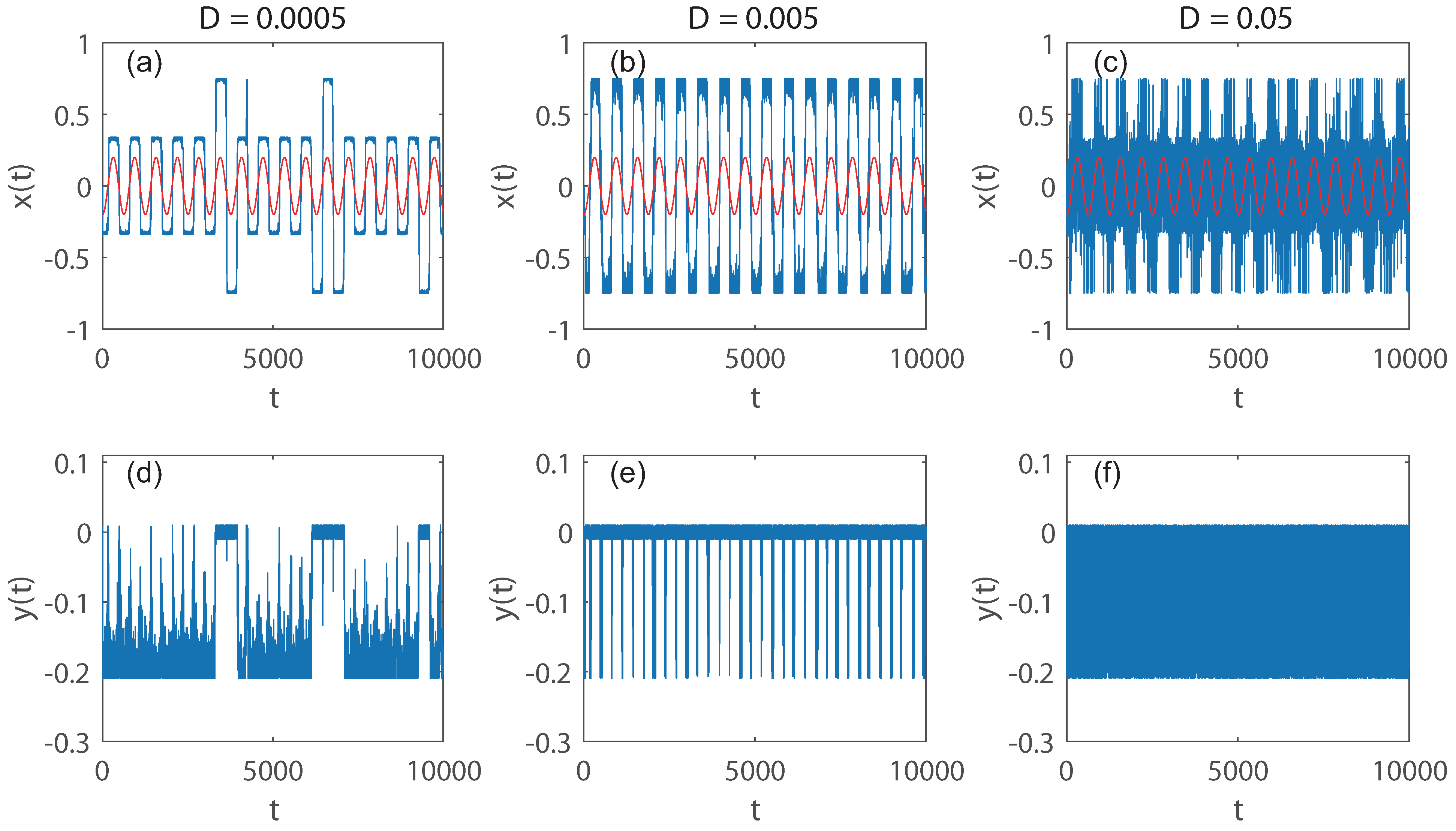
To intuitively demonstrate the stochastic resonance in a T-shaped chamber, we plotted the stochastic trajectories of particles parallel and vertical to the AC force with different noise strengths in the upper and lower panels of Figure 2. In Figure 2a,d, we set the noise as weak, $D=0.0005$. Note that the Brownian particle is trapped in the bottom of the trapezoid cavity and performs an oscillation with a short amplitude W. For an intermediate noise, such as $D=0.005$, the Brownian particle mostly stays in the upper strip cavity, and its trajectory dominates the square wave with a large amplitude L. In this case, the amplitude of the average trajectory is enhanced and synchronized with the AC force $F\left(t\right)$, indicating the occurrence of stochastic resonance. In the strong noise regime, for example, $D=0.05$, the particle is out of the control of the AC force and the constraint of the geometric structure, whose trajectory tends to be random in the chamber (Figure 2c,f).

To intuitively demonstrate the stochastic resonance in a T-shaped chamber, we plotted the stochastic trajectories of particles parallel and perpendicular to the AC force with different noise strengths in the upper and lower panels of Figure 2. In Figure 2a,d, we set the noise as weak, $D=0.0005$ (note that the Brownian particle is trapped in the bottom of the trapezoid cavity and performs an oscillation with a small amplitude W). For intermediate noise levels, such as $D=0.005$, the Brownian particle mostly stays in the upper strip cavity, and its trajectory dominates the square wave with a large amplitude L (in this case, the amplitude of the average trajectory is enhanced and synchronized with the AC force $F\left(t\right)$, indicating the occurrence of stochastic resonance). In the strong noise regime, for example, $D=0.05$, the particle is out of the control of the AC force and the constraint of the geometric structure, whose trajectory tends to be random in the chamber (Figure 2c,f).

The physics behind the phenomenon described above can be explained based on the bistable state consideration of the model. When a Brownian particle subjected to an AC force along the x-axis moves in the T-shaped chamber, it collides with the two sidewalls of the upper and lower cavities. When the AC force presses the particle against the side walls of the upper cavity, the noise can ensure that the particle is uniformly distributed on the left or right side walls of the upper cavity. In the case of the down cavity, the particle subjected to an AC force can possibly stay in the left or right inner corners of the down cavity. Therefore, under the cooperation of the pressure of the AC force and the confinement of geometry, there are two stable regions for the particle to stay in along the y-direction, which recovers the effect of an energetic bistable potential. Under the activation of sufficient weak noise, the particle cannot overcome the barrier to switch between two stable regions along the y-direction. Furthermore, we should note that the stable region of the upper cavity is adjacent to, while that of the down cavity is far away from, the peak of the barrier. Consequently, the probability of finding the particle at one of the corners of the lower cavity is maximal. For each stable region, the possible maximal displacements of the particle along the x-direction are L and W, respectively. The average displacements $\langle x\left(t\right)\rangle$ of Brownian particles exhibit two square waveforms with amplitudes L and W in the upper and lower cavities, respectively. With the help of noise, the particles will hop rather than diffuse between two stable regions along the y-direction due to the barrier between the two stable regions. Thus, the average particle displacement $\langle x\left(D\right)\rangle$ is a mix of two square waves. In this work, we set $L>W$. Hence, $L>\langle x\left(D\right)\rangle >W$ for insufficient noise.

To further investigate the underlying physics, we present the escape rate of Brownian particles passing through the middle opening from the upper and lower cavities. The escape rate, denoted as $r_K$, is defined as the inverse of the mean first passage time, $T_{MFPT}$. To numerically calculate $T_{MFPT}$, we set the initial positions of the Brownian particles at ($-L/2,dy$) and ($-W,-H$) in the upper and lower cavities, respectively. The dependence of the escape rate $r_K$ on the inverse of the noise intensity $1/D$ for different values of the driving field amplitude $F_0$ is plotted in Figure 3. It is evident that the escape rate exhibits non-Arrhenius behavior for $F_0=0$. In the low noise regime, the Arrhenius behavior gradually recovers for particles in the lower cavity with an increase in driving force. However, only a slight recovery of Arrhenius behavior occurs for middle driving strength in the case of the upper cavity. On the contrary, for lower or stronger driving forces, the non-Arrhenius behavior of the escape rate is more pronounced in the upper cavity. We can conclude that the escape rate of particles in the upper cavity is more sensitive to geometric confinement due to its narrow nature. Notably, it is observed that the escape rate in the upper cavity is lower than that in the lower cavity. This implies that the particle is more likely to remain in the upper cavity. In fact, such diffusion asymmetry has also been observed in ref. [37].

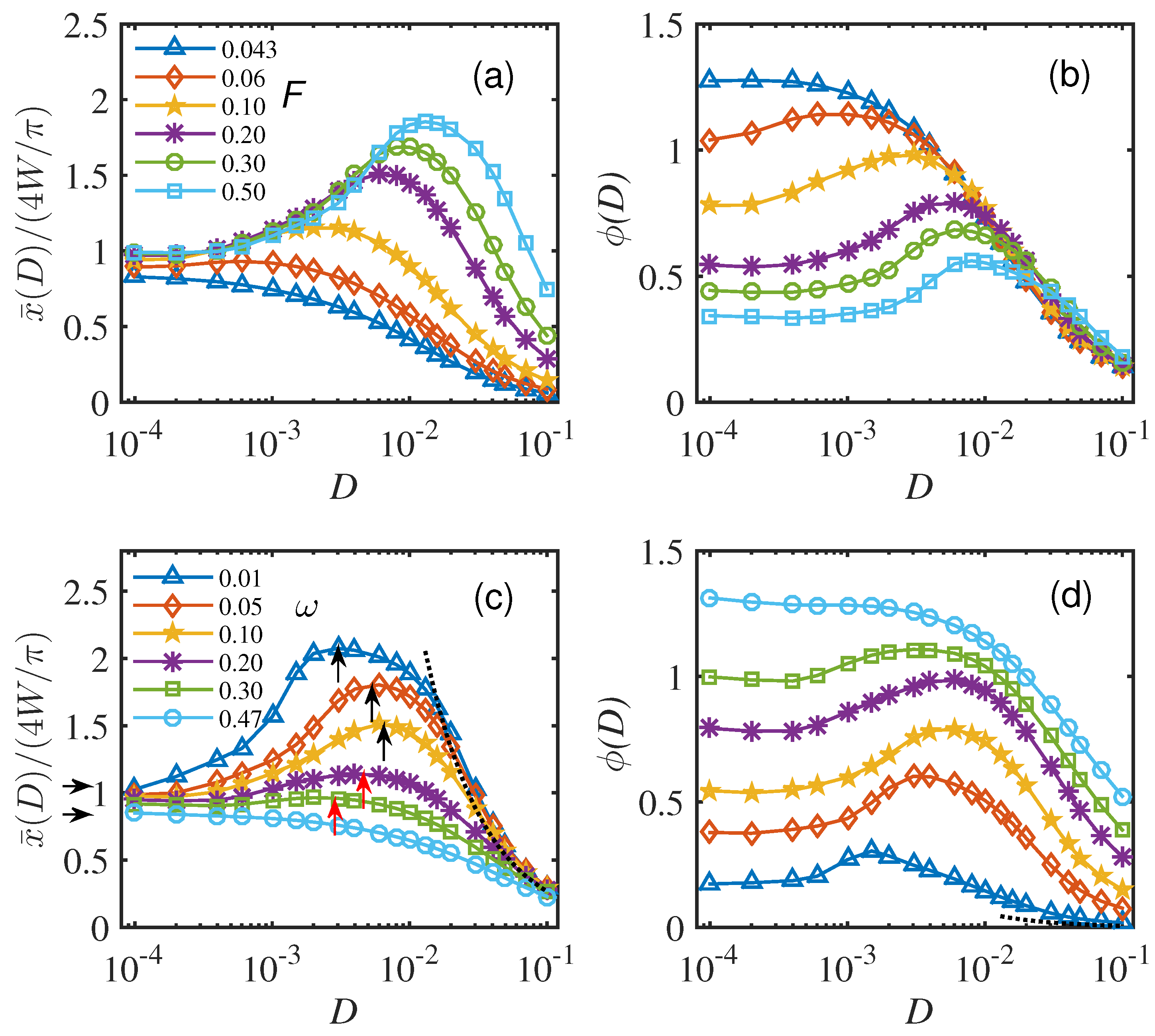
Now we explore the impact of driving force parameters on the Brownian particle dynamics in a T-shaped chamber. Figure 4 presents the response amplitude $\overline{x}\left(D\right)$ versus noise D for different strengths $F_0$ and frequencies $\omega$ of the AC driving force. Notably, the curves for $\overline{x}\left(D\right)$ exhibit stochastic resonance peaks as the noise D is varied for certain parameters. There are several noteworthy features: Firstly, there exist onset thresholds for stochastic resonance, i.e., when the external force strength $F_0>F_c$, as shown in Figure 4a, and when the frequency of the external force $\omega <{\omega }_c$, as illustrated in Figure 4c. Secondly, contrary to ordinal stochastic resonance, the curves $\overline{x}\left(0\right)$ tend toward non-vanishing values that are dependent on the geometric structure. Thirdly, the curves $\overline{x}\left(D\right)$ decay as $D^{-1}$ for large noise strengths. In addition to the response amplitude $\overline{x}\left(D\right)$, the phase delay $\varphi \left(D\right)$ peak of the average trajectory $\langle x\left(t\right)\rangle$ is also presented. From Figure 4b,d, we observe the stochastic resonance features on the phase delay $\varphi \left(D\right)$ curves. Firstly, the phase delay $\varphi \left(D\right)$ shows stochastic resonance peaks and the optimal noise $D_{max}$, as well as its variations with respect to $F_0$ and $\omega$, which are similar to the $\overline{x}\left(D\right)$ curves. Secondly, the phase peaks are suppressed at low frequencies, where the stochastic resonance signature of $\overline{x}\left(D\right)$ curves is evident. Thirdly, in the zero-noise limit, $\varphi \left(D\right)$ strongly depends on $F_0$. Finally, in the range of $F_0/\omega ⩾4L/\pi$, the phase peaks shift to the right for both increasing $F_0$ and $\omega$. These features are also observed in the system of generalized stochastic resonance [21].

We aimed to provide a semi-quantitative interpretation of the stochastic resonance behavior presented in Figure 2. By assuming the Fourier series of two square waves with a period of $2\pi /\omega$, the amplitudes of its fundamental harmonic components were calculated as $4L/\pi$ and $4W/\pi$, respectively. These results provide an upper bound to the average amplitude $\overline{x}\left(D\right)$ under the condition that $L>W$, which is given by $\overline{x}\left(D\right)\le 4L/\pi$. This prediction was confirmed by the numerical result, as demonstrated by the square symbol line in Figure 4a. The onset condition for the SR in the T-shaped chamber is assumed by the following equation:

$$F_0/\omega ⩾4W/\pi .$$

(8)

$F_0/\omega$ is the driven oscillation amplitude of a non-constrained Brownian particle. This condition is distinct from the two-cavity case [24]. According to Equation (8), with the parameters used in Figure 4, we obtain $F_c=0.043$ with $\omega =0.1$ in Figure 4a and ${\omega }_c=0.46$ with $F_0=0.2$ in Figure 4b. The numerical results in Figure 4 confirmed our assumption.

It is important to note that when the ratio $4W/\pi$ is less than $F_0/\omega$ and greater than $4L/\pi$, with a certain level of noise, the particle will frequently collide with the side walls of the upper and lower cavities. This can result in a weak enhancement of the response amplitudes and a weak SR phenomenon in the T-shaped chamber. The corresponding results are shown in Figure 4c. We can observe that, in this case, the SR peak does not shift to the right and even turns to the left as $\omega$ increases, indicated by red vertical arrows.

Next, we explained the asymptotic behavior of response amplitude $\overline{x}\left(D\right)$ in the weak and strong noise regimes in Figure 4. In the zero-noise limit case, the average displacement of particles $\overline{x}\left(D\right)$ can be estimated as follows:

$$\overline{x}(D\to 0)\simeq CW,$$

(9)

where $C\to 4/\pi$ for $\omega \to 0$, and $C\to 1$, for $\omega \to {\omega }_c$. The numerical results are consistent with Equation (9), as indicated by the horizontal arrows in Figure 4c. However, in the strong noise regime, the confinement of the geometry on the movement of Brownian particles can be ignored. The diffusion of particles along the AC force in the T-shaped chamber can be described by AC-force-damped Brownian motion with the effective damping constant ${\tau }^{-1}$. Here, $\tau$ can be obtained from the Stokes–Einstein equation $2D\tau =\langle x^2\rangle$. In this case, for a particular $\omega$, the corresponding $\langle x\left(t\right)\rangle$ are suppressed both in amplitude $F_0\tau /\sqrt{1+{\omega }^2{\tau }^2}$ and phase $\varphi \left(D\right)=\arctan \left(\omega \tau \right)$. For $\omega \ll {\omega }_c$, the response amplitudes $\overline{x}\left(D\right)$ approach to $F\tau$, which is independent on $\omega$. The analytical results are plotted with the dotted lines in Figure 4c,d.

Here we provide an explanation of the behavior of $\varphi \left(D\right)$ in Figure 4. The phase delay reflects the response of the Brownian particle to the AC drive $F\left(t\right)$. In a confined geometry, when $\varphi \left(D\right)$ is without a peak, it indicates that the particle is synchronized with $F\left(t\right)$ and the confined geometry does not pose an obstacle to the motion of the particle, or the obstacle is too strong for the particle to overcome. However, when $\varphi \left(D\right)$ shows a peak, it indicates the presence of an obstacle in the confined geometry, thus allowing the particle to experience a certain obstruction when passing through. In this case, stochastic resonance also appears.

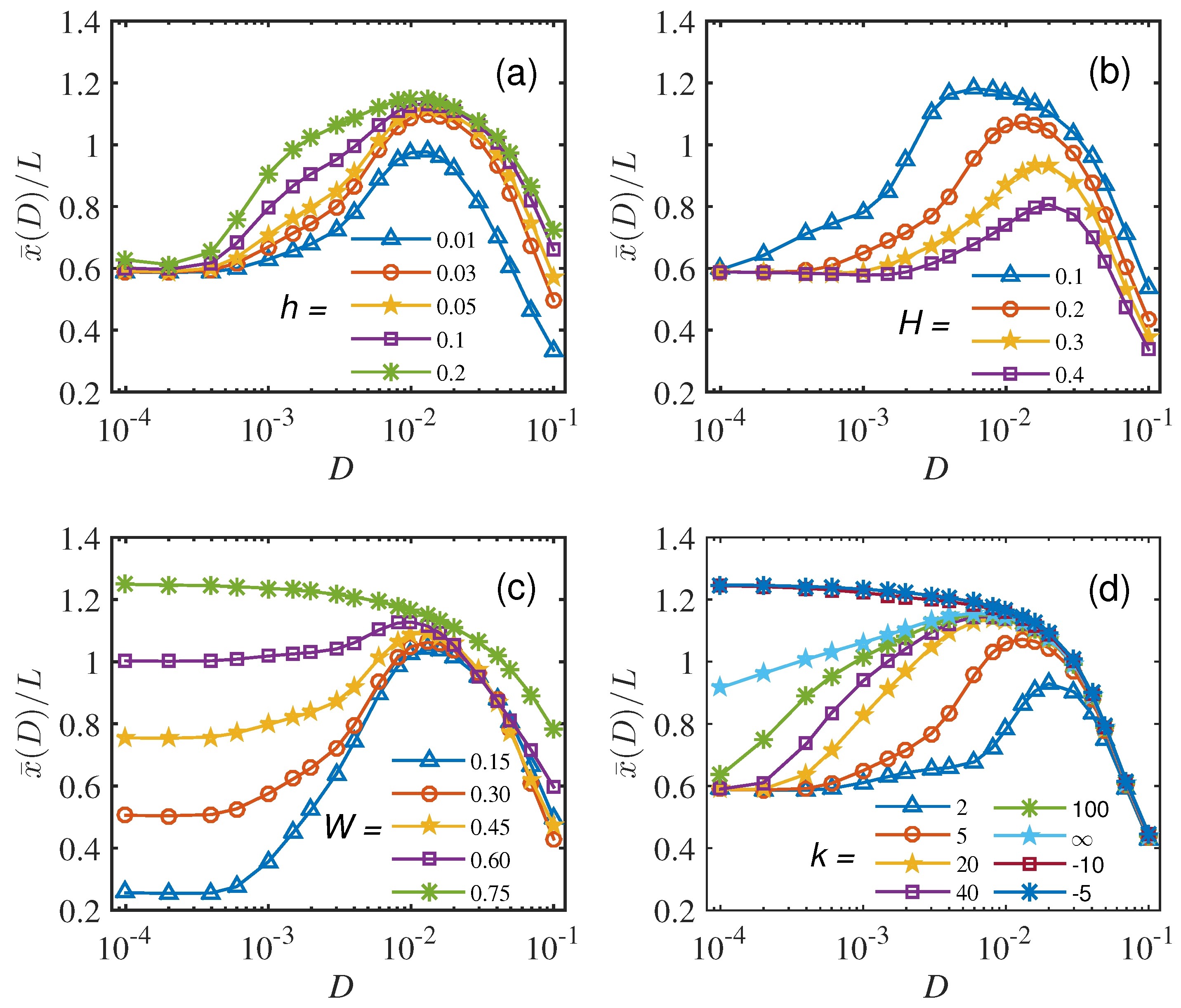
To investigate the influence of geometry on stochastic resonance, we altered the dimensions of the T-shaped chamber. Figure 5a,b display the variation of the response amplitude $\overline{x}\left(D\right)$ with respect to the height (depth) of the upper (down) cavity. We observe that the peak of the response amplitude $\overline{x}\left(D_{max}\right)$ increases as the height (depth) of the upper (down) cavity increases (decreases), while the optimal noise level and $\overline{x}\left(0\right)$ remain unchanged. Using Equation (9), we can deduce that $\overline{x}(D\to 0)$ is independent of the height (depth) of the upper (lower) cavity. However, for strong noise, particles should transition between the upper and down cavities. In this scenario, a larger h (smaller H) implies a longer residence time for particles in the upper cavity and a greater weight of the square wave with amplitude L in the average particle displacement $\langle x\left(D\right)\rangle$. Therefore, $\overline{x}\left(D_{max}\right)$ is inversely proportional to the height of the upper cavity and the depth of the down cavity.

In Figure 5c, the response amplitude $\overline{x}\left(D\right)$ is plotted against D for different bottom widths of the down cavity. It can be observed that the response amplitudes approach constant values for $D\to 0$, and the corresponding $\overline{x}\left(0\right)$ is proportional to W. This result is predicted by Equation (9). In particular, Equation (9) shows that when $W\to L$, $\overline{x}(D\to 0)=4L/\pi$, which is consistent with the numerical result as shown by the symbol ’$*-$’ in Figure 4c. We can note that when $W\to L$, there is no SR peak. When the amplitudes of the square wave in the down and upper cavities are the same, we cannot distinguish them in the $\langle x\left(t\right)\rangle$. Additionally, the ratio $\overline{x}\left(D_{max}\right)/\overline{x}\left(0\right)$ is inversely proportional to W, which implies that a smaller width W is helpful in observing strong SR in the T-shaped chamber.

The slope k of the side wall of the down cavity has different effects on the Brownian particle moving in the T-shaped chamber, corresponding to three different configurations: spout-like, square-like, and funnel-like cavities, as shown in Figure 1a–c. We explore these effects further by plotting $barx\left(D\right)$ versus D with different slopes k on the side wall of the down cavity in Figure 5d. It is observed that the peak value of SR $\overline{x}\left(D_{max}\right)$ increases with an increasing positive slope k, while $\overline{x}(D\to 0)$ decreases for a fixed W. This behavior can be explained using two states, where the height of the barrier is proportional to $k^{-1}$. As a result, the Kramers rate for the Brownian particle to transit the barrier increases with increasing k, leading to an additional weight of the square wave with amplitude L in $\langle x\left(D\right)\rangle$. Therefore, a larger slope k results in a higher $barx\left(D_{max}\right).$ Note that $\overline{x}\left(D_{max}\right)$ remains almost the same for $k\ge 20$, even when $k\to \infty$. For $k\to \infty$, the spout-like structure can approach a square-like structure, and SR can appear in both structures. In contrast, negative slopes, corresponding to funnel-like structures, do not exhibit SR, as evidenced by the curve represented by triangle symbols in Figure 5d. This can be explained using an effective bistable potential, which assumes only one stable region for funnel-like cavities along the y-direction in the T-shaped chamber. However, there are two stable regions for spout-like ($k>0$) and square-like structures ($k\to \infty$). Hence, SR cannot occur in funnel-like geometries.

In reality, ref. [26] has explored the impact of geometry on the first passage time in a conic channel geometry with unbiased AC forces. The guidance of particles along the boundaries of the geometry is a crucial factor in stochastic resonance. However, in our study, the particles in the down cavity are subjected to a biased AC force, which means that the boundaries of the geometry prevent the particles from jumping between the down cavity and the upper long channel due to the positive slope of the side wall of the down cavity. Therefore, the physics behind SRS in ref. [26] and our work differ significantly.

4. Conclusions

In this work, we observed the stimulated resonance of Brownian particles driven by an AC force moving in an asymmetric T-shaped chamber. The time series of the parallel and vertical to the AC force were presented. The results indicate that for vanishing noise, the Brownian particles localize at the down trapezoid cavity with a longitudinal oscillation amplitude of W, while they almost stay in the upper strip cavity with a longitudinal oscillation amplitude of L with proper noise. Consequently, we employed the bistable effective potential hypothesis to explain the SR in such an asymmetric geometry. The oscillation of Brownian particles is along the AC force but vertical to the two potentials in this work, which differs from the ordinary ESR or GSR. By changing the dimensions of the geometry proposed in this work, we observe that the height of the upper cavity and depth, slope, and bottom width of the down cavity can affect the height of the SR peak. Based on the effective bistable potential hypothesis, a full physical interpretation of this phenomenon is presented. Contrary to two- or multi-cavity symmetric geometric systems, the configuration of the T-shaped chamber is simple and practical for studying the resonance phenomenon of Brownian particles in microdynamic systems. The GSR in T-shaped chambers provides a new method to study SR phenomena in other asymmetric geometric structures and particle transportation in long channels with defects.