A Modified Residual Power Series Method for the Approximate Solution of Two-Dimensional Fractional Helmholtz Equations
Abstract
:1. Introduction
2. Preliminary Concept of the Shehu Transform
3. The Basic Procedure of the T-RPSM
- and for each ,
- If then ,
- .
4. Numerical Applications
4.1. Example 1
4.2. Example 2
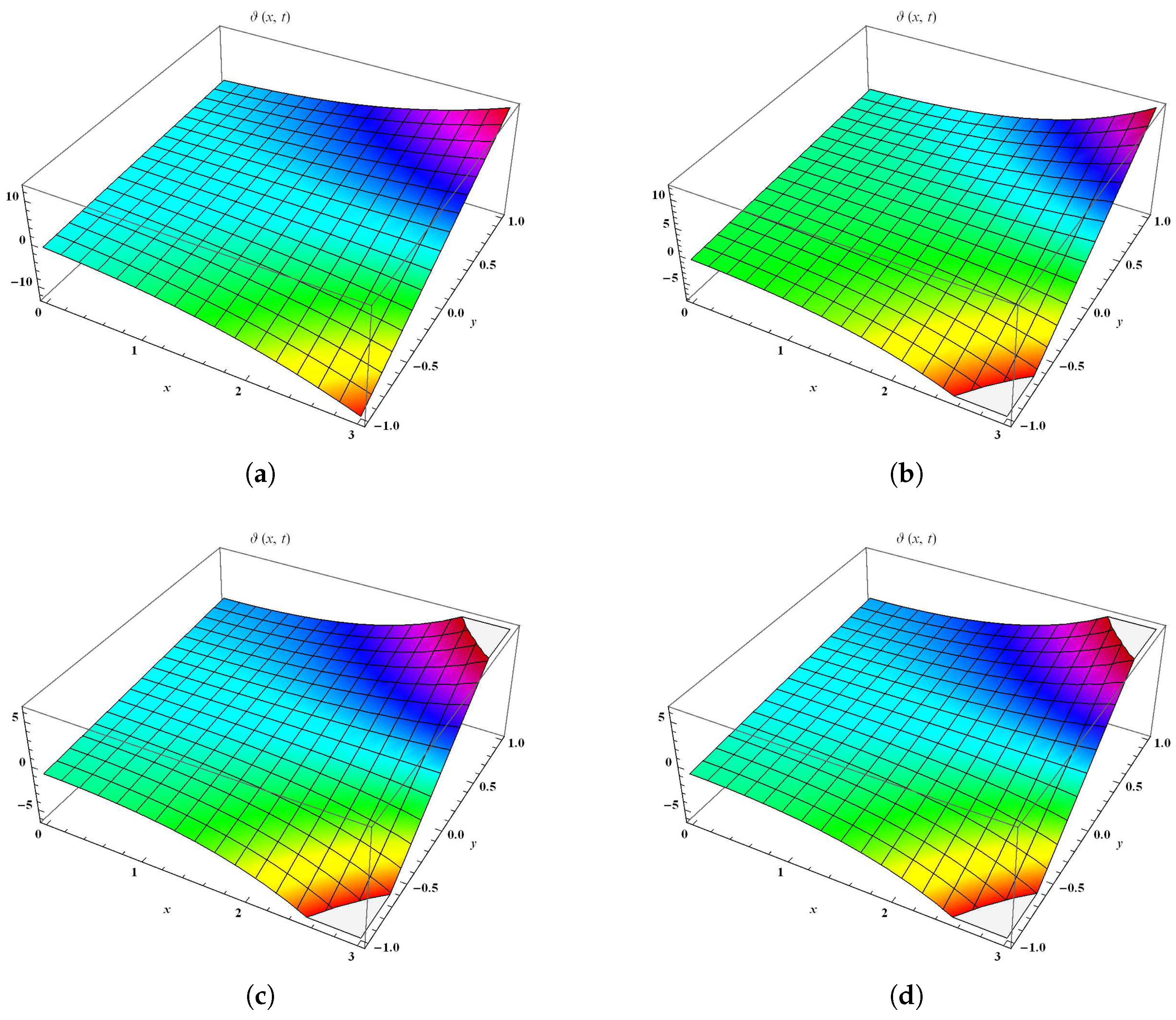
5. Description of Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ayasrah, M.; Al-Smadi, M.; Al-Omari, S.; Baleanu, D.; Momani, S. Structure of optical soliton solution for nonlinear resonant space-time Schrödinger equation in conformable sense with full nonlinearity term. Phys. Scr. 2020, 95, 105215. [Google Scholar]
- Al-Smadi, M.; Arqub, O.A. Computational algorithm for solving fredholm time-fractional partial integrodifferential equations of dirichlet functions type with error estimates. Appl. Math. Comput. 2019, 342, 280–294. [Google Scholar] [CrossRef]
- Khan, H.; Liao, S.J.; Mohapatra, R.; Vajravelu, K. An analytical solution for a nonlinear time-delay model in biology. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3141–3148. [Google Scholar] [CrossRef]
- Gu, Y.; Liao, W.; Zhu, J. An efficient high-order algorithm for solving systems of 3-D reaction–diffusion equations. J. Comput. Appl. Math. 2003, 155, 1–17. [Google Scholar] [CrossRef]
- Alaje, A.I.; Olayiwola, M.O.; Adedokun, K.A.; Adedeji, J.A.; Oladapo, A.O. Modified homotopy perturbation method and its application to analytical solitons of fractional-order Korteweg–de Vries equation. Beni-Suef Univ. J. Basic Appl. Sci. 2022, 11, 139. [Google Scholar] [CrossRef]
- Arikoglu, A.; Ozkol, I. Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals 2007, 34, 1473–1481. [Google Scholar] [CrossRef]
- Nadeem, M.; Yao, S.W. Solving the fractional heat-like and wave-like equations with variable coefficients utilizing the Laplace homotopy method. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 273–292. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S. Exact and approximate solutions of time-fractional models arising from physics via Shehu transform. Math. Methods Appl. Sci. 2020, 43, 7442–7464. [Google Scholar] [CrossRef]
- Kumar, S.; Gupta, V. An application of variational iteration method for solving fuzzy time-fractional diffusion equations. Neural Comput. Appl. 2021, 33, 17659–17668. [Google Scholar] [CrossRef]
- Singh, H. Jacobi collocation method for the fractional advection-dispersion equation arising in porous media. Numer. Methods Partial. Differ. Equ. 2022, 38, 636–653. [Google Scholar] [CrossRef]
- Sartanpara, P.P.; Meher, R. A robust computational approach for Zakharov-Kuznetsov equations of ion-acoustic waves in a magnetized plasma via the Shehu transform. J. Ocean. Eng. Sci. 2021, 8, 79–90. [Google Scholar] [CrossRef]
- Yuttanan, B.; Razzaghi, M.; Vo, T.N. Legendre wavelet method for fractional delay differential equations. Appl. Numer. Math. 2021, 168, 127–142. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.; Singh, J. Solution for fractional forced KdV equation using fractional natural decomposition method. AIMS Math. 2020, 5, 798–810. [Google Scholar] [CrossRef]
- Tandel, P.; Patel, H.; Patel, T. Tsunami wave propagation model: A fractional approach. J. Ocean. Eng. Sci. 2022, 7, 509–520. [Google Scholar] [CrossRef]
- Prakasha, D.; Veeresha, P.; Baskonus, H.M. Residual power series method for fractional Swift–Hohenberg equation. Fractal Fract. 2019, 3, 9. [Google Scholar] [CrossRef]
- Hassani, H.; Machado, J.T.; Naraghirad, E. Generalized shifted Chebyshev polynomials for fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul. 2019, 75, 50–61. [Google Scholar] [CrossRef]
- El-Sayed, S.M.; Kaya, D. Comparing numerical methods for Helmholtz equation model problem. Appl. Math. Comput. 2004, 150, 763–773. [Google Scholar] [CrossRef]
- Momani, S.; Abuasad, S. Application of He’s variational iteration method to Helmholtz equation. Chaos Solitons Fractals 2006, 27, 1119–1123. [Google Scholar] [CrossRef]
- Gupta, P.K.; Yildirim, A.; Rai, K. Application of He’s homotopy perturbation method for multi-dimensional fractional Helmholtz equation. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 424–435. [Google Scholar] [CrossRef]
- Iqbal, N.; Chughtai, M.T.; Shah, N.A. Numerical simulation of fractional-order two-dimensional Helmholtz equations. AIMS Math. 2023, 8, 13205–13218. [Google Scholar] [CrossRef]
- Alshammari, S.; Abuasad, S. Exact solutions of the 3D fractional helmholtz equation by fractional differential transform method. J. Funct. Spaces 2022, 2022, 7374751. [Google Scholar] [CrossRef]
- Khater, M.M. Computational simulations of the cubic-quintic nonlinear Helmholtz model. J. Ocean Eng. Sci. 2022. [Google Scholar] [CrossRef]
- Arqub, O.A. Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 2013, 5, 31–52. [Google Scholar] [CrossRef]
- Aggarwal, S.; Gupta, A.R. Shehu transform for solving Abel’s integral equation. J. Emerg. Technol. Innov. Res. 2019, 6, 101–110. [Google Scholar]
- Khan, H.; Farooq, U.; Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. Analytical solutions of (2+ time fractional order) dimensional physical models, using modified decomposition method. Appl. Sci. 2019, 10, 122. [Google Scholar] [CrossRef]
- Zhang, R.; Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Chung, J.D. Numerical analysis of fractional-order emden–fowler equations using modified variational iteration method. Fractals 2023, 31, 2340028. [Google Scholar] [CrossRef]
- Saadeh, R.; Ala’yed, O.; Qazza, A. Analytical solution of coupled hirota–satsuma and KdV equations. Fractal Fract. 2022, 6, 694. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, S.; Singh, M. Residual power series method for fractional Sharma-Tasso-Olever equation. Commun. Numer. Anal. 2016, 10, 1–10. [Google Scholar] [CrossRef]
- El-Ajou, A.; Arqub, O.A.; Zhour, Z.A.; Momani, S. New results on fractional power series: Theories and applications. Entropy 2013, 15, 5305–5323. [Google Scholar] [CrossRef]
- Abuasad, S.; Moaddy, K.; Hashim, I. Analytical treatment of two-dimensional fractional Helmholtz equations. J. King Saud-Univ.-Sci. 2019, 31, 659–666. [Google Scholar] [CrossRef]

| T-RPSM | T-RPSM | T-RPSM | Exact Results | Absolute Error | |
|---|---|---|---|---|---|
| (0.05, 0.05) | 0.0525636 | 0.504216 | 0.0500677 | 0.0500677 | 00000 |
| (0.10, 0.10) | 0.110517 | 0.102396 | 0.1005 | 0.1005 | 00000 |
| (0.15, 0.15) | 0.174275 | 0.15664 | 0.151691 | 0.151691 | 00000 |
| (0.20, 0.20) | 0.24428 | 0.213726 | 0.204013 | 0.204013 | 00000 |
| (0.25, 0.25) | 0.321004 | 0.274168 | 0.257853 | 0.257853 | 00000 |
| (0.30, 0.30) | 0.404951 | 0.338458 | 0.313602 | 0.313602 | 00000 |
| (0.35, 0.35) | 0.496657 | 0.407079 | 0.371657 | 0.371657 | 00000 |
| (0.40, 0.40) | 0.596693 | 0.480515 | 0.432429 | 0.432429 | 00000 |
| (0.45, 0.45) | 0.705666 | 0.559263 | 0.496337 | 0.496337 | 00000 |
| (0.50, 0.50) | 0.824219 | 0.64383 | 0.563813 | 0.563813 | 00000 |
| T-RPSM | T-RPSM | T-RPSM | Exact Results | Absolute Error | |
|---|---|---|---|---|---|
| (0.05, 0.05) | 0.0389404 | 0.479233 | 0.0496878 | 0.0496878 | 00000 |
| (0.10, 0.10) | 0.0606771 | 0.088515 | 0.0975104 | 0.0975104 | 00000 |
| (0.15, 0.15) | 0.0711182 | 0.119264 | 0.141641 | 0.141641 | 00000 |
| (0.20, 0.20) | 0.075 | 0.139052 | 0.180331 | 0.180331 | 00000 |
| (0.25, 0.25) | 0.0768636 | 0.147623 | 0.211944 | 0.211944 | 00000 |
| (0.30, 0.30) | 0.0820313 | 0.14535 | 0.234994 | 0.234994 | 00000 |
| (0.35, 0.35) | 0.097583 | 0.133078 | 0.248173 | 0.248173 | 00000 |
| (0.40, 0.40) | 0.133333 | 0.1121 | 0.250386 | 0.250386 | 00000 |
| (0.45, 0.45) | 0.202808 | 0.0836075 | 0.240772 | 0.240772 | 00000 |
| (0.50, 0.50) | 0.324219 | 0.0495244 | 0.218726 | 0.218726 | 00000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Nadeem, M.; Islam, A.; Mureşan, S.; Iambor, L.F. A Modified Residual Power Series Method for the Approximate Solution of Two-Dimensional Fractional Helmholtz Equations. Symmetry 2023, 15, 2152. https://doi.org/10.3390/sym15122152
Liu J, Nadeem M, Islam A, Mureşan S, Iambor LF. A Modified Residual Power Series Method for the Approximate Solution of Two-Dimensional Fractional Helmholtz Equations. Symmetry. 2023; 15(12):2152. https://doi.org/10.3390/sym15122152
Chicago/Turabian StyleLiu, Jinxing, Muhammad Nadeem, Asad Islam, Sorin Mureşan, and Loredana Florentina Iambor. 2023. "A Modified Residual Power Series Method for the Approximate Solution of Two-Dimensional Fractional Helmholtz Equations" Symmetry 15, no. 12: 2152. https://doi.org/10.3390/sym15122152
APA StyleLiu, J., Nadeem, M., Islam, A., Mureşan, S., & Iambor, L. F. (2023). A Modified Residual Power Series Method for the Approximate Solution of Two-Dimensional Fractional Helmholtz Equations. Symmetry, 15(12), 2152. https://doi.org/10.3390/sym15122152








