Abstract
In this paper, we consider how to find new exact solutions for nonlinear partial differential equations using the extended Kudryashov method. This method mainly uses the Riccati equation and the Bernoulli equation where there are some underdetermined constant parameters. And we also use the concept of symmetry to study its reduction equation, Lie transformation group, self-adjointness, and conservation laws. This paper mainly studies the Boussinesq class and the shallow water wave equation in (1 + 1) dimensions and tries to find new exact solutions and symmetry properties of them.
1. Introduction
As a matter of common knowledge, many methods for finding the exact solutions of nonlinear partial differential equations have been derived in recent years. In addition, the research in this area is of great significance to the isolation theory, which describes natural selection as a mechanism for ensuring the adaptation of organisms to their environment, their morphological diversity, and partial differential equations. For example, the methods for finding exact solutions include the F-expansion method [1,2], the truncated expansion method [3,4], the sine-cosine function method [5], and so on [6,7]. The idea of this paper is to use an efficient and direct method, that is, the extended Kudryashov method [8,9,10,11,12], to find the exact solution of nonlinear partial differential equations. This method presupposes the general solution form of the equation, takes the simple form of the Riccati equation and Bernoulli equation, and simultaneously obtains the exact solution of the objective equation using the reduction of the coefficient equation.
In the second part of this work, we consider how to explore other properties of the classical Boussinesq equations [13] and the shallow water wave equation [14], and use the Lie method to obtain their symmetric infinitesimal generators, Lie transformation groups, and corresponding invariant solutions [15,16,17,18,19,20,21]. Wu and Zhang [22] derived the (1 + 1)-dimensional classical Boussinesq equation, which is used to simulate nonlinear dispersive long gravity waves propagating along two horizontal directions in shallow water of a uniform depth. In recent years, many scholars have studied the equation [23,24,25]. In the third part, we calculate the self-adjoint properties and their conservation laws [26,27,28,29,30,31,32,33].
2. Simple Description of the Method
In this section, we first briefly introduce how to use the extended Kudryashov method to obtain the exact solutions of the objective equation. The idea of this method is to substitute the form of the presupposed exact solution into the objective equation to determine the form of the solution according to the determining equation of the coefficient. The principle of the earliest proposed Kudryashov method [8,9,10] is to use the polynomial form of the solution of the Riccati equation to find the exact solution of the target equation. The modified Kudryashov method [11] proposed by Kabir et al. used a similar principle, but used the polynomial of the form solution. However, the extended Kudryashov method [12] combines the above two methods to obtain a more general formal solution, and the fractional form of the solution of the Riccati equation is added. On this basis, we improve the extended Kudryashov method and add the derivative term of the Bernoulli solution to further obtain some new exact solutions of the equation.
First, we consider the nonlinear equations
Step 1. Firstly, we give the general form of the preset exact solution
where are constants to be determined; , where are also underdetermined constants; and and are the solutions of the Bernoulli and Riccati equations
Each derivative of can be expressed by the power of , for example,
where are constants to be determined. As a matter of common knowledge, the solution of Equation (3) has the following form:
where is a constant of integration. Similar to the above, we know that the solutions of Equation (4) have the following forms:
where and is an integration constant. And the solution has a special form
Step 2. Secondly, we need to use the homogeneous balance method to balance the nonlinear term with the highest derivative term in the equation, so as to determine the value of M and N and determine the form of the exact solution.
Step 3. After obtaining the general form of the solutions, we substitute them into Equations (1) and (2), and the derivative terms of and are replaced by the polynomial forms of and using the above differential equation. Then, the obtained polynomial is used to separate the power coefficients of and , and a series of determining equations concerning parameters
are obtained.
Step 4. After proposing the coefficient equation of and , we can obtain the relationship between the parameters by solving the equation simultaneously; thus, we can obtain the general expression of the solution .
3. Exact Solutions of the Boussinesq Class
In the following sections, we will use the extended Kudryashov method to deal with some different partial differential equations and obtain their exact solutions. We first study the (1 + 1)-dimensional Boussinesq class for the evolution of two horizontal nonlinear dispersive long gravity waves propagating in shallow water of uniform depth:
In order to obtain the exact solutions of the (1 + 1)-dimensional Boussinesq class, we can set
Firstly, we need to apply the homogeneous balance method to the target equation to determine the values of M and N. Then, by calculation, we can conclude that . Therefore, we can determine the exact solution of the following general form:
where ,, and the coefficients encountered in the calculation process , , , , , , , are underdetermined constants. And and are the solution of the Bernoulli and the Riccati equations, respectively. After bringing the preset exact solution form (11) into the target equation, i.e., Equation (9), we obtain a series of algebraic equations by extracting the coefficients. By solving these algebraic equations, we can obtain a series of exact solutions of Equation (9). We list some results as follows:
where
where
where
where
where
where
Figure 1 and Figure 2 show the geometries of the solutions and as determined by (12) and (13), respectively. Figure 3 and Figure 4 show the geometries of the solutions and as determined by (16) and (17), respectively. As shown in Figure 1, Figure 2, Figure 3 and Figure 4, the single lumps are localized in the plane and they are permanent lumps.
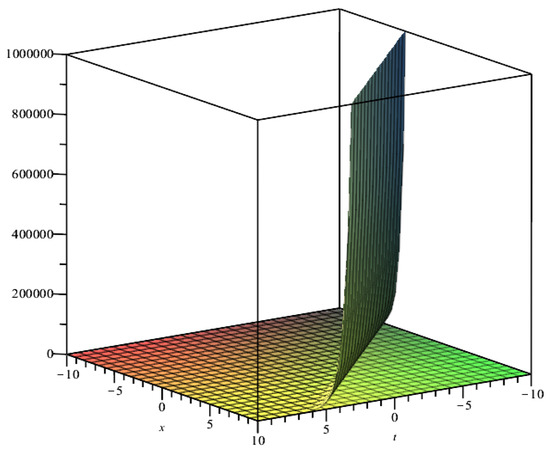
Figure 1.
Plot of for parameters .
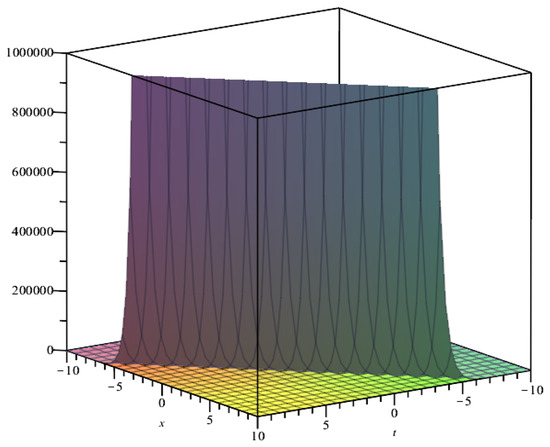
Figure 2.
Plot of for parameters .
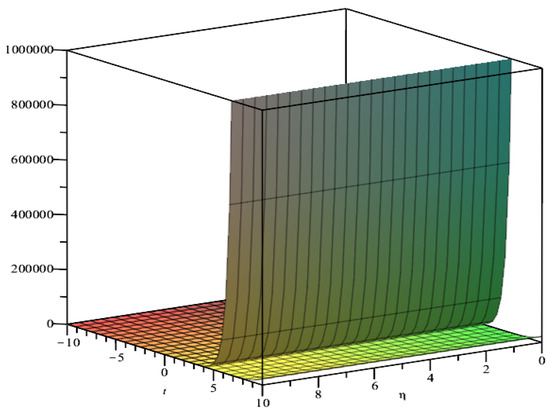
Figure 3.
Plot of for parameters .
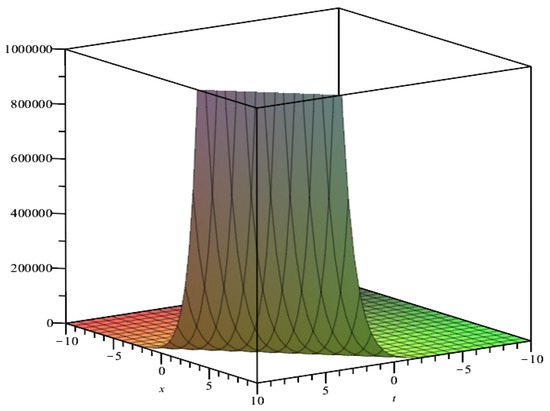
Figure 4.
Plot of for parameters .
4. Exact Solutions of the Shallow Water Wave Equation
In this section, we study the shallow water wave equation:
We will make a potential transformation on it first, i.e.,
Equation (18) can be transformed into
We study Equation (19) next. The shallow water wave equation plays a significant role in the field around the soliton. Then, we obtain some new general solutions of Equation (19) using the extended Kudryashov method. First let
Then, we also determine the value of N using the homogeneous balance method. If , we can obtain the following general solution of Equation (19):
After substituting Equation (21) into (19), we can obtain a series of coefficient equations concerning the constant coefficients Then, these equations are solved simultaneously, and the exact solution expression of u can be obtained. We list some results as follows:
where
where
where
where
where
where
where
where
where
where
where
where
where
where
where denotes the solutions of the polynomial .
where
where
where
where
where
where
where
where
where
where
where
Figure 5 and Figure 6 show the geometries of the solutions and as determined by (24) and (44), respectively. As shown in Figure 5, the single lump is localized in the plane and it is a permanent lump. And as shown in Figure 6, we observe that the breather in the plane is intermittent along the t direction and localized in the x direction.
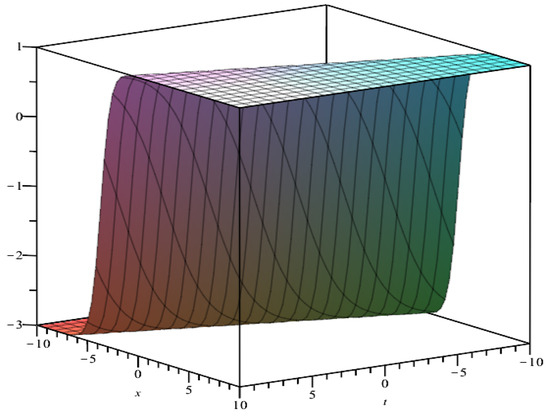
Figure 5.
Plot of for parameters .
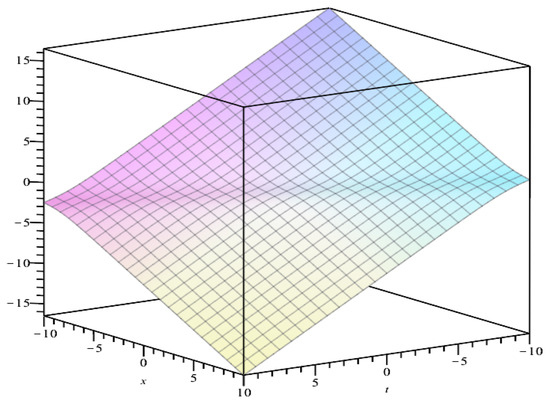
Figure 6.
Plot of for parameters .
5. Lie Symmetry Analysis
5.1. Lie Symmetry and Lie Group
In this part, we will analyze the Lie symmetry and the invariant solutions of the shallow water wave equation and the Boussinesq class. In this section, Lie symmetry analysis is performed and we consider one Lie group of the transformation parameter
with a tiny parameter . In addition, we consider the corresponding infinitesimal generator of the Lie group transformation of the form
and the corresponding Lie–Bäcklund symmetry
where denotes any order derivative of u, v with respect to the independent variables x, t. Note that (see [25,26,27,28]). Using Maple, we obtain the infinitesimal generators of Equation (9):
and the Lie–Bäcklund symmetries
In addition, we obtain the infinitesimal generators of Equation (19)
where is an arbitrary function related to t and the Lie–Bäcklund symmetries
The Lie transformation groups corresponding to the infinitesimal generator of Equation (19) are shown in the following, where corresponds to the group
where , at . Then, we can obtain
when . The transformation group calculation method corresponding to the remaining infinitesimal generators is similar. For example, when , corresponds to the group
When , corresponds to the group
And the calculation method for Equation (9) is similar. For example, corresponding to
5.2. Canonical Coordinates and Invariant Solution
Definition 1.
The change of coordinates defines a set of canonical coordinates for the one-parameter Lie group of transformations . According to such coordinates, the group becomes
Thus, we know that every symmetric infinitesimal generator can derive the corresponding canonical coordinates by computing
where X denotes the symmetric infinitesimal generator of the target equation. Next, we apply it to Equation (19). For the infinitesimal generator , when , the corresponding canonical coordinate is
We can obtain one canonical coordinate corresponding to , i.e.,
Similarly, the canonical coordinate corresponding to is
And when , the canonical coordinate corresponding to is
Then, we consider a k-order differential equation. Its form is as follows:
where u represents the dependent variable, represents n independent variables, and represents all j-order derivatives of u with respect to x. Thus, Equation (58) gives the infinitesimal generator
Definition 2.
is an invariant solution of Equation (63) corresponding to (64) as given by Equation (63) if, and only if,
- (i)
- is an invariant surface of Equation (63);
- (ii)
- solves (63). It follows that is an invariant solution of (63) under (64) if, and only if, satisfies when , i.e.,
- (iii)
- , where , for .
Then, Equation (65) is an invariant surface of the invariant solution of (63).
Then, we will consider some invariants and invariant solutions of the equations using the above method. First, we learn that Equation (9) has the following form of symmetry
Then, the corresponding characteristic equations are
We obtain the similarity variables and the similarity forms as follows:
After substituting (67) into Equation (9), we can obtain an ordinary differential equation as follows:
Then, it can be derived by calculation that Equation (68) has the following general solution:
We choose the first solution for convenience. Bringing U and Q back to Equation (68), we can obtain
Then, Formula (70) is an invariant solution of Equation (9).
Next, we use the same method to deal with Equation (19). We choose the infinitesimal generator as an example. When
The characteristic equation corresponding to this symmetry is as follows:
Its similarity variables are
Coming back to Equation (19), we can obtain
After solving (73), we have an invariant solution of Equation (19)
i.e.,
where denotes the arbitrary constants.
In addition, we find that the concept of symmetry can be used to reduce the order. First, we use transformation
where k is an arbitrary constant. Then, Equation (19) can be transformed into the following ordinary differential equation form:
It has symmetries
If we select as the symmetry used to reduce the order, then we can obtain the reduced equation
where , ,
If we select as the symmetry used to reduce the order, then we can obtain the reduced equation
where
Figure 7 and Figure 8 show the geometries of the invariant solutions (70) and (75) for Equation (9) and Equation (19), respectively. From Figure 7, we observe that the invariant solution is symmetrical about a point in space. And from Figure 8, we observe that the invariant solution (75) is a plane solution.
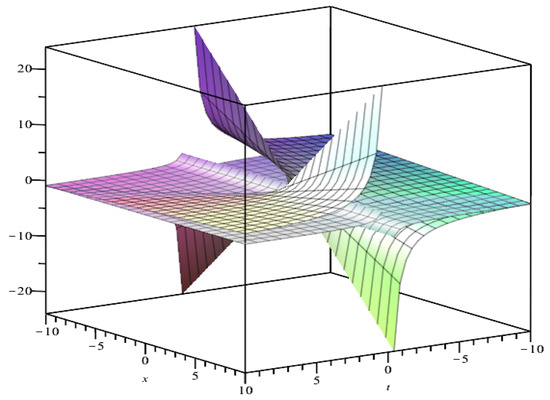
Figure 7.
Plot of the invariant solution for Equation (9) for parameters .
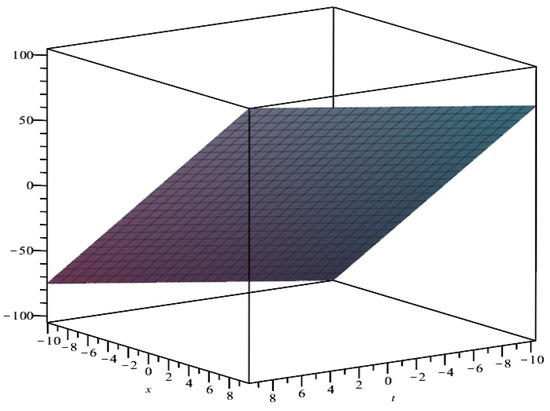
Figure 8.
Plot of the invariant solution for Equation (19) for parameters .
6. Self-Adjointness and Conservation Laws
In this section, we will calculate the self-adjoint properties and conservation laws of the objective equations using the Ibragimov method [29,30,31,32,33]. First, let us introduce some notations and definitions
where represents the total derivative operator concerning the independent variable and represents the independent variables, i.e.,
Next, we deal with a system of m differential equations. It has the following form:
which has the form of an adjoint equation
where
where denotes the formal Lagrangian for Equation (80), i.e.,
and denotes the variational derivative. It has the following form
Definition 3.
We can state that Equation (80) is strictly self-adjoint if the adjoint from Equation (81) is equivalent to Equation (82) upon the transformation
This shows that the equation
Definition 4.
Equation (80) is said to be quasi self-adjoint if the adjoint equations from Equation (81) are satisfied for all solutions u of the original equation, i.e., Equation (80) upon the substitution
such that
In other words, Equation (81) holds after the substitution (85), where not all vanish simultaneously.
Definition 5.
Equation (80) will be called nonlinearly self-adjoint if the adjoint from Equation (81) is satisfied for all solutions u of Equation (80) upon the substitution
such that
This shows that
where
Next, we use the above method to prove that
is strictly self-adjoint.
The formal Lagrangian equation of the (1 + 1)-dimensional classical Boussinesq reads
Then, i.e.,
Let
then
According to Definition 3, the (1 + 1)-dimensional Boussinesq class is strictly self-adjoint.
Similarly, we can prove that
is nonlinearly self-adjoint.
It is not difficult to verify that the (1 + 1)-dimensional shallow water wave equation does not satisfy the strictly self-adjoint condition, so we will not show this in this section. But, if we change the shallow water wave equations into the following equivalent form, we can verify its self-adjointness:
where . Then, the its Lagrangian has the following forms:
Then, we calculate its variational derivative and find
Let we obtain
Then, Equation (89) is nonlinearly self-adjoint according to Defination 5.
Theorem 1.
Any Lie point, Lie–Bäcklund, and nonlocal symmetry
of Equation (80) derives to the conservation law , i.e.,
with Lie–Bäcklund symmetry
According to the above content, we know that the (1 + 1)-dimensional Boussinesq class has a symmetry as follows:
Thus, we can discuss the symmetry . According to the calculation, it can be known that
Then,
After eliminating and of via the substitution
we have
We thus obtain the conservation law of the (1 + 1)-dimensional shallow water wave equations
and we can simply verify it as follows:
Then, the (1 + 1)-dimensional Boussinesq class has the following symmetry:
therefore, we can calculate
Then, we discuss the symmetry X. According to the calculation, it can be known that
7. Conclusions
In this paper, we mainly apply the improved extended Kudryashov method to the shallow water wave equations and the Boussinesq class to find some new exact solutions by presetting the general solution form of the objective equation. This method is convenient to apply to various nonlinear partial differential equations. This method uses the new exact solutions of the objective equation obtained when the Riccati equation and the Bernoullli equation are the simplest forms of solutions. We improve the form of the preset solution on the basis of the original method and add the term to make the form more general so as to obtain more exact solutions of the target equation.
In other parts of this paper, we can map one solution to another using the point symmetry and Lie–Bäcklund symmetry of the shallow water wave equations and the Boussinesq class solved using the Lie method. In addition, the invariant solution of the equation can be obtained using the infinitesimal generator. In the last part, we use the idea of symmetry to determine the self-adjointness of two equations and use infinitesimal generators to calculate the conservation laws of the two groups of equations.
Author Contributions
J.Z. carried out the calculation and analysis studies of equation and drafted the manuscript. L.J. conceived of the study and helped to draft and revise the manuscript. S.Z. supervised and led the planning and implementation of research activities. Y.Z. worked to publish the research results and obtain funding. All authors have read and agreed to the published version of the manuscript.
Funding
The authors thank the National Natural Science Foundation of China (Grant No. 11971475 and 12371256) and SuQian Sci&Tech Program (Grant No. K202225 and K202316).
Data Availability Statement
All data generated or analyzed during the study are included in this paper.
Conflicts of Interest
The authors declare that there are no competing interest.
References
- Zhou, Y.B.; Wang, M.L.; Wang, Y.M. Periodic wave solutions to a coupled kdv equations with variable coefficients. Phys. Lett. A 2003, 308, 31–36. [Google Scholar] [CrossRef]
- Abdel-Razek, M.A.; Seddeek, A.K.; Abdel-All, N.H. New exact jacobi elliptic function solutions for nonlinear equations using F-expansion method. Stud. Math. Sci. 2010, 2, 88–95. [Google Scholar] [CrossRef]
- Lu, B.Q.; Pan, Z.L.; Qu, B.Z.; Jiang, X.F. Solitary wave solutions for some systems of coupled nonlinear equations. Phys. Lett. A 1993, 180, 61–64. [Google Scholar] [CrossRef]
- Hassan, M.M. Exact solitary wave solutions for a generalized kdv-burgers equation. Chaos Soliton Fract. 2004, 19, 1201–1206. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The sine-cosine and the tanh methods: Reliable tools for analytic treatment of nonlinear dispersive equations. Appl. Math. Comput. 2006, 173, 150–164. [Google Scholar] [CrossRef]
- Li, Z.Q.; Tian, S.F.; Yang, J.J.; Fan, E.G. Soliton resolution for the complex short pulse equation with weighted Sobolev initial data in space-time solitonic regions. J. Differ. Equ. 2022, 329, 31–88. [Google Scholar] [CrossRef]
- Ahmed, H.A.; Mohammad, M.; Lanre, A.; Arzu, A. New solitary waves and exact solutions for the fifth-order nonlinear wave equation using two integration techniques. J. Ocean Eng. Sci. 2023, 8, 475–480. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Exact soliton solutions of the generalized evolution equation of wave dynamics. J. Appl. Math. Comp. Mec. 1988, 52, 361–365. [Google Scholar] [CrossRef]
- Kudryashov, N.A. On types of nonlinear nonintegrable equations with exact solutions. Phys. Lett. A 1991, 155, 269–275. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Loguinova, N.B. Extended simplest equation method for nonlinear differential equations. Appl. Math. Comput. 2008, 205, 396–402. [Google Scholar] [CrossRef]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Kabir, M.M.; Khajeh, A.; Aghdam, E.A.; Koma, A.Y. Modified Kudryashov method for finding exact solitary wave solutions of higher-order nonlinear equations. Math. Meth. Appl. Sci. 2011, 34, 213–219. [Google Scholar] [CrossRef]
- Roshid, H.; Rahman, M.A. The exp(−ϕ(η))-expansion method with application in the (1 + 1)-dimensional classical boussinesq equations. Results Phys. 2014, 4, 150–155. [Google Scholar] [CrossRef]
- Wazwaz, A.M. N-soliton solutions for shallow water waves equations in (1 + 1) and (2 + 1) dimensions. Appl. Math. Comput. 2011, 217, 8840–8845. [Google Scholar] [CrossRef]
- Bluman, G.W.; Kumei, S. Symmetries and differential equations. Lett. Nuovo C. 1980, 28, 507–514. [Google Scholar] [CrossRef]
- Bluman, G.; Cheviakov, A.F.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Gianni, M.; Francesco, O.; Giuseppe, S.; Raffaele, V. Ordinary differential equations described by their Lie symmetry algebra. J. Geom. Phys. 2014, 85, 2–15. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Mei, J.Q. Lie algebras and integrable systems. Commun. Theor. Phys. 2012, 57, 1012. [Google Scholar] [CrossRef]
- Wafaa, B.R.; Hamdy, M.A.; Mohammad, M.; Arzu, A.; Mir, S.H. Investigation of solitons and conservation laws in an inhomogeneous optical fiber through a generalized derivative nonlinear Schrödinger equation with quintic nonlinearity. Opt. Quant. Electron. 2023, 55, 825. [Google Scholar] [CrossRef]
- Akbulut, A.; Mirzazadeh, M.; Hashemi, M.S.; Hosseini, K.; Salahshour, S.; Park, C. Triki-Biswas model: Its symmetry reduction, Nucci’s reduction and conservation laws. Int. J. Mod. Phys. B 2022, 37, 7. [Google Scholar] [CrossRef]
- Wu, T.Y.; Zhang, J.E. Mathematics Is for Solving Problems; Cook, P., Roytburd, V., Tulin, M., Eds.; SIAM: Philadelphia, PA, USA, 1996; p. 233. [Google Scholar]
- Kumar, R.; Pandey, K.S.; Kumar, A. Dynamical Behavior of the Solutions of Coupled Boussinesq-Burgers Equations Occurring at the Seaside Beaches. Braz. J. Phys. 2022, 52, 201. [Google Scholar] [CrossRef]
- Yépez-Martínez, H.; Hashemi, M.S.; Alshomrani, A.S.; Inc, M. Analytical solutions for nonlinear systems using Nucci’s reduction approach and generalized projective Riccati equations. AIMS Math. 2023, 8, 16655–16690. [Google Scholar] [CrossRef]
- Noufe, H. Aljahdaly, Some applications of the modified (G′/G2)-expansion method in mathematical physics. Results Phys. 2019, 13, 102272. [Google Scholar] [CrossRef]
- Anco, S.C.; Bluman, G. Integrating factors and first integrals for ordinary differential equations. Eur. J. Appl. Math. 1998, 9, 245. [Google Scholar] [CrossRef]
- Anco, S.C.; Bluman, G. Direct construction of conservation laws from field equations. Phys. Rev. Lett. 1997, 78, 2869. [Google Scholar] [CrossRef]
- San, S.; Akbulut, A.; Ünsal, Ö.; Tascan, F. Conservation laws and double reduction of (2 + 1) dimensional Calogero-Bogoyavlenskii-Schiff equation. Math. Methods Appl. Sci. 2017, 40, 1703. [Google Scholar] [CrossRef]
- Ibragimov, N.H. Integrating factors, adjoint equations and lagrangians. J. Math. Anal. Appl. 2006, 318, 742–757. [Google Scholar] [CrossRef]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl. 2007, 333, 311–328. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Ibragimov, N.H.; Lukashchuk, S.Y. Nonlinear self-adjointness, conservation laws and exact solutions of time-fractional Kompaneets equations. Commun. Nonlinear Sci. 2015, 23, 153–163. [Google Scholar] [CrossRef]
- Ibragimov, N.H. Conservation laws and non-invariant solutions of anisotropic wave equations with a source. Nonlinear Anal-Real 2018, 40, 82–94. [Google Scholar] [CrossRef]
- Ibragimov, N.H. Nonlinear self-adjointness and conservation laws. J. Phys. A-Math. Theor. 2011, 44, 432002. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).