Abstract
In this paper, the formulation of Quantum Mechanics in terms of fuzzy logic and fuzzy sets is explored. A result by Pykacz, which establishes a correspondence between (quantum) logics (lattices with certain properties) and certain families of fuzzy sets, is applied to the Birkhoff–von Neumann logic, the lattice of projectors of a Hilbert space. Three cases are considered: the qubit, two qubits entangled, and a qutrit ‘nested’ inside the two entangled qubits. The membership functions of the fuzzy sets are explicitly computed and all the connectives of the fuzzy sets are interpreted as operations with these particular membership functions. In this way, a complete picture of the standard quantum logic in terms of fuzzy sets is obtained for the systems considered.
1. Introduction
In Mackey’s approach to Quantum Mechanics [1], the description of a physical system is done in terms of certain axioms. We are given two abstract sets: the set of states of the system denoted by and the set of physical quantities or observables, denoted as . The results of measurements on the physical system are assumed to be real numbers, so one considers , the family of Borel subsets of the real line. We are given a function
that is interpreted as the probability that the measurement of the observable A with the system in the state is contained in the Borel subset E. The first six axioms regard properties of the probability function, p. These axioms are natural or have physical interpretation. The first conclusion is that the physical system is described in terms of its logic , together with a convex family of probability measures on . All these terms are going to be defined in Section 2 (other sources are, for example, Refs. [2,3]).
A particular example of logic is the logic of propositions of a classical system. Propositions are such as ‘the observable A has a value in E’. If is the phase space or space of states of the classical system, the observables are functions and the proposition will be true if the system is in a state inside . In this way, physically sensible statements about the system are essentially subsets of . The logic of Classical Mechanics is the Boolean algebra of subsets of a set . This is the standard relation between sets and the propositional logic. Let U be a set and consider the subsets of it. Let A be one such subset and x an element in U. Then A can be defined as the collection of elements such that the proposition ‘’ is true.
So the first six axioms apply to Quantum Mechanics, but also to Classical Mechanics.
The next axiom of Mackey (Axiom VII) is that the logic of a quantum system is, among all possible logics, the Birkhoff–von Neumann logic of projectors of a Hilbert space. Quoting Mackey [1], “This axiom has a rather different character from Axioms I-VI. These all have some degree of physical naturalness and plausibility. Axiom VII seems completely ad hoc”.
In parallel to these logics, the many valued logics of Łukasiewicz [4] and others, where propositions are not always totally true or false, but have some degree of truth, were being developed. Intuitively, they seem related to a probabilistic theory such as Quantum Mechanics.
The same relation that the classical, two valued logic, has with set theory, has the many valued logic with fuzzy sets [5]. A fuzzy subset of a set , called the universe of discourse, is given by a map called the membership function, which associates to any element of a ‘degree of membership’ with respect to . The value means that x belongs totally to and means that x does not belong to . In between, we can have any degree of membership. If is a ‘crisp’ set, then is the characteristic function
The relationship between fuzzy sets and many valued logic was made explicit by Giles [6]. Since the introduction of both concepts, fuzzy logic has been widely used in science systems and decision making problems. In this area, for example, Ospanov et al. [7] proposed methods for the development of mathematical models to control operating modes of technological objects in the face of uncertainty, based on fuzzy information. The mathematical formulation of the problem was obtained by modifying several optimization principles centered on fuzzy sets theory.
A theorem by Pykacz [8,9] makes, finally, the connection between fuzzy sets and Quantum Mechanics. Essentially, it says that giving a logic (in the sense used before) is equivalent to giving a family of fuzzy sets with certain properties. So any logic does have a ‘representation’ in terms of fuzzy sets. Adding properties to such representation allows to further distinguish between logics. In particular, one can consider the universe of discourse to be the set of density matrices in some Hilbert space, and compute the membership functions in terms of a self-adjoint operator on such Hilbert space and a Borel subset of . Then we recover the Birkhoff–von Neumann logic. This choice is, then, equivalent to the choice of Mackey in his Axiom VII.
The aim of the present work is to clarify these abstract concepts, by giving explicitly the membership functions corresponding to the Birkhoff–von Neumann logic for different systems, all with a finite dimensional Hilbert space. The paper is organized as follows. In Section 2 we go over the definition of logic, and of observable and state over that logic. In Section 3 we deepen the understanding of the axioms of Mackey and the work of Ma̧czyński [10,11] with his experimental functions (that later will become the membership functions). In Section 4 we specify all these concepts for the Birkhoff–von Neumann logic. Section 5 is the section where the main results are reported. We compute the Ma̧czyński experimental functions for different systems. In Section 5.1 we compute the experimental functions for the qubit and in Section 5.2 we do the same for two qubits entangled, in the formalism of the Bloch matrix [12,13]. In Section 5.3 we exploit the decomposition of the Hilbert space of the two entangled qubits in terms of eigenvectors of the angular momentum operator to see how a qutrit, ‘nested’ in the system of two entangled qubits, arises [14] and easily compute its experimental functions in terms of the Bloch matrix. At this point we make a detour to study the unitary transformations of the qutrit in terms of orthogonal symmetric Lie algebras, inherited from the two entangled qubits [15]. In Section 6 we turn to the fuzzy set picture. We interpret the connectives of fuzzy sets for the case of the Birkhoff–von Neumann logic. Logic gates, essential part of quantum computers, can also be written in terms of the membership functions. We deal with a few examples and an interesting result is obtained with respect to the square root of NOT. Finally, in Section 7, we state our conclusions.
2. Logics
This section is devoted to give, briefly, the basic definitions of logic, observable and state, following some standard references [2,3,9].
Definition 1.
A partially ordered set or poset, is a set L together with a binary relation, ‘≤’, satisfying
- Reflexivity: for all ;
- Transitivity: for all such that and then ;
- Antisymmetry: if are such that and then .
The binary relation does not need to be defined for all pairs of elements in L. When it is so, it is a completely ordered set or simply an ordered set.
Example 1.
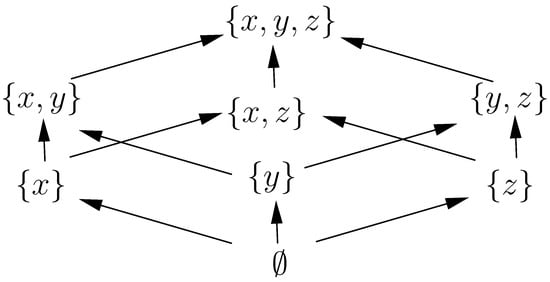
The set of all the subsets or power set of a three element set partially ordered by the inclusion relation is a poset (see Figure 1).

Figure 1.
Partial order in the power set of a three element set.
Definition 2.
If L is a poset, there exists, at most, one element called zero and denoted as ‘0’, such that In addition, there exists, at most, and element called one that will be denoted as ‘1’ such that .
In Example 1, the empty set ∅ is the 0 and the set is the 1.
Definition 3.
For S a finite subset of a poset L, the meet of S is, if it exists, an element that satisfies
- for all .
- If is such that , then .
If S has only two elements a and b, then the meet will be denoted as .
For S and L as above, the join of S is, if it exists, an element that satisfies:
- for all .
- If is such that , then .
If S has only two elements a and b then the join will be denoted as .
The meet and the join, if they exist, are unique.
Definition 4.
A poset L such that
- 0 and 1 exist, ,
- for any finite subset , and exist,
is a lattice.
Definition 5.
A complementation in a lattice L is a map
such that:
- ⊥ is bijective
- (order reversing property)
- (involutivity)
- and (complementarity).
If , we will say that .
Definition 6.
When a lattice L has a complementation, we say that L is a complemented lattice.
Definition 7.
An orthomodular lattice is a complemented lattice such that, for any with then (orthomodular law).
Definition 8.
We will say that an orthomodular lattice is σ-orthocomplete if, for every countable set of pairwise orthogonal elements, the join exists.
Definition 9.
We will say that an orthomodular, σ-orthocomplete lattice is a logic.
Example 2.
Boolean algebra of subsets of a set: classical logic. Let L be the set of subsets of a certain set X with partial ordering given by inclusion, join given by the intersection, meet by the union, and complement by the standard complement in S. The meet and the join satisfy the distributive law
which implies, together with the definition of complement, the orthomodular property. L is a logic called the classical logic.
Example 3
(Closed subspaces of a Hilbert space: Birkhoff–von Neumann logic [16]). Let be a Hilbert space, possibly of infinite dimension, and consider L be the set of its closed subspaces. There is a partial ordering given by the inclusion; then the meet is the intersection and the join the closure of the sum of vector spaces. The complement is the orthogonal complement inside the Hilbert space.
When the closed subspaces are orthogonal, the join is the direct sum of vector spaces, which is also closed.
One can show that the orthomodular law is satisfied, thus L is a logic called the standard or Birkhoff–von Neumann logic.
L does not satisfy the distributive law, which is the main difference with the classical logic.
When the Hilbert space is finite dimensional, all the subspaces are closed and the orthomodular law (Definition 7) can be replaced by the more general modular law:
Definition 10.
A probability measure in a logic L is a map such that
- for any sequence of pairwise orthogonal elements of L.
Later, we will interpret a probability measure on the Birkhoff–von Neumann logic as a state of the system. There is an important property that the states of the system must satisfy:
Definition 11.
A set of probability measures for a quantum logic L is said to be ordering (full, order determining) if and only if
Definition 12.
Let L be a logic and the set of Borel sets of the real line. A map is an L-valued measure if
- ,
- if are such that then, ,
- if is a sequence of pairwise disjoint Borel sets, then .
L-valued measures in the Birkhoff–von Neumann logic play the role of the observables of the quantum theory. Since we can identify a subspace of a Hilbert space with its orthogonal projection, an L-valued measure is, in that case, a projection valued measure.
Definition 13.
A family of L-valued measures is surjective if for each there exists and such that .
3. The Mackey Axioms and the Ma̧czyński Theorem
In Ref. [1], Mackey describes Quantum Mechanics as a rigorous mathematical system in terms of nine axioms that are, as much as possible, plausible and natural from physical considerations.
One starts with the assumption that, for each quantum system, there exists a set of states , a set of observables , and a function p such that
where denotes the family of Borel subsets of the real line. The function p has to be interpreted as the probability that the measurement of the observable A, when the system is in the state , leads to a value in the Borel set E, so
is a probability measure for each pair . We refer to Ref. [1] for the explicit formulation of the nine axioms. The first six axioms describe properties of the function p, based in physical considerations. We are not detailing those axioms here, as they are stated very clearly in the original reference [1]. Additionally, for a more modern treatment of the subject, see, for example, Ref. [3]. For example, the -orthocompleteness of Definition 8 is assumed as Axiom V. We have that defines a logic in the sense of Definition 9.
Axiom VII is, as we mentioned in the Introduction, ad hoc and does not arise from any natural, physical consideration. It says that the logic of a quantum system is the Birkhoff–von Neumann logic of closed subspaces of a Hilbert space.
Axiom VIII deals with certain observables called questions (see below) and Axiom IX, with the unitary time evolution of the system.
It is worth to mention here the definition of question by Mackey. A question is an observable Q such that takes only the values 0 or 1. It corresponds to a proposition that can be answered with ‘yes’ (1) or ‘no’ (0). Let A be any observable and E any Borel set in . Then the question is the observable that yields 1 whenever a measurement of A is in E and 0 if the measurement of A is not in E.
Let be any state and Q any question. Then the function , , defines an ordering in the space L of questions: if and only if for all . In particular, it is clear that
In the space of questions, we have an obvious complementation, , which takes the value 0 when Q takes the value 1 and vice versa. We will say that two questions are orthogonal if , that is,
for each .
In the language of Ma̧czyński [10], the functions
are called experimental functions. Notice that experimental functions are defined on the equivalence classes of pairs under the equivalence relation
The experimental function is associated to the experimental proposition ‘The result of the measurement of A lies in E′, which is one of the questions of Mackey.
In the following, we will consider finite or infinite countable sums of experimental functions, the infinite case meaning that the series is convergent. Ma̧czyński introduces two convenient definitions:
Definition 14.
A finite or countable sequence of experimental functions is orthogonal if there exists an experimental function g such that
Definition 15.
A finite or countable sequence of experimental functions is pairwise orthogonal if, for each pair , , we have that . A one element sequence is, by definition, orthogonal.
Clearly, an orthogonal sequence is pairwise orthogonal, but the contrary is not always true. Nevertheless, if an experimental proposition in an orthogonal sequence is ‘true’ in some state, that is, its experimental function takes the value 1 at such state, all the other experimental functions have to take the value 0, so the rest of the experimental propositions are ‘false’. This is the same also if the sequence is only pairwise orthogonal. Hence, according to Ma̧czyński, it makes sense to require that the set of experimental functions satisfies the postulate that both concepts are equivalent for such set. This is called by Ma̧czyński the orthogonality postulate. It is equivalent to Mackey’s fifth axiom and it allowed Ma̧czyński to prove that L is a complemented lattice. We have the following theorem by Ma̧czyński (version adapted by Pykacz [9]):
Theorem 1
(Ma̧czyński’73 [10]). Let , , and p be given as above, let L be the set of experimental functions defined by p, and assume that they satisfy the orthogonality postulate. Then,
- L is a logic with respect to the natural order of real functions, with complementation , .
- Each observable A determines a unique L-valued measure defined asThe family is surjective
- Each state determines a unique probability measure defined asThe family is ordering.
- For each , and
Conversely, if L is a logic admitting an ordering set of probability measures and is a surjective set of L-valued measures, then the function defined by
with and is a probability function that satisfies the orthogonality postulate and whose logic, , of p is isomorphic to L. Note that two logics are isomorphic if there is a bijection between them preserving the order relation and the orthocomplementation.
4. Quantum Mechanics
The VIIth axiom of Mackey says that the quantum logic is isomorphic to the Birkhoff–von Neumann logic of closed subspaces (or the projectors over such subspaces) of a certain separable Hilbert space . We saw in Example 3 that the partial ordering is given by the inclusion, the meet is the intersection, and the join is the sum. The complement is the orthogonal complement inside the Hilbert space with inner product .
We follow closely the argument of Mackey [1]. Let be a unit vector on the Hilbert space and let P be a projector. It is clear that
is a probability measure on representing the pure state . One can prove that a convex linear combination of these probability measures
defines also a probability measure on , generically corresponding to a mixed state. Now, by a theorem of Gleason [17], one can also prove that in a dimension bigger than 2, these are all the probability measures if we assume the reasonable condition that, for each non zero projector, there exists at least a vector such that . Observables are defined as valued measures, that is, projection valued measures. By the spectral theorem, there is a one-to-one correspondence between projection valued measures and self adjoint operators. Hence observables are self-adjoint operators.
We will focus on finite dimensional Hilbert spaces. General (mixed or pure) states are described by density matrices, that is, self-adjoint, non negative matrices with trace 1. If is a density matrix, A a self adjoint operator, and E a Borel subset of , and the probability function is the trace of the corresponding projector times the density matrix. In any case, , since in the standard formulation of Quantum Mechanics this quantity is a probability. We will extract some consequences from this fact.
5. The Ma̧czyński Experimental Functions
5.1. The Qubit
We want to describe the qubit system with the BvN (Hilbert space or standard) logic in terms of Ma̧czyński functional representation of Quantum Mechanics.
We then consider the Hilbert space . The set of observables is a subset (Not all self-adjoint operators have a clear meaning as observables. For example, those that violate a selection rule cannot be considered as observables of a physical theory) of the set of self-adjoint operators
In the basis of the Pauli matrices
a self-adjoint operator A can be written as ,
The set of states consists of the density matrices, that is, self-adjoint matrices that are non negative (the eigenvalues are non negative) and with trace 1:
We will write a density matrix as
with real. The trace condition implies that . From the characteristic equation
we obtain
and taking into account that , the non negativity of is equivalent to , that is,
so they can be represented as a ball of radius 1/2, the Bloch ball (see Figure 2).
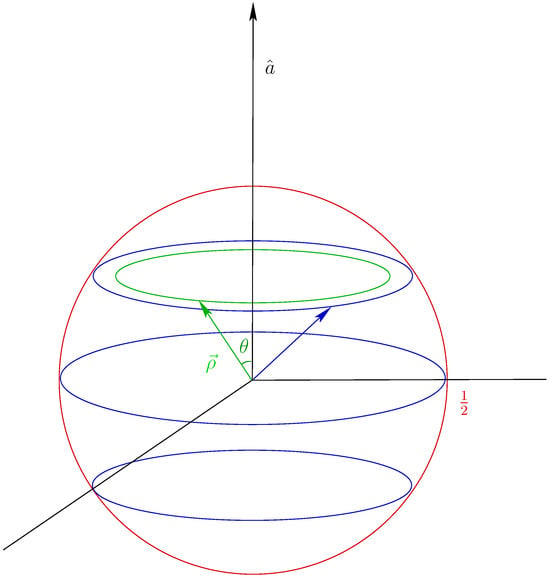
Figure 2.
Bloch ball of states and vector associated to the observable.
The pure states correspond to density matrices satisfying
They form a sphere of radius 1/2, the Bloch sphere. For these states the equality in (7) holds. Antipodal points represent mutually orthogonal states. The points inside the Bloch sphere represent mixed states and its center represents the maximally mixed state.
Let denote the set of Borel subsets of the real line. We then have four types of sets with respect to the eigenvalues :
- Borel sets such that ;
- Borel sets such that and ;
- Borel sets such that and ;
- Borel sets such that .
The projector on the subspace of eigenvectors in that correspond to eigenvalues contained in E is the same inside of each of the above four classes. We have:
Remark 1.
If the two eigenvalues coincide, then so , the observable is just and the projector is the identity. In that case only and are possible.
The experimental functions:
represent the probability that the outcome of the measurement of the observable A in a state is in the Borel subset E. This is computed as the trace of the projector times the density matrix :
Notice that changing by we switch from to , so if A is arbitrary it will be enough to consider the functions, say, .
Indeed, we see that the experimental functions, other than 0 and 1, depend only on the unit vector , with . We will denote those functions as
where , (see (7)) and is the angle between and . There is no dependence on the azimutal angle.
Let us consider the vector fixed. The function only depends on and . When we have a pure state and the set of pure states with constant is represented in the Bloch sphere of Figure 2 by the blue circles. The green vector represents an arbitrary state. One can check directly that .
If we fix , we obtain the functions in terms of only. In Figure 3 we have represented some of these functions for different values of . The function for pure states corresponds to the blue curve.
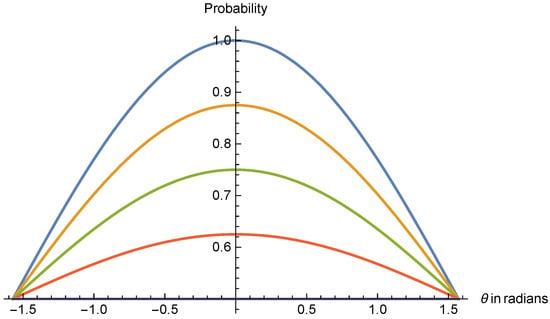
Figure 3.
Experimental functions of the qubit in terms of the angle between the Bloch vector and the unitary vector associated to the observable A [18].
The orthogonality condition is
which is only possible, for all , if .
We thus conclude that the only types of pairwise orthogonal sequences are:
- ,
- ,
- ,
- .
We recall here that a one element sequence is, by definition, orthogonal and that (7) implies that (as it should be for a probability). We observe then, that all pairwise orthogonal sequences are also orthogonal sequences, so the orthogonality postulate is satisfied.
We can restrict the experimental functions to pure states only. Let
be the standard basis in , and let . We choose
Then
If and are real, then we can parametrize the state as
and the experimental functions take the simple form
If we choose a reference frame in which only and the rest 0, we get
(This equation holds even if there is a phase between and ).
5.2. Two Qubits Entangled
We have now a Hilbert space that is a tensor product of the Hilbert spaces of the two qubits, . We will work with the basis of the matrices formed as products of the Pauli matrices (Dirac basis):
We will use Einstein’s convention, so the sum over repeated indices should be understood. Greek letters will represent indices that run from 0 to 3, while Latin letters will represent indices that run from 1 to 3. We will use the notation for the density matrix in terms of the Bloch matrix (see Ref. [12])
which is real. One has immediately that since . The vectors and can be interpreted as the Bloch vectors of the first and second (respectively) qubits. In fact, tracing out (see property 3 below) the second (first) subsystem, one obtains
which, comparing with (6), gives
is called the correlation matrix.
Using the fact that and the property 3 below, one has that
The eigenvalues of the sum of two operators have no easy expression in terms of the eigenvalues of each operator, so we will restrict our analysis to factorizable operators, that is, operators of the form . We recall that:
- ;
- ;
- ;
- If is an eigenvalue of A with eigenvectors , where a runs over the multiplicity of , and is an eigenvalue of B with eigenvectors , b running on the multiplicity of , then is an eigenvalue of and are eigenvectors of .
According to (9), we have eigenvalues for A and for B, so we have 4 eigenvalues (some of them may coincide) for ,
Example 4.
Let us consider the simple case
Then
which has two eigenvalues, , each one with degeneracy 2. Given the operator C, the decomposition is not unique, since, by the properties of the tensor product, one can rescale , and too. It may happen that there is a natural choice, as for this example. Otherwise we have to choose one such decomposition. The operators and determine, in this case, uniquely, a unitary vector of the standard basis by giving their simultaneous eigenvalues, that is, of A, of B. Whenever there is no possibility of confusion, we will denote (as usual)
Operators A and B represent the local properties of the system, that is, properties of each qubit.
So we will assume that we have chosen one such decomposition , since we are limiting our study to decomposable observables. The following analysis will have an equivalent one for every such decomposition.
It is useful to classify the Borel sets according to the eigenvalues that they enclose. Below we list the following types of Borel sets (for each type the projector is similar):
- Sets that do not contain any eigenvalue,
- Sets that contain only one eigenvalue,
- Sets that contain only the two eigenvalues of the same subsystem,
- Sets that contain only two eigenvalues, one of each subsystem,
- Sets that contain only three eigenvalues,
- Sets containing the four eigenvalues.
See Remark 1 for the case in which one of the operators has a degenerate eigenvalue. This would reduce the number of possibilities.
We compute the experimental functions for each type of Borel set:
- For type 1 we just have ,
- Type 2 corresponds to a projector in one subsystem times a projector over the eigenspace of () in the other. There are four posible combinations but the result is always 0,
- Type 3 corresponds to ,
- For type 4, let us consider , the projector onto the subspace of eigenvectors in that correspond to the eigenvalues , that is, we are considering a Borel subset E that contains only and where, according to (10), we have:We denote as , the respective unit vectors for and . The experimental functions on an arbitrary density matrix (14) can be explicitly computed as:After some algebra we getThis can be read as the probability for the observables A and B getting the values and , respectively. The observable gets the value .Unlike for the qubit, it is not straightforward to check here that , but since this is a probability, according to the Hilbert space machinery, the inequalities must be satisfied. At the end of the section we will check it for pure states. These inequalities should be related to the positivity conditions for the matrix , obtained, in the formalism of the Bloch matrix, in Ref. [13].To get the rest of the experimental functions for type 3, we only have to change in the projectors for to obtain and for to obtain .
- Type 5 are projectors of the form or . The experimental function of, say, reproduces the result of (11)
- Type 6 is just the identity.
A series of experimental functions is orthogonal if its sum is less or equal than one. This happens, for all density matrices, when we sum probabilities of events without intersection. For example,
according to the Hilbert space formalism. We can extract, as a consequence, the inequalities
In particular, choosing appropriately , we get
The same can be said about the components of .
Another case is the following sum
which implies
In particular, choosing the axes and appropriately, we have that all the entries of the correlation matrix satisfy
We can also choose and leave arbitrary; then:
where is the angle between the vectors and . This implies
The same reasoning can be done with or . We then obtain that the vectors corresponding to the rows of R, , satisfy inequalities
If instead we leave arbitrary and choose for the unit vectors of the three perpendicular axes, we will obtain that the columns of R satisfy similar inequalities,
Again, (21) and (22) are inequalities constraining the space of the density matrices, independently of any observable. In Ref. [13] the conditions of positivity for the matrix are investigated in terms of the decomposition that we are using here. One such condition is
However
hence, conditions (21) and (22) imply, in particular, that , which is consistent with the fact that . For the case where the equalities in (21) and (22) are fulfilled, one has that , which implies that so . This condition is known as the two qubits being locally maximally entangled, i.e., when tracing out one of the subsystems, the other is left in a maximally mixed state, so its density matrix is proportional to the identity (see Equation (15)).
Pure States
Let and be standard basis in and let be a unit vector representing a pure state:
for . As before, we consider the observable with
We also have the projectors onto the eigenspaces of , (see (8)), given in terms of the unitary vectors
We consider now the case . Notice that, by a change of the reference frame, we can always choose our basis in the three dimensional space, such that this condition is satisfied. Therefore we are not loosing generality. B is still general. Then we have
We compute the probability that a measurement of an observable gives the eigenvalue . To facilitate the writing, we make some definitions:
One can prove that . Then it results that
Let be the angle between and . Since, according to (23), ,
The function is the restriction to pure states of the function in (17) and we are able to check directly that it satisfies the inequalities
5.3. The ‘Nested’ Qutrit
In we consider the spin operators
In we consider the spin operators and . The standard basis is the ordered basis of eigenvectors of these operators and it is denoted as
where the indices denote the eigenvalues and , respectively. The total angular momentum , modulus squared, is given in terms of this basis as
with eigenvalues (multiplicity 1) and (multiplicity 3). A basis of eigenvectors is
Following Ref. [14], we denote this basis as the entangled basis.
As in (14), we express the density matrix of the entangled qubits in the standard basis as
Developing the last term, containing the Bloch matrix, one finds (see Ref. [13])
To change the basis from the standard to the entangled one, we compose the vertical array of unit vectors with the unitary matrix A:
Then, the density matrix in the entangled basis is . We will denote it as
One could prepare a state with . Then, it represents a qutrit inside the two entangled qubits. In Ref. [14], this ‘nested’ qutrit is studied in the context of the dipolar coupling of the two qubits. There, a family of Hamiltonians are given, for which time evolution of the system preserves the constraints defining the qutrit.
Writing the constraints in terms of the Bloch matrix, one can see that the conditions for the qutrit become simply
Hence, the experimental functions (17) are simplified. Notice that we are giving the experimental functions of a qutrit for observables that are factorized in terms of two qubits. In Ref. [14], only factorizable density matrices are studied, but with the Bloch matrix method, an arbitrary density matrix is allowed.
Unitary Transformations
It is worthy to stop here to see the form of (special) unitary transformations for the ‘nested’ qutrit.
In Ref. [15], a decomposition of the group (special unitary transformations of the two qubit system) is given in terms of a structure of orthogonal symmetric Lie algebra of the Lie algebra of , . We give here the definition [19]:
Definition 16.
Orthogonal symmetric Lie algebra. Let be a Lie algebra over and s an involutive automophism of (that is, and ). Let be the set of fixed points of s and suppose that is a compactly embedded subalgebra of . Then, the pair is an orthogonal symmetric Lie algebra.
The Lie subalgebra is the eigenvector set of eigenvalue 1 of s. The eigenvector set of eigenvalue −1 is denoted by and it is, in general, just a vector space. One has
The Lie algebra has different structures of orthogonal symmetric Lie algebra. The structure that is of interest here is the one whose involutive automorphism is . Then
A maximal abelian subspace of is the set of diagonal matrices. A basis of is given in terms of the Dirac matrices (13)
These correspond to the standard basis of (24), which is a basis of eigenvectors of
Performing a change of basis from the standard one to the Bell basis (see for example Ref. [15])
one can deduce directly the above decomposition. Let
and let
Then, by an elementary calculation, one obtains
since they are all real antisymmetric matrices. The rest
are symmetric, purely imaginary matrices. An abelian subset of is the subset of diagonal matrices
This coincides with the decomposition given in Ref. [15] in the standard basis, where the commutation relations among the generators are explicitly exhibited.
On the other hand, it is well known the isomorphism
There is a theorem (see Ref. [19], Chapter V, Theorem 6.7) that gives a decomposition of a group whose Lie algebra has the structure of an orthogonal symmetric Lie algebra. This theorem, applied to our case, asserts that admits a decomposition
The factor is a 3-torus. A unitary transformation can then be cast in the form
The transformations are interpreted as local transformations, that is, transformations involving, separately, the two subsystems of one qubit. The transformations are instead genuine non local transformations. In Ref. [13], Appendix C, the general form of such is given in terms of the Bloch matrix. For example, will transform
into
and
Such transformations preserve the qutrit condition (26), and so does a general transformation . Apparently, these transformations have three parameters, , and . Nevertheless, one can check with Ref. [13] that, if one assumes the qutrit condition, only differences among these parameters occur. So we have a two dimensional abelian group A of non local transformations. For completeness, we write here the transformations. We denote and . Then:
The local transformations are reduced to , so from (29) we are left with a decomposition of unitary transformations of the qutrit as
This is a subgroup of with 8 parameters. Since the unitary transformations for the qutrit are , the formula above is a decomposition of . The group A is a 2-torus, isomorphic to the subgroup of with .
At the infinitesimal level, the two (commuting) vectors fields, generators of the action of A on the set of Bloch matrices, satisfying the qutrit condition, are
6. The Fuzzy Set Picture
Fuzzy sets were introduced by Zadeh [5] in a different context and soon they were used in many practical applications.
Definition 17.
A fuzzy set is a pair where is a set called the universe of discourse and is a function
called the membership function. The number indicates the degree of membership with which the element x belongs to , 0 meaning no membership and 1 full membership. We will indistinctly use the notation or to refer to a fuzzy set.
Definition 18.
Let and be two fuzzy sets in the same universe of discourse .
- if an only if .
- if an only if .
- The bold union is defined as
- The bold intersection is defined as
- The complementation of is
- One defines the empty set ∅ by , and its complement is itself with ,
- and are weakly disjoint if .
The bold union and intersection [6,20] are not the union and intersection originally introduced by Zadeh, that is,
The union and intersection (31) do not satisfy the law of excluded middle and the law of contradiction,
but they are distributive (see Equation (1)); then they are not well suited to describe a quantum system.
Instead, the bold union and intersection satisfy the law of excluded middle, the law of contradiction and are not distributive.
On orthogonal sets, , one can see that the bold union is just
Our aim is to interpret them in the context of the Birkhoff–von Neumann (standard) logic.
In the fuzzy approach to Quantum Mechanics by Pykacz [8,9], the experimental functions of Theorem 1 are interpreted as membership functions of fuzzy sets in the universe of discourse formed by all the possible states of the quantum system. We quote here the theorem of Refs. [8,9], which allows for such an interpretation.
Theorem 2.
Any logic L with an ordering set of probability measures can be mapped isomorphically to a logic formed by a family of fuzzy subsets of , , that satisfies the following properties:
- ∅ belongs to the family .
- If belongs to , so does its complement .
- Given a countable family of fuzzy subsets inside which is pairwise weakly disjoint, for , then belongs to .
- If then .
Conversely, any family of fuzzy subsets of a universe , satisfying properties 1–4 above, is a logic where the partial order is the inclusion of fuzzy sets and the orthocomplementation is the complementation of fuzzy sets. The notion of orthogonality coincides with that of weak disjointness.
The set of ordering measures is given by elements of the universe as
The universe of discourse is the set of states . As stated before, given two membership functions and , the bold intersection being the empty set, implies that the bold union is
and then, the function above satisfies the conditions to be a probability measure. The same is true for an infinite countable succession of ; this is guaranteed by property 3 in Theorem 2.
In Quantum Mechanics, each state is represented by a density matrix, therefore the universe of discourse is
By stating this we have already introduced the Hilbert space. The membership functions (4) are determined by an observable A and a Borel set
where is the probability map of Mackey (2) and is the projector on the subspace of that is the sum of the eigenspaces of A in with eigenvalue in the Borel set E. So the membership function contains information about the observable A and the Borel subset E.
6.1. The Fuzzy Bit
For the qubit, the membership (experimental) functions (11) are labelled by a unit vector
where
plus the constant functions 0 and 1.
They are functions that, according to Theorem 2, can be interpreted as membership functions of fuzzy sets. These functions are orthogonal if the bold intersection of fuzzy sets is the empty set, so
Since this relation has to be satisfied for all we recover the result in (12), that is, .
If the fuzzy sets are orthogonal, then its bold union is
that is, the union is the universe of discourse S, which makes sense, since it is the probability that the eigenvalue of A is +1 or −1, which exhausts all the possibilities.
We now give some examples that help to clarify the role of the fuzzy sets for the qubit.
Example 5.
The gate NOT.We consider a qubit. Let be the ordered basis of of eigenvectors of ,
Let a vector representing a pure state, so . There is a transformation that flips the two basis states (the NOT gate). It is represented in this basis by the unitary matrix
Notice that . Its action on a density matrix is
In terms of the sigma matrices we have that
so the flip transformation takes to . In the Bloch sphere, this is a rotation of 180 around the axis.
The probability of finding the system in a state ‘+’ with respect to an arbitrary axis is
Effecting the NOT transformation changes the probability to
Notice that applying the NOT gate to the fuzzy bit is not the same than computing its complement as a fuzzy set. This has been the cause of some confusion in the literature. However, in the particular case that is the axis, , then one has that
which is equal to its complement as a fuzzy set
This probability coincides with .
Example 6.
The gate . In the same setting than the example above, one defines the square root of the gate NOT, , as a unitary transformation such that
This transformation is not unique, but it is usual to choose the following one:
(Notice that .) The sigma matrices behave, under this transformation, as
so goes to . In the Bloch sphere, this is a rotation of around the axis. It is clear that (34) is satisfied. The membership functions then change as
It is known [21,22] that the negation in fuzzy logic (orthocomplementation of fuzzy sets) does not have a square root. Particularly, Lemma 17.1.12 in Ref. [21] reads: “There is no continuous function such that for any , ”. The authors then provide an example of square root in which the function f is not continuous.
In our approach, since the NOT gate sending the fuzzy set to does not coincide with the negation, in general, a continuous square root of the gate NOT is allowed.
6.2. The Entangled Fuzzy Bits
For the entangled fuzzy bits, the membership functions of are given in terms of the two unit vectors and (17):
In the two examples (19) and (20) one can check directly that the orthogonality of the membership functions implies that the bold union is again a membership function:
that is, the sum is again a probability.
Example 7.
The CNOT gate.The Controlled NOT gate has an input of two qubits. In the ordered basis of used above, the CNOT transformation acts as
It is represented in this basis by the unitary matrix
Notice that . We want to see how the membership functions change with this transformation, so we will compute first the change in the density matrix. Let us remind the notation (14):
For the transformed matrix
we obtain [18]:
Let us consider , so . Suppressing and from the notation in (17), we get
As expected, since the first qubit is a control qubit, we have
7. Conclusions
In this paper the meaning of the relationship between Quantum Mechanics, logics, and fuzzy sets has been clarified. It results that a particular family of fuzzy sets, with universe of discourse the density matrices in a Hilbert space, can actually faithfully represent the Birkhoff–von Neumann logic of projectors of a Hilbert space. This choice is the same as the ‘ad hoc’ choice of Mackey in his Axiom VII. The membership functions of the fuzzy sets (or, equivalently, the experimental functions of Ma̧czyński) have been computed for three different systems: the qubit, two entangled qubits, and a qutrit ‘nested’ inside the entangled qubits. A decomposition of SU(3), the special unitary transformations of the qutrit, inherited from the orthogonal symmetric Lie algebra structure of , has been found. With the aid of the membership functions, we have proven that a continuous square root of NOT exists for the qubit.
We have obtained families of probability distributions for different physical systems. A possible application of our formalism would be to compute the classical Fisher information that arises in the context of parametrized probability distributions. The classical Fisher information measures the quantity of information that an observable random variable carries, conditioned to the value of the external parameters (see Ref. [23] for a pedagogical exposition of the subject). It gives the ‘distance’ between two probability distributions that are separated by a slight perturbation of the parameters. Computing this distance in terms of the distance between quantum states gives the quantum Fisher information. They are both of interest in the field of quantum information.
Author Contributions
Conceptualization, M.A. and M.A.L.; methodology, M.A. and M.A.L.; formal analysis, M.A. and M.A.L.; investigation, M.A. and M.A.L.; resources, M.A. and M.A.L.; writing—original draft preparation, M.A. and M.A.L.; writing—review and editing, M.A. and M.A.L.; supervision, M.A. and M.A.L.; project administration, M.A. and M.A.L.; funding acquisition, M.A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Spanish Grants FIS2017-84440-C2-1-P funded by MCIN/AEI/10.13039/501100011033 ‘ERDF A way of making Europe’, PID2020-116567GB-C21 funded by MCIN/AEI/10.13039/501100011033, the Project PROMETEO/2020/079 (Generalitat Valenciana) and the project CaLIGOLA, Project ID: 101086123 (HORIZON). This article is based upon work from COST Action CaLISTA CA21109 supported by COST (European Cooperation in Science and Technology). www.cost.eu, accessed on 22 November 2023.
Data Availability Statement
Data are contained within the article.
Acknowledgments
M. Aldana wants to thank the Departament de Física Teòrica, Universitat de València, for its kind hospitality. We are grateful to A. Pérez-Cañellas for interesting discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mackey, G.W. The Mathematical Foundations of Quantum Mechanics; W. A. Benjamin Inc.: New York, NY, USA, 1963. [Google Scholar]
- Varadarajan, V.S. Geometry of Quantum Theory, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Beltrametti, E.G.; Cassinelli, G. The Logic of Quantum Mechanics; Adison-Wesley: Boston, MA, USA, 1981. [Google Scholar]
- Łukasiewicz, J. Logical Foundations of Probability Theory; Akademien der Wissenschaften Schweiz: Kraków, Poland, 1913. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Giles, R. Łukasiewicz logic and fuzzy set theory. Int. J. -Man-Mach. Stud. 1976, 67, 313–327. [Google Scholar] [CrossRef]
- Ospanov, Y.A.; Orazbayev, B.B.; Orazbayeva, K.N.; Gancarczyk, T.; Shaikhanova, A.K. Control of Fuzzy Technological Objects Based on Mathematical Models. In Proceedings of the 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Republic of Korea, 16–19 October 2016; pp. 1487–1493. [Google Scholar]
- Pykacz, J. Fuzzy quantum logics and infinite-valued Łukasiewicz logic. Int. J. Theor. Phys. 1994, 33, 1403–1416. [Google Scholar] [CrossRef]
- Pykacz, J. Quantum Physics, Fuzzy Sets and Logic; Springer Briefs Series; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ma̧czyński, M.J. The orthogonality postulate in axiomatic Quantum Mechanics. Int. J. Theor. Phys. 1973, 8, 353–360. [Google Scholar] [CrossRef]
- Mączyński, M.J. Functional properties of quantum logics. Int. J. Theor. Phys. 1974, 11, 149–156. [Google Scholar] [CrossRef]
- Byrd, M.S.; Khaneja, N. Characterization of the positivity of the density matrix in terms of the coherence vector representation. Phys. Rev. A 2003, 68, 062322. [Google Scholar] [CrossRef]
- Gamel, O. Entangled Bloch spheres: Bloch matrix and two qubit state space. Phys. Rev. A 2016, 93, 062320. [Google Scholar] [CrossRef]
- Belousov, Y.; Man’ko, V.I.; Migliore, A.; Sergi, A.; Messina, A. Symmetry-induced emergence of a pseudo-qutrit in the dipolar coupling of two qubits. Entropy 2022, 24, 223. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Vala, J.; Sastry, S.; Birgitta Whaley, K. Geometric theory of non local two-qubit operations. Phyiscal Rev. A 2003, 67, 042313. [Google Scholar] [CrossRef]
- Birkhoff, G.; Von Neumann, J. The Logic of Quantum Mechanics; The Annals of Mathematics; Springer: Cham, Switzerland, 1936; Volume 37, pp. 823–843. [Google Scholar]
- Gleason, A.M. Measures on the closed subspaces of a Hilbert space. J. Math. Mech. 1957, 6, 885–893. [Google Scholar] [CrossRef]
- Graphic/Calculation Made with the Help of MATHEMATICA; Version 13.3; Wolfram Research, Inc.: Champaign, IL, USA, 2023.
- Helgason, S. Differential Geometry, Lie Groups, and Symmetric Spaces; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Zawirski, Z. Relationship between many valued logic and the calculus of probabilities. Pr. Kom. Filoz. Pozn. Tow. Przyj. Nauk. 1934, 4, 155–240. (In Polish) [Google Scholar]
- Chiara, M.L.D.; Giuntini, R.; Greechie, R. Reasoning in Quantum Theory. Sharp and Unsharp Logics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Kreinovich, V.; Kohout, L.J.; Kim, E. Square root of ‘not’: A major difference between fuzzy and quantum logics. Int. J. Gen. Syst. 2008, 40, 1–5. [Google Scholar]
- Meyer, J.J. Fisher information in noisy intermediate-scale quantum applications. Quantum 2021, 5, 539. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).