Abstract
This paper proposes a new approach to define two frequency trigonometric spline curves with interesting shape preserving properties. This construction requires the normalized B-basis of the space defined on compact intervals , where is a global shape parameter. It will be shown that the normalized B-basis can be regarded as the equivalent in the trigonometric space to the Bernstein polynomial basis and shares its well-known symmetry properties. In fact, the normalized B-basis functions converge to the Bernstein polynomials as . As a consequence, the convergence of the obtained piecewise trigonometric curves to uniform quartic B-Spline curves will be also shown. The proposed trigonometric spline curves can be used for CAM design, trajectory-generation, data fitting on the sphere and even to define new algebraic-trigonometric Pythagorean-Hodograph curves and their piecewise counterparts allowing the resolution of Hermite interpolation problems.
1. Introduction
The definition of new spaces with more flexibility than polynomials, but with the same nice structural properties, such as variation diminishing, containment in the convex-hull, affine invariance, or tangency to the control-polygon at the endpoints, is an interesting trend in Computer-Aided Geometric Design (CAGD).
For a suitable basis of a given space of functions defined on , , , provides a parametric representation of curves, where the coefficients are points in a given determining a polygon , which is called the control polygon of .
A system of functions defined on I is normalized if for all . On the other hand, a totally positive (TP) basis is a basis whose collocation matrices have nonnegative minors. We say that a basis provides a shape preserving representation if the shape of any parametric curve imitates the shape of its control polygon. Normalized and totally positive (NTP) bases provide shape preserving representations (cf. [1,2]). In [3], it was proved that a space of functions with NTP bases always has an optimal shape preserving basis that it is called the normalized B-basis and satisfies that the matrix of change of basis of any NTP basis with respect to the normalized B-basis is totally positive and stochastic. Roughly speaking, any parametric curve more faithfully imitates the shape of its control polygon with respect to the normalized B-basis than using other shape preserving representation.
The Bernstein polynomials of a given degree n on a compact interval are defined by
It is well-known that the Bernstein basis is the normalized B-basis of the space of polynomials of degree at most n on the considered interval. The B-spline basis is the normalized B-basis in the case of the space of spline polynomials.
Trigonometric functions are usually considered for the representation of closed curves and periodical functions. The space of n order trigonometric polynomials,
is a classical space of functions with applications in CAGD in order to represent approximately parametric curves arising in civil engineering and robotics, among other fields. Traditionally these curves were approximated by polynomial and rational functions.
Due to the oscillation properties of trigonometric functions, the representation of curves using trigonometric spaces is not shape preserving for very long intervals. However, using a domain of a length , the space admits a normalized B-basis and solves several shortcomings of the algebraic polynomials. Consequently, it provides an alternative to the rational model for several purposes (see [4]). In the literature one can find many papers introducing shape parameters for a more flexible design of trigonometric curves (see [5,6,7,8,9,10,11,12]). For trigonometric polynomials in , the length of the parameter domain can also be considered as a shape parameter with a tension-like effect in the parametric curves generated by the corresponding normalized B-bases. Trigonometric spline functions were introduced in [13] (see also [14]) and the recurrence relation for the trigonometric B-splines of arbitrary order was obtained in [15]. In [16,17], interested readers can find a novel technique based on the collocation finite element method for the numerical resolution of the wave equation in which trigonometric cubic B-splines are used as approximate functions.
Spline spaces provide more flexibility for curve design and then common curve and surface representations in CAGD use piecewise polynomials. Integral recurrence formulae for B-splines have been often used in the past. The definition of B-spline functions as a divided difference of a truncated power function and the Hermite–Gennochi formula lead to integral recursions. However, trigonometric polynomial spaces do not admit an integral construction. For this reason, this paper introduces NTP bases of , such that their derivatives at the ends of the interval of allow us the definition of regular piecewise trigonometric curves. In [18], one-frequency trigonometric spline curves are defined in the space . This paper proposes and analyzes piecewise trigonometric curves in providing two different frequencies for the design.
Polynomial Pythagorean-Hodograph (PH) curves have been widely analyzed (see [19,20,21,22,23,24,25] and their references). Polynomial PH curves are defined with Bernstein bases and possess a closed-form polynomial representation of their arc lengths, as well as an exact rational parameterization of their offset curves. New Pythagorean-Hodograph (PH) B-spline curves were proposed in [21]. The results in this paper will be considered in the near future to define new algebraic-trigonometric PH curves and their piecewise counterparts for the resolution of Hermite interpolation problems. Moreover, the proposed trigonometric spline curves can also be used for CAM design, trajectory generation or data fitting on the sphere where the use of trigonometric splines provide better results than the conventional polynomial counterpart (see Chapter 12 of [1]).
The paper is organized as follows. Section 2 provides the normalized B-basis of the space defined on a given interval with a length less than . A corner cutting algorithm for the evaluation and subdivision of curves generated in is also provided. This algorithm allows us to generate curves through a control polygon in a similar way to the Bézier case [26,27]. In Section 3, we introduce NTP bases of defined on appropriate intervals , and such that their derivatives at the ends of the interval allow us the definition of regular spline spaces and their bases called normalized B-spline basis. The matrices relating the normalized B-bases of and the spline spaces are also derived and their total positivity analyzed. Piecewise trigonometric curves with nice properties are also defined. Section 4 shows the convergence of the introduced trigonometric curves to polynomial B-spline curves as the parameter . Finally, Section 5 summarizes the conclusions and future work.
2. The Normalized B-Basis of the Space of Two Frequency Trigonometric Functions
Trigonometric polynomial spaces are invariant under translations and reflexions and, for this reason, they are usually analyzed on compact intervals .
We shall consider the design of parametric trigonometric curves whose components are functions in the space
In Section 4.2 of [28], the normalized B-basis of is given by:
for and . Note that the normalized B-basis can be also defined as follows:
The basis functions in (1), equivalently in (2), can be regarded as the equivalent to the Bernstein polynomial basis in due to the following properties:
- Symmetry:
- Positivity:
- Partition of unity:
Figure 1 shows the graphs of the normalized B-basis of for .
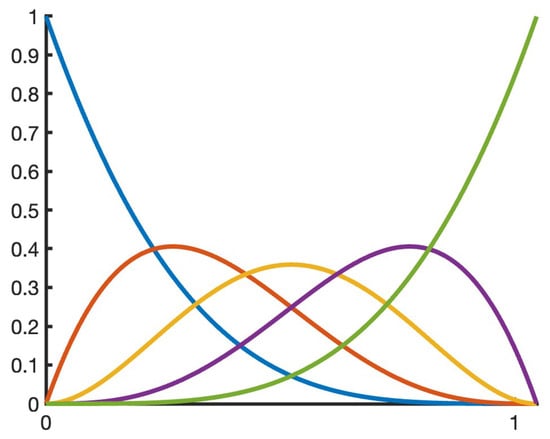
Figure 1.
Normalized B-basis of for .
Let us note that the parameter not only controls the length of the domain but also can be considered as a shape parameter with a tension-like effect in the parametric curves generated by the normalized B-basis of . The following result will explain the behavior as . In order to prevent the normalized B-bases from losing their domain intervals , we shall use a reparametrization so that the new functions are defined on allowing the parameter .
Lemma 1.
The normalized B-basis of converges uniformly to the Bernstein basis of degree 4 on the interval whenever .
Proof.
Using the change , and developing by the Taylor expansion at , we have
for . Then
and, since
we derive
By definition, , and therefore, using (4), we deduce that
Using the Taylor expansion and a similar reasoning, we can also write
Finally, from the normalization property of the bases, , , and taking into account Formulaes (4)–(6), we conclude
□
Definition 1.
Let and . Given , , we say that the parametric trigonometric curve
is a -curve.
Let us observe that, using the symmetry property (3), we can write
and derive that -curves possess a symmetry similar to that of Bézier curves. Furthermore, since -curves are curves expressed in terms of a normalized B-basis, they admit a de Casteljau-type algorithm, which is a corner cutting algorithm providing evaluation and subdivision.
Given a -curve (8), and a parameter value , the B-algorithm provides certain values that define the intermediate points of a de Casteljau-like algorithm:
where and . In fact, beginning with , this algorithm yields the final value
In addition, the two segments in which the parameter t divides the curve have control points given by and , respectively. Here we provide compact expressions of for an arbitrary :
Taking into account Lemma 1, whenever , the -curve (8) degenerates to an integral Bézier curve with control points , , and the coefficients of the algorithm degenerate to (see Figure 2). In other words, the B-algorithm reduces to the standard de Casteljau algorithm. This property can be also checked by introducing the Taylor expansion of the functions and taking limits.
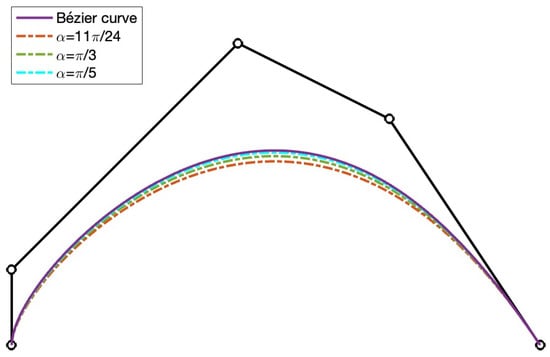
Figure 2.
-curves (8) associated to a control polygon with several parameters , as well as the Bézier curve corresponding to the mentioned control polygon.
3. Two Frequency Trigonometric Spline Curves
Now, we shall introduce NTP bases of such that their derivatives up to the third order at the ends of the interval of allow us the definition of regular piecewise curves. We shall use the following notation:
for given .
Let us define the following systems of functions on :
where is the normalized B-basis of (see (1) or (2)),
and the matrices , for , are defined as follows:
The following result proves that the systems (10) are all NTP bases of .
Theorem 1.
For , the systems and , , defined in Formula (10) are NTP basis of .
Proof.
It can be easily checked that the matrix in (11), as well as the matrices , , in (12), (13) and (14), respectively, are stochastic for . Moreover, since for
and
we conclude that they are also nonsingular matrices and the introduced systems are all bases of .
Since is the normalized B-basis of (see [4]), by Corollary 3.9 (iv) of [3], it remains to prove that the matrices are TP. Let us recall that Neville elimination is an alternative procedure to Gaussian elimination and has been used to characterize TP and STP matrices. Applying the Neville elimination to the matrix in (11), we can factorize as follows:
with
and
Additionally,
with
It can be easily checked that, for , the entries of the matrix factors in (15) are nonnegative and consequently, the bidiagonal matrices and , are TP. Taking into account that, by Theorem 3.1 of [29], the product of TP matrices is a TP matrix, we conclude that is TP.
Now, we provide the bidiagonal factorization obtained by applying Neville elimination to the matrices , . It can be checked that
where , and are the nonsingular, stochastic bidiagonal lower triangular matrices in the factorization (15). Furthermore,
where , and are the matrices in the factorization (15) and
with
Finally,
where , and are the matrices in the factorization (15) and
with
It can be easily checked that the bidiagonal matrices of the factorization (16), (17) and (18) are TP for and the result follows. □
We shall see that the NTP bases in (10) allow us to define -B-spline bases and -B-spline curves, that is, piecewise functions and curves, respectively, on . In the following result, the derivatives up to the third order of the functions of these NTP bases are provided.
Lemma 2.
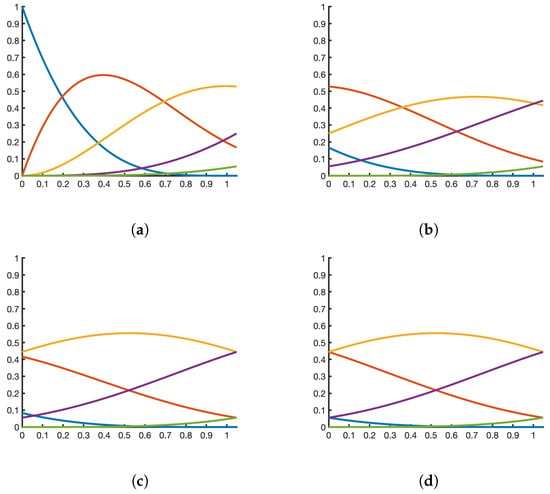
The functions , , , , of the NTP bases of defined in (10) satisfy the following properties (see Figure 3):

Figure 3.
NTP bases defined in (10) for . (a) , (b) , (c) , (d) .
- 1.
- , , .
- 2.
- , , , for .
- 3.
- , .
- 4.
- , .
- 5.
- , .
- 6.
- , .
Given , , we are going to consider the equally spaced partition
as well as the partition
with
and
Now, we define piecewise functions on either partition or . When considering the equally spaced partitions , trigonometric B-spline bases will be obtained for the shape-preserving representation of closed curves. On the other hand, using the piecewise functions on partitions , clamped trigonometric curves satisfying the tangency to the control-polygon will be defined.
For any , let
Moreover, for the partition , we consider the following piecewise functions,
for , with the convention , and
for , with the convention . In Figure 4 the piecewise functions , , are depicted.
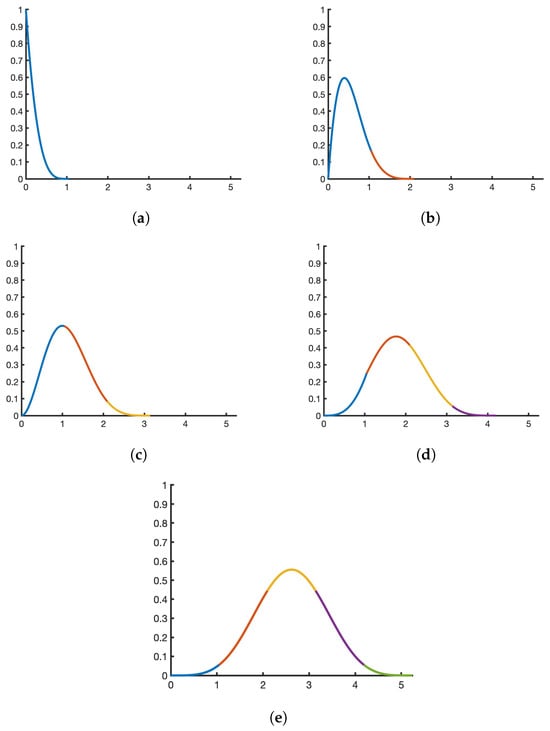
Figure 4.
Trigonometric piecewise functions (a) , (b) , (c) , (d) and (e) , for .
The following properties of the above introduced piecewise functions can be deduced from their definition and taking into account Theorem 1 and Lemma 2.
Proposition 1.
The functions , , defined in (21), and the functions , and , defined in (22) and (23) satisfy the following properties:
- 1.
- All the mentioned functions are piecewise trigonometric functions of the space .
- 2.
- The functions are symmetrical with respect to the middle of their supports and they can be obtained by translation, i.e.,
- 3.
- and for and all applicable indices i. In fact, and have minimal support .
- 4.
- for .
- 5.
- On the partitions and ,
- 6.
- On the partitions and , the functions for and for and are -continuous, where is the multiplicity of the knot in the support of the respective function.
Due to the analogy to the well-known polynomial B-splines, we will say that the introduced piecewise functions are -B-splines.
Definition 2.
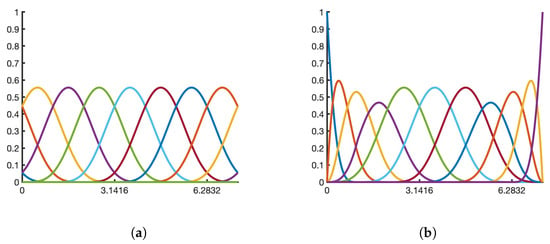
Given , , and partitions and from (19) and (20), respectively. We say that with
and defined in (21), is the normalized -B-spline basis over the partition (see Figure 5a for an illustration). On the other hand, we say that with
and defined in (22), for , and defined in (23), for , is the normalized -B-splines over the partition (see Figure 5b for an illustration).

Figure 5.
Normalized -B-splines over a partition (a), and (b) for .
The following properties guarantee shape preserving properties of normalized -B-spline systems for knot partitions and , with .
Proposition 2.
Given , the -B-spline functions and , , introduced in Definition 2, satisfy the following properties:
- 1.
- is an NTP basis of the generated space of piecewise functions on defined on .
- 2.
- is the normalized B-basis of functions on .
Proof.
Let and , , be the NTP bases of defined in (10). Given ,
for , and , we have
Consequently, taking into account Theorem 1, we deduce that the restrictions to of and the restrictions to of are NTP bases of for . Then, it can be deduced that and are NTP bases of the corresponding generated space of piecewise functions defined on .
In addition, the basis also satisfies
whenever . Then, by Theorem 3.2 of Chapter 4 of [1], is the normalized B-basis of . □
The previous result implies that the -B-spline basis has optimal shape preserving properties (see [3] and Chapter 4 of [1]) and it also has optimal stability properties for the evaluation (cf. Chapter 5 of [1]) Now, we can define the corresponding piecewise trigonometric curves.
Definition 3.
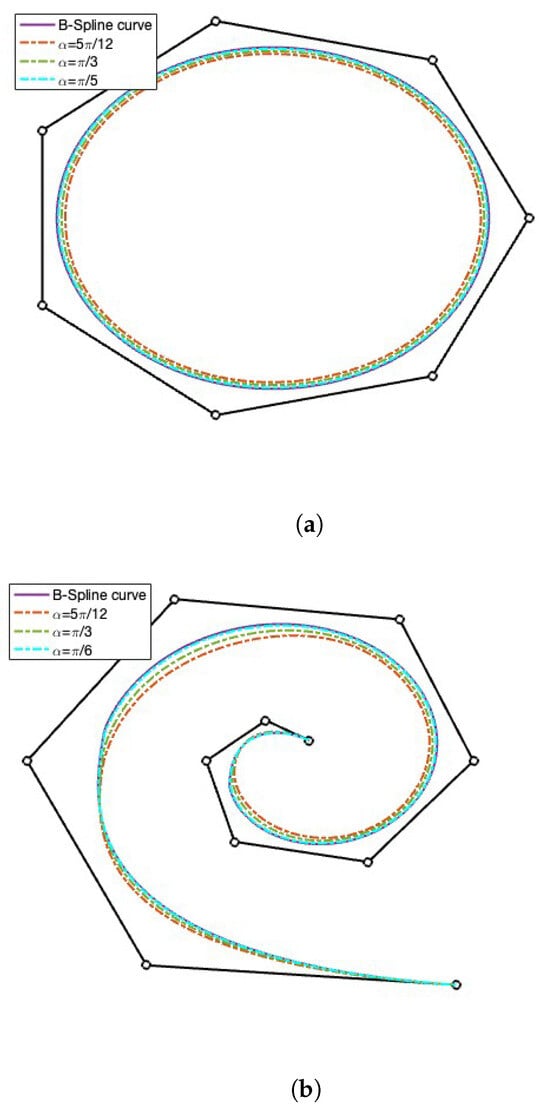
Given , , let , , and partitions and from (19) and (20), respectively. The parametric curve defined by
is called -B-spline curve with respect to the partition and control points . In particular, if , with , , then we say that is an open -B-Spline curve. If and , , we say that is a closed -B-Spline curve. See Figure 6a for an illustration of a closed -B-Spline curve.

Figure 6.
-B-splines curves (closed in (a), clamped in (b)) associated to a control polygon with several parameters , as well as the B-spline curve corresponding to the mentioned control polygon.
The parametric curve defined by
is called clamped -B-spline curve with respect to the partition and control points . See Figure 6b for an illustration of a clamped -B-Spline curve.
-B-Spline curves satisfy the following properties.
Proposition 3.
The -B-Spline curves described in Definition 2 satisfy:
- 1.
- The relation between a -B-Spline curve and its control points is affinely invariant.
- 2.
- Any -B-Spline curve is locally controlled, i.e., moving a control point only modifies the curve for , moreover for or we haveand the curve lies in the convex hull of its control points , .
- 3.
- The -B-Spline curves are monotonicity preserving: the curve has the same monotonicity as the monotone control points.
- 4.
- The length of a -B-Spline curve is bounded above by the length of its control polygon.
- 5.
- If the control polygon of a -B-Spline curve is planar and convex, then the -B-Spline curve is also planar and convex.
- 6.
- The -B-Spline curve never crosses a hyperplane more often than does the control polygon.
- 7.
- Clamped -B-Spline curves have end point and end tangent interpolation properties:
4. Convergence of -B-Spline Curves to Quartic Polynomial B-Spline Curves
In this section we prove the convergence, when , of -B-Spline curves to polynomial B-spline curves.
Theorem 2.
Let and partitions described in (19) and (20), respectively. When , the -B-Spline curve (24) and the clamped -B-Spline curve (25), with respect to and , respectively, and control points approaches uniformly to the quartic polynomial B-spline curve with knot vector and , respectively and control points .
Proof.
Let us observe that, by (26), for or , we can write
Let for reparameterizing each segment curve on the interval . By Lemma 1, as , the function approaches uniformly the Bernstein polynomial , , for all . It can be easily checked that that the matrix in (11) satisfies
and therefore for we obtain
which is the matrix form of a uniform B-spline curve of degree 4.
For , we can follow a similar reasoning taking into account that the matrices of () satisfy
and
□
5. Conclusions and Future Work
We have proposed two frequency trigonometric spline bases with shape preserving properties associated to uniform knot vectors. The corresponding parametric trigonometric spline curves have been also described. It is also shown that these curves share many properties of polynomial spline curves. In fact, they converge to uniform quartic B-spline curves.
There is some worthwhile work to study further. We want to extend the bases to knot vectors with multiple knots and to investigate whether it is possible to construct new Algebraic-Trigonometric Pythagorean-Hodograph B-Splines curves taking into account the results from [21].
Author Contributions
Conceptualization, G.A., E.M., J.M.P. and B.R.; methodology, G.A., E.M., J.M.P. and B.R.; investigation, G.A., E.M., J.M.P. and B.R.; writing—original draft, G.A., E.M., J.M.P. and B.R.; writing—review and editing, G.A., E.M., J.M.P. and B.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the CICYT under Research Grant CICYT BFM2000–1253. This research was also partially supported by Spanish research grants PGC2018-096321-B-I00 (MCIU/AEI) and RED2022-134176-T (MCI/AEI) and by Gobierno de Aragón (E41_23R).
Data Availability Statement
The data and codes used in this work are available under request. The code of the experimentation was developed in Matlab R2022b. All experiments were ran on a Apple M1 Pro chip with 10-Core CPU and 32 GB RAM.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peña, J.M. (Ed.) Shape Preserving Representations in Computer-Aided Geometric Design; Nova Science Publishers Commack: New York, NY, USA, 1999. [Google Scholar]
- Goodman, T.N.T. Shape preserving representations, In Mathematical Methods in CAGD; Lyche, T., Schumaker, L.L., Eds.; Academic Press: Boston, MA, USA, 1989; pp. 333–351. [Google Scholar]
- Carnicer, J.M.; Peña, J.M. Totally positive bases for shape preserving curve design and optimality of B-splines. Comput. Aided Geom. Des. 1994, 11, 635–656. [Google Scholar] [CrossRef]
- Sánchez-Reyes, J. Harmonic rational Bézier curves, p-Bézier curves and trigonometric polynomials. Comput. Aided Geom. Des. 1998, 9, 909–924. [Google Scholar] [CrossRef]
- Han, X.L.; Zhu, Y.P. Curve construction based on five trigonometric blending functions. Bit Numer. Math. 2012, 52, 953–979. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, G.C.; Nhon, N.T. New trigonometric basis possessing denominator shape parameters. Math. Probl. Eng. 2018. [Google Scholar] [CrossRef]
- Han, X.L.; Ma, Y.C.; Huang, X.L. The cubic trigonometric Bézier curve with two shape parameters. Appl. Math. Lett. 2008, 22, 226–231. [Google Scholar] [CrossRef]
- Han, X.L. Cubic trigonometric polynomial curves with a shape parameter. Comput. Aided Geom. Des. 2004, 21, 535–548. [Google Scholar] [CrossRef]
- Wu, X.Q.; Han, X.L.; Luo, S. Quadratic trigonometric polynomial Bézier curves with a shape parameter. Eng. Graph. 2008, 1, 82–87. [Google Scholar]
- Majeed, A.; Abbas, M.; Qayyum, F.; Miura, K.T.; Misro, M.Y.; Nazir, T. Geometric modeling using new cubic trigonometric B-spline functions with shape parameter. Mathematics 2020, 8, 2102. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Han, X.L. New trigonometric basis possessing exponential shape parameters. J. Comput. Math. 2015, 33, 642–684. [Google Scholar]
- Zhu, Y.P.; Liu, Z. A class of trigonometric Bernstein-type basis functions with four shape parameters. Math. Probl. Eng. 2019. [Google Scholar] [CrossRef]
- Schoenberg, I.J. On trigonometric spline interpolation. J. Math. Mech. 1964, 13, 795–825. [Google Scholar]
- Schumaker, L.L. Spline Functions: Basic Theory; John Wiley and Sons: New York, NY, USA, 1981. [Google Scholar]
- Lyche, T.; Winther, R. A stable recurrence relation for trigonometric B-splines. J. Approx. Theory 1979, 25, 266–279. [Google Scholar] [CrossRef]
- Yağmurlu, N.M.; Karakaş, A.S. Numerical solutions of the equal width equation by trigonometric cubic B-spline collocation method based on Rubin–Graves type linearization. Numer. Methods Partial Differ. Equ. 2020, 36, 1170–1183. [Google Scholar] [CrossRef]
- Yağmurlu, N.M.; Karakaş, A.S. A novel perspective for simulations of the MEW equation by trigonometric cubic B-spline collocation method based on Rubin-Graves type linearization. Comput. Methods Differ. Equ. 2022, 10, 1046–1058. [Google Scholar]
- Albrecht, G.; Mainar, E.; Peña, J.M.; Rubio, B. A New Class of Trigonometric B-Spline Curves. Symmetry 2023, 15, 1551. [Google Scholar] [CrossRef]
- Farouki, R.T. The conformal map of the hodograph plane. Comput. Aided Geom. Des. 1994, 11, 363–390. [Google Scholar] [CrossRef]
- Sˇir, Z.; Jüttler, B. Spatial Pythagorean Hodograph Quintics and the Approximation of Pipe Surfaces. In Mathematics of Surfaces XI. Lecture Notes in Computer Science; Martin, R., Bez, H., Sabin, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3604. [Google Scholar]
- Albrecht, G.; Beccari, C.V.; Canonne, J.C.; Romani, L. Planar Pythagorean-Hodograph B-Spline curves. Comput. Aided Geom. Des. 2017, 57, 57–77. [Google Scholar] [CrossRef]
- Farouki, R.T.; Giannelli, C.; Sestini, A. Identification and “reverse engineering” of Pythagorean-hodograph curves. Comput. Aided Geom. Des. 2015, 34, 21–36. [Google Scholar] [CrossRef]
- Farouki, R.T. Pythagorean-Hodograph Curves: Algebra and Geometry Inseparable; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Farouki, R.T.; Giannelli, C.; Sestini, A. Local modification of Pythagorean-hodograph quintic spline curves using the B-spline form. Adv. Comput. Math. 2016, 42, 199–225. [Google Scholar] [CrossRef]
- Pelosi, F.; Sampoli, M.L.; Farouki, R.T.; Manni, C. A control polygon scheme for design of planar PH quintic spline curves. Comput. Aided Geom. Des. 2007, 24, 28–52. [Google Scholar] [CrossRef]
- Farin, G. Curves and Surfaces for Computer Aided Geometric Design, 4th ed.; Academic Press: San Diego, CA, USA, 1997. [Google Scholar]
- Hoschek, J.; Lasser, D. Fundamentals of Computer Aided Geometric Design; AKPeters: Wellesley, MA, USA, 1993. [Google Scholar]
- Mainar, E.; Peña, J.M.; Sánchez-Reyes, J. Shape preserving alternatives to the rational Bézier model. Comput. Aided Geom. Des. 2001, 18, 37–60. [Google Scholar] [CrossRef]
- Ando, T. Totally positive matrices. Linear Algebra Appl. 1987, 90, 165–219. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).