Addressing Volterra Partial Integro-Differential Equations through an Innovative Extended Cubic B-Spline Collocation Technique
Abstract
1. Introduction
2. Description of the Method
Initial Vector
3. Stability Analysis
4. Convergence Analysis
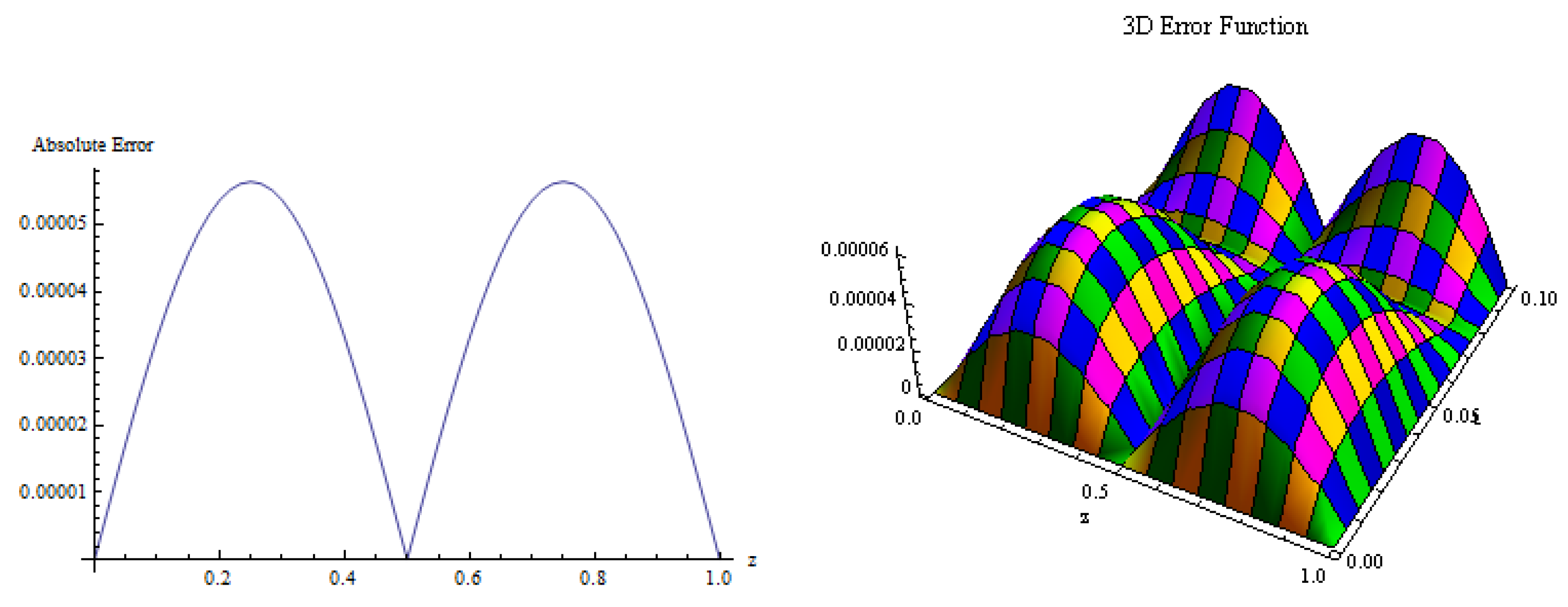
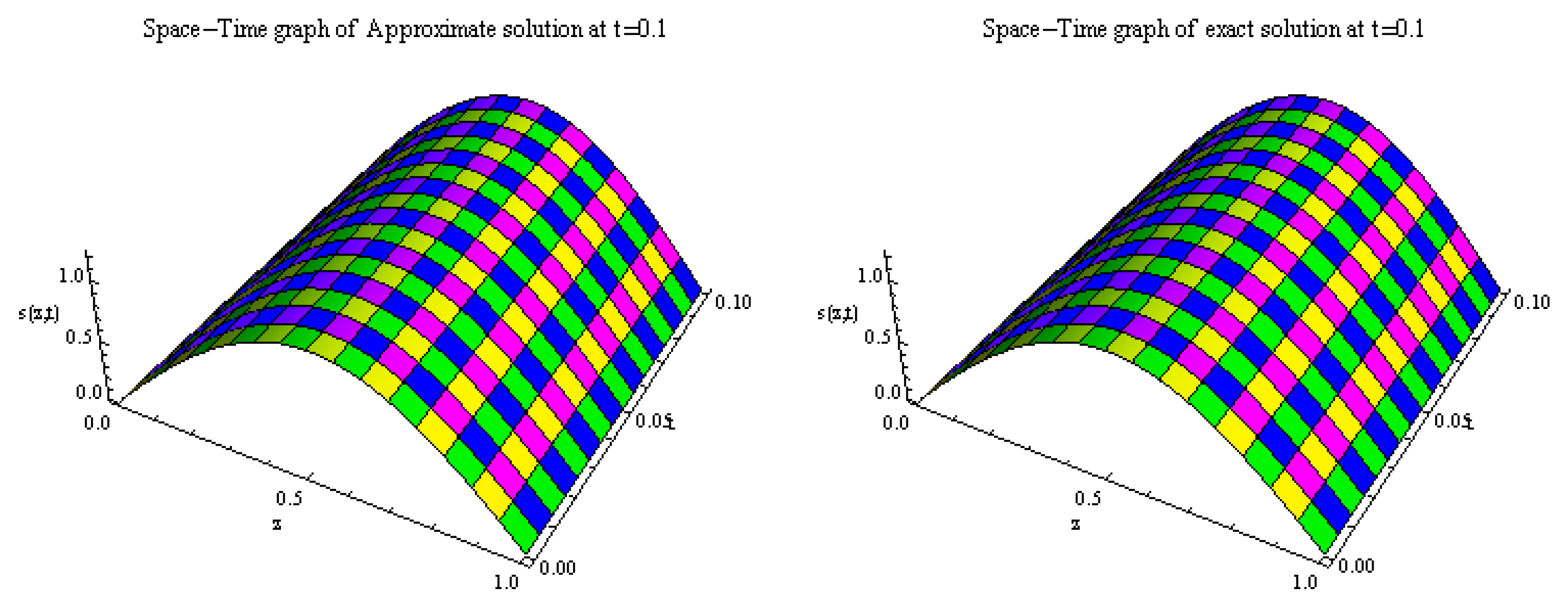
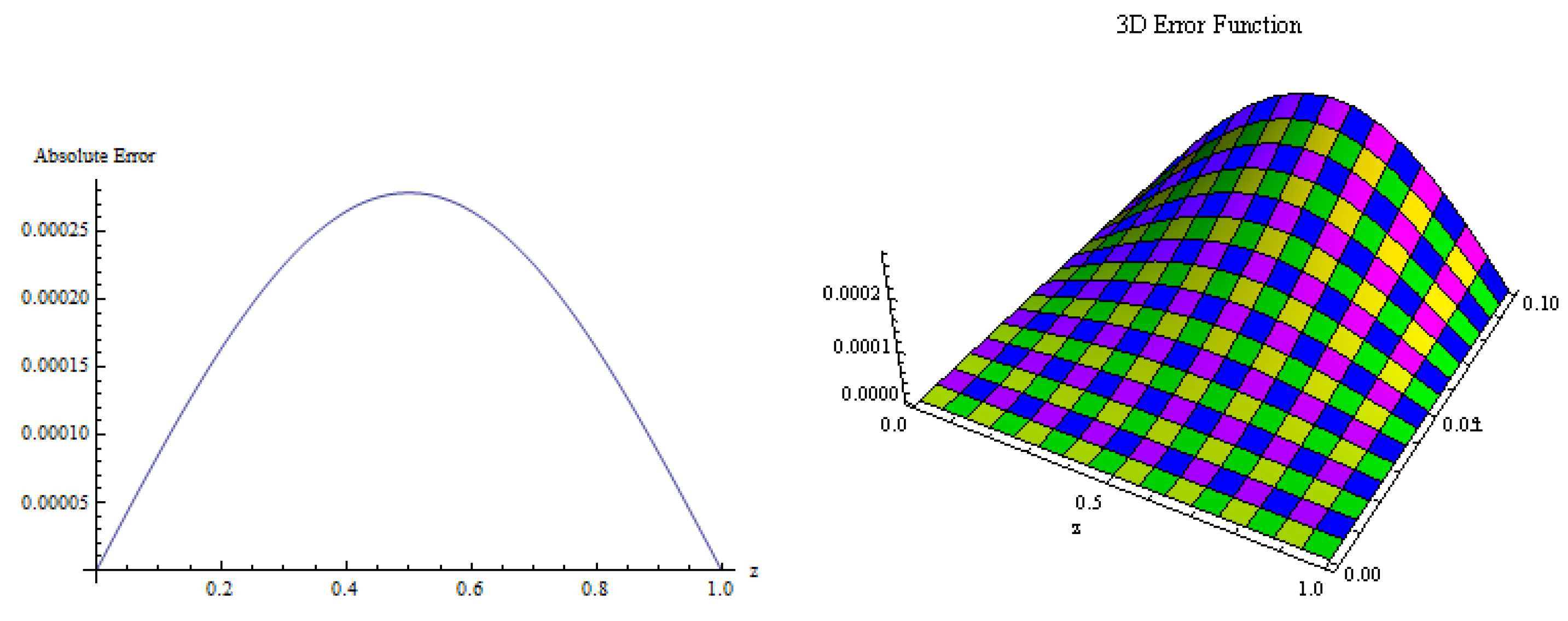
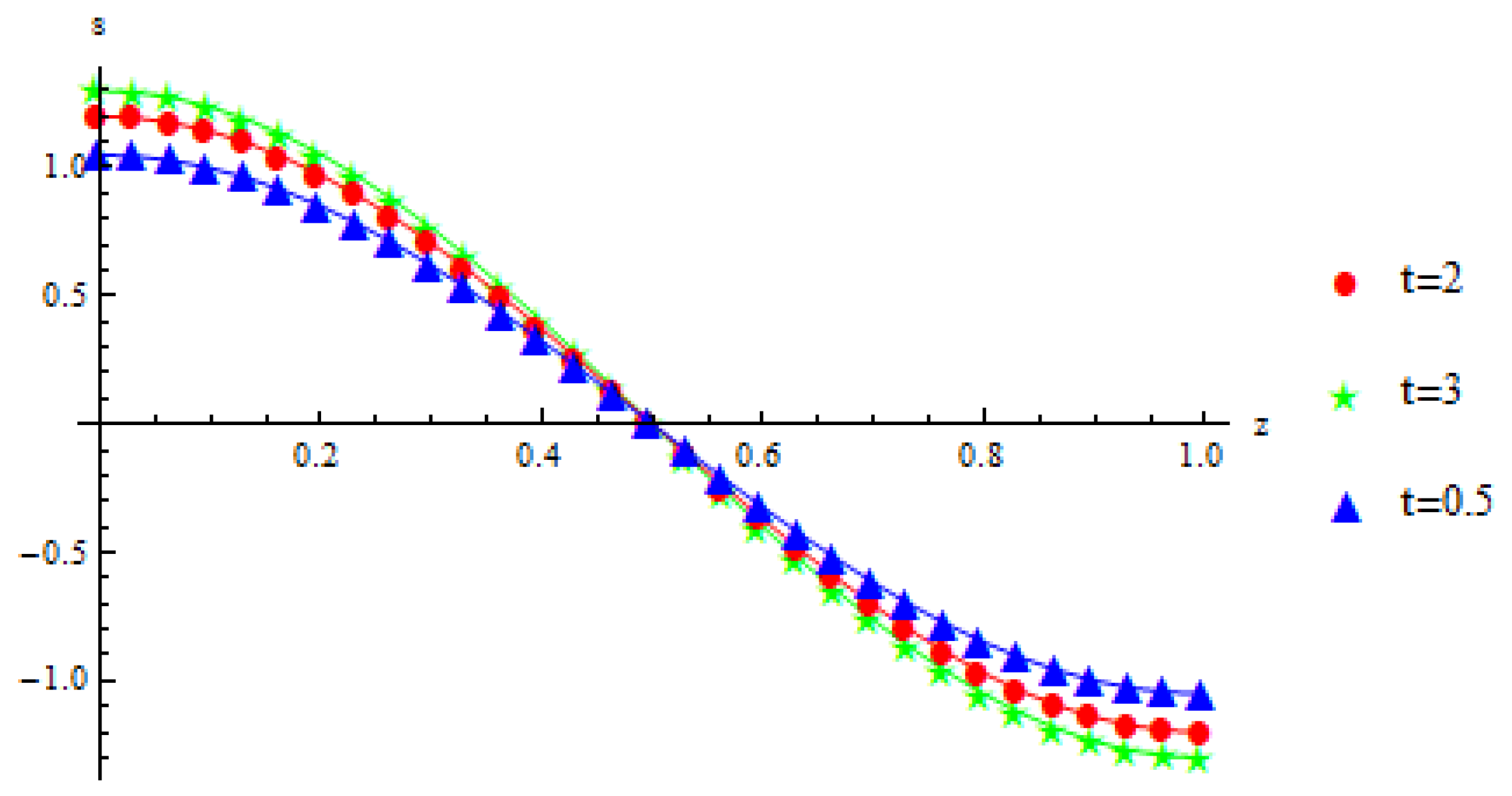
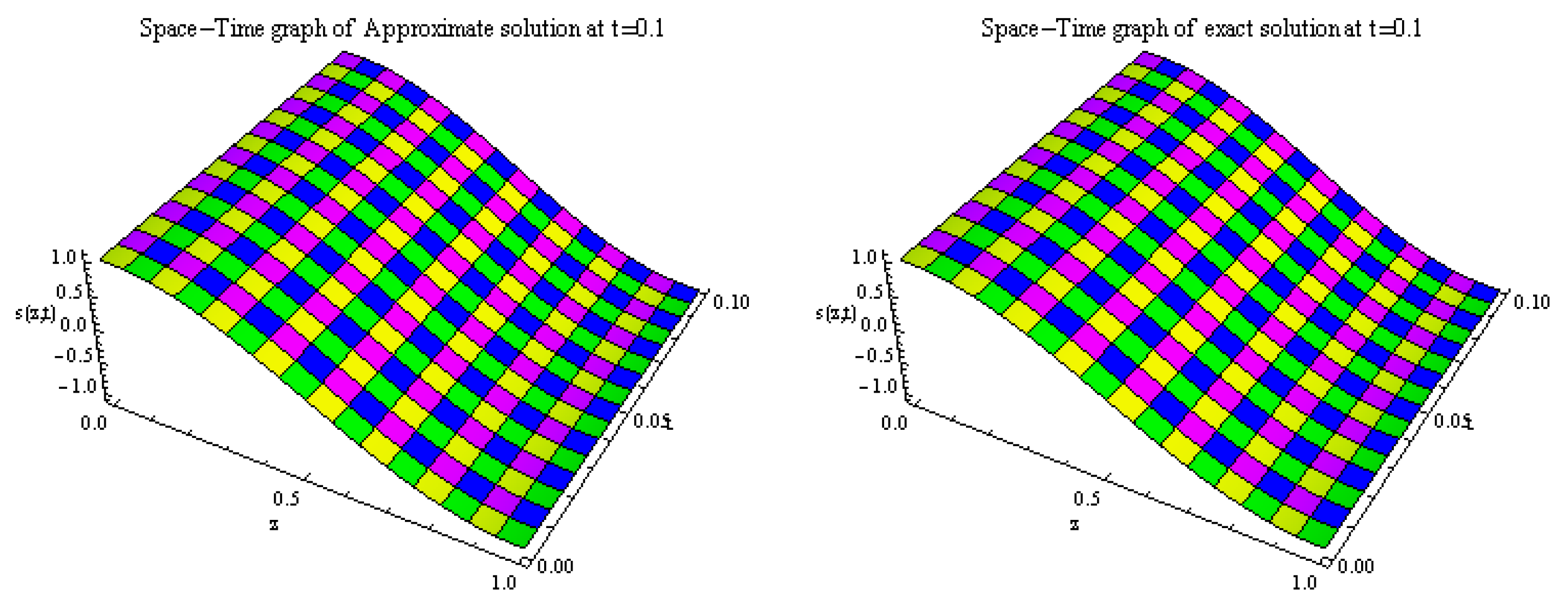
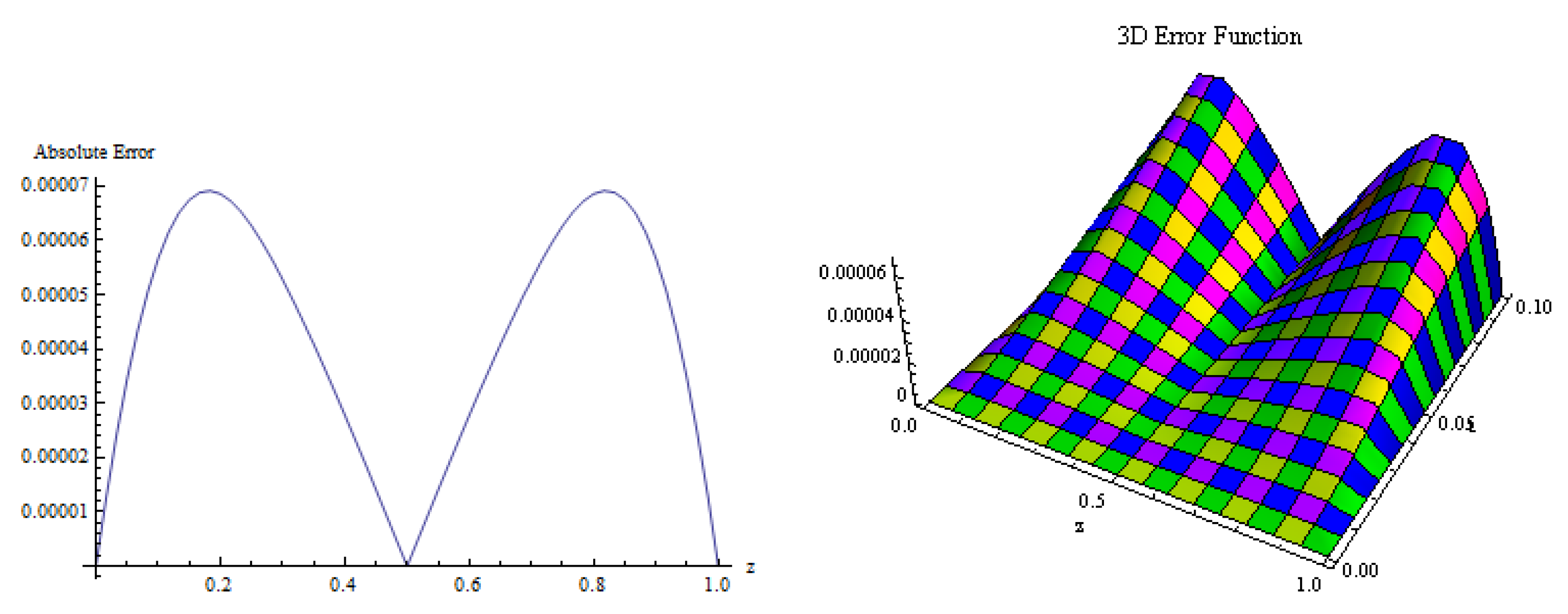
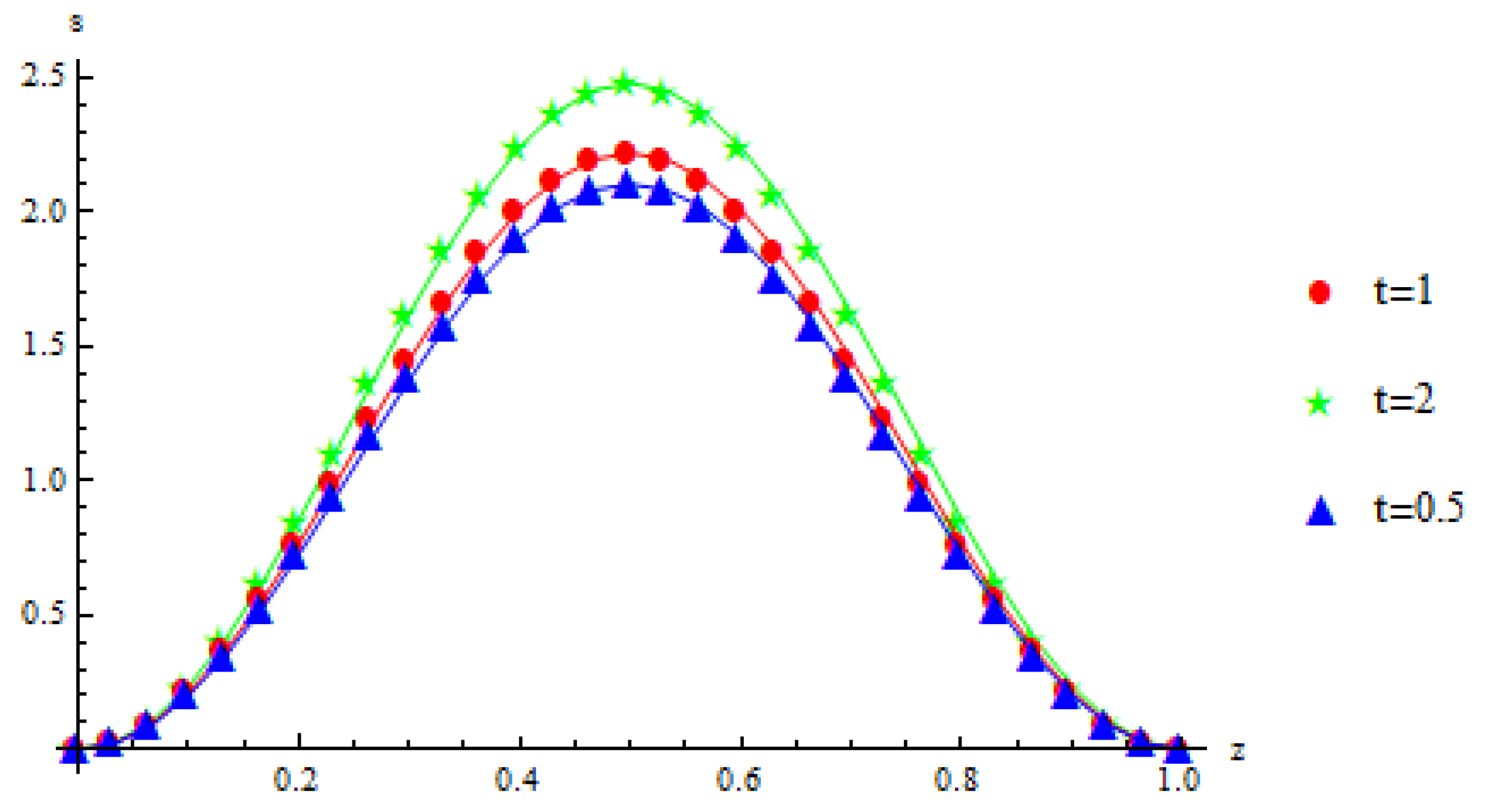
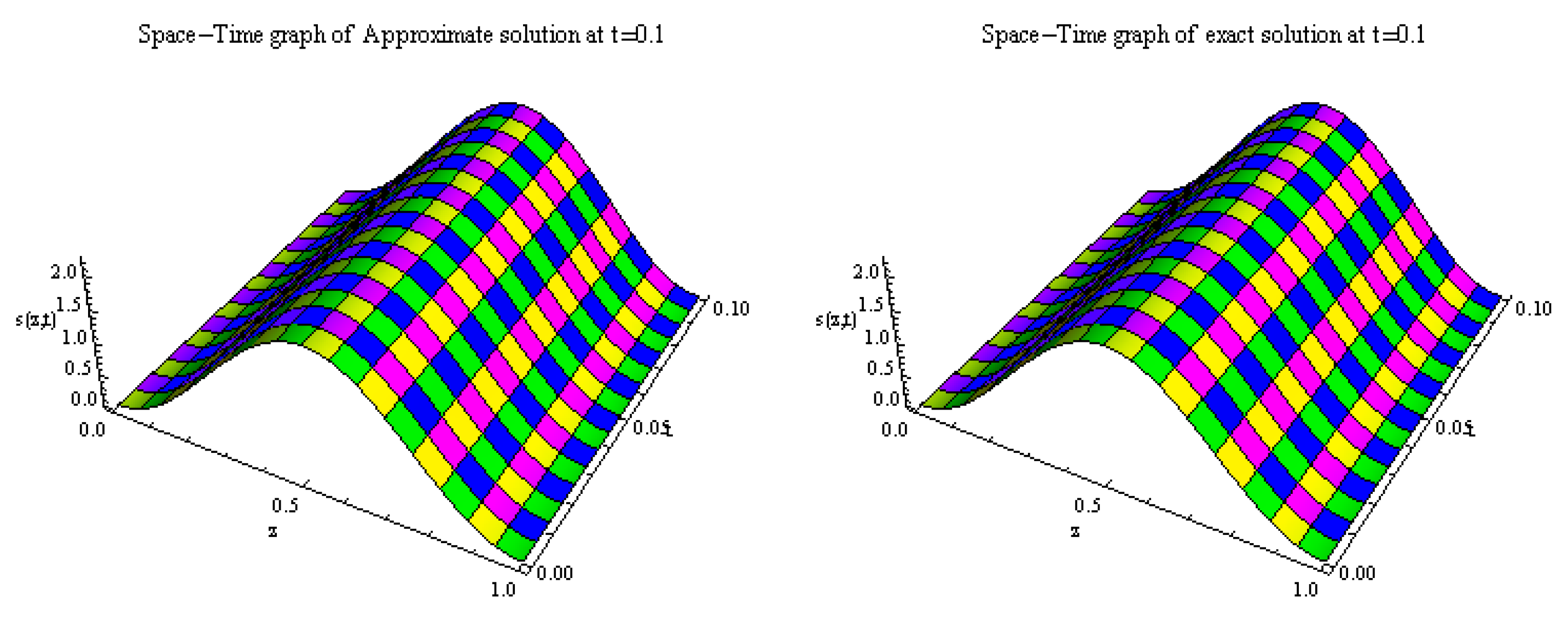
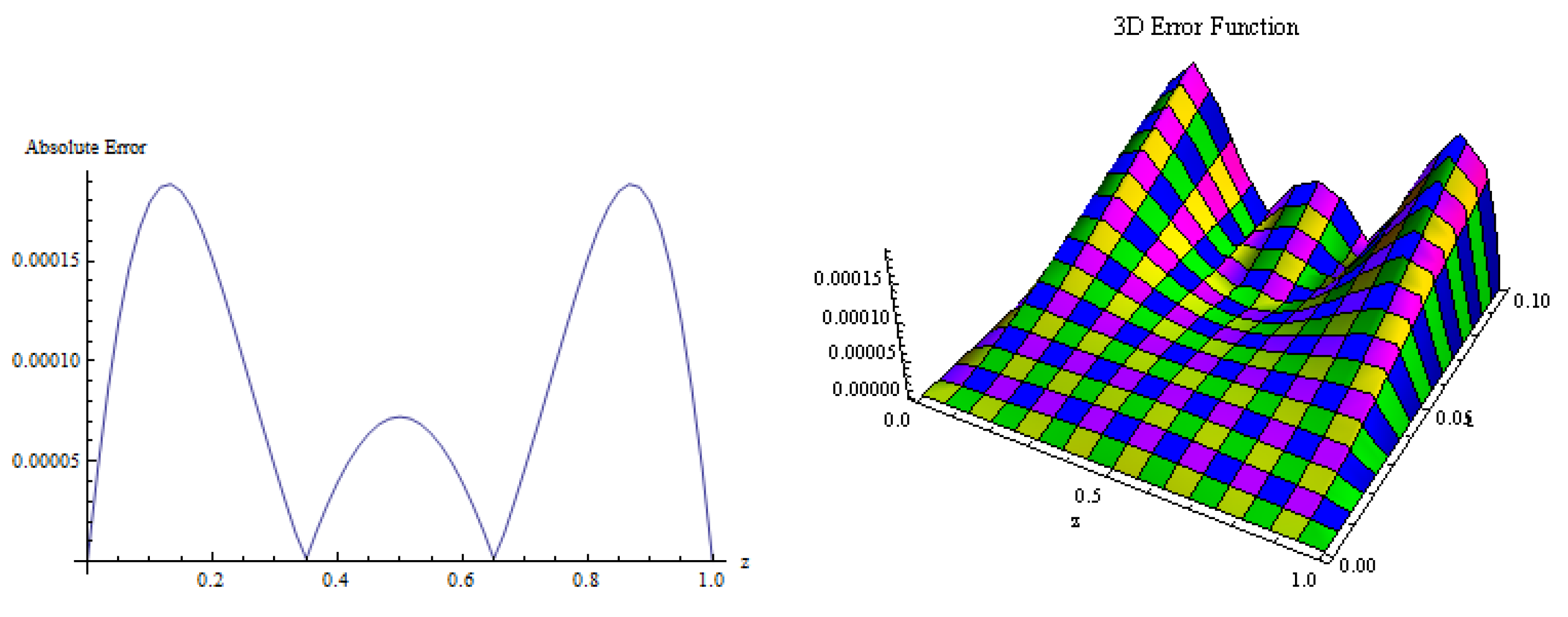
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NECuBS | New extended cubic B-Spline |
| TCuBS | Trigonometric cubic B-Spline |
| CuBS | Cubic B-Spline |
| QBS | Quartic B-Spline |
| QWM | Quasi-Wavelet Method |
References
- Lakshmikantham, V.; Rama, M. Theory of Integro-Differential Equations; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Thiem, H.R. A model for spatio spread of an epidemic. Math. Biol. 1977, 4, 337–351. [Google Scholar] [CrossRef] [PubMed]
- Sloan, I.; Thome, V. Time Discretization of an Integro-Differential Equation of Parabolic Type. SIAM J. Numer. Anal. 1986, 23, 1052–1061. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. A high order finite volume element method for solving elliptic partial integro-differential equations. Appl. Numer. Math. 2013, 65, 105–118. [Google Scholar] [CrossRef]
- Cushing, J.M. Integrodifferential Equations and Delay Models in Population Dynamics; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Dehghan, M.; Salehi, R. The numerical solution of the non-linear integro-differential equations based on the meshless method. J. Comput. Appl. Math. 2012, 236, 2367–2377. [Google Scholar] [CrossRef]
- McLean, W.; Thome, V. Numerical solution of an evolution equation with a positive-type memory term. J. Aust. Math. Soc. Ser. B 1993, 35, 23–70. [Google Scholar] [CrossRef]
- Desch, W.; Grimmer, R.; Schappacher, W. Some considerations for Linear integrodifferential equations. J. Math. Anal. 1984, 104, 219–234. [Google Scholar] [CrossRef]
- Day, J.T. Note on the numerical solution of Integro-Differential equations. J. Comput. 1967, 9, 394–395. [Google Scholar] [CrossRef][Green Version]
- Ebadi, G.; Rahimiardabili, M.; Shahmorad, S. Numerical solution of the nonlinear Volterra integro-differential equations by the tau method. Appl. Math. Comput. 2007, 188, 1580–1586. [Google Scholar]
- Siraj-ul-Islam, A.I.; Fayyaz, M. A new approach for numerical solution of integro-differential equations via Haar wavelets. Int. J. Comput. Math. 2013, 90, 1971–1989. [Google Scholar] [CrossRef]
- Von Petersdorff, T.; Schwab, C. Wavelet discretizations of parabolic integrodifferential equations. SIAM J. Numer. Anal. 2003, 41, 159–180. [Google Scholar] [CrossRef]
- Zalik, R.; Vinogradov, A. The Quasi-Elastic method of solution for a class of integrodifferential equations. J. Integral Equ. Appl. 1993, 5, 277–295. [Google Scholar] [CrossRef]
- Rostami, Y.; Maleknejad, K. Numerical solution of partial Integro-Differential equations by using projection method. Mediterr. J. Math. 2017, 14, 113. [Google Scholar] [CrossRef]
- Long, W.T.; Xu, D.; Zeng, X.Y. Quasi wavelet based numerical method for a class of partial integro-differential equation. Appl. Math. Comput. 2012, 218, 11842–11850. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Riaz, M.B.; Ismail, A.I.; Ali, N.H.M. Development and analysis of new approximation of extended cubic b-spline to the nonlinear time fractional klein–gordon equation. Fractals 2020, 28, 2040039. [Google Scholar] [CrossRef]
- Ali, A.; Ahmad, S.; Shah, S.I.; Haq, F. A Quartic B-spline collocation technique for the solution of partial integro-differential equations with a weakly kernel. Sci. Int. 2015, 27, 2953–2958. [Google Scholar]
- Gholamian, M.; Saberi-Nadjafi, J. Cubic B-splines collocation method for a class of partial integro-differential equation. Alex. Eng. J. 2017, 57, 2157–2165. [Google Scholar] [CrossRef]
- Ali, A.; Khan, K.; Haq, F.; Shah, S.I. A Computational Modeling Based on Trigonometric Cubic B-Spline Functions for the Approximate Solution of a Second Order Partial Integro-Differential Equation. In World Conference on Information Systems and Technologies; Rocha, Á., Adeli, H., Reis, L., Costanzo, S., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 930, pp. 844–854. [Google Scholar]
- de Boor, C. On the convergence of odd degree spline interpolation. J. Approx. Theory 1968, 1, 452–463. [Google Scholar] [CrossRef]
- Hall, C.A. On error bounds for spline interpolation. J. Approx. Theory 1968, 1, 209–218. [Google Scholar] [CrossRef]
- Prenter, P.M. Spline and Variational Methods; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Akram, T.; Abbas, M.; Ismail, A.I.; Ali, N.H.M.; Baleanu, D. Extended cubic B-splines in the numerical solution of time fractional telegraph equation. Adv. Differ. Equ. 2019, 2019, 365. [Google Scholar] [CrossRef]
- Wasim, I.; Abbas, M.; Iqbal, K.I. A new extended B-spline approximation technique for second order singular boundary value problems arising in physiology. J. Math. Comput. Sci. 2019, 19, 258–267. [Google Scholar] [CrossRef]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis, 3rd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]



| Q | NECuBS | TCuBS [20] | CuBS [19] | QBS [18] | QWM [16] | ||
|---|---|---|---|---|---|---|---|
| 50 | 8.40 | 1.13 | 5.96 | 8.93 | 1.24 | 1.18 | 1.58 |
| 150 | 1.48 | 2.02 | 3.09 | 4.42 | 6.34 | 6.75 | 7.89 |
| 250 | 1.93 | 2.62 | 6.65 | 9.45 | 1.36 | 1.40 | 1.61 |
| 350 | 2.29 | 3.11 | 1.10 | 1.56 | 2.25 | 2.51 | 2.53 |
| 450 | 2.59 | 3.53 | 1.60 | 2.28 | 3.28 | 3.70 | 3.46 |
| Q | NECuBS | TCuBS [20] | CuBS [19] | |||
|---|---|---|---|---|---|---|
| 150 | 5.43 | 7.68 | 2.82 | 3.99 | 3.93 | 5.56 |
| 200 | 6.13 | 8.67 | 4.56 | 6.45 | 6.26 | 8.86 |
| 250 | 6.43 | 9.06 | 6.59 | 9.31 | 8.97 | 1.27 |
| 300 | 6.38 | 9.03 | 8.86 | 1.25 | 1.20 | 1.70 |
| 350 | 6.01 | 8.50 | 1.14 | 1.61 | 1.53 | 2.17 |
| 400 | 5.34 | 7.56 | 1.41 | 1.99 | 1.89 | 2.67 |
| Q | NECuBS | TCuBS [20] | CuBS [19] | |||
|---|---|---|---|---|---|---|
| 50 | 4.42 | 1.73 | 2.73 | 4.19 | 3.48 | 5.34 |
| 100 | 1.39 | 1.73 | 8.48 | 1.26 | 1.08 | 1.61 |
| 150 | 2.70 | 1.73 | 1.64 | 2.42 | 2.09 | 3.08 |
| 200 | 4.31 | 6.27 | 2.61 | 3.82 | 3.33 | 4.87 |
| 250 | 6.16 | 9.04 | 3.73 | 5.51 | 4.76 | 7.02 |
| 300 | 8.24 | 1.20 | 4.99 | 7.33 | 6.36 | 9.35 |
| Q | NECuBS | TCuBS [20] | CuBS [19] | |||
|---|---|---|---|---|---|---|
| 50 | 5.58 | 8.51 | 2.29 | 4.26 | 2.46 | 4.53 |
| 100 | 1.06 | 1.50 | 7.89 | 1.24 | 8.44 | 1.32 |
| 150 | 1.52 | 1.97 | 1.61 | 2.50 | 1.72 | 2.67 |
| 200 | 1.97 | 2.29 | 2.66 | 3.94 | 2.84 | 4.19 |
| 250 | 2.43 | 2.53 | 3.90 | 5.74 | 4.17 | 6.12 |
| 300 | 2.89 | 3.43 | 5.33 | 7.76 | 5.69 | 8.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, I.; Yaseen, M.; Khan, S. Addressing Volterra Partial Integro-Differential Equations through an Innovative Extended Cubic B-Spline Collocation Technique. Symmetry 2023, 15, 1851. https://doi.org/10.3390/sym15101851
Ali I, Yaseen M, Khan S. Addressing Volterra Partial Integro-Differential Equations through an Innovative Extended Cubic B-Spline Collocation Technique. Symmetry. 2023; 15(10):1851. https://doi.org/10.3390/sym15101851
Chicago/Turabian StyleAli, Ishtiaq, Muhammad Yaseen, and Sana Khan. 2023. "Addressing Volterra Partial Integro-Differential Equations through an Innovative Extended Cubic B-Spline Collocation Technique" Symmetry 15, no. 10: 1851. https://doi.org/10.3390/sym15101851
APA StyleAli, I., Yaseen, M., & Khan, S. (2023). Addressing Volterra Partial Integro-Differential Equations through an Innovative Extended Cubic B-Spline Collocation Technique. Symmetry, 15(10), 1851. https://doi.org/10.3390/sym15101851







