Abstract
The present analysis deals with the study of the theory of gravity, which was recently considered by many cosmologists. In this theory of gravity, the action is taken as an arbitrary function , where Q is non-metricity and T is the trace of the energy–momentum tensor for matter fluid. In this study, we took two different forms of the function as and , and discussed the physical properties of the models. Also, we obtained the various cosmological parameters for the Friedmann–Lemaître–Robertson–Walker (FLRW) universe by defining the transit form of a scale factor that yielded the Hubble parameter in redshift form, as . We obtained the best-fit values of model parameters using the least squares method for observational constraints on available datasets, like Hubble , Supernova SNe-Ia, etc., by applying the root mean squared error formula (RMSE). For the obtained approximate best-fit values of model parameters, we observed that the deceleration parameter shows a signature-flipping (transition) point within the range of . Thus, it shows the decelerated expansion transiting into the accelerated universe expansion with as in the extreme future.
PACS:
98.80-k; 98.80.JK; 04.50.Kd
1. Introduction
Einstein’s theory of general relativity is considered the most successful theory; however, it has some limitations, such as explaining phenomena like the Big Bang singularity, ring singularity, black hole dynamics, a consistent quantum gauge field theory of gravity, etc. Modern cosmological observational data, such as type Ia supernovae [1,2,3], Wilkinson microwave anisotropy probe (WMAP) [4], and baryon acoustic oscillations (BAOs) [5,6], have confirmed that our universe is accelerating and expanding. This expansion may be driven by some unknown type of energy with negative pressure, referred to as dark energy (DE). The matter in our universe is dominated by dark energy () and dark matter () [7]. The remaining () is occupied by other ordinary matter. The problems with dark energy and dark matter are among the most difficult and unsolved problems in modern cosmology. In recent years, in order to solve these problems, different methods have been proposed by researchers, but they remain mysteries of the universe to this day. Dark energy is described by the equation of state (EoS) parameter , where p and represent the pressure and energy density of dark energy, respectively. The cosmological constant is widely used to discuss the accelerated phenomenon of the universe, which represents energy density associated with vacuum (). However, this simple dark energy model has serious issues with fine-tuning and cosmic coincidence [8,9]. Because of this, different DE models have been proposed, such as quintessence [10,11], K-essence [12,13], phantom field [14,15], the tachyon field [16], quantum field [17,18], as well as interacting dark energy models, like Chaplygin gas [19], holographic models [20,21], etc. To understand why the universe is accelerating, various cosmologists have, from time to time, proposed some well-known modified theories of gravity, like gravity [22], gravity [23], [24,25,26,27,28,29], gravity [30], gravity [31], gravity [32], gravity [33,34,35,36,37,38], and the recently proposed [39,40,41] gravity. Dark energy and dark matter refer to the unseen additives of the universe. Dark matter is an invisible, non-baryonic matter believed to explain phenomena, including gravitational lensing and galactic rotation curves. Dark energy is responsible for the accelerating expansion of the universe [1,42].
Geometric variables in symmetric teleparallel gravity reflect the physical characteristics of the gravitational interaction, which are symbolized by non-metricity Q. Non-metricity Q of the metric tensor is the non-vanishing covariant derivative of the metric tensor, i.e., . Non-metricity geometrically describes a variation of the length of a vector in parallel transport. This strategy was first presented by Nester and Yo [33]. The Lagrangian is viewed as an arbitrary function of the non-metricity in an extension of symmetric teleparallel gravity. By coupling the non-metricity Q with the trace of the energy–momentum tensor T, the theory is further extended to the theory [39].
In the present work, we study various energy conditions in the recently proposed gravity theory. Energy conditions are powerful tools used to investigate the spacetime structure and are widely used in GR to study, e.g., the emergence of Big Rip singularities and black hole dynamics [43]. Also, they provide us with some latitude in our analysis of particular notions about the nature of cosmic geometries and particular relationships that energy–momentum must satisfy under stress in order for energy density to be positive. They are typically used in general relativity to illustrate and investigate spacetime singularities [44]. Using power law in gravity, the authors of ref. [45] studied the energy condition, focusing specifically on the null energy condition for black hole thermodynamics [7], whereas the Hawking–Penrose singularity theorem invokes both the weak and strong energy conditions [46]. Ref. [31] introduced energy conditions within the FLRW universe for two models. The viability of the bounds in was investigated through energy conditions in [47]. In different modified theories of gravity, like and generalized teleparallel theory, energy conditions have been investigated [48,49,50,51].
Motivated by the preceding analysis and discussions, we, in this work, explore two different models in a flat FLRW spacetime with the proposed equation of state (EoS) , and the deceleration parameter (q) where p, , and represent cosmological pressure, energy density, and the EoS parameter; this is conducted alongside the validation of energy conditions.
The organization of the analysis is as follows: The fundamental formalism of the theory of gravity by varying actions is presented in Section 2. The gravitational field equations and the emergent scale factor are shown in Section 3. The empirical constraints that explain the model-free parameters are presented in Section 4. In Section 5, cosmological parameters are discussed. In Section 6, two models of gravity are discussed. We used a function, both linear and quadratic, as and , where , , , and are model parameters. A summary of the concluding remarks is provided in the last Section 7.
2. Basic Formalism in Gravity
The modified Einstein–Hilbert action principle for the -extended symmetric teleparallel gravity is given in [39]
where denotes the general functional form of the non-metricity scalar Q and the trace of the energy–momentum tensor T. g is the determinant of the metric tensor , i.e., , and is Lagrangian matter. The non-metricity scalar Q is defined as
where the deformation tensor is given by
The non-metricity tensor is defined by the following form
and the trace of the non-metricity tensor is obtained as
Further, we define the super potential tensor as follows:
and using this, the non-metricity scalar is
The variation of the energy–momentum tensor with respect to the metric tensor reads as follows:
The energy–momentum tensor is
and
Also, the field equations of gravity are given by varying the action, Equation (1), with respect to the metric tensor ,
where , , and denotes the covariant derivative. From Equation (11), it emerge that the field equations of depend on the tensor . Various cosmological models of gravity, depending on the nature of the source of matter, are possible. Recently, Koussour et al. [52] investigated the quintessence universe and cosmic acceleration in gravity by presuming a specific form of , where , , and are free model parameters. Also, in [53], the authors investigated energy conditions in gravity for two different forms of models.
3. Flat FLRW Universe in Cosmology
In order to find a solution for the field equations in -extended symmetric teleparallel gravity, some straightforward assumptions, such as the selection of a metric, are frequently required. Consequently, we consider the flat FLRW metric,
where is the scale factor of the metric that depends on the cosmic time (where the unit of the cosmic time is Gyr). The energy–momentum tensor of the universe for the perfect fluid is given by
Here, p and denote the pressure and energy density of the universe, respectively. Thus, for tensor , the expression is obtained as . The Einstein field equations using the metric (12) are given as follows:
Here, , , and an overhead dot represents a derivative with respect to cosmic time . In this case, and represent the differentiations of the function with respect to Q and T, respectively, and . With the help of Equations (14) and (15), the EoS parameter is expressed as
Specific Hubble Parameters and Analysis
Now we provide a glimpse of the main features of the scale factor (transit scale factor) and derive a few physical quantities from them to discuss the observed scenario. Hence, for the transit scale factor, Hubble’s parameter [54,55] is observed as follows:
where , , and are the model parameters. Keeping in mind the relation between a and z as , Equation (17) becomes
Here, represents the present Hubble constant, which explains the present expansion rate of the universe. Freedman et al. [56] and Suyu et al. [57] evaluated a value of the present Hubble constant km/s/Mpc and km/s/Mpc, where Plank [58] gives km/s/Mpc.
The model explains the accelerated universe expansion of the present era with the transition from the decelerated expansion era dominated by the dark matter in the past era. It would be interesting to check the deviation of the considered choice (Equation (17)) from the model. The universe approaches as with the transition from the decelerated phase at . The choice (Equation (17)) may also yield this kind of transitional behavior, and for , it may reproduce the effects of the model in the limit . The best-fit values of the model parameters and obtained from different observational datasets may reveal the exact nature of , compared to the model.
Using the time–redshift differential relation, , the first and second derivatives of H are obtained as
We observe and compare our investigated model with the recent observations by finding the best-fit values and the best-fit curve of the Hubble function toward the model parameters , , and , with the recent observational datasets. Hence, here, we use the most favorable Hubble and Supernovae SNe-Ia to constrain the said model parameter in the following section.
4. Observational Constraints
The accelerated expansion can be explained by a cosmological constant; alternative explanations, such as dynamical dark energy or modified gravity, can be investigated by looking at how they affect the history of the universe’s late-time expansion or the development of its structures. In order to identify constant parameters, we use the Hubble and Supernova Ia datasets in this research.
4.1. Hubble Dataset
The Hubble parameter is also related to the differential redshift, as , where is obtained from the spectroscopic surveys, and so a measurement of provides the Hubble parameter, which will be independent of the model. In fact, two methods are generally used to measure the Hubble parameter values at a certain redshift, and are extracted from , from the line-of-sight baryonic acoustic oscillation (BAO) datasets and differential age (DA) method [59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79], estimating . We notice the observational constraints on parameters , and using the latest 54 data points of in the redshift range , where 28 points are obtained using the DA method, and 26 points are obtained using BAO. The values are presented in Table 1.

Table 1.
Best-fit values of the model parameters , , and for both datasets.
We found the best-fit curve of with 54 data values shown in Table 2, using :

Table 2.
A total of 54 points of data: 28 (DA) + 26 (BAO + other).
determines the proportion of variance in the dependent variable that can be explained by the independent variable. An indicates an exact fit and pertains to the values of model parameters , , and , with respect to the OHD (observatory Hubble dataset). To find the best-fit values of , , and , we restrict the parametric spaces and . We use error bars to represent the mean point and its deviation from the mean across 54 points of the Hubble dataset and graphically compare our model with the model (with ) for km/s/Mpc, , and , where and are the density parameters of dark matter and dark energy, as shown in Figure 1 We obtain the best-fit plot for approximate values of , and , with a maximum of and an RMSE of 11.071. Therefore, km/s/Mpc deviating by from an exact fit. Figure 3 shows the (dark blue-shaded) and (sky blue-shaded) maximum likelihood contours in the -, - and - planes for the Hubble dataset.
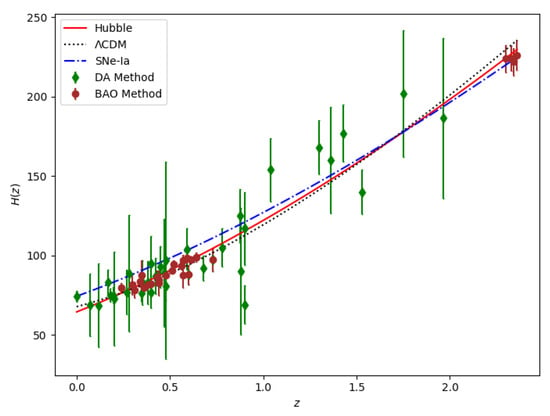
Figure 1.
The best-fit plot of the Hubble parameter versus redshift for the Hubble dataset (red); the black dotted line and blue dash-dot line show plots for the model and SNe-Ia dataset. Dots denote the Hubble datasets with the error bars.
4.2. Supernovae SNe-Ia
The distance modulus = is given by
where M is constant for all SNe-Ia. To obtain the best-fit curve, we have to consider the data frame with 580 observed entries of apparent magnitude from the Union 2.1 compilation [80], where . The [80] statistically significant value of M is −19.30.
We use error bars for 580 points from the SNe-Ia datasets and compare our model with the well-accepted model for km/s/Mpc, and as shown in Figure 2. We obtain the best-fit plot for approximate values of , , and , with a maximum and an RMSE of 0.2662. Therefore, km/s/Mpc, deviating by from an exact fit. Figure 3 shows the (dark green-shaded) and (light green-shaded) maximum likelihood contours in the -, -, and - planes for the SNe-Ia Datasets.
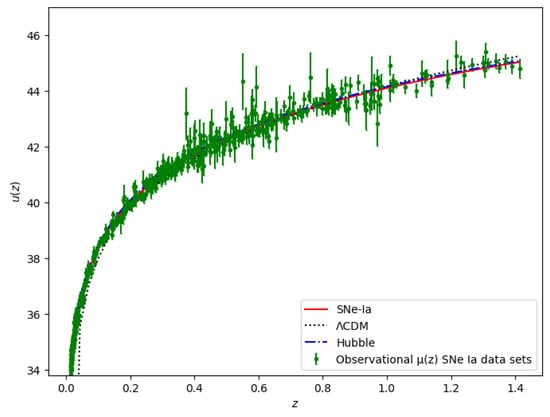
Figure 2.
The best-fit plot for luminosity distance versus redshift for SNe-Ia datasets (red); the black dotted line and blue dash-dot line show plots for the model and the Hubble dataset. Dots denote the SNe datasets with error bars.
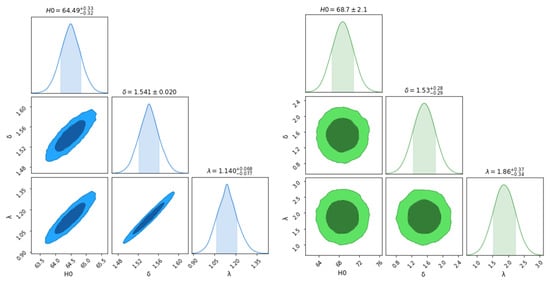
Figure 3.
The and maximum likelihood contour plots for the parameters using Hubble (left) and SNe-Ia (right) datasets.
5. Cosmic Parameters and Energy Conditions
In order to discuss how the universe has evolved in various phases, we need to discuss the behaviors of some cosmological parameters, like the deceleration parameter, statefinder parameter, etc.; these are defined as follows:
The deceleration parameter is
Here, denotes the decelerating phase of the universe, denotes the accelerating phase, represents the transition point where the universe shifts from the deceleration phase to the acceleration phase.
The statefinder parameters.
The statefinder is a novel cosmological diagnostic pair that was introduced by Sahni et al. [81]. The statefinder is a geometrical diagnostic that enables the model-independent characterization of dark energy features. It is defined as [81,82]:
The flat model is at the point where the statefinder parameters have the corresponding values. Additionally, the plane, a positive parameter s (i.e., ) with , denotes a quintessence-like model of dark energy, whereas a negative parameter s (i.e., ) with denotes a Chaplygin gas-like model of dark energy. Furthermore, by traversing the point , one can figure out different types of dark energy models.
Energy conditions
One can derive highly potent and broad theorems regarding the behaviors of massive gravitational fields and cosmic geometries using the energy conditions (ECs) of general relativity (GR). Generally speaking, ECs can be divided into
- Strong energy condition (SEC): One inequality of SEC, formulated as , asserts that gravity should always be attractive. Another component of SEC is .
- Dominant energy condition (DEC): When an observer measures, the matter–energy density will be positive and will propagate causally, which leads to , . DEC implies that the flow of sound energy will not exceed the speed of light.
- Weak energy condition (WEC): The matter–energy density measured by any time-like observer should be positive, . WEC implies that the energy density should not be negative
- Null energy condition (NEC): For a perfect fluid energy–momentum tensor, NEC is given by .
The violation of the NEC in energy conditions implies the invalidity of the given energy criteria. The current fast expansion of the universe has raised questions about the SEC. In cosmological situations during the inflationary expansion and at the present, SEC must be broken.
From Equations (18) and (19), the deceleration parameter and statefinder parameters are obtained as follows:
After the analysis of SNe-Ia data by numerous researchers, it was observed that datasets favor current acceleration for and past deceleration for . A while back, the high-z supernova search (HZSNS) team reported at the (1) confidence level [83], which was further refined to at (1 ) [83]. According to SNLS [84], as also compiled in [55], the transition redshift ≡ 0.6 (1) is in better agreement with the flat model . Another limit is (2, joint analysis) [41]. Furthermore, the transition from deceleration to acceleration (i.e., ) for our derived model is for the Hubble dataset and for supernovae, which are in agreement with the SNe-Ia supernovae observations, including the furthest-known supernova SNI997ff at [85,86]. We see that the variation of q with z in our model is compatible with the results. In our derived model, using the best-fit values of , the deceleration parameters (at ) for Hubble and Supernova are −0.2792 and −0.4774, respectively. They are compatible with [87,88]. Figure 4 shows a plot of the deceleration parameters versus redshift for both Hubble and Supernovae datasets, where the values of model parameters and are from Table 1.
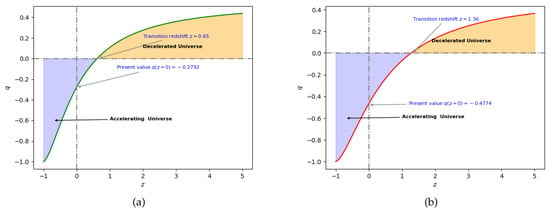
Figure 4.
Behavior of the deceleration parameter (left plot (a) for Hubble and the right plot (b) for SNe-Ia), with redshift for the best-fit values of and provided in Table 1.
In this study, the argument was made that the plane is useful for distinguishing between various models. An analysis based on has proven useful in differentiating between general relativity and modified theories of gravity. We note that for the Hubble datasets, the r and s parameters at the present epoch (i.e., z = 0) are and , while for the SNe-Ia datasets, they are and , as shown in Figure 5 for the best-fit values of from Table 1. Currently, observations are not sensitive enough to measure these parameters. However, these parameters can be deduced from future observations, which would greatly help to constrain the nature of dark energy.
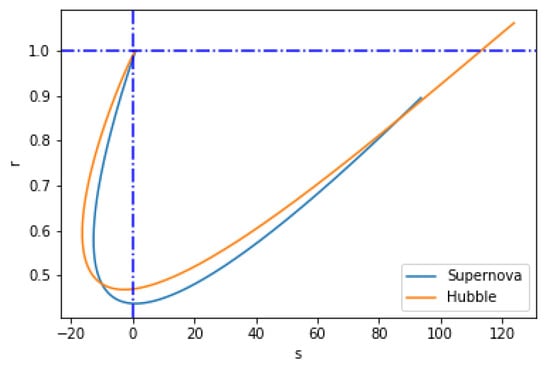
Figure 5.
Behavior of the universe in the plane for the best-fit values of and provided in Table 1.
6. Models of Gravity
In this section, we discuss some physical aspects of different models of gravity.
6.1. Model-I
Here, we consider the gravity model as
where and are arbitrary constant model parameters. For the above model, field Equations (14)–(16) take the form
Figure 6 shows the pressure versus redshift plots for both Hubble and SNe-Ia datasets. Parameters , , and are from Table 1, while model parameters = −0.0125 and = −0.012 are arbitrarily chosen, respectively.
The EoS parameter is associated with energy density and pressure p. The EoS parameter is positive in the early universe. As time evolves, it moves from the positive region into the negative region. The negative is proposed as a constant vacuum energy density. It is worth noting that shows pressureless cold matter (PCL), represents hot matter, is radiation, is the hard universe, shows stiff fluid (SF), is the Ekpyrotic matter (Ek-M), denotes the quintessence region, and denotes the phantom region, respectively; represents the cosmological constant-like fluid and is precluded by the SNe-Ia perceptions. Subsequently, the evolving range of our derived model is supportive of the ) model in both Hubble and supernova data.
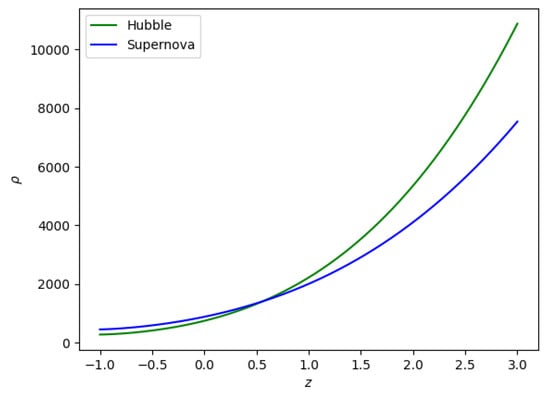
Figure 6.
Behavior of the (redshift–density) plane for the constant values , , and provided in Table 1.
From Figure 7, we can observe that the universe exits the decelerated regime and enters the accelerating phase, as studied in [89].
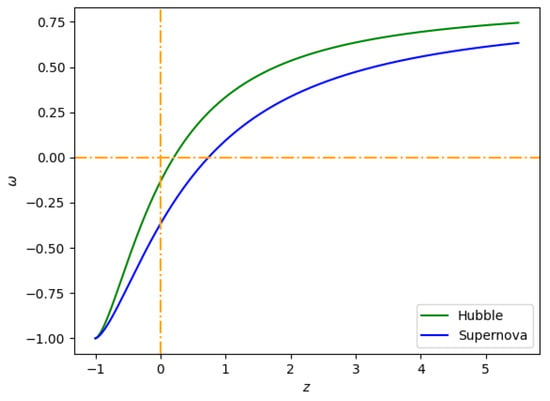
Figure 7.
Behavior of the (redshift–EoS) plane for the constant values of , , and , provided in Table 1.
Furthermore, to verify the genuineness of the model in the context of cosmic acceleration; we resolve different forms of energy conditions by calculating
and
for NEC, DEC, and SEC, respectively. Figure 8 and Figure 9 are plots of energy conditions with respect to the constants obtained from the best-fit values for the Hubble and SNe-Ia datasets, as shown in Table 1, and model parameters = −0.0125 and = −0.012, where the y-axis has a combination of pressure and density. According to the accelerating universe data, the SEC must be violated on a cosmological scale [90,91]. Also, the EoS parameter () with values of indicates that . Therefore, there is a violation of the SEC in the present era. In Figure 8 and Figure 9, we can see that both the NEC and DEC are adhered to for both Hubble and SNe-Ia datasets. The behavior of energy density is depicted in Figure 6. We examine the NEC behavior (i.e., a partial condition of WEC). Therefore, the concurrent validation of NEC and energy density results in the validation of WEC.
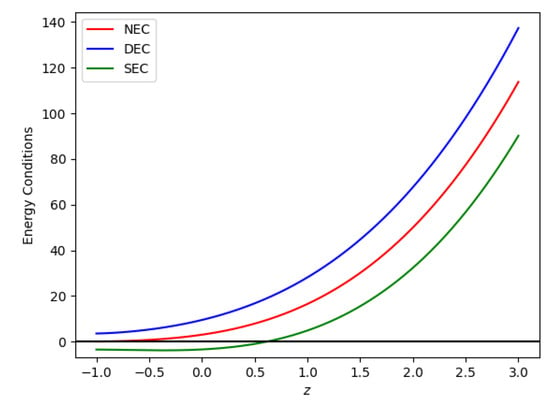
Figure 8.
Behavior of the (redshift–energy condition) plane for the Hubble dataset for = −0.0125, and = −0.012.
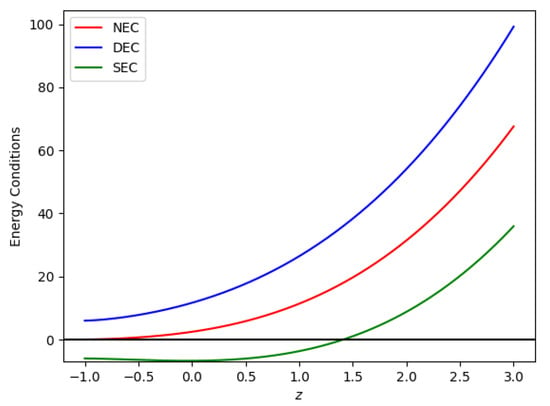
Figure 9.
Behavior of the (redshift–energy condition) plane for SNe-Ia datasets for = −0.0125, and = −0.012.
6.2. Model-II
Here, we consider the gravity model as
where and are arbitrary constant model parameters. For the above model’s field Equations (14)–(16), we take the form
Figure 10 shows the plot of density versus redshift for both Hubble and SNe-Ia datasets, with , , and taken from Table 1, while model parameters = −0.0125 and are −0.012, respectively.
As shown in Figure 11, the universe is in an accelerating mode and is about to enter a decelerating phase. Additionally, we resolve various energy conditions by calculating the model’s accuracy in the context of cosmic acceleration.
and
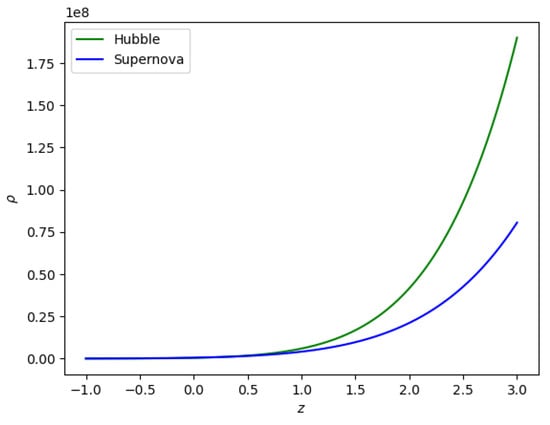
Figure 10.
Behavior of the (redshift–density) plane for the constant values of , , and , provided in Table 1.
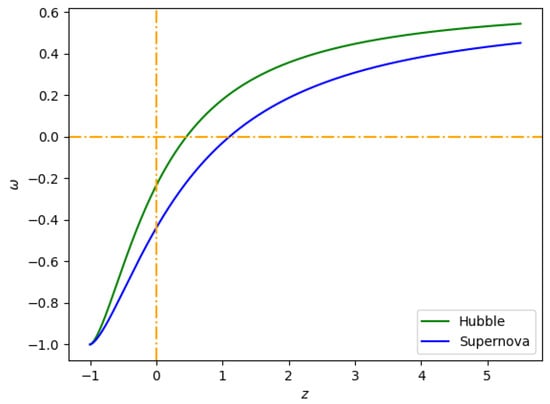
Figure 11.
Behavior of the (redshift–EoS) plane for the constant values of , , and provided in Table 1.
Figure 12 and Figure 13 show plots of energy conditions with respect to constants obtained from the best-fit values of the Hubble and SNe-Ia datasets, as shown in Table 1, and model parameters = −0.0125 and = −0.012. According to the accelerating universe data, as shown in Figure 12 and Figure 13, the SEC must be violated on a cosmological scale [55,56]. Figure 12 and Figure 13 indicate that the NEC and DEC are upheld for both Hubble and SNe-Ia datasets. We examined the NEC behavior (i.e., a partial condition of WEC). Therefore, the concurrent validation of NEC and energy density results in the validation of WEC.
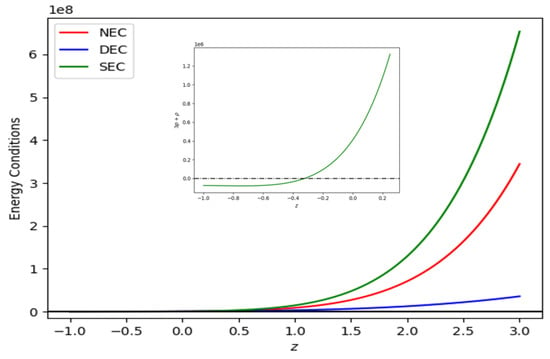
Figure 12.
Behavior of the (redshift–energy condition) plane for the Hubble dataset for = −0.0125 and = −0.012.
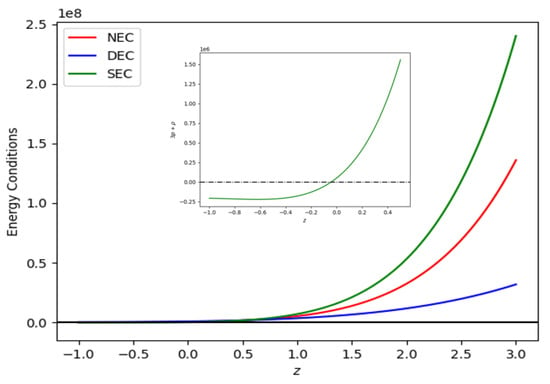
Figure 13.
Behavior of the (redshift–energy condition) plane for SNe-Ia dataset for = −0.0125 and = −0.012.
7. Conclusions
In the present work, we took a function that is both linear and quadratic, expressed as follows:
where , , , and are model parameters. In terms of redshift z, we measured several cosmological parameters in the FLRW universe, including the Hubble parameter H and the deceleration parameter q. By applying the formula for observational constraints on the model, we were able to determine the approximate best-fit values of the model parameters , utilizing datasets like the Hubble dataset and union 2.1 compilation of SNe-Ia datasets. The following are the characteristics of our cosmological model:
- The best-fit plots based on the observational datasets are presented in Figure 1 and Figure 2. We used a hybrid model of the least squares method and gradient descent for the best fit. The values for the Hubble and SNe-Ia datasets are and , respectively. SNe-Ia has 580 observations, providing the superior fit amongst the two datasets.
- The derived Hubble function is constrained by observational datasets i.e., Hubble and SNe-Ia datasets, and the present values of the Hubble constant are km/s/Mpc and km/s/Mpc, respectively, which are compatible with [56,57,58].
- The transition from early deceleration to the universe’s present acceleration is shown by the deceleration parameter and , with respect to Hubble and SNe-Ia datasets, which are compatible with [87,88].
- We considered two functional forms of gravity in Section 6.1 and Section 6.2 to observe the behaviors of energy density and the EoS parameter. In the considered models, the EoS parameter traces its journey from the matter-dominated, decelerating phase during early times to the dark energy-dominated, accelerating phase in later times. The energy density remains positive in both models, subjected to the values of model parameters.
- In both functional forms of of Section 6.1 and Section 6.2, NEC, WEC, and DEC are satisfied, whereas SEC is violated (see Figure 8, Figure 9, Figure 12 and Figure 13).
- The cosmological redshift () provides insight into the evolution of the early universe and denotes the present universe. From the cosmological redshift (), one may predict the future universe evolution. For the expanding universe, the relationship between the scale factor and cosmological redshift is . For the present universe, (by convention of the observational cosmology) [92], which will yield . For the past universe evolution, , which will yield . The future evolution of the universe may be portrayed by with (in the extreme future). For a detailed compilation of the cosmological scale issues, one may refer to Ref. [93]. In this sense, the present models are decelerating in the past and will approach the phase in the extreme future.
Author Contributions
Conceptualization, A.P.K.; writing—review and editing, A.P.K., S.H.S. and A.P.; programming, Y.S.S. and A.P.; investigation, Y.S.S.; writing-original draft, S.H.S. and A.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No advanced data are associated with this article.
Acknowledgments
The authors (H. S. Shekh and A. Pradhan) thank the IUCAA, Pune, India, for providing the facility under the associateship programs. The authors are grateful to the anonymous reviewers and editors for their valuable questions and comments, which contributed to the quality of the manuscript.
Conflicts of Interest
The authors declare that they have no personal relationships or competing financial interests that could have influenced the work reported in this paper.
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astrophys. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Tegmark, M.; Strauss, M.A.; Blanton, M.R.; Abazajian, K.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.H.; Zehavi, I.; Bahcall, N.A.; et al. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004, 69, 103501. [Google Scholar] [CrossRef]
- Bennett, C.L.; Bay, M.; Halpern, M.; Hinshaw, G.; Jackson, C.; Jarosik, N.; Kogut, A.; Limon, M.; Meyer, S.S.; Page, L.; et al. The microwave anisotropy probe* mission. Astrophys. J. 2003, 148, 1. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the baryon acoustic peak in the large-scale correlation function of SDSS luminous red galaxies. Astrophys. J. 2005, 633, 560. [Google Scholar] [CrossRef]
- Percival, W.J.; Reid, B.A.; Eisenstein, D.J.; Bahcall, N.A.; Budavari, T.; Frieman, J.A.; Fukugita, M.; Gunn, J.E.; Ivezic, Z.; Knapp, G.R.; et al. Baryon acoustic oscillations in the Sloan Digital Sky Survey Data Release 7 galaxy sample. Mon. Not. R. Astron. Soc. 2010, 401, 2148–2168. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XII. Diffuse component separation. Astron. Astrophys. 2014, 571, A12. [Google Scholar]
- Del Campo, S.; Herrera, R.; Pavon, D. Interacting models may be key to solve the cosmic coincidence problem. J. Cosmol. Astropart. Phys. 2009, 2009, 20. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Wetterich, C. Cosmology and the fate of dilatation symmetry. Nucl. Phys. B 1988, 302, 668. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A. The case for a positive cosmological Λ-term. Int. J. Mod. Phys. D 2000, 9, 373. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Quantum de Sitter cosmology and phantom matter. Phys. Lett. B 2003, 562, 147. [Google Scholar] [CrossRef]
- Padmanabhan, T.; Chaudhury, T.R. Can the clustered dark matter and the smooth dark energy arise from the same scalar field? Phys. Rev. D 2002, 66, 081301. [Google Scholar] [CrossRef]
- Anisimov, A.; Babichev, E.; Vikman, A.J. B-inflation. Cosmol. Astropart. Phys. 2005, 6, 6. [Google Scholar] [CrossRef]
- Feng, B.; Wang, X.L.; Zhang, X.M. Dark energy constraints from the cosmic age and supernova. Phys. Lett. B 2005, 607, 35. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Moschella, M.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265. [Google Scholar] [CrossRef]
- Hu, B.; Ling, Y. Interacting dark energy, holographic principle, and coincidence problem. Phys. Rev. D 2006, 73, 123510. [Google Scholar] [CrossRef]
- Kim, H.; Lee, H.W.; Myung, S.S. Equation of state for an interacting holographic dark energy model. Phys. Lett. B 2006, 632, 605. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Sasaki, M. Gauss-Bonnet dark energy. Phys. Rev. D 2005, 71, 123509. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Not. R. Astron. Soc. 1970, 150, 1–8. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.; Nojiri, S.I.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Tangphati, T.; Panotopoulos, G.; Banerjee, A.; Pradhan, A. Charged compact stars with colour-flavour-locked strange quark matter in f(R,T) gravity. Chin. J. Phys. 2023, 82, 62–74. [Google Scholar] [CrossRef]
- Pradhan, A.; Goswami, G.K.; Beesham, A. The reconstruction of constant Jerk parameter with f(R,T) gravity. J. High Energy Astrophys. 2023, 38, 12–21. [Google Scholar] [CrossRef]
- Pradhan, A.; Goswami, G.K.; Beesham, A. The reconstruction of constant Jerk parameter with f(R,T) gravity in Bianchi-I spacetime. Eur. Phys. J. Plus 2023, 138, 451. [Google Scholar] [CrossRef]
- Pradhan, A.; Goswami, G.K.; Beesham, A. Reconstruction of an observationally constrained f(R,T) gravity model. Int. J. Geom. Methods Mod. Phys. 2023, 20, 2350169. [Google Scholar] [CrossRef]
- Zubair, M.; Zeeshan, M.; Hasan, S.S.; Oikonomou, V.K. Impact of collisional matter on the late-time dynamics of f(R,T) gravity. Symmetry 2018, 10, 463. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rep. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef]
- Sharif, M.; Ikram, A. Energy conditions in f(G,T) gravity. Eur. Phys. J. C 2016, 76, 640. [Google Scholar] [CrossRef]
- Ayuso, I.; Jimenez, J.B.; Cruz-Dombriz, A. Consistency of universally nonminimally coupled f(R,T,RμνTμν) theories. Phys. Rev. D 2013, 91, 104003. [Google Scholar] [CrossRef]
- Nester, J.M.; Yo, H.J. Symmetric teleparallel general relativity. Chin. J. Phys. 1999, 37, 113. [Google Scholar]
- Pradhan, A.; Maurya, D.C.; Dixit, A. Dark energy nature of viscous Universe in f(Q)-gravity with observational constraints. Int. J. Geom. Method Mod. Phys. 2021, 18, 2150124. [Google Scholar] [CrossRef]
- Banerjee, A.; Pradhan, A.; Tangphati, T.; Rahaman, F. Wormhole geometry in f(Q) gravity and the energy conditions. Eur. Phys. J. C 2021, 81, 10131. [Google Scholar] [CrossRef]
- Dixit, A.; Maurya, D.C.; Pradhan, A. Phantom dark energy nature of bulk-viscosity universe in modified f(Q)-gravity. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250198. [Google Scholar] [CrossRef]
- Pradhan, A.; Dixit, A.; Maurya, D.C. Quintessence behaviour of an anisotropic bulk viscous cosmological model in modified f(Q)-gravity. Symmetry 2022, 14, 2630. [Google Scholar] [CrossRef]
- Shekh, S.H.; Bouali, A.; Mustafa, G.; Pradhan, A. Observational constraints in accelerated emergent f(Q) gravity model. Class. Quantum Grav. 2023, 40, 0555011. [Google Scholar] [CrossRef]
- Xu, Y.; Li, G.; Harko, T.; Liang, S. f(Q,T) gravity. Eur. Phys. J. C 2019, 79, 708. [Google Scholar] [CrossRef]
- Pradhan, A.; Dixit, A. The model of the transit cosmology along with observational constrictions in f(Q,T) gravity. Int. J. Geom. Method Mod. Phys. 2021, 18, 2150159. [Google Scholar] [CrossRef]
- Shekh, S.H.; Bouali, A.; Pradhan, A.; Beesham, A. New emergent observational constraints in f(Q,T) gravity model. J. High Energy Astrophys. 2023, 39, 53–59. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.; Casertano, S.; Lampeitl, H.; Ferguson, H.C.; Filippenko, A.V.; Jha, S.W.; Li, W.; Chornock, R. A 3% solution: Determination of the Hubble constant with the Hubble Space Telescope and Wide Field Camera 3. Astrophys. J. 2011, 730, 119. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Capozziello, S.; Nojiri, S.; Odinstov, S.D. The role of energy conditions in f(R) cosmology. Phys. Lett. B 2018, 781, 99. [Google Scholar] [CrossRef]
- Visser, M. Energy conditions in the epoch of galaxy formation. Science 1997, 276, 88–90. [Google Scholar] [CrossRef]
- Yousaf, Z.; Sharif, M.; Ilyas, M.; Zaeem-ul-Haq Bhatti, M. Energy conditions in higher derivative f(R,R,T) gravity. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850146. [Google Scholar] [CrossRef]
- Santos, J.; Alcaniz, J.S.; Reboucas, M.J.; Carvalho, F.C. Energy conditions in f(R) gravity. Phys. Rev. D 2007, 76, 083513. [Google Scholar] [CrossRef]
- Atazadeh, K.; Khaleghi, A.; Sepangi, H.R.; Tavakoli, Y. Energy conditions in f(R) gravity and Brans–Dicke theories. Int. J. Mod. Phys. D 2009, 18, 1101–1111. [Google Scholar] [CrossRef]
- Garcia, N.M.; Harko, T.; Lobo, F.S.N.; Mimoso, J.P. Energy conditions in modified Gauss-Bonnet gravity. Phys. Rev. D 2011, 83, 104032. [Google Scholar] [CrossRef]
- Liu, D.; Reboucas, M.J. Energy conditions bounds on f(T) gravity. Phys. Rev. D 2012, 86, 083515. [Google Scholar] [CrossRef]
- Koussour, M.; Myrzakulov, N.; Shekh, S.H.; Bennai, M. Quintessence universe and cosmic acceleration in f(Q,T) gravity. Int. J. Mod. Phys. D 2022, 31, 2250115. [Google Scholar] [CrossRef]
- Arora, S.; Sahoo, P.K. Energy conditions in f(Q,T) gravity. Phys. Scr. 2020, 5, 095003. [Google Scholar] [CrossRef]
- Shekh, S.; Myrzakulov, N.; Pradhan, A. Mussatayeva, Observational constraints on f(T,TG) gravity with Hubble’s parametrization. Symmetry 2023, 15, 321. [Google Scholar] [CrossRef]
- Davis, T.M.; Mrtsell, E.; Sollerman, J.; Becker, A.C.; Blondin, S.; Challis, P.; Clocchiatti, A.; Filippenko, A.V.; Foley, R.J.; Garnavich, P.M.; et al. Scrutinizing exotic cosmological models using ESSENCE supernova data combined with other cosmological probes. Astrophys. J. 2007, 666, 716. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Gibson, B.K.; Ferrarese, L.; Kelson, D.D.; Sakai, S.; Mould, J.R.; Kennicutt, R.C., Jr.; Ford, H.C.; Graham, J.A.; et al. Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant 2001. Astrophys. J. 2001, 553, 47. [Google Scholar] [CrossRef]
- Suyu, S.H.; Marshall, P.J.; Auger, M.W.; Hilbert, S.; Blandford, R.D.; Koopmans, L.V.E.; Fassnacht, C.D.; Treu, T. Dissecting the Gravitational lens B1608+656. II. Precision Measurements of the Hubble Constant, Spatial Curvature, and the Dark Energy Equation of State. Astrophys. J. 2010, 711, 201. [Google Scholar] [CrossRef]
- Ade, P.A.; Barreiro Vilas, R.B.; Curto Martin, A.; Diego Rodriguez, J.M.; Gonzalez-Nuevo Gonzalez, J.; Herranz Munoz, D.; Lopez-Caniego Alcarria, M.; Martinez Gonzalez, E.; Toffolatti, L.; Vielva Martinez, P. Planck 2013 results. XVI. Cosmological parameters. A&A 2014, 571, A16. [Google Scholar]
- Stephen, A.; Linder, E.V. The simplest non-minimal matter-geometry coupling in the f(R,T) cosmology. Phys. Rev. D 2013, 87, 023532. [Google Scholar]
- Simon, T.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Adak, D.; Bandyopadhyay, A.; Majumdar, D. Reconstructing the equation of state and density parameter for dark energy from combined analysis of recent SNe Ia, OHD and BAO data. arXiv 2011, arXiv:1102.4726. [Google Scholar]
- Amendolaand, L.; Tsujikawa, S. Dark Energy: Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Aurich, R.; Steiner, F. Dark energy in a hyperbolic universe. Mon. Not. R. Astron. Soc. 2002, 334, 735. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the Universe up to z=1.1 from the spectroscopic evolution of cosmic chronometers. J. Cosmol. Astropart. Phys. 2012, 8, 6. [Google Scholar] [CrossRef]
- Allen, S.W.; Rapetti, D.A.; Schmidt, R.W.; Ebeling, H.; Morris, R.G.; Fabian, A.C. Improved constraints on dark energy from Chandra X-ray observations of the largest relaxed galaxy clusters. Mon. Not. R. Astron. Soc. 2008, 383, 879. [Google Scholar] [CrossRef]
- Arabsalmani, M.; Sahni, V.; Saini, T.D. Reconstructing the properties of dark energy using standard sirens. Phys. Rev. D 2013, 87, 083001. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z∼2. Mon. Not. R. Astron. Soc. 2015, 450, L16–L20. [Google Scholar] [CrossRef]
- Gaztañaga, E.; Cabre, A.; Hui, L. Clustering of luminous red galaxies-IV. Baryon acoustic peak in the line-of-sight direction and a direct measurement of H(z). Mon. Not. R. Astron. Soc. 2009, 399, 1663. [Google Scholar]
- Oka, A.; Saito, S.; Nishimichi, T.; Taruya, A.; Yamamoto, K. Simultaneous constraints on the growth of structure and cosmic expansion from the multipole power spectra of the SDSS DR7 LRG sample. Mon. Not. R. Astron. Soc. 2014, 439, 2515. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, G.B.; Chuang, C.H.; Ross, A.J.; Percival, W.J.; Gil-Marin, H.; Cuesta, A.J.; Kitaura, F.S.; Rodriguez-Torres, S.; Brownstein, J.R.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Tomographic BAO analysis of DR12 combined sample in configuration space. Mon. Not. R. Astron. Soc. 2017, 469, 3762. [Google Scholar] [CrossRef]
- Chang, C.H.; Prada, F.; Pellejero-Ibanez, M.; Beutter, F.; Cuesta, A.J.; Eisenstein, D.J.; Escoffier, S.; Ho, S.; Kitaura, F.S.; Kneib, J.P.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Single-probe measurements from CMASS anisotropic galaxy clustering. Mon. Not. R. Astron. Soc. 2016, 61, 3781. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ Dark Energy Survey: Joint measurements of the expansion and growth history at z < 1. Mon. Not. R. Astron. Soc. 2012, 425, 405. [Google Scholar]
- Chuang, C.H.; Prada, F.; Cuesta, A.J.; Eisenstein, D.J.; Kazin, E.; Padmanabhan, N.; Sanchez, A.G.; Xu, X.; Beutler, F.; Manera, M.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Single-probe measurements and the strong power f(z)σ8(z). Mon. Not. R. Astron. Soc. 2013, 433, 3559. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc. 2014, 441, 24. [Google Scholar] [CrossRef]
- Busca, N.G. Baryon acoustic oscillations in the Lyα forest of BOSS quasars. Astron. Astrophys. 2013, 552, A96. [Google Scholar] [CrossRef]
- Bautista, J.E.; Guy, J.; Rich, J.; Blomqvist, M.; Des Bourboux, H.D.M.; Pieri, M.M.; Font-Ribera, A.; Bailey, S.; Delubac, T.; Kirkby, D.; et al. Measurement of baryon acoustic oscillation correlations at z = 2.3 with SDSS DR12 Lyα-Forests. Astron. Astrophys. 2017, 603, A12. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Slosar, A.; Lee, K.G.; Pieri, M.M.; Hamilton, J.C.; et al. Baryon acoustic oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef]
- Font-Ribera, A.; Kirkby, D.; Busca, N.; Miralda-Escude, J.; Ross, N.P.; Slosar, A.; Rich, J.; Aubourg, E.; Bailey, S.; Bhardwaj, V.; et al. Quasar-Lymanα forest cross-correlation from BOSS DR11: Baryon Acoustic Oscillations. J. Cosmol. Astropart. Phys. 2014, 2014, 027. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey. V. Improving the Dark-energy Constraints above z ≥ 1 and Building an Early-type-hosted Supernova Sample 2012. Astrophys. J. 2012, 85, 746. [Google Scholar]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder—A new geometrical diagnostic of dark energy. J. Exper. Theor. Phys. Lett. 2003, 77, 201. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, S.; Saini, T.D.; Starobinsky, A.A. Exploring the expanding Universe and dark energy using the statefinder diagnostic. Mon. Not. Royal Astron. Soc. 2003, 344, 1057. [Google Scholar] [CrossRef]
- Riess, A.G.; Nugent, P.E.; Gilliland, R.L.; Schmidt, B.P.; Tonry, J.; Dickinson, M.; Thompson, R.I.; Budavari, T.; Casertano, S.; Evans, A.S.; et al. The farthest known supernova: Support for an accelerating universe and a glimpse of the epoch of deceleration. Astrophys. J. 2001, 560, 49. [Google Scholar] [CrossRef]
- Amara, A.; Refregier, A. Optimal surveys for weak-lensing tomography. Mon. Not. R. Astron. Soc. 2007, 381, 1018–1026. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Jesus, J.F.; Santos, R.C.; Gill, M.S.S. Is the transition redshift a new cosmological number? arXiv 2012, arXiv:1205.4688v3. [Google Scholar]
- Amendola, L. Acceleration at z > 1? Mon. Not. R. Astron. Soc. 2003, 342, 221. [Google Scholar] [CrossRef]
- Kumar, S. Observational constraints on Hubble constant and deceleration parameter in power-law cosmology. Mon. Not. R. Astron. Soc. 2021, 422, 2532. [Google Scholar] [CrossRef]
- del Campo, S.; Duran, I.; Herrera, R.; Pavon, D. Three thermodynamically-based parametrizations of the deceleration parameter. Phys. Rev. D 2012, 86, 083509. [Google Scholar] [CrossRef]
- Capozziello, S.; Ruchika, A.; Sen, A. Model-independent constraints on dark energy evolution from low-redshift observations. Mon. Not. R. Astron. Soc. 2019, 484, 4484. [Google Scholar] [CrossRef]
- Barcelo, C.; Visser, M. Twilight for the energy conditions? Int. J. Mod. Phys. D 2002, 11, 1553. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Sahoo, P.K. The simplest non-minimal matter?geometry coupling in the f(R, T) cosmology. Eur. Phys. J. C 2017, 77, 480. [Google Scholar] [CrossRef]
- Narlikar, J.V. Introduction to Cosmology, 3rd ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Singh, A. Homogeneous and anisotropic cosmologies with affine EoS: A dynamical system perspective. Eur. Phys. J. C 2023, 83, 696. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).