Deformation of Sandy Ground Induced by Tunneling of Super-Large-Diameter Shield—Influence of Buried Depth of Tunnel and Relative Density of Sand
Abstract
1. Introduction
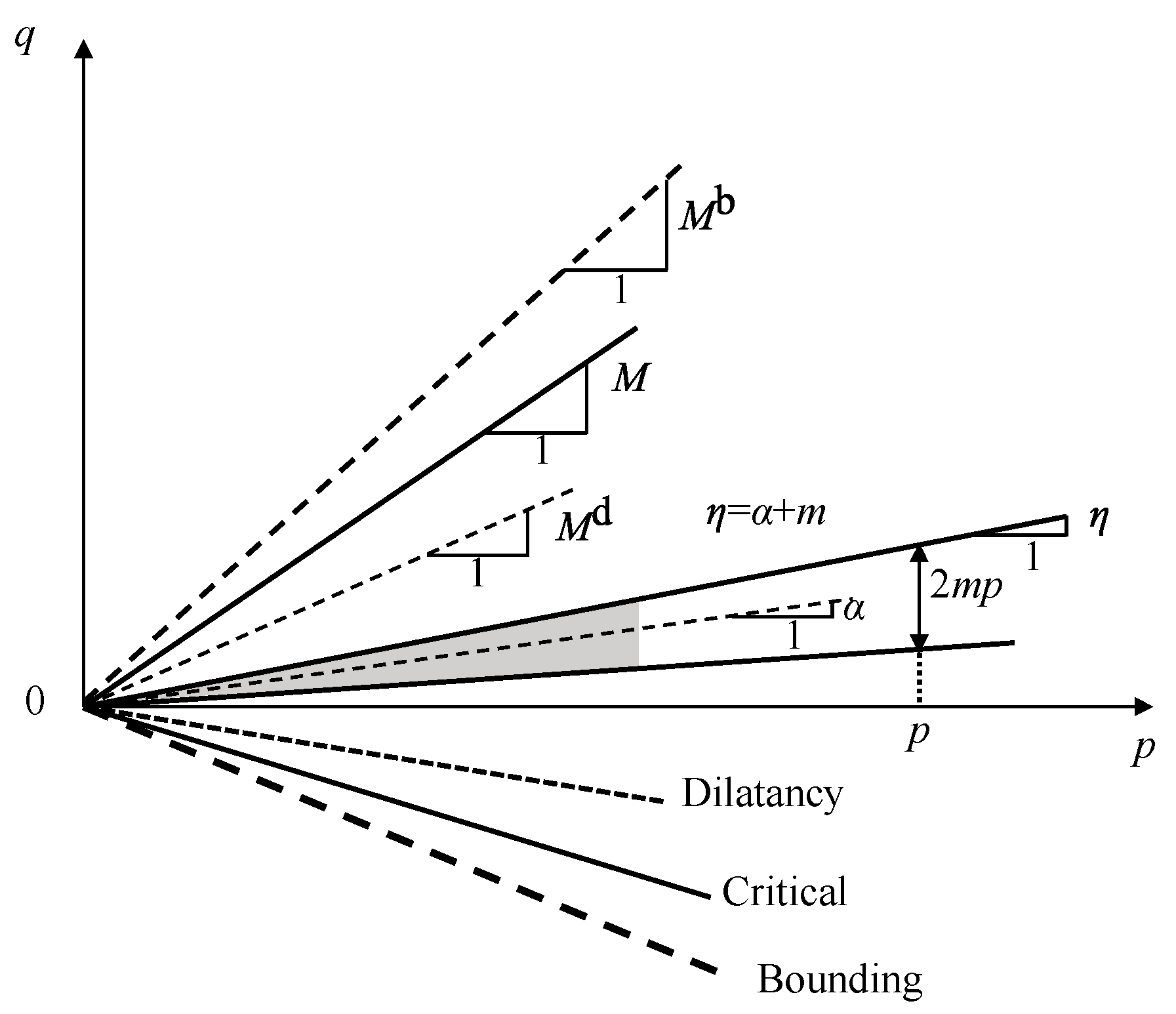
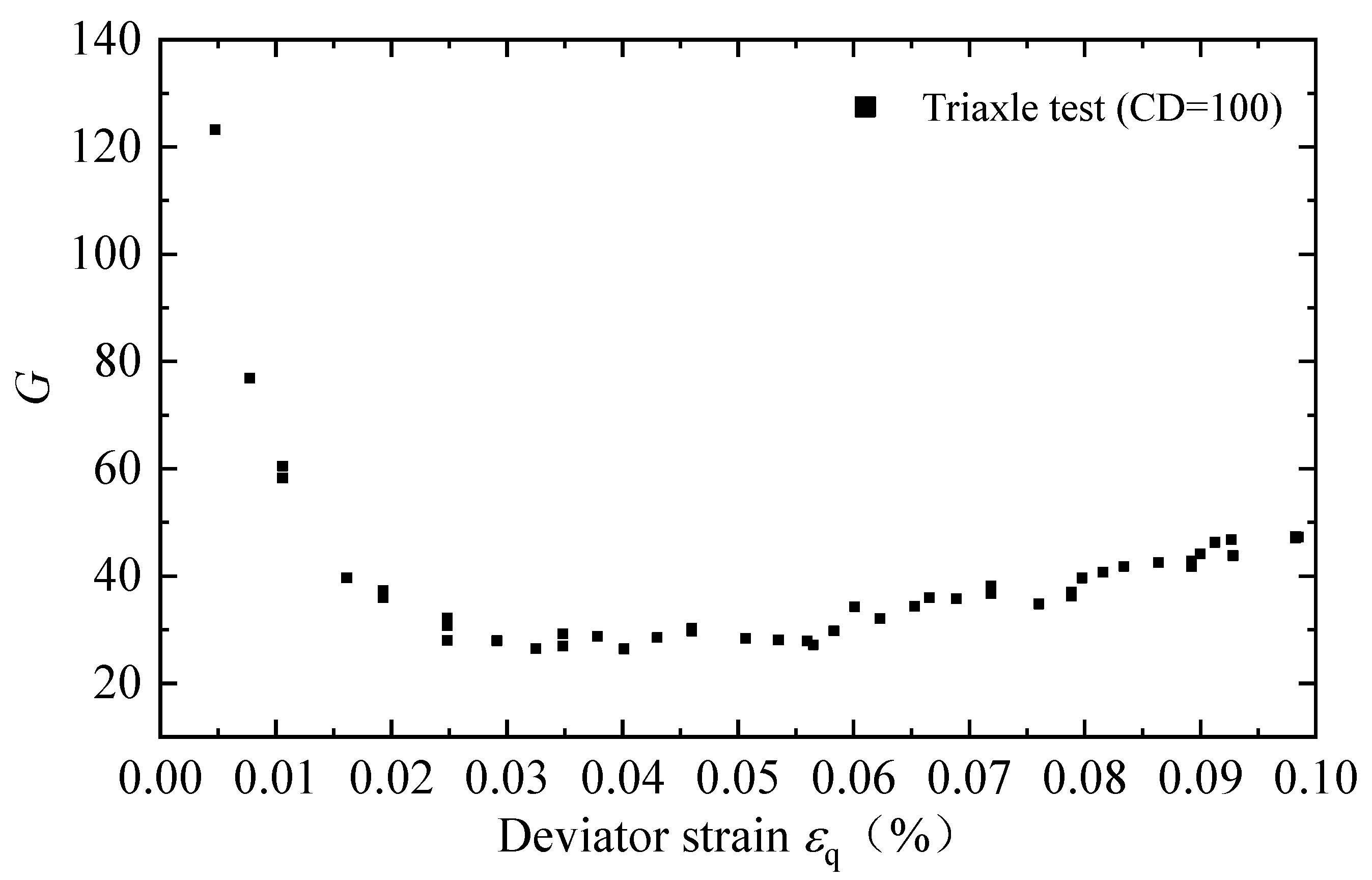
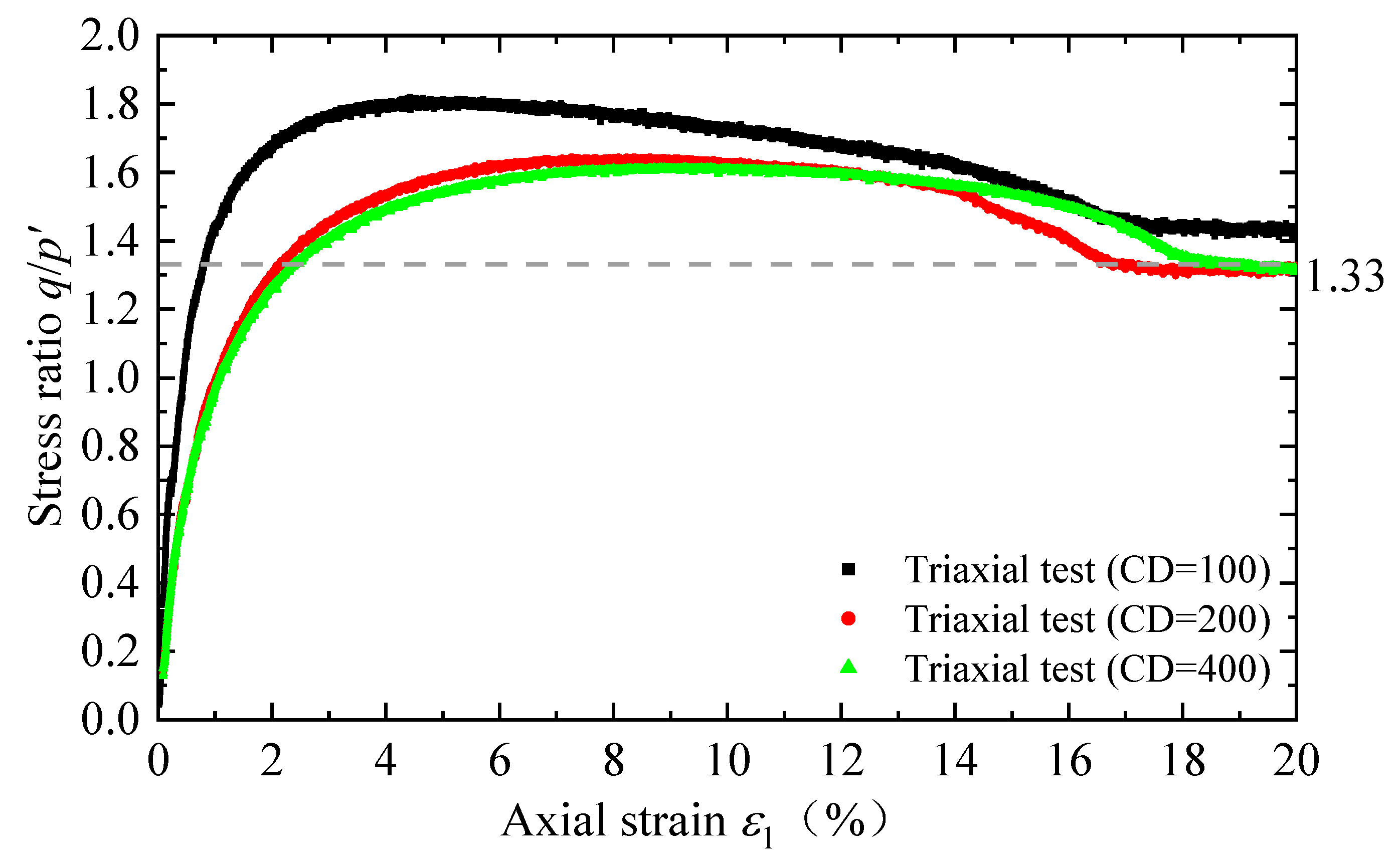
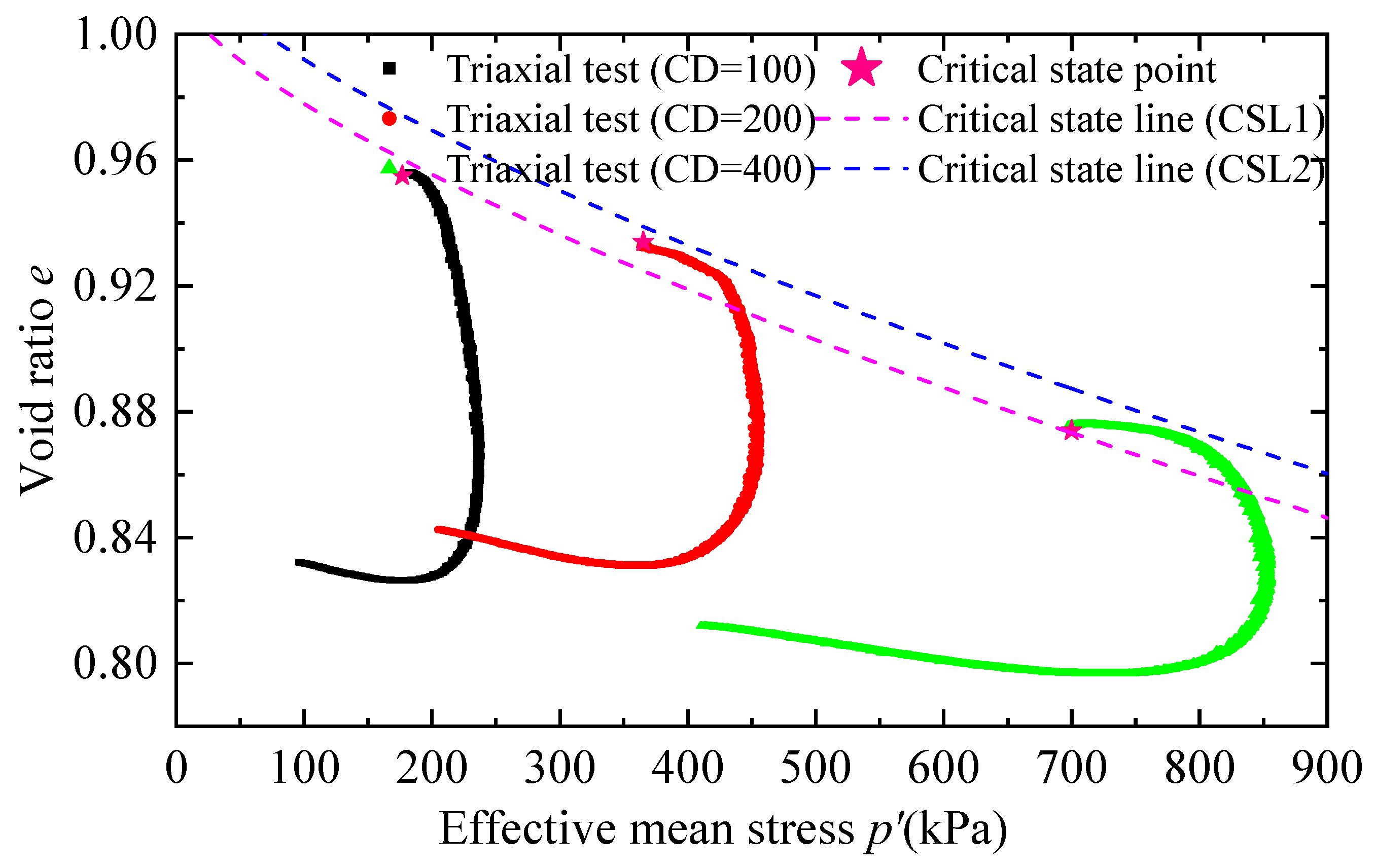
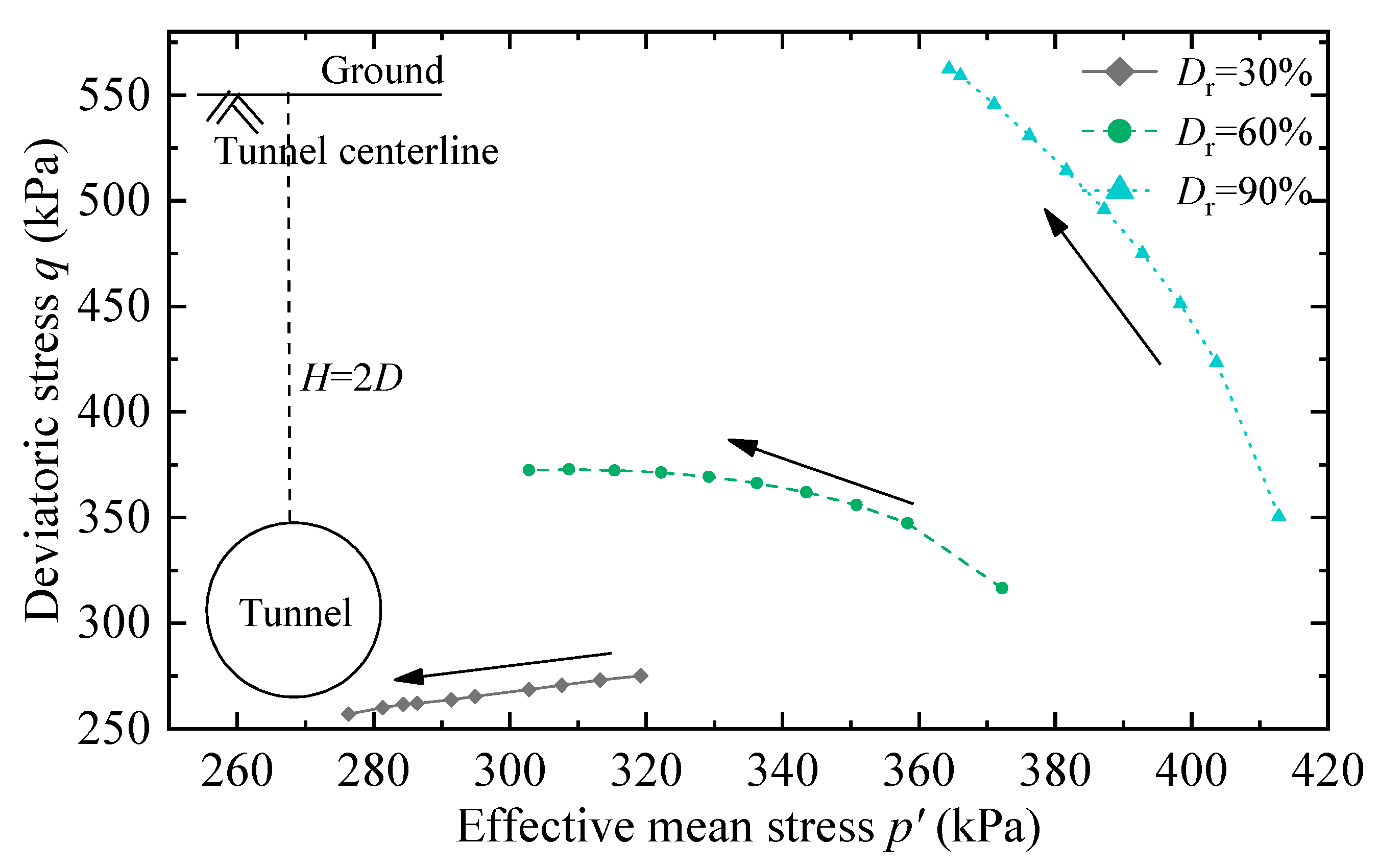
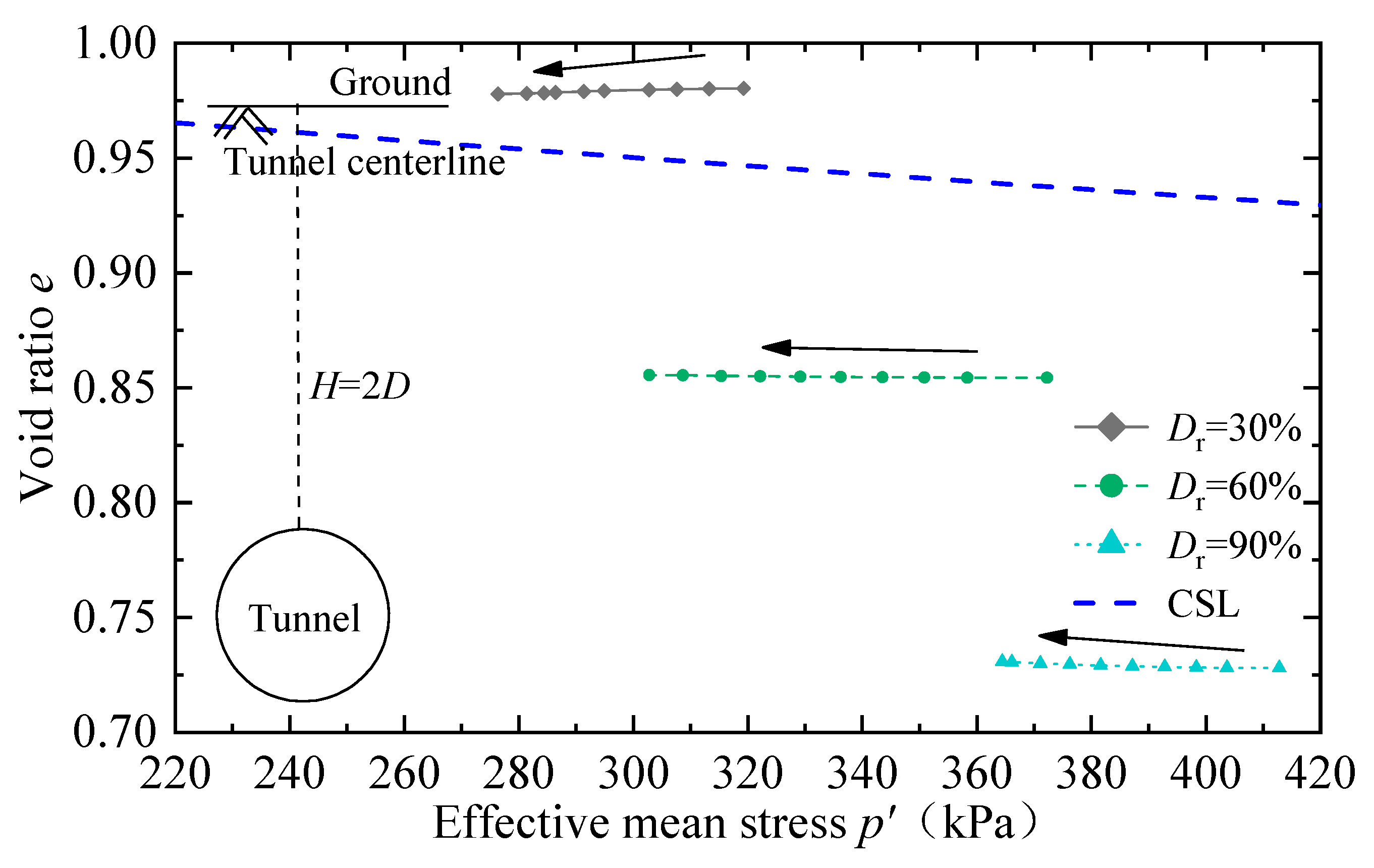
2. Calibration of SANISAND Constitutive Model by Triaxial Test
- (1)
- Elastic parameters
- (2)
- Critical state parameters
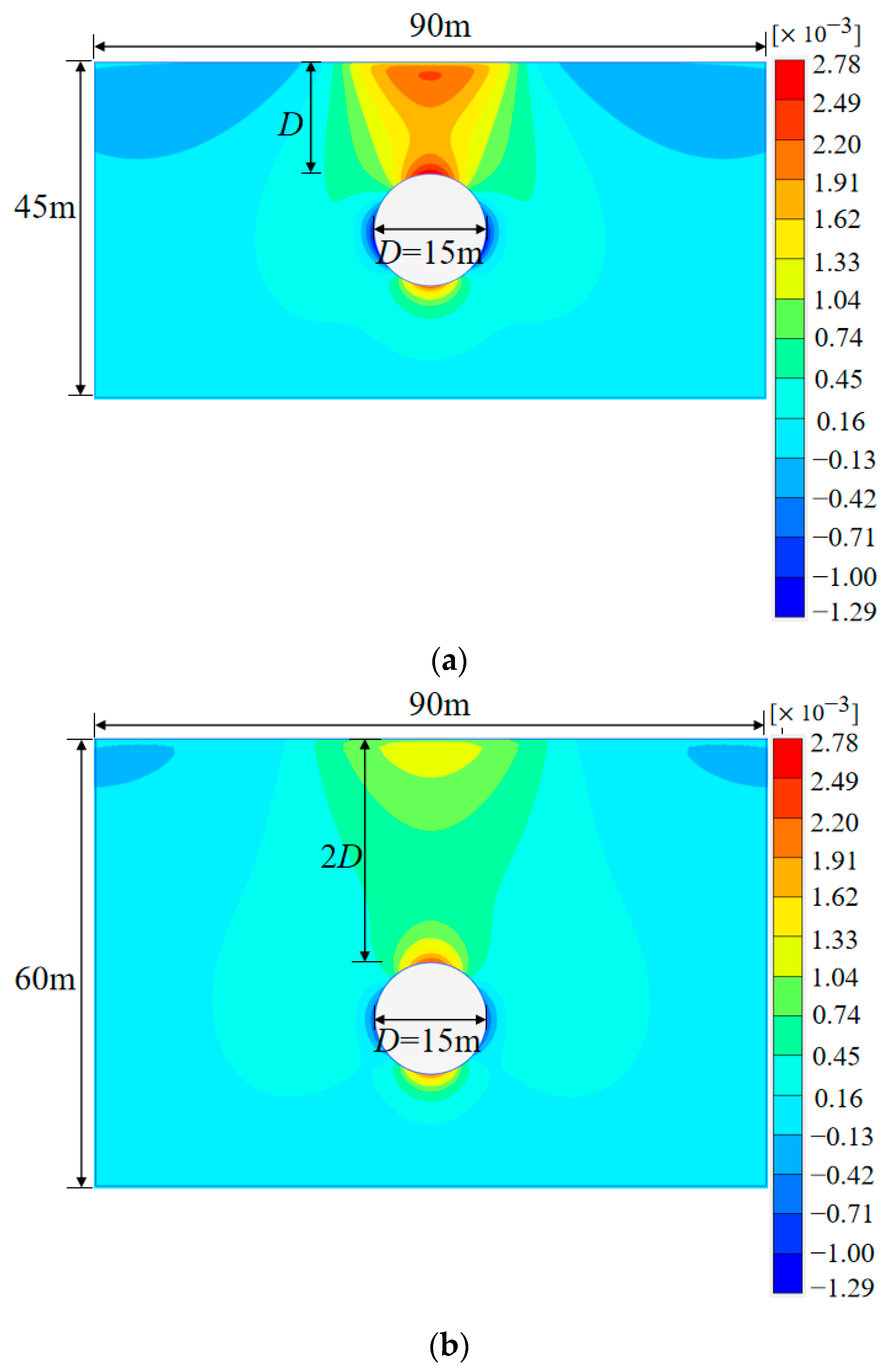
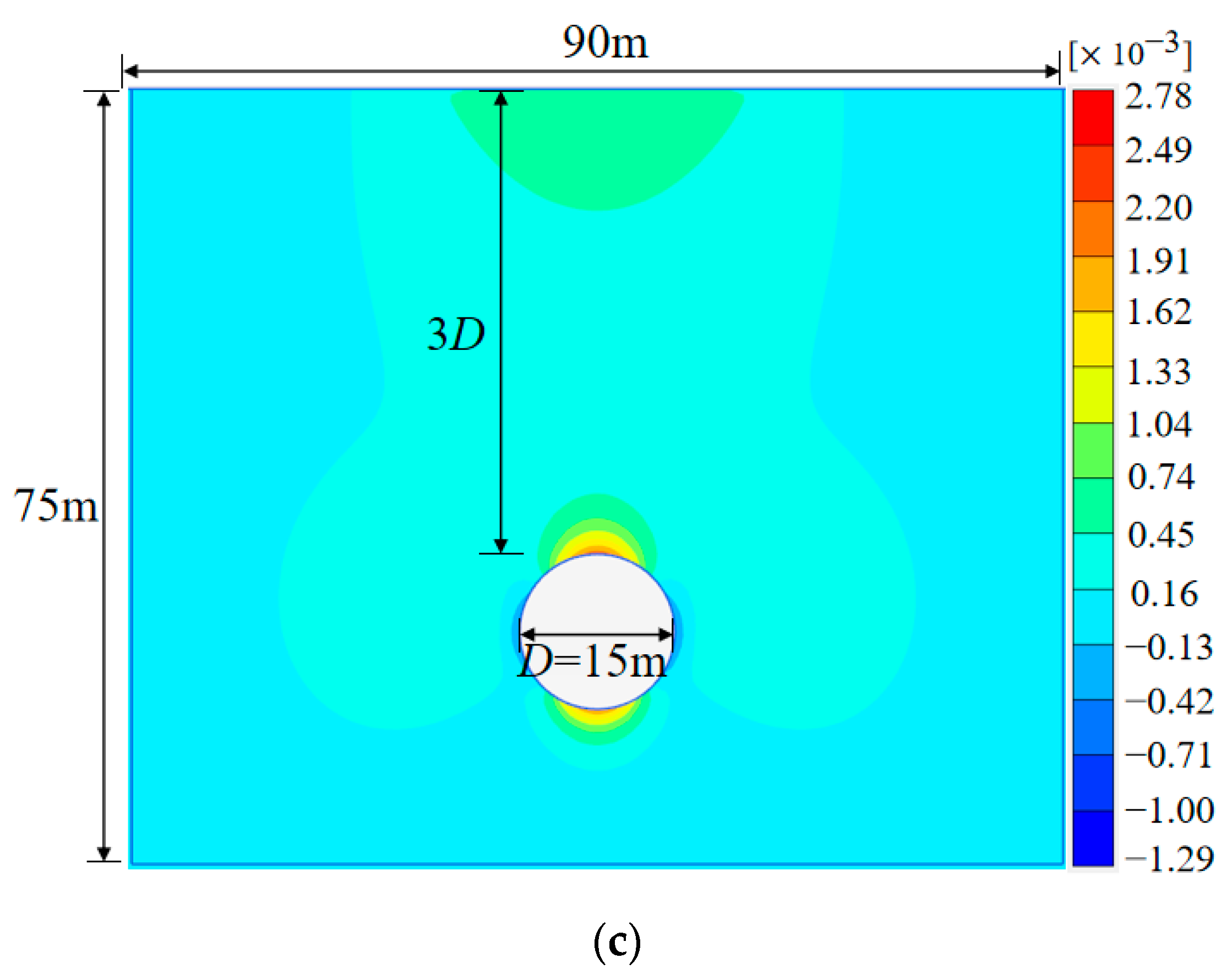
3. Establishment of Numerical Models
4. Analysis of Numerical Results
4.1. Influence of the Ratio of Buried Depth to Diameter
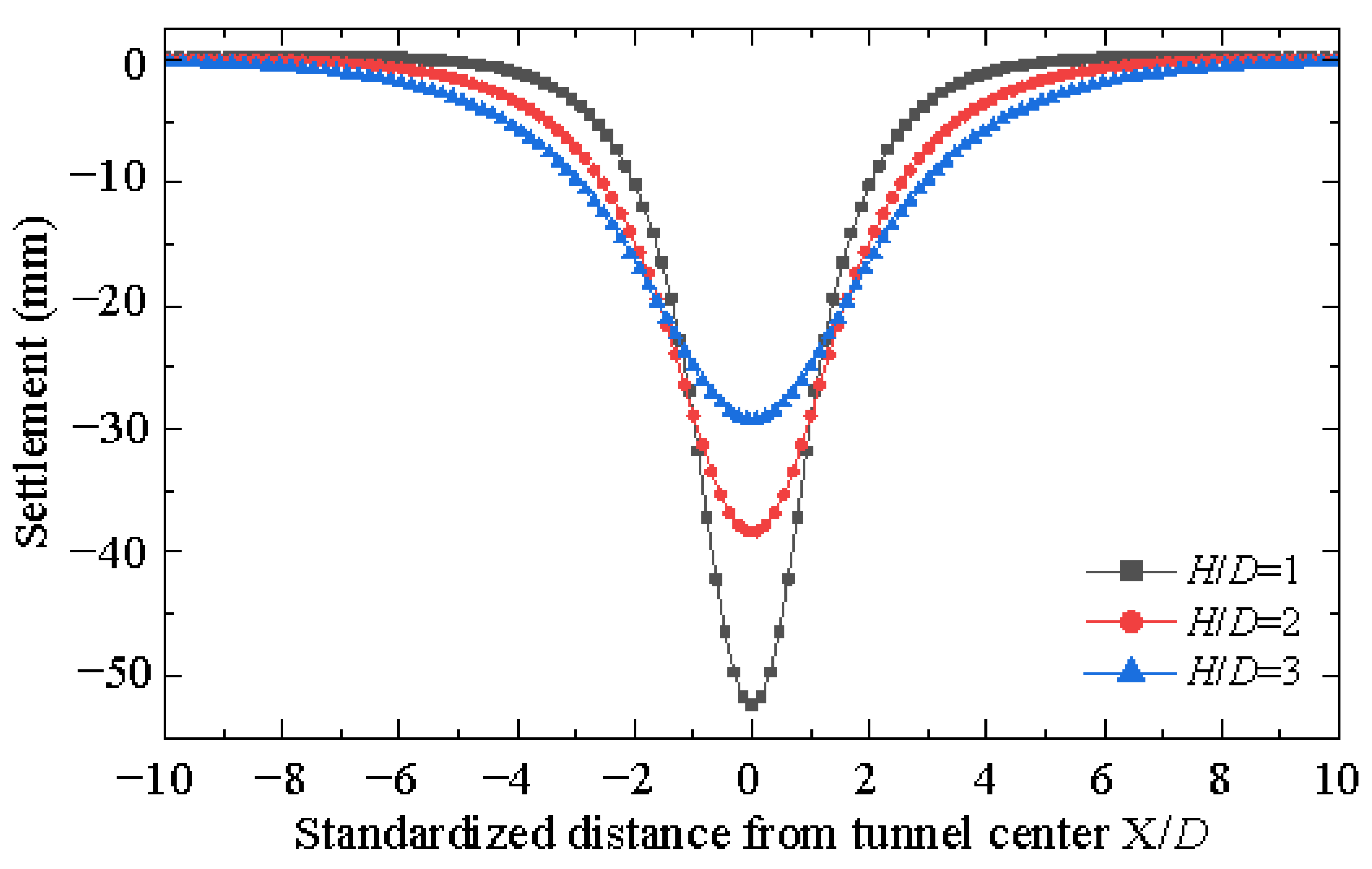
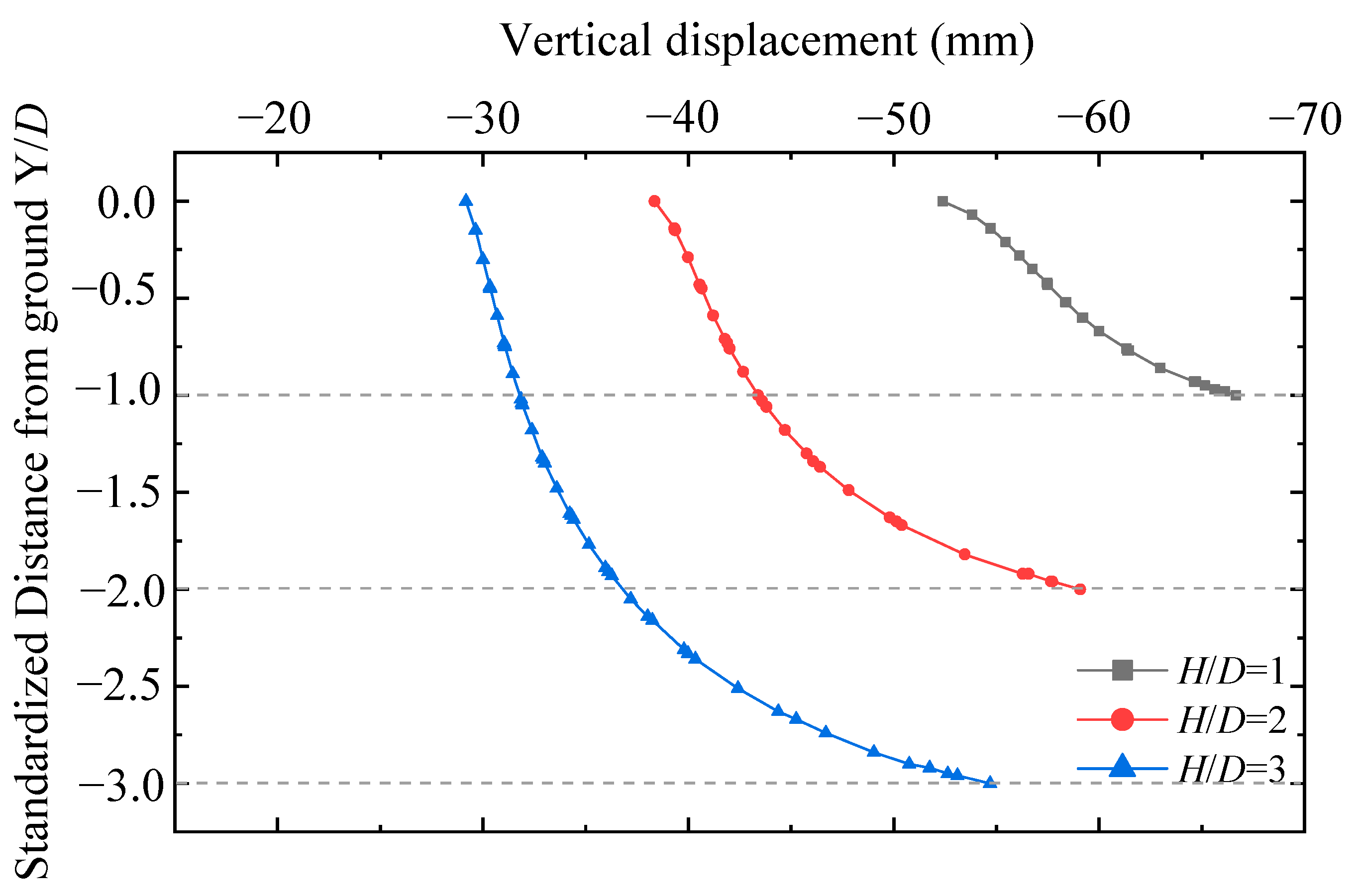
4.1.1. Ground Displacement
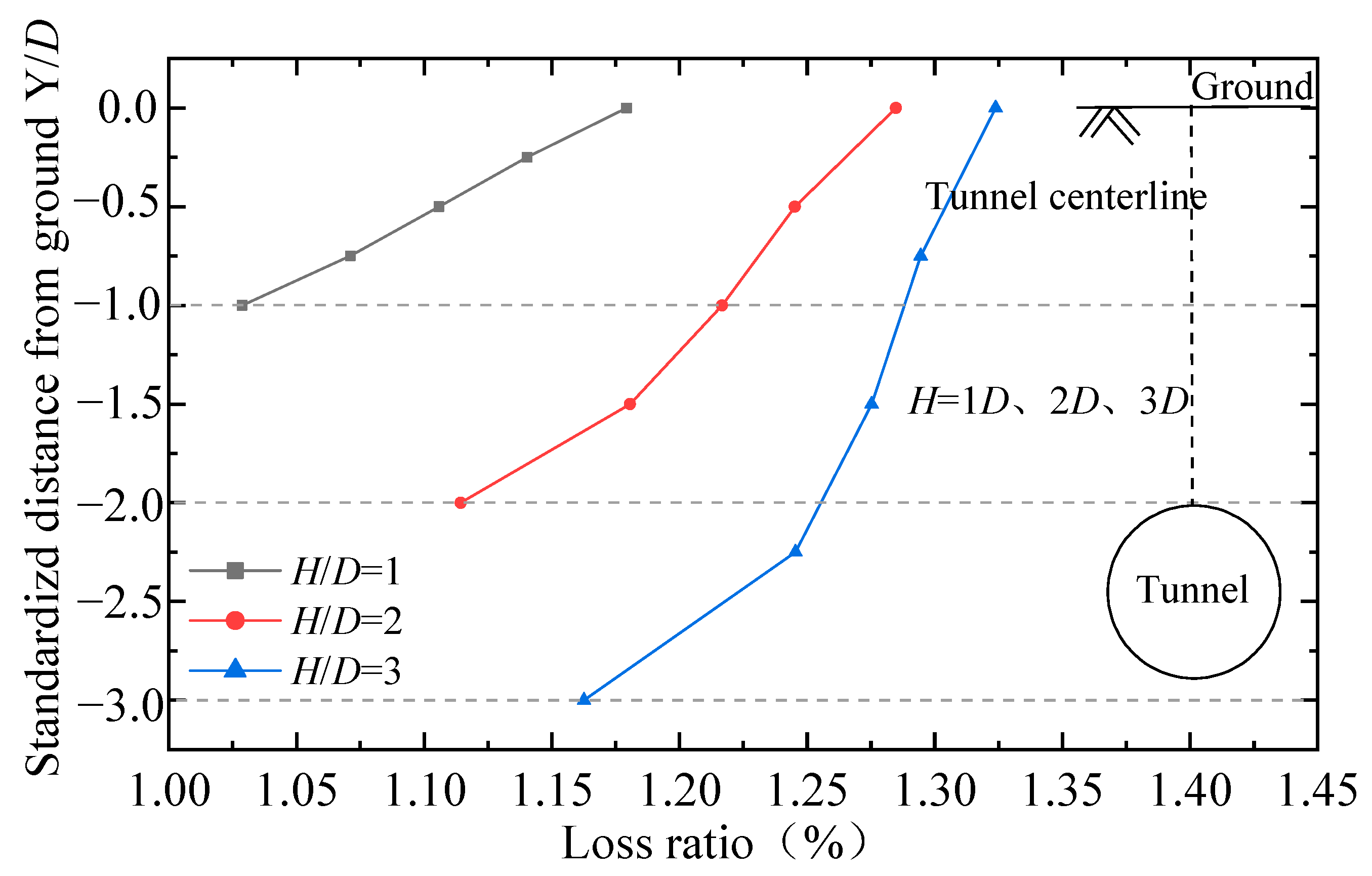
4.1.2. Ground Loss Ratio
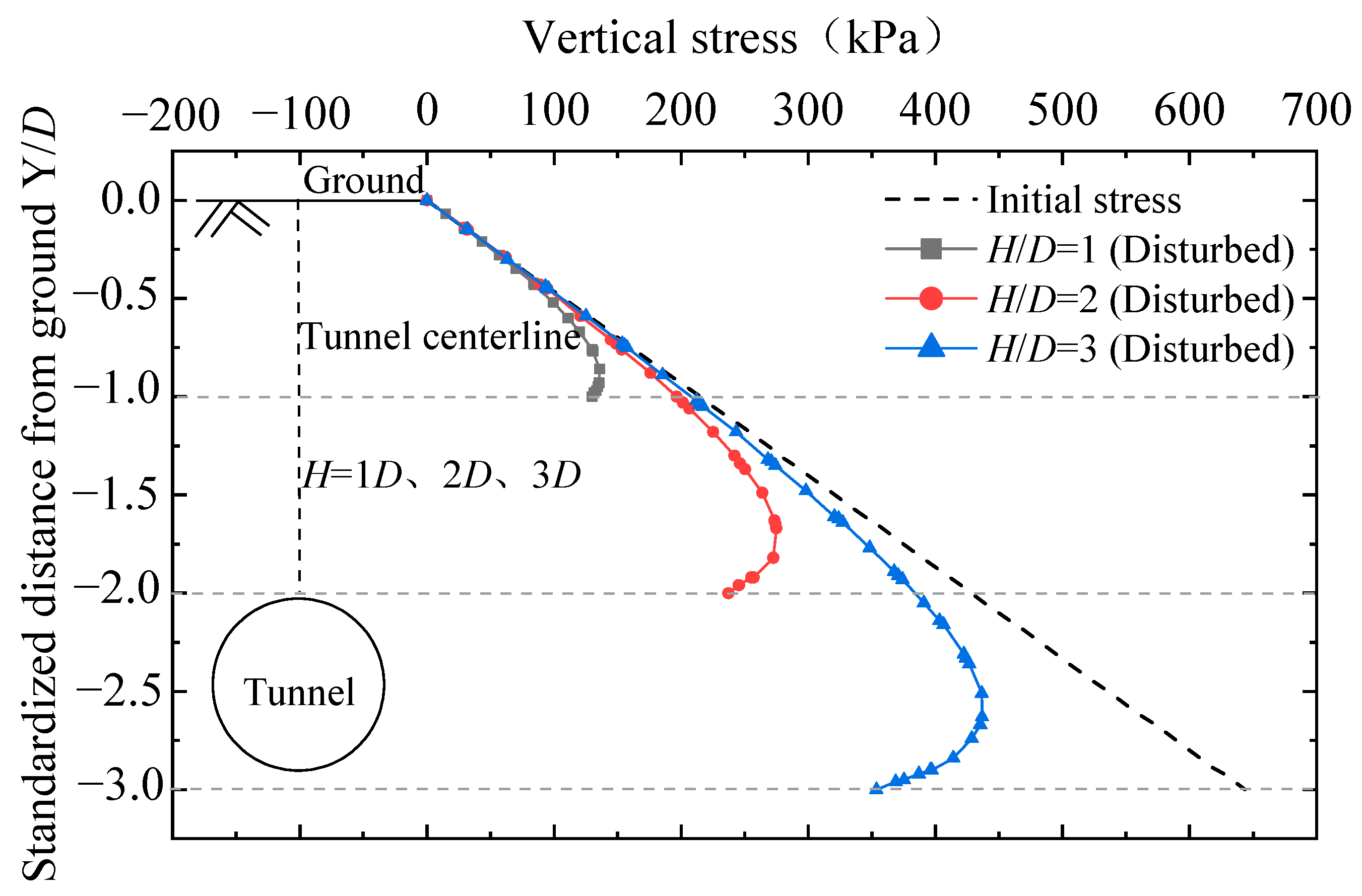
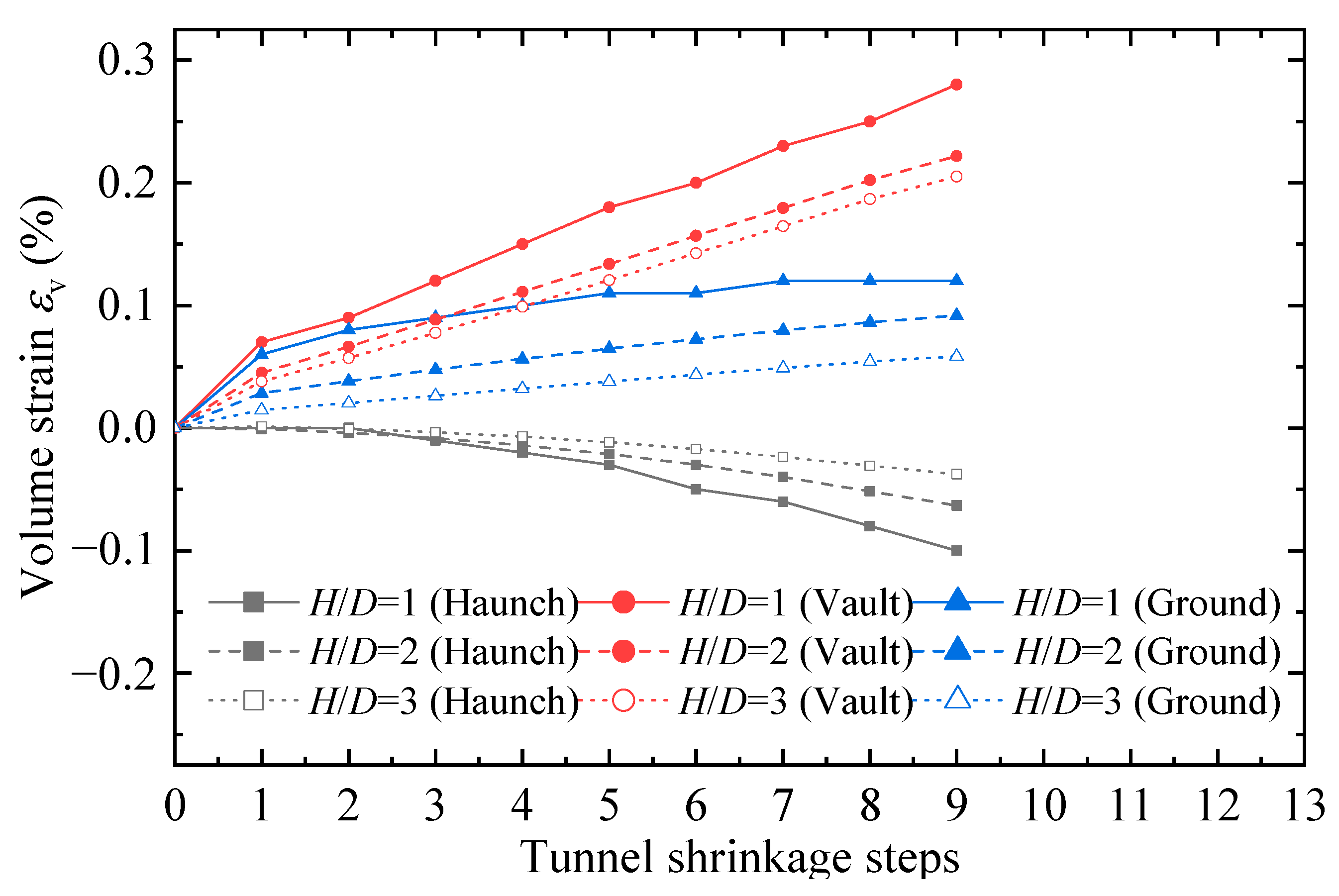
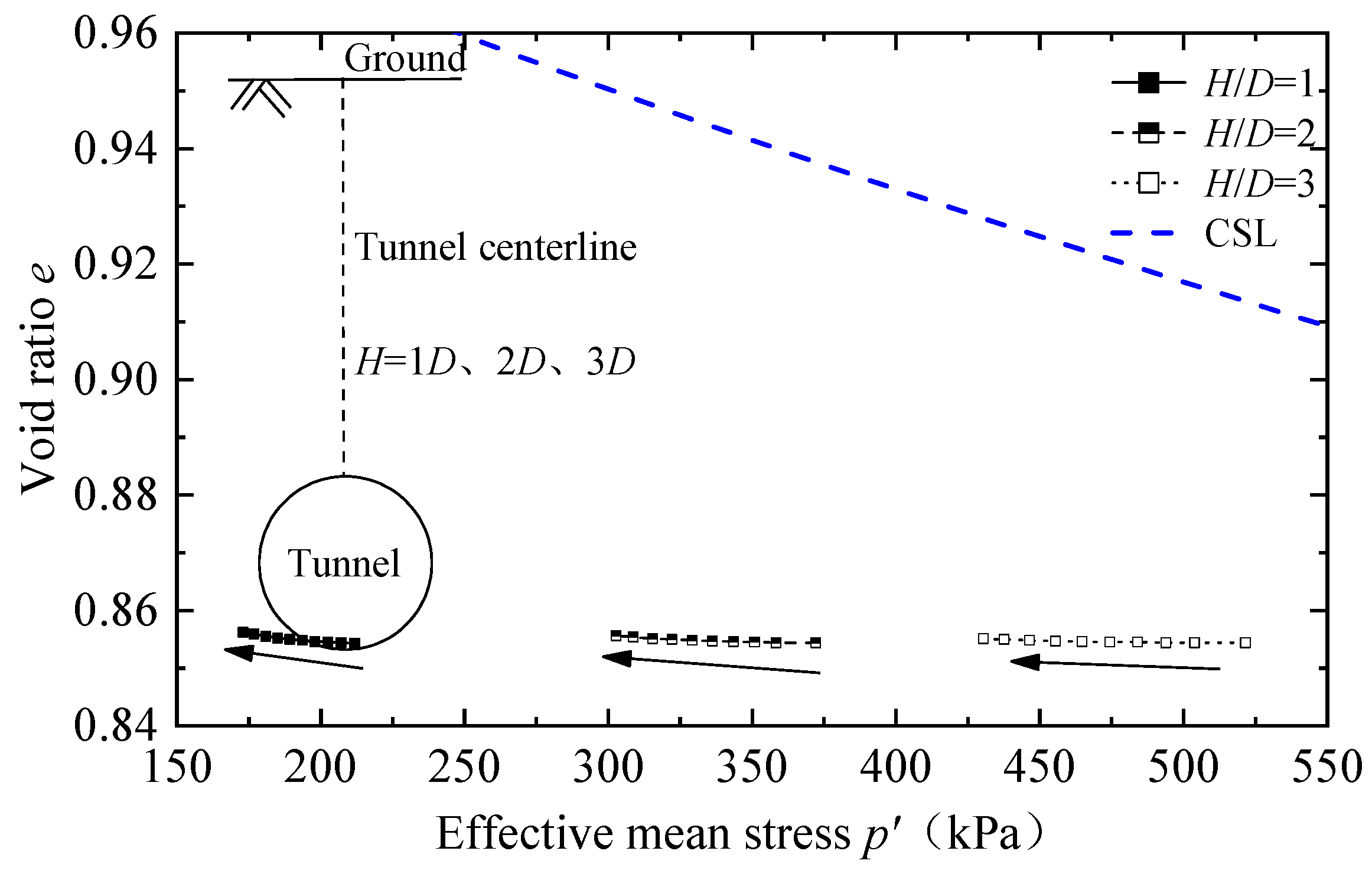
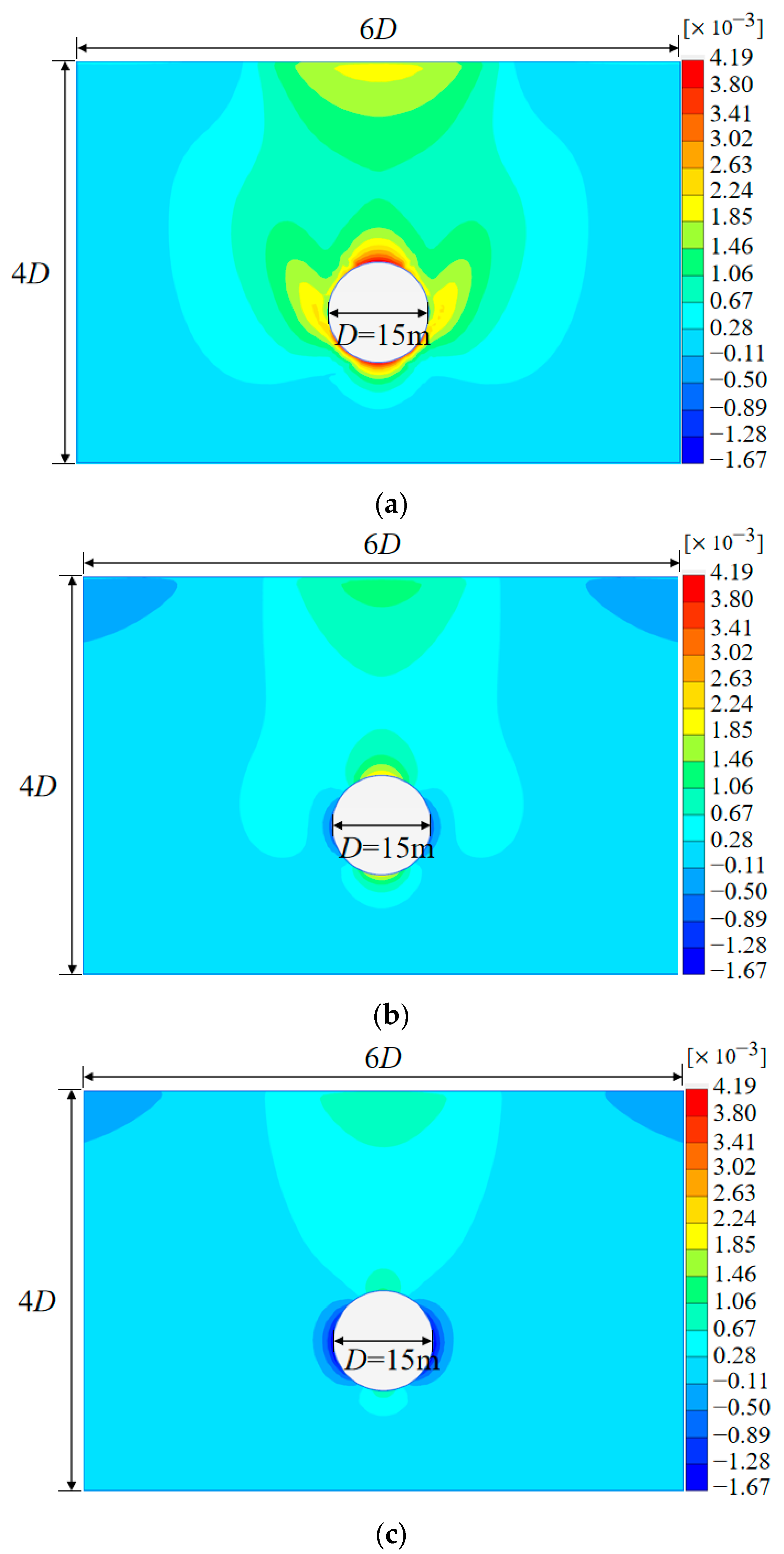
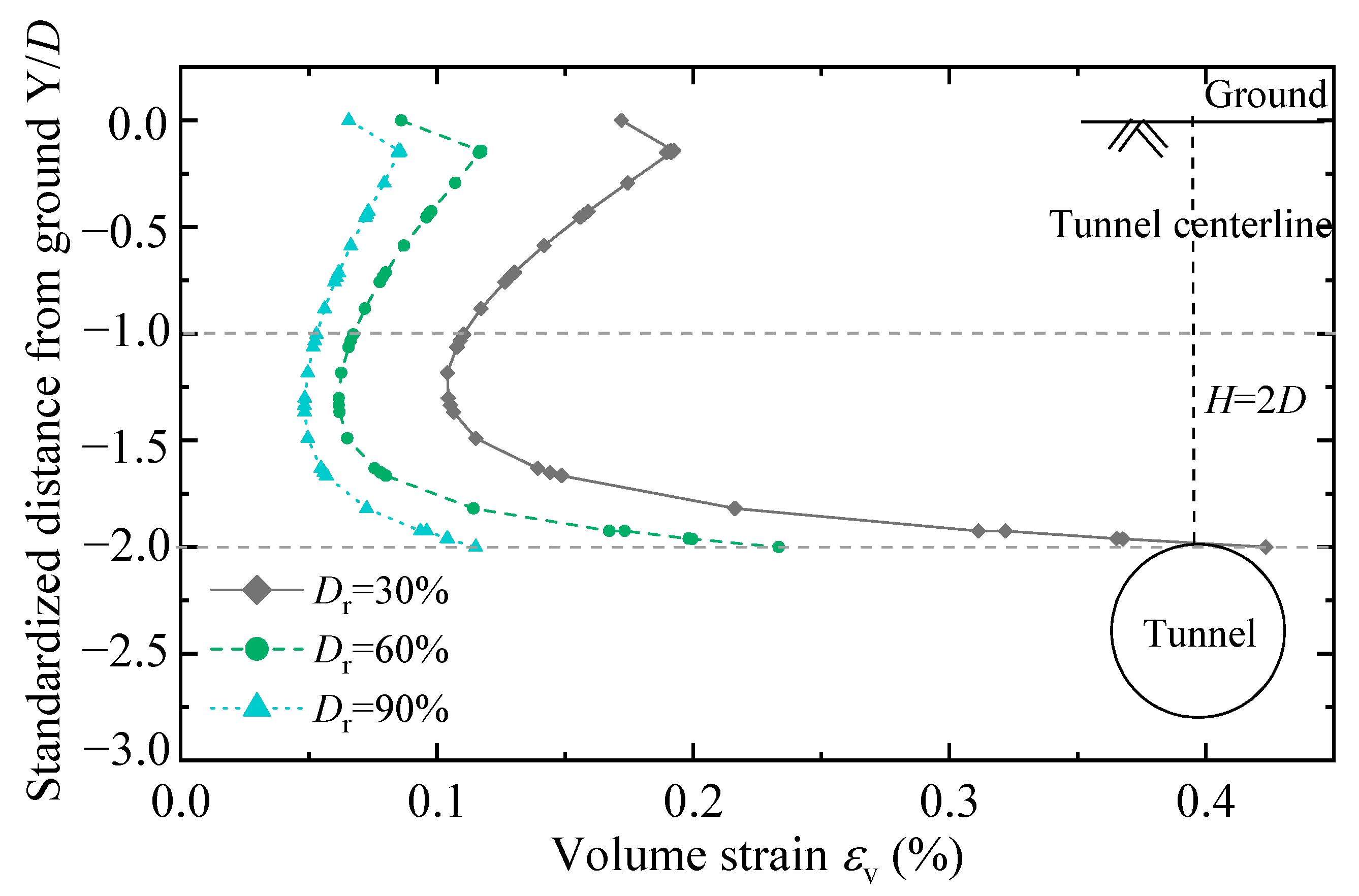
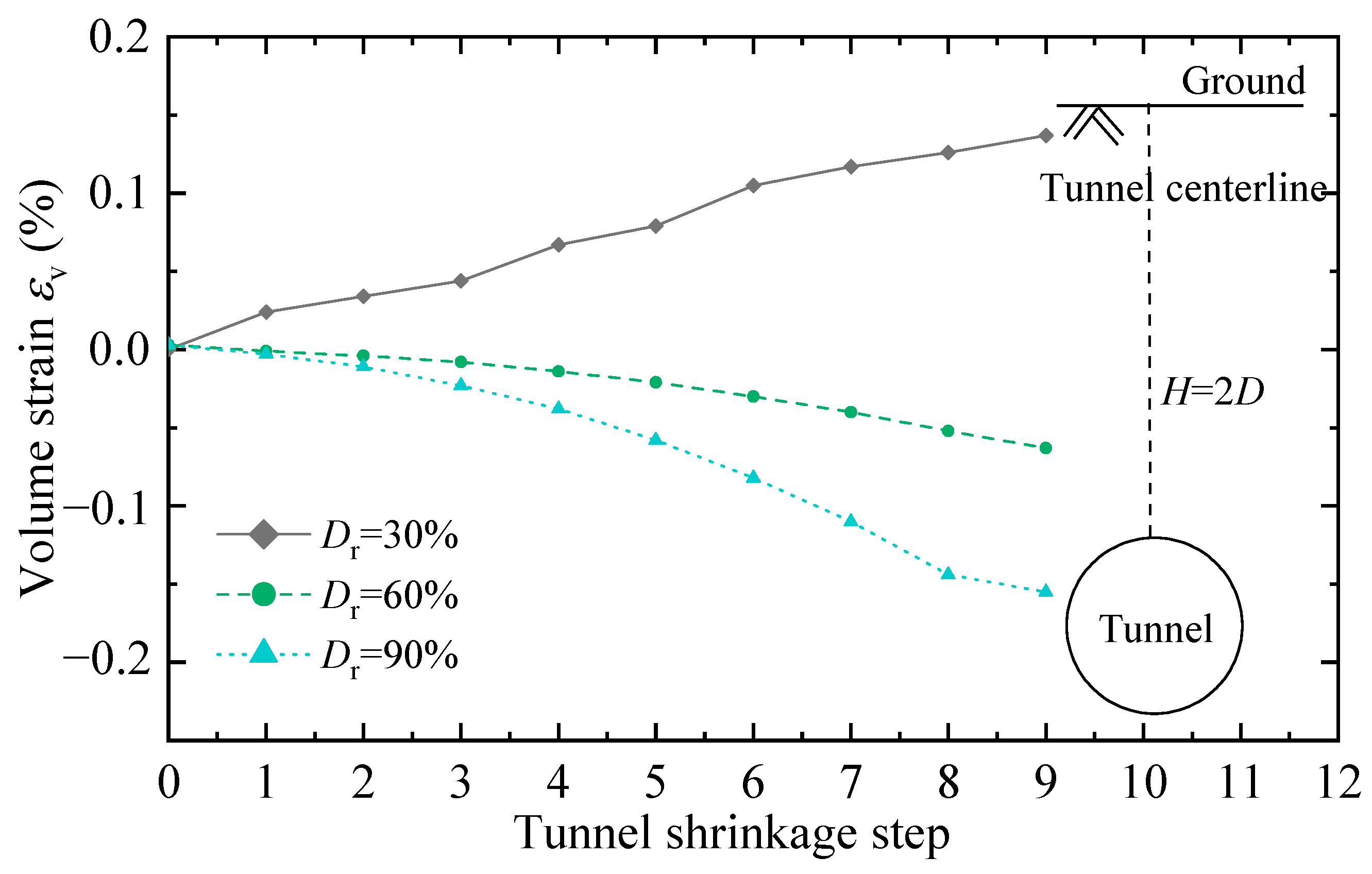
4.1.3. Soil Volume Change
4.2. Effect of Relative Density
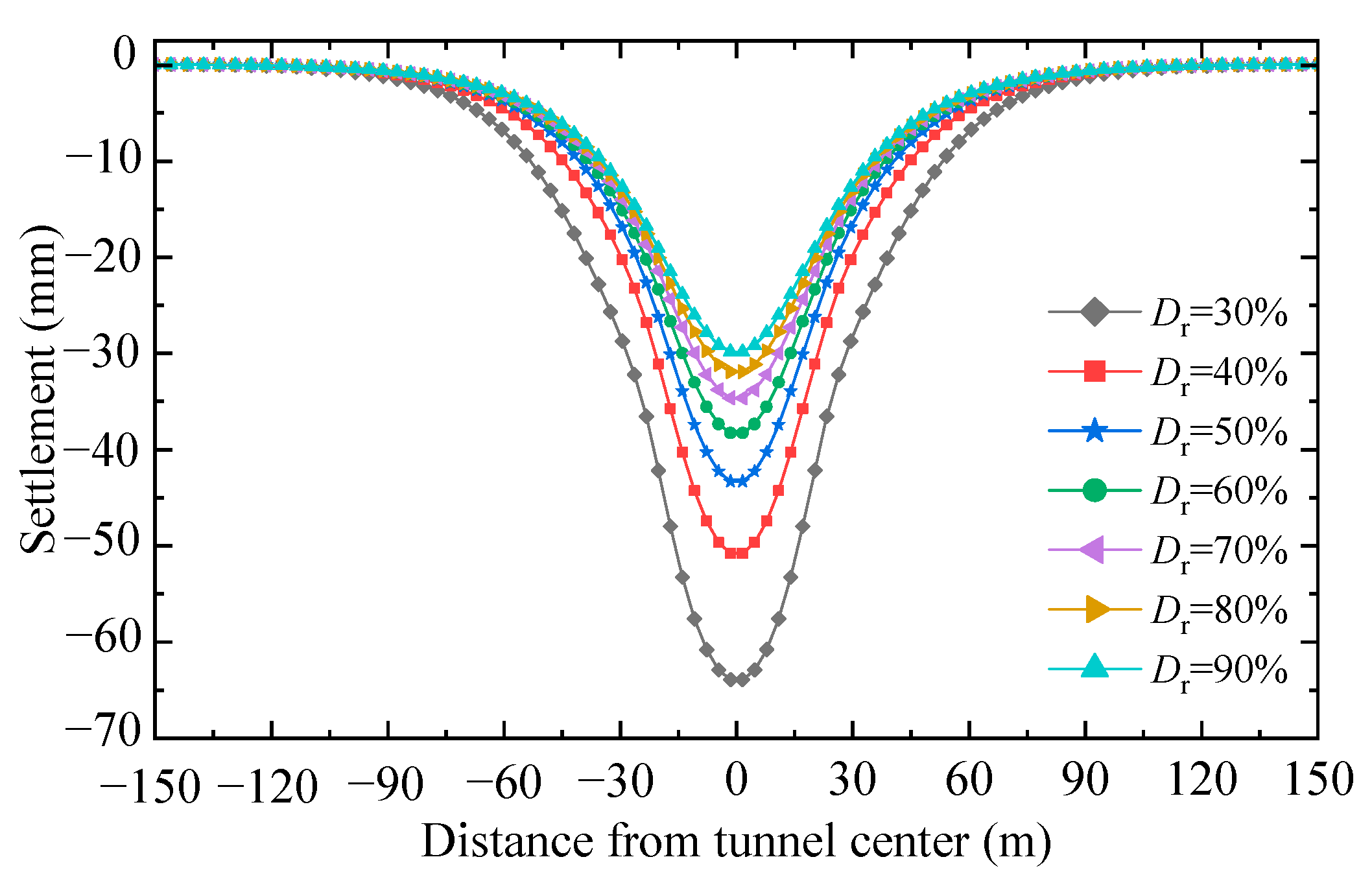
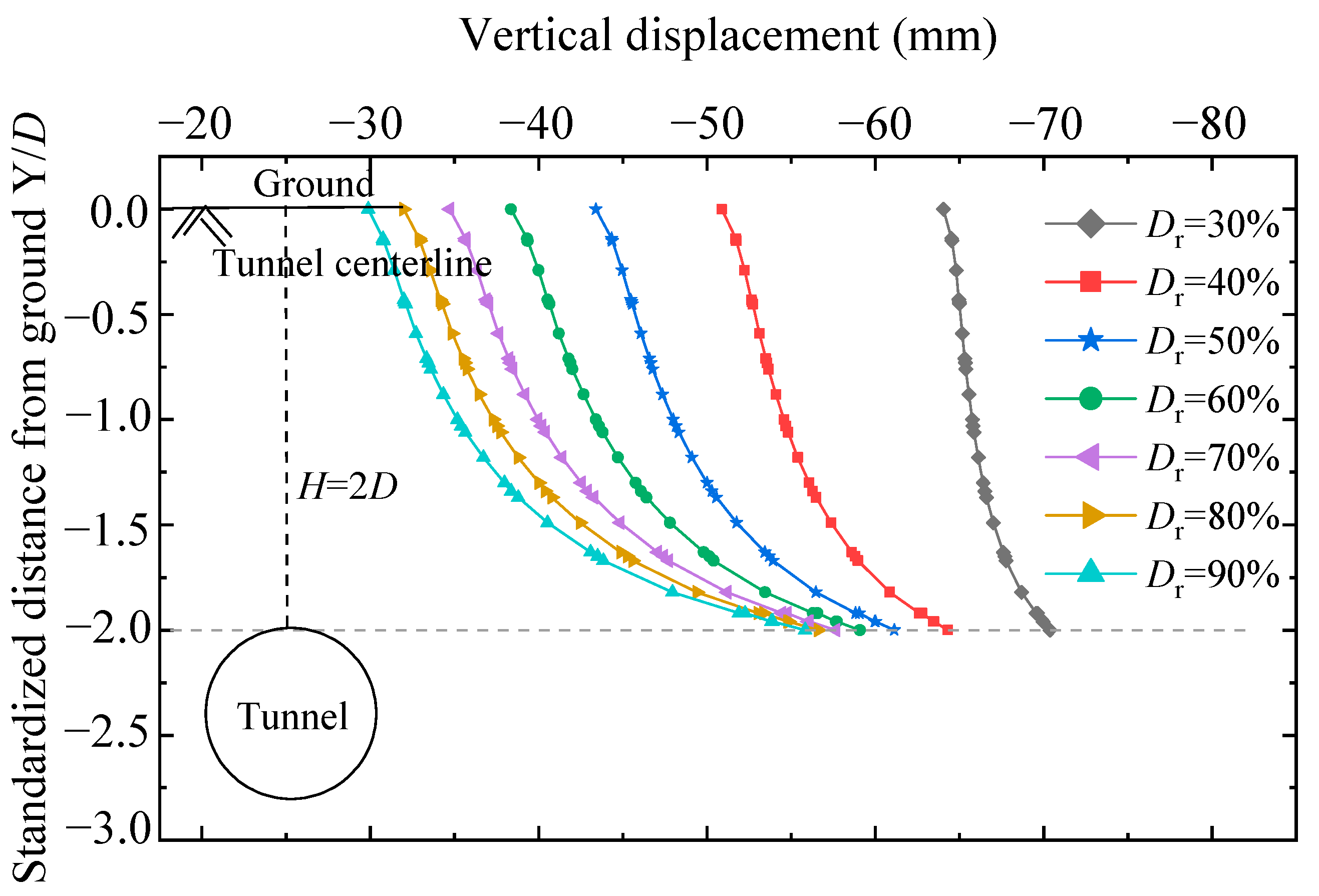
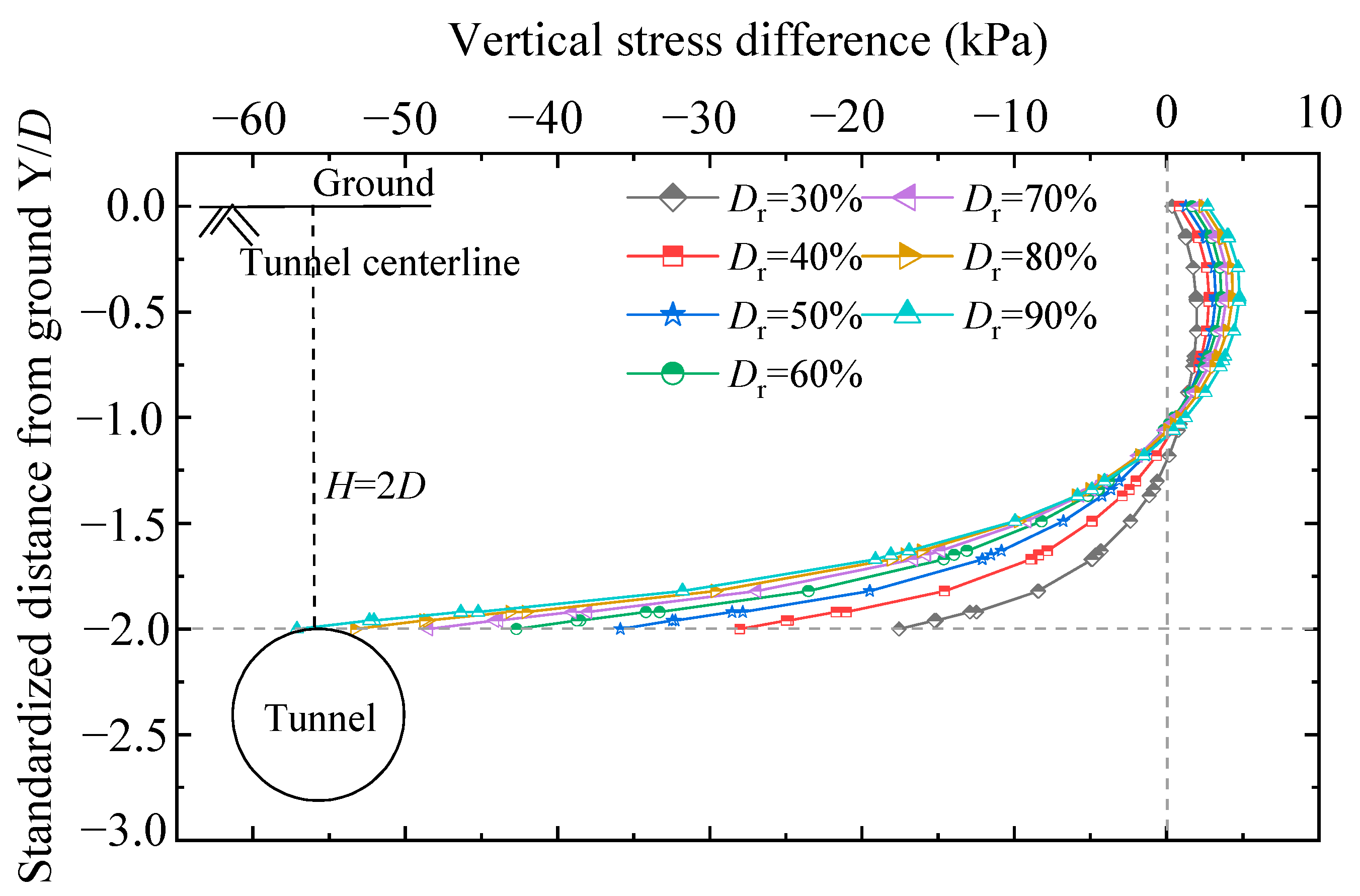
4.2.1. Ground Displacement
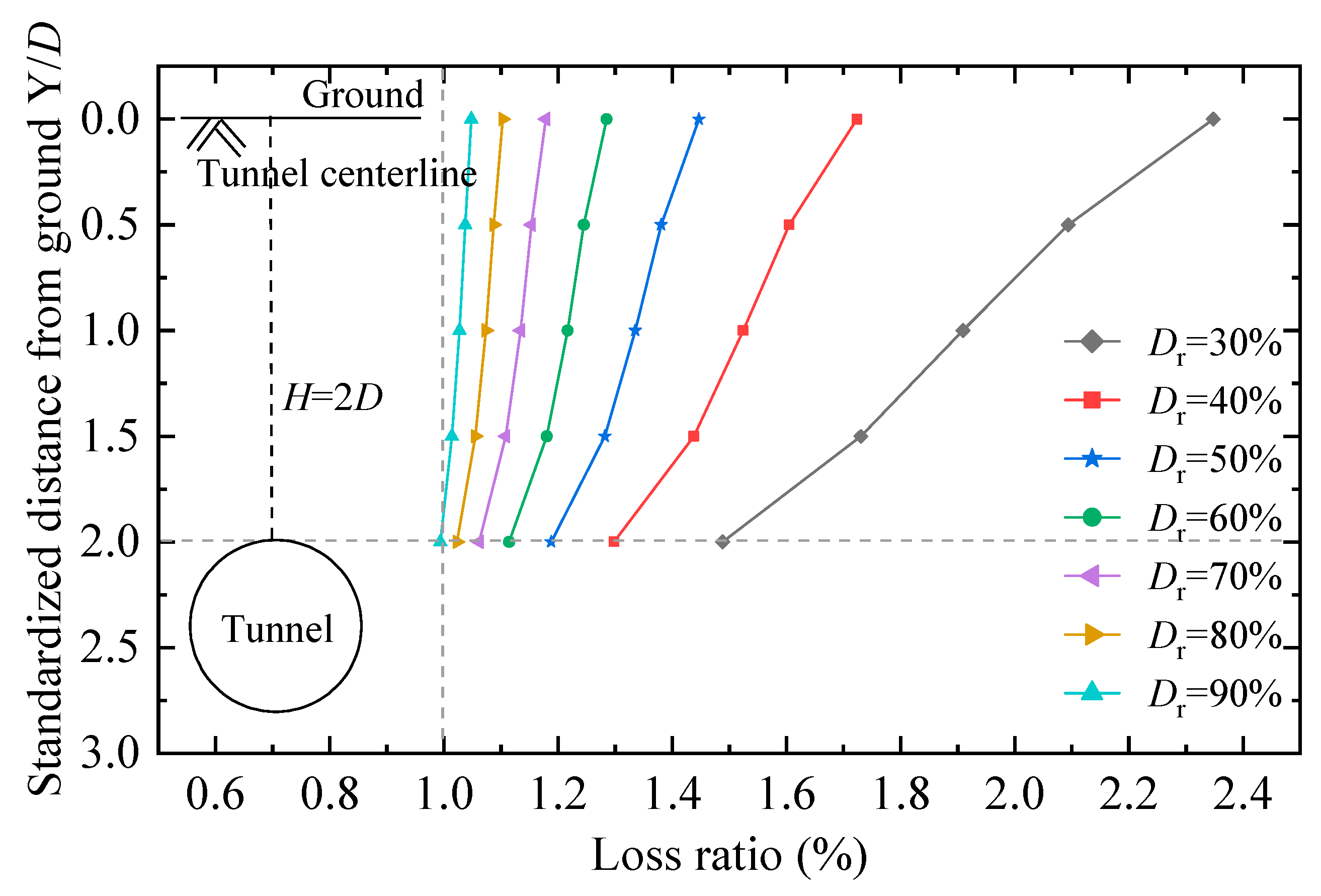
4.2.2. Ground Loss Ratio
4.2.3. Soil Volume Change
4.3. Impact of H/D and Dr on Parameters of Peck’s Formula
5. Conclusions
- (1)
- The width of the settlement trough at the ground surface is highly correlated with H/D. The half-width of the trough is about 4 D, 6 D, and 8 D for the cases of H/D = 1, 2, and 3, respectively. However, for the same H/D, Dr has no obvious impact on the width.
- (2)
- The maximum settlement at the ground surface as induced by tunneling depends on both H/D and Dr. For the same Dr, the maximum settlement decreases with the increase in H/D. For the same H/D, the maximum settlement decreases with the increase in Dr.
- (3)
- Along the centerline of tunneling, the vertical displacement (settlement) above the tunnel decreases with increasing distance from the tunnel. When H/D and Dr are larger, the “loss” in the vertical displacement becomes greater when it approaches the ground. When Dr = 60%, the loss is about 21, 35, and 46% for the cases of H/D =1, 2, and 3, respectively.
- (4)
- The ground loss ratio increases with increasing distance from the tunnel, and its variation depends on the relative density of the ground soil. From the top of the tunnel to the ground surface, the ground loss ratio increases by 0.86, 0.43, 0.26, 0.17, 0.12, 0.08, and 0.05% for ground consisting of sand with relative densities of 30, 40, 50, 60, 70, 80, and 90%.
- (5)
- In all cases, the soil above the tunnel is mainly subject to contraction. For the ground comprising dense sand, the shear-induced expansion around the tunnel haunch compensates for part of the shear-induced contraction above the tunnel, so the overall ground loss ratio is smaller than that in the ground comprising loose sand.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, Y.; Chen, Z.; Tao, L.; Cui, J.; Yan, Q. Model Tests on Longitudinal Surface Settlement Caused By Shield Tunnelling in Sandy Soil. Sustain. Cities Soc. 2019, 47, 101504. [Google Scholar] [CrossRef]
- Peck, R.B. Deep Excavation and Tunnelling in Soft Ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, State of the Arts Volume, Mexico City, Mexico; 1969. [Google Scholar]
- Fattah, M.Y.; Shlash, K.T.; Salim, N.M. Prediction of settlement trough induced by tunneling in cohesive ground. Acta Geotech. 2013, 8, 167–179. [Google Scholar] [CrossRef]
- Song, Z.; Tian, X.; Zhang, Y. A new modified Peck formula for predicting the surface settlement based on stochastic medium theory. Adv. Civ. Eng. 2019, 2019, 7328190. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, D.; Wang, D.; Zhang, L.L.; Zhang, L.M. Failure probability of transverse surface settlement induced by EPB Shield tunneling in clayey soils. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2018, 4, 04018030. [Google Scholar] [CrossRef]
- Wei, Z.; Zhu, Y. A theoretical calculation method of ground settlement based on a groundwater seepage and drainage model in tunnel engineering. Sustainability 2021, 13, 2733. [Google Scholar] [CrossRef]
- Tang, X.; Liang, J.; Liu, W.; Ye, Y.; Gan, P.; Zhao, W.; Yu, Y. Modification of Peck Formula to Predict Ground Surface Settlement of Twin Tunnels in Low Permeability Soil. Adv. Civ. Eng. 2021, 2021, 6698673. [Google Scholar] [CrossRef]
- Li, Y.; Lin, J.; Yan, S.; Du, J. Modification of the Peck Formula for a Double-Track Shield Tunnel under Expressway Subgrade. Symmetry 2022, 14, 1904. [Google Scholar] [CrossRef]
- Do, N.A.; Dias, D.; Oreste, P. 3D numerical investigation of mechanized twin tunnels in soft ground–Influence of lagging distance between two tunnel faces. Eng. Struct. 2016, 109, 117–125. [Google Scholar] [CrossRef]
- Zhang, T.; Nie, L.; Zhang, M.; Dai, S.; Xu, Y.; Du, C.; Rui, X.; He, Y. The unsymmetrical coefficient of unsymmetrical-loaded tunnel based on field monitoring and numerical simulation. Symmetry 2020, 12, 1793. [Google Scholar] [CrossRef]
- Ağbay, E.; Topal, T. Evaluation of twin tunnel-induced surface ground deformation by empirical and numerical analyses (NATM part of Eurasia tunnel, Turkey). Comput. Geotech. 2020, 119, 103367. [Google Scholar] [CrossRef]
- Khaksari, R.; Harun, Z.; Fielding, L.; Aldridge, J. Numerical Simulation of the Evacuation Process in a Tunnel during Contraflow Traffic Operations. Symmetry 2021, 13, 2392. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Zhang, H.; Yan, J.Y. A case study on the behavior of shield tunneling in sandy cobble ground. Environ. Earth Sci. 2013, 69, 1891–1900. [Google Scholar] [CrossRef]
- Zhang, P.; Pan, Y.; Yu, Z.; Guan, X.; Wang, G.; An, J.; Lei, H. Ground subsidence characteristics caused by construction of shallow-buried tunnel in a sandy soil composite formation. Arab. J. Geosci. 2020, 13, 901. [Google Scholar] [CrossRef]
- Hu, X.; He, C.; Peng, Z.; Yang, W. Analysis of ground settlement induced by Earth pressure balance shield tunneling in sandy soils with different water contents. Sustain. Cities Soc. 2019, 45, 296–306. [Google Scholar] [CrossRef]
- Moussaei, N.; Khosravi, M.H.; Hossaini, M.F. Physical modeling of tunnel induced displacement in sandy grounds. Tunn. Undergr. Space Technol. 2019, 90, 19–27. [Google Scholar] [CrossRef]
- Sun, J.; Liu, J. Visualization of tunnelling-induced ground movement in transparent sand. Tunn. Undergr. Space Technol. 2014, 40, 236–240. [Google Scholar] [CrossRef]
- Lu, H.; Shi, J.; Wang, Y.; Wang, R. Centrifuge modeling of tunneling-induced ground surface settlement in sand. Undergr. Space 2019, 4, 302–309. [Google Scholar] [CrossRef]
- Dafalias, Y.; Manzari, M. Simple Plasticity Sand Model Accounting for Fabric Change Effects. J. Eng. Mech. 2004, 130, 622–634. [Google Scholar] [CrossRef]
- Taiebat, M.; Dafalias, Y. Sanisand: Simple Anisotropic Sand Plasticity Mode. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 915–948. [Google Scholar] [CrossRef]
- Lashkari, A. A Sanisand Model with Anisotropic Elasticity. Soil Dyn. Earthq. Eng. 2010, 30, 1462–1477. [Google Scholar] [CrossRef]
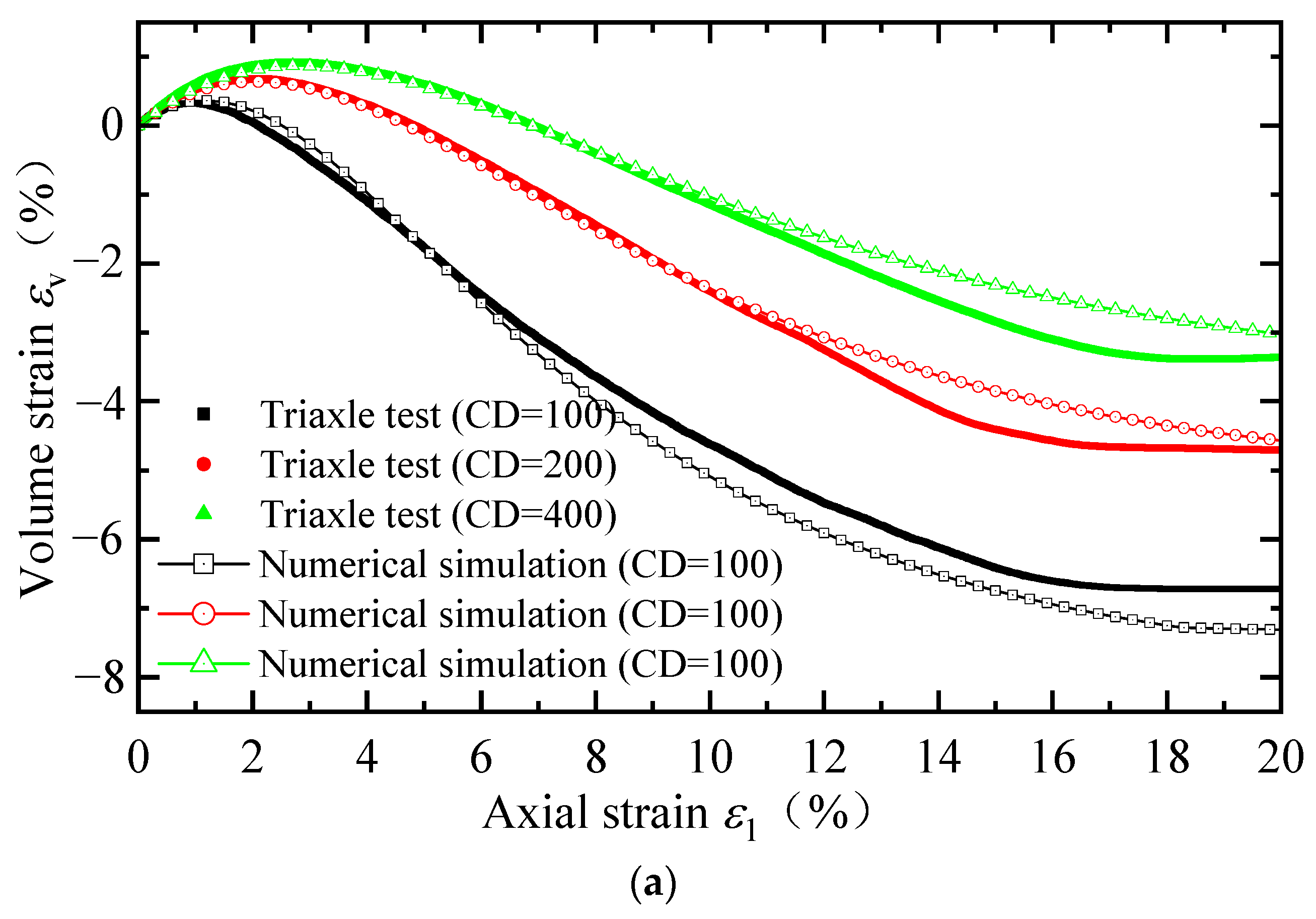
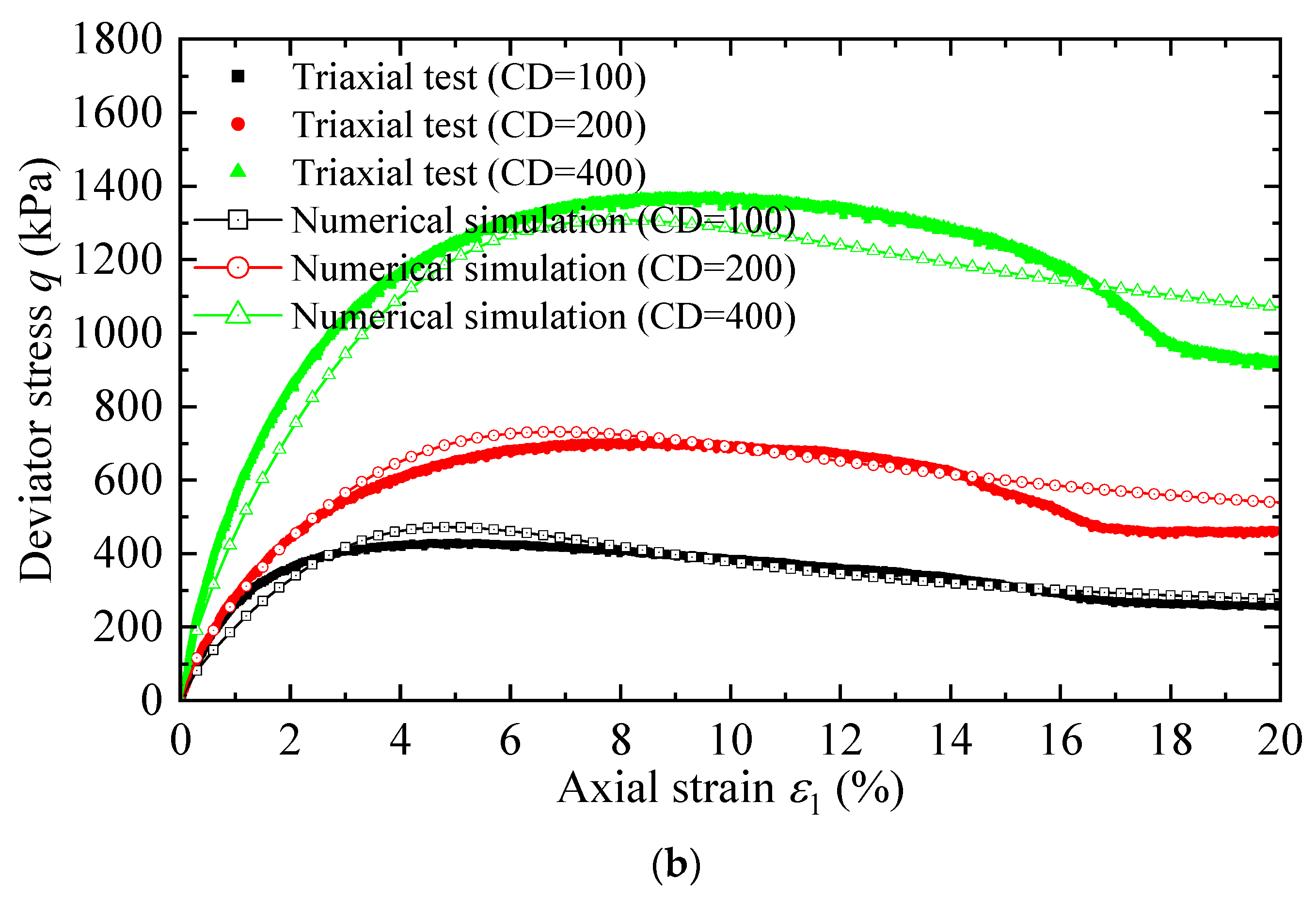
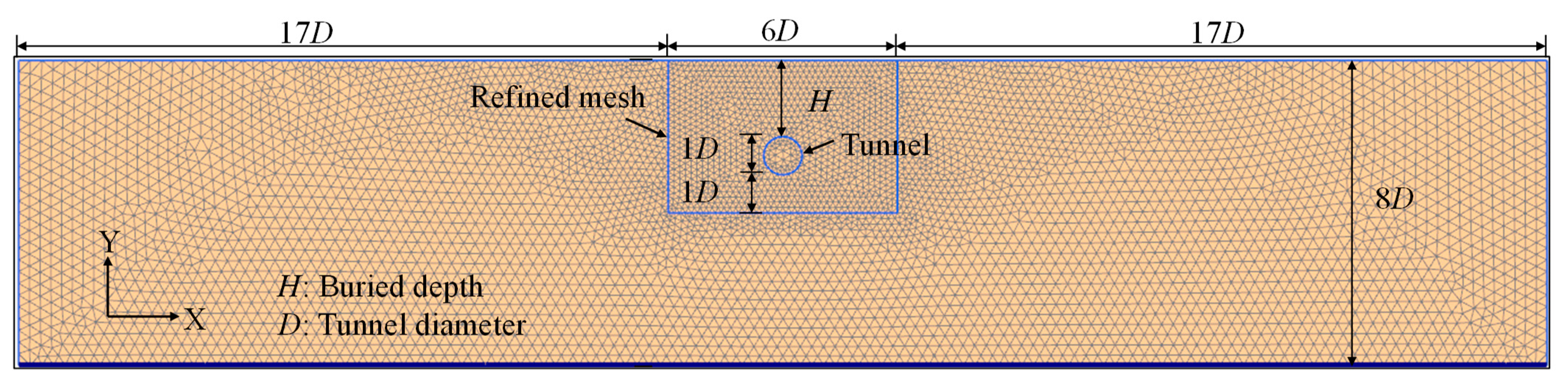
| Soil | State | emin | emax | Gs | Cu | Cc | ν | E0 |
|---|---|---|---|---|---|---|---|---|
| Silty fine sand | Loose | 0.686 | 1.107 | 2.62 | 5.33 | 3.52 | 0.32 | 4.5 |
| Elastic Parameters | Critical State Parameters | Yield Surface Parameters | Plastic Modulus Parameters | Dilatancy Parameters | Fabric Dilatancy Tensor Parameters |
|---|---|---|---|---|---|
| G0 = 120 | Mc = 1.33 | m = 0.01 | H0 = 7.04 | A0 = 1.0 | zmax = 4.0 |
| ν = 0.2 | λc = 0.036 | cH = 0.989 | nD = 1.2 | cz = 600 | |
| e0 = 1.024 | nb = 3.35 | ||||
| ξ = 0.7 |
| H/D = 1 | H/D = 2 | H/D = 3 | |
|---|---|---|---|
| D = 15 m | Dr = 30%, 60%, 90% | Dr = 30%, 40%, 50%, 60%, 70%, 80%, 90% | Dr = 30%, 60%, 90% |
| Relative Density, Dr | 30% | 40% | 50% | 60% | 70% | 80% | 90% |
|---|---|---|---|---|---|---|---|
| Void ratio, e | 0.981 | 0.939 | 0.897 | 0.854 | 0.812 | 0.770 | 0.728 |
| unit weight, γ (kN/m3) | 13.38 | 13.67 | 13.97 | 14.29 | 14.62 | 14.97 | 15.33 |
| Dr | H/D = 1 | H/D = 2 | H/D = 3 |
|---|---|---|---|
| 30% | 19.37 | 25.88 | 32.29 |
| 60% | 15.92 | 23.52 | 31.75 |
| 90% | 16.03 | 24.71 | 33.92 |
| Dr | H/D = 1 | H/D = 2 | H/D = 3 |
|---|---|---|---|
| 30% | 68.8 | 61.2 | 54.2 |
| 60% | 50.1 | 36.4 | 27.7 |
| 90% | 41.3 | 28.4 | 21.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, X.; Wen, Y.; Su, D. Deformation of Sandy Ground Induced by Tunneling of Super-Large-Diameter Shield—Influence of Buried Depth of Tunnel and Relative Density of Sand. Symmetry 2023, 15, 71. https://doi.org/10.3390/sym15010071
Li J, Li X, Wen Y, Su D. Deformation of Sandy Ground Induced by Tunneling of Super-Large-Diameter Shield—Influence of Buried Depth of Tunnel and Relative Density of Sand. Symmetry. 2023; 15(1):71. https://doi.org/10.3390/sym15010071
Chicago/Turabian StyleLi, Jiquan, Xiaolu Li, Yuqin Wen, and Dong Su. 2023. "Deformation of Sandy Ground Induced by Tunneling of Super-Large-Diameter Shield—Influence of Buried Depth of Tunnel and Relative Density of Sand" Symmetry 15, no. 1: 71. https://doi.org/10.3390/sym15010071
APA StyleLi, J., Li, X., Wen, Y., & Su, D. (2023). Deformation of Sandy Ground Induced by Tunneling of Super-Large-Diameter Shield—Influence of Buried Depth of Tunnel and Relative Density of Sand. Symmetry, 15(1), 71. https://doi.org/10.3390/sym15010071






