Model-Based Regional Control with Anomalous Diffusion of Multi-Drug Combined Cancer Therapy for Volume Predictions

Abstract

Symmetry breaking in the anatomical lung is triggered by tumorigenesis and disrupted by delivering single or multiple drugs to stop the progression of the tumor and treat cancer. In this study, a prior model of combined drug therapy is augmented to introduce tissue heterogeneity when the drug is applied in multi-drug therapy of lung cancer. Patient-related drug resistance and synergy are investigated as a function of diffusion intensity as drug molecules reach the tumor site. The results indicate that diffusion of drug molecules plays an important role next to other factors such as patient sensitivity to the drug and drug synergy effects. We conclude that the minimal model provides meaningful predictions on tumor growth at the intermediate mesoscale level. With such models at hand, it is now possible to employ model-based control algorithms to optimize the dose profiles in terms of time and amount. In this paper, we present a theoretical framework for control employing networked game theory optimality. Specific situations are discussed in terms of finding optimality at Nash equilibrium in relation to patient response and drug synergy effects.

1. Introduction

Every healthy individual cell follows a well-controlled symmetry pattern in the biological processes of conception, proliferation, differentiation, and death (the process of programmed cell death in multi-cellular organisms referred to as apoptosis). However, once developed, the cell clones may suffer a symmetry breaking due to mutational changes that lead to cancer, either genetic or other alterations.

An understanding of the growth and progression of primary and metastatic tumors requires the elucidation of mechanisms that break the symmetry in the lung and provoke tumorigenesis. Hence, the alteration of the respiratory system is characterized by the collective properties exhibited by tumorous cells and their interaction with the microenvironment and delivered treatment. In general, the tumor microenvironment can be described as a discrete stochastic accumulation of tumorous cells by continuous nonlinear displayed stromal cells. By contrast, healthy lung tissue can be described as having a fractal distribution, without disruption in the symmetry between the cells [1]. A recent study modeling different biological conditions of cancer tissue showed that the proliferation of cancer cells alters the tumor dynamics and heterogeneity [2].

The processes that govern tumor growth have been investigated and translated into mathematical models that allow analyzing of the interactions on the cancer site, and predict the evolution of the tissue and treatment outcome across multiple scales [3,4]. Monitoring pre- and post-treatment of tumorous tissue requires recursive alterations to the initially planned therapy profiles, depending on the patient’s therapeutic response [5]. In particular, for lung cancer-diagnosed patients, it has been recently suggested that a cocktail of multi-drug therapy has better outcomes in terms of clinical effect and patient recovery period [6,7]. Other recent investigations in mouse models indicated that such multi-drug therapy with adaptive protocols achieves better outcomes in terms of cell turnover and therapies which used as little drug as possible worked best [8]. However, models are scarce and the main advances are at the molecular scale of tumor dynamic profiles and dose-effect kinetics [9,10]. As part of the breathing dynamic system, the tumor volume and consistency affect respiratory mechanics [11], requiring adaptive tumor radiotherapy localization [12]. Using tissue properties in lungs [13], anomalous diffusion of the drug into the tissue and multi-drug therapy can be combined to enhance the benefits of augmented models to aid the decision making-mechanisms in therapy profiles [14,15].

Recent advances in modeling lung tumor growth dynamics have proposed simplistic yet descriptive compartmental models for characterizing the pharmacokinetics (PK) and pharmacodynamics (PD) of lung cancer therapy in non-small cell lung cancer (NSCLC). The most prevalent therapy is antiangiogenesis and a model has been proposed in [16,17]. In clinical practice, this is enhanced with periods of stereotactic body radiotherapy (SBRT) [18] and in severe cases, additional immunotherapy [19] is applied. We proposed a PKPD model encompassing all three therapies [20,21] and validated it on a set of patients with lung cancer [22]. The PKPD model was first developed and described in detail in [20]. In [22], we calibrated the model with real data measured in a clinical trial including patients with non-small cell lung cancer. The parameters capture the dynamics of the tumor and the results show the changes in patients’ responses to treatment according to tumor shrinkage. The model fitted the behavior of the lung tumors assessed by measuring the tumor volume of the patients before and after treatment from computed tomography images.

Anomalous diffusion is an important factor in describing the efficacy of a drug on the tumor volume dynamics, thus we propose to augment the model with an additional parameter related to the dose-effect intensity. Having this augmented model available at hand, we also evaluate control algorithms for optimizing multiple scenarios of therapy profiles. Distributed agent optimal control strategies often involve the existence of an equilibrium point where all agents converge towards a common objective or a self-centered objective. As such, one may project a theory that multi-agent systems seeking optimality can well approximate the multi-drug therapy protocols seeking optimal tumor volume response in patients.

In this paper, we introduce a coalition-based game optimality control theory to examine the effects of multi-drug optimal profiles on tumor volume dynamics in lung cancer. We endeavor to build a reliable mechanistic modeling framework for describing drug distribution in solid tumors due to fractional diffusion in a locally targeted approach and simulate their effects on tumor growth. We used a general pharmacokinetic-pharmacodynamic (PKPD) modeling in a tumor environment, focusing on the distribution of local targeted anti-cancer therapies and the dose-effect relationship. To evaluate the proposed rationale, we analyzed different examples simulated using both data from the literature and clinical data.

2. Materials and Methods

2.1. A Minimalistic PKPD Model of Lung Tumor Growth

A tumor volume growth model has been proposed in [20], calibrated in [22], and validated with real data from patients in [11]. It consists of first-order compartmental PK models with linear dynamics, followed by dose-effect response nonlinear gains. Although this is a well-known Wiener-type model, identification is difficult due to the lack of modalities for persistent excitation of drug dosing profiles [23,24]. The proliferating tumor volume $x_1$ in mm${}^3$ and the necrotic tumor volume $x_2$ in mm${}^3$, give the total tumor volume. The SBRT inhibitor level $x_5$ in mg/(mL·day) is expressed based on the radiation dose rate administrated $u_r$ (mg · day/mL), according to the dosing profiles adequate for NSCLC. Dosing profiles for antiangiogenic $u_a$ and immunotherapy $u_i$ give the concentrations $x_3$ and $x_4$, respectively, leading to the overall model given by:

$$\begin{array}{cccc}{\dot{x}}_1\hfill & =\hfill & (a-n)x_1\hfill & -E·x_1\hfill \\ {\dot{x}}_2\hfill & =\hfill & x_2\left(0\right)+n{x}_1\hfill & +E·x_1\hfill \\ {\dot{x}}_3\hfill & =\hfill & -c_a{x}_3\hfill & +u_a\hfill \\ {\dot{xe}}_3\hfill & =\hfill & -c_{a}x{e}_3\hfill & +E{t}_a·x_3\hfill \\ {\dot{x}}_4\hfill & =\hfill & -c_i{x}_4\hfill & +u_i\hfill \\ {\dot{xe}}_4\hfill & =\hfill & -c_{i}x{e}_4\hfill & +E{t}_i·x_4\hfill \\ {\dot{x}}_5\hfill & =\hfill & -c_r{x}_5\hfill & +u_r\hfill \\ {\dot{xe}}_5\hfill & =\hfill & -c_{r}x{e}_5\hfill & +E{t}_r·x_5\hfill \end{array}$$

(1)

where a denotes the tumor growth rate, n the necrosis rate, and $c_r$ is the clearance rate on the Michaelis–Menten kinetics $\frac{x_1{x}_3}{ED{50}_r+x_3}$ (mm${}^3$/day). As the dead cells are naturally eliminated from the body, the necrotic volume does not depend on the past value, hence $x_2\left(0\right)=0$. The parameters $x{e}_i$ and $E{t}_i$ are the effects of drug concentrations and the synergic effect between tumor cells and chosen therapy. The dose-effect PD model is in fact a nonlinear gain (for a single drug) or a nonlinear surface (for multiple drugs) and can be considered as averaged effects of all therapies (in absence of real data at the molecular level to confirm this hypothesis) for the tumor $E{t}_{all}$ and drug $E{d}_{all}$ interactions:

$$\begin{array}{ccc}E{t}_{all}\hfill & =\hfill & \frac{Eta+Eti+Etr}{3}\hfill \\ E{d}_{all}\hfill & =\hfill & \frac{Eai+Ear+Eir}{3}\hfill \\ E\hfill & =\hfill & \frac{E{t}_{all}+E{d}_{all}}{2}\hfill \end{array}$$

(2)

with $Etx$ denoting the interaction between tumor cells and each drug, while $Exy$ denotes the interaction among drugs. When surface models are used to characterize synergic effects among drugs, the effect drug concentrations $xe$ are normalized to their potency, i.e., to their corresponding half-effect concentration $C_{50}$. The combined effects of two drugs $U_A$ and $U_B$ are considered as a new drug, and expressed as a Hill curve dose–response relationship 3D surface:

$$Effect=\frac{I^{\gamma }}{1+I^{\gamma }}$$

(3)

with I denoting the interaction term:

$$I=U{n}_A+U{n}_B+\sigma U{n}_A·U{n}_B$$

(4)

with $U{n}_A=\frac{U_A}{C_{50A}}$ and $U{n}_B=\frac{U_B}{C_{50B}}$ the normalized drug effect concentrations and $C_{50}$ the concentrations at half effect 50%. The term $\gamma$ denotes the nonlinearity of the surface, which represents how a patient responds to the drug (effectiveness or resistance of therapy). The term $\sigma$ denotes the degree of synergy present between the drugs. Values for the model coefficients are those reported in [20] (open access).

2.2. Regional Anomalous Diffusion

A hybrid model for characterizing regional anomalous diffusion at the surface tension between healthy tissue and tumor tissue is proposed. Having patient-specific parameters, this model has also been validated partially to illustrate its clinical relevance. We propose here an aggregation of local diffusion phenomena to be included as part of the dose-effect relationship, i.e., (3). The effect surface depends not only on the $\gamma$ and $\sigma$ parameters characterizing drug–patient interaction but also on local effects in molecular binding between drugs and targeted treatment of the cancer tissue.

Let us assume that the effect of (2) is no longer abiding by the classical Fickean diffusion, but anomalous diffusion. When working with the surface model, it is important to understand the relationship between power-law and exponential functions, and this has been in detail discussed in [25]. Combining the theory of molecular residential time and surface interaction with simplifying algebra from [25], leads to introducing an extra parameter in the relation for $x_1$ and $x_2$, namely:

$$\begin{array}{cccc}{\dot{x}}_1\hfill & =\hfill & (a-n)x_1\hfill & -E^{(1-\alpha )}·x_1\hfill \\ {\dot{x}}_2\hfill & =\hfill & x_2\left(0\right)+n{x}_1\hfill & +E^{(1-\alpha )}·x_1\hfill \end{array}$$

(5)

whereas $\alpha$ is the coefficient of diffusion, the particular case of $\alpha =1$ giving a linear diffusion pattern along the surface (Fickean diffusion). Indeed, we verify that for $\alpha =1$, the surface remains linear along its domain, as depicted in Figure 1.

2.3. Predictive Control Strategy for Multi-Drug Therapy Optimization

Predictive control has been used in SBRT for compensating the breathing pattern effects in 3D volume changes in lung tumor tissue, to minimize towards zero the radiation of healthy tissue around the tumor [26]. The breathing pattern was identified online and the robot arm used for therapy was guided with feedforward compensation using a specially designed disturbance model in Model Predictive Control (MPC) [12]. When multiple objectives are envisaged within changing context of execution, a prioritized optimizing scheme can be used as that proposed in [27], reducing both computational and numerical complexity involved when the Pareto front is used instead.

In this paper, a centralized MPC strategy with the state-space formulation is proposed. The algorithm is derived starting from the velocity-form methodology from [28], subsequently extended to a multivariable system.

Let us consider the PKPD model from (1) described by the process model in the state-space formulation:

$$\begin{array}{c}{x}_p(k+1)=A_p{x}_p\left(k\right)+B_{p}u\left(k\right)\hfill \\ y\left(k\right)=C_p{x}_p\left(k\right)\hfill \end{array}$$

(6)

where k is the discrete-time instant, $u\in {\mathbb{R}}^{n_u}$, $y\in {\mathbb{R}}^{n_y}$ and $x_p\in {\mathbb{R}}^{n_{x_p}}$ are the input, output, and state variables, respectively. Using the methodology described in [28], the difference operation is applied on both sides of (6) resulting:

$$\begin{array}{c}\hfill \mathsf{\Delta }{x}_p(k+1)=A_p\mathsf{\Delta }{x}_p\left(k\right)+B_p\mathsf{\Delta }u\left(k\right),\\ \hfill \mathsf{\Delta }y(k+1)=C_p{A}_p\mathsf{\Delta }{x}_p\left(k\right)+C_p{B}_p\mathsf{\Delta }u\left(k\right)\end{array}$$

(7)

Note that (7) introduces the increments of the variables $x_p$, u and y, with $\mathsf{\Delta }y(k+1)=y(k+1)-y\left(k\right)$. A new state variable $x\left(k\right)={\left[\mathsf{\Delta }{x}_p{\left(k\right)}^{T}y\left(k\right)\right]}^T$ is introduced, resulting the augmented model:

$$\begin{array}{c}\hfill \underset{x(k+1)}{\underbrace{\left[\begin{array}{c}\mathsf{\Delta }{x}_p(k+1)\\ y(k+1)\end{array}\right]}}=\underset{A}{\underbrace{\left[\begin{array}{cc}{A}_p& O_{n_y\times n_{x_p}}^T\\ C_p{A}_p& 1\end{array}\right]}}\underset{x\left(k\right)}{\underbrace{\left[\begin{array}{c}\mathsf{\Delta }{x}_p\left(k\right)\\ y\left(k\right)\end{array}\right]}}\\ \hfill +\underset{B}{\underbrace{\left[\begin{array}{c}{B}_p\\ C_p{B}_p\end{array}\right]}}\mathsf{\Delta }u\left(k\right)\\ \hfill y\left(k\right)=\underset{C}{\underbrace{\left[\begin{array}{cc}{O}_{n_y\times n_{x_p}}& I_{n_y}\end{array}\right]}}\left[\begin{array}{c}\mathsf{\Delta }{x}_p\left(k\right)\\ y\left(k\right)\end{array}\right]\end{array}$$

(8)

which will be used to design the predictive controller. Note that the new input of the state-space model in velocity-form is $\mathsf{\Delta }u\left(k\right)$.

The model (8) can be written in a compressed form as:

$$\begin{array}{c}\left\{\begin{array}{c}x(k+1)=Ax\left(k\right)+B\mathsf{\Delta }u\left(k\right)\hfill \\ y\left(k\right)=Cx\left(k\right)\hfill \end{array}\right.\hfill \end{array}$$

(9)

The centralized MPC cost function is defined as:

$$\begin{array}{c}\hfill J(x\left(k\right),\mathsf{\Delta }U\left(k\right))={\left(R_s-Y\right)}^T\left(R_s-Y\right)+\\ \hfill \mathsf{\Delta }U{\left(k\right)}^{T}R\mathsf{\Delta }U\left(k\right)\end{array}$$

(10)

depending on the output future predictor

$$Y={\left[y(k+1|k)\dots y(k+N_p|k)\right]}^T$$

and the future input sequence

$$\mathsf{\Delta }U\left(k\right)={\left[\mathsf{\Delta }u\left(k\right|k)\dots \mathsf{\Delta }u(k+N_c-1|k)\right]}^T$$

with $N_p$ the prediction horizon and $N_c$ the control horizon ($N_c\le N_p$). In this paper, for simplicity, we consider $N_c=N_p$. The predicted reference trajectory $R_s\in {\mathbb{R}}^{N_p}$ assumed constant and equal with the setpoint at time instant k and the input weight matrix has the form $R=\alpha I_{N_c}$, $\alpha ⩾0$.

Using the ’velocity-form’ model (9), the prediction of state and input variables can be computed. The centralized $\mathsf{\Delta }{U}^{*}\left(k\right)$ solution is obtained:

$$\begin{array}{c}\hfill \mathsf{\Delta }{U}^{*}={({\tilde{B}}^T\tilde{B}+R)}^{-1}{\tilde{B}}^T[R_s-\tilde{A}x\left(k\right)].\end{array}$$

(11)

Following the receding horizon principle, only the first $n_u$ elements from the optimal solution vector are sent to the process [29].

2.4. Multi-Agent Nash Optimality and Coalition Control

In terms of the dose-effect relationship versus drug resistance, the problem of optimum seeking is both exploitative and explorative, as in reinforcement learning theory. Such learning schemes are highly relevant in network systems with heterogeneous entities, where these entities represent different drug therapy profiles and the agents in the network are the respective drug selection combinations. Finding the optimum implies finding an equilibrium point where the cell turnover outperforms the cell growth in tumor volume. As such, this corresponds broadly to a combination of game theoretic models with learning-based approaches, which we will employ in our analysis. In a decentralized exchange of information, it allows heterogeneous agents to strategically interact with each other, e.g., the choice of drugs affects the degree of synergy effects, and learn to adjust their behaviors, i.e., an adaptive therapy protocol strategy. Information here refers to the structure used to model the knowledge the players in the game acquire and the history of their decision-effect when they make the decisions for their next move. We introduce here some concepts used hereafter:

• Players are the participants in a game, in competition against each other. In our context these are the different multi-drug selections and protocols competing for the best patient outcome;
• Actions of a player, denoting here the drug profiles and timeline administered to the patient;
• Information in game theory refers to acquiring knowledge about the game, skills, and forecasting of move effects in finding optimality; in our context, this refers to the knowledge of how the patient responds to the drug profile both past and forecasted in optimum seeking algorithms;
• Strategy refers to the association between a player’s move and the information available at that moment; this is fairly similar in our context denoting the controller’s optimal solution-seeking protocol and can be cooperative or non-cooperative, static or adaptive, etc;
• Utility (or reward) is part of the optimization cost variable and for our case, this is the minimal amount of drug which maximizes the patient outcome, i.e., minimizes a relative ratio between volume growth and cell death rate.

It is necessary to explicitly represent the dynamic nature of the game theory parallelism to the multi-drug decision system, as it evolves over a period of time, i.e., the active treatment period in the patient. The current state of the tumor volume specifies the current situation of the dynamic game (dose-effect relationships), including the set of players (choice of drug cocktail), actions available to them (drug profiles expressed in amount and time interval dosage), and their utilities at this time (relative tumor volume reduction). As an example, a subclass of Markov games with multiagent sequential decision-making under uncertainties has been discussed in [30]. The decision-making process is based on a reinforcement learning (RL) principle, where the future choices of the actions are shaped by feedback of a reward function, in our case this being the therapeutic effect on the patient. The gradient play is most relevant here as it indicates a convergence of the RL scheme towards a Nash equilibrium in dynamic environments. The asymptotic behavior of such systems has been broadly discussed in [30].

When analyzing systems with limited resources, noncooperative games have been proven to be good candidates for reaching Nash equilibrium (NE). To minimize the risk for drug resistance and side effects of drug therapy in patients and improve the quality of life in cancer-treated patients, it is desirable to minimize the amount of drug or intensity of radiation profiles. If we have multiple players denoting multiple therapy profile strategies, reaching NE implies solving the problem of finding the best strategy for one player, given all other players move at optimality solution. That is, it needs to determine the actions that players should take to achieve the best outcome in response to other players’ actions. In terms of finding the best treatment protocols, finding NE implies having an adaptive protocol strategy. If the drug selection remains constant, it represents that the number of players is constant. If the drug selection also varies, then it represents that the number of players in the game changes as well. The coalition consists of multiple agents collectively acting as a virtual player to minimize a coalition cost function, defined as the sum of all agents’ local cost functions, as represented in Figure 2.

To analyze the number of feasible solutions and their convergence for biological applications one may employ the theory of Lyapunov analysis [31], particularly useful in designing continuous-time distributed NE-seeking algorithms. In this context, Figure 2 depicts a non-cooperative game with gradient play for an average consensus collecting the sum of all local cost functions. A convergence analysis for NE seeking in N-coalition games has been discussed in [32].

From a clinical perspective, the selection of drugs to be used in multi-drug combination therapy in cancer patients is crucial, because of their interconnected effects described by drug synergy and drug resistance. This translates to the choice of agents within a coalition set. Aggregative games are a special subclass of non-cooperative games where the decision process of each agent depends on the aggregate effect of all agents in the coalition. In this case, convergence is based on the monotonicity of convex functions, i.e., a gradient descent in tumor volume effect. Solutions for center-based NE seeking in such population games are presented in [33].

In this paper, we investigate the effect of a distributed NE-seeking problem with various coalition profiles, whereas the agents remain the same. In particular, we employ the model from (1) for a set of three drugs, with coalitions defined as cases in the next section.

3. Results

The following is a summary of the obtained results for various sets of the domain of feasible solutions within the coalition game optimality described in the prior section. The following settings were applied: sampling time of 1 day, optimality calculated per day with a recurrent prediction horizon of 7 days, fixed antiangiogenesis therapy as 0.171 mg/mL per day single dose weekly. Single-patient model settings were considered. A supporting immunotherapy profile has been administered as 0.2 mg/mL per day, a single dose weekly. The corresponding concentrations are depicted in Figure 3.

Three coalitions have been evaluated, for which the corresponding optimal profiles are given in Figure 4.

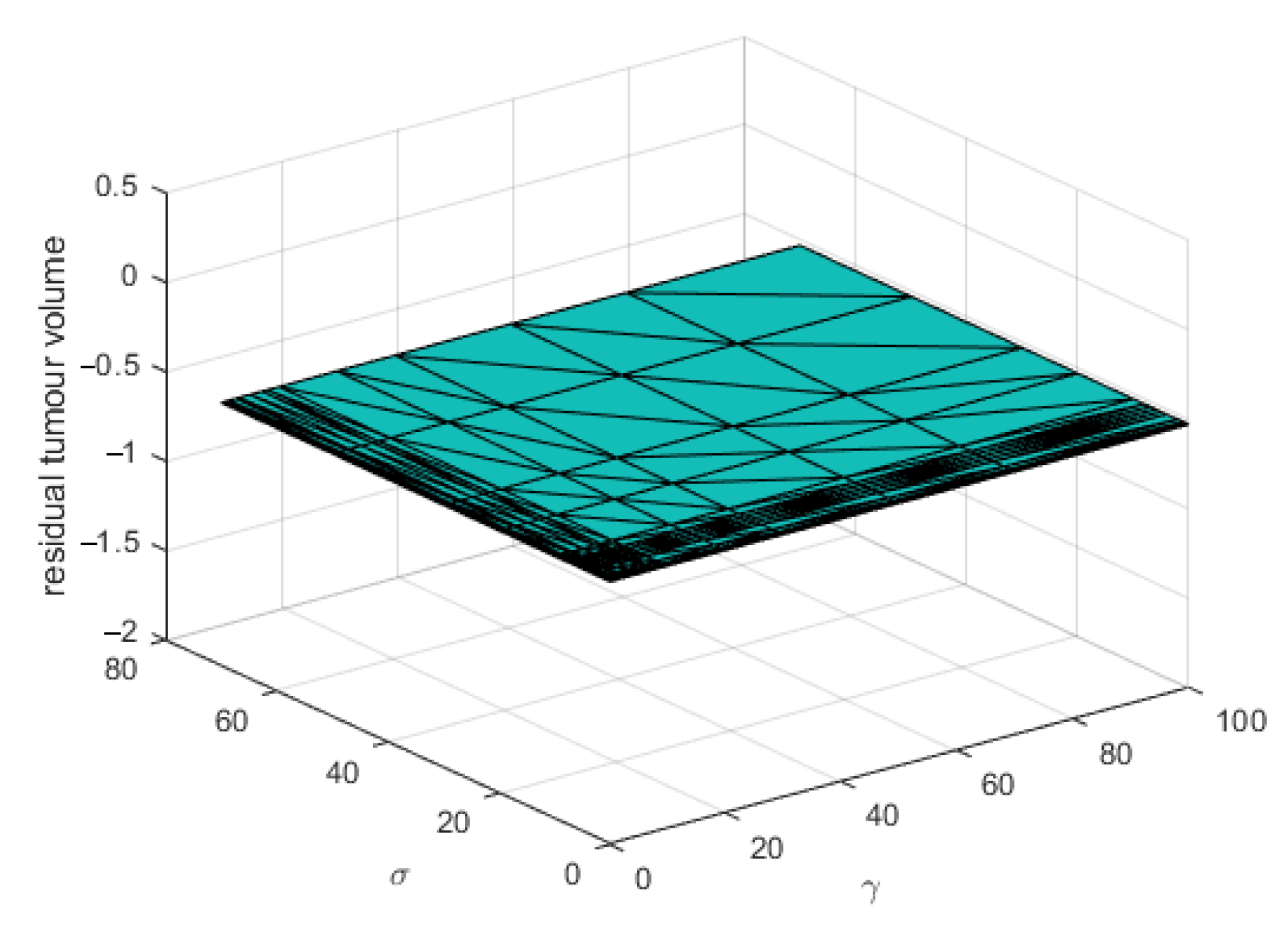
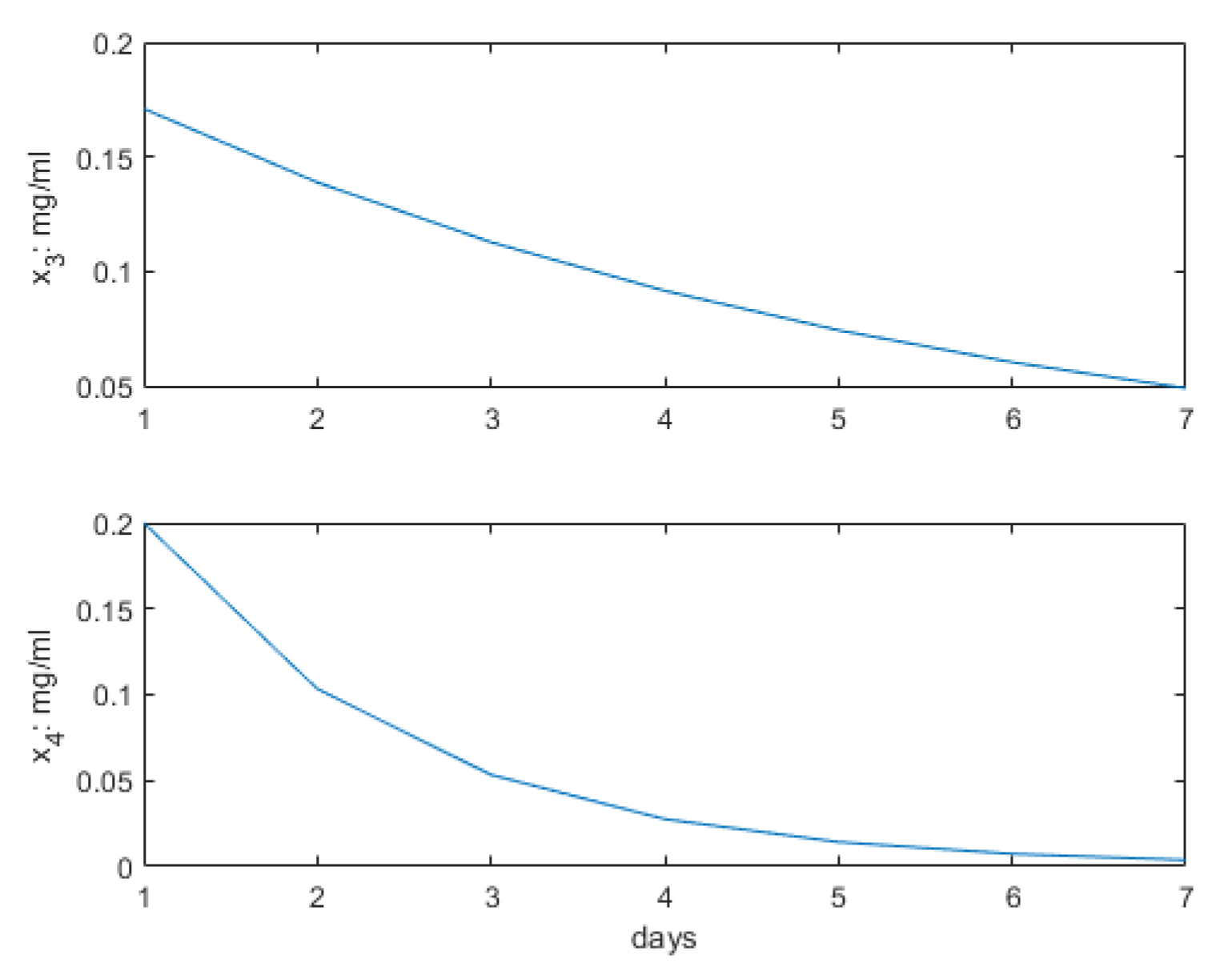
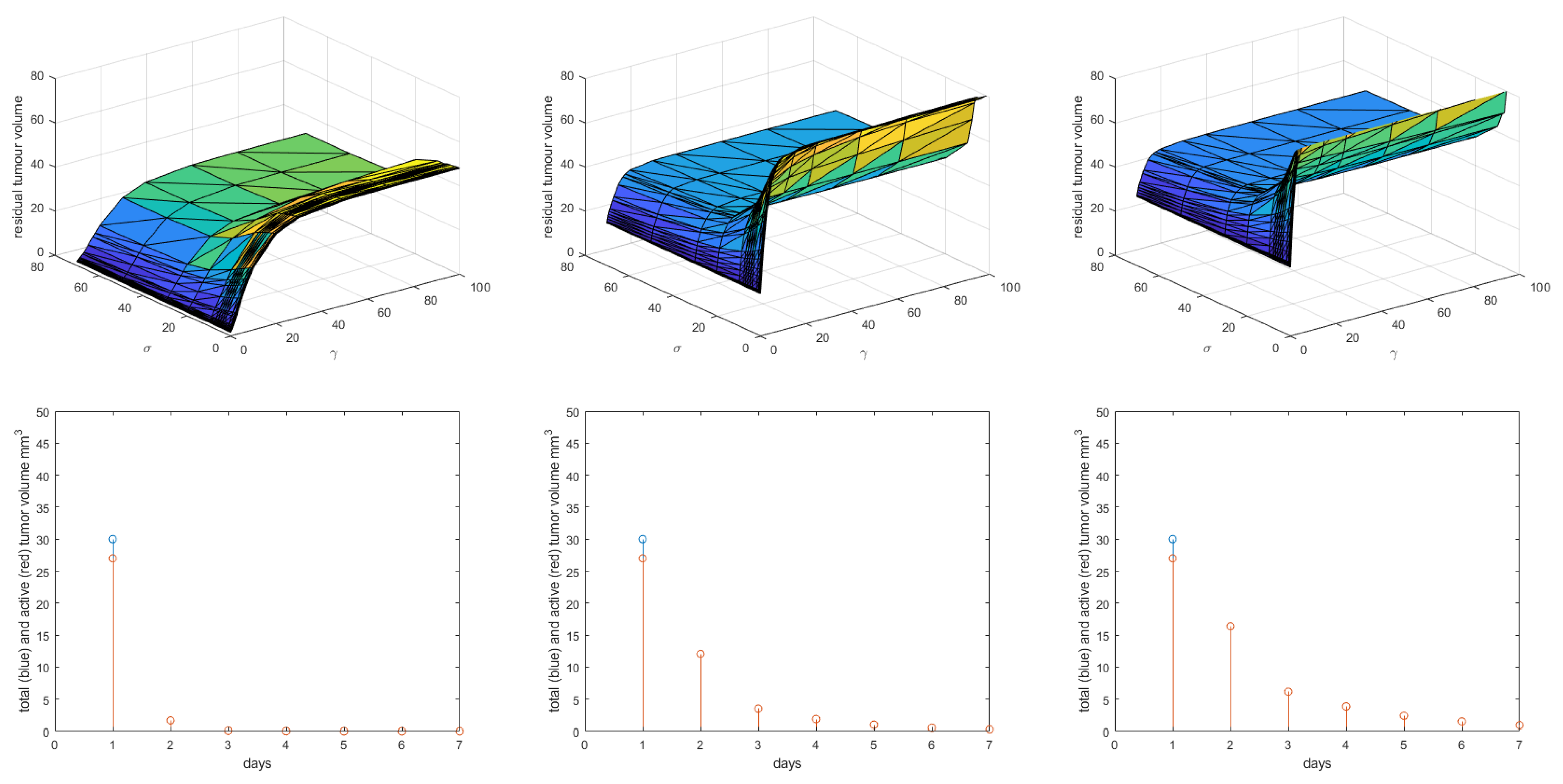
The results of the three coalitions are given in Figure 5, Figure 6 and Figure 7, respectively. The results suggest the model-based control methodology presented here has clinical relevance in analyzing the effect on short-term tumor growth dynamics.

4. Discussion

Carcinogenesis is progressively developing by acquiring specific collective characteristics of tumorous cells in order to persist within the tissue. Since all cell populations have an intrinsic self-renewal capacity, neoplastic cells will also rapidly increase, developing their blood supply for facilitating nutrient demands. The concepts promoting tumor growth and progression are important due to their involvement in multi-drug therapeutic applications, where drugs are developed to interfere with each of these capabilities of tumor growth. The formation of new multi-drug treatment options to target specific morphological and functional abnormal properties is only possible via earlier simulations of predicted optimal responses [34,35].

The augmented model provided here allows investigations into regional anomalous diffusion and dose-effect variability in patients undergoing multi-drug therapy for lung cancer. In fact, the principles governing the equations of the proposed model are generally applicable to any other kind of tumor tissue growth analysis. As such, the variability observed in terms of diffusion is rather small, given the limited scale of analysis and lack of micro-scale modeling of molecular binding patterns [36]. However, we foresee the potential of this model in being complementary to other meso- and micro-scale model analyses for a more comprehensive investigation. Residual times of drug molecules in sub-diffusive environment $\alpha \ll 1$ are not included since they cannot be validated. Diffusion can be validated through MRI data and observing patterns of enhanced colored bio-markers in the various areas of the tissue.

The projection between multi-drug optimal predictive control and multi-agent coalition (multi players) networked games is indeed novel in this application domain. A stability analysis following searchability and convergence to Nash equilibrium has not been performed. For this, more information is necessary, as to the clinically feasible knowledge domain of search for valid solutions while monotonicity must be guaranteed for convergence. As the research is in its infancy, the limited clinical data available does not allow the validation of such models.

From a modeling point of view, distributed games over networks including Nash equilibrium convergence are defined as stochastic problems, and as such, stochastic models may better fit the task. Stochastic models have been recently largely employed to characterize pandemic evolution [37]. When using multi-agent networked coalitions, this becomes a problem of decision-making of multiple self-interested decision-makers, where uncertainty and risk can be explicitly formulated under the Nash equilibrium problem [38]. However, in this control methodology, one must be aware of the difference between anticipative versus adaptive models for optimal search algorithms. In the case of the best treatment profile of combined drug therapy [39,40], the delineation between the two concepts is not yet defined, creating confusion in terminology. We expect that model-based predictive control plays the anticipative role [41], but the adaptation of the model itself to the new patient set of conditions must be integrated into a recurrent optimal search solution [42,43].

Using the conceptual framework that comprises the integral components of most forms of cancer, we envision significant advances in the development of mathematical modeling approaches in cancer research. The power of mathematics lies in its capacity to quantitatively describe the driving mechanisms investigated above, despite the complexity of cancer. Through mathematical formalism, we can address an abstraction of the underlying biological hypotheses, evaluate assumptions, investigate alternative solutions and make predictions that have to be tested and validated in multiple experiments. Individualized and targeted anti-cancer therapy requires the use of population-derived models despite the manual effort based on the clinician’s level of experience. Introducing quantitative approaches to predict tumor dynamics and patients’ responses based on mathematical models and prior data of the patient will provide model-driven predictions in the treatment planning process of cancer [44].

5. Conclusions

This study set out to prove the use of PKPD computational models and fractional tools to characterize the physiological processes of distribution and diffusion of drugs in the tumor. The variety of biological properties of cancer tissue provokes heterogeneous disparity of diffusion in space and time. We have proposed a mathematical approach to enhance drug absorption in the primary tumor and characterize the tumor dynamics under drug action. The biological events in healthy cancer tissue are influenced by microscale processes, taking into account the spatial distribution and the range of time. Moreover, the relation between multi-drug optimal predictive control and multi-agent coalition networked games brings novelty to this topic, anticipating the patient’s response to treatment and allowing its simulation. The principal theoretical implication of this study is that the proposed mathematical formulations are capable to define the macroscale properties of the anomalous tumor dynamics, capturing spatio-temporal anomalous drug diffusion, and identifying the specific response to therapy.