L(2, 1)-Labeling Halin Graphs with Maximum Degree Eight

Abstract

Suppose that T is a plane tree without vertices of degree 2 and with at least one vertex of at least degree 3, and C is the cycle obtained by connecting the leaves of T in a cyclic order. Set $G=T\cup C$, which is called a Halin graph. A k-$L(2,1)$-labeling of a graph $G=(V,E)$ is a mapping $f:V\left(G\right)\to \{0,1,\dots ,k\}$ such that, for any $x_1,x_2\in V\left(G\right)$, it holds that $|f\left(x_1\right)-f\left(x_2\right)|\ge 2$ if $x_1{x}_2\in E\left(G\right)$, and $|f\left(x_1\right)-f\left(x_2\right)|\ge 1$ if the distance between $x_1$ and $x_2$ is 2 in G. The $L(2,1)$-labeling number, denoted $\lambda \left(G\right)$, of G is the least k for which G is k-$L(2,1)$-labelable. In this paper, we prove that every Halin graph G with $\Delta =8$ has $\lambda \left(G\right)\le 10$. This improves a known result, which states that every Halin graph G with $\Delta \ge 9$ satisfies $\lambda \left(G\right)\le \Delta +2$. This result, together with some known results, shows that every Halin graph G satisfies $\lambda \left(G\right)\le \Delta +6$.

1. Introduction

Graph coloring and labeling play significant roles in graph theory and combinatorial optimization, for example, in the famous Four-Color Problem stimulating the rapid development of graph theory and network theory, where many symmetric properties are widely investigated and used, such as, symmetric graphs generated from automorphism groups, symmetric embedding, and drawings of graphs in the surface. Stanley [1] introduced a homogeneous symmetric function generalization of the chromatic polynomial of a graph to investigate the graph coloring problems. In 2018, Gross et al. [2] explored the relation between graph symmetry and colorings.

This paper focuses on simple graphs. Given a graph G, the notation $V\left(G\right)$, $E\left(G\right)$, $\left|G\right|$, and $\Delta \left(G\right)$ (or simply, $\Delta$) are used to denote the vertex set, the edge set, the vertex number, and the maximum degree of G, respectively. For a vertex v of G, let $N_G\left(v\right)$ (or simply, $N\left(v\right)$) denote the set of vertices that are adjacent to v in G. We say that v is a d-vertex, a $d^{+}$-vertex, and a $d^{-}$-vertex if the degree of v is d, at least d, and at most d, respectively. The distance, denoted $d_G(y_1,y_2)$, between two vertices $y_1$ and $y_2$, is defined as the length of a shortest path from $y_1$ to $y_2$ in G.

Assume that $k\ge 2$ is an integer. A k-$L(2,1)$-labeling of a graph G is a mapping $f:V\left(G\right)\to \{0,1,\dots ,k\}$ such that, for any $x_1,x_2\in V\left(G\right)$, it holds that $|f\left(x_1\right)-f\left(x_2\right)|\ge 2$ if $x_1{x}_2\in E\left(G\right)$, and $|f\left(x_1\right)-f\left(x_2\right)|\ge 1$ if $d_G(x_1,x_2)=2$. The $L(2,1)$-labeling number, denoted $\lambda \left(G\right)$, of G is the least k for which G is k-$L(2,1)$-labelable.

The $L(2,1)$-labeling of graphs stems from the famous frequency channel assignment problem, due to Hale [3]. By the definition, it holds trivially that $\lambda \left(G\right)\ge \Delta +1$ for any graph G. Griggs and Yeh [4] put forward the following conjecture.

Conjecture 1.

For a graph G with$\Delta \ge 2$, $\lambda \left(G\right)\le {\Delta }^2$.

Conjecture 1 remains open. In 1996, Chang and Kuo [5] first proved that $\lambda \left(G\right)\le {\Delta }^2+\Delta$ for any graph G. Later, this result was improved to $\lambda \left(G\right)\le {\Delta }^2+\Delta -1$ in [6], and furthermore to $\lambda \left(G\right)\le {\Delta }^2+\Delta -2$ in [7]. By means of probabilistic analysis, Havet et al. [8] showed that there is a constant ${\Delta }_0$ so that every graph G with $\Delta \ge {\Delta }_0$ has $\lambda \left(G\right)\le {\Delta }^2$. It was shown in [9] that $\lambda \left(G\right)\le 2\Delta +35$ for a planar graph G. Molloy and Salavatipour [10] decreased this bound to $\lambda \left(G\right)\le \lceil 5\Delta /3\rceil +95$. Wang and Lih [11] proved that if a planar graph G does not contain a cycle of length three or four, then $\lambda \left(G\right)\le \Delta +21$. Zhu et al. [12] reinforced this result by demonstrating that every planar graph G having no cycles of length four satisfies $\lambda \left(G\right)\le \Delta +19$. Wang [13] confirmed that a $\Delta \ge 3$ tree T has $\lambda \left(T\right)=\Delta +1$, provided no two $\Delta$-vertices x and y in T satisfies $d_T(x,y)\in \{1,2,4\}$.

Suppose that T is a plane tree with $\Delta \ge 3$ and without 2-vertices. Let $v\in \left(T\right)$. We say that v is a leaf if $d\left(v\right)=1$, and a handle if $d\left(v\right)\ge 2$ and v is adjacent to at most one $2^{+}$-vertex. A d-handle is a handle that is of degree d. Let C be the cycle obtained by connecting the leaves of T in a cyclic order. Define the graph $G=T\cup C$, which is called a Halin graph. The vertices in $V\left(C\right)$ and in $V\left(G\right)\backslash V\left(C\right)$ are called the outer vertices and inner vertices of G, respectively. As a special case, we call G a wheel if $\left|V\right(G)\backslash V(C\left)\right|=1$.

Halin graphs are a class of important planar graphs as they possess many interesting structural properties. It is well known that Halin graphs are minimal 3-connected graphs. Namely, every Halin graph is 3-connected, whereas each of its subgraphs is not. In an earlier paper, Bondy and Lovász [14] showed that Halin graphs are almost pancyclic with the possible exception of an even cycle. Stadler [15] proved that Halin graphs other than necklaces have a unique minimum cycle basis. Chandran et al. [16] showed that the boxicity of a Halin graph is 2. For other results on Halin graphs, the reader is referred to [17,18,19,20,21,22].

Suppose that G is a Halin graph. The third author of this paper proved in [23] that: (a) $\lambda \left(G\right)\le \Delta +7$; (b) $\lambda \left(G\right)\le \Delta +2$ for $\Delta \ge 9$; (c) $\lambda \left(G\right)\le 9$ for $\Delta =3$. Chen and Wang [24] showed that if $\Delta \le 7$, then $\lambda \left(G\right)\le 10$. The goal of this paper is to extend these results by showing the following consequences:

(1)

If G is a Halin graph with $\Delta =8$, then $\lambda \left(G\right)\le 10$;

(2)

For every Halin graph G, it holds that $\lambda \left(G\right)\le \Delta +6$.

2. Structural Analysis

The proof of the main result in this paper is by induction on the vertex number of graphs. To do this, we need to find some special structures in graphs under consideration that can be reduced in the induction process. Such special structures may consist of 14 configurations, as described in the following lemma.

Lemma 1.

Let $G=T\cup C$ be a Halin graph with $\Delta =8$ that is not a wheel. Then C contains a path $P_k=x_1{x}_2\cdots x_k$, satisfying one of the following conditions, as shown in Figure 1:

Figure 1. Configurations (C1)–(C14) in Lemma 1.

(C1) $k=4$, and there exists a vertex v adjacent to two 3-handles $u_1$ and $u_2$ such that $N\left(u_1\right)=\{v,x_1,x_2\}$ and $N\left(u_2\right)=\{v,x_3,x_4\}$.

(C2) $k=5$, and there exists a vertex v adjacent to a 3-handle $u_1$ and a 4-handle $u_2$ such that $N\left(u_1\right)=\{v,x_1,x_2\}$ and $N\left(u_2\right)=\{v,x_3,x_4,x_5\}$.

(C3) $k=6$, and there exists a vertex v adjacent to two 4-handles $u_1$ and $u_2$ such that $N\left(u_1\right)=\{v,x_1,x_2,x_3\}$ and $N\left(u_2\right)=\{v,x_4,x_5,x_6\}$.

(C4) $k=4$, and there exists a vertex v adjacent to $x_4$ and a 4-handle u such that $N\left(u\right)=\{v,x_1,x_2,x_3\}$.

(C5) $k=3$, and there exists a $5^{-}$-vertex v adjacent to $x_3$ and a 3-handle u such that $N\left(u\right)=\{v,x_1,x_2\}$.

(C6) $k=4$, and there exists a $6^{-}$-vertex v adjacent to $x_1,x_4$ and a 3-handle u such that $N\left(u\right)=\{v,x_2,x_3\}$.

(C7) $k=5$, and there exists a 7-vertex v adjacent to $x_1,x_4,x_5$ and a 3-handle u such that $N\left(u\right)=\{v,x_2,x_3\}$.

(C8) $k=6$, and there exists a 8-vertex v adjacent to $x_1,x_4,x_5,x_6$ and a 3-handle u such that $N\left(u\right)=\{v,x_2,x_3\}$.

(C9) $k=7$, and there exists a vertex v adjacent to $x_1,x_4,x_7$ and two 3-handles $u_1$ and $u_2$ such that $N\left(u_1\right)=\{v,x_2,x_3\}$ and $N\left(u_2\right)=\{v,x_5,x_6\}$.

(C10) $k=8$, and there exists a vertex v adjacent to $x_1,x_4,x_5,x_8$ and two 3-handles $u_1$ and $u_2$ such that $N\left(u_1\right)=\{v,x_2,x_3\}$ and $N_G\left(u_2\right)=\{v,x_6,x_7\}$.

(C11) $k\ge 4$, and there exists a $(k+1)$-handle u such that $N\left(u\right)=\{v,x_1,x_2,\dots ,x_k\}$.

(C12) $k\ge 7$, and there exists a vertex v adjacent to $x_3,x_4,\dots ,x_k,w$ and a 3-handle u such that $N\left(u\right)=\{v,x_1,x_2\}$ and $N\left(v\right)=\{u,x_3,\dots ,x_k,w\}$.

(C13) $k\ge 8$, and there exists a vertex v adjacent to $x_3,x_4,\dots ,x_{k-2},w$ and two 3-handles $u_1$ and $u_2$ such that $N\left(u_1\right)=\{v,x_1,x_2\}$, $N\left(u_2\right)=\{v,x_{k-1},x_k\}$, and $N\left(v\right)=\{u_1,u_2,x_3,\dots ,x_{k-2},w\}$.

(C14) $k=10$, and there exists a vertex v adjacent to $x_3,x_4,x_7,x_8,w$ and three 3-handles $u_1,u_2,u_3$ such that $N\left(u_1\right)=\{v,x_1,x_2\}$, $N\left(u_2\right)=\{v,x_5,x_6\}$, $N\left(u_3\right)=\{v,x_9,x_{10}\}$, and $N\left(v\right)=\{u_1,u_2,u_3,x_3,x_4,x_7,x_8,w\}$.

Proof. 

Since G is not a wheel, $\left|V\right(G)\backslash V(C\left)\right|\ge 2$. If $\left|V\right(G)\backslash V(C\left)\right|=2$, then (C4), (C5), or (C11) holds clearly. Thus, assume that $\left|V\right(G)\backslash V(C\left)\right|\ge 3$. Let $P=y_1{y}_2\dots y_n$ be the longest path in $G-V\left(C\right)$. Then $n\ge 3$ and $y_1,y_n$ are handles in T. Let $y_3,z_1,z_2,\dots ,z_m$ denote the neighbors of $y_2$ in T in clockwise order, where $2\le m\le 7$, and $y_1=z_l$ for some $1\le l\le m$. Thus each $z_i$ is either a handle or a leaf in T by the choice of P.

If $y_2$ is adjacent to a $5^{+}$-handle, then (C11) holds. If $y_2$ is adjacent to two consecutive $4^{-}$-handles in $N\left(y_2\right)$, then either (C1), (C2), or (C3) holds. So suppose that neither $5^{+}$-handles nor two consecutive $4^{-}$-handles are contained in $N\left(y_2\right)$. If $y_2$ is adjacent to a 4-handle, say $z_j$, then at least one of $z_{j-1}$ and $z_{j+1}$ is a leaf in T, where the indices are taken modulo m. Thus, (C4) occurs in G. Otherwise, all handles in $N\left(y_2\right)$ are 3-handles. Let $\beta$ denote the number of 3-handles in $\{z_1,z_2,\dots ,z_m\}$. Then $1\le \beta \le 4$ since $d\left(y_2\right)\le \Delta \le 8$. If $d\left(y_2\right)\le 5$, then (C5) holds obviously. Hence, assume that $6\le d\left(y_2\right)\le 8$. □

Case 1. $\beta =1$.

If $z_1$ or $z_m$ is 3-handle, then (C12) holds. Otherwise, $z_i$ is a 3-handle for some $2\le i\le m-1$. If $d\left(y_2\right)=6$, then (C6) holds. If $d\left(y_2\right)\ge 7$, then (C8) holds.

Case 2. $\beta =2$.

Suppose that $z_i$ and $z_j$ are 3-handles in $\{z_1,z_2,\dots ,z_m\}$ with $1\le i<j\le m$. Assume that $|\{z_1,z_2,\dots ,z_{i-1}\}|\le |\{z_{j+1},z_{j+2},\dots ,z_m\}|$. It suffices to consider the following three possibilities by symmetry.

• $i=1$ and $j=m$. Then (C13) holds;
• $i=1$ and $j\le m-1$. Then $z_{j-1}$ and $z_{j+1}$ are leaves in T. If $d\left(y_2\right)\le 6$, then (C6) holds. If $d\left(y_2\right)=7$, then (C7) holds. If $d\left(y_2\right)=8$, then $m=7$, we have $\left|\right\{z_2,z_3,\dots ,z_{s-1}\left\}\right|\ge 3$ or $\left|\right\{z_{s+1},z_{s+2},\dots ,z_7\left\}\right|\ge 3$. Thus, (C8) holds;
• $i\ge 2$ and $j\le m-1$. If $d\left(y_2\right)\le 6$, then (C6) holds. If $d\left(y_2\right)=7$, then (C7) holds. Otherwise, $d\left(y_2\right)=8$. Note that $2\le j-i\le 4$. If $j-i=2$, then (C9) holds. If $j-i=3$, then (C10) holds. If $j-i=4$, that is $i=2$ and $j=6$, then (C8) holds.

Case 3. $\beta =3$.

Suppose that $z_p,z_q,z_r$ are 3-handles adjacent to $y_2$ with $1\le p<q<r\le m$. Assume that $|\{z_1,z_2,\dots ,z_{p-1}\}|\le |\{z_{r+1},z_{r+2},\dots ,z_m\}|$, say. If $d\left(y_2\right)=6$, then (C6) holds. Assume that $d\left(y_2\right)=7$. Then $z_{q-1}$ and $z_{q+1}$ are leaves in T. If both $z_1$ and $z_6$ are 3-handles, then (C7) holds. Otherwise, we have $p=1$, $q=3$ and $r=5$, and hence (C9) holds. Now assume that $d\left(y_2\right)=8$. If $p\ne 1$ and $r\ne 7$, then it is easy to get that $p=2$, $q=4$, and $r=6$, and hence (C9) holds. Otherwise, we assume that $p=1$. If $r=7$, then it follows that $q\in \{3,4\}$ or $q\in \{4,5\}$, say the former holds. If $q=3$, then (C8) holds. If $q=4$, then (C14) holds. Assume that $r\le 6$. It is easy to see that $r\in \{5,6\}$. If $r=5$, then (C9) holds. If $r=6$, then (C9) or (C10) holds.

Case 4. $\beta =4$.

It is immediate to derive that $z_1,z_3,z_5,z_7$ are 3-handles, and hence (C9) holds.

3. Preliminary Results

An $L^{\ast }(2,1)$-labeling of a graph G is defined to be a one-to-one $L(2,1)$-labeling. A function L is said to be an assignment for the graph G if it assigns a list $L\left(v\right)$ of possible labels to each vertex v of G. If G has an $L(2,1)$-labeling (or $L^{\ast }(2,1)$-labeling, respectively) f such that $f\left(v\right)\in L\left(v\right)$ for all vertices v, then we say that f is an L-$L(2,1)$-labeling (or L-$L^{\ast }(2,1)$-labeling, respectively) of G. Given an integer $n\ge 1$, we use $\underline{n}$ to denote three consecutive integers $n-1,n,n+1$.

Lemma 2 below is an easy observation and hence we omit its proof.

Lemma 2.

Let L be a list assignment for an edge $xy$ such that $\left|L\right(x\left)\right|,\left|L\right(y\left)\right|\ge 2$. Then $xy$ has an L-$L(2,1)$-labeling unless $L\left(x\right)=L\left(y\right)=\{p,p+1\}$ for some integer p.

Lemma 3.

Let $P=x_1{x}_2{x}_3$ be a path. Let L be a list assignment for $V\left(P\right)$ such that $\left|L\right(x_1\left)\right|\ge 2$, $\left|L\right(x_2\left)\right|\ge 4$, and $\left|L\right(x_3\left)\right|\ge 3$. Then P has an L-$L^{\ast }(2,1)$-labeling.

Proof. 

Without loss of generality, assume that $\left|L\right(x_1\left)\right|=2$, $\left|L\right(x_2\left)\right|=4$, and $\left|L\right(x_3\left)\right|=3$. Furthermore, let $L\left(x_2\right)=\{a,b,c,d\}$ with $a<b<c<d$.

First suppose that there exists $p\in L\left(x_1\right)\backslash L\left(x_2\right)$. Label $x_1$ with p and then define a list assignment $L^{\prime }$ for $x_2$ and $x_3$: $L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \{p-1,p+1\}$ and $L^{\prime }\left(x_3\right)=L\left(x_3\right)\backslash \left\{p\right\}$. Then $|L^{\prime }\left(x_2\right)|\ge 4-2=2$ and $|L^{\prime }\left(x_3\right)|\ge 3-1=2$. By Lemma 2, $x_2$ and $x_3$ are not $L^{\prime }$-$L(2,1)$-labelable only if $L^{\prime }\left(x_2\right)=L^{\prime }\left(x_3\right)=\{q,q+1\}$ for some integer q, that is, $L\left(x_2\right)=\{p-1,p+1,q,q+1\}$ and $L\left(x_3\right)=\{p,q,q+1\}$. Since $p-1,p+1,q,q+1$ are mutually distinct, we may assume that $p+1<q$. Let $r\in L\left(x_1\right)\backslash \left\{p\right\}$. If $r<q$, then we label $x_1,x_2,x_3$ with $r,q+1,p$, respectively. Otherwise, $r\ge q$, we label $x_1$ with r, $x_2$ with $p-1$, and $x_3$ with a label in $\{q,q+1\}\backslash \left\{r\right\}.$

Next suppose that $L\left(x_1\right)\subset L\left(x_2\right)$. By symmetry, we only need to deal with the following two cases.

Case 1. $L\left(x_1\right)=\{a,t\}$ where $t\in \{b,c,d\}$.

If there exists a label $r\in L\left(x_3\right)\backslash \left\{a\right\}$ such that $r<c$, then we label $x_1$ with a, $x_2$ with d, and $x_3$ with r. Otherwise, there exist $r_1,r_2\in L\left(x_3\right)\backslash \left\{a\right\}$ such that $r_2>r_1\ge c$. There are three subcases to be considered, as follows.

• $t=b$. If $r_1>c$, or $r_2>d$, then we label $x_1$ with a, $x_2$ with c, and $x_3$ with $r_2$. Otherwise, $r_1=c$ and $r_2\le d$. If $a\in L\left(x_3\right)$, then we label $x_1$ with b, $x_2$ with d, and $x_3$ with a. So assume that $a\notin L\left(x_3\right)$. Thus, there is $r_3\in L\left(x_3\right)\backslash \{c,r_2\}$ with $r_3>c$. If $r_3>r_2$, then we label $x_1$ with a, $x_2$ with c, and $x_3$ with $r_3$. If $c<r_3<r_2$, then we label $x_1$ with a, $x_2$ with c, and $x_3$ with $r_2$;

• $t=c$. If $r_1>c$, then we label $x_1$ with a, $x_2$ with c, and $x_3$ with $r_2$. Otherwise, $r_1=c$. If $r_2\ge d$, then we label $x_1$ with c, $x_2$ with a, and $x_3$ with $r_2$. Otherwise, $c<r_2<d$, we label $x_1$ with a, $x_2$ with d, and $x_3$ with c;

• $t=d$. If $r_2>d$, then we label $x_1$ with a, $x_2$ with c, and $x_3$ with $r_2$. Otherwise, $r_2\le d$ and henceforth $c\le r_1<d$. If $r_1=c$, then we label $x_1$ with d, $x_2$ with a, and $x_3$ with c. Otherwise, $r_1>c$, we label $x_1$ with a, $x_2$ with c, and $x_3$ with $r_2$.

Case 2. $L\left(x_1\right)=\{b,c\}$.

Let $L\left(x_3\right)=\{q_1,q_2,q_3\}$ with $q_1<q_2<q_3$. If $q_3\ge d$, then we label $x_1$ with c, $x_2$ with a, and $x_3$ with $q_3$. If $q_1\le a$, then we label $x_1$ with b, $x_2$ with d, and $x_3$ with $q_1$. Otherwise, $a<q_1<q_2<q_3<d$, we label $x_1$ with b, $x_2$ with d, and $x_3$ with some label in $\{q_1,q_2\}\backslash \left\{b\right\}$. □

Lemma 4.

Let $P=x_1{x}_2{x}_3{x}_4$ be a path. Let L be a list assignment for $V\left(P\right)$ such that $\left|L\right(x_1\left)\right|\ge 2$, $|L\left(x_2\right)|,|L\left(x_3\right)|\ge 5$, and $\left|L\right(x_4\left)\right|\ge 3$. Then P has an L-$L^{\ast }(2,1)$-labeling.

Proof. 

Assume that $\left|L\right(x_1\left)\right|=2$, $|L\left(x_2\right)|=|L\left(x_3\right)|=5$, and $\left|L\right(x_4\left)\right|=3$. If there is a label $a\in L\left(x_1\right)$ such that $|L\left(x_2\right)\cap \left\{\underline{a}\right\}|\le 2$, then we label $x_1$ with a and then define a list assignment $L^{\prime }$ for $x_2,x_3,x_4$ as follows: $L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \left\{\underline{a}\right\}$, $L^{\prime }\left(x_i\right)=L\left(x_i\right)\backslash \left\{a\right\}$ for $i=3,4$. It is easy to calculate that $|L^{\prime }\left(x_2\right)|\ge 3$, $|L^{\prime }\left(x_3\right)|\ge 4$, and $|L^{\prime }\left(x_4\right)|\ge 2$. By Lemma 3, $x_2,x_3,x_4$ are $L^{\prime }$-$L(2,1)$-labelable.

If there is a label $b\in L\left(x_1\right)\backslash L\left(x_4\right)$, then we label $x_1$ with b and then define a list assignment $L^{\prime }$ for $x_2,x_3,x_4$ as follows: $L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \left\{\underline{b}\right\}$, $L^{\prime }\left(x_3\right)=L\left(x_3\right)\backslash \left\{b\right\}$, and $L^{\prime }\left(x_4\right)=L\left(x_4\right)$. Then $|L^{\prime }\left(x_2\right)|\ge 2$, $|L^{\prime }\left(x_3\right)|\ge 4$, and $|L^{\prime }\left(x_4\right)|=3$. By Lemma 3, $x_2,x_3,x_4$ are $L^{\prime }$-$L(2,1)$-labelable.

Otherwise, we have $L\left(x_1\right)\subset L\left(x_2\right)\cap L\left(x_4\right)$, and for each $a\in L\left(x_1\right)$, we have $|L\left(x_2\right)\cap \left\{\underline{a}\right\}|=3$. Let $L\left(x_1\right)=\{p,q\}$ with $p<q$. Then $p-1,p,p+1,q-1,q,q+1\in L\left(x_2\right)$. Since $\left|L\right(x_2\left)\right|=5$, we obtain that $q-p\le 2$.

Case 1. $q=p+1$, say $p=5$ and $q=6$.

Since $\left|L\right(x_3\left)\right|=5$, there must exist a label $r\in L\left(x_3\right)$ such that $r\le 4$ or $r\ge 9$, so that we can label $x_1,x_2,x_3,x_4$ with $5,7,r,6$, respectively.

Case 2. $q=p+2$, say $p=5$ and $q=7$.

It follows that $L\left(x_1\right)=\{5,7\}$, $L\left(x_2\right)=\{4,5,6,7,8\}$, and $5,7\in L\left(x_4\right)$. If there is $r\in L\left(x_3\right)$ such that $r\le 3$, then we label $x_1,x_2,x_3,x_4$ with $5,8,r,7$, respectively. If there is $r\in L\left(x_3\right)$ such that $r\ge 9$, then we label $x_1,x_2,x_3,x_4$ with $7,4,r,5$, respectively. Otherwise, $L\left(x_3\right)=\{4,5,6,7,8\}$. Let $b\in L\left(x_4\right)\backslash \{5,7\}$. If $b\le 4$, then we label $x_1,x_2,x_3,x_4$ with $5,8,6,b$, respectively. If $b\ge 8$, then we label $x_1,x_2,x_3,x_4$ with $5,7,4,b$, respectively. If $b=6$, then we label $x_1,x_2,x_3,x_4$ with $5,7,4,6$, respectively. □

Lemma 5.

Let $P=x_1{x}_2{x}_3{x}_4$ be a path. Let L be a list assignment for $V\left(P\right)$ such that $|L\left(x_1\right)|,|L\left(x_4\right)|\ge 2$ and $|L\left(x_2\right)|,|L\left(x_3\right)|\ge 5$. Then P has an L-$L(2,1)$-labeling.

Proof. 

Assume that $|L\left(x_1\right)|=|L\left(x_4\right)|=2$ and $|L\left(x_2\right)|=|L\left(x_3\right)|=5$. If there is a label $a\in L\left(x_1\right)$ such that $|L\left(x_2\right)\cap \left\{\underline{a}\right\}|\le 2$, then we label $x_1$ with a and then define a list assignment $L^{\prime }$ for $x_2,x_3,x_4$ as follows: $L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \left\{\underline{a}\right\}$, $L^{\prime }\left(x_3\right)=L\left(x_3\right)\backslash \left\{a\right\}$, and $L^{\prime }\left(x_4\right)=L\left(x_4\right)$. Then $|L^{\prime }\left(x_2\right)|\ge 3$, $|L^{\prime }\left(x_3\right)|\ge 4$, and $|L^{\prime }\left(x_4\right)|=2$. By Lemma 3, $x_2,x_3,x_4$ are $L^{\prime }$-$L(2,1)$-labelable. So suppose that $L\left(x_1\right)\subset L\left(x_2\right)$ and for each $a\in L\left(x_1\right)$, it holds that $|L\left(x_2\right)\cap \left\{\underline{a}\right\}|=3$. Similarly, $L\left(x_4\right)\subset L\left(x_3\right)$ and for each $b\in L\left(x_4\right)$, we have $|L\left(x_3\right)\cap \left\{\underline{b}\right\}|=3$. Thus, each of $L\left(x_2\right)$ and $L\left(x_3\right)$ contains at least four consecutive labels, and each of $L\left(x_1\right)$ and $L\left(x_4\right)$ consists of two labels whose difference is exactly 1 or 2.

Analogous to the proof of Lemma 4, we give the following discussion by symmetry.

Case 1. $L\left(x_1\right)=\{5,7\}$ and $L\left(x_2\right)=\{4,5,6,7,8\}$.

First assume that $L\left(x_3\right)=\{b,b+1,b+2,b+3,b+4\}$ and $L\left(x_4\right)=\{b+1,b+3\}$ for some integer b. If $b=4$, i.e., $L\left(x_3\right)=\{4,5,6,7,8\}$ and $L\left(x_4\right)=\{5,7\}$, then we label $x_1,x_2,x_3,x_4$ with $5,8,4,7$, respectively. If $b\ge 5$, then we label $x_1,x_2,x_3,x_4$ with $7,4,b+3,b+1$, respectively. If $b\le 3$, then we label $x_1,x_2,x_3,x_4$ with $5,8,b,b+3$, respectively.

Next assume that $\{b,b+1,b+2,b+3\}\subset L\left(x_3\right)$ and $L\left(x_4\right)=\{b+1,b+2\}$. If $b=4$, i.e., $L\left(x_4\right)=\{5,6\}$, then we label $x_1,x_2,x_3,x_4$ with $5,8,4,6$, respectively. If $b\ge 5$, then we label $x_1,x_2,x_3,x_4$ with $7,4,b+3,b+1$, respectively. If $b\le 3$, then we label $x_1,x_2,x_3,x_4$ with $5,8,b,b+2$, respectively.

Case 2. $L\left(x_1\right)=\{5,6\}$, $\{4,5,6,7\}\subset L\left(x_2\right)$, $L\left(x_4\right)=\{b+1,b+2\}$, and $\{b,b+1,b+2,b+3\}\subset L\left(x_3\right)$.

If $b=4$, i.e., $L\left(x_4\right)=\{5,6\}$, then we label $x_1,x_2,x_3,x_4$ with $5,7,4,6$, respectively. If $b\ge 5$, then we label $x_1,x_2,x_3,x_4$ with $6,4,b+3,b+1$, respectively. If $b\le 3$, then we label $x_1,x_2,x_3,x_4$ with $5,7,b,b+2$, respectively. □

Lemma 6.

Let $P=x_1{x}_2{x}_3{x}_4$ be a path. Let L be a list assignment for $V\left(P\right)$ such that $|L\left(x_1\right)|,|L\left(x_4\right)|\ge 2$ and $|L\left(x_2\right)|,|L\left(x_3\right)|\ge 6$. Then P has an L-$L^{\ast }(2,1)$-labeling.

Proof. 

Let $|L\left(x_1\right)|=|L\left(x_4\right)|=2$ and $|L\left(x_2\right)|=|L\left(x_3\right)|=6$. If there is a label $a\in L\left(x_1\right)$ such that $|L\left(x_2\right)\cap \left\{\underline{a}\right\}|\le 2$, then we label $x_1$ with a, $x_4$ with $b\in L\left(x_4\right)\backslash \left\{a\right\}$, and then define a list assignment $L^{\prime }$ for $x_2,x_3$ as follows: $L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \{\underline{a},b\}$, and $L^{\prime }\left(x_3\right)=L\left(x_3\right)\backslash \{\underline{b},a\}$. Then $|L^{\prime }\left(x_2\right)|\ge 3$ and $|L^{\prime }\left(x_3\right)|\ge 2$. By Lemma 2, $x_2,x_3$ are $L^{\prime }$-$L(2,1)$-labelable.

If $L\left(x_1\right)\ne L\left(x_4\right)$, then we label $x_1$ with a label $a\in L\left(x_1\right)\backslash L\left(x_4\right)$ and then define a list assignment $L^{\prime }$ for $x_2,x_3,x_4$ as follows: $L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \left\{\underline{a}\right\}$, $L^{\prime }\left(x_3\right)=L\left(x_3\right)\backslash \left\{a\right\}$, and $L^{\prime }\left(x_4\right)=L\left(x_4\right)$. Noting that $|L^{\prime }\left(x_2\right)|\ge 3$, $|L^{\prime }\left(x_3\right)|\ge 5$, and $|L^{\prime }\left(x_4\right)|=2$, $x_2,x_3,x_4$ are $L^{\prime }$-$L(2,1)$-labelable by Lemma 3.

Otherwise, we may assume that $L\left(x_1\right)=L\left(x_4\right)=\{a,b\}$ with $a<b$, and furthermore $L\left(x_2\right)=L\left(x_3\right)=\{a-1,a,a+1,b-1,b,b+1\}$. Label $x_1,x_2,x_3,x_4$ with $a,b+1,a+1,b$, respectively. □

Lemma 7.

Let $P=x_1{x}_2{x}_3{x}_4{x}_5$ be a path. If L is a list assignment for $V\left(P\right)$ satisfying the following conditions(1)and(2), then P has an L-$L^{\ast }(2,1)$-labeling.

• $\left|L\right(x_1\left)\right|\ge 2$, $|L\left(x_2\right)|,|L\left(x_3\right)|,|L\left(x_4\right)|\ge 5$, and $\left|L\right(x_5\left)\right|\ge 3$.
• $L\left(x_2\right)=L\left(x_3\right)=L\left(x_4\right)=S$ and $L\left(x_1\right),L\left(x_5\right)\subset S$.

Proof. 

Assume that $\left|L\right(x_1\left)\right|=2$, $\left|L\right(x_5\left)\right|=3$, $\left|S\right|=5$, and $S=\{a_1,a_2,a_3,a_4,a_5\}$ with $a_1<a_2<a_3<a_4<a_5$. Then the proof splits into the following two cases.

Case 1. $L\left(x_5\right)$ contains $a_1$ or $a_5$, say $a_1\in L\left(x_5\right)$.

If $a_3\in L\left(x_1\right)$, then we label $x_1,x_2,x_3,x_4,x_5$ with $a_3,a_5,a_2,a_4,a_1$, respectively. If $a_4\in L\left(x_1\right)$, then we label $x_1,x_2,x_3,x_4,x_5$ with $a_4,a_2,a_5,a_3,a_1$, respectively. Otherwise, $L\left(x_1\right)\subset \{a_1,a_2,a_5\}$.

• $L\left(x_1\right)=\{a_1,a_2\}$. If $a_3\in L\left(x_5\right)$ or $a_4\in L\left(x_5\right)$, we have a similar proof. Otherwise, $L\left(x_5\right)=\{a_1,a_2,a_5\}$. Label $x_1,x_2,x_3,x_4,x_5$ with $a_2,a_4,a_1,a_3,a_5$, respectively;
• $L\left(x_1\right)=\{a_1,a_5\}$. With the similar reasoning, we have $L\left(x_5\right)=\{a_1,a_2,a_5\}$, and $x_1,x_2,x_3,x_4,x_5$ can be labeled with $a_5,a_3,a_1,a_4,a_2$, respectively;
• $L\left(x_1\right)=\{a_2,a_5\}$. In view of the above discussion, we may assume that $L\left(x_5\right)=\{a_1,a_3,a_4\}$. It suffices to label $x_1,x_2,x_3,x_4,x_5$ with $a_2,a_4,a_1,a_5,a_3$, respectively.

Case 2. $L\left(x_5\right)=\{a_2,a_3,a_4\}$.

Note that at least one of $a_1,a_2,a_3,a_5$ is in $L\left(x_1\right)$. For each possible situation, we can construct a proper labeling for $V\left(P\right)$, similarly to the foregoing argument. □

Lemma 8.

Let $P=x_1{x}_2\dots x_7$ be a path. If L is a list assignment for $V\left(P\right)$ satisfying the following conditions (1) and (2), then P has an L-$L^{\ast }(2,1)$-labeling.

(1) $L\left(x_3\right)=L\left(x_4\right)=L\left(x_5\right)=S$, $L\left(x_1\right)\subset L\left(x_2\right)\subset S$, and $L\left(x_7\right)\subset L\left(x_6\right)\subset S$;

(2) $|L\left(x_1\right)|,|L\left(x_7\right)|\ge 2$, $|L\left(x_2\right)|,|L\left(x_6\right)|\ge 6$, and $\left|S\right|\ge 7$.

Proof. 

Assume that $|L\left(x_1\right)|=|L\left(x_7\right)|=2$, $|L\left(x_2\right)|=|L\left(x_6\right)|=6$, and $\left|S\right|=7$. In addition, let $S=\{a_1,a_2,\dots ,a_7\}$ with $a_1<a_2<\cdots <a_7$. If there is a label $p\in L\left(x_1\right)$ such that $|L\left(x_2\right)\cap \left\{\underline{p}\right\}|\le 2$, then we label $x_1$ with p and $x_7$ with $q\in L\left(x_7\right)\backslash \left\{p\right\}$, and then define a list assignment $L^{\prime }$ for $x_2,x_3,x_4,x_5,x_6$ as follows: $L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \{\underline{p},q\}$,

$L^{\prime }\left(x_6\right)=L\left(x_6\right)\backslash \{\underline{q},p\}$,

$L^{\prime }\left(x_i\right)=L\left(x_i\right)\backslash \{p,q\}$ for $i=3,4,5$.

It follows that $|L^{\prime }\left(x_2\right)|\ge 3$, $|L^{\prime }\left(x_6\right)|\ge 2$, and $\left|L\right(x_i\left)\right|\ge 5$ for $i=3,4,5$. Observing that $L^{\prime }\left(x_3\right)=L^{\prime }\left(x_4\right)=L^{\prime }\left(x_5\right)$ and $L^{\prime }\left(x_2\right),L^{\prime }\left(x_6\right)\subset L^{\prime }\left(x_3\right)$, Lemma 4 asserts that $x_2,x_3,x_4,x_5,x_6$ are $L^{\prime }$-$L^{\ast }(2,1)$-labelable. Otherwise, for any $p\in L\left(x_1\right)$ we have $|L\left(x_2\right)\cap \left\{\underline{p}\right\}|=3$, and for any $q\in L\left(x_7\right)$ we have $|L\left(x_6\right)\cap \left\{\underline{q}\right\}|=3$. Assume that $L\left(x_1\right)=\{a,b\}$ with $a<b$, and $L\left(x_7\right)=\{c,d\}$ with $c<d$. Then $L\left(x_2\right)=\{a-1,a,a+1,b-1,b,b+1\}$ and $L\left(x_6\right)=\{c-1,c,c+1,d-1,d,d+1\}$. By symmetry, we have to consider the following three cases.

Case 1. $L\left(x_1\right)=\{a_2,a_5\}$ and $L\left(x_2\right)=S\backslash \left\{a_7\right\}$.

If $L\left(x_7\right)=\{a_2,a_5\}$ and $L\left(x_6\right)=S\backslash \left\{a_7\right\}$, then we label $x_1,x_2,x_3,x_4,x_5,x_6,x_7$ with $a_2,a_6,a_4,a_7,a_1,a_3,a_5$, respectively. If $L\left(x_7\right)=\{a_2,a_6\}$ and $L\left(x_6\right)=S\backslash \left\{a_4\right\}$, then we label $x_1,x_2,x_3,x_4,x_5,x_6,x_7$ with $a_5,a_2,a_4,a_1,a_7,a_3,a_6$, respectively. If $L\left(x_7\right)=\{a_3,a_6\}$ and $L\left(x_6\right)=S\backslash \left\{a_1\right\}$, then we label $x_1,x_2,x_3,x_4,x_5,x_6,x_7$ with $a_2,a_6,a_4,a_7,a_1,a_5,a_3$, respectively.

Case 2. $L\left(x_1\right)=\{a_2,a_6\}$ and $L\left(x_2\right)=S\backslash \left\{a_4\right\}$.

If $L\left(x_7\right)=\{a_2,a_6\}$ and $L\left(x_6\right)=S\backslash \left\{a_4\right\}$, then we label $x_1,x_2,x_3,x_4,x_5,x_6,x_7$ with $a_2,a_5,a_1,a_4,a_7,a_3,a_6$, respectively. If $L\left(x_7\right)=\{a_3,a_6\}$ and $L\left(x_6\right)=S\backslash \left\{a_1\right\}$, then we label $x_1,x_2,x_3,x_4,x_5,x_6,x_7$ with $a_2,a_6,a_4,a_1,a_7,a_5,a_3$, respectively.

Case 3. $L\left(x_1\right)=L\left(x_7\right)=\{a_3,a_6\}$ and $L\left(x_2\right)=L\left(x_6\right)=S\backslash \left\{a_1\right\}$.

It suffices to label $x_1,x_2,x_3,x_4,x_5,x_6,x_7$ with $a_3,a_5,a_2,a_7,a_1,a_4,a_6$, respectively. □

Lemma 9.

Let $C=xyzx$ be a 3-cycle. Let L be a list assignment for $V\left(C\right)$ such that $\left|L\right(x\left)\right|\ge 3$, $\left|L\right(y\left)\right|\ge 4$, and $\left|L\right(z\left)\right|\ge 5$. Then C has an L-$L(2,1)$-labeling.

Proof. 

Let a denote the minimum integer in the set $L\left(x\right)\cup L\left(y\right)\cup L\left(z\right)$. The proof is split into the following three cases.

• $a\in L\left(x\right)$. Labeling x with a, we define a list assignment $L^{\prime }$ for $y,z$ as follows: $L^{\prime }\left(y\right)=L\left(y\right)\backslash \{a,a+1\}$ and $L^{\prime }\left(z\right)=L\left(z\right)\backslash \{a,a+1\}$. Then $|L^{\prime }\left(y\right)|\ge 4-2=2$ and $|L^{\prime }\left(z\right)|\ge 5-2=3$. By Lemma 2, $y,z$ are $L^{\prime }$-$L(2,1)$-labelable;
• $a\in L\left(y\right)$ and $a\notin L\left(x\right)$. Labeling y with a, we define a list assignment $L^{\prime }$ for $x,z$ as follows: $L^{\prime }\left(x\right)=L\left(x\right)\backslash \{a+1\}$ and $L^{\prime }\left(z\right)=L\left(z\right)\backslash \{a,a+1\}$. Then $|L^{\prime }\left(x\right)|\ge 3-1=2$ and $|L^{\prime }\left(z\right)|\ge 5-2=3$. By Lemma 2, $x,z$ are $L^{\prime }$-$L(2,1)$-labelable;
• $a\in L\left(z\right)$ and $a\notin L\left(x\right)\cup L\left(y\right)$. Labeling z with a, we define a list assignment $L^{\prime }$ for $x,y$ as follows: $L^{\prime }\left(x\right)=L\left(x\right)\backslash \{a+1\}$ and $L^{\prime }\left(y\right)=L\left(y\right)\backslash \{a+1\}$. Then $|L^{\prime }\left(x\right)|\ge 3-1=2$ and $|L^{\prime }\left(y\right)|\ge 4-1=3$. By Lemma 2, $x,y$ are $L^{\prime }$-$L(2,1)$-labelable.

□

Wheels are special Halin graphs, which contain only one inner vertex. The $L(2,1)$-labeling number of a wheel has been determined in [23]:

Lemma 10.

Let $W_n$ be a wheel with n vertices. Then $\lambda \left(W_n\right)=6$ if $4\le n\le 5$, and $\lambda \left(W_n\right)=\Delta \left(W_n\right)+1$ if $n\ge 6$.

4. $L(2,1)$-Labeling

Now we give the main result of this paper, i.e., Theorem 1, whose proof depends on the structural lemma in Section 2 and auxiliary lemmas in Section 3.

Theorem 1.

Let G be a Halin graph with $\Delta =8$. Then $\lambda \left(G\right)\le 10$.

Proof. 

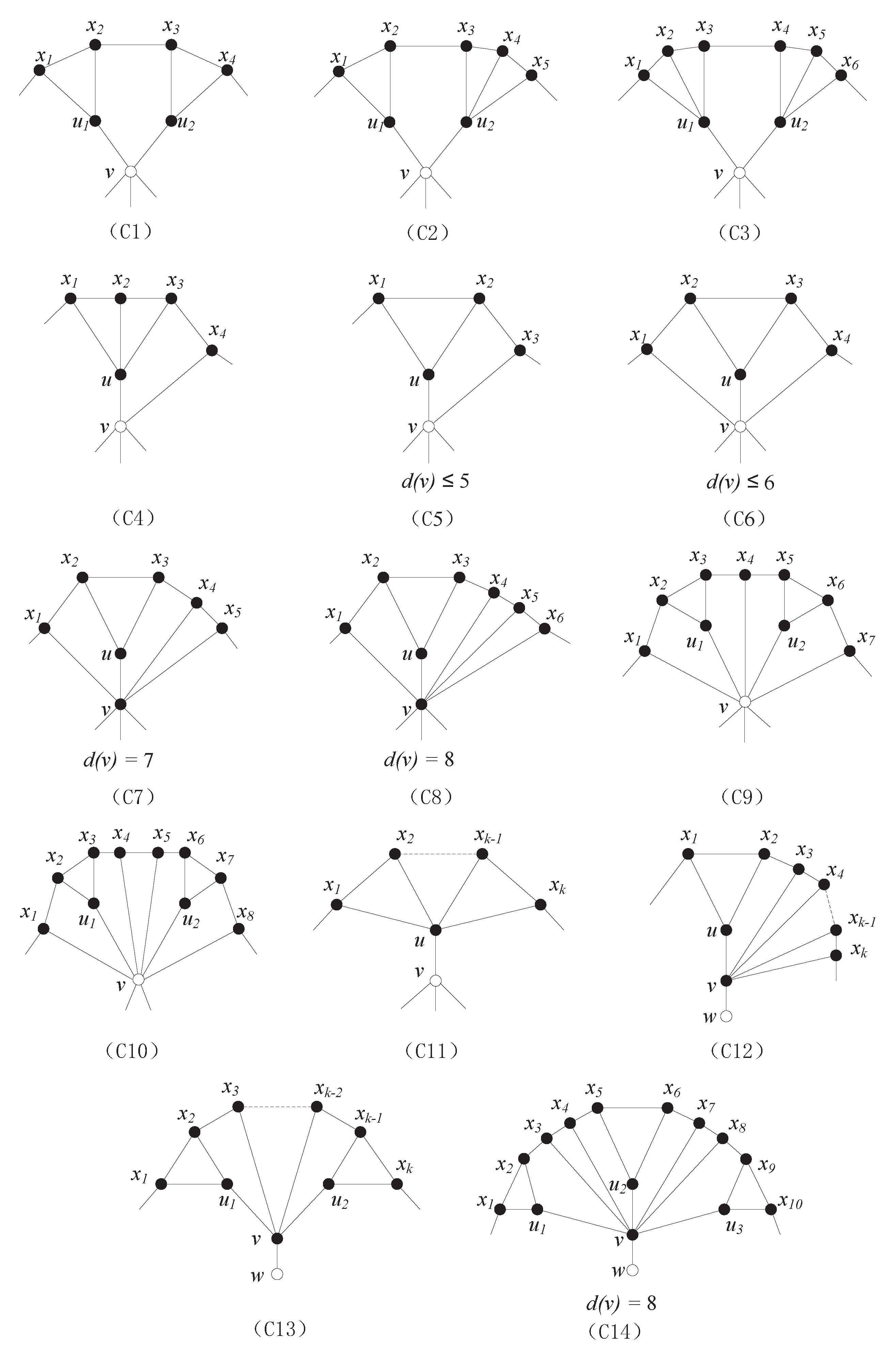
Let $B=\{0,1,\dots ,10\}$ denote a set of 11 labels. The proof is proceeded by induction on the vertex number $\left|G\right|$. Since $\Delta =8$, we see that $\left|G\right|\ge 9$. If $\left|G\right|=9$, then G is a wheel of nine vertices and hence the result holds from Lemma 10. So suppose that G is a Halin graph with $\Delta =8$ and $\left|G\right|\ge 10$. Then G is clearly not a wheel. By Lemma 1, there exists a path $x_1{x}_2\cdots x_k$ in C such that one of the conditions (C1)–(C14) holds. □

In the sequel, let $y\in N_C\left(x_1\right)\backslash \left\{x_2\right\}$, $z\in N_C\left(x_k\right)\backslash \left\{x_{k-1}\right\}$, $N_G\left(y\right)=\{x_1,y_1,y_2\}$, and $N_G\left(z\right)=\{x_k,z_1,z_2\}$. We will reduce these 14 configurations one by one.

(C1) Let $H=G-\{x_1,x_2,x_3,x_4\}+\{y{u}_1,u_1{u}_2,u_{2}z\}$. Then H is a Halin graph with $\Delta \left(H\right)=8$ and $\left|H\right|<\left|G\right|$. By the induction hypothesis, H has an $L(2,1)$-labeling f with the label set B. Define a list assignment L for $x_1,x_2,x_3,x_4$ as follows:

$L\left(x_1\right)=B\backslash \{\underline{f\left(u_1\right)},\underline{f\left(y\right)},f\left(v\right),f\left(y_1\right),f\left(y_2\right)\},$

$L\left(x_2\right)=B\backslash \{\underline{f\left(u_1\right)},f\left(y\right),f\left(v\right),f\left(u_2\right)\},$

$L\left(x_3\right)=B\backslash \{\underline{f\left(u_2\right)},f\left(z\right),f\left(v\right),f\left(u_1\right)\},$

$L\left(x_4\right)=B\backslash \{\underline{f\left(u_2\right)},\underline{f\left(z\right)},f\left(v\right),f\left(z_1\right),f\left(z_2\right)\}$.

Since $\left|B\right|\ge 11$, it follows that $\left|L\right(x_1\left)\right|\ge 11-3-3-3\ge 2$ and $\left|L\right(x_2\left)\right|\ge 11-3-3\ge 5$. Similarly, $\left|L\right(x_4\left)\right|\ge 2$ and $\left|L\right(x_3\left)\right|\ge 5$. By Lemma 5, $x_1,x_2,x_3,x_4$ are $L^{\prime }$-$L(2,1)$-labelable.

(C2) Let $H=G-x_4+x_3{x}_5$. Then H is a Halin graph with $\Delta \left(H\right)=8$ and $\left|H\right|<\left|G\right|$. By the induction hypothesis, H has an $L(2,1)$-labeling f with the label set B. Define a list assignment L for $x_2,x_3,x_4$ as follows:

$L\left(x_2\right)=B\backslash \{\underline{f\left(x_1\right)},\underline{f\left(u_1\right)},f\left(y\right),f\left(v\right),f\left(u_2\right)\},$

$L\left(x_3\right)=B\backslash \{\underline{f\left(u_2\right)},f\left(x_1\right),f\left(u_1\right),f\left(v\right),f\left(x_5\right)\},$

$L\left(x_4\right)=B\backslash \{\underline{f\left(u_2\right)},\underline{f\left(x_5\right)},f\left(v\right),f\left(z\right)\}.$

Then $\left|L\right(x_2\left)\right|\ge 11-3-3-3\ge 2$, $\left|L\right(x_3\left)\right|\ge 11-3-4\ge 4$, and $\left|L\right(x_4\left)\right|\ge 11-3-3-2\ge 5$. By Lemma 3, $x_2,x_3,x_4$ can be labeled properly.

(C3) Let $H=G-x_2+x_1{x}_3$. Then H is a Halin graph with $\Delta \left(H\right)=8$ and $\left|H\right|<\left|G\right|$. By the induction hypothesis, H has an $L(2,1)$-labeling f with the label set B. Define a list assignment L for $x_2,x_3,x_4$ as follows:

$L\left(x_2\right)=B\backslash \{\underline{f\left(x_1\right)},\underline{f\left(u_1\right)},f\left(y\right),f\left(v\right)\},$

$L\left(x_3\right)=B\backslash \{\underline{f\left(u_1\right)},f\left(x_1\right),f\left(u_2\right),f\left(v\right),f\left(x_5\right)\},$

$L\left(x_4\right)=B\backslash \{\underline{f\left(u_2\right)},\underline{f\left(x_5\right)},f\left(u_1\right),f\left(v\right),f\left(x_6\right)\}.$

Then $\left|L\right(x_2\left)\right|\ge 3$, $\left|L\right(x_3\left)\right|\ge 4$, and $\left|L\right(x_4\left)\right|\ge 2$. By Lemma 3, $x_2,x_3,x_4$ are L-$L(2,1)$-labelable.

(C4) Let $H=G-x_2+x_1{x}_3$. Then H is a Halin graph with $\Delta \left(H\right)=8$ and $\left|H\right|<\left|G\right|$. By the induction hypothesis, H has an $L(2,1)$-labeling f with the label set B. Define a list assignment L for $x_1,x_2,x_3$ as follows:

$L\left(x_1\right)=B\backslash \{\underline{f\left(y\right)},\underline{f\left(u\right)},f\left(y_1\right),f\left(y_2\right),f\left(v\right)\},$

$L\left(x_2\right)=B\backslash \{\underline{f\left(u\right)},f\left(y\right),f\left(v\right),f\left(x_4\right)\},$

$L\left(x_3\right)=B\backslash \{\underline{f\left(u\right)},\underline{f\left(x_4\right)},f\left(z\right),f\left(v\right)\}.$

Then $\left|L\right(x_1\left)\right|\ge 2$, $\left|L\right(x_2\left)\right|\ge 5$, and $\left|L\right(x_3\left)\right|\ge 3$. By Lemma 3, $x_1,x_2,x_3$ are L-$L(2,1)$-labelable.

(C5) Let $N\left(v\right)=\{u,x_3,t_1,\dots ,t_l\}$. Since $d\left(v\right)\le 5$, we see that $l\le 3$. Let $H=G-\{x_1,x_2\}+\{x_{3}u,uy\}$. Then H is a Halin graph with $\Delta \left(H\right)=8$ and $\left|H\right|<\left|G\right|$. By the induction hypothesis, H has an $L(2,1)$-labeling f using B. Erasing the label of u, we define a list assignment L for $x_1,x_2,u$ as follows:

$L\left(x_1\right)=B\backslash \{\underline{f\left(y\right)},f\left(y_1\right),f\left(y_2\right),f\left(v\right),f\left(x_3\right)\},$

$L\left(x_2\right)=B\backslash \{\underline{f\left(x_3\right)},f\left(z\right),f\left(y\right),f\left(v\right)\},$

$L\left(u\right)=B\backslash \{\underline{f\left(v\right)},f\left(y\right),f\left(x_3\right),f\left(t_1\right),\dots ,f\left(t_l\right)\}.$

Then $\left|L\right(x_1\left)\right|\ge 4$, $\left|L\right(x_2\left)\right|\ge 5$, and $\left|L\right(u\left)\right|\ge 3$. By Lemma 9, $u,x_1,x_2$ are L-$L(2,1)$-labelable.

(C6) Let $N\left(v\right)=\{u,x_1,x_4,t_1,\dots ,t_m\}$. Since $d\left(v\right)\le 6$, we see that $m\le 3$. Let $H=G-\{x_2,x_3\}+\{x_{1}u,u{x}_4\}$. Then H is a Halin graph with $\Delta \left(H\right)=8$ and $\left|H\right|<\left|G\right|$. By the induction hypothesis, H admits an $L(2,1)$-labeling f using B. Erasing the label of u, we define a list assignment L for $x_2,x_3,u$ as follows:

$L\left(x_2\right)=B\backslash \{\underline{f\left(x_1\right)},f\left(y\right),f\left(v\right),f\left(x_4\right)\},$

$L\left(x_3\right)=B\backslash \{\underline{f\left(x_4\right)},f\left(z\right),f\left(v\right),f\left(x_1\right)\},$

$L\left(u\right)=B\backslash \{\underline{f\left(v\right)},f\left(x_1\right),f\left(x_4\right),f\left(t_1\right),\dots ,f\left(t_m\right)\}.$

Since $m\le 3$, we have that $\left|L\right(u\left)\right|\ge 3$ and $|L\left(x_2\right)|,|L\left(x_3\right)|\ge 5$. By Lemma 9, $u,x_2,x_3$ are L-$L(2,1)$-labelable.

(C7) Set $N\left(v\right)=\{u,x_1,x_4,x_5,t_1,t_2,t_3\}$ because $d\left(v\right)=7$. Let $H=G-\{x_2,x_3\}+\{x_{1}u,u{x}_4\}$. Then H is a Halin graph with $\Delta \left(H\right)=8$ and $\left|H\right|<\left|G\right|$. By the induction hypothesis, H admits an $L(2,1)$-labeling f using B. Let $f\left(x_1\right)=a$, $f\left(x_4\right)=b$, and $f\left(x_5\right)=c$. Deleting the label of u, we define a list assignment L for $x_2,x_3,u$ as follows:

$L\left(x_2\right)=B\backslash \{\underline{a},b,f\left(v\right),f\left(y\right)\},$

$L\left(x_3\right)=B\backslash \{\underline{b},a,c,f\left(v\right)\},$

$L\left(u\right)=B\backslash \{\underline{f\left(v\right)},a,b,c,f\left(t_1\right),f\left(t_2\right),f\left(t_3\right)\}.$

Then $\left|L\right(u\left)\right|\ge 2$ and $|L\left(x_2\right)|,|L\left(x_3\right)|\ge 5$. It is easy to show by Lemmas 2 and 9 that $u,x_2,x_3$ cannot be labeled only if $L\left(x_2\right)=L\left(x_3\right)=S=\{i,i+1,i+2,i+3,i+4\}$ and $L\left(u\right)=\{i+1,i+3\}$ for some $i\in B$. This implies that $a-1,a,a+1,b-1,b,b+1,c\notin S$, and thus $i+1,i+3\notin \{c-1,c,c+1\}$. Let s denote the neighbor of $x_5$ other than v and $x_4$. Relabel $x_4$ with a label $p\in \{i+1,i+3\}\backslash \left\{f\right(s\left)\right\}$. If $p=i+1$, then we label u with b, $x_3$ with $i+3$, and $x_2$ with i. If $p=i+3$, then we label u with b, $x_3$ with $i+1$, and $x_2$ with $i+4$.

(C8) Set $N\left(v\right)=\{u,x_1,x_4,x_5,x_6,t_1,t_2,t_3\}$, and let $H=G-\{x_2,x_3\}+\{x_{1}u,u{x}_4\}$. Then H is a Halin graph with $\Delta \left(H\right)=8$ and $\left|H\right|<\left|G\right|$. By the induction hypothesis, H admits an $L(2,1)$-labeling f using B such that $x_1,x_4,u,x_5,$ $x_6,y,v$ are labeled by $a,b,c,d,e,g,h$, respectively. Define a list assignment L for $x_2$ and $x_3$ as follows:

$L\left(x_2\right)=B\backslash \{\underline{a},\underline{c},h,g,b\},$

$L\left(x_3\right)=B\backslash \{\underline{b},\underline{c},h,d,a\}.$

Then $\left|L\right(x_2\left)\right|\ge 2$ and $\left|L\right(x_3\left)\right|\ge 2$. By Lemma 2, $x_2$ and $x_3$ cannot be labeled only if $L\left(x_2\right)=L\left(x_3\right)=\{i,i+1\}$ for some $i\in B$. It follows that

$$\begin{array}{c}\{a-1,a+1,g\}=\{b-1,b+1,d\}\end{array}$$

(1)

Note that $a,b,c,d,e$ are distinct and $d\notin \{c-1,c,c+1\}$. Switch the labels of u and $x_4$ and then define a new list assignment $L^{\prime }$ as follows:

$L^{\prime }\left(x_2\right)=B\backslash \{\underline{a},\underline{b},h,g,c\}$,

$L^{\prime }\left(x_3\right)=L\left(x_3\right)$.

We assert that $x_2,x_3$ are $L^{\prime }$-$L(2,1)$-labelable. If not, we have that $L^{\prime }\left(x_2\right)=L^{\prime }\left(x_3\right)=L\left(x_3\right)=\{i,i+1\}$ for some $i\in B$. Thus,

$$\begin{array}{c}\{a-1,a+1,g\}=\{c-1,c+1,d\}\end{array}$$

(2)

Combining (1) and (2), we get that $\{b-1,b+1,d\}=\{c-1,c+1,d\}$, i.e., $b=c$, which contradicts the fact that $b\ne c$.

(C9) Let $H=G-\{x_2,x_3,x_5,x_6\}+\{x_1{u}_1,u_1{x}_4,x_4{u}_2,u_2{x}_7\}$. Then H is a Halin graph with $\Delta \left(H\right)=8$ and $\left|H\right|<\left|G\right|$. By the induction hypothesis, H admits an $L(2,1)$-labeling f using B such that $u_1,x_4,u_2,x_1,x_7,v,y,z$ are labeled by $a,b,c,d,e,g,h,i$, respectively. Define a list assignment L for $x_2,x_3,x_5,x_6$ as follows:

$L\left(x_2\right)=B\backslash \{\underline{a},\underline{d},b,g,h\},$

$L\left(x_3\right)=B\backslash \{\underline{a},\underline{b},d,g\},$

$L\left(x_5\right)=B\backslash \{\underline{c},\underline{b},e,g\},$

$L\left(x_6\right)=B\backslash \{\underline{c},\underline{e},b,g,i\}.$

Then $|L\left(x_2\right)|,|L\left(x_6\right)|\ge 2$ and $|L\left(x_3\right)|,|L\left(x_5\right)|\ge 3$. By Lemma 2, we can show that $x_2,x_3,x_5,x_6$ cannot be labeled only if $L\left(x_2\right)=\{i,i+1\}$, $L\left(x_3\right)=\{i,i+1,p\}$, $L\left(x_5\right)=\{j,j+1,p\}$, and $L\left(x_6\right)=\{j,j+1\}$ for some $i,j\in B$. Note that i may be equal to j. It implies that any two labels in $\{c-1,c,c+1,b-1,b,b+1,e,g\}$ are distinct, and any two labels in $\{c-1,c,c+1,e-1,e,e+1,b,g,i\}$ are distinct. A similar conclusion holds for the sets $\{a-1,a,a+1,b-1,b,b+1,d,g\}$ and $\{a-1,a,a+1,d-1,d,d+1,g,h\}$. Now we switch the labels of $x_4$ and $u_2$ and then define a new list assignment $L^{\prime }$ for $x_2,x_3,x_5,x_6$ as follows:

$L^{\prime }\left(x_2\right)=B\backslash \{\underline{a},\underline{d},c,g,h\},$

$L^{\prime }\left(x_3\right)=B\backslash \{\underline{a},\underline{c},d,g\},$

$L^{\prime }\left(x_5\right)=L\left(x_5\right),$

$L^{\prime }\left(x_6\right)=B\backslash \{\underline{b},\underline{e},c,g,i\}$.

It is easy to confirm that $L^{\prime }\left(x_2\right)=(L\left(x_2\right)\cup \left\{b\right\})\backslash \left\{c\right\}=\{i,i+1,b\}\backslash \left\{c\right\}$. If $|L^{\prime }\left(x_2\right)|\ge 3$, the proof can be reduced to the previous case. Otherwise, since $b\ne c$, we get that $c=i$ or $c=i+1$, that is, $L^{\prime }\left(x_2\right)=\{b,i+1\}$ or $L^{\prime }\left(x_2\right)=\{b,i\}$. Since $i,i+1\in L\left(x_3\right)$, we see that $|b-i|\ge 2$ and $|b-(i+1\left)\right|\ge 2$. This shows that two labels in $L^{\prime }\left(x_2\right)$ are not consecutive. Thus, $x_2,x_3,x_5,x_6$ admit an $L^{\prime }$-$L(2,1)$-labeling.

(C10) Without loss of generality, assume that $d\left(v\right)=8$ and $N\left(v\right)=\{u_1,u_2,x_1,x_4,$$x_5,x_8,t_1,t_2\}$. Let $H=G-\{u_1,u_2,x_2,x_3,\dots ,x_7\}+x_1{x}_8$. Then H is a Halin graph with $\Delta \left(H\right)\le 8$ and $\left|H\right|<\left|G\right|$. If $\Delta \left(H\right)\le 7$, then H is 10-$L(2,1)$-labelable by the result in [24]. If $\Delta \left(H\right)=8$, then H is also 10-$L(2,1)$-labelable by the induction hypothesis. Thus, H always admits an $L(2,1)$-labeling f using B such that $v,x_1,x_8,y,z,t_1,t_2$ are labeled by $i_1,i_2,i_3,i_4,i_5,i_6,i_7$, respectively. Define a list assignment L as follows:

$L\left(u_1\right)=L\left(u_2\right)=L\left(x_4\right)=L\left(x_5\right)=S=B\backslash \{\underline{i_1},i_2,i_3,i_6,i_7\}$,

$L\left(x_2\right)=B\backslash \{\underline{i_2},i_1,i_4\}$,

$L\left(x_3\right)=B\backslash \{i_1,i_2\}$,

$L\left(x_6\right)=B\backslash \{i_1,i_3\}$,

$L\left(x_7\right)=B\backslash \{\underline{i_3},i_1,i_5\}$.

It is easy to deduce that $|L\left(x_2\right)|,|L\left(x_7\right)|\ge 6$, $|L\left(x_3\right)|,|L\left(x_6\right)|\ge 9$, and $\left|S\right|\ge 4$. Assume that $\left|S\right|=4$ and $S=\{a,b,c,d\}$ with $0\le a<b<c<d\le 10$. To complete the proof, we consider the following three subcases.

(C10.1) $a=0$. (If $d=10$, we have a similar argument.)

Label $x_4$ with a, $u_1$ with b, $x_5$ with c, and $u_2$ with d. Define a list assignment $L^{\prime }$ for $x_2,x_3,x_6,x_7$ as follows:

$L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \{\underline{b},0\}$,

$L^{\prime }\left(x_3\right)=L\left(x_3\right)\backslash \{\underline{b},0,1,c\}$,

$L^{\prime }\left(x_6\right)=L\left(x_6\right)\backslash \{\underline{c},\underline{d},0\}$,

$L^{\prime }\left(x_7\right)=L\left(x_7\right)\backslash \{\underline{d},c\}$.

It is easy to show that $|L^{\prime }\left(x_3\right)|\ge 3$ and $|L^{\prime }\left(x_2\right)|,|L^{\prime }\left(x_6\right)|,|L^{\prime }\left(x_7\right)|\ge 2$. By Lemma 2, $x_2$ and $x_3$ are $L^{\prime }$-$L(2,1)$-labelable. If $x_6,x_7$ are also $L^{\prime }$-$L(2,1)$-labelable, we are done. Otherwise, by Lemma 2, we have $L^{\prime }\left(x_6\right)=L^{\prime }\left(x_7\right)=\{j,j+1\}$ for some $j\in B$. This implies that $d\ge c+3$, as otherwise we derive that $|L^{\prime }\left(x_6\right)|\ge 3$, which is impossible. Now we switch the labels of $x_5$ and $u_2$ to induce a new list assignment $L^{″}$ from $L^{\prime }$. On the one hand, it still holds that $|L^{″}\left(x_2\right)|\ge 2$ and $|L^{″}\left(x_3\right)|\ge 3$, and hence $x_2,x_3$ are $L^{″}$-$L(2,1)$-labelable. On the other hand, $L^{″}\left(x_6\right)=L^{\prime }\left(x_6\right)$, and $L^{″}\left(x_7\right)=(L^{\prime }\left(x_7\right)\cup \{d-1,d+1\})\backslash \{c-1,c+1\}=\{j,j+1,d-1,d+1\}\backslash \{c-1,c+1\}$. Since $j,j+1\notin \{c-1,c+1,d-1,d+1\}$ and $d\ge c+3$, it follows that either $|L^{″}\left(x_7\right)|\ge 3$ or $L^{″}\left(x_7\right)=\{j,k\}$ with $|j-k|\ge 2$. By Lemma 2, $x_6$ and $x_7$ are $L^{″}$-$L(2,1)$-labelable.

(C10.2) $b\le a+2$. (If $d\le c+2$, we have a similar discussion).

After $x_4,u_1,x_5,u_2$ with $a,b,c,d$, respectively, we define a list assignment $L^{\prime }$ for $x_2,x_3,x_6,x_7$ as follows:

$L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \{\underline{b},a\}$,

$L^{\prime }\left(x_3\right)=L\left(x_3\right)\backslash \{\underline{b},\underline{a},c\}$,

$L^{\prime }\left(x_6\right)=L\left(x_6\right)\backslash \{\underline{c},\underline{d},a\}$,

$L^{\prime }\left(x_7\right)=L\left(x_7\right)\backslash \{\underline{d},c\}$.

Since $b\le a+2$, it follows that $\left|\right\{a-1,a,a+1,b-1,b,b+1\left\}\right|\le 5$. Thus, $|L^{\prime }\left(x_3\right)|\ge 3$ and $|L^{\prime }\left(x_2\right)|,|L^{\prime }\left(x_6\right)|,|L^{\prime }\left(x_7\right)|\ge 2$. The remaining discussion is analogous to (C10.1).

(C10.3) $b\ge a+3$ and $c\le b+2$.

Label $x_5,x_4,u_1,u_2$ with $a,b,c,d$, respectively, and define a list assignment $L^{\prime }$ as follows:

$L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \{\underline{c},b\}$,

$L^{\prime }\left(x_3\right)=L\left(x_3\right)\backslash \{\underline{c},\underline{b},a\}$,

$L^{\prime }\left(x_6\right)=L\left(x_6\right)\backslash \{\underline{a},\underline{d},b\}$,

$L^{\prime }\left(x_7\right)=L\left(x_7\right)\backslash \{\underline{d},a\}$.

Since $c\le b+2$, we derive that $|L^{\prime }\left(x_3\right)|\ge 3$ and $|L^{\prime }\left(x_2\right)|,|L^{\prime }\left(x_6\right)|,|L^{\prime }\left(x_7\right)|\ge 2$. The remaining discussion is analogous to (C10.1).

(C11) Note that $4\le k\le 7$. Let $H=G-\{x_1,x_2,\dots ,x_k\}+\{yu,uz\}$. By the induction hypothesis or the result in [24], H has an $L(2,1)$-labeling f using B such that $u,y,z$ are labeled with $p,q,r$, respectively. Define a list assignment L for $x_1,x_2,\dots ,x_k$ as follows:

$L\left(x_1\right)=B\backslash \{\underline{p},\underline{q},f\left(v\right),f\left(y_1\right),f\left(y_2\right)\}$,

$L\left(x_k\right)=B\backslash \{\underline{p},\underline{r},f\left(v\right),f\left(z_1\right),f\left(z_2\right)\}$,

$L\left(x_2\right)=B\backslash \{\underline{p},f\left(v\right),f\left(y\right)\}$,

$L\left(x_{k-1}\right)=B\backslash \{\underline{p},f\left(v\right),f\left(z\right)\}$,

$L\left(x_i\right)=B\backslash \{\underline{p},f\left(v\right)\}$ for $i=3,4,\dots ,k-2.$

Then $|L\left(x_1\right)|,|L\left(x_k\right)|\ge 2$, $|L\left(x_2\right)|,|L\left(x_{k-1}\right)|\ge 6$, and $\left|L\right(x_i\left)\right|\ge 7$ for $i=3,4,\dots ,k-2$. According to the size of k, we have to deal with the following subcases.

(C11.1) $k=4$.

Since $|L\left(x_1\right)|,|L\left(x_4\right)|\ge 2$ and $|L\left(x_2\right)|,|L\left(x_3\right)|\ge 6$, $x_1,x_2,x_3,x_4$ are L-$L(2,1)$-labelable by Lemma 6.

(C11.2) $k=5$.

We note that $L\left(x_1\right)\subset L\left(x_2\right)\subset L\left(x_3\right)$, $L\left(x_5\right)\subset L\left(x_4\right)\subset L\left(x_3\right)$, $|L\left(x_1\right)|,|L\left(x_5\right)|\ge 2$, $|L\left(x_2\right)|,|L\left(x_4\right)|\ge 6$, and $\left|L\right(x_3\left)\right|\ge 7$. Assume, w.l.o.g., that $|L\left(x_1\right)|=|L\left(x_5\right)|=2$, $|L\left(x_2\right)|=|L\left(x_4\right)|=6$, and $\left|L\right(x_3\left)\right|=7$. If $L\left(x_1\right)\ne L\left(x_5\right)$, then we label $x_5$ with a label $a\in L\left(x_5\right)\backslash L\left(x_1\right)$ and then define a list assignment $L^{\prime }$ for $x_1,x_2,x_3,x_4$ as follows:

$L^{\prime }\left(x_1\right)=L\left(x_1\right)$,

$L^{\prime }\left(x_4\right)=L\left(x_4\right)\backslash \left\{\underline{a}\right\}$,

$L^{\prime }\left(x_i\right)=L\left(x_i\right)\backslash \left\{a\right\}$ for $i=2,3$.

Then $|L^{\prime }\left(x_1\right)|\ge 2$, $|L^{\prime }\left(x_2\right)|\ge 5$, $|L^{\prime }\left(x_3\right)|\ge 6$, and $|L^{\prime }\left(x_4\right)|\ge 3$. By Lemma 4, $x_1,x_2,x_3,x_4$ are L-$L(2,1)$-labelable. Otherwise, $L\left(x_1\right)=L\left(x_5\right)=\{p,q\}$ with $p<q$. If $|L\left(x_2\right)\cap \left\{\underline{p}\right\}|\le 2$, then we label $x_1$ with p and $x_5$ with q and then define a list assignment $L^{\prime }$ for $x_2,x_3,x_4$ as follows:

$L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \{\underline{p},q\}$,

$L^{\prime }\left(x_3\right)=L\left(x_3\right)\backslash \{p,q\}$,

$L^{\prime }\left(x_4\right)=L\left(x_4\right)\backslash \{\underline{q},p\}$.

Then $|L^{\prime }\left(x_2\right)|\ge 3$, $|L^{\prime }\left(x_3\right)|\ge 5$, and $|L^{\prime }\left(x_4\right)|\ge 2$. By Lemma 3, $x_2,x_3,x_4$ are $L^{\prime }$-$L(2,1)$-labelable. Otherwise, $|L\left(x_2\right)\cap \left\{\underline{p}\right\}|=3$. Similarly, $|L\left(x_2\right)\cap \left\{\underline{q}\right\}|=3$, $|L\left(x_4\right)\cap \left\{\underline{p}\right\}|=3$, and $|L\left(x_4\right)\cap \left\{\underline{q}\right\}|=3$. This implies that $L\left(x_2\right)=L\left(x_4\right)=\{p-1,p,p+1,q-1,q,q+1\}$, and $L\left(x_3\right)=\{p-1,p,p+1,q-1,q,q+1,r\}$. Since $p<q$, we have $p+1<q-1$. If $r>q+1$, we label $x_1$ with q, $x_2$ with $p-1$, $x_3$ with r, $x_4$ with $q-1$, and $x_5$ with p. If $r<p-1$, we have a similar labeling. If $p+1<r<q-1$, we label $x_1$ with q, $x_2$ with $p-1$, $x_3$ with r, $x_4$ with $q+1$, and $x_5$ with p.

(C11.3) $k=6$.

Assume that $|L\left(x_1\right)|=|L\left(x_6\right)|=2$, $|L\left(x_2\right)|=|L\left(x_5\right)|=6$, and $|L\left(x_3\right)|=|L\left(x_4\right)|=7$. Note that $L\left(x_3\right)=L\left(x_4\right)$, $L\left(x_1\right)\subset L\left(x_2\right)\subset L\left(x_3\right)$ and $L\left(x_6\right)\subset L\left(x_5\right)\subset L\left(x_4\right)$. If there is $a\in L\left(x_1\right)$ such that $|L\left(x_2\right)\cap \left\{\underline{a}\right\}|\le 2$, then we label $x_1$ with a, $x_6$ with $b\in L\left(x_6\right)\backslash \left\{a\right\}$, and then define a list assignment $L^{\prime }$ for $x_2,x_3,x_4,x_5$ as follows:

$L^{\prime }\left(x_2\right)=L\left(x_2\right)\backslash \{\underline{a},b\}$,

$L^{\prime }\left(x_i\right)=L\left(x_4\right)\backslash \{a,b\}$ for $i=3,4$,

$L^{\prime }\left(x_5\right)=L\left(x_5\right)\backslash \{\underline{b},a\}$,

Then $|L^{\prime }\left(x_2\right)|\ge 3$, $|L^{\prime }\left(x_3\right)|,|L^{\prime }\left(x_4\right)|\ge 5$, and $|L^{\prime }\left(x_5\right)|\ge 2$. By Lemma 4, $x_2,x_3,x_4,x_5$ are $L^{\prime }$-$L(2,1)$-labelable. Otherwise, for each $a\in L\left(x_1\right)$ we have $|L\left(x_2\right)\cap \left\{\underline{a}\right\}|=3$ and for each $b\in L\left(x_6\right)$ we have $|L\left(x_5\right)\cap \left\{\underline{b}\right\}|=3$. Let $L\left(x_3\right)=L\left(x_4\right)=S=\{b_1,b_2,\dots ,b_7\}$ with $b_1<b_2<\cdots <b_7$. Since $|L\left(x_2\right)|=|L\left(x_5\right)|=6$ and $L\left(x_2\right),L\left(x_5\right)\subset S$, we only need to consider the following cases by symmetry.

• $L\left(x_1\right)=\{b_2,b_5\}$. Then $L\left(x_2\right)=S\backslash \left\{b_7\right\}$. If $L\left(x_6\right)=\{b_2,b_5\}$, then $L\left(x_5\right)=S\backslash \left\{b_7\right\}$, we label $x_1,x_2,x_3,x_4,x_5,x_6$ with $b_2,b_6,b_4,b_1,b_3,b_5$, respectively. If $L\left(x_6\right)=\{b_2,b_6\}$, or $L\left(x_6\right)=\{b_3,b_6\}$, then $L\left(x_5\right)=S\backslash \left\{b_4\right\}$, or $L\left(x_5\right)=S\backslash \left\{b_1\right\}$, we label $x_1,x_2,x_3,x_4,x_5,x_6$ with $b_5,b_1,b_4,b_7,b_3,b_6$, respectively;
• $L\left(x_1\right)=\{b_2,b_6\}$. Then $L\left(x_2\right)=S\backslash \left\{b_4\right\}$. If $L\left(x_6\right)=\{b_2,b_6\}$, then $L\left(x_5\right)=S\backslash \left\{b_4\right\}$, we label $x_1,x_2,x_3,x_4,x_5,x_6$ with $b_2,b_7,b_3,b_5,b_1,b_6$, respectively. If $L\left(x_6\right)=\{b_3,b_6\}$, then $L\left(x_5\right)=S\backslash \left\{b_1\right\}$, we label $x_1,x_2,x_3,x_4,$$x_5,x_6$ with $b_2,b_7,b_4,b_1,b_5,b_3$, respectively;
• $L\left(x_1\right)=L\left(x_6\right)=\{b_3,b_6\}$. Then $L\left(x_2\right)=L\left(x_5\right)=S\backslash \left\{b_1\right\}$. We label $x_1,x_2,x_3,x_4,$$x_5,x_6$ with $b_3,b_7,b_5,b_1,b_4,b_6$, respectively.

(C11.4) $k=7$.

Since $|L\left(x_1\right)|,|L\left(x_7\right)|\ge 2$, $|L\left(x_2\right)|,|L\left(x_6\right)|\ge 6$, $|L\left(x_3\right)|,|L\left(x_4\right)|,|L\left(x_5\right)|\ge 7$, $L\left(x_3\right)=L\left(x_4\right)=L\left(x_5\right)$, $L\left(x_1\right)\subset L\left(x_2\right)\subset L\left(x_3\right)$, and $L\left(x_7\right)\subset L\left(x_6\right)\subset L\left(x_5\right)$, Lemma 8 guarantees that $x_1,x_2,\dots ,x_7$ are L-$L(2,1)$-labelable.

(C12) Note that $6\le k\le 8$. Let $H=G-\{u,x_1,x_2,\dots ,x_k\}$$+\{yv,vz\}$. By the induction hypothesis or the result in [24], H has an $L(2,1)$-labeling f using B such that $v,w,y,z,y_1,y_2,$$z_1,z_2$ are labeled with $a,b,c,d,c_1,c_2,d_1,d_2$, respectively. Label $x_2$ with some label in $\{a-1,a+1\}\backslash \left\{c\right\}$, say $a+1$. Then we label $x_k$ with $e\in B\backslash \{\underline{a},\underline{d},b,d_1,d_2\}$, $x_1$ with $g\in B\backslash \{\underline{c},a,a+1,c_1,c_2\}$, and u with $h\in B\backslash \{\underline{g},\underline{a},a+2,b,c,e\}$. Now we define a list assignment L for $x_3,x_4,\dots ,x_{k-1}$ as follows:

$L\left(x_3\right)=B\backslash \{\underline{a},a+2,b,e,g,h\}$,

$L\left(x_i\right)=B\backslash \{\underline{a},b,e,h\}$ for $i=4,5,\dots ,k-2,$

$L\left(x_{k-1}\right)=B\backslash \{\underline{a},\underline{e},b,d,h\}$.

It follows that $\left|L\right(x_3\left)\right|\ge 3$, $\left|L\right(x_{k-1}\left)\right|\ge 2$, and $\left|L\right(x_i\left)\right|\ge 5$ for $i=4,5,\dots ,k-2$. If $k=6$, then $x_3,x_4,x_5$ are L-$L(2,1)$-labelable by Lemma 3. If $k=7$, then $x_3,x_4,x_5,x_6$ are L-$L(2,1)$-labelable by Lemma 4. If $k=8$, then $x_3,x_4,x_5,x_6,x_7$ are L-$L(2,1)$-labelable by Lemma 7.

(C13) Note that $7\le k\le 9$. Let $H=G-\{u_1,u_2,x_1,x_2,\dots ,x_k\}$$+\{yv,vz\}$. By the induction hypothesis or the result in [24], H has an $L(2,1)$-labeling f using B such that $v,w,y,z,y_1,y_2,z_1,z_2$ are labeled with $a,b,c,d,c_1,c_2,d_1,d_2$, respectively. Label $x_2$ with some label in $\{a-1,a+1\}\backslash \left\{c\right\}$, say $a+1$, and $x_{k-1}$ with some label in $\{a-1,a+1\}\backslash \left\{c\right\}$, say $a-1$, Then we label $x_1$ with $g\in B\backslash \{\underline{c},\underline{a+1},c_1,c_2\}$, $x_k$ with $h\in B\backslash \{\underline{d},\underline{a-1},d_1,d_2\}$, $u_1$ with $e^{\prime }\in B\backslash \{\underline{e},\underline{a+1},a-1,b,c\}$, and $u_2$ with $h^{\prime }\in B\backslash \{\underline{h},\underline{a-1},a+1,b,d,e^{\prime }\}$.

Afterwards we define a list assignment L for $x_3,x_4,\dots ,x_{k-2}$ as follows:

$L\left(x_3\right)=B\backslash \{\underline{a},a+2,b,e,e^{\prime },h^{\prime }\}$,

$L\left(x_{k-2}\right)=B\backslash \{\underline{a},a-2,b,e^{\prime },h,h^{\prime }\}$,

$L\left(x_i\right)=B\backslash \{\underline{a},b,e^{\prime },h^{\prime }\}$ for $i=4,5,\dots ,k-2.$

Then $|L\left(x_3\right)|,|L\left(x_{k-2}\right)|\ge 3$, and $\left|L\right(x_i\left)\right|\ge 5$ for $i=4,5,\dots ,k-3$. If $k=7$, then $x_3,x_4,x_5$ can be L-$L(2,1)$-labeled by Lemma 3. If $k=8$, then $x_3,x_4,x_5,x_6$ can be L-$L(2,1)$-labeled by Lemma 4. If $k=9$, then $x_3,x_4,x_5,x_6,x_7$ can be L-$L(2,1)$-labeled by Lemma 7.

(C14) Let $H=G-\{u_1,u_2,u_3,x_1,x_2,\dots ,x_k\}$$+\{yv,vz\}$. By the induction hypothesis or the result in [24], H has an $L(2,1)$-labeling f using B such that $v,w,y,z,y_1,y_2,z_1,z_2$ are labeled with $a,b,c,d,c_1,c_2,d_1,d_2$, respectively. Similarly to the proof of the previous cases, we label, w.l.o.g., $x_2,x_5$ with $a+1$, $x_6,x_9$ with $a-1$, $x_1$ with g, $x_{10}$ with h, $u_1$ with $g^{\prime }$ and $u_3$ with $h^{\prime }$. Define a list assignment L for $x_3,x_4,x_7,x_8$ as follows:

$L\left(x_3\right)=B\backslash \{\underline{a},a+2,b,g,g^{\prime },h^{\prime }\}$,

$L\left(x_4\right)=B\backslash \{\underline{a},a+2,b,g^{\prime },h^{\prime }\}$,

$L\left(x_7\right)=B\backslash \{\underline{a},a-2,b,g^{\prime },h^{\prime }\}$,

$L\left(x_8\right)=B\backslash \{\underline{a},a-2,b,g^{\prime },h,h^{\prime }\}$.

It is not difficult to see that $|L\left(x_3\right)|,|L\left(x_8\right)|\ge 3$, $|L\left(x_4\right)|,|L\left(x_7\right)|\ge 4$, $L\left(x_3\right)\subset L\left(x_4\right)$, $L\left(x_8\right)\subset L\left(x_7\right)$, and $3\le |L\left(x_4\right)\cap L\left(x_7\right)|\le 4$. Assume that $|L\left(x_3\right)|=|L\left(x_8\right)|=3$, and $|L\left(x_4\right)|=|L\left(x_7\right)|=4$.

Claim 1 $x_3,x_4,x_7,x_8$ are L-$L^{\ast }(2,1)$-labelable.

Proof. 

First, assume that $L\left(x_3\right)=L\left(x_8\right)=\{\alpha ,\beta ,\gamma \}$ with $\alpha <\beta <\gamma$. Then $\alpha ,\beta ,\gamma \in L\left(x_4\right)\cap L\left(x_7\right)$. Furthermore, assume that $L\left(x_4\right)=\{\alpha ,\beta ,\gamma ,\varphi \}$. If $\varphi <\alpha$, then we label $x_3,x_4,x_7,x_8$ with $\beta ,\varphi ,\alpha ,\gamma$, respectively. If $\alpha <\varphi <\beta$, then we label $x_3,x_4,x_7,x_8$ with $\gamma ,\varphi ,\alpha ,\beta$, respectively. If $\beta <\varphi <\gamma$, then we label $x_3,x_4,x_7,x_8$ with $\alpha ,\varphi ,\beta ,\gamma$, respectively. If $\gamma <\varphi$, then we label $x_3,x_4,x_7,x_8$ with $\beta ,\varphi ,\alpha ,\gamma$, respectively.

Next assume that $L\left(x_3\right)\ne L\left(x_8\right)$. Label $x_3$ with $\alpha \in L\left(x_3\right)\backslash L\left(x_8\right)$ and $x_4$ with $\beta \in L\left(x_4\right)\backslash \left\{\underline{\alpha }\right\}$. Define a list assignment $L^{\prime }$ for $x_7,x_8$ as follows:

$L^{\prime }\left(x_7\right)=L\left(x_7\right)\backslash \{\alpha ,\beta \}$,

$L^{\prime }\left(x_8\right)=L\left(x_8\right)\backslash \left\{\beta \right\}$.

Then $|L^{\prime }\left(x_7\right)|\ge 2$ and $|L^{\prime }\left(x_8\right)|\ge 2$. By Lemma 2, $x_7,x_8$ are not $L^{\prime }$-$L(2,1)$-labelable only if $L^{\prime }\left(x_7\right)=L^{\prime }\left(x_8\right)=\{p,p+1\}$ for some $p\in B$. It turns out that $L\left(x_7\right)=\{\alpha ,\beta ,p,p+1\}$, $L\left(x_8\right)=\{\beta ,p,p+1\}$, $\alpha ,\beta \in L\left(x_4\right)$, and $\alpha \in L\left(x_3\right)$. Since $|L\left(x_4\right)\cap L\left(x_7\right)|\ge 3$ by their definitions, at least one of p and $p+1$ belongs to $L\left(x_4\right)$.

Case I. $\beta <p$.

• $\alpha <\beta$. If $p\in L\left(x_4\right)$, we label $x_3,x_4,x_7,x_8$ with $\alpha ,p,p+1,\beta$, respectively. Otherwise, $p\notin L\left(x_4\right)$. Then $p\notin L\left(x_3\right)$ since $L\left(x_3\right)\subset L\left(x_4\right)$, and $p+1\in L\left(x_4\right)$. This implies that at least one of $\beta$ and $p+1$ belongs to $L\left(x_3\right)$ since $L\left(x_3\right)\subset L\left(x_4\right)$ and $|L\left(x_4\right)\cap L\left(x_7\right)|\ge 3$. Label $x_7$ with $\alpha$, $x_8$ with p, $x_3$ with some label $\gamma \in L\left(x_3\right)\cap \{\beta ,p+1\}$, and $x_4$ with some label in $\{\beta ,p+1\}\backslash \left\{\gamma \right\}$;
• $\beta <\alpha <p$. If $p+1\in L\left(x_4\right)$, we label $x_3,x_4,x_7,x_8$ with $\alpha ,p+1,p,\beta$, respectively. Otherwise, $p+1\notin L\left(x_4\right)$ and hence $p+1\notin L\left(x_3\right)$, and $p\in L\left(x_4\right)$. If $\beta \in L\left(x_3\right)$, we label $x_3,x_4,x_7,x_8$ with $\beta ,p,\alpha ,p+1$, respectively. Otherwise, $L\left(x_3\right)=\{p,\alpha ,\gamma \}$ and $L\left(x_4\right)=\{p,\alpha ,\beta ,\gamma \}$ for some $\gamma \in B$. If $\gamma <\alpha$, then we label $x_3,x_4,x_7,x_8$ with $p,\gamma ,\beta ,p+1$, respectively. If $\gamma >p$, then we label $x_3,x_4,x_7,x_8$ with $\alpha ,p,\beta ,p+1$, respectively;
• $\alpha >p+1$. If $p\in L\left(x_4\right)$, we label $x_3,x_4,x_7,x_8$ with $\alpha ,p,p+1,\beta$, respectively. Otherwise, $p\notin L\left(x_4\right)$ and hence $p\notin L\left(x_3\right)$, and $p+1\in L\left(x_4\right)$. If $p+1\in L\left(x_3\right)$, we label $x_3,x_4,x_7,x_8$ with $p+1,\beta ,\alpha ,p$, respectively. Otherwise, $\beta \in L\left(x_3\right)$, we label $x_3,x_4,x_7,x_8$ with $\beta ,p+1,\alpha ,p$, respectively.

Case II. $\beta >p+1$.

• $\alpha <p$. If $p+1\in L\left(x_4\right)$, then we label $x_3,x_4,x_7,x_8$ with $\alpha ,p+1,\beta ,p$, respectively. Otherwise, $p+1\notin L\left(x_4\right)$, and $p\in L\left(x_4\right)$. If $\beta \in L\left(x_3\right)$, then we label $x_3,x_4,x_7,x_8$ with $\beta ,p,\alpha ,p+1$, respectively. Otherwise, $p\in L\left(x_3\right)$, then we label $x_3,x_4,x_7,x_8$ with $p,\beta ,\alpha ,p+1$, respectively;
• $p+1<\alpha <\beta$. If $p\in L\left(x_4\right)$, then we label $x_3,x_4,x_7,x_8$ with $\alpha ,p,\beta ,p+1$, respectively. Otherwise, $p\notin L\left(x_4\right)$, and $p+1\in L\left(x_4\right)$. If $\beta \in L\left(x_3\right)$, then we label $x_3,x_4,x_7,x_8$ with $\beta ,p+1,\alpha ,p$, respectively. Otherwise, $p+1\in L\left(x_3\right)$, we label $x_3,x_4,x_7,x_8$ with $p+1,\beta ,\alpha ,p$, respectively;
• $\alpha >\beta$. If $p+1\in L\left(x_4\right)$, then we label $x_3,x_4,x_7,x_8$ with $\alpha ,p+1,\beta ,p$, respectively. Otherwise, $p+1\notin L\left(x_4\right)$, and $p\in L\left(x_4\right)$. If $\beta \in L\left(x_3\right)$, then we label $x_3,x_4,x_7,x_8$ with $\beta ,p,\alpha ,p+1$, respectively. Otherwise, $p\in L\left(x_3\right)$, we label $x_3,x_4,x_7,x_8$ with $p,\beta ,\alpha ,p+1$, respectively. The completes the proof of Claim 1.

□

By Claim 1, we label $x_3,x_4,x_7,x_8$ with $p_1,p_2,p_3,p_4$, respectively. Finally, we label $u_2$ with some label in $B\backslash \{\underline{a},b,g^{\prime },h^{\prime },p_1,p_2,p_3,p_4\}$.

Combining Theorem 1 and the results in [23], we obtain easily the following:

Corollary 1.

For every Halin graph G, it holds that $\lambda \left(G\right)\le \Delta +6$.

5. Concluding  Remarks

Halin graphs are important and interesting planar graphs. The research of structures and parameters for Halin graphs has attracted considerable attention in the recent decades. The $L(2,1)$-labeling of graphs can be thought of as the generalization of the proper vertex coloring of graphs, which are of wide applications in frequency channel assignment, traffic phasing, task assignment, and other practical problems. This paper has contributed with the $L(2,1)$-labeling of Halin graphs.

We first proved that the $L(2,1)$-labeling number of each Halin graph of maximum degree 8 is at most 10. To explain that the upper bound 10 is sharp, we observed the graph $H^{\ast }$, depicted in Figure 2. Note that $H^{\ast }$ is a Halin graph consisting of three 8-vertices and twenty 3-vertices, which implies that $\Delta \left(H^{\ast }\right)=8$. It was shown in [4] that if a graph G contains a $\Delta$-vertex that is adjacent to at least two $\Delta$-vertices, then $\lambda \left(G\right)\ge \Delta +2$. This fact immediately implies that $\lambda \left(H^{\ast }\right)\ge \Delta \left(H^{\ast }\right)+2=8+2=10$. On the other hand, a 10-$L(2,1)$-labeling of $H^{\ast }$ using the labels $0,1,\dots ,10$ is constructed in Figure 2, which gives that $\lambda \left(H^{\ast }\right)\le 10$. Consequently, $\lambda \left(H^{\ast }\right)=10$.

Figure 2. A Hain graph $H^{\ast }$ with $\Delta =8$ and $\lambda \left(H^{\ast }\right)=10$.

Our Theorem 1 and the result in [23] confirm that every Halin graph G with $\Delta \ge 8$ has $\lambda \left(G\right)\le \Delta +2$. Here, the lower bound 8 for $\Delta$ does not seem like the best possibility. Thus, we would like to propose the following problem:

Problem 1.

Determine the least integer ${\Delta }_0$ such that every Halin graph G with $\Delta \left(G\right)\ge {\Delta }_0$ has $\lambda \left(G\right)\le \Delta +2$.

It is easy to check that the complete graph $K_4$ is a Halin graph with $\lambda \left(K_4\right)=6=\Delta \left(K_4\right)+3$. This fact and Theorem 1 imply that $4\le {\Delta }_0\le 8.$

The second result we establish in this paper is that every Halin graph G has $\lambda \left(G\right)\le \Delta +6$. We feel that the constant 6 in the expression can be further improved.

Problem 2.

Determine the least constant C such that every Halin graph G has $\lambda \left(G\right)\le \Delta +C$.

The above discussion clearly implies that $3\le C\le 6$.

To obtain the main contributions of this paper, we first analyzed the structures of Halin graphs with the maximum degree 8, i.e., that is, 14 inevitable configurations (C1)–(C14) were found in the graph under consideration. These structural characterizations could perhaps be applied to the study of other problems.