Abstract
Reversible data hiding in encrypted images (RDHEI) is commonly used for privacy protection in images stored on cloud storage. Currently, block permutation and co-modulation (BPCM) encryption is commonly utilized in most existing RDHEI schemes to generate encrypted images. In this paper, we analyze the vulnerabilities of RDHEI based on BPCM encryption and then propose a cryptanalysis method based on the vector quantization (VQ) attack. Unlike the existing cryptanalysis method, our method does not require the help of a plaintext image instead of adopting the symmetric property between the original cover image and the encrypted cover image. To obtain the pixel-changing pattern of a block before and after co-modulation, the concept of a pixel difference block (PDB) is first defined. Then, the VQ technique is used to estimate the content of the ciphertext block. Finally, we propose a sequence recovery method to help obtain the final recovered image based on the premise that the generator is compromised. The experimental results demonstrate that when the block size is 4 × 4, our proposed cryptanalysis method can decrypt the contents of the ciphertext image well. The average similarity can exceed 75% when comparing the edge information of the estimated image and the original image. It is concluded from our study that the BPCM encryption algorithm is not robust enough.
1. Introduction
With the rapid development of big data technology and cloud computing, cloud servers have become the most suitable option for storing data online [1,2]. The biggest advantage of cloud services is that users can access data from anywhere in the world. This not only increases productivity but also makes it easier for users to back up their data remotely. However, the leakage of private data has led to security concerns about the separation of private ownership and data management in cloud storage technologies [3]. To solve this problem, scholars began to investigate how cryptography and reversible data hiding in encrypted images (RDHEI) can be combined and applied in cloud environments. Since then, RDHEI has become a hot topic of research for scholars.
In general, RDHEI can be classified into two main categories: vacating room before encryption (VRBE) [4,5,6,7] and vacating room after encryption (VRAE) [8,9,10,11,12,13,14,15,16,17,18,19,20]. Yi et al. [21] pointed out that although a large amount of redundant space can be reserved from the original image using the VRBE-based approach, it is not feasible in practical applications. Thus, many scholars have focused on the study and development of VRAE-based schemes. Since the performance of VRAE-based RDHEI is directly affected by the encryption algorithm of the image, traditional encryption methods, e.g., the Data Encryption Standard (DES) algorithm [22] and permutation encryption [23], are difficult to use directly for RDHEI. Because the correlation between adjacent pixels is destroyed in such encrypted images, it is difficult to reserve the redundant space to carry the secret data. In order to hide data in the encrypted image and then generate the embedded encrypted image without destroying the decrypted image, special encryption algorithms need to be designed for VRAE-based RDHEI. The stream cipher technique [8,10] and block permutation operation [24,25,26] are two commonly used encryption methods in VRAE-based RDHEI.
As an example, the stream cipher technique consists of two steps: (1) generate a random sequence of the key stream and (2) encrypt each pixel using a bitwise exclusive-or operation with a key. The stream cipher technique provides high security but breaks the correlation between adjacent pixel values. With this method, data hiders can embed secret data only by changing the positions or modifying the values of the encrypted pixels. Therefore, the embedding rate of RDHEI based on the stream cipher technique is very low. For block permutation encryption, the plaintext image is divided into non-overlapping blocks. Then, these blocks are permutated using the encryption key. This type of encryption preserves the correlation within the plaintext blocks in the encrypted image. Compared with the stream cipher technique, block permutation can greatly increase the embedding rate of RDHEI.
In fact, it is a great challenge to obtain the best tradeoff between the payload, the quality of the reconstructed image and the security of the image content. In recent years, most existing VRAE-based RDHEI algorithms have been evaluated based on two conflicting measures, i.e., the embedding capability of the algorithm and the visual quality of the decrypted image. However, the security of encrypted images is also an important issue of the RDHEI algorithm that cannot be ignored because it is related to whether the privacy of the image owner can be guaranteed [27]. It is well known that known-plaintext attack (KPA) is commonly used to analyze the security of the image encryption algorithm. Li et al. pointed out in [28] that the permutation-only encryption algorithm has been shown to be unable to resist the KPA. In other words, the block permutation encryption adopted in RDHEI [24,25,26] is insecure.
To enhance the embedding capacity without compromising the security of the encrypted image, scholars have tried to design a new encryption algorithm by combining the stream cipher technique and a block permutation operation for RDHEI [29,30]. Taking the encrypted algorithm used in [29] for example, the original image with a size of is divided into non-overlapping blocks with a size of pixels, and all the blocks are shuffled using the encryption key, where H is the height and W is the width of the original image. Then, a pseudo-random matrix with a size of pixels is generated using the same encryption key, and each block is encrypted with a random number in the same position of the pseudo-random matrix by a pixel-wise modulo operation. Scholars have named this type of encryption algorithm the block permutation and co-modulation (BPCM) algorithm, which can effectively retain the correlation among the pixels inside a block. This algorithm can effectively enhance the embedding rate of RDHEI. In addition, the BPCM algorithm can effectively resist exciting KPAs [31,32]. The reasons are (1) the image block’s positions are disrupted after image encryption, which breaks the correlation between neighboring blocks; and (2) the pixel values are changed after co-modulation, which violates the premise of existing KPAs.
Recently, there have been some research reports on the security analysis of RDHEI under the assumption that the data hider may not be trusted and may be aware of one plaintext image for a given set of encrypted images [31,32,33,34]. Among them, [33] is the most representative report. In [33], the authors also assumed that the content owner used the same key to encrypt plaintext images. Based on the above assumptions, the data hider can estimate the secret key and recover all the encrypted images by comparing the plaintext image with its corresponding encrypted image. However, with the issue of information security awareness, fewer and fewer content owners continue to encrypt their images with the same secret key. In other words, the cryptanalysis proposed by [33] may not work in various situations. To analyze the security performance of BPCM, a cryptanalysis method to crack BPCM called a vector quantization attack (VQA), is proposed in this paper. Our proposed cryptanalysis algorithm can roughly recover the plaintext content of encrypted images without secret key awareness. The main contributions of this paper are summarized as follows:
- VQA: The vector quantization technique is used for the first time to estimate the plaintext of each encrypted image block.
- Direct cracking: Unlike the existing KPA algorithm [33], the cryptanalysis algorithm proposed in this paper does not require the assistance of the plaintext image when cracking the plaintext content of encrypted images.
The rest of this paper is organized as follows. Section 2 introduces the preliminary works. In Section 3, we describe in detail the cryptoanalysis based on the vector quantization attack (called VQA for short) proposed in this paper. In Section 4, the experimental results of the proposed cryptanalysis algorithm are provided. The limitations and conclusions are presented in Section 5 and Section 6, respectively.
2. Preliminary Work
In this section, we briefly analyze the characteristics and security of BPCM encryption. Then, the vector quantization technique is introduced in detail, which is the key point of our cryptanalysis method.
2.1. Analysis of BPCM Encryption
Assume the original grayscale image with a size of pixels is divided into mutually exclusive blocks , where the i-th plaintext block , and is the number of pixels in . The detailed steps of BPCM encryption are listed as follows:
Step 1: Block permutation: A permutation sequence , , is generated by a random permutation generator with a key seed . Then, the position of each block is shuffled by , and the first stage of the encryption image is obtained.
Step 2: Block co-modulation: A stream cipher is produced using a random number generator with a secret key . For each block in , all the pixels are encrypted according to Equation (1) to obtain a final encrypted block , and the final encryption image , is obtained.
In general, the BPCM algorithm has the following characteristics:
- Large encryption space. In theory, two keys of the BPCM encryption can bring different encryption results. Taking a greyscale image () as an example, when the size of the block is pixels, there are encryption results, which is much greater than . Thus, with the current level of computer hardware, it is difficult to break BPCM encryption using exhaustive brute-force attacks.
- Resisting the existing KPAs. Since the BPCM algorithm changes the pixels within each block, even if the plaintext image is obtained, the existing KPA methods [31,32] cannot estimate the permutation sequence and crack the content of the image by comparing the encrypted block with the original block.
- Increasing the embedding capacity. Although the BPCM algorithm changes the pixel values in each block, it does not destroy the correlation among the pixels inside the block. Thus, BPCM-based RDHEI schemes [29,30] can take the advantage of this characteristic to create redundant space and embed secret data. In BPCM-based schemes, the block size is usually set to in order to maintain a balance between the embedding capacity and the security. The embedding rate of such schemes can usually reach more than 2.5 bpp.
However, BPCM also has serious security problems, mainly due to the following reasons:
- The permutation sequence of BPCM is generated by a random permutation generator and a secret key . The receiver must use the same generator as the content owner when decrypting the image; therefore, the generator must be transmitted from the content owner to the receiver, which gives the attacker the possibility of stealing the generator. Once the attacker has obtained the generator, he can obtain the permutation sequence by exhaustively trying the secret key.
- The correlation of the pixels within most blocks remains unchanged, and the attacker can use these correlations to estimate the plaintext content of the block.
In Section 3, we will use the features of the BPCM algorithm discussed above to design a cracking algorithm called the vector quantization attack (VQA) algorithm.
2.2. Vector Quantization
The vector quantization algorithm is a compression technique that encodes a digital image into an index table. As shown in Figure 1, the original image is divided into exclusive non-overlapping blocks. Then, for each block, the Euclidean distance between the block and each codeword is calculated, and the index with the smallest value is recorded on the index table. With the above steps, the original image is compressed into an index table.
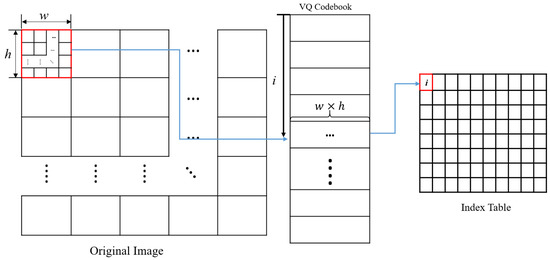
Figure 1.
An illustration of the VQ technique.
In the decoding stage, the index table is processed sequentially. According to each index value, a codeword can be arranged to reconstruct a decompressed image. The visual quality of the decompressed image depends mainly on the codewords in the codebook. The more the pixel variation characteristics of the codewords contained in the codebook match the natural image blocks and the more diversity there is, the better the approximation that is achieved.
As mentioned above, the codebook determines the quality of the compressed image. A typical strategy is to obtain a good codebook through training. The training process is as follows:
Step 1: Select four to six greyscale images as training samples.
Step 2: Divided all the images into exclusive non-overlapping blocks and derive a set of block candidates.
Step 3: Select blocks randomly from the set of block candidates generated in Step 2 as the initial centroids, where represents the number of centroids.
Step 4: Calculate the Euclidean distances between the remaining blocks and the centroids and group them according to the minimum value.
Step 5: Recalculate the new centroids.
Step 6: Repeat the above five steps until the recalculated centroids are stable.
3. Proposed Cryptanalysis Based on the VQA
The main purpose of the attack on RDHEI is to obtain the plaintext content of the ciphertext image. However, the existing cryptanalysis methods are designed based on the premise that one of the plaintext images is known. How to crack the content of the ciphertext image when the plaintext image is unknown is a problem worth investigating. To achieve our goal, we define a pixel difference block (PDB) in Section 3.1 to present the pixel-changing pattern in each image block. Later, PDB is applied and our proposed VQ attack is presented. Finally, a novel cryptanalysis method for block permutation sequence estimation is proposed. The flowchart of the proposed method is shown in Figure 2.
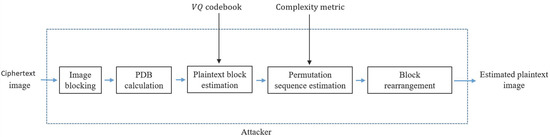
Figure 2.
Flowchart of the proposed cryptanalysis method.
3.1. Pixel Difference Block
In this subsection, we define a pixel difference block (PDB) as the structure that reflects the pixel-changing pattern in each image block. For an encrypted image block containing pixels and , its PDB of is calculated as follows:
where represents the PDB of the encrypted image block .
According to Equation (2), the ciphertext difference image is obtained by Equation (3).
where is the number of blocks.
Depending on the co-modulation key , the plaintext image block and its corresponding can be divided into two cases:
where and are the minimum and maximum pixel values in , respectively. That is, when satisfies , the PDBs of and its corresponding plaintext block are the same. When satisfies , part of the values in will overflow, which causes the PDBs of and to be different.
To illustrate Cases 1 and 2, Figure 3 shows an example (taking blocks of “Lena” for example). For plaintext block , when the block co-modulation key is and , respectively, two groups of corresponding ciphertext image blocks are generated. As shown in Figure 3, part of the values in of Case 2 are overflowed and marked in RED after co-modulation, which leads to a change in some values in its corresponding PDB. However, the values in the PDB of Case 1 do not change after co-modulation. Thus, when the ciphertext image block belongs to Case 1, the PDB of can fully reflect the changing pattern of the current plaintext block, and it can be used to estimate its corresponding plaintext content. When the ciphertext image block belongs to Case 2, the encrypted pixel has an overflow problem after co-modulation. Thus, the PDB of only reflects the partial changing pattern of the current plaintext block. Therefore, an advanced algorithm is designed and described in Section 3.2 to estimate its corresponding plaintext content.
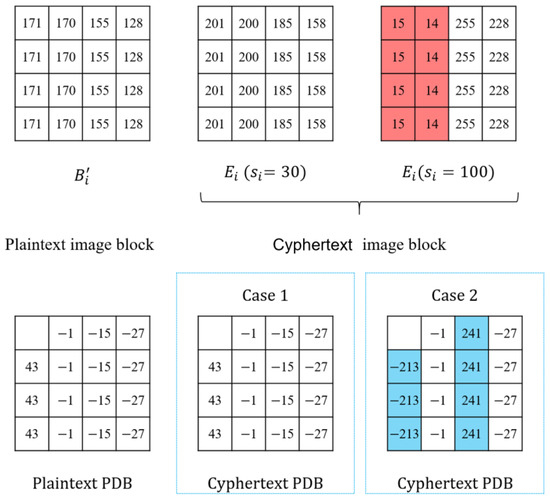
Figure 3.
PDBs of the plaintext image block and the corresponding ciphertext image block.
3.2. Plaintext Block Estimation Based on the VQ Attack
Figure 3 demonstrates that even if a plaintext image block is encrypted, its corresponding ciphertext image block may retain either all or some of the pixel-changing patterns according to the block’s type. As mentioned above, a well-trained VQ codebook can provide codewords that approximate real image blocks, and it can be used to estimate the contents of the ciphertext image blocks. If a ciphertext block belongs to Case 1, the codebook can be used directly to find the most suitable plaintext block for the current ciphertext block. If a ciphertext block belongs to Case 2, then the search range of the codebook shall be expanded to simulate the overflow problem caused by co-modulation on the image block and find the suitable plaintext block. In this section, the method of plaintext block estimation based on the VQ attack is proposed.
Assume that the length of the codeword in codebook has the same length as the number of pixels in the ciphertext image block. The PDBs of can be calculated by Equation (2), where is the number of codewords. The detailed steps of the plaintext block estimation are as follows:
Step 1: For a ciphertext block , calculate the complex of according to Equation (6).
If the value of does not exceed the threshold th, then treat as a normal block; otherwise, treat as an abnormal block.
Step 2: Calculate the PDBs and of and , respectively.
Step 3.1: If is a normal block, compare and according to Equation (7) until the that is closest to is found. Then, mark the according to .
Step 3.2: If is an abnormal block, expand each codeword to , as shown in Equation (8), and calculate the PDBs of the new codebook .
Step 3.3: Compare and to find the that is closest to as Step 4.1. Then, mark the from the original codebook according to Equation (10).
Step 4: Replace with .
3.3. Block Permutation Sequence Estimation
By estimating the block content of the ciphertext block, each ciphertext block is replaced by a VQ codeword that reflects the pixel-changing pattern of and its corresponding plaintext block . Next, we can roughly recover the content of the image by obtaining the block permutation sequence .
In our hypothesis, the attacker can obtain the random permutation generator . Therefore, the attacker can obtain all the permutation sequences generated from by exhausting all the secret keys. It is worth mentioning that the current encryption software is limited to the length of the secret key, so it takes less time to exhaustively try all the secret keys than to try all the permutations. For example, in MATLAB, the length of the secret key cannot exceed , and the type must be an integer. After obtaining , we only need to try all the secret keys to generate sequences and find the most suitable one instead of finding one among the original sequences. However, it is an extremely difficult task to find the most suitable sequence among results by manual inspection. Therefore, a screen idea is proposed below to reduce the search scope.
In a normal image, the pixel values between adjacent blocks are highly close to each other. Abrupt changes only appear at the edge positions, which are relatively rare according to the statistics. We propose a complexity detection method based on this characteristic of the adjacent blocks. As illustrated in Figure 4a, the green pixel sequence in the top-left block is and the adjacent pixel sequence is . Note that, is the mean value of the two pixels that are adjacent to . The complexity of the region where the current block is located is defined as:
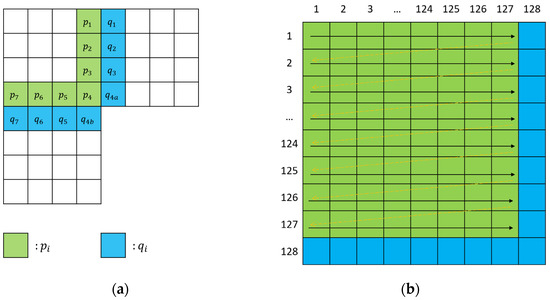
Figure 4.
An illustration of the complexity calculation. (a) Complexity of each block; (b) Complexity of the whole image.
Next, as shown in Figure 4b, add the of all the blocks to represent the complexity of the whole image. Finally, the complexity of the recovered image is calculated for each sequence key, and the minimum 5% of the images with the smallest complexity are selected for manual screening.
4. Experimental Results
In this section, some experiments are conducted to evaluate the situation of information leakage under the VQA. As shown in Figure 5, five 512 × 512 sized grayscale standard test images are used: Airplane, Lena, Peppers, Baboon and Elaine. All the programs are implemented with MATLAB R2017a.

Figure 5.
Five 512 × 512 sized grayscale standard test images. (a) Airplane; (b) Lena; (c) Peppers; (d) Baboon; (e) Elaine.
4.1. Analysis of the PDBs of Ciphertext Image
In this section, the characteristics of the PDB are analyzed. The experimental results of “Lena” are shown in Figure 6, where the histograms together with the 3D views of the pixel values of the plaintext image and its corresponding ciphertext image, generated by the BPCM encryption under a 4 × 4 block size, are given. We first observe the histograms of the test images. As shown in the figure, the histogram of the ciphertext image is uniform and like the distribution of white noise.
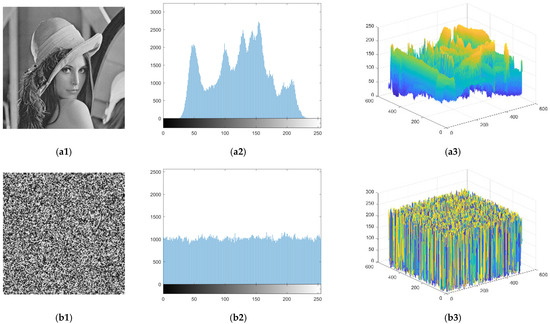
Figure 6.
Results of the test image “Lena”. (a1) Plaintext image; (b1) Ciphertext image; (a2, b2) The corresponding histograms; (a3, b3) 3D view of the pixel values.
The distribution of the histogram shows that the BPCM encryption is effective. However, when we analyze the PDB of the image blocks of the ciphertext image, we find that the PDB of most of the image blocks does not change after encryption. Figure 7 is given to illustrate the distribution of the blocks belonging to Case 2. As shown in the figure, the white and black blocks represent that the current block belongs to the above-mentioned Cases 1 and 2 after encryption, respectively. Figure 7a illustrates that the image blocks belonging to Case 2 are mostly distributed in the regions where the textures are complex. Thus, in an encrypted image, we can obtain the changing pattern in most of the encrypted blocks, which helps to crack the plaintext content of the whole ciphertext image.

Figure 7.
The distribution of the two cases of the blocks after encryption in “Lena”. (a) Before permutation; (b) After permutation.
4.2. Analysis of the Estimation of the Plaintext Block
With our proposed VQA, when the attacker obtains a ciphertext image encrypted by BPCM, the attacker first divides the image into blocks and uses the PDB of each block to find the most suitable VQ codeword instead of this block. The experimental results of the test images “Lena” and “Airplane” are shown in Figure 8, where the histograms of the pixel values of the ciphertext image and the estimated image are given. As shown in the figure, the histograms of the estimated image become irregular, which means that each encrypted block is replaced by a suitable plaintext block.
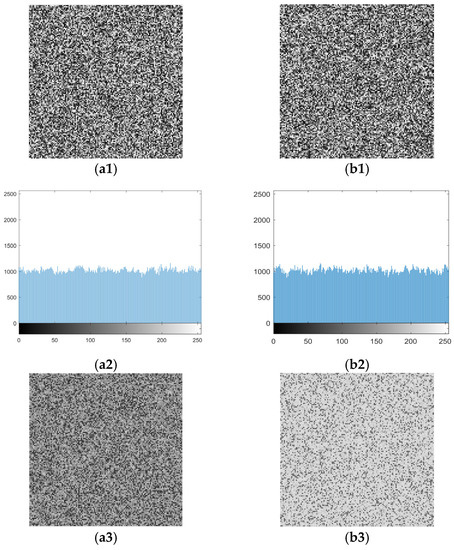
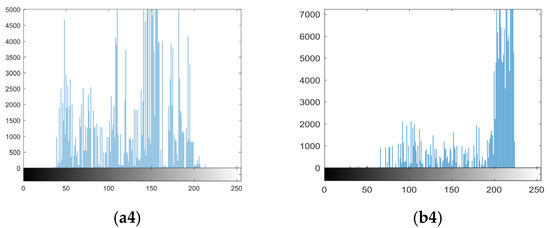
Figure 8.
Results of the test images. (a1) Ciphertext image of “Lena”; (b1) Ciphertext image of “Airplane”; (a2) Histogram of (a1); (b2) Histogram of (b1); (a3) Estimated image of “Lena”; (b3) Estimated image of “Airplane”; (a4) Histogram of (a3); (b4) Histogram of (b3).
4.3. Analysis of the Estimation of Permutation Sequence
Once the estimated image is obtained, the attacker uses the block permutation sequence estimation method described in Section 3.3 to find the most suitable sequence Ω from the sequence generator. After obtaining the sequence Ω, the attacker can recover the estimated image as a fuzzy plaintext image to successfully crack the plaintext image content. Figure 9 shows the recovery result of “Lena” (the size of the codebook = 100). As shown in Figure 9c, we can obtain the content of the original image from the recovered fuzzy plaintext image. In addition, we mark the edge of the recovered fuzzy plaintext image by the pixel difference (PD) within each block:
where
represents the j-th pixel in the i-th block. After calculating the PD of each block, we mark the block as white when the PD of the block is greater than the APD (average pixel difference), and vice versa.

Figure 9.
Results of the test image “Lena” (the size of codebook = 100). (a) Original image; (b) Edges of (a); (c) Estimated image; (d) Recovered fuzzy plaintext image; (e) Edges of (d), similarity = 83%.
To test the effect of the generated codebook on the recovery results, we conduct three sets of experiments, where the codebook is trained by the plaintext images related to the encrypted images; the codebook is trained by the plaintext images that are completely unrelated to the encrypted images; and the codebook is trained with larger size blocks. We use the edge similarity to evaluate the accuracy of the recovered fuzzy plaintext image, which is defined as:
where represents the Hamming distance between the edge of the original plaintext image and the recovered fuzzy plaintext image. By comparing the similarity, we can see that they are close (similarity = 83%).
As shown in Figure 10 and Figure 11, when we use a small-sized codebook (with a block size = 4 × 4), the diversity of the recovered image blocks is decreased; however, better recovery results are achieved for smooth images (e.g., Airplane). When we increase the block size to 8 × 8 pixels and train the codebook, as shown in Figure 12, there is an obvious block effect in the recovery results, so the visual quality of the decrypted image decreased. In other words, we can conclude that a better recovered image can be obtained when the block size is 4 × 4 compared with a block size of 8 × 8. Moreover, the smaller codebook provides relatively better image quality for the recovered image than the larger codebook, no matter what kind of source of codebook training.


Figure 10.
Experimental results using different sizes of codebooks that are trained by “Lena” and “Airplane”. (Block size = 4 × 4). (a1–a5) are the edges of the original images; (b1–b5) are the estimated images when the size of codebook is 100; (c1–c5) are the edges of (b1–b5); (d1–d5) are the estimated images when the size of codebook is 64; (e1–e5) are the edges of (d1–d5); (f1–f5) are the estimated images when the size of codebook is 32; (g1–g5) are the edges of (f1–f5).


Figure 11.
Experimental results using different sizes of codebooks that are trained by (h). (Block size = 4 × 4). (a1–a5) are the edges of the original images; (b1–b5) are the estimated images when the size of codebook is 100; (c1–c5) are the edges of (b1–b5); (d1–d5) are the estimated images when the size of codebook is 64; (e1–e5) are the edges of (d1–d5); (f1–f5) are the estimated images when the size of codebook is 32; (g1–g5) are the edges of (f1–f5). (h) training sample of VQ codebook.


Figure 12.
Experimental results using different sizes of codebooks that are trained by (h). (Block size = 8 × 8). (a1–a5) are the edges of the original images; (b1–b5) are the estimated images when the size of codebook is 100; (c1–c5) are the edges of (b1–b5); (d1–d5) are the estimated images when the size of codebook is 64; (e1–e5) are the edges of (d1–d5); (f1–f5) are the estimated images when the size of codebook is 32; (g1–g5) are the edges of (f1–f5). (h) training sample of VQ codebook.
We also list the comparative results under different categories in Table 1. When we set the size of the codebook to 100, 64 and 32, respectively, we find that the best recovery results are achieved with the 64-sized codebook when the block size is set to 4 × 4. When we set the block size to 8 × 8, the size of the codebook has relatively little effect on the recovery results.

Table 1.
Comparative results under different categories.
4.4. Characteristics Analysis
The proposed cryptanalysis scheme aims to estimate the plaintext content of the ciphertext image. In this subsection, we compare the performance with several cryptanalysis schemes [31,32,33,34]. Table 2 shows the characteristics of the proposed scheme and the compared schemes. The cryptanalysis schemes proposed in [31,32] are only suitable for permutation-only encryption and, therefore, they cannot crack the plaintext content of the ciphertext image encrypted by BPCM. For the BPCM encryption algorithm, the image quality of the estimated plaintext content of Qu et al.’s scheme [33] is better than ours. However, Qu et al.’s scheme [33] can only be utilized with the help of a plaintext image, and all the encrypted images must be encrypted with the same encryption key. In other words, once either the plaintext image cannot be accessed or the encryption key is not the right one, the analysis results cannot be derived. Compared to Qu et al.’s scheme [33], we can estimate the plaintext content of encrypted ciphertext images generated by any key without the help of the plaintext image, which is more applicable than [33]. Moreover, our evaluation results are more stable than those offered by Qu et al.’s scheme [33]. As for Xiang et al.’s scheme [34], they also analyzed the insecurity of the BPCM encryption algorithm, which also proved the feasibility of our scheme. Although they did not conduct the cryptanalysis as our scheme does, and they evaluated BPCM from the BPCM algorithm itself and pointed out the insecurity of the BPCM encryption algorithm, we still included it in Table 2.

Table 2.
Comparison of scheme characteristics.
5. Limitations
Although the proposed cryptanalysis algorithm can roughly capture the contents of the ciphertext image, the visual quality of the estimated plaintext image is low. In addition, estimating the permutation sequence is time-consuming and requires powerful hardware support.
6. Conclusions
BPCM is an encryption algorithm that has been commonly used in RDHEI. In this paper, we analyzed the security of BPCM and proposed a new cryptanalysis algorithm based on the VQ attack. Unlike other cryptanalysis methods, our proposed VQA method does not require the plaintext image to obtain the contents of the ciphertext image. The experimental results demonstrate that under a block size of 4×4 pixels, our VQA method can capture the contents of the ciphertext image well. The average similarity can exceed 75% when comparing the edge information of the estimated image and the original image. The conclusion drawn from the research in this paper is that the security offered by the BPCM encryption algorithm leaves a leakage risk. This allows researchers to consider its security aspects in the future to develop more robust techniques.
In the future, our work will focus on designing a better cryptanalysis algorithm to improve the visual quality of the estimated plaintext image.
Author Contributions
Conceptualization, C.-C.C.; methodology, C.-C.C.; software, K.G.; validation, C.-C.C., K.G. and C.-C.L.; formal analysis, K.G. and C.-C.L.; investigation, K.G.; resources, C.-C.C. and C.-C.L.; data curation, K.G.; writing—original draft preparation, K.G.; writing—review and editing, C.-C.C., K.G. and C.-C.L.; visualization, C.-C.C., K.G. and C.-C.L.; supervision, C.-C.C. and C.-C.L.; project administration, C.-C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gharehpasha, S.; Masdari, M.; Jafarian, A. Power efficient virtual machine placement in cloud data centers with a discrete and chaotic hybrid optimization algorithm. Clust. Comput. 2021, 24, 1293–1315. [Google Scholar] [CrossRef]
- Gharehpasha, S.; Masdari, M.; Jafarian, A. Virtual machine placement in cloud data centers using a hybrid multi-verse optimization algorithm. Artif. Intell. Rev. 2021, 54, 2221–2257. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, H.; Hou, D.; Yu, N. Reversible data hiding in encrypted images by reversible image transformation. IEEE Trans. Multimed. 2016, 18, 1469–1479. [Google Scholar] [CrossRef]
- Zhang, W.M.; Ma, K.; Yu, N. Reversibility improved data hiding in encrypted images. Signal Process. 2014, 94, 118–127. [Google Scholar] [CrossRef]
- Cao, X.C.; Du, L.; Wei, X.X.; Meng, D.; Guo, X.J. High capacity reversible data hiding in encrypted images by patch-level sparse representation. IEEE Trans. Cybern. 2015, 46, 1132–1143. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Zhou, Y.C. Binary-block embedding for reversible data hiding in encrypted images. Signal Process. 2017, 133, 40–51. [Google Scholar] [CrossRef]
- Qiu, Y.Q.; Qian, Z.; Zeng, H.; Lin, X.; Zhang, X. Reversible data hiding in encrypted images using adaptive reversible integer transformation. Signal Process. 2020, 167, 107288. [Google Scholar] [CrossRef]
- Zhang, X.P. Reversible data hiding in encrypted image. IEEE Signal Process. Lett. 2011, 18, 255–258. [Google Scholar] [CrossRef]
- Hong, W.; Chen, T.-S.; Wu, H.-Y. An improved reversible data hiding in encrypted images using side match. IEEE Signal Process. Lett. 2012, 19, 199–202. [Google Scholar] [CrossRef]
- Zhang, X.P. Separable reversible data hiding in encrypted image. IEEE Trans. Inf. Forensics Secur. 2011, 7, 826–832. [Google Scholar] [CrossRef]
- Wu, X.; Sun, W. High-capacity reversible data hiding in encrypted images by prediction error. Signal Process. 2014, 104, 387–400. [Google Scholar] [CrossRef]
- Qin, C.; Zhang, X. Effective reversible data hiding in encrypted image with privacy protection for image content. J. Vis. Commun. Image Represent. 2015, 31, 154–164. [Google Scholar] [CrossRef]
- Qian, Z.; Zhang, X. Reversible data hiding in encrypted images with distributed source encoding. IEEE Trans. Circuits Syst. Video Technol. 2015, 26, 636–646. [Google Scholar] [CrossRef]
- Huang, F.; Huang, J.; Shi, Y.-Q. New framework for reversible data hiding in encrypted domain. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2777–2789. [Google Scholar] [CrossRef]
- Ge, H.; Chen, Y.; Qian, Z.; Wang, J. A high capacity multi-level approach for reversible data hiding in encrypted images. IEEE Trans. Circuits Syst. Video Technol. 2019, 29, 2285–2295. [Google Scholar] [CrossRef]
- Chen, K.-M. High capacity reversible data hiding based on the compression of pixel Differences. Mathematics 2020, 8, 1435. [Google Scholar] [CrossRef]
- Wang, Y.M.; He, W.G. High capacity reversible data hiding in encrypted image based on adaptive MSB prediction. IEEE Trans. Multimed. 2021, 24, 1288–1298. [Google Scholar] [CrossRef]
- Fu, Y.J.; Kong, P.; Yao, H.; Tang, Z.J.; Qin, C. Effective reversible data hiding in encrypted image with adaptive encoding strategy. Inf. Sci. 2019, 494, 21–36. [Google Scholar] [CrossRef]
- Pun, C.-M. Reversible data hiding in encrypted images using chunk encryption and redundancy matrix representation. IEEE Trans. Dependable Secur. Comput. 2020, 19, 1382–1394. [Google Scholar]
- Wang, Y.M.; Cai, Z.C.; He, W.G. High capacity reversible data hiding in encrypted image based on intra-block lossless compression. IEEE Trans. Multimed. 2020, 23, 1466–1473. [Google Scholar] [CrossRef]
- Yi, S.; Zhou, Y. Separable and reversible data hiding in encrypted images using parametric binary tree labeling. IEEE Trans. Multimed. 2019, 21, 51–64. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology. “FIPS-46: Data Encryption Standard (DES).” Revised as FIPS 46-1:1988, FIPS 46-2:1993, FIPS 46-3:1999. 1979. Available online: http://csrc.nist.gov/publications/fips/fips46-3/fips46-3.pdf (accessed on 15 January 1977).
- Jolfaei, A.; Wu, X.; Muthukkumarasamy, V. On the security of permutation-only image encryption schemes. IEEE Trans. Inf. Forensics Secur. 2016, 11, 235–246. [Google Scholar] [CrossRef]
- TableYin, Z.X.; Abel, A.; Tang, J.; Zhang, X.P.; Luo, B. Reversible data hiding in encrypted images based on multi-level encryption and block histogram modification. Multimed. Tools Appl. 2017, 76, 1–22. [Google Scholar]
- Yin, Z.X.; Abel, A.; Zhang, X.P.; Luo, B. Reversible data hiding in encrypted image based on block histogram shifting. IEEE Int. Conf. Acoust. Speech Signal Process. 2016, 2016, 2129–2133. [Google Scholar]
- Liu, Z.; Pun, C. Reversible data-hiding in encrypted images by redundant space transfer. Inf. Sci. 2018, 433–434, 188–203. [Google Scholar] [CrossRef]
- Dragoi, I.; Coltuc, D. On the Security of Reversible Data Hiding in Encrypted Images by MSB Prediction. IEEE Trans. Inf. Forensics Secur. 2021, 16, 187–189. [Google Scholar] [CrossRef]
- Li, S.J.; Li, C.Q.; Chen, G.R.; Bourbakis, N.G.; Lo, K.-T. A general quantitative cryptanalysis of permutation-only multimedia ciphers against plaintext attacks. Signal Process. Image Commun. 2008, 23, 212–223. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, X.; Li, G.; Zhan, S.; Tang, Z. Reversible data hiding with adaptive difference recovery for encrypted images. Inf. Sci. 2022, 584, 89–110. [Google Scholar] [CrossRef]
- Wang, X.; Chang, C.-C.; Lin, C.-C. Reversible data hiding in encrypted images with block-based adaptive MSB encoding. Inf. Sci. 2021, 567, 375–394. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Liu, Y.S.; Wang, C.; Zhou, J.T.; Zhang, Y.S.; Chen, G.R. Improved known-plaintext attack to permutation-only multimedia ciphers. Inf. Sci. 2018, 430–431, 228–239. [Google Scholar] [CrossRef]
- Qu, L.; Chen, F.; He, H. Security analysis of multiple permutation encryption adopt in reversible data hiding. Multimed. Tools Appl. 2020, 79, 29451–29471. [Google Scholar]
- Qu, L.F.; Chen, F.; Zhang, S.J.; He, H.J. Cryptanalysis of reversible data hiding in encrypted images by block permutation and co-modulation. IEEE Trans. Multimed. 2021, 24, 2924–2937. [Google Scholar]
- Xiang, Y.P.; Xiao, D.; Zhang, R.; Liang, J.; Liu, R. Cryptanalysis and improvement of a reversible data-hiding scheme in encrypted images by redundant space transfer. Inf. Sci. 2021, 545, 188–206. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).