Calculating Crossing Numbers of Graphs Using Their Redrawings

Abstract

The main aim of the paper is to give the crossing number of the join product $G^{*}+D_n$. The connected graph $G^{*}$ of order six is isomorphic to $K_{3,3}\backslash e$ obtained by removing one edge from the complete bipartite graph $K_{3,3}$, and the discrete graph $D_n$ consists of n isolated vertices. The proofs were carried out with the help of several possible redrawings of the graph $G^{*}$ with respect to its many symmetries.

1. Introduction

The problem of reducing the number of crossings is interesting in many areas. One of the most popular areas is the implementation of the VLSI layout, which has revolutionized circuit design and has had a strong impact on parallel computing. Crossing numbers were also studied to improve the readability of hierarchical structures and automated graphs. The visualized graph should be easy to read and understand. For the sake of the clarity of the graphical drawings, the reduction in crossings is likely the most important. Therefore, the investigation on the crossing number of simple graphs is a classical but very difficult problem. Garey and Johnson [1] proved that determining $\mathrm{cr}\left(G\right)$ is an NP-complete problem.

Let G be a simple graph. We use $V\left(G\right)$ and $E\left(G\right)$ to denote the vertex set and the edge set of G, respectively. A drawing of G is a representation of G in the plane such that its vertices are represented by distinct points and its edges by simple continuous arcs connecting the corresponding point pairs. The crossing number $\mathrm{cr}\left(G\right)$ is the smallest number of crossings of edge crossings in any drawing of G in the plane. It is easy to see that a drawing with a minimum number of crossings (an optimal drawing) is always a good drawing, meaning that no edge crosses itself, no two edges cross more than once, and no two edges are incident with the same vertex cross. Let D be a good drawing of the graph G. We denote the number of crossings in D by ${\mathrm{cr}}_D\left(G\right)$. Let $G_i$ and $G_j$ be edge-disjoint subgraphs of G. We denote the number of crossings between edges of $G_i$ and edges of $G_j$ by ${\mathrm{cr}}_D(G_i,G_j)$, and the number of crossings among edges of $G_i$ in D by ${\mathrm{cr}}_D\left(G_i\right)$. It is easy to see that. for any three mutually edge-disjoint subgraphs $G_i$, $G_j$, and $G_k$ of G, the following equations hold:

$${\mathrm{cr}}_D(G_i\cup G_j)={\mathrm{cr}}_D\left(G_i\right)+{\mathrm{cr}}_D\left(G_j\right)+{\mathrm{cr}}_D(G_i,G_j),$$

$${\mathrm{cr}}_D(G_i\cup G_j,G_k)={\mathrm{cr}}_D(G_i,G_k)+{\mathrm{cr}}_D(G_j,G_k).$$

It was Turán [2] who introduced the concept of crossing numbers. In his Brick Factory Problem, he investigated the minimal number of crossings among edges of the complete bipartite graphs $K_{m,n}$. Kleitman in [3] showed that

$$\mathrm{cr}\left(K_{m,n}\right)=⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋,\mathrm{if}min\{m,n\}\le 6.$$

(1)

For an overview of several exact values of crossing numbers for some families of graphs, see Clancy [4]. The main aim of this survey was to compile all such published results for crossing numbers together with references. The join product of two graphs $G_i$ and $G_j$, denoted $G_i+G_j$, is obtained from vertex-disjoint copies of $G_i$ and $G_j$ by adding all edges between $V\left(G_i\right)$ and $V\left(G_j\right)$. For $\left|V\right(G_i\left)\right|=m$ and $\left|V\right(G_j\left)\right|=n$, the edge set of $G_i+G_j$ is the union of the disjoint edge sets of the graphs $G_i$, $G_j$, and the complete bipartite graph $K_{m,n}$. Let $D_n$ denote the discrete graph (sometimes called empty graph) on n vertices, and let $K_n$ be the complete graph on n vertices. The exact values for crossing numbers of $G+D_n$ for all graphs G of an order of at most four are given by Klešč and Schrötter [5], and also for some connected graphs G of order five and six [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. The main aim of this paper is to extend the known results concerning this topic to new connected graphs. Note also that $\mathrm{cr}(G+D_n)$ are known only for some disconnected graphs G; see [30,31,32].

Recently, the crossing numbers of complete multipartite graphs have attracted much attention. Note that the crossing numbers of complete tripartite graphs $K_{k,l,n}$ were determined for all cases where $k+l\le 6$, except for $K_{3,3,n}$. In the case of complete fourpartite graphs, $K_{k,l,m,n}$ for all cases where $k+l+m\le 6$, except for $K_{1,2,3,n}$. Ho [33] already conjectured that the crossing number of $K_{3,3,n}$ is equal to $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+2⌊\frac{n}{2}⌋+1$ for all $n\ge 1$. He also showed that $\mathrm{cr}\left(K_{3,3,n}\right)$ can be determined if the equality (1) holds for $m=7$ and $n\le 20$. To date, this is not known to be true, and so the crossing number of $K_{3,3,n}$ can only be given as a conjecture. Much attention began to focus on the crossing number of $G\backslash e$ obtained by removing one edge e from graph G. Conjectures about the crossing numbers of $K_n\backslash e$ and $K_{m,n}\backslash e$ are established, but not yet for tripartite graphs without one edge. Recently, the crossing numbers of $K_{1,4,n}\backslash e$ and $K_{2,3,n}\backslash e$ have been well-known by Su [34], and he also stated a question considering the exact values of the crossing numbers of $K_{1,5,n}\backslash e$, $K_{2,4,n}\backslash e$ and $K_{3,3,n}\backslash e$. A partial answer to his question is offered in this paper for the last mentioned graph $K_{3,3,n}\backslash e$.

Let $G^{*}=(V\left(G^{*}\right),E\left(G^{*}\right))$ be the connected graph of order six isomorphic to $K_{3,3}\backslash e$ obtained by removing one edge from the complete bipartite graph $K_{3,3}$, and also let $V\left(G^{*}\right)=\{v_1,v_2,\dots ,v_6\}$. Many possible drawings of the graph $G^{*}$ are partially solved using several redrawings of $G^{*}$ in Figure 1, Figure 2 and Figure 3, thanks to which, it is not necessary to deal with the considered drawings of $G^{*}$ in any optimal drawing of $G^{*}+D_n$. The crossing number of $G^{*}+D_n$ equal to $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ is determined in Theorem 1 with proof that is strongly based on properties of cyclic permutations. Certain parts of the statements could also be simplified with the help of software COGA by Berežný and Buša [35], generating all cyclic permutations of six elements. In the statements of the paper, the term “region” is also used for nonplanar drawings. In this case, crossings are considered to be vertices of the “map”. Two regions are neighboring if their boundaries have a common edge or a segment of an edge.

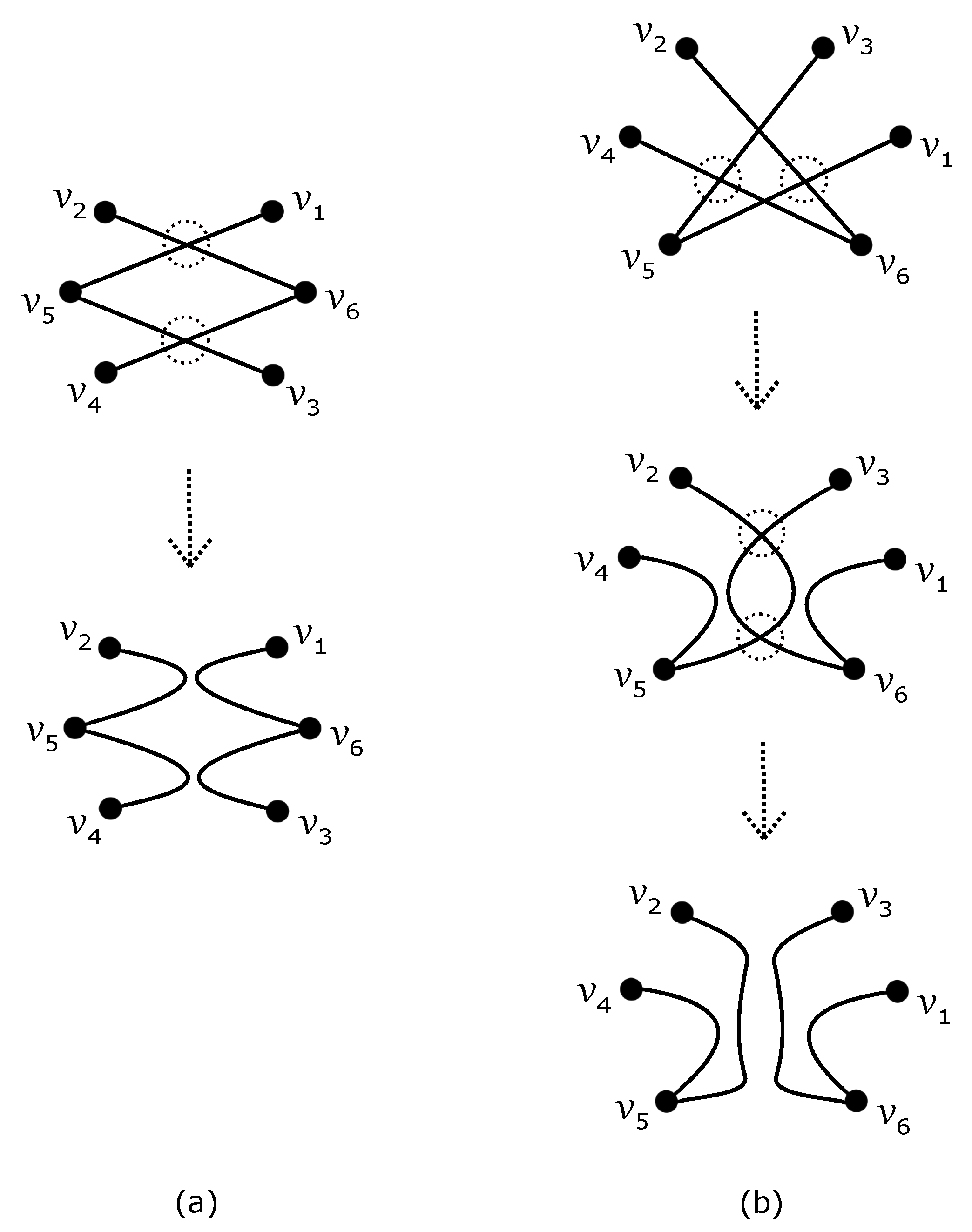
2. Cyclic Permutations and Possible Drawings of ${\mathit{G}}^{*}$

The join product $G^{*}+D_n$ (sometimes used notation $G^{*}+n{K}_1$) consists of one copy of the graph $G^{*}$ and n vertices $t_1,t_2,\dots ,t_n$, and any vertex $t_i$ is adjacent to every vertex of the graph $G^{*}$. Let $T^i$, $1\le i\le n$, denote the subgraph induced by the six edges incident with the vertex $t_i$. Thus, $T^1\cup T^2\cup \cdots \cup T^n$ is isomorphic to the complete bipartite graph $K_{6,n}$, which yields that

$$G^{*}+D_n=G^{*}\cup \left(\bigcup _{i=1}^n{T}^i\right).$$

(2)

We consider a good drawing D of $G^{*}+D_n$. The rotation ${\mathrm{rot}}_D\left(t_i\right)$ of a vertex $t_i$ in the drawing D as the cyclic permutation that records the (cyclic) counter-clockwise order in which the edges leave $t_i$ was defined by Hernández-Vélez et al. [36] or Woodall [37]. We use the notation $\left(123456\right)$ if the counter-clockwise order of the edges incident with the vertex $t_i$ is $t_i{v}_1$, $t_i{v}_2$, $t_i{v}_3$, $t_i{v}_4$, $t_i{v}_5$, and $t_i{v}_6$. We have to emphasize that rotation is a cyclic permutation. Let ${\overline{\mathrm{rot}}}_D\left(t_i\right)$ denote the inverse permutation of ${\mathrm{rot}}_D\left(t_i\right)$. In the given drawing D, it is highly desirable to separate n subgraphs $T^i$ into four mutually disjoint subsets depending on how many times edges of $G^{*}$ could be crossed by $T^i$ in D. Let us denote by $R_D$, $S_D$, and $T_D$ the set of subgraphs for which ${\mathrm{cr}}_D(G^{*},T^i)=0$, ${\mathrm{cr}}_D(G^{*},T^i)=1$, and ${\mathrm{cr}}_D(G^{*},T^i)=2$, respectively. Edges of $G^{*}$ are crossed by each remaining subgraph $T^i$ at least three times in D. Moreover, let $F^i$ denote the subgraph $G^{*}\cup T^i$ for $T^i\in R_D\cup S_D$, where $i\in \{1,\dots ,n\}$.

First, note that if D is a good drawing of $G^{*}+D_n$ with the empty set $R_D\cup S_D$, then ${\displaystyle {\sum }_{i=1}^n}{\mathrm{cr}}_D(G^{*},T^i)\ge 2n$ implies at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings in D provided by

$${\mathrm{cr}}_D(G^{*}+D_n)={\mathrm{cr}}_D\left(K_{6,n}\right)+{\mathrm{cr}}_D(G^{*},K_{6,n})+{\mathrm{cr}}_D\left(G^{*}\right)$$

$$\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋.$$

Taking into account the expected result of the main Theorem 1, this leads to a consideration of the nonempty set $R_D\cup S_D$ in all good drawings of $G^{*}+D_n$.

Let us discuss all possible drawings of $G^{*}$ induced by D with the degree sequence $(2,2,3,3,3,3)$. The graph $G^{*}$ contains a cycle $C_4$ induced on four vertices of degree 3 as a subgraph (for brevity, we write $C_4\left(G^{*}\right)$), and let $v_1$, $v_2$, $v_3$, and $v_4$ be their vertex notation in the appropriate order of the cycle $C_4\left(G^{*}\right)$. In the rest of the paper, suppose also that $\mathrm{deg}\left(v_5\right)=2$ and $\mathrm{deg}\left(v_6\right)=2$ for $v_1{v}_5,v_3{v}_5\in E\left(G^{*}\right)$ and $v_2{v}_6,v_4{v}_6\in E\left(G^{*}\right)$. Note that edges of $C_4\left(G^{*}\right)$ can cross each other in some discussed good subdrawings $D\left(G^{*}\right)$.

In Figure 1, we can redraw two crossings on four edges incident with different vertices of $C_4\left(G^{*}\right)$ to obtain a new drawing of $G^{*}$ induced by D (with the vertex notation in a different order for both bottom drawings) with fewer edge crossings. Based on this argument, these four edges of $G^{*}$ do not cross each other in such a way in any optimal drawing of $G^{*}+D_n$. Both redrawings of the graph $G^{*}$ in Figure 1 give almost no constraints on the behavior of the four remaining edges of the cycle $C_4\left(G^{*}\right)$, and so many subdrawings of $G^{*}$ induced by D are eliminated. Clearly, we also have other possibilities for some special redrawings of $G^{*}$ presented in Figure 2 and Figure 3.

Taking into account the assumption that it does not matter which of the regions in $D\left(G^{*}\right)$ are unbounded in our considerations, we will deal with the subdrawings of $G^{*}$ given in Figure 4 and Figure 5. Since the graph $G^{*}$ consists of the edge disjoint subgraphs $C_4\left(G^{*}\right)$ and $2P_3$, we only need to consider possibilities of crossings between subdrawings of subgraphs $C_4\left(G^{*}\right)$ and $2P_3$ (the edges of both paths $P_3$ can cross themselves in the considered subdrawings). If we consider a good subdrawing of $G^{*}$ in which edges of $C_4\left(G^{*}\right)$ cross each other, then edges of $2P_3$ do not cross edges of $C_4\left(G^{*}\right)$ only in one case, which is shown in Figure 4a. If edges of $C_4\left(G^{*}\right)$ are crossed at least once by some edge of $2P_3$, then there are four next possibilities due to all previous restrictions, and they are shown in Figure 4b–e. Similarly, using all previous observations, if edges of $C_4\left(G^{*}\right)$ do not cross each other, then we obtain seven other possible nonplanar subdrawings of $G^{*}$ induced by D in Figure 5.

Lemma 1.

For $n\ge 1$, let D be a good drawing of $G^{*}+D_n$. If the vertices $v_5$ and $v_6$ are placed in different regions of the good subdrawing $D\left(C_4\left(G^{*}\right)\right)$ except for the drawing of $G^{*}$ given in Figure 4b, then there are at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings in D.

Proof. 

The set $R_D$ must be empty assuming that vertices $v_5$ and $v_6$ are located in different regions of $D\left(C_4\left(G^{*}\right)\right)$. For easier reading, let $s=\left|S_D\right|$ and $t=\left|T_D\right|$. Now, we discuss two cases.

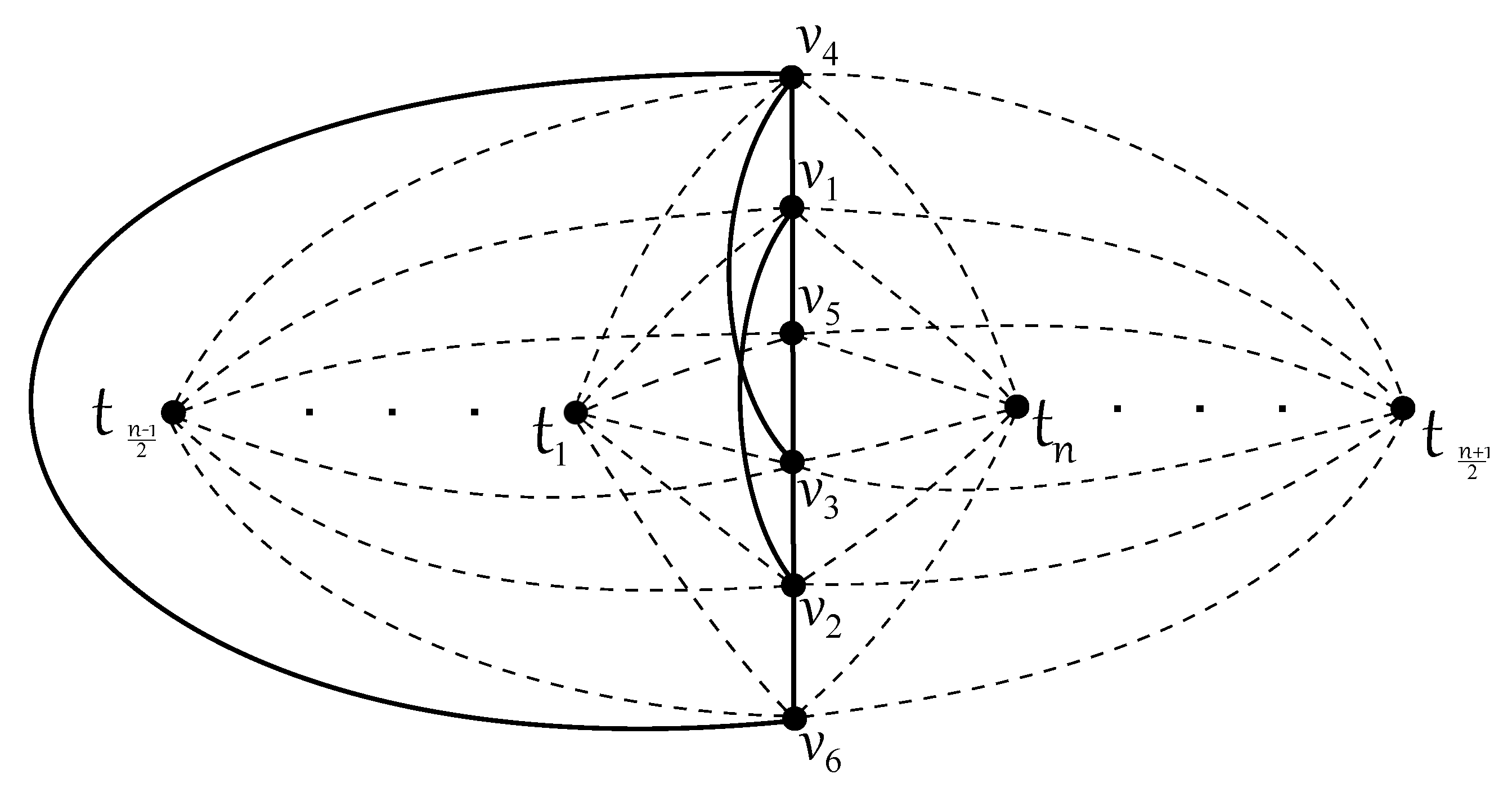
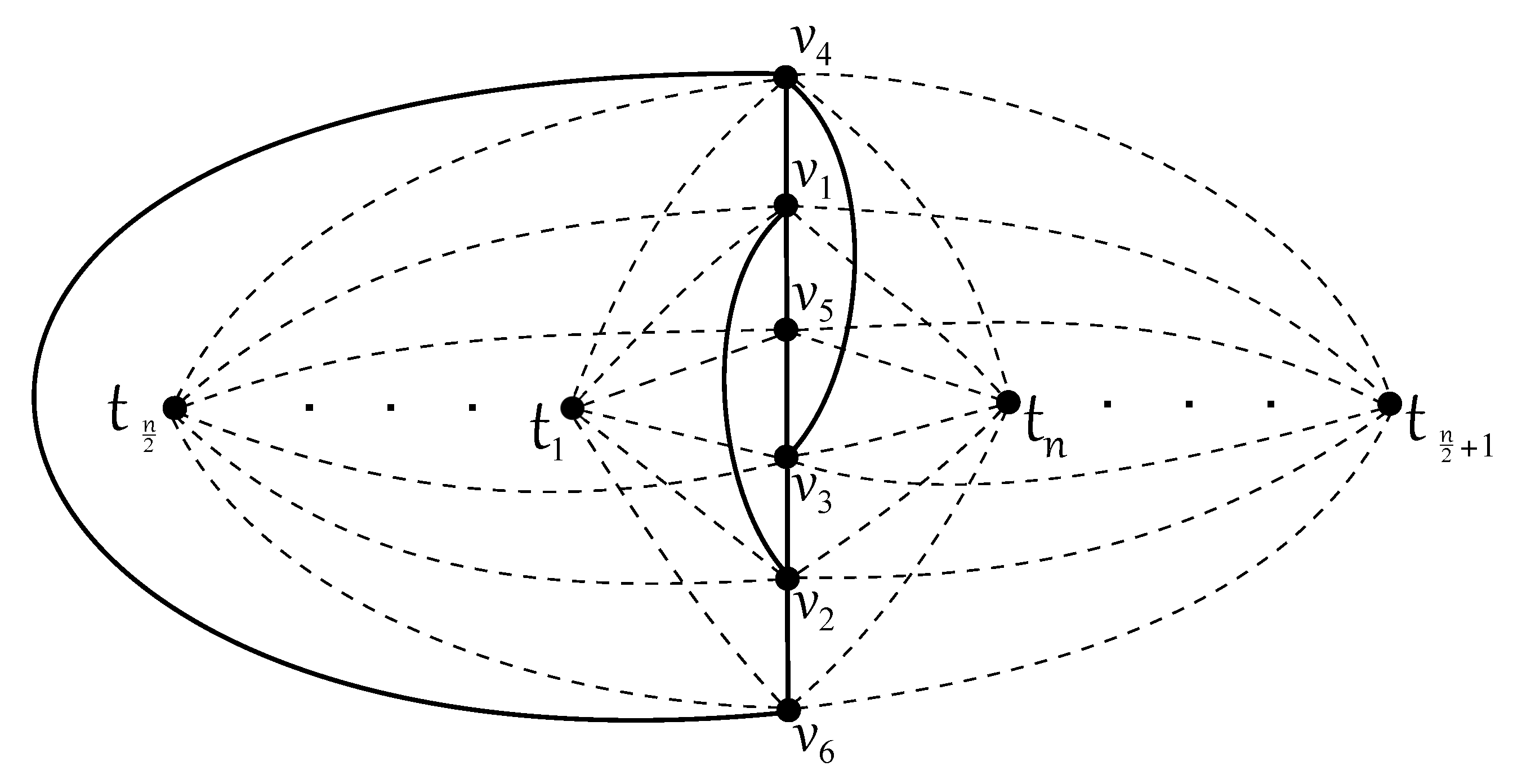
• Let us first suppose that $2s+t\le 2\lceil \frac{n}{2}\rceil$; that is, $-2s-t\ge -2\lceil \frac{n}{2}\rceil$. The number of crossings in D satisfies

  $${\mathrm{cr}}_D(G^{*}+D_n)={\mathrm{cr}}_D\left(K_{6,n}\right)+{\mathrm{cr}}_D(K_{6,n},G^{*})+{\mathrm{cr}}_D\left(G^{*}\right)\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+1s+2t+3(n-s-t)$$

  $$=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3n-2s-t\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+3n-2⌈\frac{n}{2}⌉\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋.$$
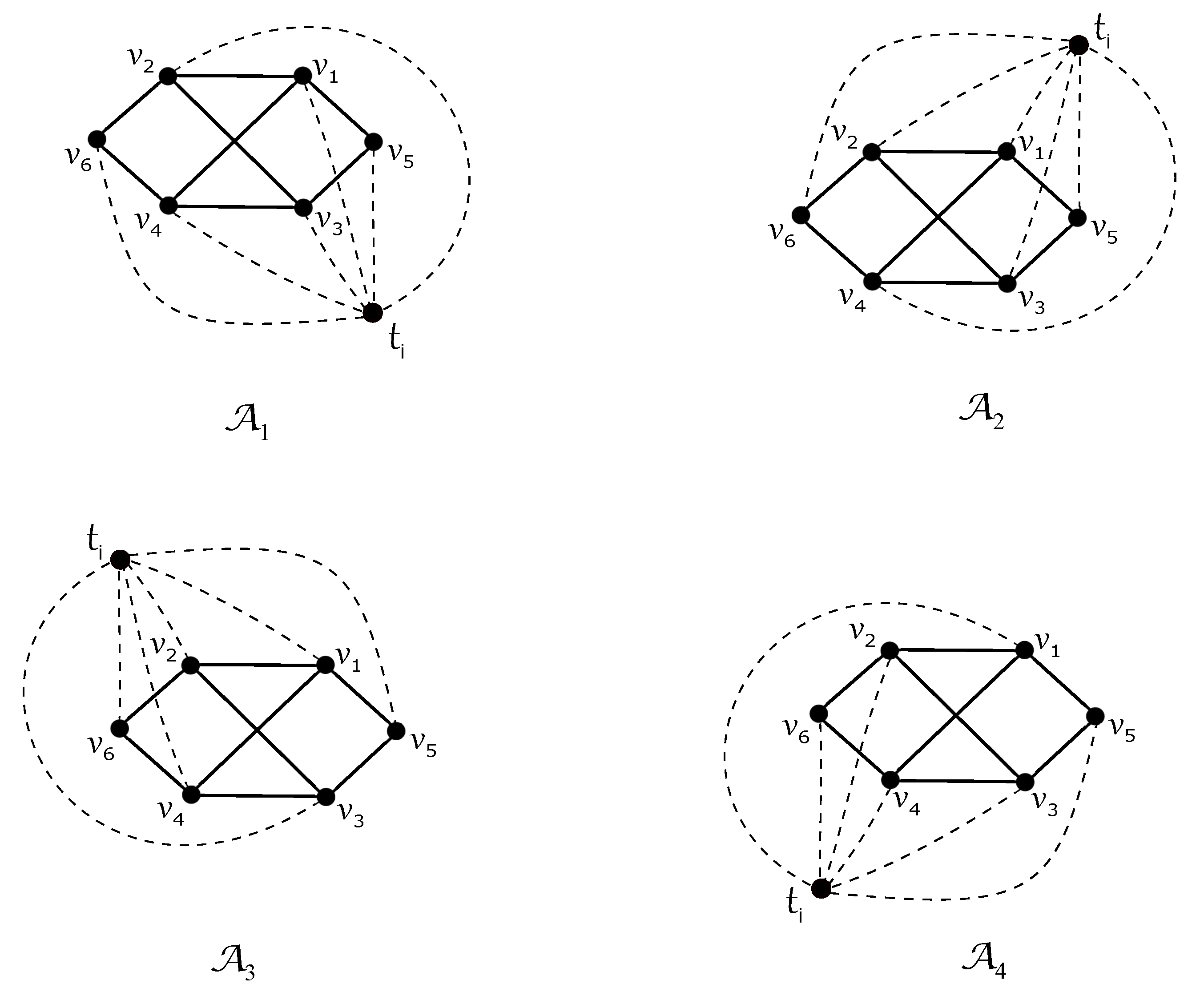
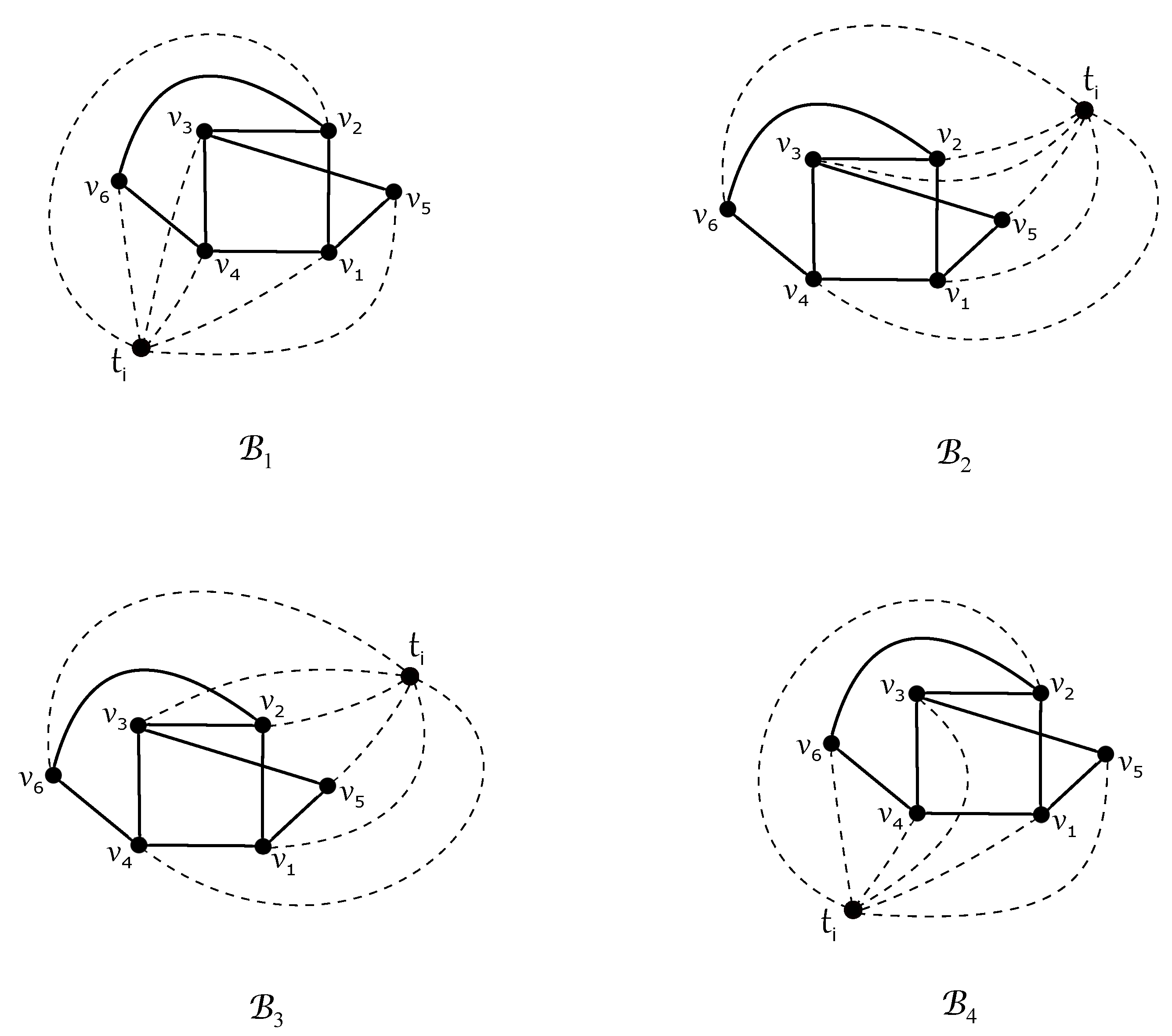
• Now, let $2s+t>2\lceil \frac{n}{2}\rceil$, which yields that $2s+t\ge 2\lceil \frac{n}{2}\rceil +1$ and also that $s\ge 1$. By fixing the subgraph $G^{*}\cup T^i$ for some $T^i\in S_D$, we have

  $${\mathrm{cr}}_D(G^{*}+D_n)={\mathrm{cr}}_D\left(K_{6,n-1}\right)+{\mathrm{cr}}_D(K_{6,n-1},G^{*}\cup T^i)+{\mathrm{cr}}_D(G^{*}\cup T^i)$$

  $$\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+6(s-1)+5t+4(n-s-t)+1=6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4n+2s+t-5$$

  $$\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4n+2⌈\frac{n}{2}⌉+1-5\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋,$$

  where we can verify over all possible regions of $D(G^{*}\cup T^i)$ that the edges of $G^{*}\cup T^i$ are crossed at least six, five, and four times by each subgraph $T^j\in S_D$, $j\ne i$, $T^k\in T_D$, and $T^l\notin S_D\cup T_D$, respectively.

The results of both subcases complete the proof of Lemma 1. □

We have to emphasize that, in Lemma 1, the assumption except for the drawing of $G^{*}$ given in Figure 4b is inevitable. In this case, we cannot use the idea presented in the second part of the proof mentioned above because there is a possibility of an existence of subgraph $T^l\notin S_D\cup T_D$ with ${\mathrm{cr}}_D(G^{*}\cup T^i,T^l)=3$ for some fixed subgraph $T^i\in S_D$ with ${\mathrm{rot}}_D\left(t_i\right)=\left(153462\right)$. This subcase will be solved by fixing the subgraph $T^i\cup T^j$ in the proof of Theorem 1.

Since the same argument with at least five crossings on edges between two different subgraphs from the nonempty set $S_D$ can also be applied for other drawings of $G^{*}$ induced by D, the proofs of Corollaries 1 and 2 can be omitted.

Corollary 1.

For $n\ge 1$, let D be a good drawing of $G^{*}+D_n$ such that both vertices $v_5$ and $v_6$ are placed in the same region of $D\left(C_4\left(G^{*}\right)\right)$. If exactly one of them is not contained in the region of $D\left(G^{*}\right)$ with five vertices of $G^{*}$ on its boundary, then there are at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings in D.

Corollary 2.

For $n\ge 1$, let D be a good drawing of $G^{*}+D_n$ such that both vertices $v_5$ and $v_6$ are contained in the region of $D\left(G^{*}\right)$ with five vertices of $G^{*}$ on its boundary. If there are at most two possibilities of crossing one edge of $G^{*}$ in an effort to obtain a subdrawing $G^{*}\cup T^i$ for some subgraph $T^i\in S_D$, then there are at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings in D.

Assume that there is a good drawing D of the join product $G^{*}+D_n$ with $D\left(G^{*}\right)=1$ only among edges of the cycle $C_4\left(G^{*}\right)$. For this purpose, let us consider the nonplanar drawing of the graph $G^{*}$ as shown in Figure 4a. For subgraphs $T^i\in S_D$, we establish all possible rotations ${\mathrm{rot}}_D\left(t_i\right)$ that could appear in the considered drawing D. There is only one subdrawing of $F^i\backslash \{v_1,v_2,v_3,v_4\}$, and, therefore, we have just four possibilities of obtaining a subdrawing of $F^i$ depending on which of the edges $v_3{v}_5$, $v_1{v}_5$, $v_2{v}_6$, and $v_4{v}_6$ is crossed by edge $t_i{v}_1$, $t_i{v}_3$, $t_i{v}_4$, and $t_i{v}_2$, respectively. These four possibilities under our consideration can be denoted by ${\mathcal{A}}_p$ for $p=1,2,3,4$. We will call them the configurations of corresponding subdrawings of the subgraph $F^i$ in D and suppose that their drawings are as shown in Figure 6 because it does not matter which of the regions in $D\left(F^i\right)$ is unbounded in our considerations.

In the rest of the paper, we present a cyclic permutation by the permutation with 1 in the first position. Thus, the configurations ${\mathcal{A}}_1$, ${\mathcal{A}}_2$, ${\mathcal{A}}_3$, and ${\mathcal{A}}_4$ are represented by the cyclic permutations $\left(134625\right)$, $\left(135462\right)$, $\left(153642\right)$, and $\left(153426\right)$, respectively. Clearly, in a fixed drawing of the graph $G^{*}+D_n$, some configurations from $\mathcal{M}=\{{\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3,{\mathcal{A}}_4\}$ need not appear. We denote by ${\mathcal{M}}_D$ the set of all configurations that exist in the drawing D belonging to the set $\mathcal{M}$.

Our aim is to establish a minimum number of edge crossings between two different subgraphs $F^i$ and $F^j$ using the idea of mentioned configurations. For two configurations $\mathcal{X}$ and $\mathcal{Y}$ from ${\mathcal{M}}_D$ (not necessarily different), let ${\mathrm{cr}}_D(\mathcal{X},\mathcal{Y})$ denote the number of edge crossings in $D(T^i\cup T^j)$ for two different subgraphs $T^i,T^j\in S_D$ such that $F^i$, $F^j$ have configurations $\mathcal{X}$, $\mathcal{Y}$, respectively. We denote by $\mathrm{cr}(\mathcal{X},\mathcal{Y})$ the minimum value of ${\mathrm{cr}}_D(\mathcal{X},\mathcal{Y})$ over all pairs $\mathcal{X}$ and $\mathcal{Y}$ from $\mathcal{M}$ among all good drawings D of the join product $G^{*}+D_n$. In the following, our goal is to determine the lower bounds of $\mathrm{cr}(\mathcal{X},\mathcal{Y})$ for all possible pairs $\mathcal{X},\mathcal{Y}\in \mathcal{M}$. In particular, the configurations ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ are represented by the cyclic permutations $\left(134625\right)$ and $\left(135462\right)$, respectively. Each subgraph $T^j$ with $\mathrm{conf}\left(F^j\right)={\mathcal{A}}_2$ crosses edges of each $T^i$ with $\mathrm{conf}\left(F^i\right)={\mathcal{A}}_1$ at least four times provided that the minimum number of interchanges of adjacent elements of $\left(134625\right)$ required to produce $\overline{\left(135462\right)}=\left(126453\right)$ is four, i.e., $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_2)\ge 4$. For more details, see also Woodall [37]. The same reason gives $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_3)\ge 4$, $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_4)\ge 4$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_3)\ge 4$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_4)\ge 4$, and $\mathrm{cr}({\mathcal{A}}_3,{\mathcal{A}}_4)\ge 4$. Clearly, also $\mathrm{cr}({\mathcal{A}}_p,{\mathcal{A}}_p)\ge 6$ for any $p=1,2,3,4$. Moreover, by a discussion of possible subdrawings, we can verify that $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_4)\ge 5$ and $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_3)\ge 5$.

Now, assume that the nonplanar subdrawing of the graph $G^{*}$ induced by a drawing D of $G^{*}+D_n$ are as shown in Figure 5a. For $T^i\in S_D$, again, we only have four possibilities of obtaining a subdrawing of $F^i$ depending on which of the edges $v_4{v}_6$, $v_1{v}_2$, $v_2{v}_6$, or $v_1{v}_4$ is crossed by the edge $t_i{v}_3$. These four ways under our consideration are denoted by ${\mathcal{B}}_p$ for $p=1,2,3,4$, and we assume that their drawings are as shown in Figure 7. Thus, the configurations ${\mathcal{B}}_1$, ${\mathcal{B}}_2$, ${\mathcal{B}}_3$, and ${\mathcal{B}}_4$ are described by the cyclic permutations $\left(143625\right)$, $\left(146235\right)$, $\left(146325\right)$, and $\left(134625\right)$, respectively. Because some configurations from $\mathcal{N}=\{{\mathcal{B}}_1,{\mathcal{B}}_2,{\mathcal{B}}_3,{\mathcal{B}}_4\}$ may not appear in a fixed drawing of $G^{*}+D_n$, we denote by ${\mathcal{N}}_D$ the subset of $\mathcal{N}$ consisting of all configurations that exist in the drawing D.

The verification of the lower bounds for the number of crossings between two configurations from $\mathcal{N}$ proceeds in the same way as above. Thus, all lower bounds for the number of crossings between two configurations from $\mathcal{M}$ as well as from $\mathcal{N}$ are summarized in the common symmetric

Table 1. The minimum number of crossings between $T^i$ and $T^j$ for two configurations ${\mathcal{X}}_p$ and ${\mathcal{X}}_q$ of subgraphs $F^i=G^{*}\cup T^i$ and $F^j=G^{*}\cup T^j$, where $\mathcal{X}=\mathcal{A}$ and $\mathcal{X}=\mathcal{B}$ for configurations in $\mathcal{M}$ and $\mathcal{N}$, respectively.

-	${\mathcal{X}}_1$	${\mathcal{X}}_2$	${\mathcal{X}}_3$	${\mathcal{X}}_4$
${\mathcal{X}}_1$	6	4	4	5
${\mathcal{X}}_2$	4	6	5	4
${\mathcal{X}}_3$	4	5	6	4
${\mathcal{X}}_4$	5	4	4	6

.

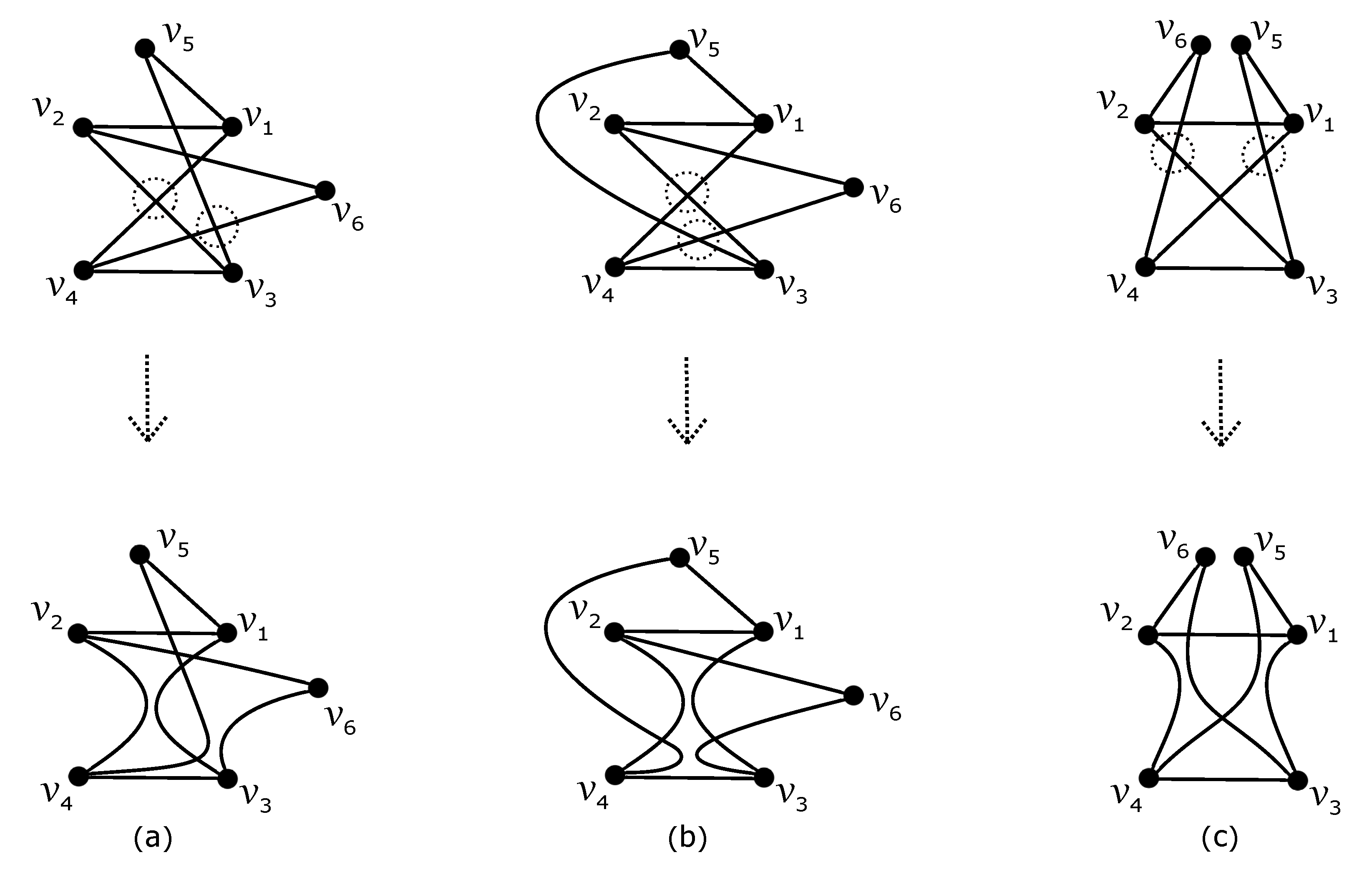
3. The Crossing Number of ${\mathit{G}}^{*}+{\mathit{D}}_{\mathit{n}}$

In the following, we are able to compute the exact values of crossing numbers of join products of the graph $G^{*}$ with both discrete graphs $D_1$ and $D_2$ using the algorithm located on the website http://crossings.uos.de/ (accessed on 26 May 2022). This algorithm can find the crossing numbers of small undirected graphs. It uses an ILP formulation, based on Kuratowski subgraphs, and solves it via branch-and-cut-and-price. The system also generates verifiable formal proofs, as described by Chimani and Wiedera [38].

Lemma 2.

$\mathrm{cr}(G^{*}+D_1)=1$ and $\mathrm{cr}(G^{*}+D_2)=4$.

Theorem 1.

$\mathrm{cr}(G^{*}+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ for $n\ge 1$.

Proof. 

In Figure 8, the edges of $K_{6,n}$ cross each other

$$6\left(\genfrac{}{}{0pt}{}{\lceil \frac{n}{2}\rceil }{2}\right)+6\left(\genfrac{}{}{0pt}{}{\lfloor \frac{n}{2}\rfloor }{2}\right)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$$

times, each subgraph $T^i$, $i=1,\dots ,\frac{n-1}{2}$ on the left side crosses edges of $G^{*}$ exactly four times, and each subgraph $T^i$, $i=\frac{n+1}{2},\dots ,n$ on the right side does not cross edges of $G^{*}$. The edges of $G^{*}$ cross each other once, and so $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings appear among edges of the graph $G^{*}+D_n$ in this drawing for n odd. In Figure 9, we also obtain the drawing of $G^{*}+D_n$ with the same number of crossings because each subgraph $T^i$ crosses edges of $G^{*}$ twice. Lemma 2 confirms the result for $n=1$ and $n=2$. To prove the reverse inequality by induction on n, suppose now that there is a good drawing D of $G^{*}+D_n$ with

$${\mathrm{cr}}_D(G^{*}+D_n)<6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋\mathrm{for}\mathrm{some}n\ge 3,$$

(3)

and that

$$\mathrm{cr}(G^{*}+D_m)=6⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+m+2⌊\frac{m}{2}⌋\mathrm{for}\mathrm{any}\mathrm{positive}\mathrm{integer}m<n.$$

(4)

For easier reading, if $r = |R_D|$ and $s = |S_D|$, then the assumption (3) together with ${\mathrm{cr}}_D\left(K_{6,n}\right)\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ using (1) imply the following relation with respect to the edge crossings of $G^{*}$ in D:

$${\mathrm{cr}}_D\left(G^{*}\right)+\sum _{T^i\in R_D\cup S_D}{\mathrm{cr}}_D(G^{*},T^i)+\sum _{T^i\notin R_D\cup S_D}{\mathrm{cr}}_D(G^{*},T^i)<n+2⌊\frac{n}{2}⌋,$$

i.e.,

$${\mathrm{cr}}_D\left(G^{*}\right)+0r+1s+2(n-r-s)<n+2⌊\frac{n}{2}⌋.$$

(5)

The obtained inequality (5) forces $r+s\ge 1$, and so there is at least one subgraph $T^i$ by which edges of $G^{*}$ are crossed at most once in D. Now, we will show that a contradiction with the assumption (3) can be obtained in all following subcases:

Case 1: ${\mathrm{cr}}_D\left(G^{*}\right)=1$. Let us first consider the subdrawing of $G^{*}$ induced by D given in Figure 4a. Since the set $R_D\cup S_D$ is nonempty, two possible subcases may occur.

(a)

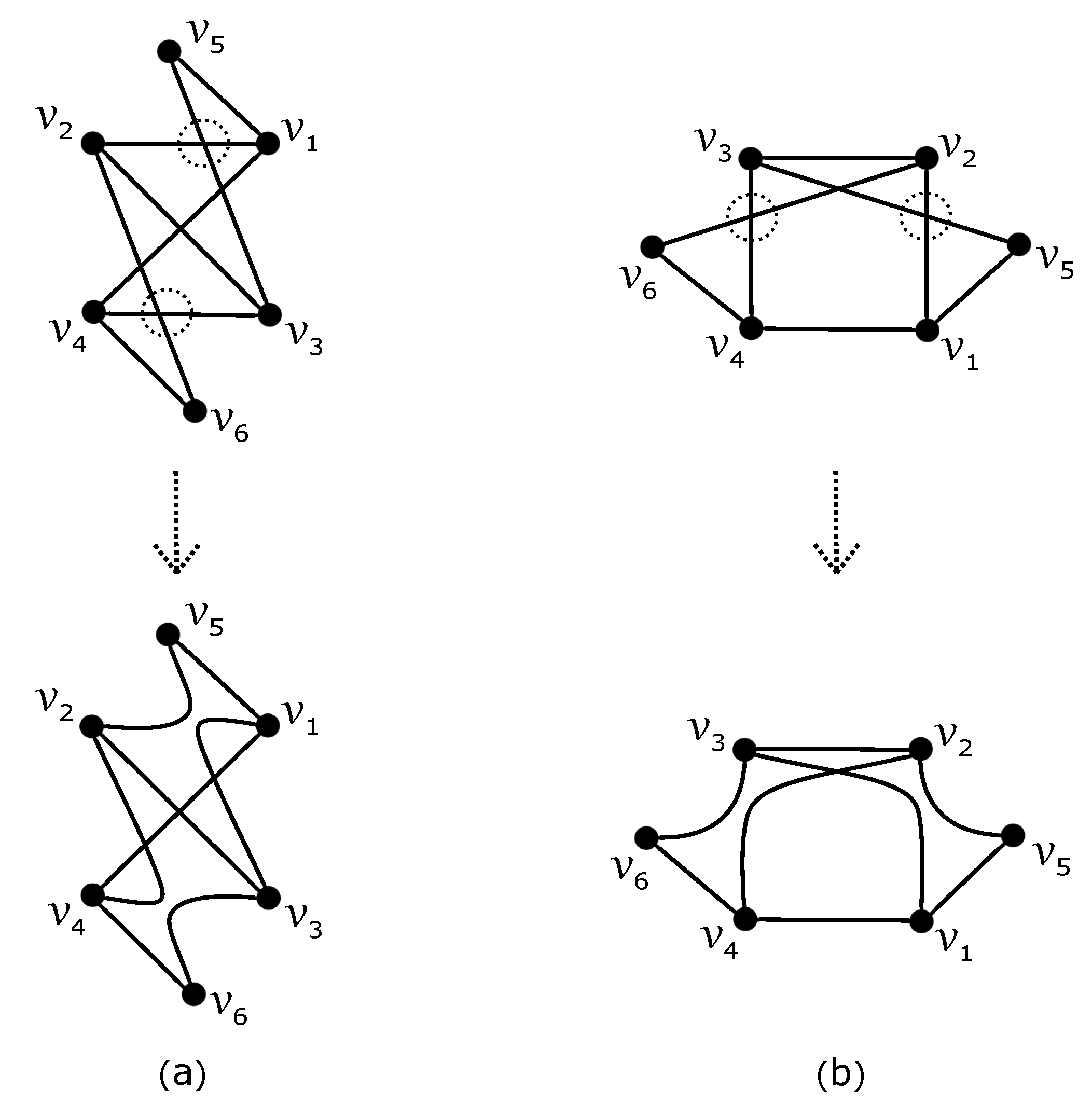
Let $R_D$ be the nonempty set; that is, there is a subgraph $T^i\in R_D$. The reader can easily see that the subgraph $F^i=G^{*}\cup T^i$ is uniquely represented by ${\mathrm{rot}}_D\left(t_i\right)=\left(153462\right)$. By fixing the subgraph $G^{*}\cup T^i$, if edges of $G^{*}\cup T^i$ are crossed by any other subgraph $T^j$ at least five times, we obtain

$${\mathrm{cr}}_D(G^{*}+D_n)={\mathrm{cr}}_D\left(K_{5,n-1}\right)+{\mathrm{cr}}_D(K_{5,n-1},G^{*}\cup T^i)+{\mathrm{cr}}_D(G^{*}\cup T^i)$$

$$\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+5(n-1)+1\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋.$$

If there is some subgraph $T^j$ with ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)<5$, then the vertex $t_j$ cannot be placed in the outer region of subdrawing $D\left(G^{*}\right)$ with all six vertices of $G^{*}$ on its boundary, and ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)=4$ enforces ${\mathrm{cr}}_D(T^i,T^j)=0$. Thus, by fixing the subgraph $T^i\cup T^j$, we have

$${\mathrm{cr}}_D(G^{*}+D_{n-2})+{\mathrm{cr}}_D(T^i\cup T^j)+{\mathrm{cr}}_D(K_{6,n-2},T^i\cup T^j)+{\mathrm{cr}}_D(G^{*},T^i\cup T^j)$$

$$\ge 6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+n-2+2⌊\frac{n-2}{2}⌋+6(n-2)+4=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋,$$

where edges of $T^i\cup T^j$ are crossed by each other subgraph $T^k$ at least six times using ${\mathrm{cr}}_D\left(K_{6,3}\right)\ge 6$ again due to (1). Both considered subcases contradict the assumption (3) in D.

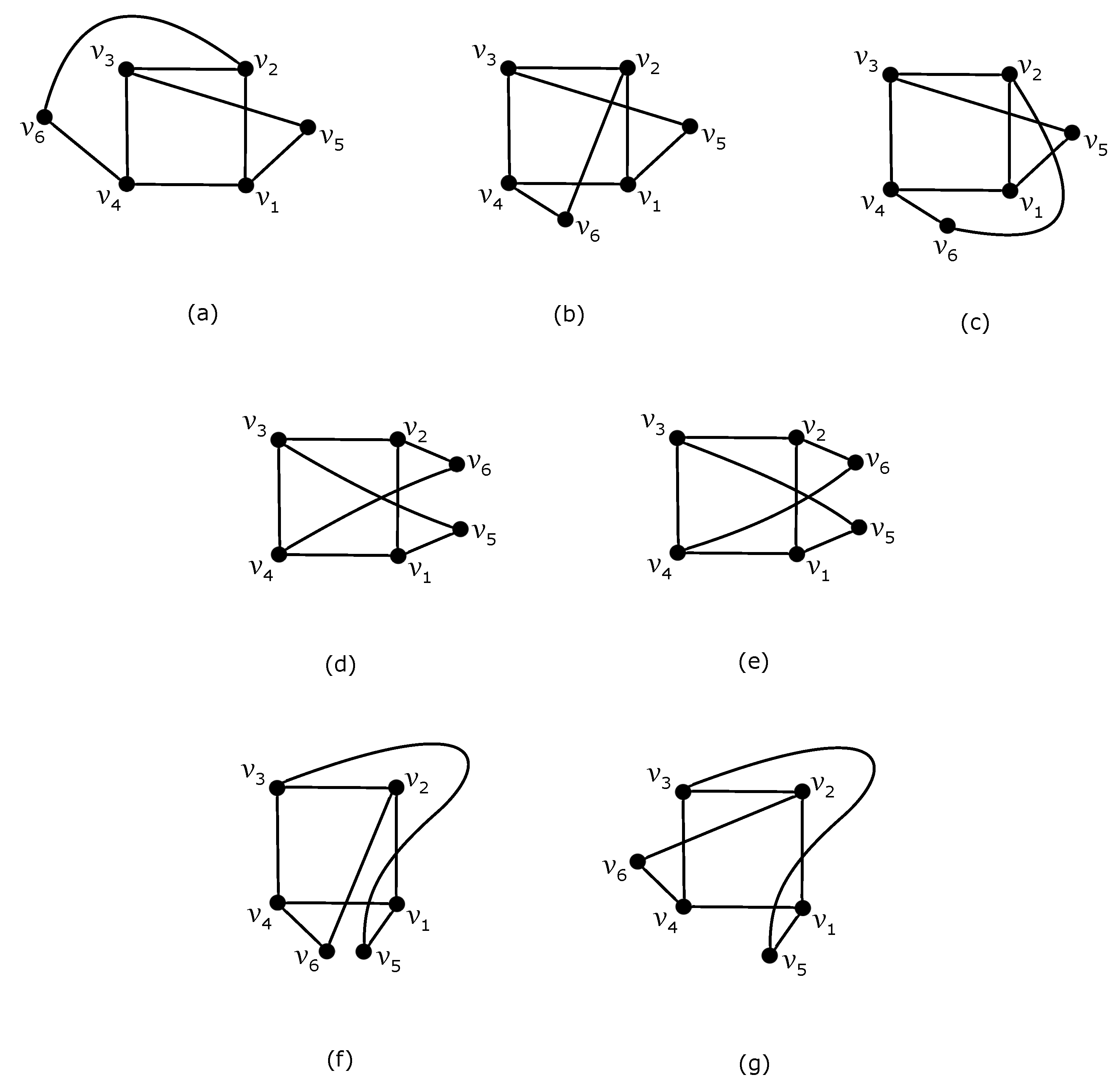
(b)

Let $R_D$ be the empty set; that is, there is a subgraph $T^i\in S_D$. As $s\ge 1$, we deal with possible configurations ${\mathcal{A}}_p$ from the nonempty set ${\mathcal{M}}_D$. For any $p\in \{1,2,3,4\}$, if there is a subgraph $T^j$, $j\ne i$ such that ${\mathrm{cr}}_D(G^{*}\cup T^i,T^j)<5$ and ${\mathrm{cr}}_D(T^i,T^j)=0$ with $\mathrm{conf}\left(F^i\right)={\mathcal{A}}_p$, the same fixation of $T^i\cup T^j$ like in the previous case also confirms a contradiction with (3) in D.

Now, let us turn to the possibility of obtaining the minimum value 4 in Table 1; that is, $\mathrm{cr}({\mathcal{A}}_p,{\mathcal{A}}_q)=4$ could be achieved in D for two different ${\mathcal{A}}_p,{\mathcal{A}}_q\in {\mathcal{M}}_D$. In the rest of the paper, assume that there are two different subgraphs $T^i,T^j\in S_D$ such that $F^i$ and $F^j$ have mentioned configurations ${\mathcal{A}}_p$ and ${\mathcal{A}}_q$, respectively. Then, ${\mathrm{cr}}_D(T^i\cup T^j,T^k)\ge 9$ holds for any $T^k\in S_D$ with $k\ne i,j$ by summing two corresponding values in Table 1. We can easily verify in six possible regions of $D(G^{*}\cup T^i)$ and $D(G^{*}\cup T^j)$ that ${\mathrm{cr}}_D(G^{*}\cup T^i,T^k)\ge 2+3=5$ and ${\mathrm{cr}}_D(G^{*}\cup T^j,T^k)\ge 2+3=5$ are fulfilling for any $T^k\in T_D$, which yields that ${\mathrm{cr}}_D(G^{*}\cup T^i\cup T^j,T^k)\ge 2+3+3=8$ trivially holds for any such subgraph $T^k$. Moreover, each of $n-s-t$ subgraphs $T^k\notin S_D\cup T_D$ of $K_{6,n-2}$ crosses $G^{*}\cup T^i\cup T^j$ at least six times. As ${\mathrm{cr}}_D(G^{*}\cup T^i\cup T^j)\ge 7$, by fixing the subgraph $G^{*}\cup T^i\cup T^j$, we have

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+10(s-2)+8t+6(n-s-t)+7$$

$$\ge 6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+6n+2\left(2⌈\frac{n}{2}⌉+1\right)-13\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋,$$

where the modified inequality (5), for $1s+2t+3(n-r-s-t)<n+2\lfloor \frac{n}{2}\rfloor$, forces $2s+t>2\lceil \frac{n}{2}\rceil$ if $r=0$ and $t = |T_D|$.

The obtained number of crossings contradicts the assumption (3). Finally, let us consider that $\mathrm{cr}({\mathcal{A}}_p,{\mathcal{A}}_q)\ge 5$ holds for all ${\mathcal{A}}_p,{\mathcal{A}}_q\in {\mathcal{M}}_D$ with $p,q\in \{1,2,3,4\}$. By fixing the subgraph $G^{*}\cup T^i$ for some $T^i\in S_D$, we have

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+6(s-1)+5t+4(n-s-t)+2$$

$$\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4n+2⌈\frac{n}{2}⌉+1-4\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋.$$

This again confirms a contradiction with (3) in D.

If we assume the subdrawing of the graph $G^{*}$ induced by D given in Figure 5a, the set $R_D$ is empty, which is caused by at most five vertices of $G^{*}$ on the boundary of each region in $D\left(G^{*}\right)$. As the set $S_D$ must be nonempty, the proof can proceed similarly for possible configurations ${\mathcal{B}}_p$ from the nonempty set ${\mathcal{N}}_D$ like in the previous subcase for configurations ${\mathcal{A}}_p\in {\mathcal{M}}_D$.

Case 2: ${\mathrm{cr}}_D\left(G^{*}\right)\ge 2$. For all such subdrawings of the graph $G^{*}$ in Figure 4 and Figure 5, if all six vertices of $G^{*}$ are included in one region of $D\left(G^{*}\right)$ and the set $R_D$ is nonempty, then the same technique like in the first part of Case 1 can be applied. To finish the proof of this case, let $R_D$ be the empty set. Let any subgraph $T^i\in S_D$ be crossed at least once by each other subgraph $T^j$, because otherwise fixing $T^i\cup T^j$ results in at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings in D. This assumption solves the problem of the drawing of $G^{*}$ given in Figure 4b described above after the proof of Lemma 1. Finally, for all remaining subdrawings of $G^{*}$ induced by D with any $T^i\in S_D$, we can verify over all possible regions of $D(G^{*}\cup T^i)$ that the edges of $G^{*}\cup T^i$ are crossed at least five times by each other subgraph $T^j$, $j\ne i$. Again, by fixing the subgraph $G^{*}\cup T^i$, we have

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+5(n-1)+2\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋.$$

We have shown that there are at least $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+2⌊\frac{n}{2}⌋$ crossings in each good drawing D of $G^{*}+D_n$, and this completes the proof of Theorem 1. □

4. Conclusions

We expect that similar forms of discussions can be used to estimate unknown values of the crossing numbers of other graphs on six vertices with a much larger number of edges in join products with discrete graphs, and also with paths and cycles. The result of $K_{3,3}\backslash e+D_n$ could also be useful for confirming Ho’s conjecture [33] mentioned in Section 1 for the complete tripartite graph $K_{3,3,n}$.