Abstract
An essential element for driver safety is represented by the Impact Attenuator (especially for race cars). The effect of the Impact Attenuator can be seen in the behavior of a dummy, tied with a seat belt, in a frontal collision with a rigid wall. The loads that act on the dummy are determined and checked to see if they fall within the values recommended by existing standards. The car is considered a structure with a dummy fixed with a seat belt and equipped with an Impact Attenuator. Two types of Impact Attenuator having constructive similarity and symmetries are studied, made up of three different materials and different thicknesses of material. The behavior of the dummy was studied, considering a frontal collision of the car–dummy assembly, in accordance with existing standards. Using simulation software, the accelerations were determined at various points on the mannequin’s body and the force appearing on the seat belts was determined. The Gibbs–Appell equations are the method used to determine the dynamic response in this problem involving shocks.
1. Introduction
Passenger safety is an essential objective in automotive engineering. If you take into account the development that the automotive industry has undergone, the importance of this aspect requires, in manufacturing, additional knowledge that can be obtained through studies oriented towards the safety of passengers and the development of various safety systems. The simplest are passive safety systems, which play a very important role in reducing the damage or injuries caused to the occupants of the vehicle but also to pedestrians if an accident occurs. Passive safety systems consist of airbags (of all kinds), anti-lock braking systems (ABS), traction control, electronic stability control (ESC), seat belts and crash protection systems. The first safety element, simple and relatively cheap, that experienced spectacular development in the industry was the safety belt. The emergence of safety belts determined the outcomes of numerous studies and research in order to improve the constructive variants and the performance of these passive safety elements [1,2,3].
The role of the safety belt has proven to be of crucial importance, especially in the case of overweight people. Evaluations were made from a biomechanical point of view to determine the role played by the safety belt [4]. The experimental checks were made using an 80 kg dummy. It has been found that a force greater than 1000 N produces a bending or folding of the belt, so the impact of its role decreases.
The literature that deals with improving the performance of seat belts is rich. For example, in [5], improvement of the mechanical properties of the material used through a process of topological optimization of the fabric was studied. A significant improvement in the performance of the belt was, thus, achieved. In works [6,7,8], the operation of seat belts in different possible situations is studied, experimental verifications are presented in [9,10,11], and various other aspects related to the operation of seat belts in service are presented in [12,13].
For the study of safety in operation of the belt, special attention is required from the design phase. In [14], a CAE method is used for the analysis, even during the first phases, of the conception and design. HyperWorks software (which uses finite element methods) is used as a tool, and the effect of using the belt on the upper limbs and buttocks of the mannequins is studied. Thus, the development costs are reduced and the design development cycle is shortened. As part of the work, a stand for belt testing was designed and built. An excellent analysis of the efficiency as well as the limitations imposed on these safety systems was made in [15]. Post-accident inspections of these systems were used as the research method. Following the analysis of a large number of events, solutions were proposed for design improvements. An extensive study on the role of the seat belt in Formula Student racing cars was carried out in [16].
The element studied in the current work is the Impact Attenuator (IA). It is analyzed how such an element ensures the safety of the driver in a racing car. The IA can be mounted separately or can be incorporated into the bumper. In the form of a front bumper, it is an indispensable element in modern automobiles and provides shock absorption/mitigation.
In [17], the behavior of a roll cage equipped onto a SUPRA racing car is investigated. Based on the research conducted, an improved design solution is proposed to ensure safety in the event of an impact—front, back and side. ANSYS 18.1 software was used. Of course, the materials used for manufacturing IAs are of great importance regarding their behavior in case of shocks. For example, in [18], a CFRP composite was studied, aiming to use it in automotive engineering. This composite was used in the construction of a monocoque chassis. The car on which this chassis was used competed in the Formula Student competition. The goal was to meet the safety requirements set by Formula SAE. The analytical study was carried out with the finite element method and an optimization was made of the shape and dimensions of the chassis. Experimental verifications in impact tests for a car used in Formula Student can be found in [19]. The objective of an IA is to ensure a high rate of energy absorption during impact. There are also medical aspects in the case of using IAs as shock absorbers, as described in [20,21]. In the papers [22,23], various modern aspects of IA computation are discussed, and relevant designs are presented in [24,25].
Energy considerations are widely used in shock problems. In addition, regarding problems with rapid variations in acceleration, the notion of energy of accelerations is of interest in the study of biological phenomena. Calculation methods of this energy are presented in [26,27,28,29,30].
The traffic safety of the driver and passengers remains an objective of particular interest for researchers and the automotive industry. As a result, the literature presents the results of recent research in the field, i.e., [31,32,33,34,35,36].
The purpose of this work is to determine the role of an IA and the forces to which a car driver is subjected after a frontal collision. Two special geometric variants for an IA made of three different materials and having different thicknesses were studied. A total of 24 variants of an IA are, thus, studied to see their effect on the dummy. For this, the finite element method (FEM) was used for modeling the entire system, including the car equipped with the IA, the car driver and the safety belt with four-point fastening. The study was conducted on a racing car used by Transilvania University in the Formula Student competitions. The effect of the airbags was not considered, considering the first part of the impact, when the demands are the highest. It was sought to determine if the system can ensure satisfactory safety in a race, in case of an impact. The behavior of the entire system is influenced by a multitude of factors whose influence is insufficiently studied. A mathematical model using the Gibbs–Appell method is used, allowing the rapid determination of the forces loading the system, which are then used in the FEM model [37,38,39,40,41,42,43,44,45,46,47,48]. The obtained results were used to design and calculate the performance of a racing car used in Formula Student competitions. The problems surrounding the biological effects of the accelerations experienced by the driver or passenger were not addressed in the paper. At the present moment, soft actuators have undergone special development; they were originally inspired by soft-bodied animals and human muscles. They have the property of being agile, reconfigurable and multifunctional and their use is found in numerous applications such as artificial muscles, wearable devices, haptic devices and innovative medical devices. Until now, however, synthetic models could not rise, in terms of performance, to the level of complex biological systems. The challenges and opportunities offered by soft actuators are widely presented in specialized works in the literature [49,50].
In the paper, two types of IA with constructive similarity and symmetries are developed and studied, considering three different materials and four different thicknesses of the material. A frontal collision of the car–dummy assembly with a vertical wall is considered, in accordance with the standards. Using simulation software, accelerations were determined at various points on the mannequin’s body.
2. Materials and Methods
An IA has the role of absorbing the energy in the event of an accident and transmitting the impact forces to the body structure. If the car has low speed, then the role of the IA is to minimize these damages, and at high speed, it must transmit the forces generated by the impact to the body structure without destroying it and, thus, prevent the death of the driver.
People are generally very sensitive to various shock requests from the external environment. The human body is vulnerable to shocks, mechanical shocks and acceleration. If an accident occurs, particularly involving dramatic shocks, accelerations occur that can negatively affect the health of the driver or passengers and can, in some cases, even lead to death. Of course, the automotive industry, in its development over the last hundred years, has perfected systems to protect the people in the vehicle. As a result, anthropomorphic test devices, called “dummies”, were designed and made. With their help, a series of practical situations were modeled and very effective safety systems were created. The development of the calculation technique and the software used has allowed the creation of virtual mannequins, from which a multitude of useful results and conclusions can be obtained.
Dummies can be very precise from the point of view of kinematics and can give values very close to real-world values of kinematic quantities, especially accelerations. There are “front impact dummies”, “side impact dummies” and “aerospace dummies”. For different situations and studies, customized mannequins are created for men, women and children.
Specialized works in the literature present a series of such dummies and their behavior in experiments in the case of some shocks. For the racing cars considered in this article, relevant results are presented in [51,52]. A standard average-sized adult mannequin, having the average height and weight of the US adult male population, is used in the studies. Despite the fact that this presents a major disadvantage in that a real human body is not used to test systems and conduct experiments to study the influence of various factors, the subject would obviously be seriously injured or even die in such an experiment. One solution would be to use corpses, but the results obtained were not satisfactory.
For the analysis of the passenger’s behavior in the case of a frontal collision, a dummy discretized with the FEM was used (Figure 1). In addition to the dummy, the entire racing car, equipped with an IA placed in the front of the car, is considered (Figure 2). The dummy is fixed to the car seat with a three-point safety belt. The purpose of the IA is to reduce the impact energy that is transmitted to the dummy after a frontal impact with a rigid wall as much as possible. In the case of the present study, one of the FE Hybrid III 50th Male-type dummies was chosen from the many types of dummies that can be used. This represents the average adult male (and is the most used model by researchers in works related to frontal impact tests [53]). Normally, the three-point seat belt is not used in car racing. For car races, a four-point seat belt is the accepted solution. The purpose of the presentation is to highlight the disadvantages of using this belt in practice.
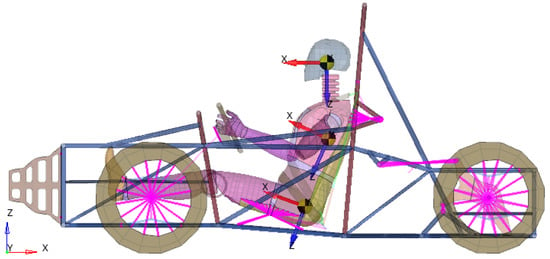
Figure 1.
A dummy with a three-point seat belt and a square IA.

Figure 2.
The racing car equipped with a three-point seat belt and a square IA.
A FE model using Altair Hyperworks [54,55,56] is used to study the system. Based on this model, different parameters are used to observe the behavior of the dummy in different situations that may arise. The analysis conducted is an explicit analysis using RADIOSS from the Altair Hyperworks package. The type of elements used for this analysis is CQUAD4, a shell element with four corner nodes with six DOF. These element types have been used for most components of the model, excluding the upper and lower arm of the suspension, which was simulated as a CBAR element, a 1D element with two end nodes with six DOF. Materials used in comparative analysis are shown in the paper. In the FE model, simulation material for IA was considered non-linear and the card image of material used in the solver is M36_PLAS_TAB. Furthermore, a non-linear material with a similar card image was used for the chassis. The following types of material were considered for other components of the model:
- -
- For the dummy—M1_ELAST;
- -
- For arms suspension—nonlinear steel using M2-John-Zeril Card Image Material. Ultimate stress considered is 450 MPa;
- -
- For tires—nonlinear rubber considering M2-John-Zeril as the card image. Properties of the material for linear zones are as follows: Young’s modulus of 200 MPa, Poisson ratio of 0.49. A unitary hardening exponent was considered to define the plasticity zone.
The interactions between elements were made through self-contact elements node-to-surface with an image card—TYPE7.
Based on this complex model, which analyzes the deformability of the structure, the forces that appear in the safety belt and the accelerations of different points of the dummy at the same time, the results presented in the following section are obtained—results that give us indications of the demands that appear in such a system.
3. Results
The three-point safety belt is the unanimously accepted solution in the automotive industry. The solution has shown its validity and advantages throughout the history of this industry. However, in the case of automobile racing, the safety belt used utilizes four-point fastening. This is because in the case of very large shocks, the upper part of the accent does not fulfill its role, and the dummy comes out from under the belt. To be able to make a comparison between the behaviors of the mannequin equipped with the two types of safety belt, a calculation of the system equipped with the belt fixed at three points is first conducted. The IA used is a square-shaped shock absorber. The kinematics of the frontal impact with a rigid wall of the dummy model are presented in Figure 3, Figure 4, Figure 5 and Figure 6.

Figure 3.
Deformation of IA after 25 ms.

Figure 4.
Deformation of IA after 50 ms.

Figure 5.
Deformation of IA after 75 ms.

Figure 6.
Deformation of IA after 100 ms.
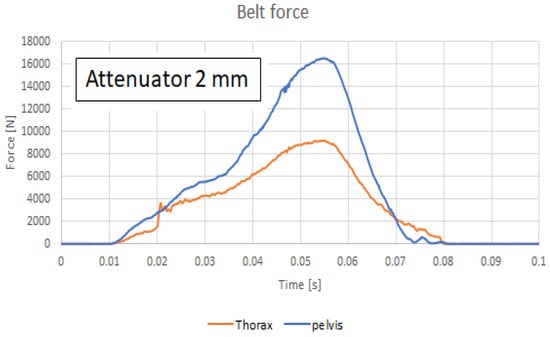
Figure 7.
Belt force using an IA having 2 mm thickness.
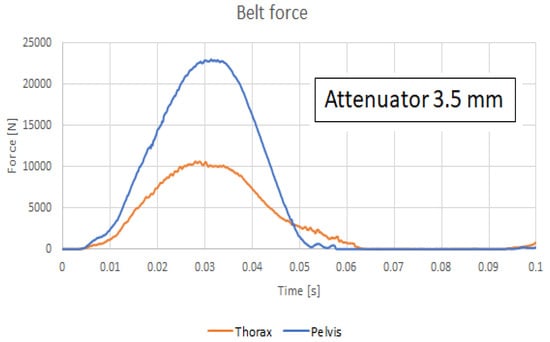
Figure 8.
Belt force using an IA having 3.5 mm thickness.
The problem that occurs when fixing the mannequin with a three-point fastening belt was reported by [4,13,15] and represents the folding of the safety belt. This phenomenon can also be observed in our case, which is why the study only considers belts that are fixed at four points in the discussion that follows, a model that is mainly used in cars used in competitions.
In order to comply with the ruleset for the Formula Student competition, the speed the car must have at the moment of impact is 7 m/s (25.2 km/h). The belt is considered to be made of the material M19_fabri, having a Young’s moduli E11 = E22 = 2500 MPa, a Poisson ratio ν = 0.2, a bending modulus G = 1040 MPa and a density of ρ = 1000 kg/m3. The representation of the belt force at ifferent moments of time are presented in Figure 9 and a comparison considering the two IA with two different thickness is presente in Figure 10.
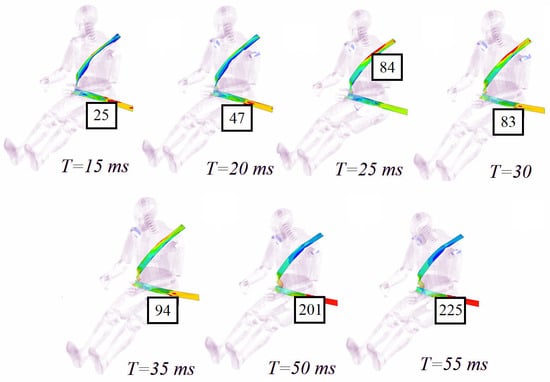
Figure 9.
Belt stress using an IA having 3.5 mm thickness (in MPa).
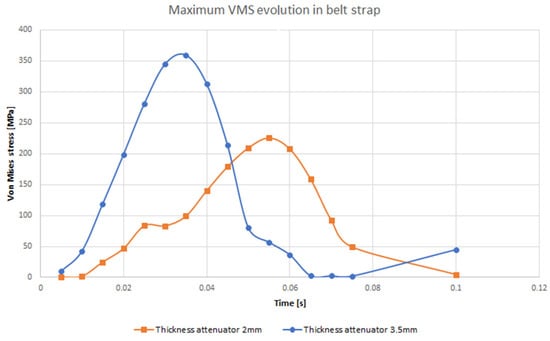
Figure 10.
Maximum evolution of VMS (von Mises stress) for crash time; crash analysis in the range [0–0.1] s.
Following the criteria established for the Formula Student competition, we obtain the following results:
Acceptance criteria according to Formula Student Rules T3.19.1/2022 Version: 0.9: Deceleration of vehicle: average deceleration: 20 g, and peak deceleration: 40 g. For the shock absorber with a thickness of 3.5 mm, the rules are not respected.
The accelerations are supported by several significant points of the dummy and are presented in Figure 11, Figure 12, Figure 13 and Figure 14.
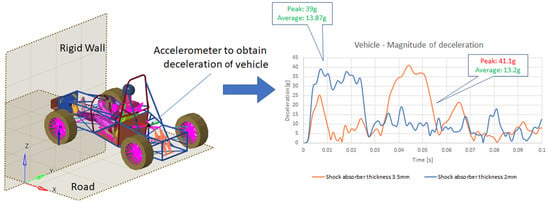
Figure 11.
The decelerations of the car considering two different thickness of the square-shaped IA.
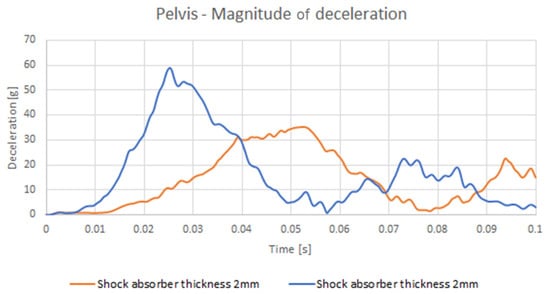
Figure 12.
The decelerations of the pelvis.
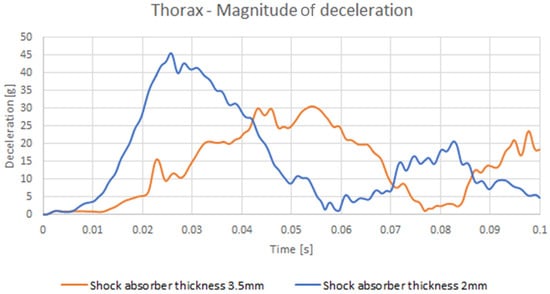
Figure 13.
The decelerations of the thorax.
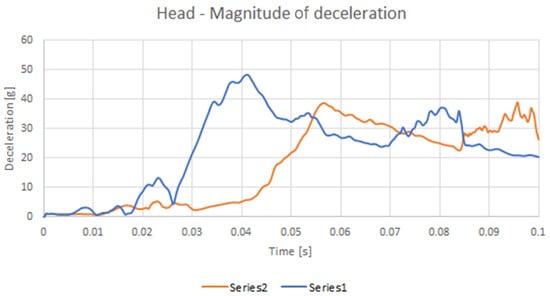
Figure 14.
The decelerations of the head.
The deformation of the IA at different moments in time are presented in Figure 15, Figure 16, Figure 17 and Figure 18.
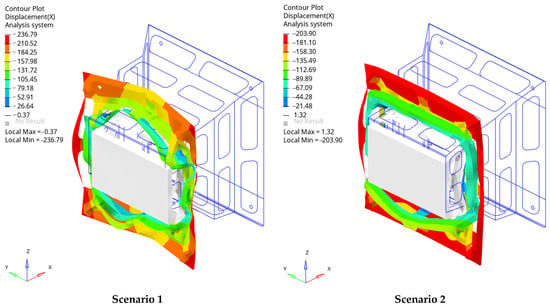
Figure 15.
The deformation of the IA at t = 0.05 s: Scenarios 1 and 2.
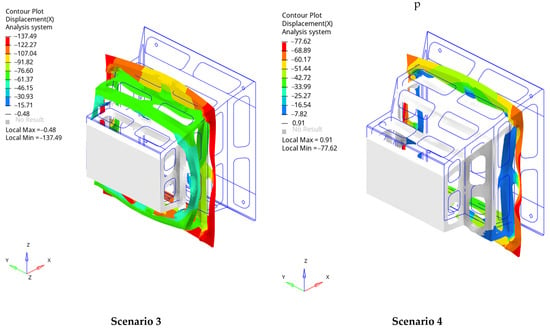
Figure 16.
The deformation of the IA at t = 0.05 s: Scenarios 3 and 4.
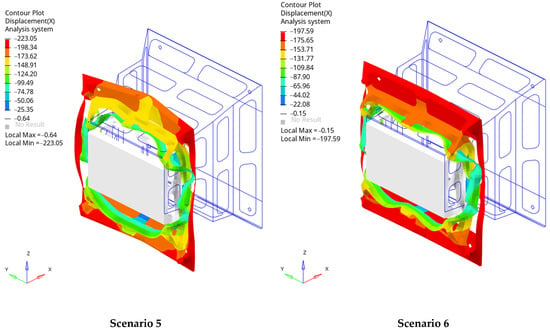
Figure 17.
The deformation of the IA at t = 0.05 s: Scenarios 5 and 6.
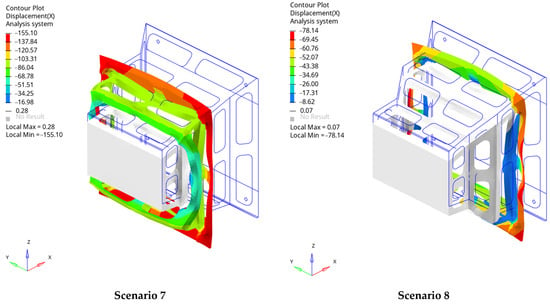
Figure 18.
The deformation of the IA at t = 0.05 s: Scenarios 7 and 8.
In the work, 24 constructive variants are presented. Two types of IA are studied, one of rectangular shape and the other of cylindrical shape. Three materials used with the properties shown in Table 1 are studied. For these variants, the calculation is made for four different wall thicknesses.

Table 1.
The mechanical properties of the material used for IA.

Table 2.
The first 12 scenarios for rectangular IA.

Table 3.
The next 12 scenarios for cylindrical IA.
In the following, the dummy used for the study (Figure 19 and Figure 20) is presented, fastened with a four-point safety belt and for which the fulfillment of the conditions required by the regulations of the Formula Student competition were studied.
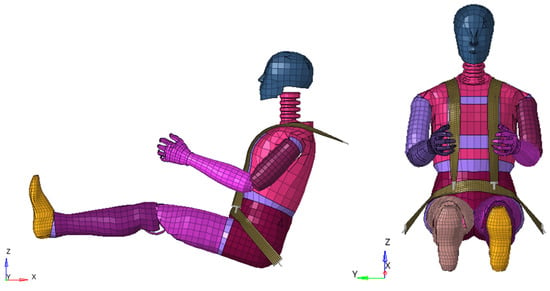
Figure 19.
Articulated Total Body (ATB) of Hybrid III used to model the driver or the passenger.
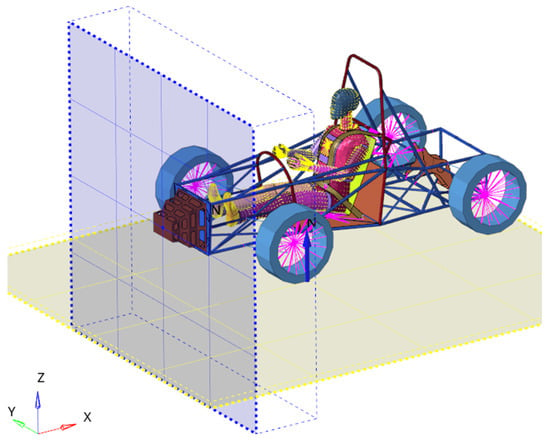
Figure 20.
The model of the dummy and of the car.
The Peak and Average deceleration for the car in 24 scenarios are presented in Figure 21 and the Internal Energy in Table 4 and Table 5.
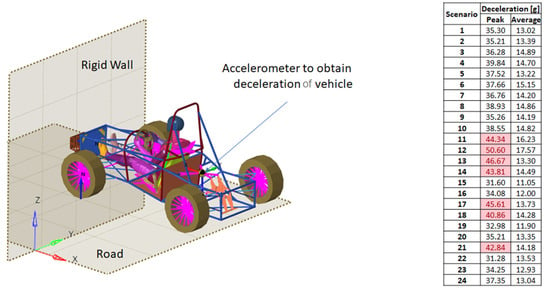
Figure 21.
The Peak and Average deceleration for the car in 24 scenarios.

Table 4.
The Internal Energy for the first 12 scenarios (for the rectangular IA). The colored numbers represent the case when the limit value is exceeded.

Table 5.
The Internal Energy for the next 12 scenarios (for the cylindrical IA).
The situations in which the internal energy is higher than that accepted by the standards are presented in the tables in red (Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30, Figure 31, Figure 32 and Figure 33).
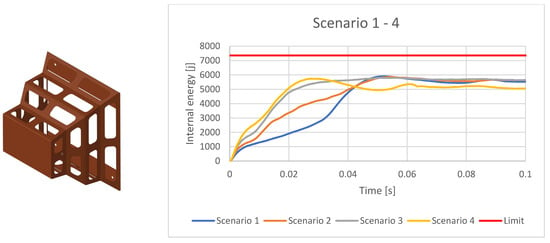
Figure 22.
Internal Energy for the rectangular IA with Al7050 material for different scenarios.
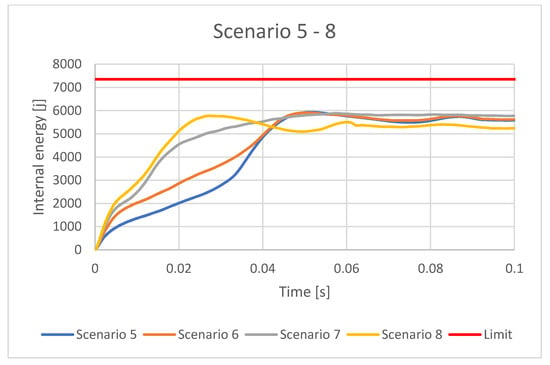
Figure 23.
Internal Energy for the rectangular IA with OL37 material for different scenarios.
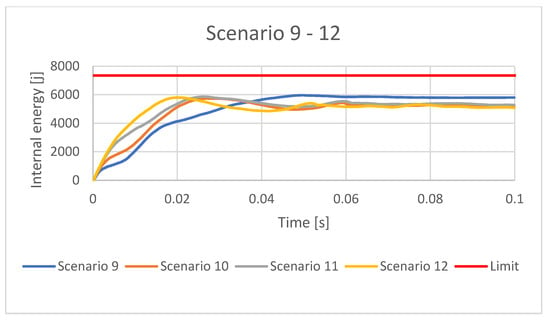
Figure 24.
Internal Energy for the rectangular IA with OL50 material for different scenarios.
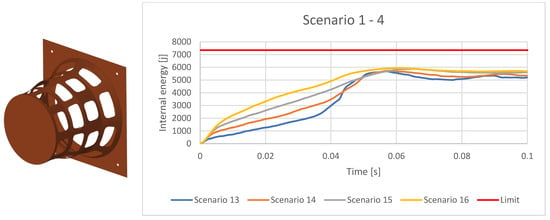
Figure 25.
Internal Energy for the cylindrical IA with AI7050 for different scenarios.
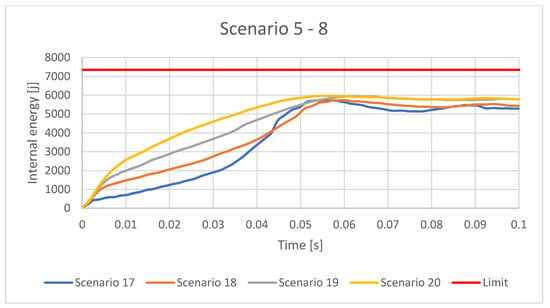
Figure 26.
Internal Energy for the cylindrical IA with OL37 material for different scenarios.
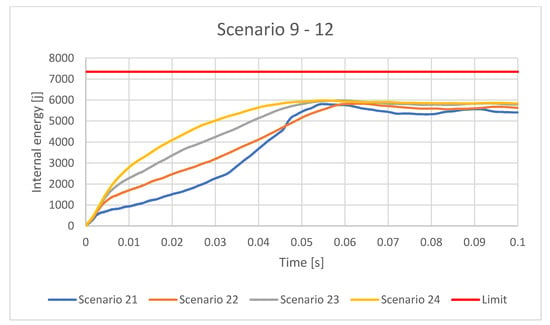
Figure 27.
Internal Energy for the cylindrical IA with Ol50 material for different scenarios.
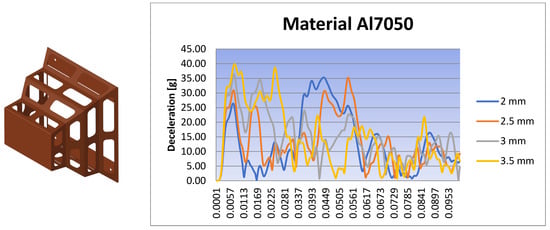
Figure 28.
Deceleration for the rectangular IA with Al5070 material for different scenarios.
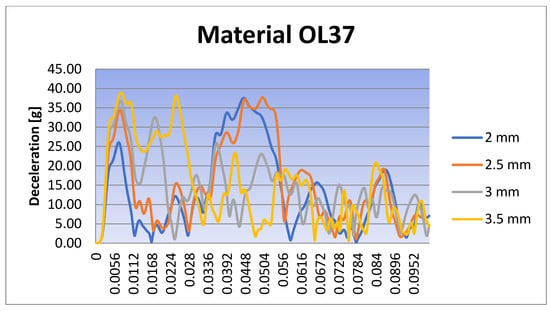
Figure 29.
Deceleration for the rectangular IA with Ol37 material for different scenarios.
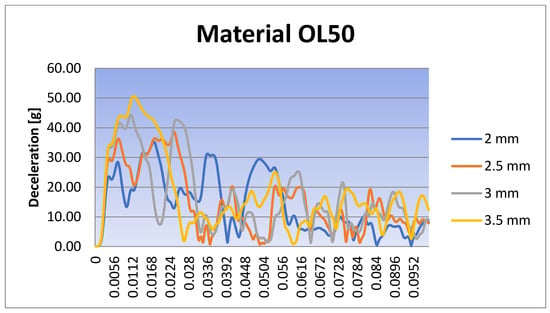
Figure 30.
Deceleration for the rectangular IA with OL50 material for different scenarios.
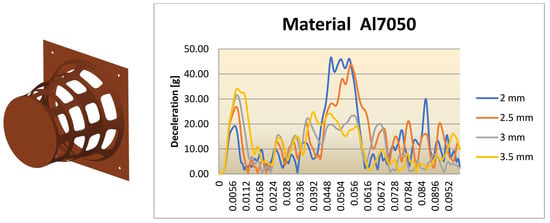
Figure 31.
Deceleration for the cylindrical IA with Al5070 material for different scenarios.
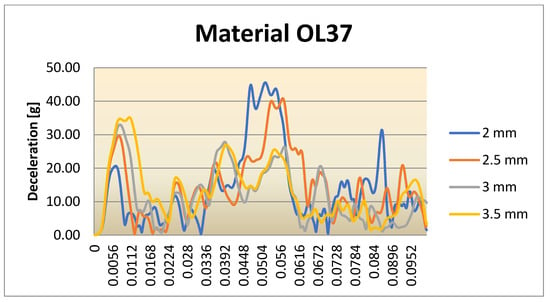
Figure 32.
Deceleration for the cylindrical IA with OL37 material for different scenarios.
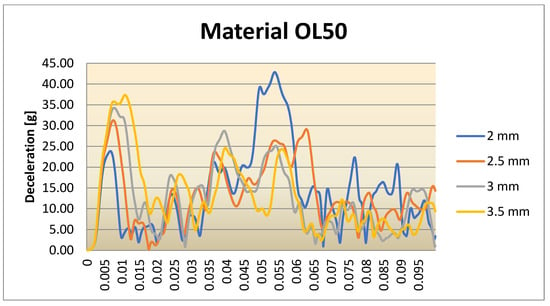
Figure 33.
Deceleration for the cylindrical IA with OL50 material for different scenarios.
The internal lost energy is less than 7350 J in our results. However, we must consider that the dummy and structure have 270 Kg together, so this limit energy can be decreased by 10%. Even in this version, the minimum wasted energy does not have the desired value, so a redesign of the IA with a resizing is required. Because the difference in additional energy that must be obtained is small, it is assumed that a minor resizing of the absorber will be sufficient to achieve the condition. In the paper, several types of shock absorption systems were studied for different IA wall thicknesses and for different materials. It is found that a better steel in terms of strength leads to a worse behavior in terms of shock absorption and the use of thicker-walled IAs can also lead to a worse behavior in terms of shock absorption.
Based on the study, an optimal variant of the absorber can be chosen that complies with the conditions imposed by the standards. During the study, it was found that a number of constructive types do not meet the conditions imposed on the project.
4. Conclusions
The aim of the work was to determine the behavior of a passenger wearing a seat belt in a vehicle equipped with an IA in the front, as well as the loads that appear in such a scenario. In the paper, the effect that IAs can have, in different variants, on the damages that can occur in the case of a frontal collision was determined. The forces occurring in the seat belt and in the IA were also calculated. The calculation method was FEM, a method that has proven its effectiveness and consistency in many practical applications. The Gibbs–Appell method was used to determine the forces that the system experienced during the shock. Several variants of IAs with different wall thicknesses were studied. In the case analyzed in the paper (a mannequin sitting in a Formula Student racing car), the criteria stipulated by the Formula Student regulations are respected for most of the cases studied. Two different structural models of IA, made of three different materials and with four different wall thicknesses, were analyzed. The results obtained indicate the variants that correspond to the standards that apply to these racing cars. The biological effects, important in such cases, were not studied, as they do not represent the subject of analysis of the paper, but the values obtained in the study can be used by researchers in respective fields. Thus, a satisfactory design was proposed for this IA to provide optimal behavior of a racing car in the case of a frontal impact with a wall. In this way, a certification of the fact that the IA works properly for the type of car studied is made. The IA has been studied to determine what effects its existence has on the occupant of a car. An optimal shape for better shock absorption in the event of a collision is proposed. In racing cars, the IA is a separate element, which must be equipped to such a car and which must ensure the safety of the occupants in the event of an accident.
Based on the results obtained, we can make the observation that a better material for IAs from the point of view of material resistance can lead to a worse behavior from the point of view of shock behavior of the absorber. It is, therefore, necessary to reach an optimal compromise between the choice of several types of materials, so that the system meets all requirements.
The research presented in the work and the results obtained offer a wide horizon for research. The number of parameters involved in such a study is very large and the results obtained are, at the moment, insufficient but extremely necessary for designers.
Author Contributions
Conceptualization, C.I. and S.V.; formal analysis, S.V.; investigation, C.I.; methodology, C.I. and S.V.; software, C.I.; supervision, C.I. and S.V.; validation, C.I. and S.V.; visualization, C.I. and S.V.; writing—original draft, C.I. and S.V.; writing—review and editing, C.I. and S.V. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Transilvania University of Brasov.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ashley, S. Mechanical Seat-Belt Tensioner. Mech. Eng. 1992, 114, 24. [Google Scholar]
- DeGaspari, J. ‘Smarter’ seat belt fiber. Mech. Eng. 2002, 124, 22–30. [Google Scholar]
- Takimizu, Y. Retraction performance of motor vehicle seat belt. J. Jpn. Soc. Tribol. 1997, 42, 625–630. [Google Scholar]
- Sances, A.; Kumaresan, S.; Herbst, B.; Meyer, S.; Hock, D. Biomechanics of seat belt restraint system. In Proceedings of the 41st Annual Rocky Mountain Bioengineering Symposium/41st International ISA Biomedical Sciences Instrumentation Symposium, Ft Collins, CO, USA, 23–25 April 2004; Volume 449, pp. 377–380. [Google Scholar]
- Zhao, F.; Jiao, H.Y. Topography Optimization of Automobile Seat Belt Bracket. In Proceedings of the 2017 International Conference on Mechanical, Electronic, Control and Automation Engineering (MECAE 2017), Beijing, China, 25–26 March 2017; Volume 61, pp. 10–14. [Google Scholar]
- Dubois, D.; Gross, P.; Tramecon, A.; Markiewicz, E. Finite element analysis of seat belt bunching phenomena. Int. J. Crashworthiness 2006, 11, 519–528. [Google Scholar] [CrossRef]
- Kang, S.J.; Chun, B.K. Strength analysis of automotive seat belt anchorage. Int. J. Veh. Des. 2001, 26, 496–508. [Google Scholar] [CrossRef]
- Roberts, A.; Partain, M.; Batzer, S.; Renfroe, D. Failure analysis of seat belt buckle inertial release. Eng. Fail. Anal. 2007, 14, 1135–1143. [Google Scholar] [CrossRef]
- Dubois, D.; Zellmer, H.; Markiewicz, E. Experimental and numerical analysis of seat belt bunching phenomenon. Int. J. Impact Eng. 2009, 36, 763–774. [Google Scholar] [CrossRef]
- Cao, L.G.; Feng, H. Torque performance measurement system for spring in seat belt. In Proceedings of the 3rd International Conference on Advances in Materials Manufacturing (ICAMMP 2012), Beihai, China, 22–23 December 2012; Volume 655–657, pp. 1149–1152. [Google Scholar] [CrossRef]
- Tang, Y.M.; Lv, N.; Xue, Q.; Wang, T.; Tan, W.F. Experiment Simulation of Seat Belt and ISOFIX Anchorage for a Commercial Vehicle. In Proceedings of the 8th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Macau, China, 11–12 March 2016; pp. 282–285. [Google Scholar] [CrossRef]
- Jung, S.P.; Park, T.W.; Park, C.S. Dynamic analysis and design optimisation of the seat belt pretensioner. Veh. Syst. Dyn. 2010, 48, 65–78. [Google Scholar] [CrossRef]
- Meyer, S.E.; Hock, D.; Forrest, S.; Herbst, B. Motor vehicle seat belt restraint system analysis during rollover. In Proceedings of the 40th Annual Rocky Mountain Bioengineering Symposium/40th International ISA Biomedical Sciences Instrumentation Symposium, Biloxi, MS, USA, 10–13 April 2003; Biomedical Sciences Instrumentation, Book Series. Volume 39, pp. 229–240. [Google Scholar]
- Shi, P.C.; Xu, Z.W. Analysis of Seat. In Proceedings of the 5th Annual International Conference on Material Science and Environmental Engineering (MSEE 2017), Xiamen, China, 15–17 October 2017; Volume 301, p. 012127. [Google Scholar] [CrossRef]
- Huston, R.L. A Review of the effectiveness of seat belt systems: Design and safety considerations. Int. J. Crashworthiness 2001, 6, 243–252. [Google Scholar] [CrossRef]
- Itu, C.; Toderita, A.; Melnic, L.-V.; Vlase, S. Effects of Seat Belts and Shock Absorbers on the Safety of Racing Car Drivers. Mathematics 2022, 10, 3593. [Google Scholar] [CrossRef]
- Karishma, P.; Venugopal, K.V.; Raju, I.R.K. Optimization and Impact Analysis of a Roll Cage Model. Int. Res. J. Eng. Technol. (IRJET) 2018, 5, 526–543. [Google Scholar]
- Kanketr, T.; Phongphinnittana, E.; Patamaprohm, B. Design of a CFRP composite monocoque: Simulation approach. In Proceedings of the 9th Thai-Society-of-Mechanical-Engineers International Conference on Mechanical Engineering (TSME-ICoME), Phuket, Thailand, 11–14 December 2018; IOP Conference Series-Materials Science and Engineering. Volume 501, p. 012014. [Google Scholar] [CrossRef]
- Lufinka, A. Crash Test of the Student Racing Car Impact Attenuator. In Proceedings of the 58th International Conference of Machine Design Departments (ICMD 2017), Prague, Czech Republic, 6–8 September 2017; pp. 210–213. [Google Scholar]
- Kaul, A.; Abbas, A.; Smith, G.; Manjila, S.; Pace, J.; Steinmetz, M. A revolution in preventing fatal craniovertebral junction injuries: Lessons learned from the Head and Neck Support device in professional auto racing. J. Neurosurgey-Spine 2016, 25, 756–761. [Google Scholar] [CrossRef] [PubMed]
- Mihradi, S.; Golfianto, H.; Mahyuddin, A.I.; Dirgantara, T. Head Injury Analysis of Vehicle Occupant in Frontal Crash Simulation: Case Study of ITB’s Formula SAE Race Car. J. Eng. Technol. Sci. 2017, 49, 534–545. [Google Scholar] [CrossRef]
- Guegan, P.; Lebreton, D.; Pasco, F.; Othman, R.; Le Corre, S.; Poitou, A. Metallic energy-absorbing inserts for Formula One tyre barriers. Proceeding Inst. Mech. Eng. Part D-J. Automob. Eng. 2008, 222, 699–704. [Google Scholar] [CrossRef]
- Davies, H.C.; Bryant, M.; Hope, M.; Meiller, C. Design, development, and manufacture of an aluminium honeycomb sandwich panel monocoque chassis for Formula Student competition. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2012, 226, 325–337. [Google Scholar] [CrossRef]
- Albak, E.I.; Solmaz, E.; Kaya, N.; Ozturk, F. Impact attenuator conceptual design using lightweight materials and meta-modeling technique. Mater. Test. 2019, 61, 621–626. [Google Scholar] [CrossRef]
- Switek, W.; Vallejo, R. Finite element dynamic simulation of a race car. In Proceedings of the Computer Aided Optimum Design of Structures VIII, Structures and Materials, Dearborn, MI, USA, 19–21 May 2003; Volume 13, pp. 115–122. [Google Scholar]
- Nguyen, H.C.; Vo-Minh, T. The use of the node-based smoothed finite element method to estimate static and seismic bearing capacities of shallow strip footings. J. Rock Mech. Geotech. Eng. 2022, 14, 180–196. [Google Scholar] [CrossRef]
- Iorio, L. Revisiting the 2PN Pericenter Precession in View of Possible Future Measurements. Universe 2020, 6, 53. [Google Scholar] [CrossRef]
- Negrean, I. Formulations about Elastodynamics in Robotics. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 2019, 62, 237–250. [Google Scholar]
- Hassan, M.; Bruni, S. Experimental and numerical investigation of the possibilities for the structural health monitoring of railway axles based on acceleration measurements. Struct. Health Monit. Int. J. 2019, 18, 902–919. [Google Scholar] [CrossRef]
- Xiao, M.L.; Zhang, Y.; Zhu, H.Y. The mechanism of hindering occupants’ evacuation from seismic responses of building. Nat. Hazards 2019, 96, 669–692. [Google Scholar] [CrossRef]
- Filben, T.M.; Pritchard, N.S.; Oravec, C.S.; Hile, C.W.; Bercaw, J.R.; Zoch, S.R.; Miller, L.E.; Bullock, G.S.; Flashman, L.A.; Miles, C.M.; et al. Pilot characterization of head kinematics in grassroots dirt track racing traffic injury prevention. Traffic Inj. Prev. 2022, in press. [Google Scholar] [CrossRef] [PubMed]
- Bhat, A.; Gupta, V.; Aulakh, S.S.; Elsen, R.S. Generative design and analysis of a double-wishbone suspension assembly: A methodology for developing constraint oriented solutions for optimum material distribution. J. Eng. Des. Tecnol. 2021, in press. [Google Scholar] [CrossRef]
- Drage, T.; Lim, K.L.; Koh, J.E.H.; Gregory, D.; Brogle, C.; Braunl, T. Integrated Modular Safety System Design for Intelligent Autonomous Vehicles. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium (IV), Nagoya, Japan, 11–17 July 2021; pp. 258–265. [Google Scholar] [CrossRef]
- Vaverka, O.; Koutny, D.; Palousek, D. Topologically optimized axle carrier for Formula Student produced by selective laser melting. Rapid Prototyp. J. 2019, 25, 1545–1551. [Google Scholar] [CrossRef]
- Vlase, S.; Teodorescu, P.P. Elasto-Dynamics of a Solid with a General “RIGID” Motion using FEM Model. Part I. Theoretical Approach. Rom. J. Phys. 2013, 58, 872–881. [Google Scholar]
- Vlase, S.; Negrean, I.; Marin, M.; Scutaru, M.L. Energy of Accelerations Used to Obtain the Motion Equations of a Three- Dimensional Finite Element. Symmetry 2020, 12, 321. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the fundamental formulae of dynamics. Am. J. Math. 1879, 2, 49–64. [Google Scholar] [CrossRef]
- Appell, P. Sur une forme générale des equations de la dynamique. C.R. Acad. Sci. Paris 1899, 129, 317–320. [Google Scholar]
- Mirtaheri, S.M.; Zohoor, H. The Explicit Gibbs-Appell Equations of Motion for Rigid-Body Constrained Mechanical System. In Proceedings of the RSI International Conference on Robotics and Mechatronics ICRoM, Piscataway, NJ, USA, 23–25 October 2018; pp. 304–309. [Google Scholar]
- Korayem, M.H.; Dehkordi, S.F. Motion equations of cooperative multi flexible mobile manipulator via recursive Gibbs-Appell formulation. Appl. Math. Model. 2019, 65, 443–463. [Google Scholar] [CrossRef]
- Shafei, A.M.; Shafei, H.R. A systematic method for the hybrid dynamic modeling of open kinematic chains confined in a closed environment. Multibody Syst. Dyn. 2017, 38, 21–42. [Google Scholar] [CrossRef]
- Korayem, M.H.; Dehkordi, S.F. Derivation of dynamic equation of viscoelastic manipulator with revolute-prismatic joint using recursive Gibbs-Appell formulation. Nonlinear Dyn. 2017, 89, 2041–2064. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Scutaru, M.L. Maggi’s equations used in the finite element analysis of the multibody systems with elastic elements. Mathematics 2020, 8, 399. [Google Scholar] [CrossRef]
- Ursu-Fisher, N. Elements of Analytical Mechanics; House of Science Book Press: Cluj-Napoca, Romania, 2015. [Google Scholar]
- Negrean, I.; Crișan, A.-D.; Vlase, S. A New Approach in Analytical Dynamics of Mechanical Systems. Symmetry 2020, 12, 95. [Google Scholar] [CrossRef]
- Vlase, S.; Negrean, I.; Marin, M.; Nastac, S. Kane’s Method-Based Simulation and Modeling Robots with Elastic Elements, Using Finite Element Method. Mathematics 2020, 8, 805. [Google Scholar] [CrossRef]
- European New Car Assessment Programme (Euro NCAP), Frontal Impact Testing Protocol Version 6.0 August. Available online: https://cdn.euroncap.com/media/1457/euro-ncap-frontal-protocol-version-60.pdf (accessed on 29 September 2022).
- Kallieris, D.; Rizzetti, A.; Mattern, R. The Biofidelity of Hybrid III Dummies, Institute of Legal Medicine University of Heidelberg. Available online: http://www.ircobi.org/wordpress/downloads/irc1995/pdf_files/1995_10.pdf (accessed on 29 September 2022).
- Fortuna, L.; Buscarino, A. Microrobots in Micromachines. Micromachines 2022, 13, 1207. [Google Scholar] [CrossRef] [PubMed]
- Fortuna, L.; Buscarino, A. Smart Materials. Materials 2022, 15, 6307. [Google Scholar] [CrossRef] [PubMed]
- Injury Criteria for Side Impact Dummies, May 2004, By Shashi Kuppa. Available online: https://www.nhtsa.gov/ (accessed on 29 September 2022).
- Hybrid III 50th Male FE|Humanetics. Available online: humaneticsgroup.com (accessed on 25 September 2022).
- Li, X. Simulation System of Car Crash Test in C-NCAP Analysis Based on an Improved Apriori Algorithm. Phys. Procedia 2012, 25, 2066–2071. [Google Scholar] [CrossRef]
- Untaroiu, C.D.; Shina, J.; Ivarssona, J.; Crandalla, J.R.; Subita, D.; Takahashib, Y.; Akiyamab, A.; Kikuchi, Y. A study of the pedestrian impact kinematics using finite element dummy models: The corridors and dimensional analysis scaling of upper-body trajectories. Int. J. Crashworthiness 2008, 13, 469–478. [Google Scholar] [CrossRef]
- Quoc, P.M.; Krzikalla, D.; Mesicek, J.; Petru, J.; Smiraus, J.; Sliva, A.; Poruba, Z. On Aluminum Honeycomb Impact Attenuator Designs for Formula Student Competitions. Symmetry 2020, 12, 1647. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Marin, M.; Zeeshan, A.; Abdelsalam, S.I. Recent trends in computational fluid dynamics. Front. Phys. 2020, 8, 593111. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).