New Differentially 4-Uniform Piecewise Permutations over ${\mathbb{F}}_{2^{2k}}$ from the Inverse Function

Abstract

Permutations with low differential uniformity, high nonlinearity and high algebraic degree over ${\mathbb{F}}_{2^{2k}}$ are preferred substitution boxes in modern block ciphers. In this paper, we study the bijectivity and the difference uniformity of piecewise function with the help of permutation group theory. Based on our results, We found many at least differentially 6-uniform and differentially 4-uniform permutations over ${\mathbb{F}}_{2^{2k}}$, which can be chosen as the substitution boxes.

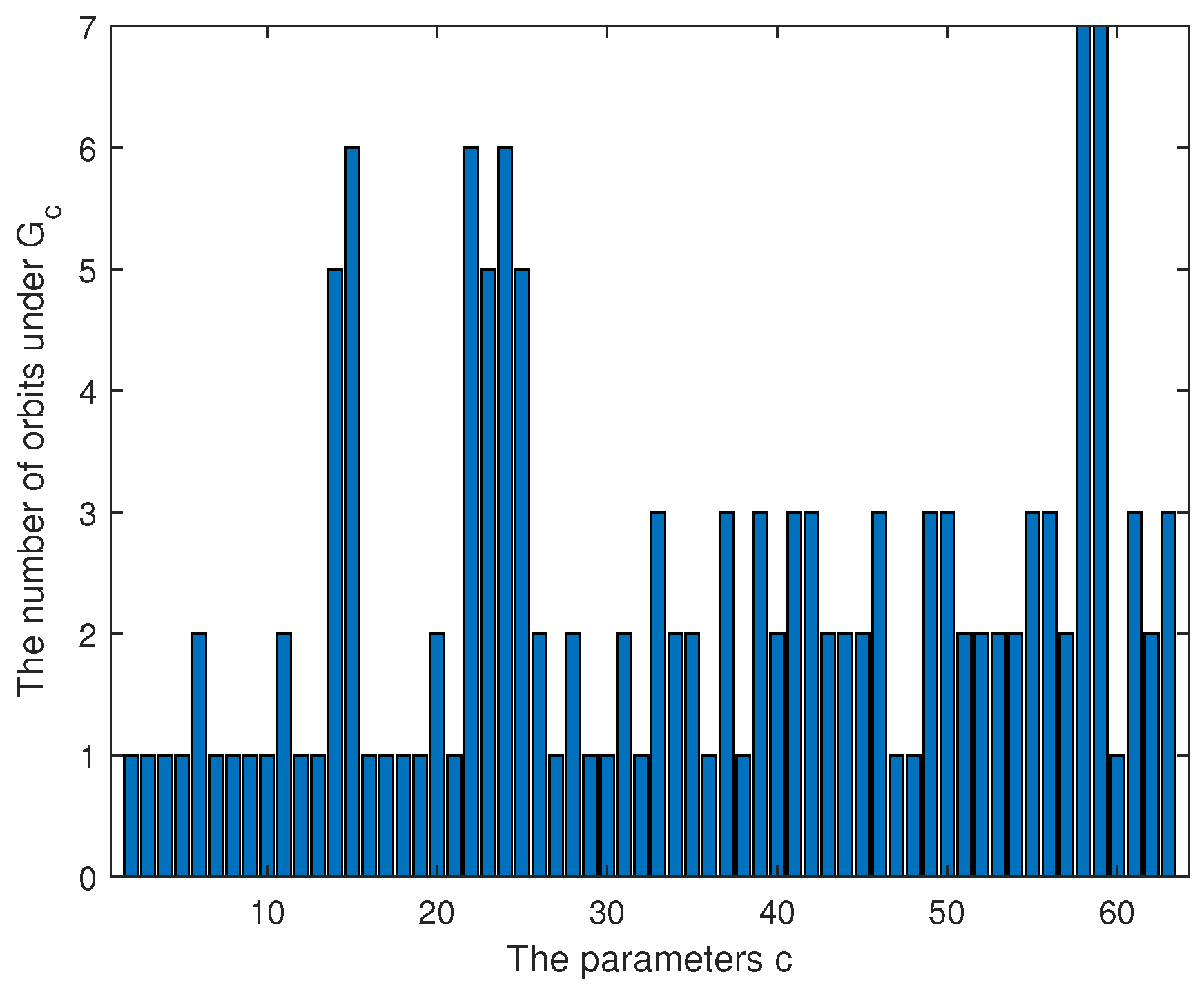
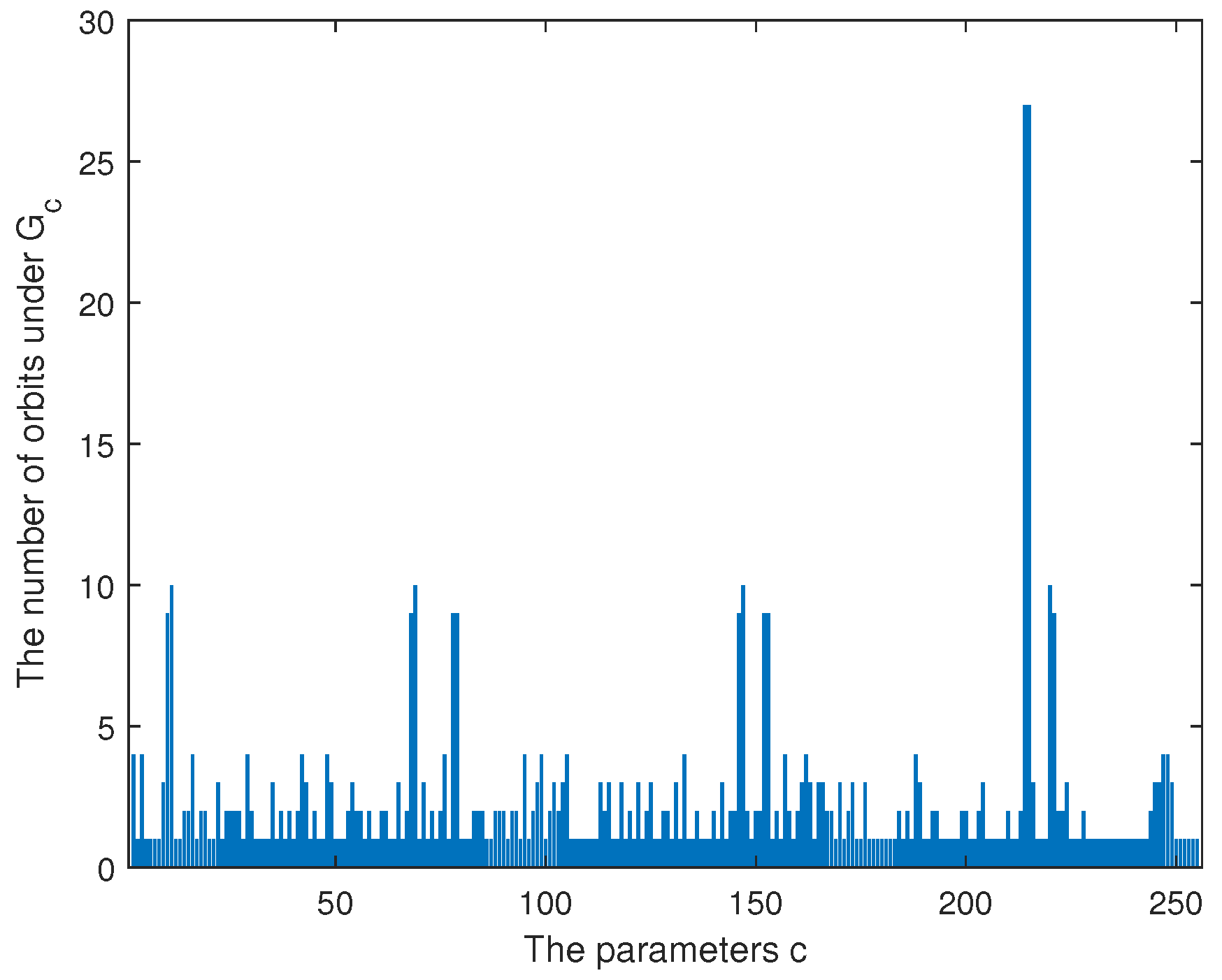
1. Introduction

Modern block cipher is an important way to ensure information security in various environments [1,2]. The substitution boxes (S-boxes) with good cryptographic properties play a crucial role in modern block ciphers. S-boxes with good cryptographic properties must have low differential uniformity [3], high nonlinearity [4] and high algebraic degree [5] to resist differential attacks, linear attacks and higher-order differential attacks, respectively. In practice, permutations over ${\mathbb{F}}_{2^n}$ with even n are used as S-boxes.

A function f from ${\mathbb{F}}_{2^n}$ to itself is called differentially $\delta$-uniform and $\delta$ is called the differential uniformity of f if the equation $f(x+a)+f(x)=b$ has at most $\delta$ solutions for every nonzero a and every b in ${\mathbb{F}}_{2^n}$. In particular, a differentially 2-uniform function is called almost perfect nonlinear (APN). APN functions have the theoretical lowest differential uniformity and the strongest resistance to differential attacks. However, finding APN permutations over ${\mathbb{F}}_{2^n}$ for even $n\ge 8$ is a famous open problem, i.e., the big APN problem. Then, differentially 4-uniform permutations are often chosen as S-boxes.

A lot of work has been devoted to find new differentially 4-uniform permutations over ${\mathbb{F}}_{2^n}$ with even n. The switching method proposed by Claude Carlet [6] is an efficient way to construct differentially 4-uniform permutations. Several classes of differential 4-uniformity permutations have been constructed using the switching method [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. Differential 4-uniformity permutations based on the switch method can be expressed as piecewise functions, i.e.,

$$\begin{array}{c}\hfill f(x)=\left\{\begin{array}{cc}{g}_1(x),\hfill & \hfill x\in U\\ g_2(x),\hfill & \hfill x\notin U\end{array}\right.,\end{array}$$

(1)

where $g_1$ and $g_2$ are known permutations over ${\mathbb{F}}_{2^n}$, and U is a specific subset of ${\mathbb{F}}_{2^n}$. In most existing work, the subset U is either obtained from the subfield of ${\mathbb{F}}_{2^n}$ [6,7,8,9,10,11,12,13,14,15,16,17] or a small subset ${\mathbb{F}}_{2^n}$ [18,19,20,21,22]. In other words, the subset U has special properties, and is not general.

In this paper, we focus on the conditions of the subset U in Equation (1) such that f is a permutation with low differential uniformity. First, we study the bijectivity and the difference uniformity of f from known $g_1$ and $g_2$ based on permutation group theory. Then, we construct at least differentially 6-uniform and differentially 4-uniform piecewise permutations from the inverse function and a function that is affine equivalent to the inverse function, and present the algorithm for constructing differentially 4-uniform piecewise permutations over ${\mathbb{F}}_{2^{2k}}$ from the inverse function. Finally, we discuss the number of at least differentially 6-uniform piecewise permutations, and calculate the differential spectrum and extend Walsh spectrum of some differentially 4-uniform piecewise permutations. The main contributions of this paper are as follows:

• Based on permutation group theory, we determine the conditions for constructing piecewise permutations with low difference uniformity from known permutations.
• Based on our results, we construct many at least differentially 6-uniform and differentially 4-uniform piecewise permutations over ${\mathbb{F}}_{2^{2k}}$ from the inverse function.

The rest of this paper is as follows. Section 2 presents necessary notations and results. Section 3 studies the bijectivity and the difference uniformity of piecewise functions from known permutations. Section 4 constructs at least differentially 6-uniform and differentially 4-uniform piecewise permutations over ${\mathbb{F}}_{2^{2k}}$ from the inverse function. Section 5 presents some numerical results on our construction. The last section is the conclusions of this paper.

2. Preliminaries

Given a positive integer n, let ${\mathbb{F}}_{2^n}$ denote the finite field of order $2^n$; and let ${\mathbb{F}}_{2^n}^{\ast }$ denote the set of nonzero elements in ${\mathbb{F}}_{2^n}$. We will use $a+b$ and $ab$ to denote the sum and the product of a and b in ${\mathbb{F}}_{2^n}$, respectively.

The finite field ${\mathbb{F}}_{2^n}$ can be identified with the vector space ${\mathbb{F}}_2^n$. The elements of ${\mathbb{F}}_2^n$ can be written as the integers in the range from 0 to $2^n-1$ with the element $(x_1,\cdots ,x_n)$ in ${\mathbb{F}}_2^n$ corresponding to the integer ${\sum }_{i=1}^n{x}_i{2}^{n-i}$. In this sense, ${\mathbb{F}}_{2^n}=\{0,1,\cdots ,2^n-1\}$.

Let ${\mathfrak{F}}_{{\mathbb{F}}_{2^n}}$ denote the set of all functions from ${\mathbb{F}}_{2^n}$ to itself; and let ${\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$ denote the set of all permutations of ${\mathbb{F}}_{2^n}$. For $f,g\in {\mathfrak{F}}_{{\mathbb{F}}_{2^n}}$, let $fg$ denote the composition of f and g, i.e., $fg(x)=f(g(x))$ for every $x\in {\mathbb{F}}_{2^n}$. The set ${\mathfrak{F}}_{{\mathbb{F}}_{2^n}}$ with composition forms a monoid, and ${\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$ with composition forms a group, which is called the symmetric group on ${\mathbb{F}}_{2^n}$ [29].

For $f\in {\mathfrak{F}}_{{\mathbb{F}}_{2^n}}$, we can identify a polynomial of degree $2^n-1$ over ${\mathbb{F}}_{2^n}$ with f, i.e.,

$$\begin{array}{c}\hfill f(x)=\sum _{i=0}^{2^n-1}{a}_i{x}^i\mathrm{for}\mathrm{every}x\in {\mathbb{F}}_{2^n}.\end{array}$$

Definition 1. 

For $f\in {\mathfrak{F}}_{{\mathbb{F}}_{2^n}}$, the differential uniformity of f is defined by

$$\begin{array}{c}\hfill \delta (f)=\underset{a\in {\mathbb{F}}_{2^n}^{\ast },b\in {\mathbb{F}}_{2^n}}{max}\left|{\Delta }_f(a,b)\right|,\end{array}$$

where

$$\begin{array}{c}\hfill {\Delta }_f(a,b)=\{x\in {\mathbb{F}}_{2^n}:f(x+a)+f(x)=b\}.\end{array}$$

The multi-set $\{\ast |{\Delta }_f(a,b)|:a\in {\mathbb{F}}_{2^n}^{\ast },b\in {\mathbb{F}}_{2^n}\ast \}$ is called the differential spectrum of f.

Definition 2. 

For $f\in {\mathfrak{F}}_{{\mathbb{F}}_{2^n}}$, the nonlinearity of f is defined by

$$\begin{array}{c}\hfill nl(f)=2^{n-1}-\frac{1}{2}\underset{a\in {\mathbb{F}}_{2^n},b\in {\mathbb{F}}_{2^n}^{\ast }}{max}\left|W_f(a,b)\right|,\end{array}$$

where

$$\begin{array}{c}\hfill W_f(a,b)=\sum _{x\in {\mathbb{F}}_{2^n}}{(-1)}^{a·x+b·f(x)}.\end{array}$$

The multi-set $\{\ast |W_f(a,b)|:a\in {\mathbb{F}}_{2^n},b\in {\mathbb{F}}_{2^n}\ast \}$ is called the extended Walsh spectrum of f.

For $f,g\in {\mathfrak{F}}_{{\mathbb{F}}_{2^n}}$, we say that they are affine equivalent if there exist affine permutations $h_1,h_2$ such that $g(x)=h_1(f(h_2(x)))$ for every $x\in {\mathbb{F}}_{2^n}$; we say that they are extended affine (EA) equivalent if there exist affine permutations $h_1,h_2$ and an affine function $h_3$ such that $g(x)=h_1(f(h_2(x)))+h_3(x)$ for every $x\in {\mathbb{F}}_{2^n}$; and we say that they are Carlet–Charpin–Zinoviev (CCZ) equivalent [30] if the graphs $\{(x,y)\in {\mathbb{F}}_{2^n}\times {\mathbb{F}}_{2^n}:y=f(x)\}$ and $\{(x,y)\in {\mathbb{F}}_{2^n}\times {\mathbb{F}}_{2^n}:y=g(x)\}$ are affine equivalent.

It is known that differential uniformity and nonlinearity are affine, EA and CCZ invariant, the algebraic degree is affine and EA invariant but not CCZ invariant, and the bijectivity is affine invariant but neither EA nor CCZ invariant. In addition, a permutation and its inverse are CCZ equivalent [31].

If $G\le {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$, i.e., G is a permutation group, then G acts on ${\mathbb{F}}_{2^n}$ [29].

For $x\in {\mathbb{F}}_{2^n}$ and $G\le {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$, the orbit of x under G is denoted by $x^G=\{g(x):g\in G\}$.

For $X\subseteq {\mathbb{F}}_{2^n}$ and $G\le {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$, denote $X^G=\{g(x):x\in X,g\in G\}$; and X is called to be invariant under G if $X^G=X$. It is known that any invariant subset of ${\mathbb{F}}_{2^n}$ under G is a union of orbits of G.

For $X\subseteq {\mathbb{F}}_{2^n}$ and $f\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$, denote $X^f=\{f(x):x\in X\}$. If $X^f=X$, then $X^{f^k}=X$ for all integer k. In other words, X is invariant under the cyclic group generated by f. Then, X is a union of orbits of the cyclic group generated by f.

We will use $id$ to denote the identity function $id(x)=x,x\in {\mathbb{F}}_{2^n}$.

We will use p to denote the inverse function $p(x)=x^{2^n-2},x\in {\mathbb{F}}_{2^n}$. It is obvious that $p\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$ and $p^2=id$. We will also use $\frac{1}{x}$ to denote $p(x)$ when $x\ne 0$.

We will use $tr$ to denote the trace function

$$\begin{array}{c}\hfill tr(x)=\sum _{i=0}^{n-1}{x}^{2^i},x\in {\mathbb{F}}_{2^n}.\end{array}$$

For $a\in {\mathbb{F}}_{2^n}^{\ast }$, we will use $m_a$ to denote the linear function $m_a(x)=ax,x\in {\mathbb{F}}_{2^n}$. It is obvious that $m_a\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$, $m_a^{-1}=m_{\frac{1}{a}}$, $m_{a}p{m}_a=p$ for all $a\in {\mathbb{F}}_{2^n}^{\ast }$, $m_{a_1}{m}_{a_2}=m_{a_2}{m}_{a_1}=m_{a_1{a}_2}$ for all $a_1,a_2\in {\mathbb{F}}_{2^n}^{\ast }$,

For $b\in {\mathbb{F}}_{2^n}$, we will use $t_b$ to denote the affine function $t_b(x)=x+b,x\in {\mathbb{F}}_{2^n}$. It is obvious that $t_b\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$, $t_b^{-1}=t_b$, $h{t}_b{h}^{-1}=t_{h(b)}$ for all $b\in {\mathbb{F}}_{2^n}$ and linear permutation h, $t_{b_1}{t}_{b_2}=t_{b_2}{t}_{b_1}=t_{b_1+b_2}$ for all $b_1,b_2\in {\mathbb{F}}_{2^n}$.

For $X\subseteq {\mathbb{F}}_{2^n}$, we will use $\overline{X}$ to denote the complement of X in ${\mathbb{F}}_{2^n}$.

We will use $\omega$ to denote the solution of equation $x^2+x+1=0$ in ${\mathbb{F}}_{2^n}$ with even n.

3. Piecewise Permutations

In this section, we study the bijectivity and the difference uniformity of piecewise functions from known permutations.

First, we consider the bijectivity of f in Equation (1).

Proposition 1. 

For $g_1,g_2\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$ and $U\subseteq {\mathbb{F}}_{2^n}$, let f is defined by

$$f(x)=\left\{\begin{array}{cc}{g}_1(x),\hfill & \hfill x\in U\\ g_2(x),\hfill & \hfill x\in \overline{U}\end{array}\right..$$

Then, $f\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$ if $U^{g_2^{-1}{g}_1}=U$.

Proof. 

For $g\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$ and $U\subseteq {\mathbb{F}}_{2^n}$, let $g_U$ is defined by

$$g_U(x)=\left\{\begin{array}{cc}g(x),\hfill & \hfill x\in U\\ x,\hfill & \hfill x\in \overline{U}\end{array}\right..$$

It can be verified that $g_U\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$ if $U^g=U$.

Denote $g=g_2^{-1}{g}_1$, then $f=g_2{g}_U\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$. □

There is a conclusion similar to Proposition 1. In [27], $f\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$ if U is a union of some cycle sets of $g_1$ related to $g_2$. It can be seen that the so-called cyclic sets is actually the orbits of the cyclic group generated by $g_2^{-1}{g}_1$.

It is difficult to determine the differential uniformity of f in Equation (1) if both $g_1$ and $g_2$ are arbitrary permutations. Next, we consider the case that $g_1$ and $g_2$ are affine equivalent.

Proposition 2. 

For $g\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$, $c_0,c_1\in {\mathbb{F}}_{2^n}$, $U\subseteq {\mathbb{F}}_{2^n}$, $U^{g^{-1}{t}_{c_1}g{t}_{c_0}}=U$, let f is defined by

$$f(x)=\left\{\begin{array}{cc}{t}_{c_1}g{t}_{c_0}(x),\hfill & \hfill x\in U\\ g(x),\hfill & \hfill x\in \overline{U}\end{array}\right..$$

(2)

Then, $f\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$ and

$$|{\Delta }_f(a,b)|\le |{\Delta }_g(a,b)|+|{\Delta }_g(a+c_0,b+c_1)|$$

(3)

for every $a,b\in {\mathbb{F}}_{2^n}$ if $U^{t_{c_0}}=U$.

Proof. 

By Proposition 1, we have $f\in {\mathfrak{S}}_{{\mathbb{F}}_{2^n}}$.

When $x+a\notin U$ and $x\notin U$, i.e., $x\in {\overline{U}}^{t_a}\cap \overline{U}$, we have

$${\Delta }_f(a,b)=\{x\in {\mathbb{F}}_{2^n}:g(x+a)+g(x)=b\}={\Delta }_g(a,b);$$

when $x+a\in U$ and $x\in U$, i.e., $x\in U^{t_a}\cap U$, we have

$${\Delta }_f(a,b)=\{x\in {\mathbb{F}}_{2^n}:g(x+c_0+a)+c_1+g(x+c_0)+c_1=b\}={\Delta }_g^{t_{c_0}}(a,b);$$

when $x+a\in U$ and $x\notin U$, i.e., $x\in U^{t_a}\cap \overline{U}$, we have

$${\Delta }_f(a,b)=\{x\in {\mathbb{F}}_{2^n}:g(x+c_0+a)+c_1+g(x)=b\}={\Delta }_g(a+c_0,b+c_1);$$

when $x+a\notin U$ and $x\in U$, i.e., $x\in {\overline{U}}^{t_a}\cap U$, we have

$${\Delta }_f(a,b)=\{x\in {\mathbb{F}}_{2^n}:g(x+a)+g(x+c_0)+c_1=b\}={\Delta }_g^{t_{c_0}}(a+c_0,b+c_1).$$

Denote

$$\left\{\begin{array}{cc}{Q}_f(a,b)=({\overline{U}}^{t_a}\cap \overline{U}\cap {\Delta }_g(a,b))\cup (U^{t_a}\cap U\cap {\Delta }_g^{t_{c_0}}(a,b)),\hfill & \\ R_f(a,b)=(U^{t_a}\cap \overline{U}\cap {\Delta }_g(a+c_0,b+c_1))\cup ({\overline{U}}^{t_a}\cap U\cap {\Delta }_g^{t_{c_0}}(a+c_0,b+c_1)),\hfill \end{array}\right.$$

then

$$\left\{\begin{array}{cc}{Q}_f(a,b)\cap R_f(a,b)=\varnothing ,\hfill & \\ Q_f(a,b)\cup R_f(a,b)={\Delta }_f(a,b),\hfill \end{array}\right.$$

for every $a,b\in {\mathbb{F}}_{2^n}$.

Given $a,b\in {\mathbb{F}}_{2^n}$, if $a=0$ or $c_0$, then ${\Delta }_g^{t_{c_0}}(a,b)={\Delta }_g(a,b)$ and ${\Delta }_g^{t_{c_0}}(a+c_0,b+c_1)={\Delta }_p(a+c_0,b+c_1)$, thus $Q_f(a,b)\subseteq {\Delta }_g(a,b)$ and $R_f(a,b)\subseteq {\Delta }_g(a+c_0,b+c_1)$. It is obvious that Equation (3) holds.

Given $a,b\in {\mathbb{F}}_{2^n}$, if $a\ne 0$ and $c_0$, then $U^{t_{c_0}}=U$ implies that ${\overline{U}}^{t_{c_0}}=\overline{U}$, ${(U^{t_a})}^{t_{c_0}}=U^{t_a}$, and ${({\overline{U}}^{t_a})}^{t_{c_0}}={\overline{U}}^{t_a}$. If we show that $x\in Q_f(a,b)$ implies that $x+c_0\notin Q_f(a,b)$ and $x\in R_f(a,b)$ implies that $x+c_0\notin R_f(a,b)$, then

$$\left\{\begin{array}{cc}|Q_f(a,b)|\le \frac{1}{2}|{\Delta }_g(a,b)\cup {\Delta }_g^{t_{c_0}}(a,b)|\le |{\Delta }_g(a,b)|,\hfill & \\ |R_f(a,b)|\le \frac{1}{2}|{\Delta }_g(a+c_0,b+c_1)\cup {\Delta }_g^{t_{c_0}}(a+c_0,b+c_1)|\le |{\Delta }_g(a+c_0,b+c_1)|,\hfill \end{array}\right.$$

it means that Equation (3) holds.

If $x\in Q_f(a,b)$, then either $x\in {\overline{U}}^{t_a}\cap \overline{U}\cap {\Delta }_g(a,b)$ or $x\in U^{t_a}\cap U\cap {\Delta }_g^{t_{c_0}}(a,b)$.

For $x\in {\overline{U}}^{t_a}\cap \overline{U}\cap {\Delta }_g(a,b)$, $x\in {\overline{U}}^{t_a}\cap \overline{U}$ implies that $x+c_0\in {\overline{U}}^{t_a}\cap \overline{U}$, i.e., $x+c_0\notin U^{t_a}\cap U\cap {\Delta }_p^{t_{c_0}}(a,b)$; and $x\in {\Delta }_g(a,b)$ and $a\ne 0,c_0$ implies that $x+c_0\notin {\Delta }_g(a,b)$, i.e., $x+c_0\notin {\overline{U}}^{t_a}\cap \overline{U}\cap {\Delta }_g(a,b)$, thus $x+c_0\notin Q_f(a,b)$.

For $x\in U^{t_a}\cap U\cap {\Delta }_p^{t_{c_0}}(a,b)$, $x\in U^{t_a}\cap U$ implies that $x+c_0\in U^{t_a}\cap U$, i.e., $x+c_0\notin {\overline{U}}^{t_a}\cap \overline{U}\cap {\Delta }_g(a,b)$; and $x\in {\Delta }_g^{t_{c_0}}(a,b)$ and $a\ne 0,c_0$ implies that $x+c_0\notin {\Delta }_g^{t_{c_0}}(a,b)$, i.e., $x+c_0\notin U^{t_a}\cap U\cap {\Delta }_g^{t_{c_0}}(a,b)$, thus $x+c_0\notin Q_f(a,b)$.

In both cases, $x\in Q_f(a,b)$ implies that $x+c_0\notin Q_f(a,b)$.

Similarity, $x\in R_f(a,b)$ implies that $x+c_0\notin R_f(a,b)$.

In summary, this theorem holds. □

By Proposition 2, f in Equation (2) is at least differentially $2\delta$-uniform if g is differentially $\delta$-uniform. Specifically, we can obtain differentially 4-uniform permutations from APN permutations.

4. Differentially 4-Uniform Piecewise Permutations from the Inverse Function

Based on Proposition 1 and 2, we construct differentially 4-uniform piecewise permutations over ${\mathbb{F}}_{2^{2k}}$ from the inverse function in this section.

Definition 3. 

For $c\in {\mathbb{F}}_{2^{2k}}$, $U\subseteq {\mathbb{F}}_{2^{2k}}$, $U^{p{t}_{c}p{t}_1}=U$ and $0\in U$, let f is defined by

$$f(x)=\left\{\begin{array}{cc}{t}_{c}p{t}_1(x),\hfill & \hfill x\in U\\ p(x),\hfill & \hfill x\in \overline{U}\end{array}\right..$$

(4)

Proposition 3. 

For $g\in {\mathfrak{S}}_{{\mathbb{F}}_{2^{2k}}}$, $c_0,c_1\in {\mathbb{F}}_{2^{2k}}$, $c_0$ and $c_1$ are not simultaneously equal to zero, $U\subseteq {\mathbb{F}}_{2^{2k}}$, $U^{g^{-1}{t}_{c_1}g{t}_{c_0}}=U$, let $f_g$ is defined by

$$f_g(x)=\left\{\begin{array}{cc}{t}_{c_1}g{t}_{c_0}(x),\hfill & \hfill x\in U\\ g(x),\hfill & \hfill x\in \overline{U}\end{array}\right..$$

Then, $f_g$ and f in Definition 3 are CCZ equivalent if g and p are affine equivalent.

Proof. 

If g and p are CCZ are affine equivalent, then there exist linear permutations $h_0,h_1$, and $d_0,d_1\in {\mathbb{F}}_{2^{2k}}$ such that $g=h_1{t}_{d_1}p{h}_0{t}_{d_0}$, i.e., $t_{d_1}{h}_1^{-1}g{t}_{d_0}{h}_0^{-1}=p$. Thus,

$$t_{d_1}{h}_1^{-1}{f}_g{t}_{d_0}{h}_0^{-1}(x)=\left\{\begin{array}{cc}{t}_{h_1^{-1}(c_1)}p{t}_{h_0(c_0)}(x),\hfill & \hfill x\in U^{t_{d_0}{h}_0^{-1}}\\ p(x),\hfill & \hfill x\in {\overline{U}}^{t_{d_0}{h}_0^{-1}}\end{array}\right..$$

It is trivial that $f_g=g$ if $c_0=0$ and $c_1=0$.

When $c_0\ne 0$, we have $h_0(c_0)\ne 0$ and

$$m_{h_0(c_0)}{t}_{d_1}{h}_1^{-1}{f}_g{t}_{d_0}{h}_0^{-1}{m}_{h_0(c_0)}(x)=\left\{\begin{array}{cc}{t}_{c}p{t}_1(x),\hfill & \hfill x\in U^{m_{\frac{1}{h_0(c_0)}}{t}_{c_3}}\\ p(x),\hfill & \hfill x\in {\overline{U}}^{m_{\frac{1}{h_0(c_0)}}{t}_{c_3}}\end{array}\right.;$$

and when $c_1\ne 0$, we have $h_1^{-1}(c_1)\ne 0$ and

$$m_{h_1^{-1}(c_1)}{t}_{d_1}{h}_1^{-1}{f}_g{t}_{d_0}{h}_0^{-1}{m}_{h_1^{-1}(c_1)}(x)=\left\{\begin{array}{cc}{t}_{1}p{t}_c(x),\hfill & \hfill x\in U^{m_{\frac{1}{h_1^{-1}(c_1)}}{t}_{c_3}}\\ p(x),\hfill & \hfill x\in {\overline{U}}^{m_{\frac{1}{h_1^{-1}(c_1)}}{t}_{c_3}}\end{array}\right.,$$

where $c=h_0(c_0)h_1^{-1}(c_1)$.

Note that the inverse of f in Definition 3 is given by

$$f^{-1}(x)=\left\{\begin{array}{cc}{t}_{1}p{t}_c(x),\hfill & \hfill x\in U^p\\ p(x),\hfill & \hfill x\in {\overline{U}}^p\end{array}\right..$$

In addition, if $0\notin U$, i.e., $0\in \overline{U}$, then

$$t_{c}f{t}_1(x)=\left\{\begin{array}{cc}p(x),\hfill & \hfill x\in U^{t_1}\\ t_{c}p{t}_1(x),\hfill & \hfill x\in {\overline{U}}^{t_1}\end{array}\right..$$

Therefore, $f_g$ and f in Definition 3 are CCZ-equivalent because a permutation and its inverse are CCZ equivalent. □

By Proposition 3, f in Definition 3 and every non-trivial piecewise permutation from a permutation that is affine equivalent to the inverse function in Equation (2) are CCZ-equivalent. Then, we focus on permutations in Definition 3.

Theorem 1. 

Let f be defined by Definition 3. Then, f is at least differentially 6-uniform if $U^{t_1}=U$.

Proof. 

It can be verified that

$${\Delta }_p(a,b)=\left\{\begin{array}{cc}{\mathbb{F}}_{2^{2k}},\hfill & \hfill a=0,b=0,\\ \varnothing ,\hfill & \hfill a=0,b\ne 0,\\ \varnothing ,\hfill & \hfill a\ne 0,b=0,\\ \{0,a,a\omega ,a{\omega }^2\},\hfill & \hfill a\ne 0,b=\frac{1}{a},\\ \{\lambda ,\lambda +a\},\hfill & \hfill a\ne 0,b\ne 0,\frac{1}{a},tr(\frac{1}{ab})=0,\\ \varnothing ,\hfill & \hfill a\ne 0,b\ne 0,\frac{1}{a},tr(\frac{1}{ab})=1,\end{array}\right.$$

for every $a,b\in {\mathbb{F}}_{2^{2k}}$.

Obviously, there are 6 cases for ${\Delta }_p(a,b)$.

By Equation (3), we need to consider $6\times 6$ cases to determine the value of $|{\Delta }_f(a,b)|$ for every $a,b\in {\mathbb{F}}_{2^{2k}}$.

Note that f is permutation. Then, we only need to consider $3\times 6$ cases where $ab\ne 0$ to determine the differential uniformity of f.

Additionally, $U^{t_1}=U$ implies that $U^{t_1}\cap \overline{U}=\varnothing$ and ${\overline{U}}^{t_1}\cap U=\varnothing$, it means that ${\Delta }_f(a,b)=Q_f(a,b)\subseteq {\Delta }_p(a,b)$ for $a=1$. Then, we only need to consider 12 cases where $ab\ne 0$ and $a\ne 1$ to determine the differential uniformity of f.

Denote

$$H_c=\{x\in {\mathbb{F}}_{2^{2k}}:x\ne 0,1,p(c),\frac{1}{x+1}+\frac{1}{x}\ne c,tr(\frac{1}{(x+1)(\frac{1}{x}+c)})=0\}.$$

It can be verified that $|{\Delta }_f(a,b)|\le 4$ for all $ab\ne 0$ and $a\ne 1$ except for the following three cases:

Case 1. 

$a\ne 0,b=\frac{1}{a},a+1\ne 0,b+c\ne 0,\frac{1}{a+1},tr(\frac{1}{(a+1)(b+c)})=0$, it means that $a\in H_c$ and $b=\frac{1}{a}$;

Case 2. 

$a\ne 0,b\ne 0,\frac{1}{a},tr(\frac{1}{ab})=0,a+1\ne 0,b+c=\frac{1}{a+1}$, it means that $a\in H_c^{t_1}$ and $b=\frac{1}{a+1}+c$;

Case 3. 

$a\ne 0,b=\frac{1}{a},a+1\ne 0,b+c=\frac{1}{a+1}$, it means that $a\ne 0,1,p(c),p(c)+1$, $\frac{1}{a+1}+\frac{1}{a}=c$, and $b=\frac{1}{a}$.

It can be seen that $|{\Delta }_f(a,b)|\le 6$ for Cases 1 and 2, and $|{\Delta }_f(a,b)|\le 8$ for Case 3. Then, we only need to show that $|{\Delta }_f(a,b)|<8$ for Case 3 to prove that f is at least differentially 6-uniform.

As in Proposition 2, for Case 3, we have $0\in {\Delta }_p(a,b)$ and $0\in {\Delta }_p(a+1,b+c)$; then, 0 or $1\in Q_f(a,b)$ implies that 0 and $1\notin R_f(a,b)$, and 0 or $1\in R_f(a,b)$ implies that 0 and $1\notin Q_f(a,b)$; thus, only one of 0 and 1 belongs to ${\Delta }_f(a,b)$; therefore, $|{\Delta }_f(a,b)|\le \frac{4+4}{2}+\frac{4+4}{2}-1<8$.

In summary, this theorem holds. □

By Theorem 1, we can obtain different at least differentially 6-uniform permutation from the inverse function from different U for a given c. Next, we show how to construct U satisfying the condition of Theorem 1.

Remark 1 

(The construction of U). By Theorem 1, we have $U^{p{t}_{c}p{t}_1}$ and $U^{t_1}$. Then, U is invariant under the group generated by $p{t}_{c}p{t}_1$ and $t_1$. Thus, U is a union of orbits under $G_c$, where $G_c$ is generated by $p{t}_{c}p{t}_1$ and $t_1$. Assume that the order of $p{t}_{c}p{t}_1$ is $ord$, i.e., ${(p{t}_{c}p{t}_1)}^{ord}=id$. For $x\in {\mathbb{F}}_{2^{2k}}$, the orbit of x under $G_c$ is

$$x^{G_c}=\{{(p{t}_{c}p{t}_1)}^i(x):0\le i<ord\}\cup \{{(p{t}_{c}p{t}_1)}^i{t}_1(x):0\le i<ord\}.$$

(5)

In the proof of Theorem 1, it can be seen that f is differentially 4-uniform if $|{\Delta }_f(a,b)|<6$ for Cases 1, 2, and 3. In fact, we can prove the following conclusions.

Proposition 4. 

Let f is defined by Definition 3. Then f is differentially 4-uniform if $c=1$ and $U^{t_1}=U$.

Proof. 

By the proof of Theorem 1, we need to show that $|{\Delta }_f(a,b)|<6$ for Cases 1, 2, and 3 to prove that f is differentially 4-uniform.

It can be seen that $c=1$ implies that Case 1 means that $a\in H_c$ and $b=\frac{1}{a}$, where

$$H_c=\{x\in {\mathbb{F}}_{2^{2k}}:x\ne 0,1,\frac{1}{x+1}+\frac{1}{x}\ne 1,tr(\frac{x}{x^2+1})=0\}.$$

Note that $tr(\frac{x}{x^2+1})=tr(\frac{1}{x+1}+\frac{1}{x^2+1})=0$ for every $x\in {\mathbb{F}}_{2^{2k}}$. Then, Case 1 means that $a\notin \{0,1,\omega ,{\omega }^2\}$ and $b=\frac{1}{a}$.

As in Proposition 2, for case 1, it can be verified that $a\in {\Delta }_p(a,b)$ and $a\in {\Delta }_p(a+1,b+1)$; then, a or $a+1\in Q_f(a,b)$ implies that a and $a+1\notin R_f(a,b)$, and a or $a+1\in R_f(a,b)$ implies that a and $a+1\notin Q_f(a,b)$; thus, only one of a and $a+1$ belongs to ${\Delta }_f(a,b)$; therefore, $|{\Delta }_p(a,b)|\le \frac{4+4}{2}+\frac{2+2}{2}-1<6$.

Similarly, $|{\Delta }_p(a,b)|<6$ for Case 2.

It is obvious that $c=1$ also implies that Case 3 means that $a\in \{\omega ,{\omega }^2\}$ and $b=\frac{1}{a}$. Note that ${\Delta }_p(\omega ,\frac{1}{\omega })={\Delta }_p({\omega }^2,\frac{1}{{\omega }^2})=\{0,1,\omega ,{\omega }^2\}$. By the proof of Theorem 1, ${\Delta }_f(a,b)={\Delta }_p(a,b)$ for Case 3.

In summary, this theorem holds. □

Theorem 2. 

Let f be defined by Definition 3. Then, f is differentially 4-uniform if

1. 

$c\ne 1$ and $U^{t_1}=U$,

2. 

$U\cap {\Pi }_a\ne \{{\lambda }_a\},\{{\lambda }_a+a\},\{a\omega ,a{\omega }^2,{\lambda }_a\}$, and $\{a\omega ,a{\omega }^2,{\lambda }_a+a\}$ for every $a\in U\cap H$,

3. 

$U\cap {\Pi }_a\ne \{a\omega \},\{a{\omega }^2\},\{a\omega ,{\lambda }_a,{\lambda }_a+a\}$, and $\{a{\omega }^2,{\lambda }_a,{\lambda }_a+a\}$ for every $a\in \overline{U}\cap H$,

where ${\lambda }_a$ is the solution of the equation $(\frac{1}{a}+c)x^2+(\frac{1}{a}+c)(a+1)x+a+1=0$ in ${\mathbb{F}}_{2^{2k}}$ and

$$\begin{array}{ccc}\hfill {\Pi }_a=& \{a\omega ,a{\omega }^2,{\lambda }_a,{\lambda }_a+a\},\hfill & \\ \hfill H=& \{x\in {\mathbb{F}}_{2^{2k}}:x\ne 0,1,p(c),tr(\frac{1}{(x+1)(\frac{1}{x}+c)})=0\}.\hfill & \end{array}$$

Proof. 

By the proof of Theorem 1, we need to show that $|{\Delta }_f(a,b)|<6$ for Cases 1, 2, and 3 to prove that f is differentially 4-uniform.

Note that Case 1 means that $a\in H_c$ and $b=\frac{1}{a}$, and Case 2 means that $a\in H_c^{t_1}$ and $b=\frac{1}{a+1}+c$, where

$$H_c=\{x\in {\mathbb{F}}_{2^{2k}}:x\ne 0,1,p(c),\frac{1}{x+1}+\frac{1}{x}\ne c,tr(\frac{1}{(x+1)(\frac{1}{x}+c)})=0\}.$$

Then, we need to show that $|{\Delta }_f(a,\frac{1}{a})|<6$ for $a\in H_c$ and $|{\Delta }_f(a,\frac{1}{a+1}+c)|<6$ for $a\in H_c^{t_1}$ to prove that $|{\Delta }_f(a,b)|<6$ for Cases 1 and 2.

In the proof of Proposition 2, we can verify that $U^{t_1}=U$ implies that x or $x+1\in Q_f(a,b)$ if and only if $U\cap \{x,x+a\}=\varnothing$ or $\{x,x+a\}$ for $x\in {\Delta }_p(a,b)$, and x or $x+1\in R_f(a,b)$ if and only if $U\cap \{x,x+a\}=\{x\}$ or $\{x+a\}$ for $x\in {\Delta }_p(a+1,b+c)$.

If there exists $a\in H_c$ such that $|{\Delta }_f(a,\frac{1}{a})|=6$, then x or $x+1\in Q_f(a,\frac{1}{a})$ for every $x\in {\Delta }_p(a,\frac{1}{a})$ and y or $y+1\in R_f(a,\frac{1}{a})$ for every $y\in {\Delta }_p(a+1,\frac{1}{a}+c)$, it implies that $U\cap \{0,a\}=\{0,a\}$, $U\cap \{a\omega ,a{\omega }^2\}=\varnothing$ or $\{a\omega ,a{\omega }^2\}$, and $U\cap \{{\lambda }_a,{\lambda }_a+a\}=\{{\lambda }_a\}$ or $\{{\lambda }_a+a\}$, it also means that there exists $a\in U$ such that $U\cap {\Pi }_a=\{{\lambda }_a\},\{{\lambda }_a+a\},\{a\omega ,a{\omega }^2,{\lambda }_a\}$, or $\{a\omega ,a{\omega }^2,{\lambda }_a+a\}$. In other words, if $U\cap {\Pi }_a\ne \{{\lambda }_a\},\{{\lambda }_a+a\},\{a\omega ,a{\omega }^2,{\lambda }_a\}$, and $\{a\omega ,a{\omega }^2,{\lambda }_a+a\}$ for every $a\in U\cap H_c$ then $|{\Delta }_f(a,\frac{1}{a})|<6$ for every $a\in H_c$.

If there exists $a\in H_c^{t_1}$ such that $|{\Delta }_f(a,\frac{1}{a+1}+c)|=6$, then there exists $a^{\prime }=a+1\in H_c$ such that $|{\Delta }_f(a^{\prime }+1,\frac{1}{a^{\prime }}+c)|=6$, thus x or $x+1\in Q_f(a^{\prime }+1,\frac{1}{a^{\prime }}+c)$ for every $x\in {\Delta }_p(a^{\prime }+1,\frac{1}{a^{\prime }}+c)$ and y or $y+1\in R_f(a^{\prime }+1,\frac{1}{a^{\prime }}+c)$ for every $y\in {\Delta }_p(a^{\prime },\frac{1}{a^{\prime }})$, it implies that $U\cap \{{\lambda }_{a^{\prime }},{\lambda }_{a^{\prime }}+a^{\prime }\}=\varnothing$ or $\{{\lambda }_{a^{\prime }},{\lambda }_{a^{\prime }}+a^{\prime }\}$, $U\cap \{0,a^{\prime }\}=\{0\}$, and $U\cap \{a^{\prime }\omega ,a^{\prime }{\omega }^2\}=\{a^{\prime }\omega \}$ or $\{a^{\prime }{\omega }^2\}$, it also means that there exists $a^{\prime }\in \overline{U}$ such that $U\cap {\Pi }_{a^{\prime }}=\{a\omega \},\{a{\omega }^2\},\{a\omega ,{\lambda }_a,{\lambda }_a+a\}$, or $\{a{\omega }^2,{\lambda }_a,{\lambda }_a+a\}$. In other words, if $U\cap {\Pi }_{a^{\prime }}\ne \{a^{\prime }\omega \},\{a^{\prime }{\omega }^2\},\{a^{\prime }\omega ,{\lambda }_{a^{\prime }},{\lambda }_{a^{\prime }}+a^{\prime }\}$, and $\{a^{\prime }{\omega }^2,{\lambda }_{a^{\prime }},{\lambda }_{a^{\prime }}+a^{\prime }\}$ for every $a^{\prime }\in \overline{U}\cap H_c$, then $|{\Delta }_f(a,\frac{1}{a+1}+c)|<6$ for every $a\in H_c^{t_1}$.

When $c=0$ or $tr(\frac{1}{c})=1$, Case 3 does not occur and $H=H_c$. When $c\ne 0,1$ and $tr(\frac{1}{c})=0$, Case 3 means that $a\in \{{\chi }_c,{\chi }_c+1\}$ and $b=\frac{1}{a}$, and $H=H_c\cup \{{\chi }_c,{\chi }_c+1\}$, where ${\chi }_c$ and ${\chi }_c+1$ are the solution of the equation $x^2+x+\frac{1}{c}=0$ in ${\mathbb{F}}_{2^{2k}}$. Then, we need to show that $|{\Delta }_f({\chi }_c,\frac{1}{{\chi }_c})|<6$ to prove that $|{\Delta }_f(a,b)|<6$ for Case 3.

Note that ${\lambda }_{{\chi }_c}=({\chi }_c+1)\omega$ and ${\lambda }_{{\chi }_c+1}={\chi }_c\omega$. If $|{\Delta }_f({\chi }_c,\frac{1}{{\chi }_c}))|=6$, then either $\{0,{\chi }_c,{\chi }_c\omega ,{\chi }_c{\omega }^2\}\subseteq Q_f({\chi }_c,\frac{1}{{\chi }_c})$ and $\{{\lambda }_{{\chi }_c},{\lambda }_{{\chi }_c}+{\chi }_c\}\subseteq R_f({\chi }_c,\frac{1}{{\chi }_c})$, or $\{{\lambda }_{{\chi }_c+1},{\lambda }_{{\chi }_c+1}+{\chi }_c+1\}\subseteq Q_f({\chi }_c,\frac{1}{{\chi }_c})$ and $\{0,{\chi }_c+1,({\chi }_c+1)\omega ,({\chi }_c+1){\omega }^2\}\subseteq R_f({\chi }_c,\frac{1}{{\chi }_c})$. The former implies that $U\cap \{0,{\chi }_c\}=\{0,{\chi }_c\}$, $U\cap \{{\chi }_c\omega ,{\chi }_c{\omega }^2\}=\varnothing$ or $\{{\chi }_c\omega ,{\chi }_c{\omega }^2\}$, and $U\cap \{{\lambda }_{{\chi }_c},{\lambda }_{{\chi }_c}+{\chi }_c\}=\{{\lambda }_{{\chi }_c}\}$ or $\{{\lambda }_{{\chi }_c}+{\chi }_c\}$, it means that ${\chi }_c\in U$ and $U\cap {\Pi }_{{\chi }_c}=\{{\lambda }_{{\chi }_c}\},\{{\lambda }_{{\chi }_c}+{\chi }_c\},\{{\chi }_c\omega ,{\chi }_c{\omega }^2,{\lambda }_{{\chi }_c}\}$, or $\{{\chi }_c\omega ,{\chi }_c{\omega }^2,{\lambda }_{{\chi }_c}+{\chi }_c\}$. The latter implies that $U\cap \{{\lambda }_{{\chi }_c+1},{\lambda }_{{\chi }_c+1}+{\chi }_c+1\}=\varnothing$ or $\{{\lambda }_{{\chi }_c+1},{\lambda }_{{\chi }_c+1}+{\chi }_c+1\}$, $U\cap \{0,{\chi }_c+1\}=\{0\}$, and $U\cap \{({\chi }_c+1)\omega ,({\chi }_c+1){\omega }^2\}=\{({\chi }_c+1)\omega \}$ or $\{({\chi }_c+1){\omega }^2\}$, it means that ${\chi }_c+1\in \overline{U}$ and $U\cap {\Pi }_{{\chi }_c+1}=\{({\chi }_c+1)\omega \},\{({\chi }_c+1){\omega }^2\},\{({\chi }_c+1)\omega ,{\lambda }_{{\chi }_c+1},{\lambda }_{{\chi }_c+1}+{\chi }_c+1\}$, and $\{({\chi }_c+1){\omega }^2,{\lambda }_{{\chi }_c+1},{\lambda }_{{\chi }_c+1}+{\chi }_c+1\}$. In other words, if $U\cap {\Pi }_a\ne \{{\lambda }_a\},\{{\lambda }_a+a\},\{a\omega ,a{\omega }^2,{\lambda }_a\}$, and $\{a\omega ,a{\omega }^2,{\lambda }_a+a\}$ for every $a\in U\cap \{{\chi }_c,{\chi }_c+1\}$, and $U\cap {\Pi }_a\ne \{a\omega \},\{a{\omega }^2\},\{a\omega ,{\lambda }_a,{\lambda }_a+a\}$, and $\{a{\omega }^2,{\lambda }_a,{\lambda }_a+a\}$ for every $a\in \overline{U}\cap \{{\chi }_c,{\chi }_c+1\}$, then $|{\Delta }_f({\chi }_c,\frac{1}{{\chi }_c})|<6$.

In summary, this theorem holds. □

There is a conclusion similar to Proposition 4. In [26], f is differentially 4-uniform permutation if U is the union of some non-trivial minimum stable sets of $f\in {\mathfrak{S}}_{{\mathbb{F}}_{2^{2k}}}$. It can be seen that the so-called minimum stable subsets is actually the orbits of the group generated by $p{t}_{c}p{t}_1$ and $t_1$ where $c=1$.

Deng Tang et al. [23] and Jie Peng et al. [28] have studied the case that $c=0$. However, the condition of U in [23,28] is a sufficient condition of U in Theorem 2. Then, Theorem 2 constructs more differentially 4-uniform permutations.

By Theorem 2, we have Algorithm 1 for constructing differentially 4-uniform piecewise permutations over ${\mathbb{F}}_{2^{2k}}$ from the inverse function.

Algorithm 1. Constructing algorithm of differentially 4-uniform piecewise permutations over ${\mathbb{F}}_{2^{2k}}$

1: Select the parameter $c\in {\mathbb{F}}_{2^{2k}}\backslash \{1\}$;

2: Calculate all orbits under the group generated by $p{t}_{c}p{t}_1$ and $t_1$ using Equation (5);

3: Select some orbits to obtain an invariant subset U of ${\mathbb{F}}_{2^{2k}}$;

4: if U satisfies the conditions 2 and 3 in Theorem 2

5:        Construct f by Definition 3;

6: else

7:         Back to step 3;

8: end if

9: return f.

5. Numerical Results

In this section, we show some numerical results. As Remark 1, let $G_c$ be the group generated by $p{t}_{c}p{t}_1$ and $t_1$.

For $c\in {\mathbb{F}}_{2^{2k}}$, if the number of orbits under $G_c$ equals r, then the number of invariant sets under $G_c$ equals $2^r$. Note that it is trivial that $f=p$ in Definition 3 if $U={\mathbb{F}}_{2^{2k}}$. Thus, the number of non-trivial at least differentially 6-uniform permutations constructed by Theorem 1 equals $2^{r-1}-1$. It can be verified that, the number of orbits under $G_c$ equals $2^{2k-1}$ when $c=0$; the number of orbits under $G_c$ equals $\frac{2^{2k-4}}{6}+2$ when $c=1$; and the number of orbits under $G_c$ takes the maximum value when $c=\omega$ or $\omega +1$ for all $c\in {\mathbb{F}}_{2^{2k}}\backslash \{0,1\}$. Figure 1 and Figure 2 show the relation between $c\in {\mathbb{F}}_{2^{2k}}\backslash \{0,1\}$ and the number of orbits under $G_c$ for $k=3$ and 4, respectively. It can be seen that we can obtain a lot of at least differentially 6-uniform permutation from the inverse function.

Differentially 4-uniform piecewise permutations can be obtained by verifying whether the union of orbits under $G_c$ satisfies the conditions in Theorem 2. It can be seen that the number of invariant sets under $G_c$ is large for $c\in \{0,1\}\subseteq {\mathbb{F}}_{2^6}$ and $c\in \{0,1,\omega ,\omega +1\}\subseteq {\mathbb{F}}_{2^8}$.

Table 1. Extended Walsh spectrum of differential 4-uniformity permutations over ${\mathbb{F}}_{2^6}$ obtained from Theorem 2.

c	No.	Extended Walsh Spectrum
6	1	{*16[189],12[882],8[1008],4[1134],0[819]*}
14	1	{*24[4],20[24],16[245],12[698],8[972],4[1294],0[795]*}
	1	{*28[4],24[0],20[28],16[197],12[742],8[1040],4[1242],0[779]*}
15	2	{*20[52],16[209],12[694],8[992],4[1270],0[815]*}
	3	{*24[4],20[44],16[209],12[702],8[988],4[1270],0[815]*}
	4	{*20[48],16[213],12[690],8[1008],4[1278],0[795]*}
33	1	{*24[2],20[34],16[197],12[748],8[1022],4[1234],0[795]*}
	1	{*20[24],16[167],12[834],8[1048],4[1158],0[801]*}
58	2	{*24[2],20[44],16[193],12[718],8[1038],4[1254],0[783]*}
	3	{*20[42],16[213],12[708],8[1008],4[1266],0[795]*}

shows the extended Walsh spectrum of differential 4-uniformity permutations over ${\mathbb{F}}_{2^6}$ obtained from Theorem 2 for $c\in {\mathbb{F}}_{2^6}\backslash \{0,1\}$.

Table 2. Differential spectrum of differential 4-uniformity permutations over ${\mathbb{F}}_{2^8}$ obtained from Theorem 2.

c	No.	Differential Spectrum
2	1	{*0[32895],2[32130],4[255]*}
	1	{*0[34317],2[29286],4[1677]*}
10	2	{*0[36093],2[25734],4[3453]*}
	3	{*0[36129],2[25662],4[3489]*}
11	1	{*0[34125],2[29670],4[1485]*}
	2	{*0[36231],2[25458],4[3591]*}
78	1	{*0[34335],2[29250],4[1695]*}
	2	{*0[35649],2[26622],4[3009]*}

shows the differential spectrum of differential 4-uniformity permutations over ${\mathbb{F}}_{2^8}$ obtained from Theorem 2 for $c\in {\mathbb{F}}_{2^8}\backslash \{0,1,\omega ,\omega +1\}$. It is know that CCZ equivalent permutations possess the same differential spectrum and extended Walsh spectrum. Then, permutations with different differential spectrum and extended Walsh spectrum are CCZ inequivalent. Therefore, differential 4-uniformity permutations in Table 1 and Table 2 are CCZ inequivalent.

6. Conclusions

In this paper, we study the bijectivity and the difference uniformity of f in Equation (2) from known g based on permutation group theory. We show that f in Equation (2) is at least differentially $2\delta$-uniform if g is differentially $\delta$-uniform. Then, we construct at least differentially 6-uniform and differentially 4-uniform piecewise permutations over ${\mathbb{F}}_{2^{2k}}$ from the inverse function and a function that is affine equivalent to the inverse function in Theorems 1 and 2. Finally, numerical results shows that we obtain a lot of at least differentially 6-uniform and differentially 4-uniform permutations over ${\mathbb{F}}_{2^{2k}}$.